Геометрия
7 класс
Урок № 26
Расстояние от точки до прямой. Расстояние между параллельными прямыми
Перечень рассматриваемых вопросов:
- Понятие наклонной.
- Расстояние от точки до прямой.
- Расстояние между параллельными прямыми.
- Теорема о равноудалённости точек параллельных прямых.
Тезаурус:
Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямойине являющийся перпендикуляром к прямой.
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Расстояние между двумя точками – длина отрезка, соединяющего эти точки. Введём также следующие понятия:
1) расстояние от точки до прямой;
2) расстояние между параллельными прямыми.
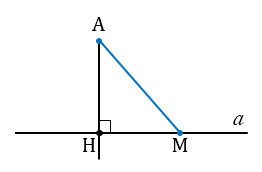
Пусть отрезок АН – перпендикуляр, проведённый из точки А к прямой а, М – любая точка прямой а, отличная от Н. Отрезок АМ называется наклонной, проведённой из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы АМ. Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.
Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.
На рисунке расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.
Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.
Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Доказательство. Рассмотрим параллельные прямые а и b. Отметим на прямой a точку A и проведём из этой точки перпендикуляр AB к прямой b. Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.
Проведём из точки Х перпендикуляр XY к прямой b. Так как XY перпендикулярно b, то XY перпендикулярно а. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY). Следовательно, XY = AB.
Итак, любая точка X прямой a находится на расстоянии AB от прямой b. Очевидно, что все точки прямой b находятся на таком же расстоянии от прямой a. Теорема доказана.
Из доказанной теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Отметим, что расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.
Замечание. Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.
Дано:
AA1= BB1= CC1
Доказать: точкиA, B, C– принадлежатодной прямой, АА1║ ВВ1║СС1.
Доказательство: по аксиоме параллельных прямых, через точку A проведем прямую b, b║a, тогда все точки b║a равноудаленыот точек прямой a. Докажем, что B, C∈ b.
Пусть B∉ b, C∉ b, значит, расстояние от точки B до a и C будет больше или меньше, чем расстояние h. Но это противоречит AA1 = BB1 = CC1.
Следовательно, наше предположение неверно и A, B и С ∈ b || a, что и требовалось доказать.
Разбор заданий тренировочного модуля.
В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 12 см. Найти расстояние от точки A до прямой BC.
Объяснение: равносторонним треугольником называется треугольник с тремя равными сторонами (значит, и с тремя равными углами, то есть – по 60°). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD⊥BC
Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую AC, то DH – данное расстояние. Рассмотрим треугольник AHD. В нём угол H = 90°, так как DH – перпендикуляр к AC (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла DAH = 30°, поэтому AD = 2 ∙ 12= 24см (по свойству).
Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD⊥ BC, значит, AD = 24 см.
Ответ: 24 см.
«Расстояние от точки до прямой
(решения задач по теме)»
Расстояние от точки до прямой — длина перпендикуляра, проведенного из данной точки к прямой.
Если точка лежит на прямой, то считают, что расстояние от этой точки до прямой равно 0.
Теорема. Все точки каждой из двух параллельных прямых находятся на равном расстоянии от другой прямой.
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
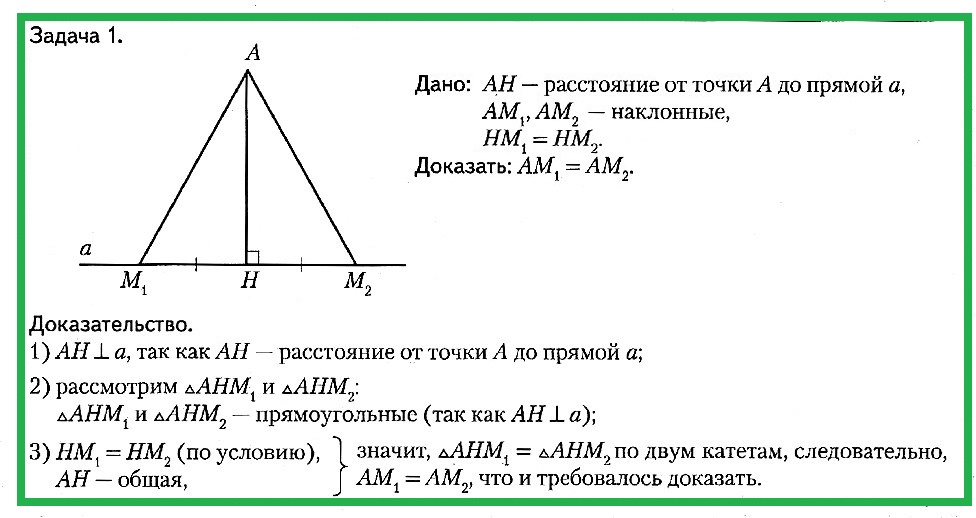
Задача № 1.
Дано: АН — расстояние от точки А до прямой а, АМ1, АМ2 — наклонные, НМ1 = НМ2. Доказать: АМ1 = АМ2.
Задача № 2.
Дано: АН — расстояние от точки А до прямой а, HМ1 < HМ2. Доказать: АМ1 < АМ2.
Задача № 3.
Дано: Δ АВС — равносторонний, AD — биссектриса, DH — расстояние от точки D до АС, DH = 6 см. Найти: AD.
Это конспект по теме «Расстояние от точки до прямoй (ЗАДАЧИ)». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Геометрия 7 класс: ЗАДАЧИ на построение
- Вернуться к Списку конспектов по геометрии
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Расстояние от точки до прямой
Пусть нам даны прямая 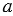
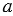
Отрезок АМ называется наклонной, проведенной из точки А к прямой 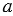
Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
Расстояние от точки до прямой — это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой.
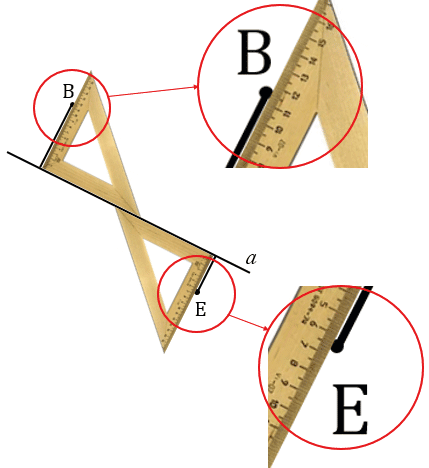
Для того, чтобы найти расстояние от точки до прямой, нужно с помощью чертежного угольника провести перпендикуляр из данной точки к данной прямой, а затем измерить длину этого перпендикуляра.
Расстояние от точки Е до прямой 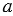
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 275,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 301,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 308,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 357,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 434,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 631,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 633,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Решение задач по математике у учащихся часто сопровождается многими трудностями. Помочь учащемуся справиться с этими трудности, а так же научить применять имеющиеся у него теоретические знания при решении конкретных задач по всем разделам курса предмета «Математика» – основное назначение нашего сайта.
Приступая к решению задач по теме «Расстояние между двумя точками на плоскости», учащиеся должны уметь строить точку на плоскости по ее координатам, а так же находить координаты заданной точки.
Вычисление расстояния между взятыми на плоскости двумя точками А(хА; уА) и В(хВ; уВ), выполняется по формуле d = √((хА – хВ)2 + (уА – уВ)2), где d – длина отрезка, который соединяет эти точки на плоскости.
Если один из концов отрезка совпадает с началом координат, а другой имеет координаты М(хМ; уМ), то формула для вычисления d примет вид ОМ = √(хМ2 + уМ2).
1. Вычисление расстояния между двумя точками по данным координатам этих точек
Пример 1.
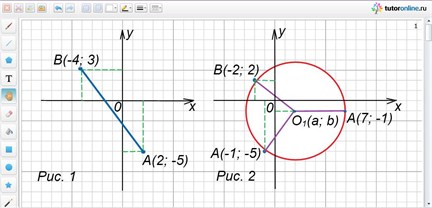
Найти длину отрезка, который соединяет на координатной плоскости точки А(2; -5) и В(-4; 3) (рис. 1).
Решение.
В условии задачи дано: хА = 2; хВ = -4; уА = -5 и уВ = 3. Найти d.
Применив формулу d = √((хА – хВ)2 + (уА – уВ)2), получим:
d = АВ = √((2 – (-4))2 + (-5 – 3)2) = 10.
2. Вычисление координат точки, которая равноудалена от трех заданных точек
Пример 2.
Найти координаты точки О1, которая равноудалена от трех точек А(7; -1) и В(-2; 2) и С(-1; -5).
Решение.
Из формулировки условия задачи следует, что О1А = О1В = О1С. Пусть искомая точка О1 имеет координаты (а; b). По формуле d = √((хА – хВ)2 + (уА – уВ)2) найдем:
О1А = √((а – 7)2 + (b + 1)2);
О1В = √((а + 2)2 + (b – 2)2);
О1С = √((а + 1)2 + (b + 5)2).
Составим систему из двух уравнений:
{√((а – 7)2 + (b + 1)2) = √((а + 2)2 + (b – 2)2),
{√((а – 7)2 + (b + 1)2) = √((а + 1)2 + (b + 5)2).
После возведения в квадрат левой и правой частей уравнений запишем:
{(а – 7)2 + (b + 1)2 = (а + 2)2 + (b – 2)2,
{(а – 7)2 + (b + 1)2 = (а + 1)2 + (b + 5)2.
Упростив, запишем
{-3а + b + 7 = 0,
{-2а – b + 3 = 0.
Решив систему, получим: а = 2; b = -1.
Точка О1(2; -1) равноудалена от трех заданных в условии точек, которые не лежат на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные точки (рис. 2).
3. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на заданном расстоянии от данной точки
Пример 3.
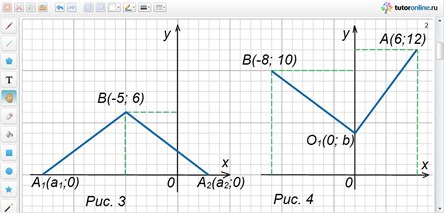
Расстояние от точки В(-5; 6) до точки А, лежащей на оси Ох равно 10. Найти точку А.
Решение.
Из формулировки условия задачи следует, что ордината точки А равна нулю и АВ = 10.
Обозначив абсциссу точки А через а, запишем А(а; 0).
По формуле d = √((хА – хВ)2 + (уА – уВ)2) находим:
АВ = √((а + 5)2 + (0 – 6)2) = √((а + 5)2 + 36).
Получаем уравнение √((а + 5)2 + 36) = 10. Упростив его, имеем
а2 + 10а – 39 = 0.
Корни этого уравнения а1 = -13; а2 = 3.
Получаем две точки А1(-13; 0) и А2(3; 0).
Проверка:
А1В = √((-13 + 5)2 + (0 – 6)2) = 10.
А2В = √((3 + 5)2 + (0 – 6)2) = 10.
Обе полученные точки подходят по условию задачи (рис. 3).
4. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на одинаковом расстоянии от двух заданных точек
Пример 4.
Найти на оси Оу точку, которая находится на одинаковом расстоянии от точек А(6; 12) и В(-8; 10).
Решение.
Пусть координаты нужной по условию задачи точки, лежащей на оси Оу, будут О1(0; b) (у точки, лежащей на оси Оу, абсцисса равна нулю). Из условия следует, что О1А = О1В.
По формуле d = √((хА – хВ)2 + (уА – уВ)2) находим:
О1А = √((0 – 6)2 + (b – 12)2) = √(36 + (b – 12)2);
О1В = √((а + 
Имеем уравнение √(36 + (b – 12)2) = √(64 + (b – 10)2) или 36 + (b – 12)2 = 64 + (b – 10)2.
После упрощения получим: b – 4 = 0, b = 4.
Необходимая по условию задачи точка О1(0; 4) (рис. 4).
5. Вычисление координат точки, которая находится на одинаковом расстоянии от осей координат и некоторой заданной точки
Пример 5.
Найти точку М, расположенную на координатной плоскости на одинаковом расстоянии от осей координат и от точки А(-2; 1).
Решение.
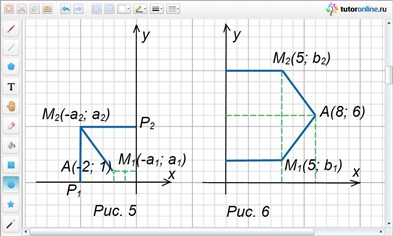
Необходимая точка М, как и точка А(-2; 1), располагается во втором координатном углу, так как она равноудалена от точек А, Р1 и Р2 (рис. 5). Расстояния точки М от осей координат одинаковые, следовательно, ее координатами будут (-a; a), где а > 0.
Из условия задачи следует, что МА = МР1 = МР2, МР1 = а; МР2 = |-a|,
т.е. |-a| = а.
По формуле d = √((хА – хВ)2 + (уА – уВ)2) находим:
МА = √((-а + 2)2 + (а – 1)2).
Составим уравнение:
√((-а + 2)2 + (а – 1)2) = а.
После возведения в квадрат и упрощения имеем: а2 – 6а + 5 = 0. Решим уравнение, найдем а1 = 1; а2 = 5.
Получаем две точки М1(-1; 1) и М2(-5; 5), удовлетворяющие условию задачи.
6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки
Пример 6.
Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.
Решение.
Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).
По формуле d = √((хА – хВ)2 + (уА – уВ)2) имеем:
МА = √((5 – 
Составим уравнение:
√((5 – 
Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.
Остались вопросы? Не знаете, как найти расстояние между двумя точками на плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определение:
Расстоянием
между двумя точками А и В является длина отрезка АВ,
соединяющего эти точки.
При
этом следует отметить, что точки А и В можно соединить
и таким образом:
Но
именно кратчайший путь, то есть отрезок АВ, является расстоянием между данными
точками.
Возьмём
некоторую прямую b
и
точку А, которая не лежит на этой прямой. Опустим
перпендикуляр из точки А к прямой b:
Полученный
отрезок АН и будет называться расстоянием
от точки А до
прямой, так как это кратчайшее расстояние между данными точкой и прямой.
Действительно
так. Отметим точку В на прямой b и рассмотрим прямоугольный
треугольник АНВ:
АВ
— гипотенуза, а АН — катет этого треугольника. Известно, что катет всегда
меньше гипотенузы.
Отрезок
АВ называется наклонной, проведённой из точки А к
прямой b.
Перпендикуляр,
проведённый из точки к прямой, меньше любой наклонной, проведённой из той же
точки к этой прямой.,
Определение:
Длина
перпендикуляра, проведённого из точки к прямой,
называется расстоянием от этой точки до прямой.
Обозначают
следующим образом:
Пусть
а и b
—
параллельные прямые. Отметим на прямой а две точки А
и В и опустим из них перпендикуляры АМ и BN на
прямую b:
Если
прямая a||b,
а отрезки AM⊥b, BN⊥b, то АМ=BN и равняется расстоянию между
параллельными прямыми а и b.
Проведём
отрезок АN
и
рассмотрим полученные треугольники АBN и АМN:
Так
как AM⊥b, а a||b, то AM⊥a. То есть ВN⊥b, а a||b, то и ВN⊥a.
Получили,
что АBN
и АМN
—
прямоугольные треугольники. У них сторона АN —
общая, она является гипотенузой для обоих треугольников. Углы ВАN и АNМ равны, так как являются
внутренними накрест лежащими при параллельных прямых
АВ и MN
и секущей АN.
Следовательно,
получаем, что прямоугольные треугольники АBN и АМN равны по гипотенузе и острому
углу. Из этого следует, что АМ=ВN.
Получили,
что отрезки АМ и BN
равны.
Расстоянием между параллельными прямыми
является длина их общего перпендикуляра.
Обозначают
следующим образом:
Верно
и обратное утверждение:
Все
точки плоскости, расположенные по одну сторону от прямой и находящиеся на
равном расстоянии от неё, лежат на прямой параллельной
данной.
Пример.
На
рисунке отрезок АВ=6 см, ∠В=30 градусов. Найти
расстояние от точки А до прямой а.
Опустим
из точки А к прямой а перпендикуляр АС, который
и есть расстояние от точки А до прямой а:
Получили
прямоугольный треугольник АВС. У которого ∠В=30
градусов, АВ=6см.
Известно,
что катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен
половине гипотенузы. Получаем:
Пример.
На
рисунке расстояние между параллельными прямыми а
и b
равно 5 сантиметров, а расстояние между параллельными прямыми а и с
равно 9 сантиметров. Чему равно расстояние между параллельными
прямыми b
и с?
Известно,
что:
Из
этого следует: