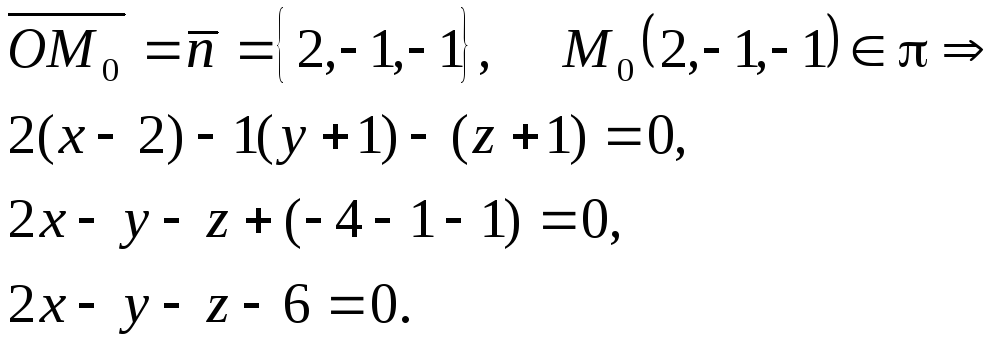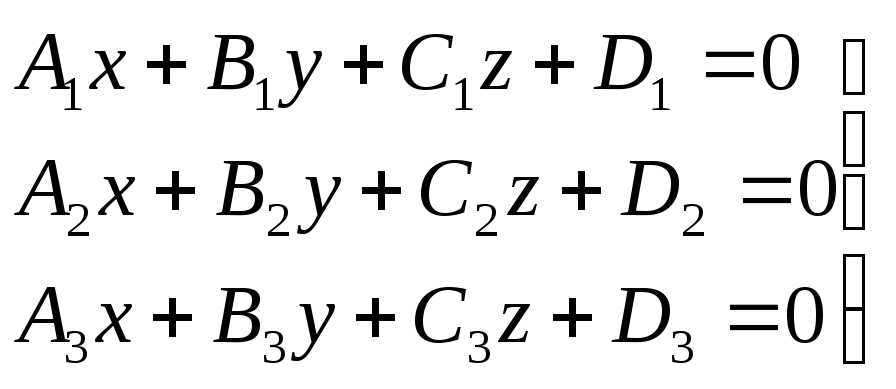Как найти расстояние по нормали - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти расстояние от точки (A) до плоскости, определенной вектором нормали (NormalVector) и точкой (P) лежащей на этой плоскости?

0xdb

51.4k194 золотых знака56 серебряных знаков232 бронзовых знака

задан 4 фев 2018 в 10:18

Воспользуйтесь канонической формулой расстояния до плоскости:

В ней есть всё, что вам нужно:

Нормаль N = (A; B; C);
Точка P = (x₀; y₀; z₀) в плоскости;
Точка A = (x; y; z), до которой надо найти расстояние;
Собственно, расстояние d.

Два важных момента:

Если нормаль не нормирована (то есть A² + B² + C² ≠ 1), то вам потребуется разделить вычисленное расстояние d на sqrt(A² + B² + C²);
Расстояние d — знаковое. Причём знак обозначает, по какую сторону от плоскости находится точка (больше нуля — по ту сторону, куда смотрит нормаль). Если же вам необходимо просто расстояние, возьмите модуль от d.

VladD

206k27 золотых знаков289 серебряных знаков521 бронзовый знак

ответ дан 4 фев 2018 в 12:16

ArhadthedevArhadthedev

11.4k8 золотых знаков42 серебряных знака69 бронзовых знаков

Ещё один подход такой. Ваше искомое расстояние — проекция вектора AP на нормаль. Длина проекции вектора на (единичный) вектор рассчитывается как скалярное произведение. Итого:

|(P - A) ⋅ NormalVector|

Если вам нужно ориентированное расстояние (положительное с одной стороны и отрицательное с другой), уберите модуль.

NormalVector должен быть, понятно, единичный.

ответ дан 4 фев 2018 в 12:26

VladDVladD

206k27 золотых знаков289 серебряных знаков521 бронзовый знак

Источник

Анна Кирпиченкова

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Очень часто на практике необходимо найти расстояние между точкой и некой прямой линией или между двумя прямыми линиями в пространстве, например, иногда определять расстояние между двумя линиями приходится и в реальной жизни. Хорошая иллюстрация такого примера — это знак, который вешают на мосты для грузовиков, указывающий максимальную высоту грузовика, которая может проехать под данным мостом.

Расстояние от верхней грани грузовика и нижней грани в данном случае определяют как расстояние между двумя прямыми.

Расстояние между 2 прямыми в пространстве — это отрезок, соединяющий две прямые линии по наикратчайшему расстоянию между ними, то есть перпендикулярный к обеим прямым.

Определение 1

Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной заданной прямой и плоскостью, в которой лежит вторая прямая.

Чтобы было чуть проще понять, что это такое, давайте повторим определение скрещивающихся прямых:

Определение 2

Скрещивающиеся прямые — это две прямые, которые не лежат в одной плоскости и не имеют каких-либо совместных друг для друга точек.

Соответственно, для того чтобы найти расстояние между скрещивающимися прямыми в пространстве, необходимо от одной из прямых опустить перпендикуляр на плоскость, в которой лежит другая прямая.

Расстояние же между двумя параллельными прямыми в пространстве является одинаковым на протяжении всей длины параллельных прямых, то есть перпендикуляр, опущенный из одной параллельной прямой на другую, всегда будет одной и той же длины вне зависимости от того, из какой именно точки его опустили.

Метод координат для определения расстояния между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми в пространстве можно найти используя метод координат, для этого необходимо:

«Расстояние между 2 прямыми в пространстве» 👇

Найти координаты точек $M_1$ и $M_2$, лежащих на прямых $a$ и $b$ соответственно.
Вычислить икс, игрек и зет направляющих векторов для прямых $a$ и $b$.
С помощью векторного произведения векторов $overline{a}$ и $overline{b}$ нужно найти вектор-нормаль для плоскости, в которой лежит прямая $b$. Затем необходимо записать общее уравнение плоскости: $A (x – x_0) + B(y – y_0) + C(z – z_0) = 0$, и от него перейти к нормированному виду уравнения плоскости следующего вида: $ x cdot cos α + y cdot cos β + z cdot cos{γ} – p = 0$, где $cos α, cos β$ и $cos γ$ — координаты единичного нормального вектора плоскости, а $p$ — свободный член, это число равно расстоянию от точки начала координат до плоскости.
Для вычисления расстояния от точки $M$ до искомой плоскости, нужно воспользоваться следующим уравнением:
$M_1H_1 = |x_1 cdot cos α + y_1 cdot cos β + z_1 cdot cos{γ} – p|$, где $x_1, y_1, z_1$ – координаты точки $M_1$, лежащей на прямой $a$, а $H_1$ — точка, лежащая на искомой плоскости.

Пример 1

Найти расстояние между двумя скрещивающимися прямыми, заданными уравнениями:
$d_1$:
$frac {x-2}{2} = frac {y + 1}{-3} = frac{z}{-1}$

и $d_2$: $begin{cases} frac{x + 1}{1} = frac{y}{-2} \ z – 1 = 0 end{cases}$

Рисунок 1. Расстояние между двумя скрещивающимися прямыми в пространстве

Для этого воспользуемся следующей формулой:

$ ρ(d_1d_2) = frac{| overline{p_1} cdot overline{p_2} cdot overline{M_1M_2}|}{[overline{p_1} × overline{p_2}]}$

Сначала найдём смешанное произведение векторов. Для этого найдём точки, лежащие на данных прямых, и их направляющие вектора:

$d_1$: $frac {x-2}{2} = frac {y + 1}{-3} = frac{z}{-1}$, точка, лежащая на прямой — $M_1$ с координатами $(2;-1;0)$, а направляющий вектор — $overline{p_1}$ с координатами $(2; -3; -1)$

$d_2$: $begin{cases} frac{x + 1}{1} = frac{y}{-2} \ z – 1 = 0 end{cases}$, точка, лежающая на прямой — $M_2$ с координатами $(-1; 0; 1)$,

а её направляющий вектор — $overline{p_2}$ с координатами $(1; -2; 0)$

Теперь найдём вектор $overline{M_1M_2}$:

$overline{M_1M_2} = (-1-2;0-(-1);1-0) = (-3; 1; 1)$

Найдём смешанное произведение векторов:

$overline{p_1} cdot overline{p_2} cdot overline{M_1M_2} = begin{array}{|ccc|} 2& 1 & -3 \ -3& -2 & 1 \ -1 & 0 & 1 \ end{array} = — begin{array}{|cc|} 1 & -3 \ -2 & 1 \ end{array} + begin{array}{|cc|} 2 & 1 \ -3 & -2 \ end{array} = -(1 — 6) + (4 + 3) = 4$

Теперь найдём векторное произведение векторов:

$[|overline{p_1} × overline{p_2}|] = begin{array}{|ccc|} i& j & k \ 2 & -3 & -1 \ 1 & -2 & 0 end{array} = begin{array}{|cc|} -3 & -1 \ -2 & 0 end{array} cdot overline{i} — begin{array}{|cc|} 2 & -1 \ 1 & 0 end{array} cdot overline{j} + begin{array}{|cc|} 2 & -3 \ 1 & -2 end{array} cdot overline{k}$

$[|overline{p_1} × overline{p_2} |]= -2 overline{i} — overline{j} — overline{k}$

Длина этого векторного произведения составит:

$overline{p_1} × overline{p_2} = sqrt{(-2)^2 + (-1)^2 + (-1)^2} = sqrt{6}$

Соответственно, длина между скрещивающимися прямыми составит:

$ ρ(d_1d_2) = frac{|4|}{sqrt{6}} ≈ 1,63$

Пример 2

Даны две параллельные несовпадающие прямые $g$ и $m$, ниже приведены уравнения для них. Определить расстояние между ними.

$g$: $frac{x-1}{4} = frac{y + 1}{6}= frac{z+3}{8}$

$m$: $frac{x+1}{2} = frac{y — 1}{3}= frac{z — 3}{4}$

Расстояние в этом случае для них вычисляется по следующей формуле:

$ρ(m;g) =frac{|[overline{r_2} — overline{r_1} × overline{s_1}]|}{|overline{s_1}|}$, где

$overline{r_2}, overline{r_1}$ — радиус-векторы для каждой прямой, а $s_1$ — направляющий вектор.

Радиус-вектор для первой прямой будет $r_1={1; -1; -3}$, а направляющий вектор $s_1 = {4; 6; 8}$.

Радиус-вектор для второй прямой будет $r_2={-1; 1; 3}$, а направляющий вектор $s_2 = {2; 3; 4}$.

Найдём векторную разность радиус-векторов:

$overline{r_2} — overline{r_1} = {-1; 1; 3} — {1; -1; -3} = {-2;0;0}$

Теперь найдём её произведение с направляющим вектором для первой прямой:

$[overline{r_2} — overline{r_1} × overline{s_1}] = begin{array}{|ccc|} i & j & k \ -2 & 0 & 0 \ 4 & 6 & 8 \ end{array} = — 16j – 12k = {0;-16;-12}$

$|[overline{r_2} — overline{r_1} × overline{s_1}]| = sqrt{(-16)^2 + (-12)^2} = 20$

$|overline{s_1}| = sqrt{4^2 + 6^2 +8^2} = 2sqrt{29}$

$ρ(m;g) = frac{20}{2sqrt{29}} = frac{10}{sqrt{29}} ≈ 1.85$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Нормальное уравнение плоскости. Расстояние от точки до плоскости.

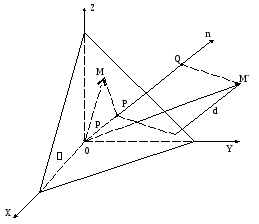
Пусть
существует плоскость
.
Проведем нормальчерез начало координат О. Пусть заданы– углы, образованные нормальюс осями координат..
Пусть–
длина отрезка нормалидо пересечения с плоскостью. Считая
известными направляющие косинусы
нормали,
выведем уравнение плоскости.

Пусть
)
– произвольная точка плоскости. Вектор
единичной нормали имеет координаты.
Найдем проекцию вектора
на нормаль.

Поскольку
точка М
принадлежит плоскости, то

(8)

Это
и есть уравнение заданной плоскости,
называющееся нормальным.

Расстояние от точки до плоскости

Пусть
дана плоскость
,М*– точка пространства,d
– её расстояние
от плоскости.

Определение.
Отклонением
точки М*
от плоскости называется
число (+d),
если M*
лежит по ту сторону от плоскости, куда
указывает положительное направление
нормали
,
и число (-d),
если точка расположена по другую сторону
плоскости:

Теорема.
Пусть
плоскость
с единичной нормальюзадана нормальным уравнением:

Пусть
М*– точка пространства Отклонение т.M*
от плоскости задаётся выражением

. (9)

Доказательство.
Проекцию т.
*
на нормаль обозначимQ.
Отклонение точки М*
от плоскости равно

;

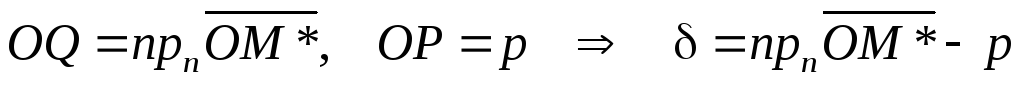
(9)

Правило.
Чтобы найти отклонение
т. M*
от плоскости, нужно в нормальное уравнение
плоскости подставить координаты т. M*.
Расстояние от точки до плоскости равно
.

Приведение общего уравнения плоскости к нормальному виду

Пусть
одна и та же плоскость задана двумя
уравнениями:

—
общее уравнение,

—
нормальное уравнение.

Поскольку оба
уравнения задают одну плоскость, их
коэффициенты пропорциональны:

Первые три равенства
возведем в квадрат и сложим:

Отсюда
найдем
– нормирующий множитель:

. (10)

Умножив
общее уравнение плоскости на нормирующий
множитель, получим нормальное уравнение
плоскости:

Примеры задач на тему «Плоскость».

Пример
1. Составить
уравнение плоскости
,
проходящей через заданную точку(2,1,-1)
и параллельной плоскости.

Решение.
Нормаль к плоскости
:.
Поскольку плоскости параллельны, то
нормальявляется и нормалью к искомой плоскости.
Используя уравнение плоскости, проходящей
через заданную точку (3), получим для
плоскостиуравнение:

Ответ:

Пример
2. Основанием
перпендикуляра, опущенного из начала
координат на плоскость
,
является точка.
Найти уравнение плоскости.

Решение.
Вектор
является нормалью к плоскости.
ТочкаМ₀
принадлежит плоскости. Можно воспользоваться
уравнением плоскости, проходящей через
заданную точку (3):

Ответ:

Пример
3. Построить
плоскость
,
проходящую через точкии перпендикулярную
плоскости
:.

Следовательно,
чтобы некоторая точка М
(x, y,
z)
принадлежала плоскости
,
необходимо, чтобы три векторабыли
компланарны:

=0.

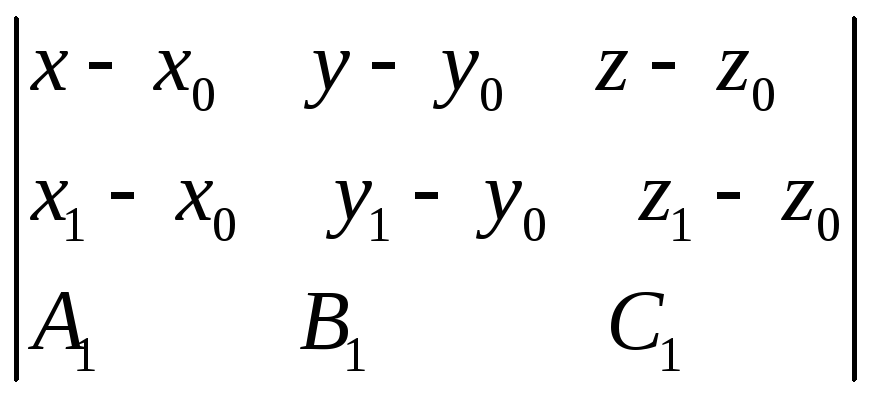
Осталось
раскрыть определитель и привести
полученное выражение к виду общего
уравнения (1).

Пример
4. Плоскость
задана
общим уравнением:

Найти
отклонение точки
от заданной плоскости.

Решение.
Приведем уравнение плоскости к нормальному
виду.

Подставим
в полученное нормальное уравнение
координаты точки М*.

Ответ:
.

Пример
5. Пересекает
ли плоскость
отрезок.

Решение.
Чтобы отрезок АВ
пересекал плоскость, отклонения
иот плоскостидолжны иметь разные знаки:

Пример
6. Пересечение
трех плоскостей в одной точке.

Система
имеет единственное решение, следовательно,
три плоскости имеют одну общую точку.

Пример
7. Нахождение
биссектрис двугранного угла, образованного
двумя заданными плоскостями.

Пусть
и— отклонение некоторой точкиот первой и второй плоскостей.

На одной из
биссектральных плоскостей (отвечающей
тому углу, в котором лежит начало
координат) эти отклонения равны по
модулю и знаку, а на другой – равны по
модулю и противоположны по знаку.

— это уравнение
первой биссектральной плоскости.

— это уравнение
второй биссектральной плоскости.

Пример
8. Определение
местоположения двух данных точек
иотносительно двугранных углов,
образованных данными плоскостями.

Пусть
.
Определить: в одном, в смежных или в
вертикальных углах находятся точкии.

Находим
и,и— это отклонения точекА
и В от
плоскостей
и.

а).
Если
илежат по одну сторону оти от,
то они лежат в одном двугранном углу.

б).
Если
илежат по одну сторону оти по разные от,
то они лежат в смежных углах.

в).
Если
илежат по разные стороны оти,
то они лежат в вертикальных углах.

Системы
координат 3

Линии
на плоскости 8

Линии
первого порядка. Прямые на плоскости. 10

Угол
между прямыми 12

Общее
уравнение прямой 13

Неполное
уравнение первой степени 14

Уравнение
прямой “в отрезках” 14

Совместное
исследование уравнений двух прямых 15

Нормаль
к прямой 15

Угол
между двумя прямыми 16

Каноническое
уравнение прямой 16

Параметрические
уравнения прямой 17

Нормальное
(нормированное) уравнение прямой 18

Расстояние
от точки до прямой 19

Уравнение
пучка прямых 20

Примеры
задач на тему «прямая на плоскости» 22

Векторное
произведение векторов 24

Свойства
векторного произведения 24

Геометрические
свойства 24

Алгебраические
свойства 25

Выражение
векторного произведения через координаты
сомножителей 26

Смешанное
произведение трёх векторов 28

Геометрический
смысл смешанного произведения 28

Выражение
смешанного произведения через координаты
векторов 29

Примеры
решения задач по теме: «Векторная
алгебра». 30

Поверхности
в пространстве 33

Плоскость 33

Неполные
уравнения плоскости 35

Уравнение
плоскости в «отрезках» 35

Угол
между плоскостями 36

Уравнение
плоскости, проходящей через три точки,
не принадлежащие одной прямой 37

Нормальное
уравнение плоскости. Расстояние от
точки до плоскости. 38

Расстояние
от точки до плоскости 39

Приведение
общего уравнения плоскости к нормальному
виду 40

Примеры
задач на тему «Плоскость». 40

Линии
в пространстве. Прямая в пространстве 46

Канонические
уравнения прямой в пространстве 47

Параметрические
уравнения прямой 48

Уравнения
прямой, проходящей через две заданные
точки 48

Угол
между двумя прямыми в пространстве 49

Угол
между прямой и плоскостью 49

Условие
принадлежности двух прямых одной
плоскости 50

Некоторые
задачи на построение прямых и плоскостей 50

Примеры
решения задач по теме «Аналитическая
геометрия» 55

Кривые
второго порядка 59

Пример
приведения общего уравнения линии
второго порядка к каноническому виду 59

Эллипс 62

Вывод
уравнения эллипса 62

Гипербола 64

Парабола 65

Примеры
решения задач на тему «Кривые второго
порядка». 66

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

956 Определить, какие из следующих
уравнений плоскостей являются нормальными: 956.1

; 956.2

; 956.3

; 956.4

; 956.5

; 956.6

; 956.7

; 956.8

;

. 956.9

; 956.10

; 956.11

; 956.12

. 957 Привести каждое из
следующих уравнений плоскостей к нормальному
виду: 957.1

; 957.2

; 957.3

; 957.4

; 957.5

; 957.6

; 957.7

; 957.8

; 957.9

; 957.10

. 958 Для каждой из
следующих плоскостей вычислить углы

, образуемые нормальню с осями
координат, и расстояние р от начала координат: 958.1

; 958.2

; 958.3

; 958.4

; 958.5

; 958.6

; 958.7

; 958.8

; 958.9

; 958.10

. 959 Вычислиь величину
отклонения

и расстояние d от точки до
плоскости в каждом из следующих случаев:М₂(2;
-1; -1),

; 959.1 М₁(-2;
-4; 3),

; 959.2 М₃(1;
2; -3),

; 959.3 М₃(1; 2;
-3),

; 959.4 М₄(3;
-6; 7),

; 959.5 М₅(9;
2; -2),

. 960 Вычислить
расстояние d от точки Р(-1; 1; -2) до плоскости,
проходящей через точки М₁(1; -1; 1),
М₂(-2; 1; 3), М₃(4;
-5; -2). 961 Определить, лежит
ли точка Q(2; -1; 1) и начало координат по одну или по
разные стороны относительно каждой из следующих
плоскостей: 961.1

; 961.2

; 961.3

; 961.4

; 961.5

; 961.6

. 962 Доказать, что
плоскость

пересекает отрезок,
ограниченный точками М₁(3; -2; 1) и М₂(-2; 5; 2). 963 Доказать, что
плоскость

не пересекает отрезка,
ограниченного точками М₁(1; 4; -3) и М₂(2; 5; 0). 964 В каждом из
следующих случаев вычислить расстояние между
параллельными плоскостями: 964.1

; 964.2

; 964.3

; 964.4

; 964.5

; 964.6

. 965 Две грани куба
лежат на плоскостях

. Вычислить объем
этого куба. 966 На оси Оу найти
точку, отстоящую от плоскости

на
расстояние d=4. 967 На оси Oz найти
точку, равноудаленную от точки М(1; -2; 0) и от
плоскости

. 968 На оси Ох найти
точку, равноудаленную от двух плоскостей

. 969 Вывести уравнение
геометрического места точек, отклонение которых
от плоскости

равно 2. 970 Вывести уравнение
геометрического места точек, отклонение которых
от плоскости

равено –3. 971 Составить
уравнения плоскостей, параллельных плоскости

и отстоящих от нее на расстояние d=5. 972 В каждом из
следующих случаев составить уравнение
геометрического места точек, равноудаленных от
двух параллельных плоскостей: 972.1

; 972.2

; 972.3

. 973 В каждом из
следующих случаев составить уравнения
плоскостей, которые делят пополам двугранные
углы, образованные двумя пересекающимися
плоскостями: 973.1

; 973.2

; 973.3

. 974 В каждом из
следующих случаев определить, лежат ли точка М(2;
-1; 3) и начало координат в одном, в смежных или
вертикальных двугранных углах, образованных при
пересечении двух плоскостей: 974.1

; 974.2

; 974.3

. 975 В каждом из
следующих случаев определить, лежат ли точки М(2;
-1; 1) и N(1; 2; -3) в одном, в смежных или вертикальных
двугранных углах, образованных при пересечении
двух плоскостей: 975.1

; 975.2

. 976 Определить, лежит
ли начало координат внутри острого или тупого
угла, образованного двумя плоскостями

. 977 Определить, лежит
ли точка М(3; 2; -1) внутри острого или тупого угла,
образованного двумя плоскостями

. 978 Составить
уравнение плоскости, делящей пополам тот
двугранный угол между двумя плоскостями

, в
котором лежит начало координат. 979 Составить
уравнение плоскости, делящей пополам тот
двугранный угол между двумя плоскостями

, в
котором лежит точка М(1; 2; -3). 980 Составить
уравнение плоскости, которая делит пополам
острый двугранный угол, образованный двумя
плоскостями

. 981 Составить
уравнение плоскости, которая делит пополам тупой
двугранный угол, образованный двумя плоскостями

Источник

I feel like this has probably been answered, but I searched and couldn’t find an exact solution.

What I want is a quick way to take a selected set of faces on an object (or the vertices that make up the faces), typically ones that are connected along a particular side of a rectangular-shaped object, and move each of them along the face normal until they’re a fixed distance away from the surface of whatever object is in that particular direction.

I found an addon that moves faces along the face normal, so I was hoping to add a little bit of code to create a modified addon that would do the job. OR, maybe there’s an easy way to do this already in the Blender interface, and I’m overlooking it.

I created an addon for Blender several years ago, but I’m a little rusty now. Seems like this should be easy to do, yet my searches have come up empty so far.

Thanks for the help!
-Mike

Источник