|
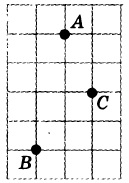
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах квадратных. Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой. Весьма хитрая задача. На плане обозначен прямоугольный стол со сторонами 3 и 4 клеток, а длина измеряется не в квадратных метрах, а просто в метрах. Длина между углами данного стола представляет собой гипотенузу прямоугольного треугольника и равна корню квадратному из суммы квадратов катетов. Так гласит формула теоремы Пифагора. Подставляем значения: √ (3²+ 4²) = √ (9 + 16) = √ (25) = 5. Конечно любой знакомый с математикой не станет это вычислять. Ведь перед ним магический квадрат — 3, 4, 5. Теперь зная размер гипотенузы мы вычислим длину в метрах: 5 * 0.3 = 1.5 метра или 150 сантиметров или 15 дециметров. автор вопроса выбрал этот ответ лучшим Simple Ein более года назад Из условия задачи понятно, что обеденный стол обозначен цифрой 4. Обеденный стол со сторонами 3 и 4 клетки. Сторона каждой клетки равна 0,3 м. Получается, одна сторона стола равна 0,3*3=0,9 м. Вторая — 0,4*3=1,2 м. Определить расстояние между противоположными углами у стола можно по теореме Пифагора. Получается √ (0,9²+ 1,2²) = √ (2,25) =1,5 метра. Пашенька более года назад Пояснение к задаче нам подсказывает, что обеденный стол на схеме расположен в центре кухни, поэтому можем смело утверждать, что нас интересует объект под номером 4. Из условия задания нам известно, что клетка имеет размер — 0.3м. Для подсчета нам необходимо рассчитать размеры стола. В клеточках это 3х4, в метрах:
Далее учитываем, что стол — это прямоугольник, где расстояние между углами — это гипотенуза, а стороны стола — катеты. Следовательно, на основании теоремы Пифагора мы имеем возможность рассчитать длину-гипотенузу. Находим сумму квадратов катетов и извлекаем квадратный корень.
Ответ: 1.5. Stan1711 3 года назад Длина измеряется в метрах.Из плана видно что размеры ободеного стола равны 3 клетки на 4.Стол прямоугльный.Тогда размер диагонали от одного угла до другого будет ровна 5 клеткам (как соотношение в прямоугольном треугольнике — 3:4:5.)Учитывая размер клетки 0,3м. мы получим ответ на вопрос 5*0,3 =1,5м. Знаете ответ? |
2. Определение тангенса угла
Что нужно вспомнить:
• Тангенс угла в прямоугольном
треугольнике — отношение противолежащего катета к прилежащему.

прямоугольный треугольник.
Задача 1
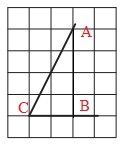
Найдите тангенс угла А треугольника ABC,
изображённого на рисунке 1.
|
Решение:
Ответ: 0,4. |
Рис.1 |
Задача 2
Найдите тангенс угла B треугольника ABC,
изображённого на рисунке 2.
|
Решение:
Ответ: 3,5. |
Рис. 2 |
Задача 3
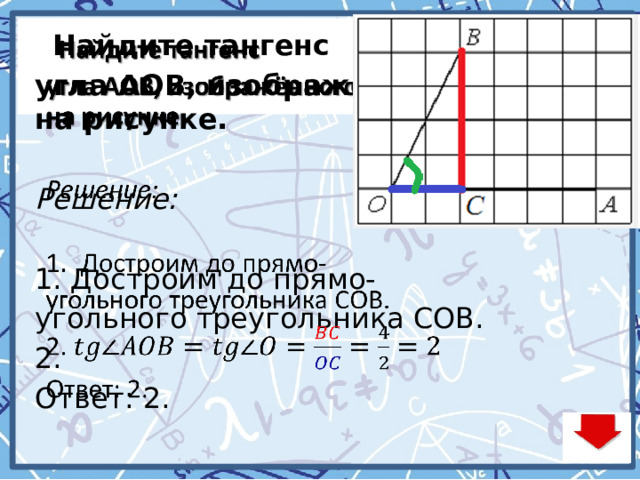
Найдите тангенс угла AOB, изображённого
на рисунке 3.
|
Решение: 1. 2. Ответ: 2. |
Рис. 3 |
Задача 4
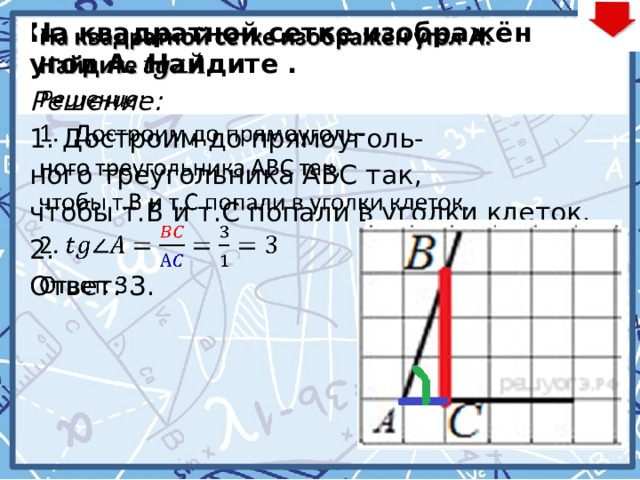
На квадратной сетке изображён угол А
(рис.4). Найдите .
|
Решение: 1. 2. Ответ: 3. |
Рис. 4 |
Задача 5
Найдите тангенс угла, изображённого
на рисунке 5.
|
Решение: 1. 2. Значит,
Ответ: -3. |
Рис. 5 Рис. 5.1 |
Задача 6
Найдите тангенс угла АОВ (рис. 6).
|
Решение: Найдём каждую из сторон треугольника АОВ, чтобы показать, что он прямоугольный: Таким образом Ответ: 0,5. |
Рис. 6 |
8. Определение градусной меры
вписанного угла
Что нужно вспомнить:
• Вписанный угол – угол, вершина которого
лежит на окружности, а стороны её пересекают.
• Центральный угол – угол, вершина которого
совпадает с центром окружности, а стороны её пересекают.
Вписанный угол равен половине дуги, на которую опирается.
Задача 1:
Найдите угол ABC (рис.
20). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол ABC — Ответ: 45. |
Рис. 20 |
Задача 2:
Найдите угол ABC (рис.
21). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол BAC — Треугольник ABC Ответ: 67,5. |
Рис. 21 |
Задача 3:
Найдите угол ABC (рис.22).
Ответ дайте в градусах.
|
Решение: Угол ABC — опирается на большую Проведём вспомогательное построение. Заметим, что дуга АC составляет Угол AВC — вписанный, поэтому он равен Ответ: 135. |
Рис. 22 |
Задача 4:
Найдите угол ABC (рис.
23). Ответ дайте в градусах.
|
Решение: Проведём вспомогательное Угол АВС опирается на ту же дугу, Ответ: 22,5. |
Рис. 23 |
9. Задачи для самостоятельно решения
I.
Определение
тангенса угла
1.

рисунке.
2.

на рисунке.
3.

4.

5.

6.
Найдите
тангенс угла AOB, изображённого на рисунке.
 |
7.

8.

9.

10.
Найдите
тангенс угла, изображённого на рисунке.

II.
Определение
площади фигуры (ромба, трапеции, параллелограмма, треугольника)
1.
На
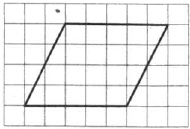
клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его
площадь.
 |
2.

треугольник. Найдите его площадь.
3.
На
клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.
 |
4.

ромб. Найдите его площадь.
5.

ромб. Найдите длину его большей диагонали.
6.

трапеция. Найдите её площадь.
7.

трапеция. Найдите её площадь.
III.
Определение
расстояния от точки до прямой (отрезка)
1.
На клетчатой
бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой ВС. Ответ выразите
в сантиметрах.
 |
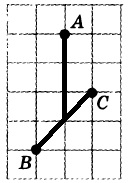
2.

отмечены точки А, В и С. Найдите расстояние
от точки А до прямой ВС. Ответ выразите в
сантиметрах.
3.
На клетчатой
бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
 |
4.

см отмечены точки А, В и С. Найдите
расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
5.
На клетчатой
бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С.
Найдите расстояние от точки А до прямой BC. Ответ выразите
в сантиметрах.
 |
IV.
Определение
длины средней линии треугольника и трапеции
1.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
2.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
3.

изображён треугольник ABC. Найдите длину его средней линии,
параллельной стороне AC.
4.

трапеция. Найдите длину её средней линии.
5.

трапеция. Найдите длину её средней линии.
6.

трапеция. Найдите длину её средней линии.
V.
Определение
длины большего катета, большей диагонали
1.

прямоугольный треугольник. Найдите длину его большего катета.
2.

прямоугольный треугольник. Найдите длину его большего катета.
3.

прямоугольный треугольник. Найдите длину его большего катета.
4.
На
клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его
большей диагонали.
 |
5.

ромб. Найдите длину его большей диагонали.
VI.
Определение
площади сложных или составных фигур
1.

фигура. Найдите её площадь.
2.

фигура. Найдите её площадь.
3.
На
клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

4.
На клетчатой
бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

5.

изображённой на рисунке.
6.

изображённой на рисунке.
VII.
Определение
площади сложных или составных фигур
1.
Найдите
угол ABC. Ответ дайте в градусах.
 |
2.

3.

4.
Найдите
угол ABC. Ответ дайте в градусах.
 |
5.
Найдите
угол ABC. Ответ дайте в градусах.
 |
6.
Найдите
угол ABC. Ответ дайте в градусах.
 |
II. Определение площади фигуры (ромба, трапеции, параллелограмма,
треугольника
III. Определение расстояния от
точки до прямой (отрезка)
IV. Определение расстояния от
точки до прямой (отрезка)
V. Определение длины большего катета,
большей диагонали
VII. Определение площади сложных
или составных фигур
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Бакирова Лариса Дамировна , МБОУ СОШ №11, Серовский ГО
Подготовка к ОГЭ. Задание №18 «Фигуры на квадратной решётке»
Задание 18 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. Данные в таких задачах даются в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи. К этим задачам вплотную примыкают задания на вычисление элементов плоских фигур по готовому чертежу, на котором указаны координаты некоторых точек фигуры (например, вершин треугольника или четырёхугольника), позволяющие после выполнения несложных вычислений ответить на вопрос задачи. При этом, как правило, не требуется применения дополнительных формул метода координат.
Основные типы задач
- Определение тангенса угла;
- Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);
- Определение расстояния от точки до прямой (отрезка);
- Определение длины средней линии треугольника и трапеции;
- Определение длины большего катета, большей диагонали;
- Определение площади сложных или составных фигур;
- Определение градусной меры вписанного угла.
- При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь.
- По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.
Расстояние от точки до прямой
Средняя линия треугольника
Средняя линия трапеции
Диагонали ромба
Определение расстояния от точки до прямой (отрезка)
Что нужно вспомнить:
- Расстояние от точки до прямой равно перпендикуляру, опущенному из этой точки на прямую.
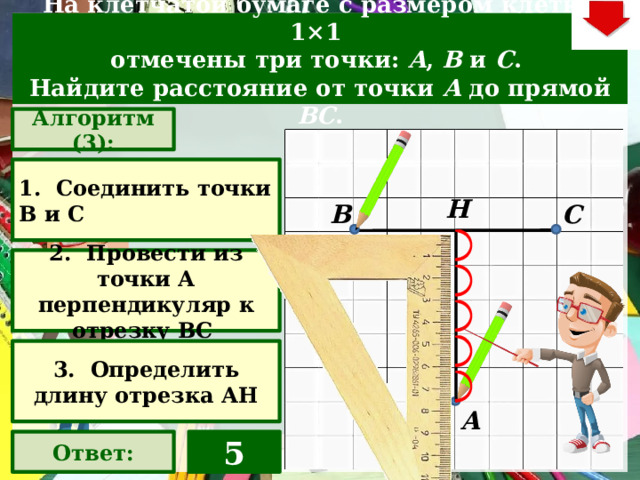
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Алгоритм (3):
1. Соединить точки В и С
Н
В
С
2. Провести из точки А перпендикуляр к отрезку ВС
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм – последовательно три раза
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
А
5
Ответ:
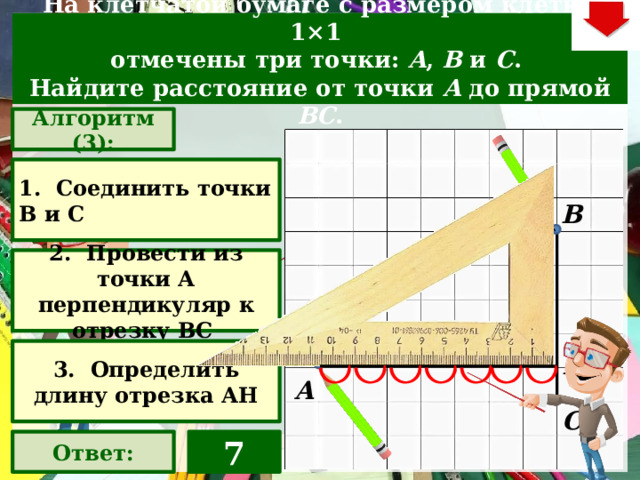
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Алгоритм (3):
1. Соединить точки В и С
В
2. Провести из точки А перпендикуляр к отрезку ВС
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм – последовательно три раза
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
Н
А
С
Ответ:
7
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
Ответ:
6
Проверка (3):
Н
С
В
1. Соединить точки В и С
2. Провести из точки А перпендикуляр к отрезку ВС
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза.
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
6
3. Определить длину отрезка АН
А
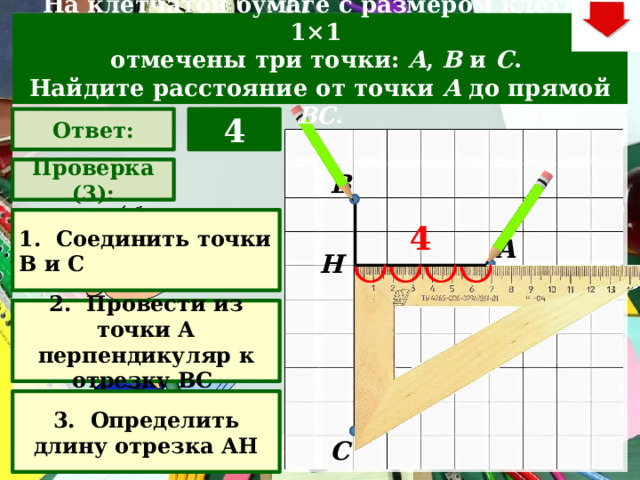
На клетчатой бумаге с размером клетки 1×1
отмечены три точки: A , B и C .
Найдите расстояние от точки A до прямой BC .
4
Ответ:
Проверка (3):
В
1. Соединить точки В и С
4
А
Н
2. Провести из точки А перпендикуляр к отрезку ВС
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза.
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Определить длину отрезка АН
С
Определение длины средней линии треугольника и трапеции
Что нужно вспомнить:
- Средняя линия треугольника параллельна третьей стороне и равна её половине;
- Средняя линия трапеции равна полусумме оснований.
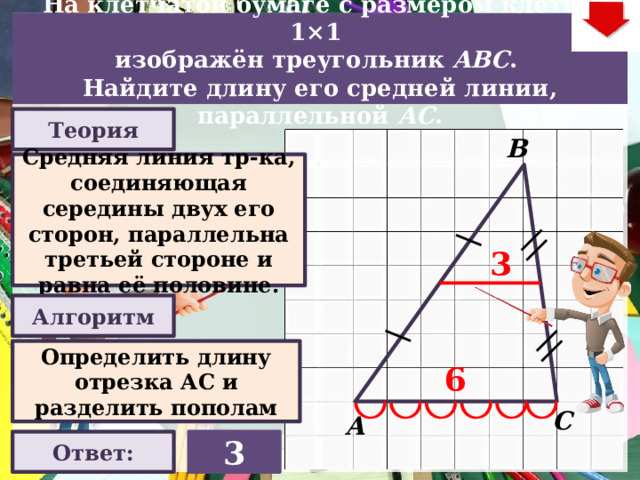
На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
Теория
В
Средняя линия тр-ка, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
4
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
Определить длину отрезка АС и разделить пополам
С
А
4
Ответ:
На клетчатой бумаге с размером клетки 1×1
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
Теория
В
Средняя линия тр-ка, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
3
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Определить длину отрезка АС и разделить пополам
6
С
А
3
Ответ:
На клетчатой бумаге с размером клетки 1×1
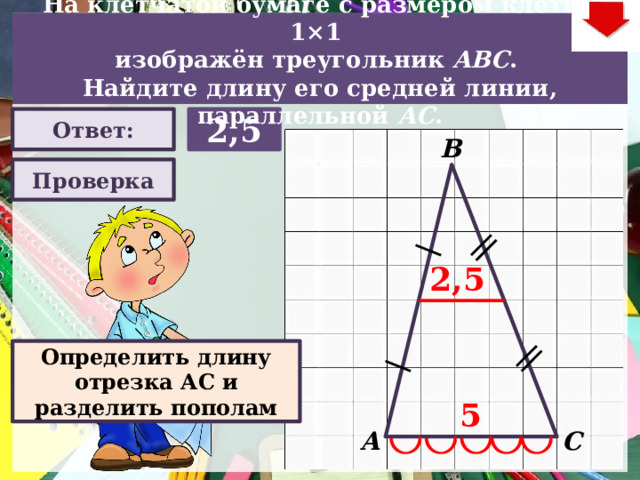
изображён треугольник ABC .
Найдите длину его средней линии, параллельной АC .
2,5
Ответ:
В
Проверка
2,5
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка)
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Определить длину отрезка АС и разделить пополам
5
А
С
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
Теория
5
Средняя линия трапеции равна полусумме её оснований
Алгоритм (2)
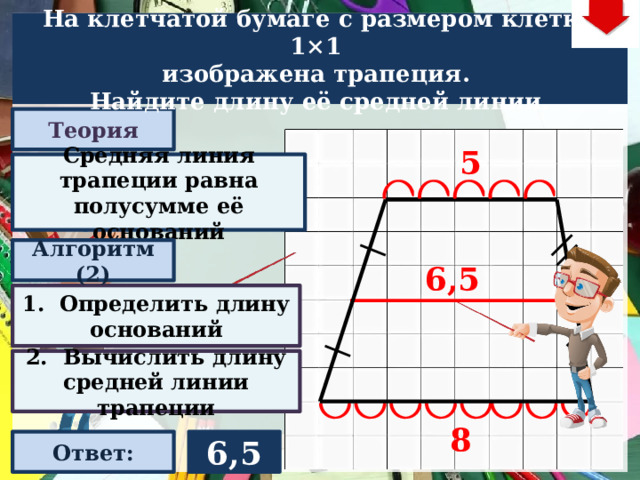
6,5
1. Определить длину оснований
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» — последовательно 3 раза — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Вычислить длину средней линии трапеции
8
Ответ:
6,5
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
Теория
Средняя линия трапеции равна полусумме её оснований
1
Алгоритм (2)
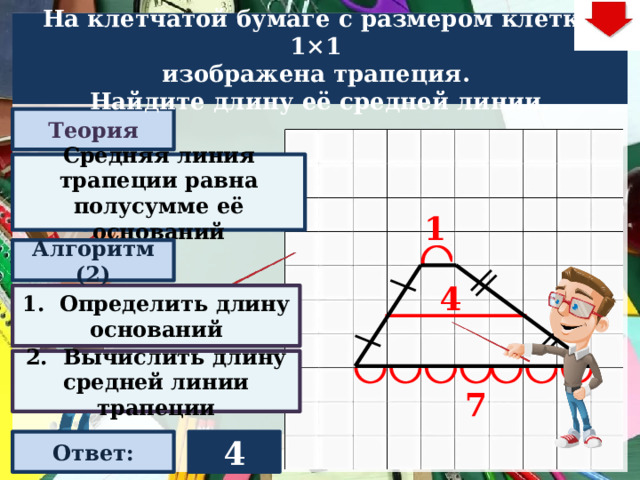
4
1. Определить длину оснований
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Теория!
- «Алгоритм» — последовательно 3 раза — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Вычислить длину средней линии трапеции
7
Ответ:
4
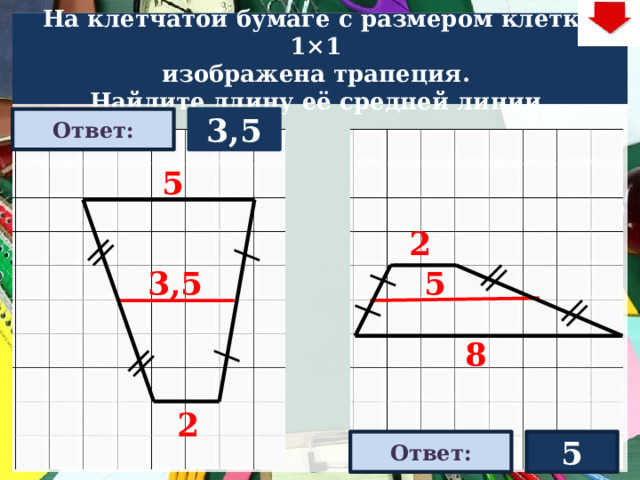
На клетчатой бумаге с размером клетки 1×1
изображена трапеция.
Найдите длину её средней линии.
3,5
Ответ:
5
2
3,5
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
2
Ответ:
5
Определение длины большего катета, большей диагонали
Что нужно вспомнить:
- Стороны прямоугольного треугольника: катеты – образуют прямой угол:
гипотенуза – лежит напротив прямого угла.
- Диагональ – отрезок соединяющий две не соседние вершины.

На клетчатой бумаге с размером клетки 1×1
изображён ромб.
Найдите длину его большей стороны.
Алгоритм (2)
8 4
1. Определить длину диагоналей ромба
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» — последовательно 2 раза — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Сравнить длины диагоналей
Ответ:
8
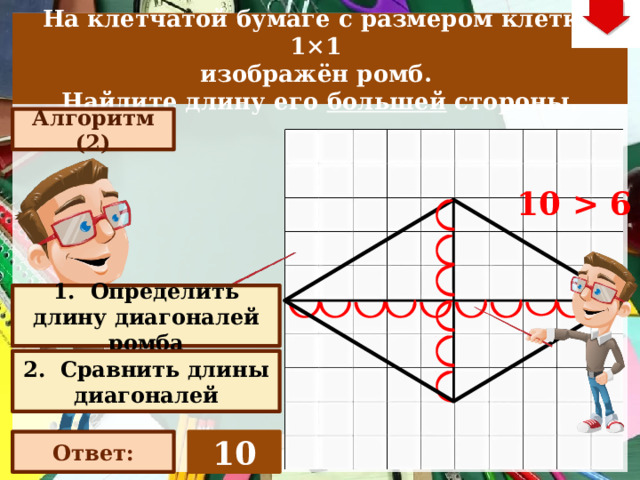
На клетчатой бумаге с размером клетки 1×1
изображён ромб.
Найдите длину его большей стороны.
Алгоритм (2)
10 6
1. Определить длину диагоналей ромба
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» — последовательно 2 раза — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
2. Сравнить длины диагоналей
10
Ответ:
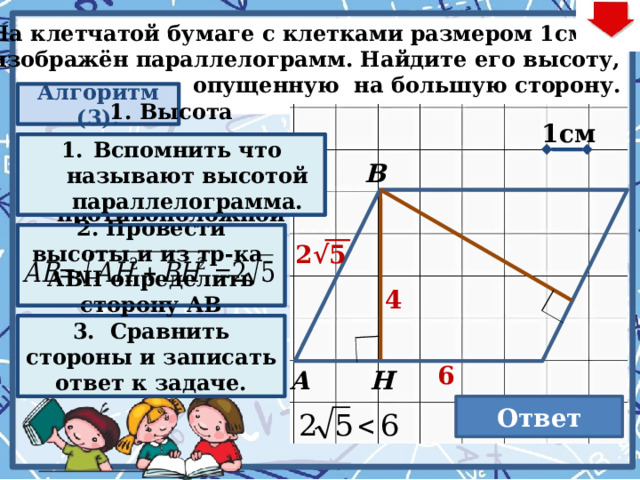
На клетчатой бумаге с клетками размером 1см×1см
изображён параллелограмм. Найдите его высоту,
опущенную на большую сторону.
Алгоритм (3):
1cм
1. Высота параллелограмма – перпендикуляр из вершины к противоположной стороне.
- Вспомнить что называют высотой параллелограмма.
В
2. Провести высоты и из тр-ка АВН определить
сторону АВ
2√5
4
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – 3 раза для визуализации ответов и решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Сравнить стороны и записать ответ к задаче.
6
Н
А
Ответ
4
22
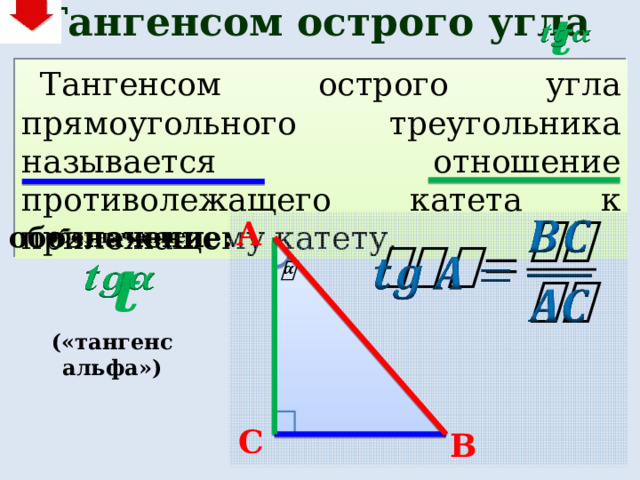
Тангенсом острого угла
t
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
A
обозначение:
t
(«тангенс альфа»)
C
B
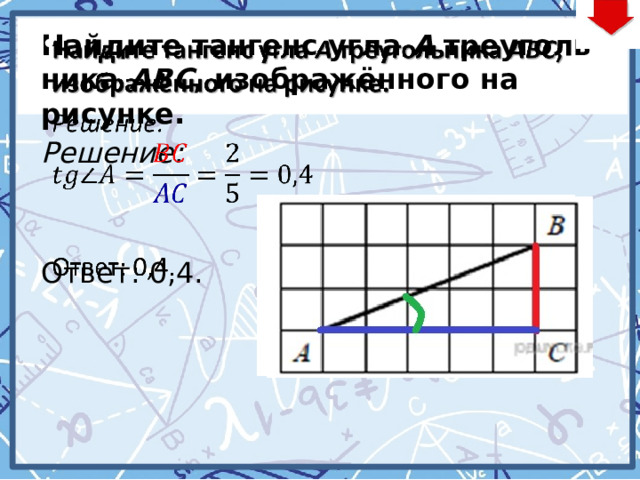
Найдите тангенс угла А треугольника ABC , изображённого на рисунке.
Решение:
Ответ: 0,4.
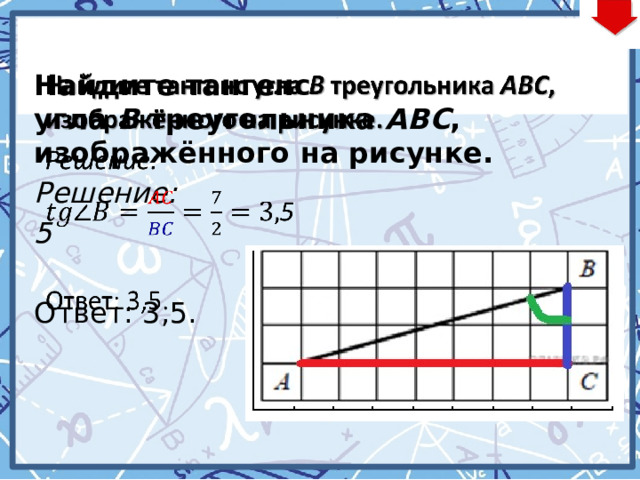
Найдите тангенс угла B треугольника ABC , изображённого на рисунке.
Решение:
5
Ответ: 3,5.
Найдите тангенс
угла AOB, изображённого на рисунке.
Решение:
- Достроим до прямо-
угольного треугольника СОВ.
2.
Ответ: 2.
На квадратной сетке изображён угол А. Найдите .
Решение:
- Достроим до прямоуголь-
ного треугольника АВС так,
чтобы т.В и т.С попали в уголки клеток.
2.
Ответ: 3.
Площадь треугольника
Площадь параллелограмма
Площадь трапеции
Площадь фигуры
Определение площади фигуры
Нужно вспомнить формулы площадей фигур:
- параллелограмм треугольник — ромб — трапеция —
- параллелограмм
- треугольник —
- ромб —
- трапеция —
На клетчатой бумаге с размером клетки 1×1
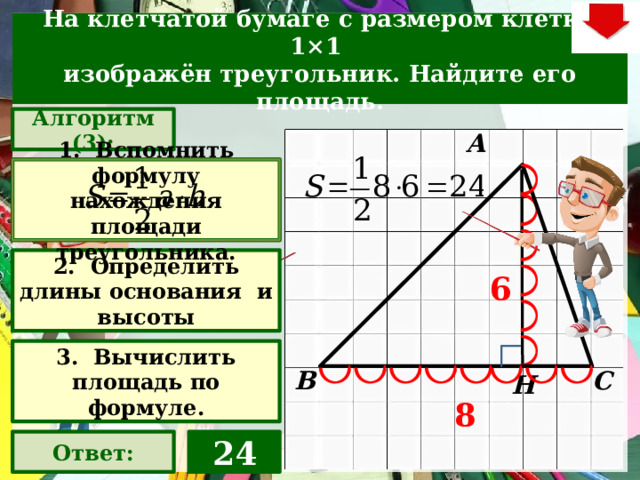
изображён треугольник. Найдите его площадь.
Алгоритм (3):
А
1. Вспомнить формулу нахождения площади треугольника.
2. Определить длины основания и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади треугольника. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
В
С
Н
8
24
Ответ:
22
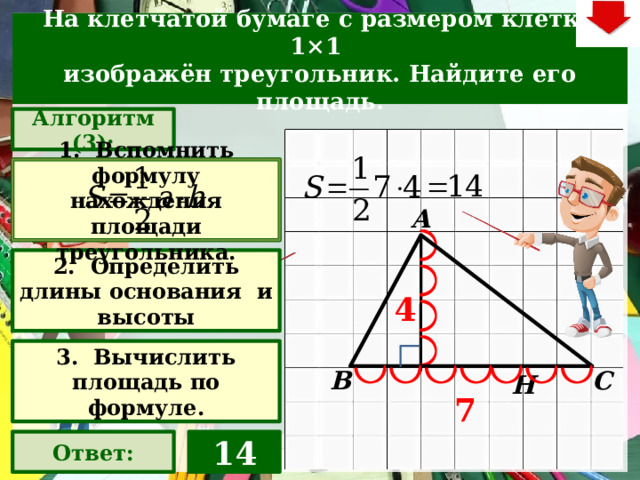
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Алгоритм (3):
1. Вспомнить формулу нахождения площади треугольника.
А
2. Определить длины основания и высоты
4
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм@ – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади треугольника. При появлении второй и третьей подсказки нажииать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
В
С
Н
7
14
Ответ:
22
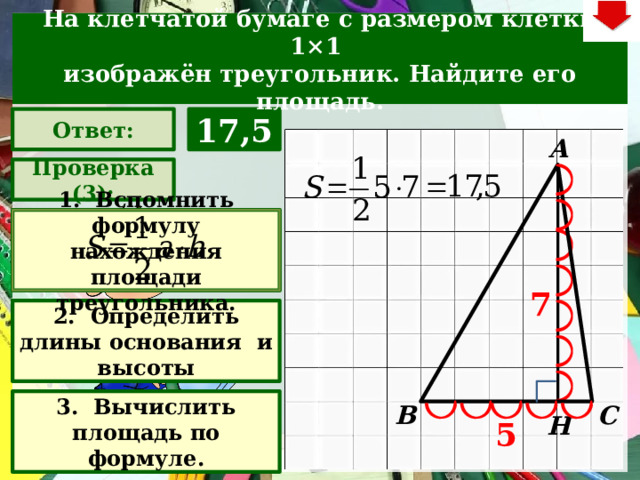
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
Ответ:
17,5
А
Проверка (3):
1. Вспомнить формулу нахождения площади треугольника.
7
2. Определить длины основания и высоты
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза. После появления первого прямоугольника– нажмите на него – появится формула нахождения площади треугольника. При появлении второго и третьего прямоугольников нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
С
В
Н
5
22
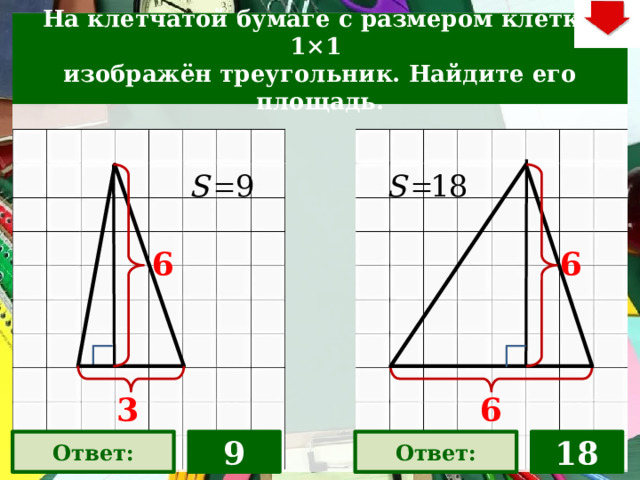
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
6
6
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3
6
9
Ответ:
Ответ:
18
22
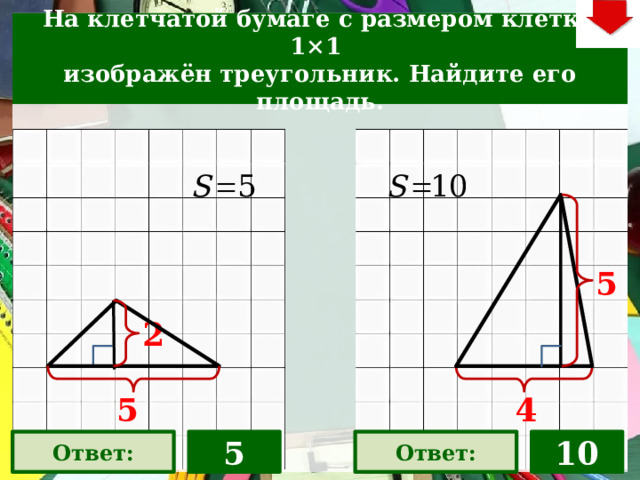
На клетчатой бумаге с размером клетки 1×1
изображён треугольник. Найдите его площадь.
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможет только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
2
5
4
Ответ:
5
Ответ:
10
22
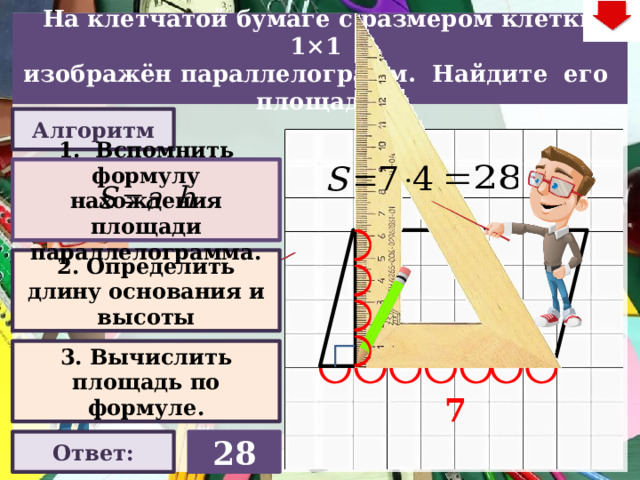
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Алгоритм
1. Вспомнить формулу нахождения площади параллелограмма.
2. Определить длину основания и высоты
4
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади параллелограмма. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
7
Ответ:
28
22
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Алгоритм
1. Вспомнить формулу нахождения площади параллелограмма.
2. Определить длину основания и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади параллелограмма. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
3. Вычислить площадь по формуле.
5
Ответ:
30
22
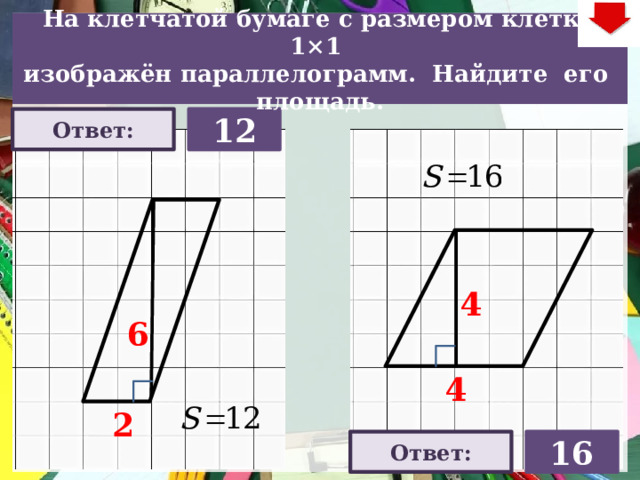
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Ответ:
12
4
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
6
4
2
16
Ответ:
22
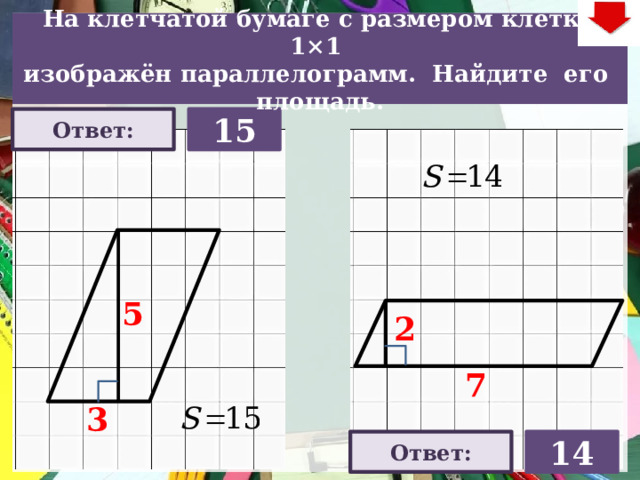
На клетчатой бумаге с размером клетки 1×1
изображён параллелограмм. Найдите его площадь.
Ответ:
15
5
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможен только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
2
7
3
14
Ответ:
22
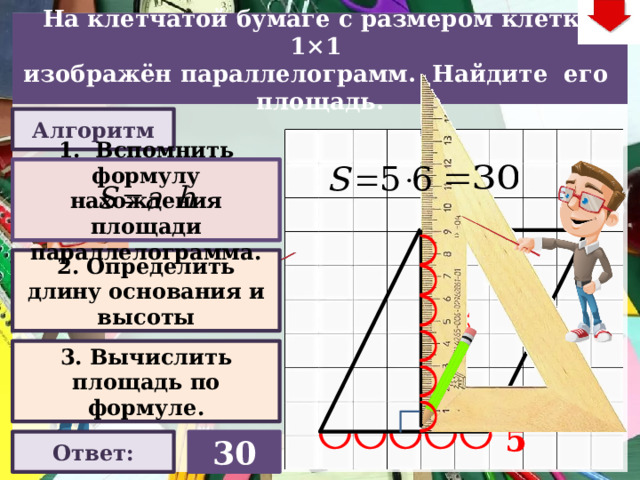
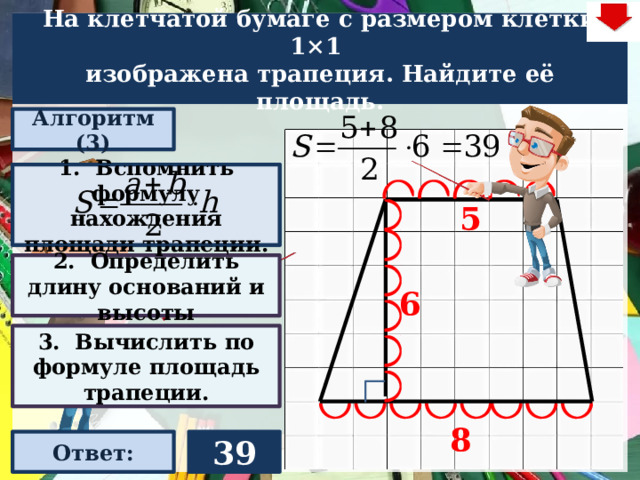
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
Алгоритм (3)
1. Вспомнить формулу нахождения площади трапеции.
5
2. Определить длину оснований и высоты
6
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади трапеции. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
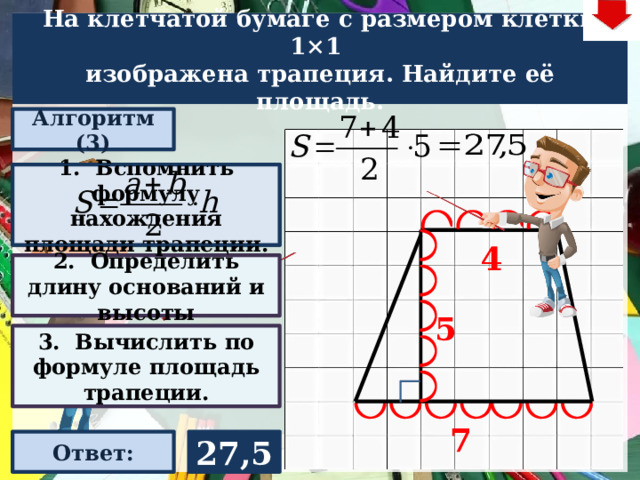
3. Вычислить по формуле площадь трапеции.
8
Ответ:
39
22
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
Алгоритм (3)
1. Вспомнить формулу нахождения площади трапеции.
4
2. Определить длину оснований и высоты
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
- Нажимает на прямоугольник «Алгоритм» – последовательно три раза. После появления первой подсказки – нажмите на неё – появится формула нахождения площади трапеции. При появлении второй и третьей подсказки нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
5
3. Вычислить по формуле площадь трапеции.
7
27,5
Ответ:
22
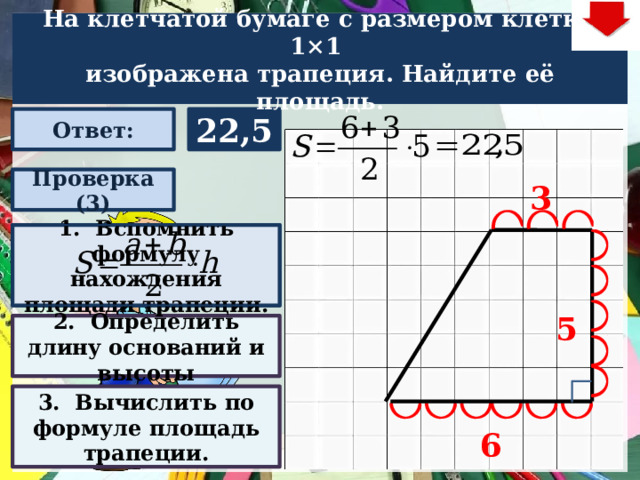
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
22,5
Ответ:
Проверка (3)
3
1. Вспомнить формулу нахождения площади трапеции.
Задача. Решают учащиеся самостоятельно. После озвучивания и визуализации ответа (кнопка «Ответ»), необходимо визуализировать решение задачи (для всего класса) – нажимаем на прямоугольник «Проверка» – последовательно три раза. После появления первого прямоугольника– нажмите на него – появится формула нахождения площади трапеции. При появлении второго и третьего прямоугольников нажимать на них не надо. Действия на слайде настроены в автоматическом режиме
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ вернуться на слайд выбора следующей задачи
5
2. Определить длину оснований и высоты
3. Вычислить по формуле площадь трапеции.
6
22
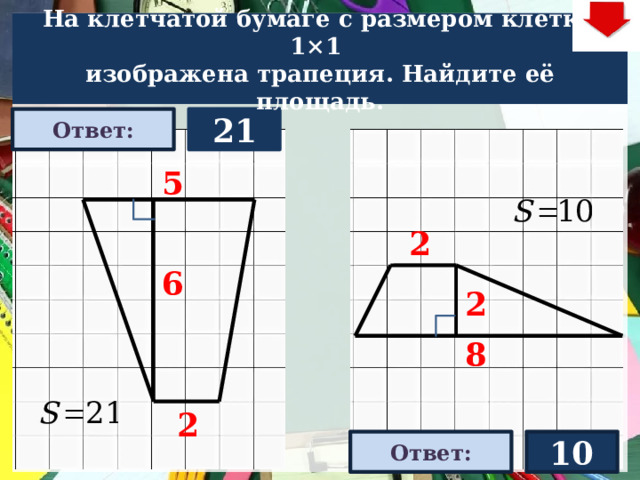
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
21
Ответ:
5
2
6
2
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
8
2
Ответ:
10
22
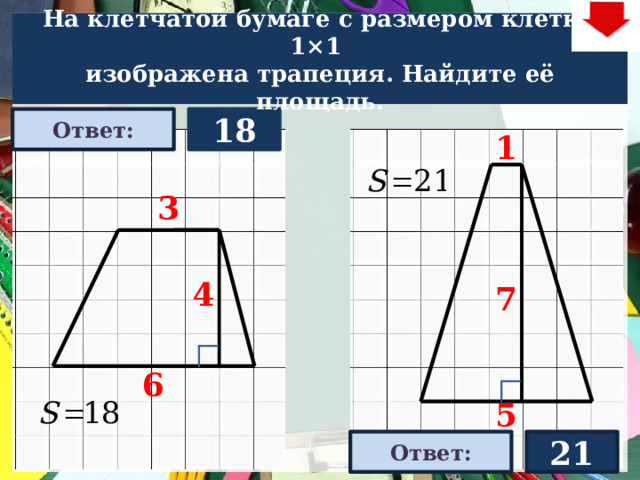
На клетчатой бумаге с размером клетки 1×1
изображена трапеция. Найдите её площадь.
18
Ответ:
1
3
4
7
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможен только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
6
5
21
Ответ:
22
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Сосчитать количество клеточек из которых состоит фигура
19
Ответ:
22
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
Алгоритм
Слайд объяснения решения задачи. Выполнена настройка триггеров, поэтому учитель сам может организовать сценарий решения задачи.
Можно самому объяснить последовательно визуализируя этапы решения задачи, можно наводящими вопросами получить ответы от учеников, а можно предложить учащимся объяснить решения задачи.
Алгоритм работы с триггерами
1. «Алгоритм» — визуализация исполнения решения настроена автоматически.
- «Ответ»
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Сосчитать количество клеточек из которых состоит фигура
20
Ответ:
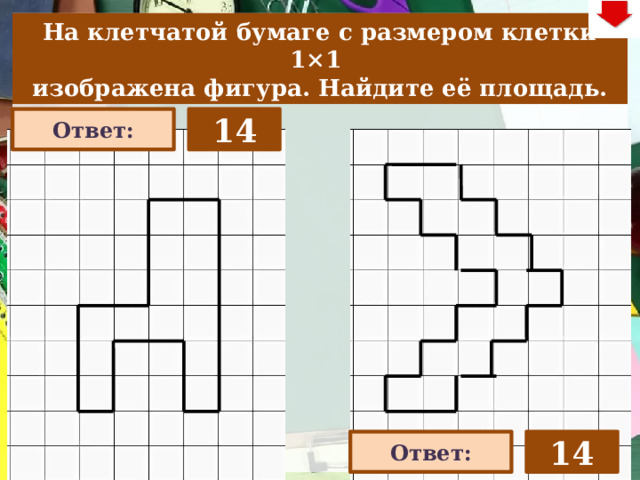
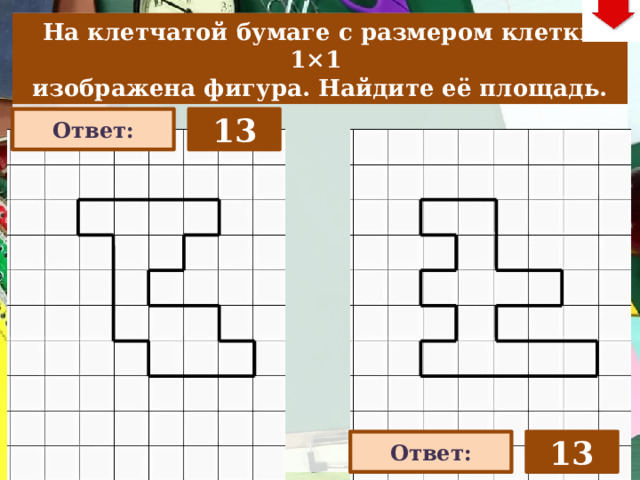
22
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
14
Ответ:
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
В зависимости от сценария урока возможно перейти к следующей задаче – по управляющей кнопке в правом верхнем углу слайда ИЛИ
вернуться на слайд выбора следующей задачи
Ответ:
14
22
На клетчатой бумаге с размером клетки 1×1
изображена фигура. Найдите её площадь.
13
Ответ:
На слайде две задачи. Можно предложить учащимся работу по вариантам, работу в мини-группах (по партам)
На слайде представлена только визуализация правильных ответов
С данного слайда возможет только возврат к слайду выбора следующей задачи (правый верхний угол слайда – кнопка «6»).
13
Ответ:
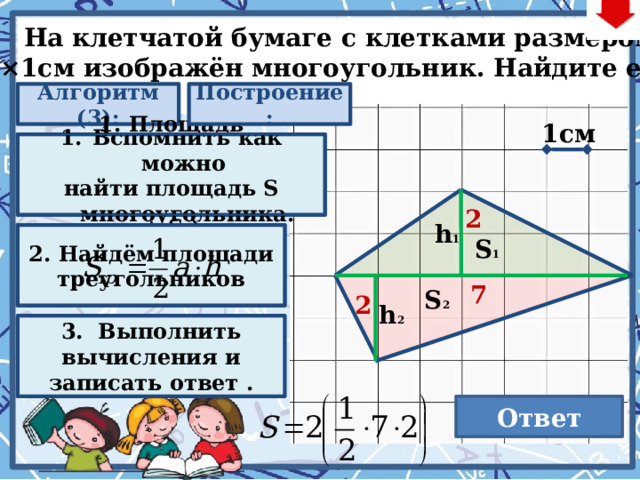
22
На клетчатой бумаге с клетками размером
1см×1см изображён многоугольник. Найдите его S.
Алгоритм (3):
Построение:
1cм
- Вспомнить как можно
1. Площадь многоугольника равна сумме площадей фигур из которых состоит (S 1 + S 2 )
найти площадь S многоугольника.
2
h 1
2. Найдём площади треугольников
S 1
7
S 2
2
h 2
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Построение»
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – 3 раза для визуализации ответов и решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Выполнить вычисления и записать ответ .
Ответ
14
22
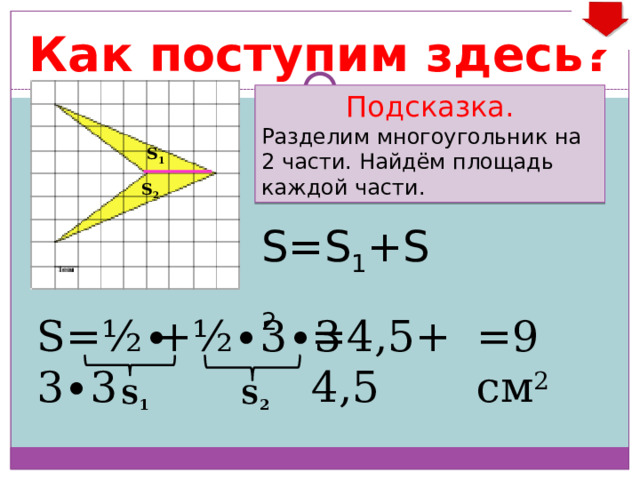
Как поступим здесь?
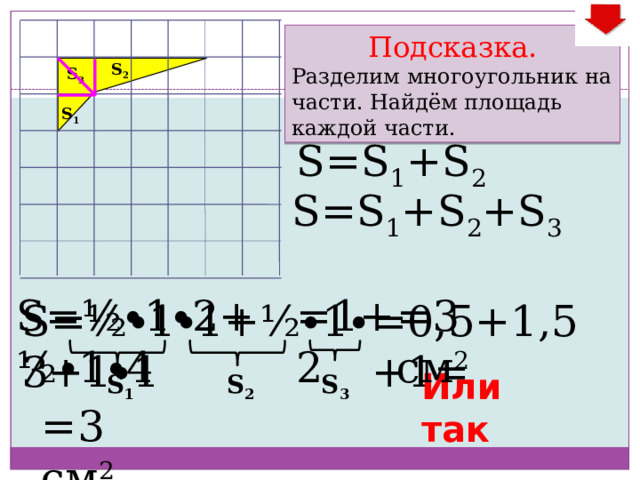
Подсказка.
Разделим многоугольник на 2 части. Найдём площадь каждой части.
S 1
S 2
S=S 1 +S 2
=4,5+4,5
S=½ ∙ 3 ∙ 3
=9 см 2
+½ ∙ 3 ∙ 3
S 1
S 2
Подсказка.
Разделим многоугольник на части. Найдём площадь каждой части.
S 2
S 3
S 1
S=S 1 +S 2
S=S 1 +S 2 +S 3
S=½ ∙ 1 ∙ 2+½ ∙ 1 ∙ 4
=1+2
=3 см 2
=0,5+1,5+1=
S=½ ∙ 1 ∙ 1+½ ∙ 1 ∙ 3+1 ∙ 1
Или так
S 1
S 2
S 3
=3 см 2
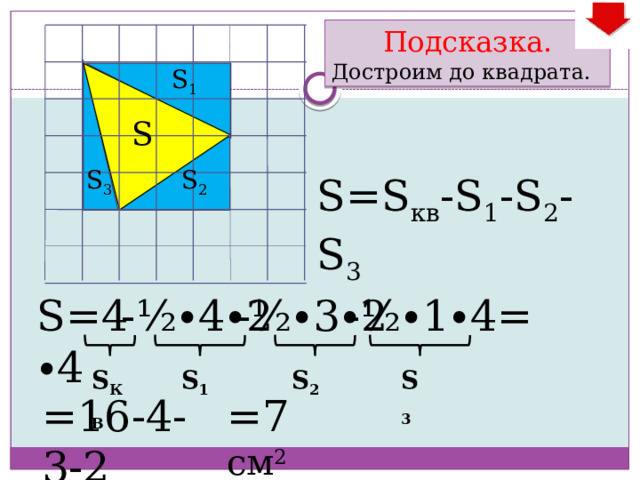
Подсказка.
Достроим до квадрата.
S 1
S
S 3
S 2
S=S кв -S 1 -S 2 -S 3
S= 4∙4
-½∙4∙2
-½∙3∙2
-½∙1∙4=
S КВ
S 1
S 3
S 2
=7 см 2
=16-4-3-2
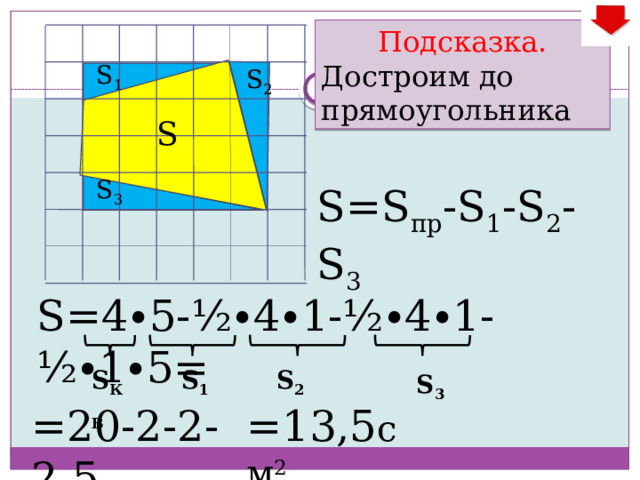
Подсказка.
Достроим до прямоугольника
S 1
S 2
S
S 3
S=S пр -S 1 -S 2 -S 3
S=4∙5-½∙4∙1-½∙4∙1- ½∙1∙5=
S КВ
S 2
S 1
S 3
=13,5 см 2
=20-2-2-2,5
А всегда ли Удобно
Таким способом находить площади фигур?
S 1
S 5
S 2
S 4
S
S=S кв -S 1 -S 2 -S 3 -S 4
S 3
S=5 ∙ 5-½ ∙ 3∙1-½ ∙ 5∙1- ½∙2∙5 — ½∙1∙2-1∙1=
S 2
S 5
S 1
S 4
S 3
S КВ
=13,5см 2
=25-1,5-2,5-5-1-1
Формула Пика
Позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.
Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить до прямоугольника, квадрата …
Формула Пика
Определение: Точка координатной плоскости называется целочисленной, если обе её координаты целые числа.
Площадь многоугольника с целочисленными вершинами равна
где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Г
– 1
B
+
2
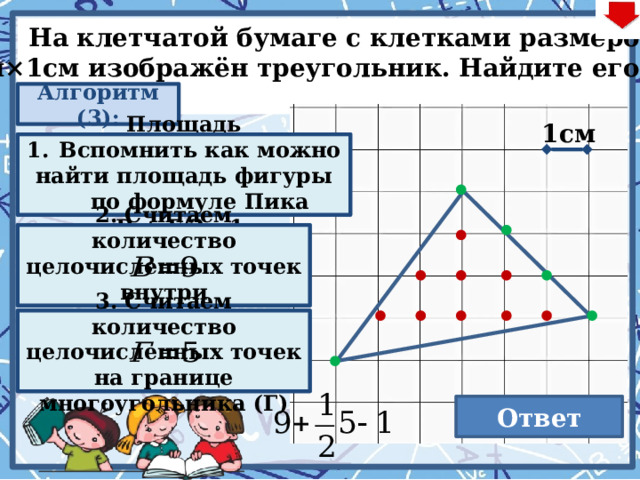
На клетчатой бумаге с клетками размером
1см×1см изображён треугольник. Найдите его S.
Алгоритм (3):
1cм
Площадь многоугоугольника с целочисленными вершинами равна сумме В + Г/2 – 1
- Вспомнить как можно
найти площадь фигуры по формуле Пика
2. Считаем количество целочисленных точек внутри многоугольника (В)
.
Последовательность действий на слайде:
- Нажимаем кнопку «Алгоритм»
- Нажимаем на появившийся прямоугольник (анимированная сорбонка) – 3 раза (можно два – в зависимости от целей демонстрации)
- Нажимаем кнопку «Алгоритм»
- Нажимаем на второй появившийся прямоугольник (анимированныя сорбонка) – количество определяете в зависимости от целей демонстрации
- Нажимаем кнопку «Алгоритм»
- Нажимаем на третий появившийся прямоугольник (анимированныя сорбонка) – для визуализации решений
- Нажимаем кнопку «Ответ». При этом не забываем выполнить условие задачи.
3. Считаем количество целочисленных точек на границе многоугольника (Г)
Ответ
10,5
55
Площадь многоугольника с целочисленными вершинами равна
В + Г /2 − 1
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника.
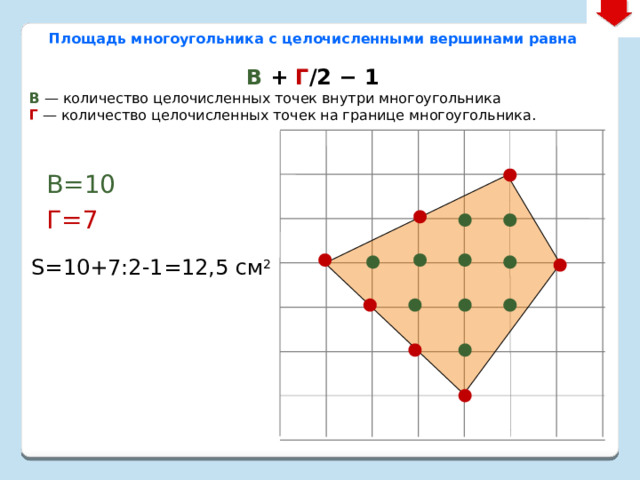
В=10
Г=7
S=10+7:2-1=12,5 см 2
Площадь многоугольника с целочисленными вершинами равна
В + Г /2 − 1
В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника.
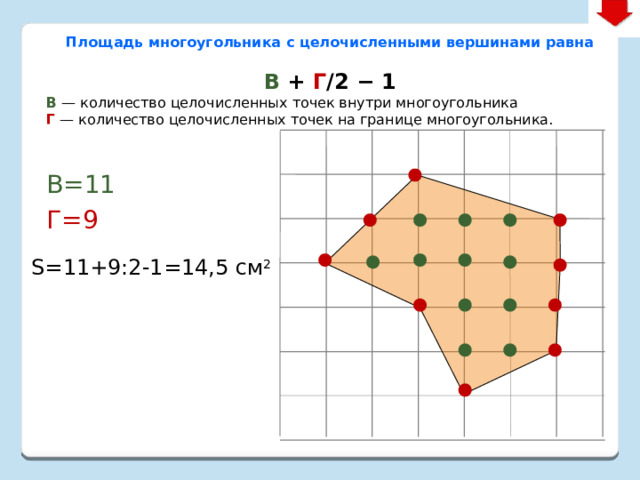
В=11
Г=9
S=11+9:2-1=14,5 см 2
На клетчатой бумаге нарисовано два круга.
Площадь внутреннего круга равна 27. Найдите S
закрашенной фигуры. (π =3)
Алгоритм (3):
S = S б – S м
- Вспомнить как можно
найти площадь S закрашенной фигуры.
4
2. Определим по рис. центр бóльшего круга и найдём его площадь .
Действия на слайде – по аналогии с предыдущими…
3. Выполнить вычисления и записать ответ .
21
Ответ
55
Определение градусной меры вписанного угла
Что нужно вспомнить:
- Вписанный угол – угол, вершина которого лежит на окружности, а стороны её пересекают.
- Центральный угол – угол, вершина которого совпадает с центром окружности, а стороны её пересекают.
Вписанный угол равен половине дуги, на которую опирается.
Определение градусной меры вписанного угла
Задача 1:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Проведём вспомогательное
построение. Заметим, что
дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.
Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC : 90°/2 = 45°.
Ответ: 45.
Определение градусной меры вписанного угла
Задача 2:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Угол ABC — опирается на большую дугу АC.
Проведём вспомогательное построение. Заметим, что дуга А C составляет всей окружности, следовательно, она равна
Угол AВC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине большой дуги АC : 270°/2 = 135°.
Ответ: 135.
Определение градусной меры вписанного угла
Задача 3:
Найдите угол ABC . Ответ дайте
в градусах.
Решение:
Проведём вспомогательное построение. Угол АОС – центральный и равен .
Угол АВС опирается на ту же дугу, что и угол АОС, но является вписанным, поутому равен половине угла АОС , т.е. .
Ответ: 22,5.
Всё возможно! Только смело На ОГЭ иди! Вперед ! Будь спокоен и без нервов! Голова не подведет!!!
Если учил уроки и…
ответственно готовился к экзамену!
Удачи!
Как найти расстояние по диагонали по клеткам
Найдите расстояние между противоположными углами гаража (длину диагонали) в метрах.
На плане изображено домохозяйство по адресу с. Иволгино, 5-й Заречный пер, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится сарай, а справа — гараж. Площадь, занятая гаражом, равна 48 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Перед гаражом имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и отмеченная на плане цифрой 6.
Тип 1 № 369666
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | гараж | теплица | жилой дом | сарай |
|---|---|---|---|---|
| Цифры |
При входе на участок слева от ворот находится сарай, а справа — гараж. Значит, сарай отмечен цифрой 3, а гараж — цифрой 2. Жилой дом находится в глубине территории, поэтому жилой дом отмечен цифрой 4. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Следовательно, теплица отмечена цифрой 1.
Задание №19 ОГЭ по математике
В 19 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания. Давайте на них посмотрим.
Разбор типовых вариантов задания №19 ОГЭ по математике
Первый вариант задания
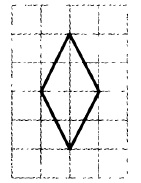
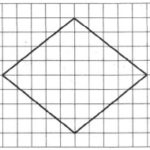
На клетчатой бумаге размером 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4.
Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
Второй вариант задания
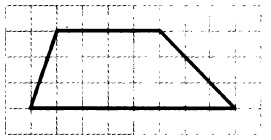
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии.
Решение:
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8 клеткам, а верхнее — 4 клеткам. Полусумма оснований:
Третий вариант задания
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Проведем необходимые отрезки:
Из рисунка можно вычислить длину — это 3.
Демонстрационный вариант ОГЭ 2019
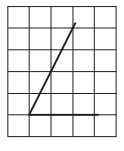
Найдите тангенс острого угла, изображённого на рисунке.
Решение:
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС:
Чтобы получить ответ на вопрос задачи, требуется найти tg∠C.
Согласно определению тангенса, из треугольника ∆АВС можем записать:
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
Четвертый вариант задания
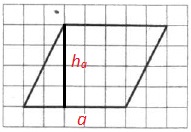
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма вычисляется так:
Теперь определим их длины по рисунку:
Вычисляем искомую площадь:
Пятый вариант задания
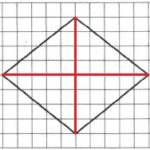
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба будем искать через его диагонали:
Линии диагоналей обозначим на рисунке красным:
Обозначим меньшую диагональ через d1, большую – через d2 (можно наоборот). Определим их длины из рисунка:
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Решение.
Найдём расстояние между противоположными углами участка по теореме Пифагора: