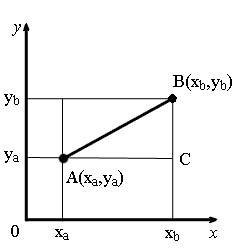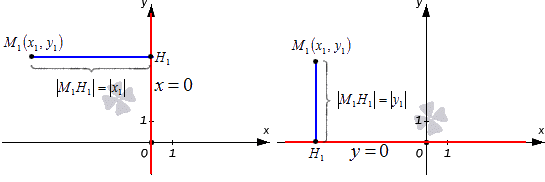|
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах квадратных. Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой. Весьма хитрая задача. На плане обозначен прямоугольный стол со сторонами 3 и 4 клеток, а длина измеряется не в квадратных метрах, а просто в метрах. Длина между углами данного стола представляет собой гипотенузу прямоугольного треугольника и равна корню квадратному из суммы квадратов катетов. Так гласит формула теоремы Пифагора. Подставляем значения: √ (3²+ 4²) = √ (9 + 16) = √ (25) = 5. Конечно любой знакомый с математикой не станет это вычислять. Ведь перед ним магический квадрат — 3, 4, 5. Теперь зная размер гипотенузы мы вычислим длину в метрах: 5 * 0.3 = 1.5 метра или 150 сантиметров или 15 дециметров. автор вопроса выбрал этот ответ лучшим Simple Ein более года назад Из условия задачи понятно, что обеденный стол обозначен цифрой 4. Обеденный стол со сторонами 3 и 4 клетки. Сторона каждой клетки равна 0,3 м. Получается, одна сторона стола равна 0,3*3=0,9 м. Вторая — 0,4*3=1,2 м. Определить расстояние между противоположными углами у стола можно по теореме Пифагора. Получается √ (0,9²+ 1,2²) = √ (2,25) =1,5 метра. Пашенька более года назад Пояснение к задаче нам подсказывает, что обеденный стол на схеме расположен в центре кухни, поэтому можем смело утверждать, что нас интересует объект под номером 4. Из условия задания нам известно, что клетка имеет размер — 0.3м. Для подсчета нам необходимо рассчитать размеры стола. В клеточках это 3х4, в метрах:
Далее учитываем, что стол — это прямоугольник, где расстояние между углами — это гипотенуза, а стороны стола — катеты. Следовательно, на основании теоремы Пифагора мы имеем возможность рассчитать длину-гипотенузу. Находим сумму квадратов катетов и извлекаем квадратный корень.
Ответ: 1.5. Stan1711 3 года назад Длина измеряется в метрах.Из плана видно что размеры ободеного стола равны 3 клетки на 4.Стол прямоугльный.Тогда размер диагонали от одного угла до другого будет ровна 5 клеткам (как соотношение в прямоугольном треугольнике — 3:4:5.)Учитывая размер клетки 0,3м. мы получим ответ на вопрос 5*0,3 =1,5м. Знаете ответ? |
Загрузить PDF
Загрузить PDF
Расстояние (обозначим как d) – это длина прямой между двумя точками. Расстояние можно найти между двумя неподвижными точками, а можно найти расстояние, пройденное движущимся телом. В большинстве случаев расстояние может быть вычислено по следующим формулам: d = s × t, где d — расстояние, s – скорость, t – время; d = √((x2 — x1)2 + (y2 — y1)2, где (x1, y1) и (x2, y2) – координаты двух точек.
-
1
Чтобы вычислить расстояние, пройденное движущимся телом, вам необходимо знать скорость тела и время в пути, чтобы подставить их в формулу d = s × t.
- Пример. Автомобиль едет со скоростью 120 км/ч в течение 30 минут. Необходимо вычислить пройденное расстояние.
-
2
Перемножьте скорость и время и вы найдете пройденное расстояние.
- Обратите внимание на единицы измерения величин. Если они различны, вам необходимо конвертировать одну из них так, чтобы она соответствовала другой единице. В нашем примере скорость измеряется в километрах в час, а время – в минутах. Поэтому необходимо конвертировать минуты в часы; для этого значение времени в минутах необходимо разделить на 60 и вы получите значение времени в часах: 30/60 = 0,5 часов.
- В нашем примере: 120 км/ч х 0,5 ч = 60 км. Обратите внимание, что единица измерения «час» сокращается и остается единица измерения «км» (то есть расстояние).
-
3
Описанную формулу можно использовать для вычисления входящих в нее величин. Для этого обособьте нужную величину на одной стороне формулы и подставьте в нее значения двух других величин. Например, для вычисления скорости используйте формулу s = d/t, а для вычисления времени – t = d/s.
- Пример. Автомобиль проехал 60 км за 50 минут. В этом случае его скорость равна s = d/t = 60/50 = 1,2 км/мин.
- Обратите внимание, что результат измеряется в км/мин. Чтобы конвертировать эту единицу измерения в км/ч, умножьте результат на 60 и получите 72 км/ч.
-
4
Данная формула вычисляет среднюю скорость, то есть предполагается, что в течение всего времени в пути тело имеет постоянную (неизменную) скорость. Это годится в случае абстрактных задач и моделирования движения тел. В реальной жизни скорость тела может меняться, то есть тело может ускоряться, замедляться, останавливаться или двигаться в обратном направлении.
- В предыдущем примере мы нашли, что автомобиль, проехавший 60 км за 50 минут, ехал со скоростью 72 км/ч. Это справедливо только при условии, что с течением времени скорость автомобиля не менялась. Например, если в течение 25 минут (0,42 часов) автомобиль ехал со скорость 80 км/ч, а в течение еще 25 минут (0,42 часов) – со скоростью 64 км/час, он тоже проедет 60 км за 50 минут (80 х 0,42 + 64 х 0,42 = 60).
- Для решения задач, включающих меняющуюся скорость тела, лучше использовать производные, а не формулу для вычисления скорости по расстоянию и времени.
Реклама
-
1
Найдите две точки пространственных координат. Если вам даны две неподвижные точки, то, чтобы вычислить расстояние между этими точками, необходимо знать их координаты; в одномерном пространстве (на числовой прямой) вам понадобятся координаты x1 и x2, в двумерном пространстве – координаты (x1,y1) и (x2,y2), в трехмерном пространстве – координаты (x1,y1,z1) и (x2,y2,z2).
-
2
Вычислите расстояние в одномерном пространстве (точки лежат на одной горизонтальной прямой) по формуле: d = |x2 — x1|, то есть вы вычитаете «х» координаты, а затем находите модуль полученного значения.
- Обратите внимание, что в формулу включены скобки модуля (абсолютного значения). Модуль числа – это неотрицательное значение этого числа (то есть модуль отрицательного числа равен этому числу со знаком плюс).
- Пример. Машина находится между двумя городами. До города, который находится перед ней, 5 км, а до города за ней – 1 км. Вычислите расстояние между городами. Если взять машину за точку отсчета (за 0), то координата первого города x1 = 5, а второго x2 = -1. Расстояние между городами:
- d = |x2 — x1|
- = |-1 — 5|
- = |-6| = 6 км.
-
3
Вычислите расстояние в двумерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2). То есть вы вычитаете «х» координаты, вычитаете «у» координаты, возводите полученные значения в квадрат, складываете квадраты, а затем из полученного значения извлекаете квадратный корень.
- Формула для вычисления расстояния в двумерном пространстве основана на теореме Пифагора, которая гласит, что гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов обоих катетов.
- Пример. Найдите расстояние между двумя точками с координатами (3, -10) и (11, 7) (центр окружности и точка на окружности, соответственно).
- d = √((x2 — x1)2 + (y2 — y1)2)
- d = √((11 — 3)2 + (7 — -10)2)
- d = √(64 + 289)
- d = √(353) = 18,79
-
4
Вычислите расстояние в трехмерном пространстве по формуле: d = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2). Эта формула является видоизмененной формулой для вычисления расстояния в двумерном пространстве с добавлением третьей координаты «z».
- Пример. Космонавт находится в открытом космосе недалеко от двух астероидов. Первый из них расположен в 8 километрах перед космонавтом, в 2 км справа от него и в 5 км ниже него; второй астероид находится в 3 км позади космонавта, в 3 км слева от него, и в 4 км выше него. Таким образом, координаты астероидов (8,2,-5) и (-3,-3,4). Расстояние между астероидами вычисляется следующим образом:
- d = √((-3 —
2 + (-3 — 2)2 + (4 — -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15,07 км
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 61 245 раз.
Была ли эта статья полезной?
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
Расстояние между точками A и В равно:
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
B этом случае рассояние между точками A и B равно:
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
Ответ: 11.
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
Тогда, учитывая (8), получим:
Откуда:
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
Ответ: 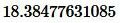
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
Но AM=A’B’. Тогда из (10) и (11) следует:
Откуда:
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
Ответ: 
Ответы 2
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Объяснение:
это длина гипотенузы соответствующего прямоугольного треугольника
(треугольник «египетский» — катеты 6 и 8; гипотенуза 10))
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
10 м
Объяснение:
кратчайшее расстояние по прямой от входа до ближайшей точки пруда (2) — по диагонали 8 клеток/плиток 1м по вертикали и 6 по горизонтали, значит L=√(8²+6²)= 10 м

Другие вопросы по Алгебре

Укажите верный промежуток-решение неравенства: |2x — 3| < 5…
Ответов: 2

Функция задана формулой y=3(x-1)+5(-0,2x-1) а. значение уесли х=-1. б. значение аргумента, при котором значениие, функции равно 2. в. значение аргумента, при котором значение функц…
Ответов: 4

Баночка йогурта стоит 4р. 2к. какое наибольшее количество таких баночек можно купить на 20 рублей?…
Ответов: 3

Y=sin(3x)cos(5x)+cos(3x)sin(5x) №42.5(а) 10-11 класс мордкович профильный уровень…
Ответов: 3

Решите уравнение f(x)=g(x) если f(x)=x^2 — 10 и g(x)=3x-5…
Ответов: 4

Как с чашечных весов и гири в 1 кг за 7 взвешиваний отмерить 100 кг сахара…
Ответов: 2
Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления расстояния между двумя точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb — xa)2 + (yb — ya)2
- Формула вычисления расстояния между двумя точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb — xa;
BC = yb — ya.
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
AB = √AC2 + BC2.
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Примеры задач на вычисление расстояния между двумя точками
Примеры вычисления расстояния между двумя точками на плоскости
Пример 1.
Найти расстояние между точками A(-1, 3) и B(6,2).
Решение.
AB = √(xb — xa)2 + (yb — ya)2 = √(6 — (-1))2 + (2 — 3)2 = √72 + 12 = √50 = 5√2
Ответ: AB = 5√2.
Пример 2.
Найти расстояние между точками A(0, 1) и B(2,-2).
Решение.
AB = √(xb — xa)2 + (yb — ya)2 = √(2 — 0)2 + (-2 — 1)2 = √22 + (-3)2 = √13
Ответ: AB = √13.
Примеры вычисления расстояния между двумя точками в пространстве
Пример 3.
Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).
Решение.
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 =
= √(6 — (-1))2 + (2 — 3)2 + (-2 — 3)2 = √72 + 12 + 52 = √75 = 5√3
Ответ: AB = 5√3.
Пример 4.
Найти расстояние между точками A(0, -3, 3) и B(3, 1, 3).
Решение.
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 =
= √(3 — 0)2 + (1 — (-3))2 + (3 — 3)2 = √32 + 42 + 02 = √25 = 5
Ответ: AB = 5.
Похожие вопросы:
Алгебра, 04.03.2019 09:10
Найдите угловой коэффициэнт прямой проходящей через точки а (2; 3) и в(-3; 7)
Ответов: 3
Алгебра, 07.03.2019 23:40
Впрогрессии дан первый член и знаменатель. запишите первые пять членов этой прогрессии, если: b1=3, q=2
Ответов: 4
Алгебра, 08.03.2019 01:50
Напишите уравнение прямой, проходящей через точку а(4: -2) и точку в(-1; 3)
Ответов: 3
Алгебра, 08.03.2019 21:50
Из формулы площади треугольника s=1/2 ah выразить сторону а
Ответов: 4
Алгебра, 08.03.2019 23:00
Вквадрате со стороной a см соединили последовательно середины сторон. оцените площадь образовавщегося четырёхугольника, если известно, что 1,2
Ответов: 4
Алгебра, 09.03.2019 21:30
Решить систему уравнений методом сложения 4x+2y=-22 3x-17=-5
Ответов: 4
Алгебра, 10.03.2019 07:30
4в степени х минус 2 в степени х минус 12 = 0
Ответов: 3
Алгебра, 10.03.2019 11:20
Разложите на множителе квадратный трехчлен -5х² — 14х +3
Ответов: 2
Алгебра, 10.03.2019 12:30
Мне сколько рулонов обоев потребуется для того чтобы оклеить стены квадратной комнаты, h=3м, s пола 9м квадратным,
Ответов: 4
Алгебра, 11.03.2019 19:10
Разложить на множители 5a-5b-c(a-b) a(в кубе)-а(в квадрате)-4а+4
Ответов: 1
Алгебра, 12.03.2019 00:20
При каких значениях c парабола y=x^2-8x+c расположена выше прямой y=8? прямой y=-26?
Ответов: 1
Алгебра, 12.03.2019 09:24
Оцените периметр и площадь прямоугольника со сторонами a см и b см, если известно ,что 2,62,7,1,2
Ответов: 1
Вопросы по другим предметам:
Другие предметы, 01.05.2021 08:51
Английский язык, 01.05.2021 08:56
Литература, 01.05.2021 08:56
Русский язык, 01.05.2021 08:56
История, 01.05.2021 09:04
Қазақ тiлi, 01.05.2021 09:04
Қазақ тiлi, 01.05.2021 09:04
Математика, 01.05.2021 09:05
Задание № 26380
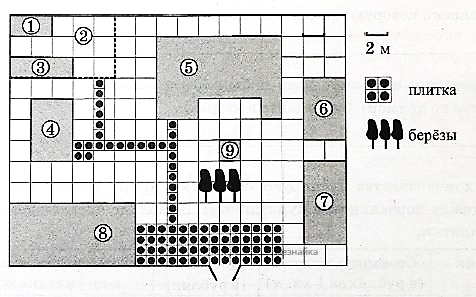
Найдите расстояние от жилого дома до огорода (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Показать ответ
Комментарий:
Жилой дом расположен под цифрой 5, а огород — 2. Между ними 2 клеточки, значит расстояние между ними — 2м•2=4 м.
Ответ: 4
Улучши свой результат с курсами ЕГЭ/ОГЭ/ВПР на egevpare.ru
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Предложи свой вариант решения в комментариях 👇🏻
На этой странице вы узнаете
- Как найти расстояние между мухой и столбом?
- Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
- Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?
Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее?
Расстояния между фигурами
Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое.
Таким образом, мы получаем расстояние между двумя точками.
Расстояние между точками — это длина отрезка, заключенного между ними.

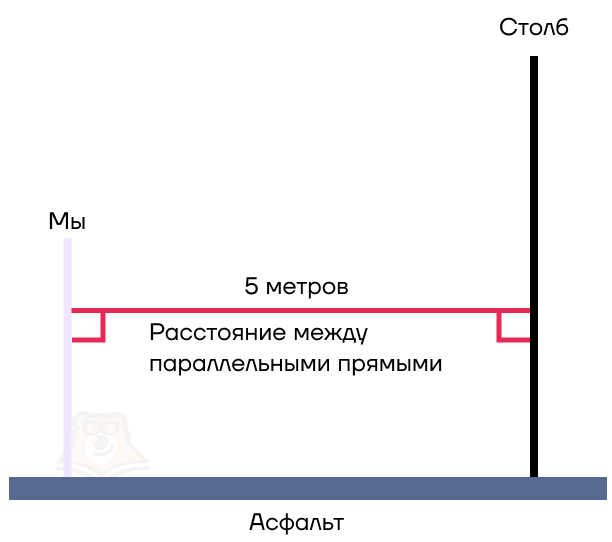
Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров.
Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми.
Следовательно, мы пришли к выводу, что:
Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.
Иными словами, это отрезок, который мы прошли по асфальту.
Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление.
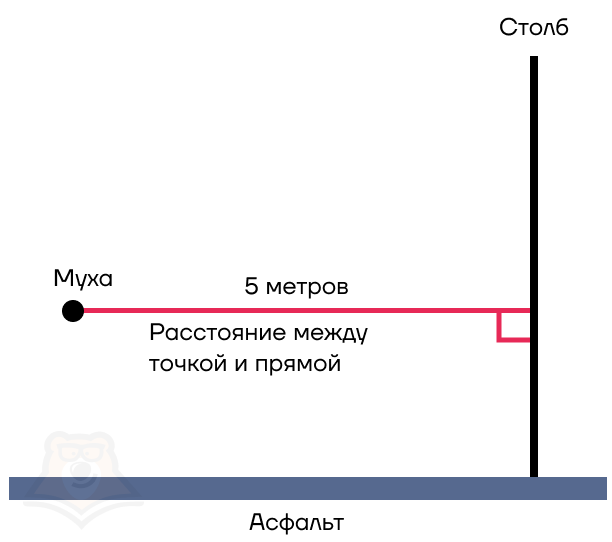
Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.
Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.
Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую.
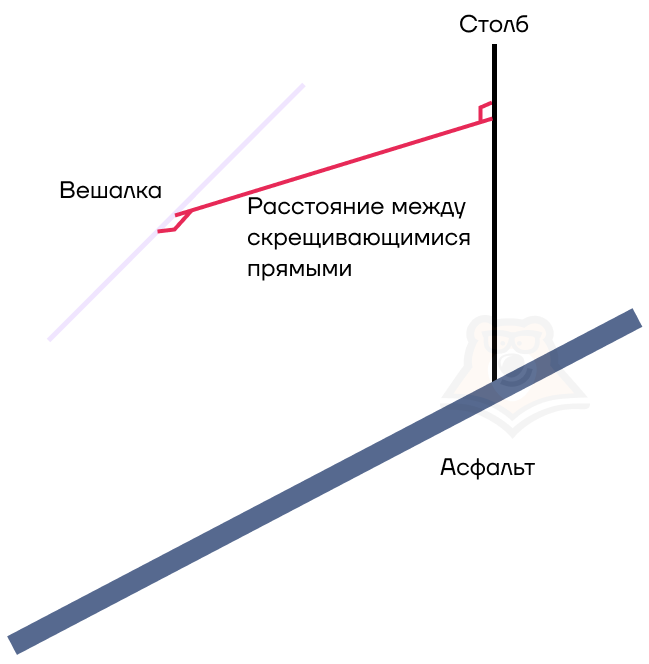
Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?
Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке.
Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии. Прямые и плоскости в пространстве».
Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай.
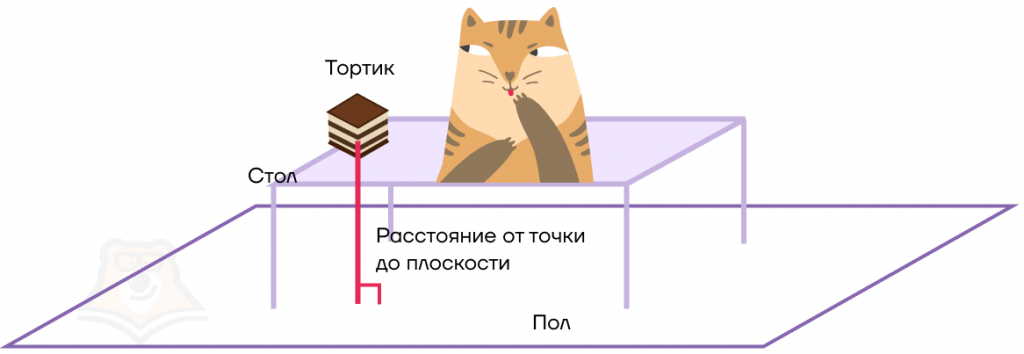
В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола.
Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола.
Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.
Расстояние от рулетика до пола можно было найти и другим способом, а именно найти расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу.
Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
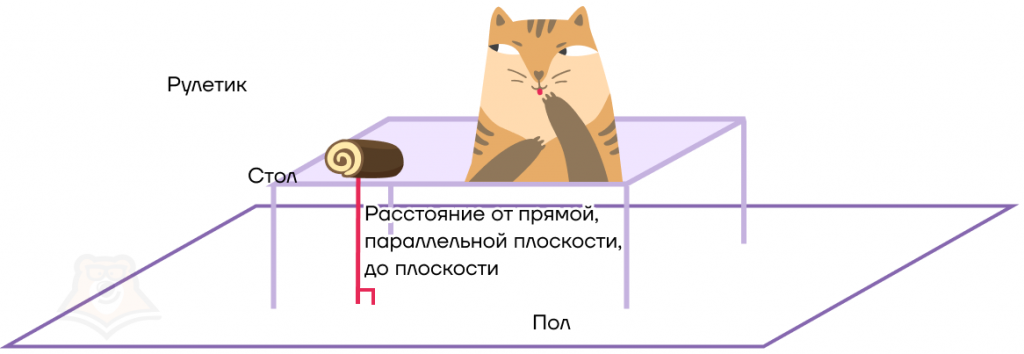
Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет.
Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола!
Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок.
Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике.
Теперь нам нужно найти расстояние между параллельными плоскостями.
Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
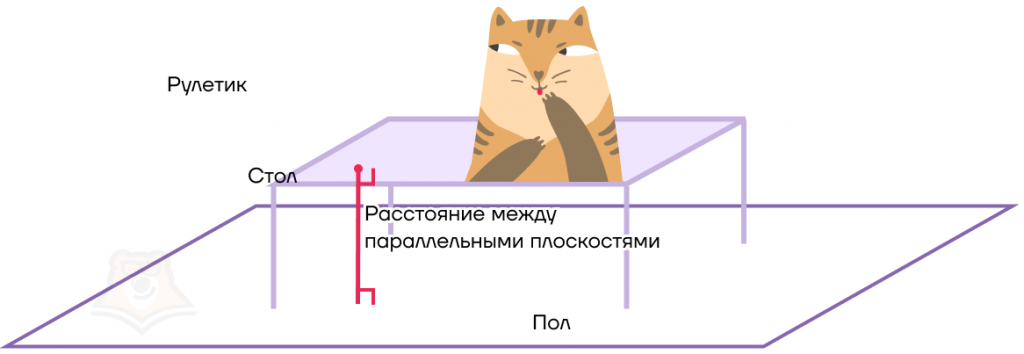
Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость.
Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами. Ничего сложного, верно?
При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.
Фактчек
- Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую.
- Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра.
- Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
Проверь себя
Задание 1.
Как найти расстояние между точкой и прямой?
- Найти длину любой линии от этой точки до прямой.
- Найти длину перпендикуляра, опущенного из этой точки на прямую.
- Невозможно найти расстояние между точкой и прямой.
- Ни один из вышеперечисленных вариантов.
Задание 2.
Как найти расстояние между скрещивающимися прямыми?
- Найти длину произвольной прямой между ними.
- Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
- Найти длину их общего перпендикуляра.
- Невозможно найти расстояние между скрещивающимися прямыми.
Задание 3.
Как найти расстояние от точки до плоскости?
- Найти длину перпендикуляра, опущенного из этой точки на плоскость.
- Найти длину произвольной линии, проведенной из точки к плоскости.
- Найти расстояние от точки до любой прямой, лежащей в плоскости.
- Невозможно найти расстояние между точкой и плоскостью.
Задание 4.
Как найти расстояние от прямой до плоскости?
- Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
- Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
- Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
- Невозможно найти расстояние между прямой и плоскостью.
Задание 5.
Как найти расстояние между параллельными плоскостями?
- Невозможно найти расстояние между параллельными плоскостями.
- Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
- Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
- Найти длину отрезка, соединяющего две произвольные прямые в плоскостях.
Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2
Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.
Расстояние от точки до прямой – определение
Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.
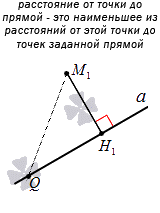
Пусть имеется прямая a и точка М1, не принадлежащая заданной прямой. Через нее проведем прямую b, расположенную перпендикулярно относительно прямой a. Точка пересечения прямых возьмем за Н1. Получим, что М1Н1 является перпендикуляром, который опустили из точки М1 к прямой a.
Расстоянием от точки М1 к прямой a называется расстояние между точками М1 и Н1.
Бывают записи определения с фигурированием длины перпендикуляра.
Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.
Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.
Если взять точку Q, лежащую на прямой a, не совпадающую с точкой М1, тогда получим, что отрезок М1Q называется наклонной, опущенной из М1 к прямой a. Необходимо обозначить, что перпендикуляр из точки М1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.
Чтобы доказать это, рассмотрим треугольник М1Q1Н1, где М1Q1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M1H1<M1Q. Рассмотрим рисунок, приведенный ниже.
Расстояние от точки до прямой на плоскости – теория, примеры, решения
Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.
Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М1 к прямой a. Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.
Если на плоскости имеется точка с координатами M1(x1, y1), расположенная в прямоугольной системе координат, прямая a, а необходимо найти расстояние M1H1, можно произвести вычисление двумя способами. Рассмотрим их.
Первый способ
Если имеются координаты точки H1, равные x2, y2, тогда расстояние от точки до прямой вычисляется по координатам из формулы M1H1=(x2-x1)2+(y2-y1)2.
Теперь перейдем к нахождению координат точки Н1.
Известно, что прямая линия в Оху соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М1 перпендикулярно заданной прямой a. Прямую обозначим буковой b. Н1 является точкой пересечения прямых a и b, значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Видно, что алгоритм нахождения расстояния от заданной точки M1(x1, y1) до прямой a проводится согласно пунктам:
- нахождение общего уравнения прямой a, имеющее вид A1x+B1y+C1=0 ,или уравнение с угловым коэффициентом, имеющее вид y=k1x+b1;
- получение общего уравнения прямой b, имеющее вид A2x+B2y+C2=0 или уравнение с угловым коэффициентом y=k2x+b2, если прямая b пересекает точку М1 и является перпендикулярной к заданной прямой a;
- определение координат x2, y2 точки Н1, являющейся точкой пересечения a и b, для этого производится решение системы линейных уравнений A1x+B1y+C1=0A2x+B2y+C2=0 или y=k1x+b1y=k2x+b2;
- вычисление искомого расстояния от точки до прямой, используя формулу M1H1=(x2-x1)2+(y2-y1)2.
Второй способ
Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.
Прямоугольная система координат имеет Оху имеет точку M1(x1, y1), из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α·x+cos β·y-p=0, равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x=x1, y=y1, значит, что M1H1=cos α·x1+cos β·y1-p.
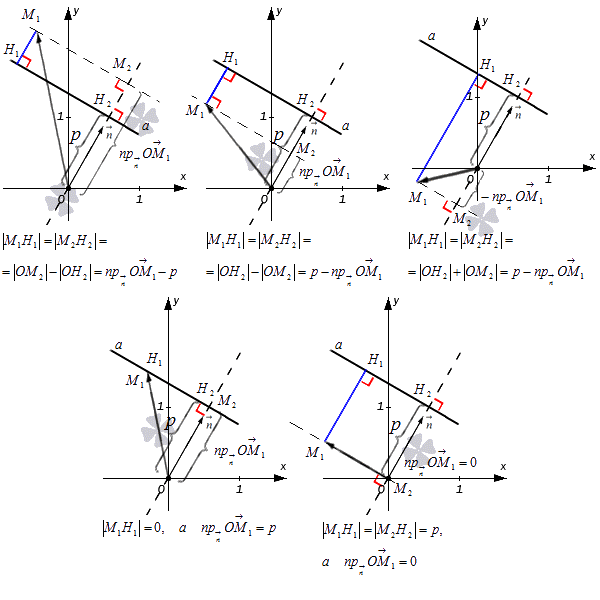
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α·x+cos β·y-p=0, тогда n→=(cos α, cos β) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M1(x1, y1), где радиус-вектор точки М1 — OM1→=(x1, y1). Необходимо провести прямую от точки до прямой, которое обозначим M1H1. Необходимо показать проекции М2 и Н2 точек М1 и Н2 на прямую, проходящую через точку O с направляющим вектором вида n→=(cos α, cos β), а числовую проекцию вектора обозначим как OM1→=(x1, y1) к направлению n→=(cos α, cos β) как npn→OM1→.
Вариации зависят от расположения самой точки М1. Рассмотрим на рисунке, приведенном ниже.
Результаты фиксируем при помощи формулы M1H1=npn→OM→1-p. После чего приводим равенство к такому виду M1H1=cos α·x1+cos β·y1-p для того, чтобы получить npn→OM→1=cos α·x1+cos β·y1.
Скалярное произведение векторов в результате дает преобразованную формулу вида n→, OM→1=n→·npn→OM1→=1·npn→OM1→=npn→OM1→, которая является произведением в координатной форме вида n→, OM1→=cos α·x1+cos β·y1. Значит, получаем, что npn→OM1→=cos α·x1+cos β·y1. Отсюда следует, что M1H1=npn→OM1→-p=cos α·x1+cos β·y1-p. Теорема доказана.
Получаем, что для нахождения расстояния от точки M1(x1, y1) к прямой a на плоскости необходимо выполнить несколько действий:
- получение нормального уравнения прямой a cos α·x+cos β·y-p=0, при условии, что его нет в задании;
- вычисление выраженияcos α·x1+cos β·y1-p, где полученное значение принимает M1H1.
Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.
Найти расстояние от точки с координатами M1(-1, 2) к прямой 4x-3y+35=0.
Решение
Применим первый способ для решения.
Для этого необходимо найти общее уравнение прямой b, которая проходит через заданную точку M1(-1, 2), перпендикулярно прямой 4x-3y+35=0. Из условия видно, что прямая b является перпендикулярной прямой a, тогда ее направляющий вектор имеет координаты, равные(4, -3). Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М1, принадлежит прямой b. Определим координаты направляющего вектора прямой b. Получим, что x-(-1)4=y-2-3⇔x+14=y-2-3. Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
x+14=y-2-3⇔-3·(x+1)=4·(y-2)⇔3x+4y-5=0
Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н1. Преобразования выглядят таким образом:
4x-3y+35=03x+4y-5=0⇔x=34y-3543x+4y-5=0⇔x=34y-3543·34y-354+4y-5=0⇔⇔x=34y-354y=5⇔x=34·5-354y=5⇔x=-5y=5
Из выше написанного имеем, что координаты точки Н1 равны (-5;5).
Необходимо вычислить расстояние от точки М1 к прямой a. Имеем, что координаты точек M1(-1, 2) и H1(-5, 5), тогда подставляем в формулу для нахождения расстояния и получаем, что
M1H1=(-5-(-1)2+(5-2)2=25=5
Второй способ решения.
Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4x-3y+35=0. Отсюда получим, что нормирующий множитель равен -142+(-3)2=-15, а нормальное уравнение будет вида -15·4x-3y+35=-15·0⇔-45x+35y-7=0.
По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x=-1, y=2. Тогда получаем, что
-45·-1+35·2-7=-5
Отсюда получаем, что расстояние от точки M1(-1, 2) к заданной прямой 4x-3y+35=0 имеет значение -5=5.
Ответ: 5.
Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.
На плоскости имеется прямоугольная система координат Оху с точкой M1(8, 0) и прямой y=12x+1. Найти расстояние от заданной точки до прямой.
Решение
Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.
Если произведение угловых коэффициентов перпендикулярных прямых имеют значение -1, значит угловой коэффициент прямой перпендикулярной заданной y=12x+1 имеет значение 2. Теперь получим уравнение прямой, проходящее через точку с координатами M1(8, 0). Имеем, что y-0=-2·(x-8)⇔y=-2x+16.
Переходим к нахождению координат точки Н1, то есть точкам пересечения y=-2x+16 и y=12x+1. Составляем систему уравнений и получаем:
y=12x+1y=-2x+16⇔y=12x+112x+1=-2x+16⇔y=12x+1x=6⇔⇔y=12·6+1x=6=y=4x=6⇒H1(6, 4)
Отсюда следует, что расстояние от точки с координатами M1(8, 0) к прямой y=12x+1 равно расстоянию от точки начала и точки конца с координатами M1(8, 0) и H1(6, 4). Вычислим и получим, что M1H1=6-82+(4-0)220=25.
Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y=12x+1⇔12x-y+1=0, тогда значение нормирующего множителя будет -1122+(-1)2=-25. Отсюда следует, что нормальное уравнение прямой принимает вид -25·12x-y+1=-25·0⇔-15x+25y-25=0. Произведем вычисление от точки M18, 0 к прямой вида -15x+25y-25=0. Получаем:
M1H1=-15·8+25·0-25=-105=25
Ответ: 25.
Необходимо вычислить расстояние от точки с координатами M1(-2, 4) к прямым 2x-3=0 и y+1=0.
Решение
Получаем уравнение нормального вида прямой 2x-3=0:
2x-3=0⇔12·2x-3=12·0⇔x-32=0
После чего переходим к вычислению расстояния от точки M1-2, 4 к прямой x-32=0. Получаем:
M1H1=-2-32=312
Уравнение прямой y+1=0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид -y-1=0. Переходим к вычислению расстояния от точки M1(-2, 4) к прямой -y-1=0. Получим, что оно равняется -4-1=5.
Ответ: 312 и 5.
Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям Ох и Оу.
В прямоугольной системе координат у оси Оу имеется уравнение прямой, которое является неполным имеет вида х=0, а Ох — y=0. Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M1x1, y1 до прямых. Это производится, исходя из формул M1H1=x1 и M1H1=y1. Рассмотрим на рисунке, приведенном ниже.
Найти расстояние от точки M1(6, -7) до координатных прямых, расположенных в плоскости Оху.
Решение
Так как уравнение у=0 относится к прямой Ох, можно найти расстояние от M1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6=6.
Так как уравнение х=0 относится к прямой Оу, то можно найти расстояние от М1 к этой прямой по формуле. Тогда получим, что -7=7.
Ответ: расстояние от М1 к Ох имеет значение 6, а от М1 к Оу имеет значение 7.
Расстояние от точки до прямой в пространстве – теория, примеры, решения
Когда в трехмерном пространстве имеем точку с координатами M1(x1, y1, z1), необходимо найти расстояние от точки A до прямой a.
Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a, расположенной в пространстве. Первый случай рассматривает расстояние от точки М1 к прямой, где точка на прямой называется Н1 и является основанием перпендикуляра, проведенного из точки М1 на прямую a. Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.
Первый способ
Из определения имеем, что расстояние от точки М1, расположенной на прямой а, является длиной перпендикуляра М1Н1, тогда получим, что при найденных координатах точки Н1 , тогда найдем расстояние между M1(x1, y1, z1) и H1(x1, y1, z1), исходя из формулы M1H1=x2-x12+y2-y12+z2-z12.
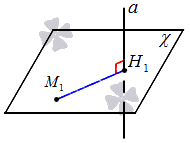
Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М1 на прямую a. Это производится следующим образом: Н1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.
Значит, алгоритм определения расстояния от точки M1(x1, y1, z1) к прямой a пространства подразумевает несколько пунктов:
- составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
- определение координат (x2, y2, z2), принадлежавших точке Н1, которая является точкой пересечения прямой a и плоскости χ;
- вычисление расстояния от точки до прямой при помощи формулы M1H1=x2-x12+y2-y12+z2-z12.
Второй способ
Из условия имеем прямую a, тогда можем определить направляющий вектор a→=ax, ay, az с координатами x3, y3, z3 и определенной точки М3,принадлежащей прямой a. При наличии координат точек M1(x1, y1) и M3x3, y3, z3 можно произвести вычисление M3M1→:
M3M1→=(x1-x3, y1-y3, z1-z3)
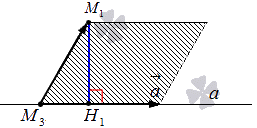
Следует отложить векторы a→=ax, ay, az и M3M1→=x1-x3, y1-y3, z1-z3 из точки М3, соединим и получим фигуру параллелограмма. М1Н1 является высотой параллелограмма.
Рассмотрим на рисунке, приведенном ниже.
Имеем, что высота М1Н1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M1H1.
Обозначим площадь параллелограмма за букву S, находится по формуле, используя вектор a→=(ax, ay, az) и M3M1→=x1-x3. y1-y3, z1-z3. Формула площади имеет вид S=a→×M3M1→. Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S=a→·M1H1 с a→=ax2+ay2+az2, являющимся длиной вектора a→=(ax, ay, az), являющейся равной стороне параллелограмма. Значит, M1H1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M1H1=a→×M3M1→a→.
Для нахождения расстояния от точки с координатами M1(x1, y1, z1) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:
- определение направляющего вектора прямой a — a→=(ax, ay, az);
- вычисление длины направляющего вектора a→=ax2+ay2+az2;
- получение координат x3, y3, z3, принадлежавших точке М3, находящейся на прямой а;
- вычисление координат вектора M3M1→;
- нахождение векторного произведения векторов a→(ax, ay, az) и M3M1→=x1-x3, y1-y3, z1-z3 в качестве a→×M3M1→=i→j→k→axayazx1-x3y1-y3z1-z3 для получения длины по формуле a→×M3M1→;
- вычисление расстояния от точки до прямой M1H1=a→×M3M1→a→.
Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Найти расстояние от точки с координатами M12, -4, -1 к прямой x+12=y-1=z+55.
Решение
Первый способ начинается с записи уравнения плоскости χ, проходящей через М1 и перпендикулярно заданной точке. Получаем выражение вида:
2·(x-2)-1·(y-(-4))+5·(z-(-1))=0⇔2x-y+5z-3=0
Нужно найти координаты точки H1, являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:
x+12=y-1=z+55⇔-1·(x+1)=2·y5·(x+1)=2·(z+5)5·y=-1·(z+5)⇔x+2y+1=05x-2z-5=05y+z+5=0⇔x+2y+1=05x-2z-5=0
Необходимо вычислить систему x+2y+1=05x-2z-5=02x-y+5z-3=0⇔x+2y=-15x-2z=52x-y+5z=3 по методу Крамера, тогда получаем, что:
∆=12050-22-15=-60∆x=-12050-23-15=-60⇔x=∆x∆=-60-60=1∆y=1-10552235=60⇒y=∆y∆=60-60=-1∆z=12-15052-13=0⇒z=∆z∆=0-60=0
Отсюда имеем, что H1(1, -1, 0).
Необходимо рассчитать расстояние между точками с координатами M1(2, -4, -1) и H1(1, -1, 0) по формуле:
M1H1=1-22+-1—42+0—12=11
Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a→=2, -1, 5 является направляющим вектором прямой x+12=y-1=z+55. Необходимо вычислить длину по формуле a→=22+(-1)2+52=30.
Понятно, что прямая x+12=y-1=z+55 пересекает точку M3(-1, 0, -5), отсюда имеем, что вектор с началом координат M3(-1, 0, -5) и его концом в точке M12, -4, -1 является M3M1→=3, -4, 4. Находим векторное произведение a→=(2, -1, 5) и M3M1→=(3, -4, 4).
Мы получаем выражение вида a→×M3M1→=i→j→k→2-153-44=-4·i→+15·j→-8·k→+20·i→-8·j→=16·i→+7·j→-5·k→
получаем, что длина векторного произведения равняется a→×M3M1→=162+72+-52=330.
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
M1H1=a→×M3M1→a→=33030=11
Ответ: 11.










 2 + (-3 — 2)2 + (4 — -5)2)
2 + (-3 — 2)2 + (4 — -5)2)