Как найти расстояние по теореме пифагора

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

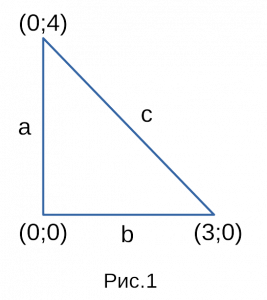
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
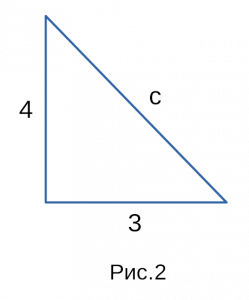
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. ​Взгляните на формулу,
которая получилась:

( с^2 = (y2-y1)^2 + (x2-x1)^2 )

Подставляем наши координаты:

( с^2 = (0-4)^2 + (3-0)^2 )

​( с^2 = -4^2 + 3^2 )​

( с^2 = 16 + 9 )

( с^2 = 25 )

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Была ли эта статья полезной?

Договорившись о системе координат, можно определить расстояние между двумя точками. В одномерном пространстве расстояние между двумя точками — это длина соединяющего их отрезка. Рассмотрим точки P и Q. Расстояние между ними, которое мы обозначим как d (Р, Q), будет вычисляться как абсолютная величина разности: d (Р, Q)=|P-Q|.

Мы помним, что абсолютная величина числа равна положительному значению этого числа. Например, |3|=3 и |-3|=3. Для того, чтобы расстояние было определено однозначно, необходимо, чтобы d (Р, Q)=d (Q,P), то есть величина расстояния между точками не должна зависеть от порядка перечисления этих точек.

Кроме того, расстояние всегда должно быть положительной величиной. Именно поэтому расстояние вычисляют с помощью модуля. Например, расстояние между точками 4 и 9 будет определяться не как: 4-9=-5, а по нашему определению: d (4,9)=|4-9|=|-5|=5.

Давайте посмотрим, как определяется расстояние между двумя точками в двумерном пространстве, то есть между точками на плоскости. Предположим, что у нас есть две точки P и Q, координаты которых заданы как (a, b) и (c, d).

Расположив обе точки на декартовой плоскости, мы можем построить прямоугольный треугольник РОQ. Длины катетов этого треугольника известны: РО=c-a и OQ=d-b.
Чтобы найти значение гипотенузы РQ, применим теорему Пифагора:
$(PQ)^2=(PO)^2+(OQ)^2=(c-a)^2+(d-b)^2$, откуда $d(PQ) =sqrt {(c-a)^2+(d-b)^2}$.
Таким образом, мы получили формулу для вычисления расстояния между двумя любыми точками на плоскости. Например, расстояние между точками Р (3, 5) и Q(-2,7) в соответствии с этой формулой вычисляется так:
$d(PQ) =sqrt {(-2-3)^2+(7-5)^2}=sqrt {(-5)^2+(2)^2}=sqrt {25+4}=sqrt {29}$.

Посмотрим, что произойдет в трехмерном пространстве. Предположим, что мы хотим вычислить расстояние между точками Р (a, b, c) и Q(d, e, f).

Здесь мы также будем опираться на теорему Пифагора, но применим ее в два последователь­ных этапа.

Расстояние, которое нам нужно найти, явля­ется диагональю в параллелепипеде (это фигура, похожая на обувную коробку). Два прямоуголь­ных треугольника, к которым мы будем приме­нять теорему Пифагора, закрашены на рисунке разными цветами. Фиолетовый треугольник рас­положен горизонтально, желтый — вертикально. В фиолетовом треугольнике значения катетов та­ковы: |d-a| и |e-b|. Поэтому длина гипотенузы вычисляется как $(d-a)^2+(e-b)^2$

Рассмотрим теперь желтый прямоугольный треугольник. Длину одного из двух его катетов мы только что рассчитали. Другой катет, вертикальный, имеет длину |f-c|. Вновь применим теорему Пифагора и получим искомое значение гипотенузы: $sqrt{[ sqrt{(d-a)^2+(e-b)^2}]^2+(f-c)^2}=sqrt{(d-a)^2+(e-b)^2+(f-c)^2}$.
Таким образом, мы получили формулу для вычисления расстояния между двумя любыми точками трехмерного пространства:
$d(PQ)=sqrt{(d-a)^2+(e-b)^2+(f-c)^2}$.
Например, расстояние между точками Р (2, -1,6) и Q(1, 5, 3) будет равно:
$d(PQ)=sqrt{(1-2)^2+(5-(-1))^2+(3-6)^2}=sqrt{(-1)^2+6^2+(-3)^2}=sqrt{1+36+9}=sqrt{46}$.
Этот способ определения расстояния между точками можно применять к пространствам любого измерения. Обычно для n-мерного пространства
расстояние между точками $Р (x_1, x_2,…, x_n)$ и $Q(y_1, y_2, …, y_n)$ задается формулой:
$d(PQ)=sqrt{(x_1-y_1)^2+…+(x_n-y_n)^2}$.
Заметим, что применяя теорему Пифагора для получения формул для вычисления расстояния между двумя точками в двух- и трехмерном про-странствах, мы получили обобщение данной теоремы для n-мерных пространств, где n>2.

Материалы по теме:

• Теорема Пифагора
• Теорема невесты!
• Многообразия и подмногообразия
• Координатная геометрия

22 января 2014

Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)

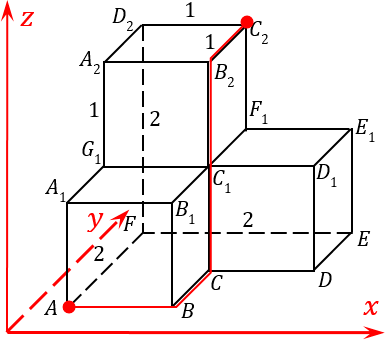
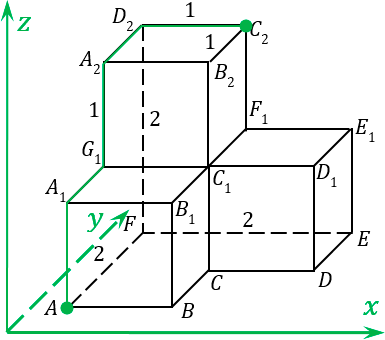
Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами
A
и C2 отличается от квадрата расстояния между вершинами
E
и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами
a
,
b
и гипотенузой
c
:

В этом случае квадрат гипотенузы равен сумме квадратов катетов:

c

² =
a

² +
b

²

Теорема Пифагора в пространстве

Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.

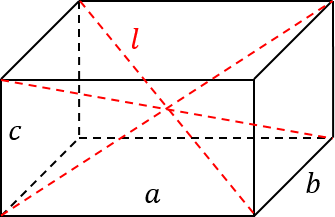
Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами
a
,
b
и
c
. Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.

Диагональ обозначим буквой
l
. В этом случае можно записать формулу:

l

² =
a

² +
b

² +
c

²

Как связана теорема Пифагора и расстояния между точками в пространстве

Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами
a
,
b
и
c
? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза
c
является диагональю на прямоугольнике.

Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:

Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками
a
и
b
. Разумеется, при условии, что точка
A
лежала бы в начале координат, а точка
B
имела координаты, равные длинам сторон нашего параллелепипеда:

A
= (0; 0; 0);

B
= (
a
,
b
,
c
).

Однако ничего удивительного в этом нет, потому что длина диагонали
l
— это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.

Метод обхода точек

Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки
A
до точки
C

₂. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.

Метод обхода точек заключается в следующем:

1. Построим систему координат с осями, параллельными ребрам нашего многогранника. Назовем эти оси x, y и z.
2. А теперь давайте поставим ручку в нашу точку A и попытаемся каким-то образом, двигаясь по ребрам, добраться до точки C
   ₂.

Нахождение диагонали методом обхода точек

Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке
B
, затем к точке
C
, затем вверх до точки
B

₂ и, наконец, двигаться вдаль — и мы попадем в точку
C

₂:

Давайте разметим, полученный нами путь:

1. Из точки A в точку B мы двигались вдоль оси x в положительном направлении. Запишем: 1x;
2. От точки B в точку C мы двигались вдоль оси игрек опять же по положительному направлению, то есть вглубь. Так и запишем 1y;
3. Затем мы шагнули на два шага вверх из точки C в точку B
   ₂. так и напишем: 2z;
4. Еще один шаг из точки B
   ₂ в точку C
   ₂ вдоль y, т. е. вглубь нашего рисунка. Запишем: 1y.

А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки
A
и
C

₂, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:

1. x: 1;
2. y: 1 + 1 = 2;
3. z: 2.

Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси
x
,
y
и
z
— это, по сути,
a
,
b
и
c
, т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:

Вот и все! Мы получили расстояние от точки
A
до
C

₂, согласно рисунку нашего многогранника.

Диагональ параллелепипеда не зависит от маршрута обхода

Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки
A
до точки
C

₂ можно идти и другим путем: сначала вверх до точки
A
₁, затем вглубь до точки
G

₁, затем вверх до точки
A

₂, затем снова в глубину до точки
D

₂, и, наконец вправо до точки
C

₂:

Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат
x
,
y
и
z
, и, соответственно, другое значение
l
? Давайте проверим.

Размечаем наш второй маршрут:

1. из точки A в точку A
   ₁ мы попадаем, смещением оси z на единичку: 1z;
2. из точки A
   ₁ в точку G
   ₁ мы попадаем, смещением по y на единичку: 1y;
3. из точки G
   ₁ в точку A
   ₂ — смещение по z: 1z;
4. из точки A
   ₂ в точку D
   ₂ — смещение по y: 1y;
5. от D
   ₂ до C
   ₂ — смещение вправо, т.е. в положительную сторону по x: 1x.

Выписываем полученные смещения:

1. x: 1
2. y: 1 + 1 = 2
3. z: 1 + 1 = 2

Итого выражение для диагонали
l
получилось в точности тем же самым:

Таким образом, мы убедились, что итоговое значение величины
l
, т. е. расстояние между точками
A
и
C

₂ не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.

Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.

Вычисление квадрата расстояния методом обхода точек

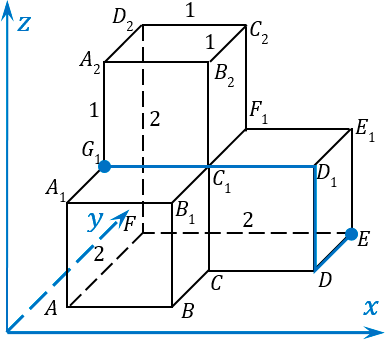
Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой
E
и точкой
G

₁. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки
E
, будем двигаться к точке
D
, потом из точки
D
в точку
D

₁, и потом от
D

₁ напрямую в точку
G

₁:

Размечаем нашу ломанную:

1. из точки E в точку D мы попадаем смещением по оси y на единицу в сторону, противоположную положительному направлению оси: -1y;
2. затем мы поднимаемся вверх на одну единицу по оси z, т. е. этот отрезок ломанной обозначаем как 1z;
3. потом мы смещаемся влево из точки D
   ₁ в точку G
   ₁ на две единицы вдоль оси x и получаем -2x.

Давайте запишем, что у нас получилось:

1. x: -2
2. y: -1
3. z: 1

По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки
E
и
G

₁. Давайте назовем этот отрезок
l

₂. Его длина равна:

Окончательное решение задачи B13

Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:

l

₂
² = 6

При произведении в квадрат корень исчезает.

Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.

Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:

∆ = 6 − 3 = 3

Вот мы и нашли ответ — он равен 3.

Ключевой прием — обход точек

Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.

При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.

Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.

Краткая сводка по задачам B13

Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:

1. Добавить к рисунку оси координат, параллельные ребрам многогранника;
2. Начертить «траекторию движения» от одной точки до другой, двигаясь исключительно по ребрам исходного многогранника;
3. Выяснить, вдоль какой оси происходит смещение на каждом отрезке полученной ломаной, и посчитать общее смещение;
4. Найти итоговое расстояние по обобщенной теореме Пифагора: l
   ² = a
   ² + b
   ² + c
   ², где a, b, c — суммарные смещения вдоль каждой из осей.

Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.

В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.

Смотрите также:

1. Обход точек в стереометрии — 2
2. Разбор задачи 8 из ЕГЭ на площадь полной поверхности призмы/параллелепипеда.
3. Решение ЕГЭ-2011: вариант 1, часть B
4. Метод коэффициентов, часть 1
5. Задача B5: площадь сектора
6. Решение задач на движение по воде

Что такое расстояние от точки до прямой

При этом перпендикуляр – это наименьшее из расстояний от этой точки до точек прямой.

Расстояние от точки до прямой на плоскости, методы нахождения

Найти расстояние от точки до прямой можно двумя способами. С помощью теоремы Пифагора или прямоугольной системы координат. Рассмотрим первый метод.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема Пифагора гласит, что прямоугольная система координат OXY имеет точку М₁ (x₁, y₁). Из нее к плоскости проведена прямая а. Уравнение плоскости имеет вид:

cos ax + cos by — p = 0.

Это уравнение равно по модулю значению, которое получается в левой части уравнения прямой при x = x₁, а y = y₁. Это значит, что:

M₁H₁ = cos ax₁ + cos by₁ — p

Доказательство

Прямой а соответствует уравнение плоскости, которое имеет вид:

cos ax + cos by — p = 0.

Тогда n → = (сos a, cos b) – это нормальный вектор прямой а с расстоянием от начала координат до прямой а с р единицами. При этом радиус вектор точки М₁ — ОМ₁ → = (х₁, у₁).

М₁Н₁ – прямая от точки до прямой. Проекции М₂ и Н₂ точек М₁ и Н₁ проходят через точку О с направляющим вектором n → = (cos a, cos b). Числовая проекция вектора ОМ₁ → = (х₁, у₁) направлена к n → = (cos a, cos b) как npn → OM₁ →. В итоге получаем М₁Н₁ = npn → ОМ → 1 — р.

Далее приводим равенство к виду М₁Н₁ = cos x₁ + cos b₁ — p. Из этого выходит npn → OM → 1 = cos ax₁ + cos by₁. Cкалярное произведение векторов дает формулу n → OM → 1 = n → npn → OM₁ → = 1npn → OM₁ → = npn → OM1 →.

Эта формула – произведение в координатной форме вида n →, OM₁ → = cos ax₁ + cos by₁. Из этого npn → OM₁ → = cos ax₁ +cos by₁. Отсюда следует, что M₁H₁ = npn → OM₁ → — p = cos ax1 + cos by1 — p.

Что и следовало доказать.

Согласно теореме Пифагора, чтобы найти расстояние от точки до прямой, нужно совершить следующие шаги:

1. Вывести уравнение прямой cos ax + cos by — p = 0, если его нет в задании.
2. Вычислить cos ax + cos by — p, где значение принимает М₁Н₁.

Рассмотрим второй метод. Если у точки Н₁ есть координаты (х₂, у₂), тогда расстояние от точки до прямой можно найти по формуле:

(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})

Найдем координаты точки Н1.

Прямая линия в ОХУ равна уравнению прямой на плоскости. Необходимо составить уравнение прямой b, проходящей через точку М₁ перпендикулярно прямой а. Н₁ – это точка пересечения прямых a и b. Для начала нужно найти общее уравнение прямой а, которое имеет вид А₁х + В₁у + С₁ = 0. Либо можно воспользоваться уравнением с угловым коэффициентом у = k₁x + b₁. 

Далее нужно вывести уравнение прямой b, которое имеет вид А₂х + В₂у + С₂ = 0. Либо можно использовать уравнение по аналогии с прямой а: у = k₂x + b₂. Чтобы определить координаты точки Р1, нужно решить систему линейных уравнений:

(left{begin{array}{lc}А1х;+;В1у;+;С1;=;0&\А2х;+;В2у;+;С2;=;0&end{array}right.) либо ( left{begin{array}{l}у;=;k1x;+;b1\у;=;k2x;+;b2end{array}right.)

Конечное расстояние получают с помощью формулы:

(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})

Формулы для нахождения расстояния

Длину перпендикуляра также можно найти с помощью следующей формулы:

(d;=;;frac{left|Atimes M_x+Btimes M_y+Cright|}{sqrt{A^2+B^2}})

Решение уравнений

Пример 1

Вычислить расстояние между прямой 3x + 4y — 6 = 0 и точкой M(-1, 3).

Решение

(d;=;;frac{left|3times(-1)+4times3-6right|}{sqrt{3^2+4^2}}=frac{left|-3+12-6right|}{sqrt{9+16}}=frac{left|3right|}{sqrt{25}}=frac{left|3right|}5=0,6)

Ответ: 0,6.

Пример 2

Найти расстояние между прямой 12x + 5y — 17 = 0 и точкой M(-3, 8).

Решение

(d;=;;frac{left|12times(-3)+5times8-17right|}{sqrt{12^2+5^2}}=frac{left|-36+40-17right|}{sqrt{144+25}}=frac{left|-13right|}{sqrt{169}}=frac{left|13right|}{13}=1)

Ответ: 1.

Пример 3

Вычислить расстояние между прямой 4x + 3y — 3 = 0 и точкой M(-2, 5).

Решение

(d;=;;frac{left|4times(-2)+3times5-3right|}{sqrt{4^2+3^2}}=frac{left|-8+15-3right|}{sqrt{16+9}}=frac{left|4right|}{sqrt{25}}=frac{left|4right|}5=0,8)

Ответ: 0,8.

Примеры задач для нахождения расстояния от точки до прямой

Задача 1

Дана треугольная пирамида АВСD. Ее грани ABС и ABD представляют собой равные равнобедренные треугольники с прямыми углами при вершине A.

Найти расстояние от точки A до грани ACD, если высота пирамиды равна h и равна CD.

Решение

Так как △BCD равнобедренный, то BC ⊥ CD, K – середина CD. Так же AK ⊥ CD. Получается, перпендикуляр BH на плоскость ACD упадет на прямую AK (удовлетворяет теореме о трех перпендикулярах: HK – проекция, BK – наклонная, обе перпендикулярны CD).

По теореме Пифагора (BK=frac{hsqrt3}2).

Тогда (tg ∠ AKB = frac{AB}{BK}=frac{2sqrt3}3=frac{BH}{HK}).

Значит, (BH = 2sqrt3x), (HK = 3x).

По теореме Пифагора из △ BHK находим (x = frac1{2sqrt7}h ⇒ BH = sqrt{frac37}h).

Ответ: (sqrt{frac37}h).

Задача 2

Дана правильная четырехугольная пирамида ABCDE с вершиной A. Через точку пересечения диагоналей основания провели плоскость α перпендикулярно ребру AB.

Найти расстояние от точки N до плоскости α, если N – середина (BE = 2sqrt2), а высота пирамиды равна 11.

Решение

По теореме о трех перпендикулярах AB ⊥ CE как наклонная (AO ⊥ (BCD), OB ⊥ CE – проекция). Получаем две пересекающиеся прямые OK и СЕ из плоскости α. Значит, сечением является треугольник СKЕ.

Проведем MN ∥ СЕ. Тогда MN ∥ α. Так как расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то:

ρ(N,α)=ρ(Q,α)

где ρ — расстояние.

Т.к. по условию SA⊥α, то проведем QH∥SA⇒QH⊥α. По построению MN – средняя линия △BAD, следовательно:

ВQ = QO ⇒ QH – средняя линия △ KВO ⇒ QH = frac12 ВK.

Рассмотрим △ АВO = 2. Из △ ВKO ∼ △ ВАO (⇒ frac{ВК}{ВО}=frac{ВО}{ВА} ⇒ ВK = frac{4sqrt5}{25} ⇒ QH = frac{2sqrt5}{25}).

Ответ: (frac{2sqrt5}{25}).

Задача 3

Дано: в цилиндре параллельно диаметру ВС = 10 в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках Р и Z, причем PZ = 6. Через отрезок PZ проведена плоскость α под углом 15 градусов к плоскости осевого сечения ВСDE.

Найти расстояние от центра нижнего основания до плоскости α.

Решение

Обозначим за OQ – ось цилиндра. Тогда OQ ⊥ BC ⇒ OQ ⊥ p (OQ ∩ p = L).

Проведем OR ⊥ PZ ⇒ по теореме о трех перпендикулярах RL ⊥ PZ ⇒ RL ⊥ p ⇒ ∠ RLO – угол между плоскостями BCDE и α.

Так как и OR⊥PZ и LR⊥PZ, то перпендикуляр из точки O на плоскость α упадет на прямую LR.

Рассмотрим △ OPR: OP = 5, PR = 3, ∠ ORP = 90° ⇒ OR = 4.

Рассмотрим △ LOR: (∠ HOR = ∠ RLO = 15° ⇒ OH = OR ⋅ cos⁡15° = 4 ⋅ cos⁡(45° − 30°) = sqrt6+sqrt2).

Ответ: (sqrt6+sqrt2).