to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Формула перемещения
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
v = v0 ± at
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает вид:
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
t1 = t – t2
Когда тело тормозит, через некоторое время t1 оно останавливается. Поэтому скорость в момент времени t1 равна 0:
0 = v01 – at1
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
t2 = t – t1
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
v = at2
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
s = |s1 – s2|
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
l = s1 + s2
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с2. Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
v02 = v01 + a1t1 = a1t1 (так как v01 = 0)
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с2. Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:
Задание EF18553

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18831
На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t1=20 с до t2=50 с.
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
Исходные данные:
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s = s1 + s2
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1 и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1 и s2, а затем сложим их:
s1 + s2 = 100 + 100 = 200 (м)
Ответ: 200
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 25.5k
Перейти к содержимому
Задача №34. Ускорение при торможении и длина пути торможения автомобиля
Определить ускорение автомобиля при торможении и длину пути торможения, если автомобиль за время торможения равное 5 секундам снизил скорость с 10 метров в секунду до 5 метров в секунду.
Дано: v0=10 м/с; v1=5 м/с; t=5 с
Найти: a — ?; L — ?
Решение:
Ускорение при торможении определяем по формуле

Путь при торможении определяем по формуле

Ответ: ускорение автомобиля при торможении составило -1 метр в секунду в квадрате, путь при торможении равен 37,5 метрам
МУНИЦИПАЛЬНОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ПЕНЗЯТСКАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА» ЛЯМБИРСКОГО
МУНИЦИПАЛЬНОГО РАЙОНА РЕСПУБЛИКИ МОРДОВИЯ
Исследовательский проект
Тормозной
путь
Выполнил:
ученик 9 класса
Муртазин
Тимур
Руководитель
: учитель физики
Заликова
Р.А.
Пензятка,2021
Содержание
I.
Введение…………………………………………………………………………………………….3
II.
Основная часть……………………………………………………………………………5
1.
Теоретическая часть
1.1 Что такое тормозной путь……………………………………………………………..
1.2 Зависимости тормозного пути………………………………….
1.3 Расчет
тормозного пути
2.
Исследовательская часть
2.1
Описание эксперимента
2.2
Результаты эксперимента
III. Заключение. Выводы
IV.Список
литературы
Исследовательский проект по физике
Тормозной путь.
I.Введение.
С каждым годом на дорогах нашей страны
увеличивается количество транспортных средств, что можно видеть, проведя анализ
статистических данных, взятых из официальных новостных интернет-источников:
А вместе с этим повысился и процент
травматизма людей на дорогах, а также общее количество
дорожно-транспортных происшествий.
Дороги всегда были объектом повышенной
опасности, и не зря из года в год разрабатываются и усовершенствуются правила
дорожной безопасности, как для водителей, так и для пешеходов.
Но почему нельзя переходить проезжую часть
дороги перед близко идущим транспортом, даже по пешеходному переходу? Какое
минимальное расстояние до движущегося транспортного средства считается
безопасным? Почему мы наблюдаем высокий процент травматизма на дорогах и
дорожно-транспортных происшествий?
Задавая себе эти вопросы, я пришел к
выводу, что ответы на эти вопросы, связанные с движением тел, могут дать законы
механики (раздел физики).
Актуальность моей работы заключается в том, что изучение данной темы поможет
раскрыть основную суть тормозного пути и даст возможность на практике
определить наличие (или отсутствие) зависимости тормозного пути от скорости
движущего транспорта и коэффициента сцепления.
Многие в будущем станут водителями или
пешеходами, которые обязаны знать, что тормозной путь зависит от
скорости движущегося транспорта и коэффициента сцепления шин с
дорогой.
Проблема:
Можно ли определить безопасное расстояние движения пешехода перед движущимся
дорожным транспортом. Важно ли учитывать тормозной путь, когда мы
пользуемся личным транспортом или переходим дорогу перед транспортом.
Цель проекта: научиться определять тормозной путь и его зависимость от
таких факторов, как скорость движущегося транспорта и коэффициент сцепления
шин с дорогой.
Задачи проекта:
1. Изучить специализированную литературу по
данному вопросу.
3. Дать ответ на вопросы:
— Что такое тормозной путь?
— В соответствии с законом физики, от каких
факторов и как зависит тормозной путь движущегося дорожного транспорта?
4. Провести теоретический расчет тормозного
пути автомашины.
5. Организовать эксперимент, подтверждающий
сделанные ранее выводы.
II. Основная часть.
1. Теоретическая часть.
1.1. Что такое тормозной путь
Тормозной путь — это
путь, пройденный автомобилем от начала торможения
до его полной остановки.
Началом тормозного пути называется момент
срабатывания тормозной системы автомобиля, а его концом – момент полной
остановки машины.
1.2. Зависимости тормозного пути
транспортного средства
Тормозной путь транспортного средства
зависит от многих факторов:
1- скорость движения
2- дорожное покрытие
3- погодные условия
4- состояние колес и тормозной системы
5- способ торможения
1.3. Расчет тормозного пути.
Тормозной путь автомобиля пропорционален
квадрату скорости. Это следует из самого обычного уравнения равноускоренного
(равнозамедленного) движения:
Допустим, что после того, как Вы нажали на
педаль тормоза, торможение автомобиля происходит равнозамедленно, с каким-то
постоянным, равным по величине замедлением (отрицательным ускорением) a.
Тогда тормозной путь автомобиля с начала момента торможения составит:
Учитывая, что конечная скорость автомобиля
равна 0:
Соответственно, получаем
Но необходимо помнить, что время торможения
будет всегда положительным числом, при замедлении движения
величина a всегда отрицательная:
И, соответственно::
То есть тормозной путь при всех прочих
одинаковых параметрах торможения машины действительно пропорционален квадрату
начальной скорости, то есть скорости, с которой автомобиль начал
торможение.
На практике принято использовать полученное
уравнение в виде:
полагая, что на самом деле в уравнении
используется не собственно ускорение a, а его модуль |a|.
Поэтому более правильной с точки зрения математики была бы запись:
В основе расчета тормозного пути лежит
второй закон Ньютона. Так как при торможении на автомобиль действует сила
трения скольжения, поэтому: µmg = ma, откуда а = µg. Путь до полной остановки
рассчитывается по формуле: S = v2/2a, поэтому основной тормозной путь автомобиля можно определить по формуле:
S
= v ²/2gµ,
где:
S — тормозной путь в
метрах;
v — скорость движения автомобиля в момент
начала торможения в м/сек;
g — ускорение силы
тяжести, равное 9,81 м/с2;
µ — коэффициент сцепления
шин с дорогой.
Приведенная формула годится лишь при
одновременном торможении всех колес до «юза».
Из формулы видно, что тормозной путь
зависит только от скорости и коэффициента сцепления шин с дорогой, при этом,
значение последнего может измениться в зависимости от вида и состояния дорожного
покрытия, типа шин автомобиля и давления воздуха в них.
Таким образом, согласно
классической теории трения, масса автомобиля никак не влияет на длину
тормозного пути. А длина тормозного пути определяется прежде всего,
скоростью движения, причем зависимость тут – квадратичная. И также определяется
коэффициентом (продольного) сцепления, как принято называть µ в
среде профессиональных автодорожников и автомобилистов.
Для иллюстрации полученного и осмысления
важности этого уравнения приведен график (см. ниже) зависимости тормозного
пути от коэффициента трения между покрышкой и асфальтом при разных начальных
скоростях без учета конструктивных особенностей покрышек и массы автомобиля
Из графика видно, что на скользких
поверхностях (лед, снег, мокрый грунт) качество резины не существенно и только
трением машину на льду не остановить. Нужно применять другие принципы —
протектор, цепляющийся за неровности покрытия, грунтозацепы, цепи или шипы,
вгрызающиеся в лед. Участок с коэффициентом трения до 0,8 примерно
характеризует поведение обычного автомобиля на асфальте. Для сравнения
приведены показатели болида формулы 1.»
Упрощённая таблица величин коэффициентов
сцепления приведена выше. Будущим автомобилистам никогда не стоит забывать, что
на мокрой дороге коэффициент сцепления уменьшается примерно вдвое, а на
обледенелой дороге падает до катастрофической величины 0,08…0,1.
Необходимо обратить внимание на
следующие моменты : что в условиях гололедицы, не столь уж редким явлением на
всей территории Российской Федерации, при коэффициенте сцепления 0,08 – 0,10,
даже при скорости 60 км/час тормозной путь составит 140 метров, а при скорости
80 км/час – почти 400.
Необходимо также учитывать, что в месте
контакта шины с дорогой происходит ее растяжение, деформация и сжатие, из-за
чего на некотором участке шина проскальзывает (возникает скольжение). Все это
зависит от нагрузки на шину и способность покрышки не подвергаться этим
влияниям характеризуется ее индексом нагрузки. Также очень существенно — на
коэффициент трения влияет температура. Вообще коэффициент не является
константой и находится в сложной зависимости от очень многих факторов и
условий.
Почему тормозной
путь автомобиля не зависит от его массы, хотя большинство водителей
считают, что зависит. Попытаемся пояснить справедливость этого
утверждения, прибегнув к физическим понятиям.
Подчеркнем, что речь идет о кратчайшем,
экстренном, то есть минимально возможном тормозном пути. То есть о тормозном
пути при торможении на грани блокировки колес. В современных машинах при
таком торможении срабатывает АБС (антиблокировочная система тормозов), а
классические машины либо срываются в «юз», либо остаются на грани «юза», в
зависимости от действий водителя.
Утяжеляя
машину, мы, с одной стороны, увеличиваем ее инертность и
осложняем торможение. С другой стороны, мы сильнее прижимаем шины к дороге,
увеличиваем сцепление шин с дорогой и повышаем тормозные возможности машины.
Эти два эффекта компенсируют друг друга в равной степени, и, в конечном итоге,
масса не влияет на длину тормозного пути
От чего же зависит тормозной путь?
1.4. Теоретический расчет
тормозного пути автомобиля
Коэффициенты сцепления шин взяты из ГОСТ
50597-93 (среднее значение).
Были получены следующие данные (см. таблицу
№ 1):
|
Скорость движения автомобиля, км/ч |
30 |
60 |
80 |
100 |
Коэффициент сцепления шин |
|
Тормозной путь по сухой дороге, м |
5 |
20 |
36 |
56 |
0,7 |
|
Тормозной путь по мокрой дороге, м |
8,8 |
35 |
63 |
98 |
0,4 |
|
Тормозной путь по зимней укатанной |
11,8 |
47 |
84 |
131 |
0,3 |
|
Тормозной путь по дороге, покрытой |
35 |
141,6 |
251,7 |
393,3 |
0,1 |
По данному расчету можно сделать вывод, что
чем больше скорость и хуже погодные условия, тем длиннее тормозной путь. При
движении автомобиля и по сухой летней, и по скользкой зимней дороге тормозной
путь и время торможения зависят от начальной скорости, причём тормозной путь
прямо пропорционален квадрату начальной скорости. При движении автомобиля со
скоростью 60 км/ч (средняя скорость по городу) тормозной путь составляет не
менее 20 метров по сухой дороге летом. Поэтому при переходе дороги пешеходу
просто необходимо внимательно смотреть по сторонам, и если машина едет на
высокой скорости, то начинать переходить дорогу по пешеходному переходу можно
только, если машина находится на расстоянии не ближе 30 метров в хорошую погоду
и не ближе 50-100 метров в плохую (дождливую, снежную).
2. Исследовательская часть
2.1. Описание эксперимента
Я провел теоретический расчет тормозного
пути для автомобиля и чтобы подтвердить соответствие данной закономерности на
практике, провел эксперимент по определению тормозного пути велосипеда с
помощью рулетки и секундомера.
Эксперимент был проведен в двух погодных
условиях — хорошая сухая и с ледяным покрытием дороги.
Этапы проведения эксперимента:
1. Был выбран и рассчитан удобный маршрут
движения велосипеда расстоянием 1 километр.
2. С помощью секундомера замерялось время
движения велосипеда по данному маршруту.
3. По формуле V = S/t, где V – скорость
движения, S – расстояние (равное 1
км), t – время в пути (замеренное с
помощью секундомера).
4. Набрав равномерную скорость (3 раза), в
момент достижения отметки в 1 километр я нажимал на тормоз и с помощью рулетки
измерял тормозной путь.
5. Данные действия были проведены в хорошую
сухую погоду и в гололед, то есть с ледяным покрытием дороги.
2.2. Результаты эксперимента
Результаты своего эксперимента я записал в
таблицу № 2.
Таблица № 2
|
Скорость движения велосипеда, км/ч |
8 |
12 |
15 |
|
Тормозной путь по сухой дороге, м |
0,30 |
0,55 |
0,88 |
|
Тормозной путь по ледяной дороге, м |
0,65 |
1,26 |
1,7 |
Анализируя данные можно сделать вывод, что
при увеличении скорости движения велосипеда и ухудшении погодных условий
сохраняется зависимость, установленная ранее по теории, а именно, тормозной
путь неизменно увеличивается.
III. Заключение. Выводы
Многих аварий можно было бы избежать, если
бы водители следовали золотому правилу — держи дистанцию. В работе мы выяснили,
какую дистанцию нужно соблюдать для собственной безопасности и как можно
определить нужную дистанцию, а также на практике подтвердили установленную
зависимость тормозного пути от таких факторов как скорость движения транспорта
и погодные условия. Я провел серию экспериментов, которые подтвердили все
утверждения, высказанные в ходе работы.
Поэтому, можно определенно сказать, что
движущийся автомобиль на большой скорости не сможет мгновенно остановиться, а
еще некоторое расстояние будет продолжать движение. Например, если мы
представим, что современный легковой автомобиль движется по дороге со скоростью
100 км/час, то за одну секунду он проезжает до 28 метров, и когда водитель
нажмет на тормоз, машина (как и любое транспортное средство) по инерции
еще будет продолжать движение определенное расстояние.
При этом, согласно закону физики,
рассмотренного в пункте 1.3. проекта, его величина находится в прямой
зависимости от скорости движения, коэффициента сцепления шин с дорожным
покрытием (который в свою очередь зависит от дорожных условий). Например, при
скорости 50 км/ч средний тормозной путь будет составлять около 15 м, а при
скорости 100 км/ч около 60 м, т.е. больше в четыре раза. Длина тормозного
пути часто оказывается решающим фактором в критической ситуации на дороге.
Лишний метр, прочерченный покрышками по
асфальту, может стоить не только разбитого бампера, но и человеческой жизни.
IV.
Список литературы.
- Элементарный учебник физики: Учебное
пособие. В 3-хт. /Под ред.Г.С.Ландсберга. Т.1 Механика. Молекулярная
физика.М.:Наука, 1985, 218 с. - Иванов А.С., Проказа А.Т. Мир механики и
техники: Кн. для учащихся. – М.: Просвещение, 1993. - Бытько Н.Д. Физика, ч.1 и 2. Механика.
Молекулярная физика и теплота.М.: Высшая школа, 1972, 336 с. - https://ria.ru/society/20160220/1377940767.html
- http://avtonov.info/teorija-dvizhenija-avtomobilja
При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a
Задача «Разгон»
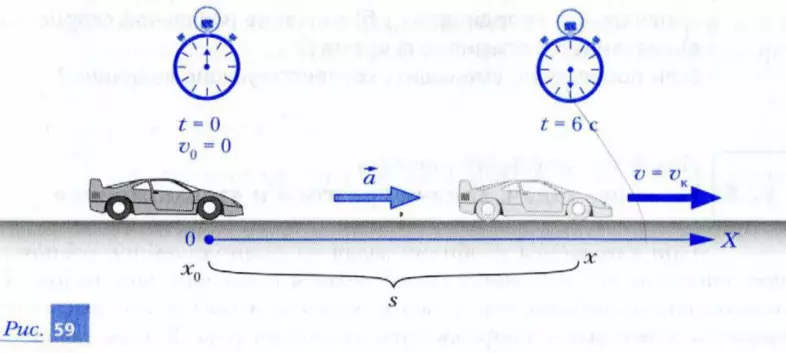
Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.
Решение.
Используем известную нам схему решения кинематических задач.
Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x0 = 0.
Шаг 3. По условию начальная скорость автомобиля v0 = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.
Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:
x = x0 + v0 · t + (a · t2) / 2 = 0 + 0 + (a · t2) / 2 = (a · t2) / 2.
Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:
v = v0 + a · t = 0 + a · t = a · t.
Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).
Шаг 5. Условие окончания разгона до скорости vк имеет вид:
v = vк.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = (a · t2) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = vк. (3) (условие окончания разгона)
Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:
vк = a · t,
a = vк/t; a = 30/6 = 5 (м/с2).
Подставив полученное значение a в уравнение (1), находим:
x = (a · t2) / 2 = (5 · 62) / 2 = 90 (м).
Ясно, что s = x — x0 = 90 — 0 = 90 (м).
Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.
Задача «Торможение»
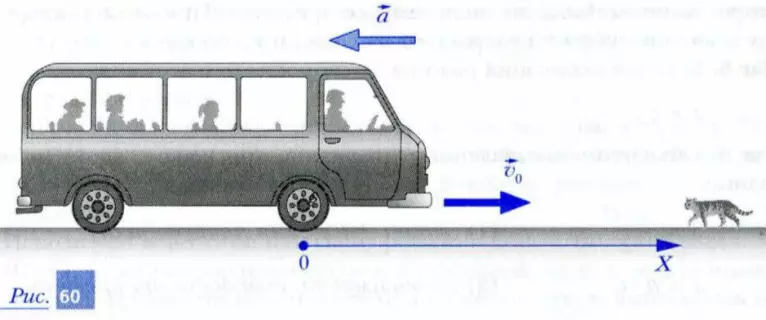
Автобус движется со скоростью, модуль которой равен 20 м/с (72 км/ч). Водитель автобуса замечает на дороге кошку и нажимает на педаль тормоза. Определите длину тормозного пути автобуса, если модуль ускорения при торможении |a| = 4 м/с2.
Решение.
Шаг 1. Систему отсчета выберем так, как показано на рис. 60.
Шаг 2. Начальная координата автобуса x0 = 0.
Шаг 3. Значение начальной скорости автобуса v0 = 20 м/с.
Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:
x = x0 + v0 · t + (a · t2) / 2 = 0 + 20 · t — (4 · t2) / 2.
Внимание! Значение скорости автобуса уменьшается. Значит, направление вектора ускорения автобуса противоположно положительному направлению оси X. Поэтому мы подставили в формулу отрицательное значение ускорения (a = -4 м/с2). При этом направление вектора начальной скорости совпадает с положительным направлением оси X. Поэтому значение скорости v0 положительно. Такие же знаки у величин v0 и a будут и в шаге 4*.
Шаг 4* (новый). Зависимость значения скорости от времени имеет вид:
v = v0 + a · t = 20 — 4 · t.
Видно, что при отрицательном значении ускорения a = -4 м/с2 скорость автобуса со временем уменьшается. При этом за каждую секунду значение скорости изменяется на величину -4 м/с, т. е. уменьшается на 4 м/с.
Шаг 5. Запишем условие окончания торможения: v = 0, так как в искомый момент времени t автобус должен остановиться.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = 0 + 20 · t — (4 · t2) / 2, (1) (закон движения автобуса)
v = v0 + a · t = 20 — 4 · t, (2) (зависимость скорости от времени)
v = 0. (3) (условие окончания торможения)
Шаг 7. Решение уравнений. Чтобы найти тормозной путь, необходимо подставить в уравнение (1) время торможения автобуса. Эта величина нам неизвестна, но ее можно найти из уравнений (2) и (3). Для этого необходимо подставить в зависимость скорости от времени значение скорости в момент окончания торможения v = 0, после чего решить полученное уравнение:
20 — 4 · t = 0, t = 5 c.
Таким образом, автобус остановится через время t = 5 с.
Подставим найденное время торможения t = 5 с в уравнение (1) и найдем тормозной путь:
x = 20 · 5 — (4 · 52) / 2 = 50 (м).
Таким образом, длина тормозного пути автобуса равна 50 м.
Итоги
Если положительное направление оси X выбрать совпадающим с направлением движения тела, то все задачи на равноускоренное движение можно свести к двум типам:
1) задача «разгон» (a > 0, скорость тела увеличивается с течением времени);
2) задача «торможение» (a
Если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы, в течение каждого из которых тело движется только в одном направлении. При этом задача разделяется на несколько задач.
Упражнения
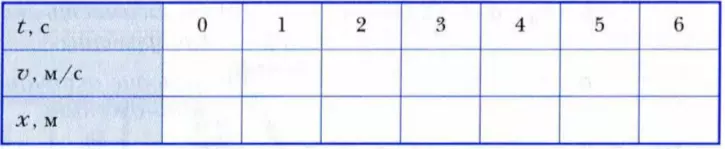
1. Заполните таблицу для разгоняющегося автомобиля, используя условия задачи 1 («разгон»). Как изменяются со временем: значение скорости; координата разгоняющегося автомобиля?
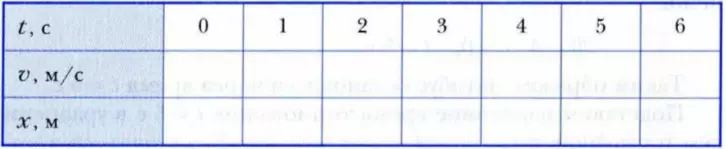
2. Заполните таблицу для тормозящего автобуса, используя условия задачи 2 («торможение»). Ответьте на вопросы: как изменяются со временем: значение скорости; координата тормозящего автобуса?
3. Найдите координату x автомобиля (см. рис. 57) в моменты времени 3, 5 и 8 с, если его начальная координата x0 = 30 м, значение начальной скорости v0 = 10 м/с, а значение ускорения a = 3 м/с2.
4. Решите задачу 2 («торможение») в общем виде. Представьте полученный ответ в виде
s = v02 / (2 · a).
Проведите анализ полученного ответа. Определите тормозной путь автобуса, если: а) v0 = 16 м/с; б) v0 = 115,2 км/ч.
5. Найдите путь, пройденный автомобилем, движение которого задано в упражнении 3, за промежуток времени от t1 = 2 с до t2 =5 с.
6. Два мотоциклиста, двигавшиеся прямолинейно, начинают одновременно тормозить перед светофором и так же одновременно останавливаются, проехав расстояние s = 100 м. Первый мотоциклист перед торможением двигался со скоростью, имеющей значение v1 = 72 км/ч, второй – со скоростью, имеющей значение v2 = 108 км/ч. Найдите значения ускорений мотоциклистов.