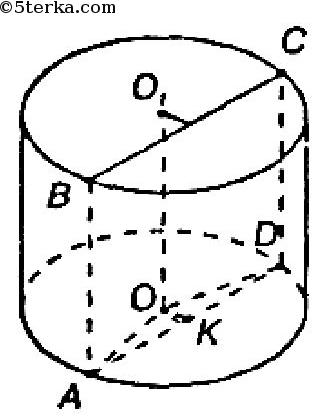
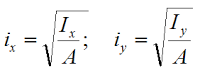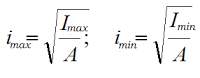Так как в сечении квадрат ABCD, то AB=AD=8 дм. В равнобедренном ΔAOD проведем OK⊥AD.
Тогда
Далее, по теореме Пифагора
Ответ: 3 дм.
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
В прошлой статье “цикла в цикле” мы разобрали площадь сечения, кратко коснулись её использования для определения напряжений и повторили как с помощью интегрирования определить площадь сложного сечения. В этой статье речь пойдет о статических моментах. И первое, что стоит о них сказать — это то, что, в отличие от площади и размеров сечения, статический момент достаточно абстрактная величина, то есть их нельзя измерить неким прибором, увидеть или ощутить тактильно. Единственный путь определения статического момента — бусидо расчет. Однако для того, чтобы получить ответ на вопрос “сломается ли деталь” при изгибах и кручении, эта величина очень удобна.
Сначала немного теории
Проясним физический смысл величины.
Статические моменты выражают действие момента собственного веса стержня относительно некоторых осей. Впрочем, тут стоит всё же разобраться более подробно:
Представим, что у нас есть стержень какого-то сложного сечения. Мы также произвольно построим систему координат (но желательно всё же, чтобы она проходила близко к сечению нашего стержня). А теперь важный момент: стержень жестко закреплен основанием на осях, которыми мы задались.
На такой стержень действует сила тяжести, вызывая момент. Что это такое мы уже выяснили в части, посвященной изгибу. Для тех, кто заметку про изгиб не читал: момент силы — это произведение силы на плечо (расстояние от точки приложения силы до рассматриваемой точки). Для всего стержня он будет:
g – ускорение свободного падения
ρ – плотность (объёмный вес) материала стержня
l – длина стержня
e – плечо момента. Если стержень “закреплен” на оси, то плечо будет равно расстоянию до этой оси (x или y). е — потому что эксцентриситет!
F – площадь поперечного сечения стержня.
При этом мы можем заметить следующее:
- Плотность материала для любого куска стержня пусть будет одинакова, как и его длина, а значит они вместе с ускорением свободного падения будут константами для моментов каждой точки поперечного сечения стержня и не повлияют на разницу в величине моментов разных точек. По сути, их можно вынести за скобки и рассматривать только произведение площади на расстояние до оси.
- Если расстояние до осей не очень велико по сравнению с размерами сечения, то каждая материальная точка будет иметь свой момент (потому что точки находятся на неодинаковом расстоянии до оси). Это значит, что для определения момента от собственного веса нужно разделить сечение на как можно большее количество элементарных площадок, умножить площадь каждой из них на расстояние до оси и, затем, просуммировать получившиеся произведения.
А сумма произведений предельно малых площадей сечения на расстояние до оси – это интеграл, следовательнодля определения моментов относительно системы координат xOy нам необходимо прежде всего вычислить такие два интеграла:
Каждый из этих интегралов как раз и представляет собой сумму произведений элементарных площадок dF на расстояние до соответствующей оси (x или y).
Элементарная площадка – это кусок сечения с очень малой площадью. Настолько малой, что она меньше всякой возможности её измерить и меньше всякого конечного значения вообще. Но нулю она не равна.
Эти интегралы называются соответственно – статические моменты сечения относительно осей x и y.
Статический момент может быть как положительным, так и отрицательным. Величина статического момента зависит от выбора системы координат. Имеет размерность см3.
Теперь попробуем параллельно перенести оси так, чтобы расстояния между ними были a и b. Теперь x1=x-a, y1=y-b. Изменятся ли статические моменты в таком случае? Если изменятся, то как? И что нам может дать такое изменение расположения осей? Давайте посмотрим:
Значит при переносе осей без их поворота статический момент изменяется на величину, равную произведению площади всего сечения на расстояние между осями.
Можно подобрать оси (а, следовательно и величины a и b) так, что b*F=Sx и a*F=Sy .
В таком случае статический момент сечения относительно осей будет равен нулю. Такие оси будут называться центральными, а начало отсчета такой системы координат – центром тяжести сечения.
Т.е. статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если оно закреплено (опирается) в точке центра тяжести. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение равно нулю.
Тут нам важно одно свойство центра тяжести – если сечение имеет ось симметрии, то центр тяжести всегда лежит на ней. Если осей симметрии целых две, (а они вообще-то должны пересекаться) то точка их пересечения – центр тяжести. Следовательно чтобы найти статический момент сложного сечения, состоящего из нескольких простых, симметричных – нужно найти его центр тяжести из выражений:
х1, y1 и x2, y2 – это координаты центров тяжести простых сечений, входящих в состав сложного.
После преобразования получим формулы для координат центра тяжести:
Далее, нужно непосредственно найти статический момент:
Где, x’ и y’ – оси, относительно которых нужно найти статический момент.
Находим статический момент
Пример:
Найти статический момент сечения неравнополочного уголка 14/9 толщиной 10 мм по ГОСТ 8510-86 без учета скруглений относительно осей, указанных на рисунке:
Определим площади и положение центров тяжести двух частей сечения – прямоугольников 130х10 и 90х10:
Координаты центра тяжести сечения определяем по формулам:
Если перенести ось Х на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 4.58 см.
Если перенести ось Y на внешнюю грань уголка, то положение центра тяжести:
По сортаменту положение центра тяжести с учетом закруглений – 2.12 см.
Найдем статические моменты сечения:
Подведём итоги
Статический момент — величина, характеризующая положение выбранных осей относительно центра тяжести сечения. Статический момент относительно центра тяжести равен нулю. Посчитать его мы можем как произведение площади сечения на расстояние от центра сечения до выбранной оси, но когда расстояние до оси сравнимо с размерами сечения нужно всё же взять интеграл.
Статический момент, кроме определения центра тяжести, используется для расчётов касательных напряжений, что на практике выливается также в расчеты на скалывание (конструкций из дерева).
На очереди моменты инерции.
Автор: Марк Ершов
Редактор, факт-чекер: Кирилл Овчинников
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 719
В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:
Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.
Радиусом инерции i называют расстояние от соответствующей оси до точки, концентрация всей площади сечения в которой, даст такой же момент инерции, как и для всей площади рассматриваемой фигуры.
Отсюда:
Здесь:
A — площадь поперечного сечения;
Ix, Iy — осевые моменты инерции.
При расчете относительно главных осей сечения получаем главные радиусы инерции:
где Imax и Imin — соответственно максимальный и минимальный осевые моменты инерции фигуры.
Размерность — метр (либо кратные — см, мм).
Для стандартных прокатных профилей (например: двутавр или швеллер) значения радиусов инерции указаны в соответствующем сортаменте.
Понятие радиуса инерции часто используется в сопромате при расчетах на устойчивость и внецентренное нагружение.
Моменты инерции плоских сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее