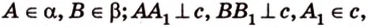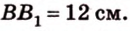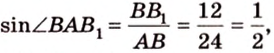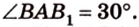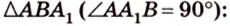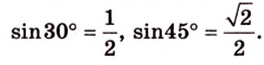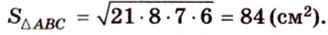Содержание:
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
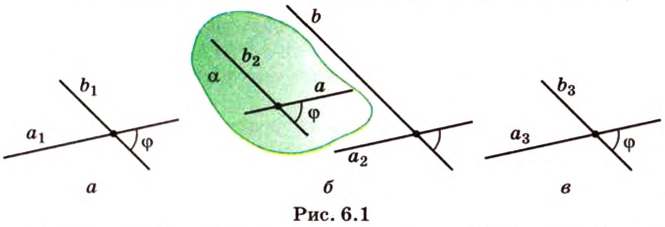
Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 
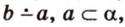
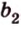
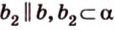
Итак,
Если 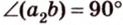
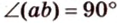
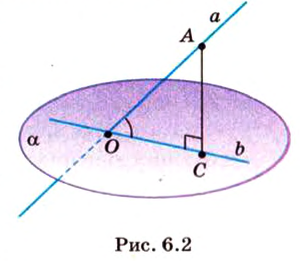
Угол между прямой и плоскостью в пространстве
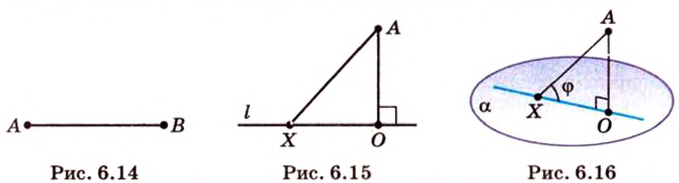
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 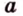
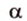
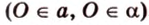
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 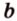
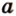
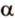
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 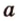
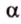
Угол между прямой 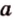
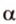
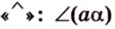
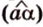
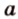
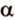
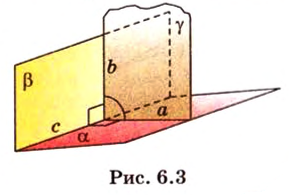
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например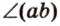
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
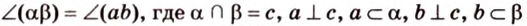
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
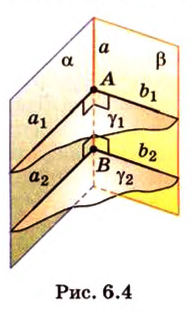
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 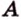
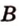
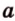
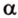
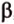
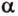
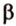
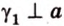
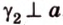
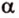
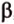
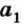
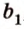
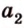
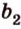
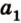
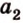
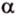
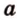
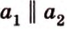
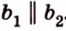
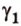
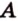
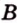
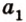
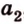
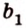
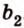
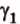
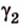
Пример №1
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 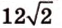
Дано: 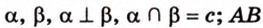

Найти: углы, образованные отрезком 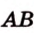
Решение:
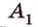
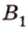
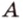
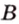
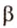
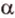
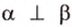
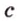
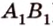
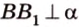
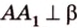
Итак, 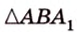
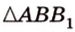
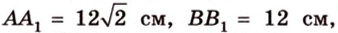
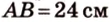
Из 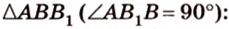
Из 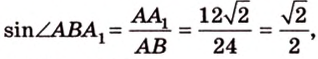
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 
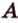
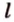
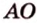
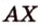
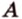
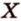
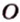
Рассмотрим плоскость 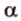
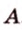
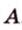
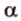
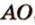
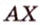
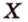
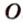
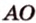
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 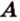
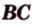
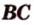
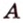
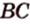
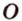
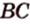
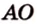
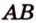

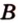
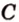
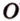
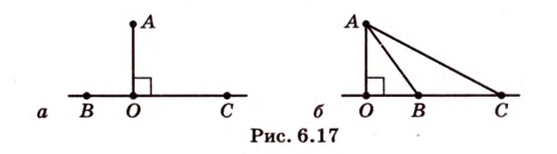
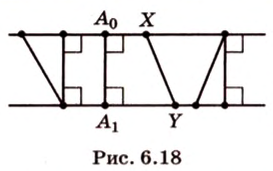
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 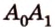
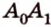
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 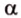
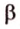
и второй, то перпендикуляр 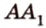
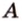
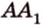
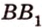
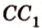
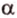
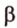
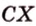
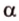
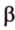
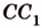
А это вытекает из того, что перпендикуляр 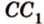
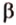
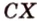
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
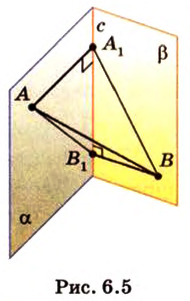
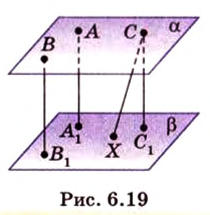
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
Действительно, пусть 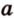
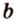
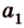
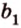
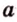
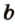
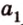
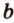
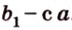
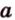
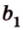
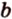
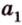
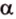
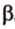
Плоскости 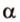
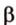
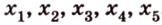
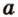
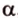
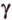
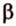
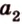
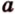
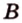
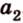
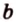
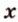
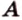
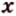
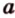
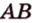
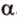
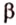
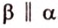
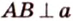
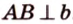
Отрезок 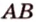
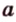
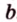
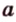
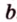
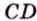
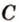
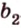
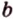

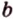
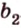
Поскольку она перпендикулярна прямым 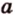
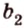

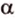




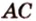
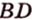
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
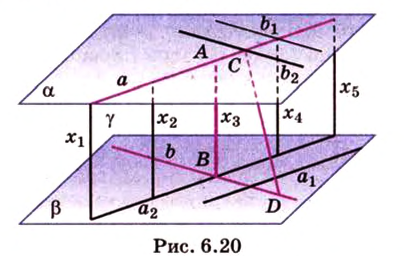
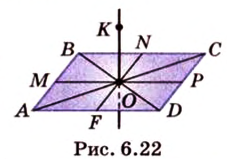
Пример №2
Отрезок 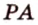
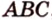
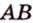
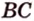
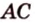
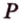
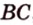
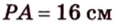
Решение:
Пусть 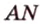
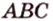
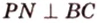
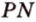
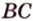
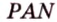
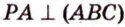
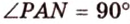
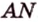
Из формулы для площади треугольника 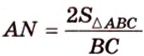
Необходимую площадь определим по формуле Герона:
Тогда 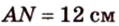
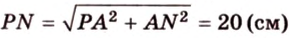
Ответ. 20 см.
Пример №3
Прямая 
Доказательство:
Пусть 
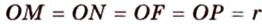
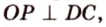
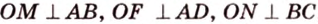
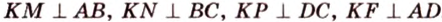
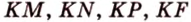
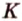
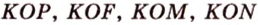
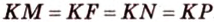
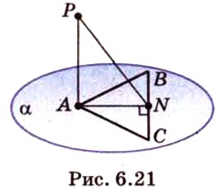
Пример №4
Точка 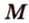
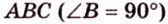
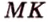
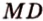
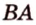
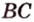
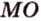
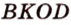
Доказательство:
Поскольку отрезки 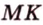
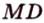
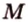
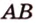
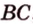
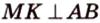
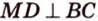
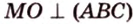
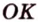
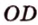
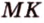
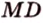
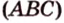
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
Как найти расстояние между двумя точками?
Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
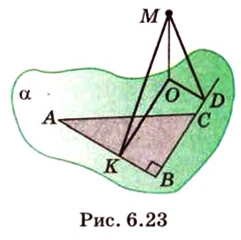
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.
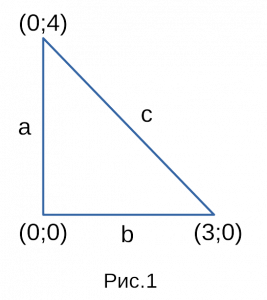
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
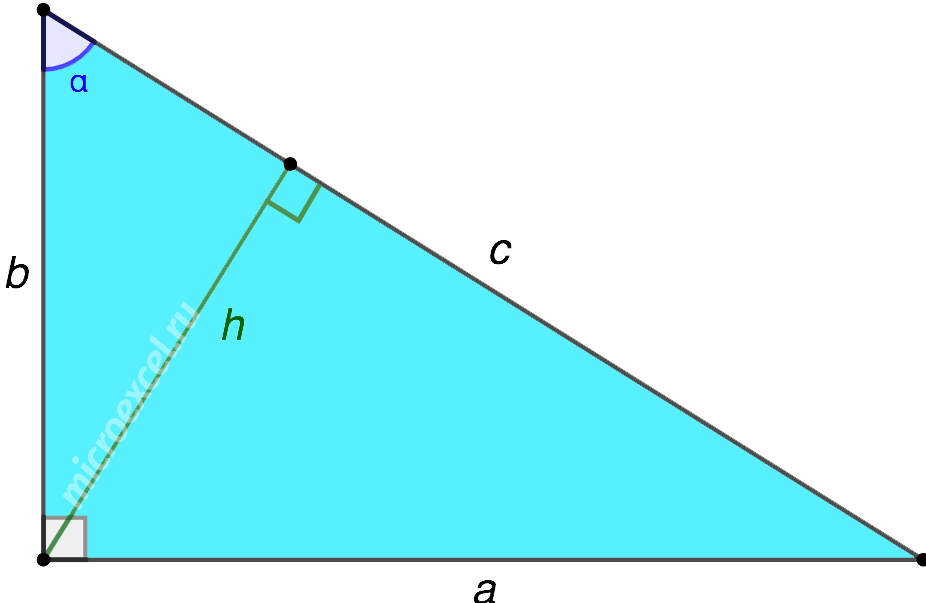
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.
Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
2. Через длины сторон треугольника:
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :
Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
http://poschitat.online/storony-pryamougolnogo-treugolnika
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
Страница 1 из 2
-
Форумчанин
- Регистрация:
- 28 ноя 2018
- Сообщения:
- 395
- Симпатии:
- 15
добрый день, подскажите как получить координаты пикета. Делал съемку и угол дома записал по углу, а расстояния нет. Можно как то вручную посчитать зная угол и координаты точки стояния?
Вложения:
-
image.jpg
- Размер файла:
- 898,6 КБ
- Просмотров:
- 41
#1
-
Форумчанин
Нет, нельзя.
Но если сняты другие углы дома, то можно искомый угол потом получить по построениям.
Надеюсь, при производстве съемки вы учитываете требования НТД и кроме собственно съемки делаете линейные обмеры снимаемых зданий-сооружений?#2
-
Форумчанин
#3
Мимокрокодил нравится это.
-
Форумчанин
- Регистрация:
- 28 ноя 2018
- Сообщения:
- 395
- Симпатии:
- 15
У меня сняты два угла на одной прямой ,третьего нет, что бы получить четвёртый
#4
-
Форумчанин
- Регистрация:
- 26 мар 2009
- Сообщения:
- 2.456
- Симпатии:
- 1.044
- Адрес:
-
Киев
Если известны координаты двух углов дома и измерен гор. угол на третий угол дома, то:
1. Вбиваешь в кредо для пикета V22 произвольное расстояние.
2. Сбрасываешь пикеты углов дома, пикет V22 и точку стояния в автокад.
3. Рисуешь линию между двумя известными углами дома
4. Рисуешь линию от точки стояния через пикет V22
4. Рисуешь с привязкой «перпендикуляр» линию к известному углу дома
5. Снимаешь в автокаде координаты пересечения линий или подрезаешь синию линию и снимаешь координаты конца линии.#5
Последнее редактирование: 17 май 2019
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
Если съёмка двух углов здания и направление на третий угол выполнялись с одной станции, то всё можно решить прямо в Кредо_ДАТ, не используя автокад, что будет гораздо проще.
#6
-
Форумчанин
Господа, хватит ТС-а халтуре учить.
При съемке застройки положено делать обмеры. Если бы это было сделано, никаких вопросов-проблем бы не возникло.
От ошибок при съемке никакая электроника полностью не застрахует.
А как вылезет пара судебных дел из-за неточностей топосъемки, тогда и наступит вразумление в головах вкупе с ветром в карманах.А что ему делать сейчас?
Ехать в поле с обмерами и досъемкой!
#7
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
Тем более надо определить третий угол, решением засечки.
Это будет контроль посадки здания на план. По двум привязанным углам, обмеры не гарантируют от разворота здания в случае каких-то ошибок измерений. Да и здания не всегда бывают прямоугольными.
А три снятых угла плюс обмеры — хорошая страховка.#8
-
Форумчанин
Согласен.
Андрей12344, вот так всегда и делайте. Это на будущее.Кстати, когда я сам работал в геослужбе городской, при съемках для землеустройства даже все заборы дополнительно обмеряли, не говоря уж о любых строениях, делали даже избыточные диагональные стяжки между углами контуров, плюс обязательно с высоткой, чтобы можно было учесть изменение площади на негоризонтальной поверхности. Когда соседи за 1м2 годами судятся, наши планы были реально истиной в последней инстанции, которую суды безоговорочно принимали. Частной застройки в городе до хренища, поэтому задача точности было на особом контроле.
Давным-давно уж ушел с этой отрасли, но остатки закалки остались.
Кстати, часть города у нас на новые планшеты еще ГУГК снимал в 70-80-е (ОКЭ-148 от 8 предприятия), качество отменное. И нам просто нельзя было что-то ухудшать.
#9
-
Форумчанин
- Регистрация:
- 28 ноя 2018
- Сообщения:
- 395
- Симпатии:
- 15
Третий угол дома взял по углу, этот момент упустил при съемки, обмеры в этом случаи не помогут, это уж точно. Ну остаётся только выезжать и доснимать. А способом вычислением в кредо дате модно попробовать «найти» этот угол )
#10
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
Если направление (без расстояния) на третий угол здания измерялось с той же станции, что на другие два угла здания, то задача с вычислением координат третьего угла решается прямо в Кредо_ДАТ путём добавления в программу ручных обмеров здания, либо условной станции с измерением прямого угла.
А если добавить и обмеры и условную станцию, то появляются избыточные данные, то есть контроль.#11
-
Форумчанин
Да ну!
См.Обленились, блин, землеустроители…#12
-
Форумчанин
- Регистрация:
- 26 мар 2009
- Сообщения:
- 2.456
- Симпатии:
- 1.044
- Адрес:
-
Киев
Как по мне, измерения с одной станции не обязательны. Нужно скопировать измерения на пикеты углов (1 и 2) в ПВО и добавить доп. станцию на пикете одного угла здания (2) с ориентировкой на пикет другого угла (1).
#13
Последнее редактирование модератором: 18 май 2019
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
-
Форумчанин
Прямая засечка с условных 1, 2, 3 на А, 3 дирекционных угла на нее известны.
Рассчитываем расстояния А-1, А-2, А-3.И делаем полярки уже с исходной А на1, 2, 3.
Избыток — измеренные линии 1-2 и 2-3, а также угол 1-2-3.#16
Последнее редактирование: 19 май 2019
-
Форумчанин
Прямая засечка с условных 1, 2, 3 на А, 3 дирекционных угла на нее получаем по приведенным измерениям.
Рассчитываем расстояния А-1, А-2, А-3.И делаем полярки уже с исходной А на 1, 2, 3.
Избыток — измеренные линии 1-2 и 2-3, а также угол 1-2-3.З.Ы. за другие способы думать лениво, спать давно пора.
#17
-
Форумчанин
- Регистрация:
- 26 мар 2009
- Сообщения:
- 2.456
- Симпатии:
- 1.044
- Адрес:
-
Киев
#18
Последнее редактирование: 20 май 2019
-
Форумчанин
- Регистрация:
- 28 фев 2010
- Сообщения:
- 4.525
- Симпатии:
- 5.000
Enot, ivsem, всё как бы так, но
Где вычисленные координаты?
Есть ещё, как минимум два способа в Кредо_ДАТ.
1. Придать условные координаты углам здания (для прямоугольного с известными сторонами это просто). По условным координатам решить обратную угловую засечку для точки А и вычислить координаты В в условной системе. Затем, по точкам А и В преобразовать всё из условной системы в нужную СК.
2. По измеренным углам на точке А рассчитать дирекционные направления на точки 1, 2, 3 и задать эти дирекционные условия в проекте ДАТ. Ещё по данным обмеров задать условную станцию 2 (угол здания) и измерения с неё на другие два угла здания. Остаётся лишь нажать Предобработку и Уравнивание.Как видите, даже при отсутствии прямых измерений расстояния до углов здания, есть много способов получения координат этих углов.
А вот можно ли определить координаты углов без линейных измерений, имея только два (три) исходных пункта, без взаимной видимости между ними, и измеренные направления?#19
-
Форумчанин
- Регистрация:
- 26 мар 2009
- Сообщения:
- 2.456
- Симпатии:
- 1.044
- Адрес:
-
Киев
Вот графические координаты.
#20
Страница 1 из 2
Поделиться этой страницей

Когда мы строим ломаную или кривую, иногда необходимо вместо привычных декартовых X,Y-координат задавать точку кривой через угол и расстояние. Ни в GDI, ни в GDI+, нет инструментов, чтобы задать координаты точки по углу от произвольной прямой и расстоянию.
Зато координаты можно очень легко посчитать. Вот этим сейчас и займемся. А потом найдем угол между двумя прямыми.
Найти координаты по углу и расстоянию
Если прямая, от которой необходимо отложить угол, параллельна оси X, формулы для нахождения координат достаточно очевидны.
Рис1. Прямая отстоит на угол от оси X
Где:
L — расстояние, или длина прямой (P1, P2)
А — угол, на который отстоит прямая (P1, P2) от прямой (P0, P1). Отрицательное значение угла означает — против часовой стрелки.
Теперь придадим прямой (P0, P1) наклон.
A (синий) — это угол, на который отстоит (P1, P2) от прямой (P0, P1);
В (красный) — угол на между прямой (P0, P1) и осью X;
C (оранжевый) — угол на между прямой (P1, P2) и осью X.
Задача сводится к нахождению угла C. Как нетрудно убедится по рисунку:
Угол А нам известен. Угол B найдем через arctan2. Функция arctan2 есть во множестве языков. Возможно, будет называться atan2.
Таким образом, функция для нахождения координат точки выглядит так:
|
// Посчитать координаты по углу и расстоянию // P0,P1 — прямая, точка считается от P1 // A — угол отклонения от (P0,P1), градусы // L — расстояние до точки function CalcPolarCoord(const P0, P1: TPointF; A, L: Single): TPointF; var B, C: Single; begin B := arctan2(p0.Y—p1.Y, p0.X—p1.x); C := A * PI/180 + B; Result.X := p1.X + cos(C) * L; Result.Y := p1.Y + sin(C) * L; end; |
И что, всегда работает? Всегда.
Найти угол по трем координатам
Рассмотрим процесс, обратный нахождению координаты по углу. Теперь будем находить угол между отрезками ломаной. Мы в плоскости работаем в декартовых координатах. Меняем мышкой координаты X, Y. А ситуация может возникнуть такая, что для предметной области важно хранить данные в полярных координатах.
Функция такая:
|
// Нахождение угла между тремя точками в градусах // Точки заданы массивом из трех элементов function CalcPolarAngle(const pnt: Array of TPointF): Single; var a1, a2: Single; begin if Length(pnt)<3 then Exit; a1 := ArcTan2(pnt[0].y—pnt[1].y, pnt[0].x—pnt[1].x) * 180/PI; a2 := ArcTan2(pnt[2].y—pnt[1].y, pnt[2].x—pnt[1].x) * 180/PI; Result := (a2 — a1); end; |
Более продвинутую функцию можно найти в статье Пересечение прямых, угол и координаты пересечения.

Друзья, спасибо за внимание!
Оставляйте комментарии. Подписывайтесь на телегу.
В группе комментариев уже потихоньку становится интересно )))
|
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах квадратных. Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой. Весьма хитрая задача. На плане обозначен прямоугольный стол со сторонами 3 и 4 клеток, а длина измеряется не в квадратных метрах, а просто в метрах. Длина между углами данного стола представляет собой гипотенузу прямоугольного треугольника и равна корню квадратному из суммы квадратов катетов. Так гласит формула теоремы Пифагора. Подставляем значения: √ (3²+ 4²) = √ (9 + 16) = √ (25) = 5. Конечно любой знакомый с математикой не станет это вычислять. Ведь перед ним магический квадрат — 3, 4, 5. Теперь зная размер гипотенузы мы вычислим длину в метрах: 5 * 0.3 = 1.5 метра или 150 сантиметров или 15 дециметров. автор вопроса выбрал этот ответ лучшим Simple Ein более года назад Из условия задачи понятно, что обеденный стол обозначен цифрой 4. Обеденный стол со сторонами 3 и 4 клетки. Сторона каждой клетки равна 0,3 м. Получается, одна сторона стола равна 0,3*3=0,9 м. Вторая — 0,4*3=1,2 м. Определить расстояние между противоположными углами у стола можно по теореме Пифагора. Получается √ (0,9²+ 1,2²) = √ (2,25) =1,5 метра. Пашенька более года назад Пояснение к задаче нам подсказывает, что обеденный стол на схеме расположен в центре кухни, поэтому можем смело утверждать, что нас интересует объект под номером 4. Из условия задания нам известно, что клетка имеет размер — 0.3м. Для подсчета нам необходимо рассчитать размеры стола. В клеточках это 3х4, в метрах:
Далее учитываем, что стол — это прямоугольник, где расстояние между углами — это гипотенуза, а стороны стола — катеты. Следовательно, на основании теоремы Пифагора мы имеем возможность рассчитать длину-гипотенузу. Находим сумму квадратов катетов и извлекаем квадратный корень.
Ответ: 1.5. Stan1711 3 года назад Длина измеряется в метрах.Из плана видно что размеры ободеного стола равны 3 клетки на 4.Стол прямоугльный.Тогда размер диагонали от одного угла до другого будет ровна 5 клеткам (как соотношение в прямоугольном треугольнике — 3:4:5.)Учитывая размер клетки 0,3м. мы получим ответ на вопрос 5*0,3 =1,5м. Знаете ответ? |

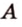 прямой
прямой 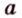
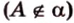 ;
;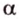
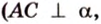
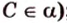 ;
;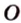 и
и  прямую
прямую 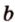 .
.