Как найти расстояние точки от координатной плоскости

Расстояние от точки до плоскости. Метод координат. Задание 14

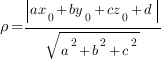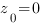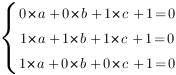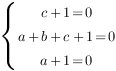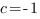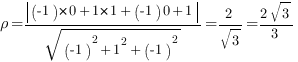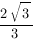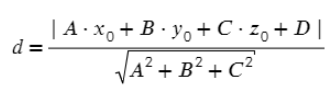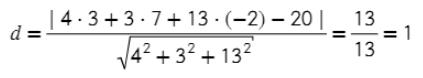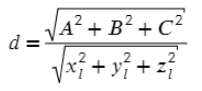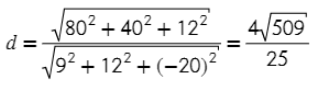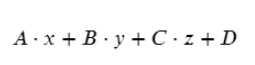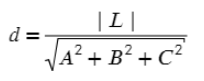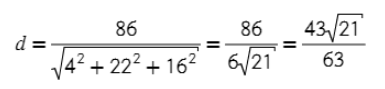
В этой статье мы поговорим о том, как найти расстояние от точки до плоскости с помощью метода координат. О том как находить расстояние от точки до плоскости геометрическим способом, вы можете прочитать здесь.

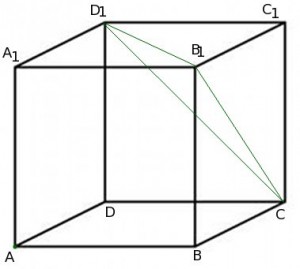
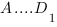
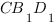
Решим задачу: в единичном кубе найдите расстояние от точки до плоскости .

На этот раз давайте решим ее с помощью метода координат.

Сначала немного теории.

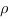
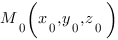
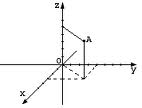
Рассстояние  от точки  до плоскости вычисляется по такой формуле:

Чтобы воспользоваться этой формулой, поместим наш куб в систему координат:

В нашей задаче роль точки  играет точка . То есть ,  ,  

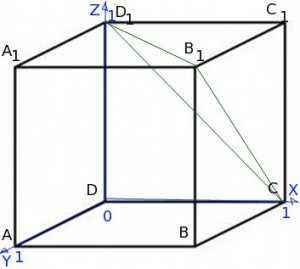
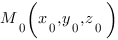
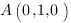
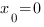
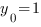
Теперь наша задача найти коэффициенты ,   ,   и в уравнении  плоскости .

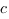
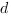
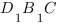
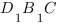
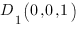
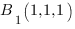
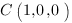
Плоскость   определяется тремя точками  ,    и . Если мы координаты точек подставим в уравнение плоскости , то получим верное равенство.

Коэффициент 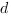 в уравнении плоскости мы можем принять равным 1.

Чтобы найти коэффициенты  ,   и  , подставим координаты точек  ,    и в уравнение плоскости . Получим систему уравнений:

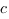
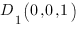
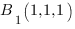
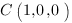
Отсюда: ,  ,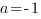  

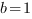
Подставим координаты точки 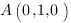 и значения коэффициентов в формулу для расстояния:

Ответ: 

И.В. Фельдман, репетитор по математике.

Поиск расстояния от точки до плоскости — частая задача, возникающая при решении различных задач аналитической геометрии, например, к этой задаче можно свести нахождение расстояния между двумя скрещивающимися прямыми или между прямой и параллельной ей плоскостью.

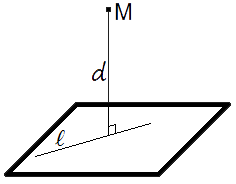
Рассмотрим плоскость $β$ и точку $M_0$ с координатами $(x_0;y_0; z_0)$, не принадлежащую плоскости $β$.

Ниже рассмотрено как найти расстояние от точки до плоскости координатным методом.

Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве

Перпендикуляр из точки $M_0$, пересекающийся с плоскостью $β$ в точке $M_1$ с координатами $(x_1;y_1; z_1)$, лежит на прямой, направляющим вектором которой является нормальный вектор плоскости $β$. При этом длина единичного вектора $n$ равна единице. Соответственно этому, расстояние от $β$ до точки $M_0$ составит:

$ρ= |vec{n} cdot vec{M_1M_0}|left(1right)$, где $vec{M_1M_0}$ — нормальный вектор плоскости $β$, а $vec{n}$ — единичный нормальный вектор рассматриваемой плоскости.

В случае, когда уравнение плоскости задано в общем виде $Ax+ By + Cz + D=0$, координаты нормального вектора плоскости представляют собой коэффициенты уравнения ${A;B;C}$, а единичный нормальный вектор в этом случае имеет координаты, вычисляемые по следующему уравнению:

$vec{n}= frac{{A;B;C}}{sqrt{A^2 + B^2 + C^2}}left(2right)$.

Теперь можно найти координаты нормального вектора $vec{M_1M_0}$:

«Расстояние от точки до плоскости» 👇

$vec{M_0M_1}= {x_0 – x_1;y_0-y_1;z_0-z_1}left(3right)$.

Также выразим коэффициент $D$, используя координаты точки, лежащей в плоскости $β$:

$D= Ax_1+By_1+Cz_1$

Координаты единичного нормального вектора из равенства $(2)$ можно подставить в уравнение плоскости $β$, тогда мы имеем:

$ρ= frac{|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|}{sqrt{A^2+B^2+C^2}}= frac{|Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|}{sqrt{A^2+B^2+C^2}} = frac{Ax_0+ By_0 + Cz_0 + D}{sqrt{A^2+B^2+C^2}}left(4right)$

Равенство $(4)$ является формулой для нахождения расстояния от точки до плоскости в пространстве.

Общий алгоритм для нахождения расстояния от точки $M_0$ до плоскости

1. Если уравнение плоскости задано не в общей форме, для начала необходимо привести его к общей.
2. После этого необходимо выразить из общего уравнения плоскости нормальный вектор данной плоскости через точку $M_0$ и точку, принадлежащую заданной плоскости, для этого нужно воспользоваться равенством $(3)$.
3. Следующий этап — поиск координат единичного нормального вектора плоскости по формуле $(2)$.
4. Наконец, можно приступить к поиску расстояния от точки до плоскости, это осуществляется с помощью вычисления скалярного произведения векторов $vec{n}$ и $vec{M_1M_0}$.

Расстояние между точкой и плоскостью.

Расстояние между точкой и прямой.

Расстояние между двумя прямыми.

---

Первое, что полезно знать, это как найти расстояние от точки до плоскости: 

Значения A, B, C, D — коэффициенты плоскости

x, y, z — координаты точки

Задача. Найти расстояние между точкой А = (3; 7; −2) и плоскостью 4x + 3y + 13z — 20 = 0.

Все дано, можно сразу подставить значения в уравнение:

Задача. Найдите расстояние от точки К = (1; −2; 7) до прямой, проходящей через точки V = (8; 6; −13) и T = (−1; −6; 7).

1. Находим вектор прямой.
2. Вычисляем вектор, проходящий через искомую точку и любую точку на прямой. 
   
3. Задаем матрицу и находим определитель по двум полученным векторам в 1-ом и 2-ом пункте.
4. Расстояние получим, когда квадратный корень из суммы квадратов коэффициентов матрицы поделим на длину вектора, который задает прямую (Думаю непонятно, поэтому перейдем к конкретному примеру).

1) TV = (8−(−1); 6−(−6); -13-7) = (9; 12; −20)

2) Вектор найдем через точки K и T, хотя так же можно было бы через K и V или любую другую точку на данной прямой.

TK = (1−(−1); −2−(−6); 7-7) = (2; 4; 0)

3) Получится матрица без коэффициента D (здесь он не нужен для решения):

Если непонятно, как получить матрицу и ее определитель, смотрите здесь более подробный разбор.

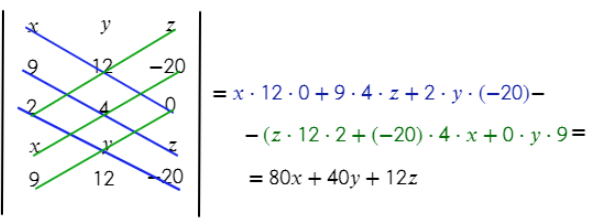
4) Плоскость получилась с коэффициентами А = 80, В = 40, С = 12,

x, y, z — координаты вектора прямой, в данном случае — вектор TV имеет координаты (9; 12; −20)

Задача. Найти расстояние между прямой, проходящей через точки Е = (1; 0; −2), G = (2; 2; −1), и прямой, проходящей через точки M = (4; −1; 4), L = (−2; 3; 0).

1. Задаем векторы обеих прямых.
2. Находим вектор, взяв по одной точке с каждой прямой.
3. Записываем матрицу из 3-х векторов (две строчки из 1-го пункта, одна строчка из 2-го) и находим ее численный определитель.
4. Задаем матрицу из двух первых векторов (в пункте 1). Первую строчку задаем как x, y, z.
5. Расстояние получим, когда разделим получившееся значение из пункта 3 по модулю на квадратный корень из суммы квадратов пункта 4. 

Перейдем к цифрам:

1) EG = (2−1; 2−0; −1−2) = (1; 2; −3)

ML = (−2−4; 3−(−1); 0−4) = (−6; 4; −4) 

2) Найдем вектор EM (можно было так же найти EL или GM, или GL).

EM = (1−4; 0−(−1); −2−4) = (−3; 1; −6)

3) Составляем матрицу из трех выше найденных векторов и находим определитель.

4) Составляем матрицу из первых двух выше найденных векторов и находим определитель 

без коэффициента D (здесь он не нужен для решения).

Вспомним, что уравнение плоскости задается так:

В нашем случае А = 4, В = 22, С = 16, D = 0.

5) Итоговая формула выглядит так, где L= −86 (из 3 пункта)

Будь в курсе новых статеек, видео и легкого математического юмора.

§ 26.Расстояние от точки до плоскости в координатах

Напомним, что расстояние от данной точки M0 до плоскости α равно длине перпендикуляра M0M1 (M1∈ α), опущенного из точки M0 на плоскость α (рис. 228).

Проведём через точку M0(x0; y0; z0), не лежащую на плоскости α, прямую h, перпендикулярную α. Так как вектор нормали плоскости α является направляющим вектором прямой h, то для поиска координат x1, y1, z1 точки M1 пересечения прямой h и плоскости α достаточно, как и в предыдущем параграфе, решить систему уравнений относительно параметра t:

Решением этой системы является

t0 =  = ,

что позволяет нам найти искомые координаты точки пересечения прямой h и плоскости α:

Тогда находим длину отрезка M0M1, равную искомому расстоянию d от точки M0 до плоскости α:

d = | M0M1 | =

= =

=  = 

= |t0| =

= •=

= .

Если точка M0 лежит на данной плоскости, то

Ax0 + By0 + Cz0 + D = 0

и искомое расстояние равно нулю, что также следует из полученной формулы

d = .

Расстояние от начала координат O(0; 0; 0) до плоскости α равно

.

Приведём ещё один способ рассуждений.

Расстояние от точки M0 до плоскости α обозначим: d = | M0; α | = | M0M1|, где точка M1 — основание перпендикуляра, опущенного из точки M0 на плоскость α (см. рис. 228).

Пусть в системе координат Oxyz плоскость α задана уравнением

Ax + By + Cz + D = 0,(1)

точки M0 и M1 имеют координаты: M0(x0; y0; z0), M1(x1; y1; z1).

Заметим, что

M1 ∈ α ⇒ Ax1 + By1 + Cz1 + D = 0.(2)

Вектор (x0 – x1; y0 – y1; z0 – z1) и вектор нормали (A; B; C) плоскости α коллинеарны, так как каждый из них перпендикулярен плоскости α, поэтому

• = |  |•|  |•(±1) = ±d•|  |;

(+1, если  ↑↑ ; – 1, если  ↑↓ ).

Тогда

|M0; α | = d = |  | =  = .

Раскроем в числителе скобки и, пользуясь соотношением (2), заменим выражение –Ax1 – By1 – Cz1 числом D. Получаем

d = .(3)

Сравните два приведённых способа рассуждений и выберите для себя наиболее понятный.

ЗадаЧа 7.182. Найти расстояние от точки K(1; –2; 3) до плоскости 3x + 2y – 6z + 5 = 0.

Решение. Находим координаты вектора нормали плоскости: (3; 2; –6). Тогда

d =  =  = 2.

Ответ: 2.

ЗадаЧа 7.183. Найти множество точек, равноудалённых от плоскостей 2x + 2y – z – 3 = 0 и 3x + 4y + 12z – 13 = 0.

Решение. Пусть точка M(x; y; z) равноудалена от данных плоскостей, тогда

 = , т. е.

 = .

Данное уравнение распадается на совокупность двух уравнений

 = ,

или  = – .

После упрощения получим уравнения двух плоскостей

17x + 14y – 49z = 0 и 35x + 38y + 23z – 78 = 0.

Подумайте, почему эти плоскости получились взаимно перпендикулярными и как они связаны с данными в задаче плоскостями.

Задания для работы с интернет-ресурсами

1. Вы можете найти в Интернете дополнительный материал по темам «Декартова прямоугольная система координат в пространстве», «Координаты вектора», «Условие параллельности двух векторов в координатах», «Скалярное произведение векторов в координатах», «Условие перпендикулярности двух векторов в координатах», «Проекция вектора на ось в координатах».

2. Найдите и изучите дополнительные материалы и презентации по темам: «Простейшие задачи стереометрии в координатах», «Уравнения и неравенства, задающие множества точек в пространстве», «Уравнение сферы и неравенство шара».

3. Найдите и выпишите знакомые и незнакомые формулы по теме «Плоскость в пространстве в координатах».

4. Найдите и выпишите знакомые и незнакомые формулы по темам «Прямая в координатах», «Взаимное расположение прямой и плоскости в координатах».

5. Набрав в поисковой системе слова «Прямая и плоскость в пространстве», «Параллельность прямой и плоскости», вы увидите, как можно использовать векторы и координаты при изучении вопросов параллельности прямой и плоскости.

6. Посмотрите статьи по теме «Аналитическая геометрия». Этот раздел математики вы будете изучать в высших учебных заведениях, но многими формулами и приёмами координатного метода изучения свойств геометрических фигур вы владеете уже сейчас. Попытайтесь узнать об этом ещё больше.

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2. Что нового вы узнали в этой главе?

3. Как могут пригодиться вам эти знания в повседневной жизни?

4. Какие задания в этой главе были для вас самыми трудными? Почему?

5. Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6. Обращались ли вы за помощью к одноклассникам, родителям, учителю?

Расстояние от точки до плоскости

Определение.

Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.

Формула для вычисления расстояния от точки до плоскости

Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(M_x, M_y, M_z) до плоскости можно найти, используя следующую формулу:

d =	|A·Mx + B·My + C·Mz + D|
√A2 + B2 + C2

Примеры задач на вычисление расстояния от точки до плоскости

Пример 1.

Найти расстояние между плоскостью 2x + 4y — 4z — 6 = 0 и точкой M(0, 3, 6).

Решение. Подставим в формулу коэффициенты плоскости и координаты точки

d =

|2·0 + 4·3 + (-4)·6 — 6|√4 + 16 + 16

=

|0 + 12 — 24 — 6|√36

=

|-18|6

= 3

Ответ: расстояние от точки до плоскости равно 3.