Как найти расстояние точки от начала координат - Исправление недочетов и поиск решений вместе с Examum.ru

Расстояние от точки (x_M;y_M) до начала координат можно найти по формуле расстояние между точками.

Подставив в формулу

$[MO = sqrt {{{({x_O} - {x_M})}^2} + {{({y_O} - {y_M})}^2}} ]$

координаты точек M(x_M;y_M) и O(0;0)

$[MO = sqrt {{{(0 - {x_M})}^2} + {{(0 - {y_M})}^2}} ,]$

получаем формулу для нахождения расстояния от точки M до начала отсчёта — точки O:

$[MO = sqrt {{x_M}^2 + {y_M}^2} .]$

Пример 1.

Найти расстояние от точки F(-5; 12) до начала координат.

Решение:

$[FO = sqrt {{x_F}^2 + {y_F}^2} ,]$

$[FO = sqrt {{{( - 5)}^2} + {{12}^2}} = sqrt {169} = 13.]$

Ответ: 13.

Эту же формулу можно получить, руководствуясь непосредственно геометрическими соображениями.

Из прямоугольного треугольника OMM₁по теореме Пифагора

$[M{O^2} = O{M^2} + MM_1^2.]$

OM₁=x_M, MM₁=y_M,

$[MO = sqrt {{x_M}^2 + {y_M}^2} .]$

Пример 2.

На координатной плоскости отмечена точка A. Найти расстояние от точки A до начала координат.

Решение:

Координаты точки C — x_C =4, y_C=3.

$[CO = sqrt {x_C^2 + y_C^2} ,]$

$[CO = sqrt {{4^2} + {3^2}} = 5.]$

Ответ: 5.

Источник

We will discuss here how to find the distance of a point
from the origin.

The distance of a point A (x, y) from the origin O (0, 0) is
given by OA = (sqrt{(x — 0)^{2} + (y — 0)^{2}})

i.e., OP = (sqrt{x^{2} + y^{2}})

Consider some of the following examples:

1. Find the distance of the point (6, -6) from the origin.

Solution:

Let M (6, -6) be the given point and O (0, 0) be the origin.

The distance from M to O = OM

= (sqrt{(6 — 0)^{2} + (-6 —
0)^{2}})

= (sqrt{(6)^{2} + (-6)^{2}})

= (sqrt{36 + 36})

= (sqrt{72})

= (sqrt{2 × 2 × 2 × 3 × 3})

= 6(sqrt{2}) units.

2. Find the distance between the point (-12, 5) and the
origin.

Solution:

Let M (-12, 5) be the given point and O (0, 0) be the
origin.

The distance from M to O = OM = (sqrt{(-12 — 0)^{2} + (5 —
0)^{2}}) = (sqrt{(-12)^{2} + (5)^{2}})

= (sqrt{144 + 25})

= (sqrt{169})

= (sqrt{13 × 13})

= 13 units.

3. Find the distance between the point (15, -8) and the
origin.

Solution:

Let M (15, be the given point and O (0, 0) be the origin.

The distance from M to O = OM = (sqrt{(15 — 0)^{2} + (-8 —
0)^{2}}) = (sqrt{(15)^{2} + (-8)^{2}})

= (sqrt{225 + 64})

= (sqrt{289})

= (sqrt{17 × 17})

= 17 units.

● Distance and Section Formulae

Distance Formula
Distance Properties in some Geometrical Figures
Conditions of Collinearity of Three Points
Problems on Distance Formula
Distance of a Point from the Origin
Distance Formula in Geometry
Section Formula
Midpoint Formula
Centroid of a Triangle
Worksheet on Distance Formula
Worksheet on Collinearity of Three Points
Worksheet on Finding the Centroid of a Triangle
Worksheet on Section Formula

Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

Источник

Расстояние от точки до начала координат

Расстояние от точки (x_M;y_M) до начала координат можно найти по формуле расстояние между точками.

Подставив в формулу

получаем формулу для нахождения расстояния от точки M до начала отсчёта — точки O:

Найти расстояние от точки F(-5; 12) до начала координат.

Эту же формулу можно получить, руководствуясь непосредственно геометрическими соображениями.

Из прямоугольного треугольника OMM₁ по теореме Пифагора

На координатной плоскости отмечена точка A. Найти расстояние от точки A до начала координат.

Координаты точки C — x_C =4, y_C=3.

Как рассчитать координаты точек окружности

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Уравнение окружности по трем точкам

Калькулятор расчета онлайн уравнения окружности по трем заданным точкам, а также нахождение координат точки центра и радиус окружности.

Уравнение окружности

r 2 = (x — h) 2 + (y — k) 2

h,k — координаты центра Окружности
x,y — координаты точки окружности
r — радиус

Пример

Найдите координаты точки центра окружности, радиус и уравнение окружности, если известны координаты трех точек A (2,2), B (2,4) и C (5,5)

Решение :

Подставляем координаты точек в формулу

(2 — h) 2 + (2 — k) 2 = r 2
(2 — h) 2 + (4 — k) 2 = r 2
(5 — h) 2 + (5 — k) 2 = r 2

Шаг :2

Найдем значение k упрощая 1 и 2 уравнения

(2 — h) 2 + (2 — k) 2 = (2 — h) 2 + (4 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 4 — 4h + h 2 +16 — 8k + k 2
8 — 4k = 20 — 8k
k= 3

Шаг :3

Найдем значение h упрощая уравнения 2 и 3

(2 — h) 2 + (2 — k) 2 = (5 — h) 2 + (5 — k) 2
4 — 4h + h 2 + 4 — 4k + k 2 = 25 — 10h + h 2 + 25 — 10k + k 2
8 — 4k — 4h = 50 — 10h — 10k
6k + 6h = 42

Подставив значение k=3 в уравнение

Получаем координаты точки центра (h,k) = ( 4,3 )

Шаг :4

Подставим значения h,k в формулу

r 2 = (x — h) 2 + (y — k) 2
r 2 = (2 — 4) 2 + (2 — 3) 2
r 2 = (-2) 2 + (-1) 2
r 2 = 5
r = 2.24

Шаг :5

Подставим значения h, k в уравнение окружности

(x — h) 2 + (y — k) 2

Уравнение окружности = (x — 4) 2 + (y — 3) 2

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O. Ее координаты равны нулю: O (0,0).
Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Прямоугольная декартова система координат на плоскости

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

источники:

http://b4.cooksy.ru/articles/kak-rasschitat-koordinaty-tochek-okruzhnosti

http://www.resolventa.ru/demo/him/diagege.htm

Источник

Это последовательный пост, связанный с Координатная геометрия, особенно на Балы. Мы уже обсуждали несколько тем ранее в посте «Полное руководство по координатной геометрии». В этом посте мы обсудим оставшиеся темы.

Все основные формулы для точек в аналитической геометрии описаны здесь, и для легкого и быстрого изучения формул a ‘Таблица формул по точкам’ с графическим объяснением представлено ниже.

Формулы расстояния между двумя точками | Аналитическая геометрия:

Расстояние — это измерение, позволяющее определить, насколько далеко друг от друга находятся объекты, места и т. Д. Имеет числовое значение с единицами измерения. В координатной геометрии или аналитической геометрии в 2D есть формула, выведенная из теоремы Пифагора, для вычисления расстояния между двумя точками. мы можем записать это как «Расстояние» d = √ [(x₂-x₁)²+ (y₂-y₁)²] , Где (x₁,y₁) и (x₂,y₂) две точки на плоскости xy. После краткого графического объяснения следует ‘Таблица формул по пунктам тема № 1’ внизу.

Расстояние точки от начала координат | Координатная геометрия:

Если мы начнем наше путешествие с исходной точки в плоскости xy и закончим с любой точкой этой плоскости, расстояние между исходной точкой и точкой также можно будет найти по формуле «Расстояние». OP = √ (x²+ у²), который также является сокращенной формой «Формулы расстояния между двумя точками» с одной точкой в (0,0). После краткого графического объяснения следует ‘Таблица формул по пунктам тема № 2’ внизу.

Формулы сечения точек | Координатная геометрия:

Если точка разделяет линейный сегмент, соединяющий две заданные точки в некотором соотношении, мы можем использовать формулы сечения, чтобы найти координаты этой точки, в то время как соотношение, на которое делится линейный сегмент, задается и наоборот. Существует вероятность того, что отрезок линии может быть разделен точкой внутри или снаружи. Когда точка лежит на отрезке линии между двумя заданными точками, используются формулы внутреннего сечения, т. Е.

х = мх₂+ nx₁/(м+п)

у = мой₂+ ny₁/(м+п)

И когда точка лежит на внешней части отрезка прямой, соединяющего две заданные точки, используются формулы внешнего сечения, т.е.

у = мой₂-ни₁/(млн)

Где (x, y) — требуемые координаты точки. Это очень необходимые формулы для нахождения центра тяжести, центра окружности, центра описанной окружности треугольника, а также центра масс систем, точек равновесия и т. Д. В физике. Обязательно посмотрите краткий обзор различных типов формул сечения с графиками, приведенными ниже в ‘Таблица формул по пунктам темы № 3; случай-I и случай-II ‘.

Формула средней точки | Координатная Геометрия:

Это простая формула, полученная из описанных выше формул раздела внутренних точек. Хотя нам нужно найти среднюю точку линейного сегмента, то есть координату точки, которая равноудалена от двух заданных точек на линейном сегменте, то есть соотношение принимает форму 1: 1, тогда эта формула требуется. Формула имеет вид

Если точка разделяет линейный сегмент, соединяющий две заданные точки в некотором соотношении, мы можем использовать формулы сечения, чтобы найти координаты этой точки, в то время как соотношение, на которое делится линейный сегмент, задается и наоборот. Существует вероятность того, что отрезок линии может быть разделен точкой внутри или снаружи. Когда точка лежит на отрезке линии между двумя заданными точками, используются формулы внутреннего сечения, т. Е.

х = мх₂+ nx₁/(м+п)

у = мой₂+ ny₁/(м+п)

х = мх₂-nx₁/(млн)

у = мой₂-ни₁/(млн)

Формула средней точки | Координатная Геометрия:

Это простая формула, полученная из описанных выше формул раздела внутренних точек. Хотя нам нужно найти среднюю точку линейного сегмента, то есть координату точки, которая равноудалена от двух заданных точек на линейном сегменте, то есть соотношение принимает форму 1: 1, тогда эта формула требуется. Формула имеет вид

х = х₁+x₂/2

х = у₁+y₂/2

Пройдите через «Таблица формул по пунктам темы № 3 — случай-III» ниже, чтобы получить графическое представление об этом.

Площадь треугольника в координатной геометрии:

Треугольник имеет три стороны и три вершины на плоскости или в двумерном поле. Площадь треугольника — это внутреннее пространство, окруженное этими тремя сторонами. Основная формула вычисления площади треугольника: (2/1 X Основание X Высота). В аналитической геометрии, если заданы координаты всех трех вершин, площадь треугольника можно легко вычислить по формуле Площадь Треугольника = | ½ [x₁ (y₂– y₃ ) + x₂ (y₃– y₂) + x₃ (y₂-y ₁)] | , на самом деле это может быть получено из основной формулы площади треугольника с использованием формулы расстояния между двумя точками в координатной геометрии. Оба случая графически описаны в ‘Таблица формул по теме 4’ внизу.

Коллинеарность точек (Три точки) | Координатная геометрия:

Коллинеарность означает «находиться на одной линии». В геометрии, если три точки лежат на одной единственной линии в плоскости, они никогда не могут образовать треугольник с площадью, отличной от нуля, т.е. если формула площади треугольника заменяется координатами трех коллинеарных точек, результат для площади воображаемый треугольник, образованный этими точками, будет иметь только ноль. Таким образом, формула выглядит как ½ [x₁ (y₂– y₃ ) + x₂ (y₃– y₂) + x₃ (y₂-y ₁)] = 0 Чтобы получить более четкое представление о графическом представлении, пройдите через «Таблица формул по пунктам темы № 5» внизу.

Центроид треугольника | Формула:

Три медианы * треугольника всегда пересекаются в точке, находящейся внутри треугольника, и делят медианное значение в соотношении 2: 1 от любой вершины до середины противоположной стороны. Эта точка называется центром тяжести треугольника. Формула для определения координат центроида:

х = х₁+x₂+x₃/3

х = у₁+y₂+y₃/3

В разделе «Таблица формул по пунктам темы № 6» ниже вышеуказанная тема описывается графически для лучшего понимания и для быстрого просмотра.

Центр треугольника | Формула:

Это центр самой большой вписанной окружности треугольника, которая помещается внутри треугольника. Это также точка пересечения трех биссектрис внутренних углов треугольника. Формула, используемая для нахождения центра треугольника:

х=топор₁+ bx₂+сх₃/а+б+в

х=ау₁+от₂+cy₃/а+б+в

Для удобства графического объяснения ниже «Таблица формул по пунктам темы № 7» нужно видеть.

Формула смещения происхождения | Координатная геометрия:

Мы уже узнали в предыдущем посте «Полное руководство по координатной геометрии» что начало координат лежит в точке (0,0), которая является точкой пересечения осей на плоскости. мы можем переместить начало координат во всех квадрантах плоскости относительно начала координат, что даст новый набор осей через него.

Для точек в вышеупомянутой плоскости ее координаты изменятся вместе с новым началом и осями, и это может быть вычислено по формуле, новые координаты точки P (x₁,y₁) Он x₁= х- а; у₁ = у- b где координаты новой точки отсчета (a, b). Чтобы иметь четкое представление об этой теме, желательно увидеть графическое представление ниже в «Таблица формул по пунктам темы № 8» .

`Formulae table on Points in Coordinate Geometry in 2D`:

﹡ Окружность треугольника:

Это точка пересечения трех серединных перпендикуляров стороны треугольника. Это также центр описанной окружности треугольника, которая касается только вершин треугольника.

﹡ Медианы:

Медиана — это отрезок прямой, соединяющий вершину треугольника с серединой или точкой, делающей пополам противоположную сторону вершины. В каждом треугольнике есть три медианы, которые всегда пересекаются в центре тяжести одного и того же треугольника.

Решенные задачи о точках координатной геометрии в 2D.

Для лучшего изучения точек в 2D, здесь шаг за шагом решается один базовый пример, а для самостоятельной практики есть больше проблем с ответами по каждой формуле. В следующих статьях должны появиться сложные проблемы с решением сразу после получения базового и ясного представления по теме точек в координатной геометрии 2D.

Основные примеры по формулам «Расстояние между двумя точками»

Проблемы 1: Вычислите расстояние между двумя заданными точками (1,2) и (6, -3).

Решение: Мы уже знаем, что формула расстояния между двумя точками (x₁,y₁) и (x₂,y₂) is d = √ [(x₂-x₁)²+ (y₂-y₁)²]… (1)

(См. Таблицу формул выше) Здесь можно считать, что (x₁,y₁) ≌ (1,2) и (x₂,y₂) ≌ (6, -3) т.е. x₁= 1, у₁= 2 и x₂= 6, у₂ = -3, если мы поместим все эти значения в уравнение (1), мы получим требуемое расстояние.

Следовательно, расстояние между двумя точками (1,2) и (6, -3) равно

= √ [(6-1)²+ (- 3-2)²] единицы измерения

= √ [(5)²+ (- 5)²] единицы измерения

= √ [25 + 25] единицы измерения

= √ [50] единицы измерения

= √ [2 × 5²] единицы измерения

= 5√2 шт. (Отв.)

Примечание: За расстоянием всегда следуют единицы.

Дополнительные ответы на вопросы (базовые) приведены ниже для дальнейшей практики с использованием процедуры, описанной выше. Проблема 1:-

Задача 2: Найдите расстояние между двумя точками (2,8) и (5,10).

Ответ √13 единиц

Задача 3: Найдите расстояние между двумя точками (-3, -7) и (1, -10).

Отв. 5 единиц

Задача 4: Найдите расстояние между двумя точками (2,0) и (-3,4).

Ответ √41 единиц

Задача 5: Найдите расстояние между двумя точками (2, -4) и (0,0).

Отв. 2√5 единиц

Задача 6: Найдите расстояние между двумя точками (10,100) и (-10,100,).

Отв. 20 единиц

Задача 7: Найдите расстояние между двумя точками (√5,1) и (2√5,1).

Ответ √5 единиц

Задача 8: Найдите расстояние между двумя точками (2√7,2) и (3√7, -1).

Ответ 4 единиц

Задача 9: Найдите расстояние между двумя точками (2 + √10, 0) и (2-√10, 0).

Ответ 2√10 единиц

Задача 10: Найдите расстояние между двумя точками (2 + 3i, 0) и (2-3i, 10). {я = √-1}

Отв. 8 единиц

Задача 11: Найдите расстояние между двумя точками (2 + i, -5) и (2-i, -7). {я = √-1}

Ответ 0 единиц

Задача 12: Найдите расстояние между двумя точками (7 + 4i, 2i) и (7-4i, 2i). {я = √-1}

Ответ 8i единиц

Задача 13: Найдите расстояние между двумя точками (√3 + i, 3) и (2√3 + i, 5). {я = √-1}

Ответ √7 единиц

Задача 14: Найдите расстояние между двумя точками (5 + √2, 3 + i) и (2 + √2, 7 + 2i). {я = √-1}

Ответ 2√ (6 + 2i) единиц

Основные примеры формул «Расстояние точки от начала координат»

Задача 15: Найдите расстояние точки (3,4) от начала координат.

Решение:

У нас есть формула расстояния точки от начала координат, OP = √ (x²+ у²) (См. Таблицу формул выше) Итак, здесь мы можем считать (x, y) ≌ (3,4), т.е. x = 3 и y = 4

Следовательно, подставляя эти значения x и y в приведенное выше уравнение, мы получаем требуемое расстояние

=√ (3²+ 4²) единицы измерения

= √ (9+ 16) шт.

= √ (25) единиц

= 5 единиц

Примечание. За расстоянием всегда следуют единицы измерения.

Примечание. Расстояние от точки до начала координат — это фактически расстояние между точкой и исходной точкой, т. Е. (0,0)

Дополнительные ответы на вопросы приведены ниже для дальнейшей практики с использованием процедуры, описанной выше.

Проблема
15:-

Задача 16: Найдите расстояние точки (1,8) от начала координат.

Ответ √65 единиц

Задача 17: Найдите расстояние точки (0,7) от начала координат.

Ответ 7 единиц

Задача 18: Найдите расстояние точки (-3, -4) от начала координат.

Ответ 5 единиц

Задача 19: Найдите расстояние точки (10,0) от начала координат.

Ответ 10 единиц

Задача 20: Найдите расстояние точки (0,0) от начала координат.

Ответ 0 единиц

___________________________________________________________

Основные примеры других формул баллов описано выше и несколько сложных вопросов по этой теме в координатной геометрии, следуют следующие сообщения.

Источник

Таблицы DPVA.ru — Инженерный Справочник

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты… / / Метод координат на плоскости. Расстояние между точками. Расстояние до точки от начала координат. Координаты точки, делящей отрезок в отношении λ . Координаты середины отрезка. Координаты центра тяжести треугольника.

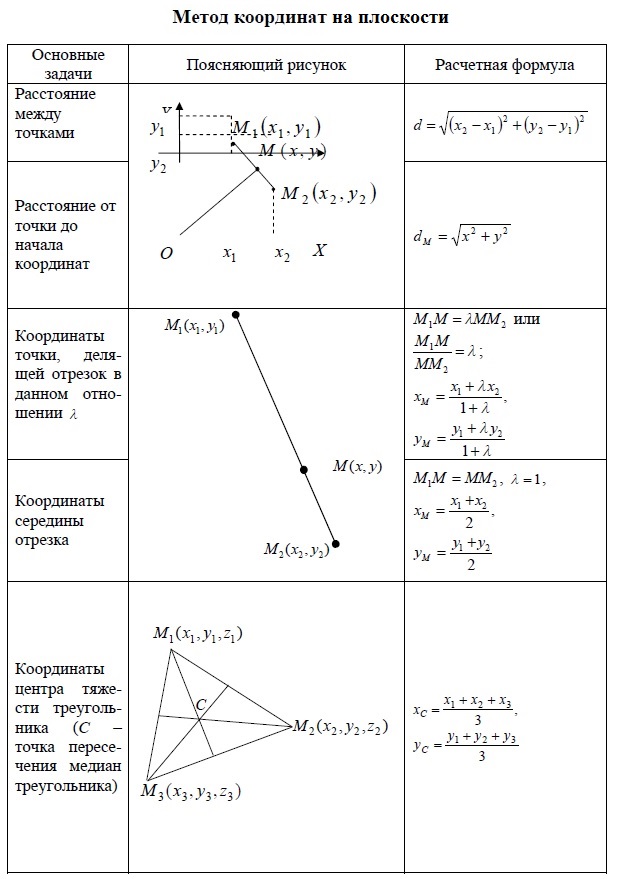
Метод координат на плоскости. Расстояние между точками. Расстояние до точки от начала координат. Координаты точки, делящей отрезок в отношении λ . Координаты середины отрезка. Координаты центра тяжести треугольника.

Метод координат на плоскости. Расстояние между точками. Расстояние до точки от начала координат. Координаты точки, делящей отрезок в отношении λ . Координаты середины отрезка = координаты точки, делящей отрезок пополам. Координаты центра тяжести треугольника = координаты точки пересечения медиан.

название задачи,
рисунок, поясняющий метод,
расчетная формула

*Бабичева, Болдовская, Справочник по математике. СибАДИ, 2010. (классная книга)

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.

Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator

Источник

Расстояние от точки до начала координат

Как рассчитать координаты точек окружности

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Уравнение окружности по трем точкам

Уравнение окружности

Пример

Решение :

Шаг :2

Шаг :3

Шаг :4

Шаг :5

Как найти координаты точки?

Понятие системы координат

Определение координат точки

Особые случаи расположения точек

Способы нахождения точки по её координатам

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Формулы расстояния между двумя точками | Аналитическая геометрия:

Расстояние точки от начала координат | Координатная геометрия:

Формулы сечения точек | Координатная геометрия:

Формула средней точки | Координатная Геометрия:

Формула средней точки | Координатная Геометрия:

Площадь треугольника в координатной геометрии:

Коллинеарность точек (Три точки) | Координатная геометрия:

Центроид треугольника | Формула:

Центр треугольника | Формула:

Формула смещения происхождения | Координатная геометрия:

Formulae table on Points in Coordinate Geometry in 2D:

﹡ Окружность треугольника:

﹡ Медианы:

Решенные задачи о точках координатной геометрии в 2D.

Основные примеры по формулам «Расстояние между двумя точками»

Проблемы 1: Вычислите расстояние между двумя заданными точками (1,2) и (6, -3).

Дополнительные ответы на вопросы (базовые) приведены ниже для дальнейшей практики с использованием процедуры, описанной выше. Проблема 1:-

Задача 2: Найдите расстояние между двумя точками (2,8) и (5,10).

Задача 3: Найдите расстояние между двумя точками (-3, -7) и (1, -10).

Задача 4: Найдите расстояние между двумя точками (2,0) и (-3,4).

Задача 5: Найдите расстояние между двумя точками (2, -4) и (0,0).

Задача 6: Найдите расстояние между двумя точками (10,100) и (-10,100,).

Задача 7: Найдите расстояние между двумя точками (√5,1) и (2√5,1).

Задача 8: Найдите расстояние между двумя точками (2√7,2) и (3√7, -1).

Задача 9: Найдите расстояние между двумя точками (2 + √10, 0) и (2-√10, 0).

Задача 10: Найдите расстояние между двумя точками (2 + 3i, 0) и (2-3i, 10). {я = √-1}

Задача 11: Найдите расстояние между двумя точками (2 + i, -5) и (2-i, -7). {я = √-1}

Задача 12: Найдите расстояние между двумя точками (7 + 4i, 2i) и (7-4i, 2i). {я = √-1}

Задача 13: Найдите расстояние между двумя точками (√3 + i, 3) и (2√3 + i, 5). {я = √-1}

Задача 14: Найдите расстояние между двумя точками (5 + √2, 3 + i) и (2 + √2, 7 + 2i). {я = √-1}

Основные примеры формул «Расстояние точки от начала координат»

Задача 15: Найдите расстояние точки (3,4) от начала координат.

Дополнительные ответы на вопросы приведены ниже для дальнейшей практики с использованием процедуры, описанной выше.

Проблема 15:-

Задача 16: Найдите расстояние точки (1,8) от начала координат.

Задача 17: Найдите расстояние точки (0,7) от начала координат.

Задача 18: Найдите расстояние точки (-3, -4) от начала координат.

Задача 19: Найдите расстояние точки (10,0) от начала координат.

Задача 20: Найдите расстояние точки (0,0) от начала координат.

Основные примеры других формул баллов описано выше и несколько сложных вопросов по этой теме в координатной геометрии, следуют следующие сообщения.

`Formulae table on Points in Coordinate Geometry in 2D`:

Проблема
15:-