Как найти расстояние в действительности

При разработке маршрута для похода немаловажным критерием является его длинна. В зависимости от этого рассчитываются сложность и длительность предстоящего маршрута, определяется время, необходимое для его прохождения, необходимая средняя скорость движения, запас воды и продовольствия, определяется минимально допустимая степень подготовленности будущих участников. Способы и методы разработки самого маршрута могут быть различными, но все упирается в расстояние, которое вы готовы преодолеть за время, отведенное для его прохождения. От точности произведенных вами замеров и проведенных расчетов, будет зависеть многое, в частности, успеете ли вы на запланированную обратную электричку или вам придется искать место в гастинице или сидеть на платформе  в ожидании утреннего поезда.

Существует множество средств и способов измерения расстояний по карте, но не все они одинаково применимы и удобны для точного измерения длинны будущих маршрутов по извилистым дорогам.

В качестве средств для измерения отрезков на карте можно использовать привычные линейку или циркуль. Но как не сложно догадаться, все эти приспособления предназначены для измерения прямых отрезков, а велосипедный маршрут редко представляет из себя набор прямых, если только вы не катаетесь по улицам города. При измерении маршрута проходящего по извилистым дорогам и тропам при помощи линейных инструментов вы непременно столкнетесь с необходимостью дополнительных вычислений, в том числе с определением величины погрешности ваших измерений, так как обычный плавный изгиб дороги при измерении линейкой будет выглядеть как ломаная, состоящая из множества коротких прямых отрезков. При этом, чем длиннее и извилистее маршрут, тем большая погрешность будет допущена в ваших измерениях и тем приблизительнее будет определена общая длинна маршрута, особенно, если вы используете для прокладки маршрута карту небольшого масштаба.

Более точные результаты можно получить при использовании нитки с заранее нанесенными на нее с помощью все той же линейки поперечными штихами-делениями, соответствующими сантиметровой шкале. Однако, в этом случае точность измерения будет напрямую зависеть от вашей аккуратности и терпения при раскладывании нитки на поверхности карты.

К счастью, уже давно существует специальный несложный прибор, предназначенный как раз для проведения измерений на карте как прямых так и извилистых отрезков под названием курвиметр. Курвиметр (от лат. curvus — кривой и …метр), прибор для измерения длин отрезков кривых и извилистых линий на топографических планах, картах и графических документах.

Курвиметр изготовляют с круговыми и прямолинейными шкалами. Курвиметр каждого типа выпускаются в двух исполнениях: с неподвижным циферблатом и подвижной стрелкой или индексом; с подвижным циферблатом и неподвижным индексом. Для измерения длины линии колесико Курвиметра прокатывают по этой линии. Измеряемое Курвиметром расстояние за один оборот соответствует длине шкалы в 100 см . Погрешность измерения отрезка прямой линии длиной не менее 50 см — не более 0,25 см .

Курвиметр механический (изображенный на рисунке) имеет метрическую и дюймовую шкалу. Цена деления метрической шкалы соответствует 1 см , дюймовой 0.05 дюйма . Погрешность измерения отрезка длиною 50 см не превышает 0.5%.

Таким образом, при использовании курвиметра вы с наименьшими затратами сможете измерить необходимый вам извилистый отрезок маршрута и с наибольшей точностью. Однако и здесь следует помнить несколько несложных правил измерения маршрута с помощью этого приспособления.

Во-первых, измеряя общую длину маршрута не пытайтесь измерить сразу всю его длину от начала и до конца. Лучше мерить отрезками – от одного важного ориентира к другому. И дело вовсе не в том, что вам может не хватить длинны шкалы. Просто с увеличением длинны измеряемого отрезка увеличивается степень погрешности измерения, неудобное положение, усталость или дрожь руки так же не лучшим образом могут сказаться на точности измерений.

Во-вторых, по возможности используйте карту большего масштаба. На практике, карта масштабом 1:50 000 (пятьсотметровка) или 1: 100 000 (километровка) вполне сгодятся. Только не ленитесь тщательно обводить курвиметром все изгибы дороги.

В –третьих, не поленитесь перемерить каждый отрезок несколько раз. Так вы исключите случайную ошибку. Если вы используете обычный механический курвиметр, а не электронный аналог позволяющий измерять с десятыми и даже тысячными долями, определяя на глаз оставшийся «хвостик» на глазок, что весьма актуально на картах масштабом менее 1:100 000, не стремитесь округлять всегда в одну сторону (большую или меньшую) используйте хотя бы примерные десятые доли.

В-четвертых, в отрезках между основными ориентирами не поленитесь отдельно замерить расстояния до второстепенных ориентиров по пути следования, например, мост через протоку, перекресток дорог, глубокий овраг, и т.д. Таким образом, как уже упоминалось выше, вы сможете постоянно контролировать свое местоположение на маршруте и иметь точное представление об оставшимся до финиша расстоянии и без GPS — приемника а только с помощью карты с нанесенными на нее расстояниями до ориентиров.

При нанесении на карту результатов замеров представляется удобным использование дробной записи А/В., где А — расстояние от предыдущего ориентира, а В — расстояние от точки начала маршрута. Подобный способ позволяет легко ориентироваться в пространстве без лишних математических вычислений. Это актуально, в случае, например, когда вам необходимо сообщить своим попутчикам, особенно любителям вырываться вперед от основной группы, точное расстояние до ориентира возле которого необходимо свернуть, дождаться группу и т.п. Кроме того, если вы на каком либо из отрезков маршрута совершали радиальные вылазки или случайно сделали незапланированный крюк, например в обход размытого участка дороги, вам не придется вносить коррективы в заранее нанесенные отметки на карте, перезаписывать их или постоянно держать в голове число «лишних» километров, на которое придется постоянно делать поправку.

Пример замера и нанесения его результатов на карту:

Старт (0/0) — поворот направо, съезд с асфальтового шоссе на грунтовую дорогу (3/3) — мост через реку (2/5) — деревня Дубки (7/13) – поселок Лесной (14/27) – мост через ручей (5/32) – перекресток с асфальтовым шоссе (8/40) – ж/д станция Конечная (10/50).

И несколько слов о многообразии форм и разновидностей курвиметров, которые представлены сегодня на российском рынке.

Как уже упоминалось выше, существуют два основных типа курвиметров: механический и электронный.

В устройстве механических курвиметров, вне зависимости от конкретной модели, нет особых принципиальных различий, за исключением типа шкалы (прямолинейная и круговая) и принципа отображения результатов замеров (с неподвижным циферблатом и подвижной стрелкой или индексом; с подвижным циферблатом и неподвижным индексом). Как правило, это пластмассовый прибор весом около 50 грамм довольно скромных размеров. Например курвиметр КУ-А российского производства изображенный на рисунке имеет габариты 50х20х100 (в футляре).

Данный курвиметр выпускается в нашей стране уже не первое десятилетие в неизменном виде, разве что теперь без знака качества СССР, и входил в обязательный перечень предметов в составе офицерского планшета. Он был стандартизирован еще в советские времена и соответствует ТУ 25-07-1039-74. Стоимость данного экземпляра составляет около до 500 рублей.

Примерно так же устроен курвиметр шведской фирмы Silva. Однако, неподвижный циферблат имеет более сложную разметку для измерений в восьми масштабах.

Стоимость такого курвиметра составляет порядка 1000 рублей.

Еще один образец механического курвиметра российского производства выполненный в виде брелока и снабженный дополнительно компасом. https://vizhivai.com/shop/-/988-kurvimetr-mexanicheskij-i-kompas

Циферблат курвиметра имеет шкалы для карт масштаба 1:5000, 1:20000 и 1:50000. а так же метрическую шкалу, цена деления которой соответствует 1 сантиметру .

Стоимость его составляет 120 рублей.

еще один образец с выживай.сом

https://vizhivai.com/shop/-/565-kurvimetr-mexanicheskij

— Измерение расстояния в мм., см., м. милях и км. 
— Диапазон измерений: 10 м. (актуальный размер) 
— Возможности: установка масштаба
— Металлическое колесико для измерений 

Диаметр 4,5см

Длина 9,7см

Вес 30гр.

Материалы: пластик, сталь, стекло пластиковое.

цена 215,00 р. 

В целом, у механических курвиметров можно выделить несколько основных преимуществ: 
— простота конструкции и использования; 
— отсутствие электронных цепей и иных сложных элементов, предполагает возможность его использования в любых климатических, погодных и температурных условиях; 
— полная энергонезависимость в связи с отсутствием элементов питания как таковых; 
— хорошая ударопрочность и невозможность выведения его из строя в результате водных процедур. 

Все вышеперечисленное делает механический курвиметр наиболее пригодным для использования в полевых условиях. Основной и наверное единственный недостаток такого курвиметра это необходимость определять десятые доли цены деления «на глазок».

А теперь обратимся к многообразию электронных курвиметров. Здесь стоимость одного экземпляра колеблется от трехсот до пяти тысяч рублей в зависимости от сложности прибора и количества основных и дополнительных функций в нем. Как и при производстве многих других электронных приборов, производители электронных курвиметров редко избегают соблазна наделить его массой дополнительных функций, как полезных, так и не очень.

Например, один из простейших электронных курвиметров все той же шведской фирмы Silva, под названием«Silva Digital Map Measurer» выполненный в виде брелока, и по мимо выполнения основной функции – измерения расстояния по карте дополнительно снабжен:

— калькулятором; 
— мини фонариком; 
— компасом.

Его стоимость составляет порядка >2000рублей.

Гораздо более сложный высокоточный курвиметр производства США под названием «Scal Master II», предназначен для выполнения сложных графических замеров и вычислений, имеет собственное программное обеспечение, возможность подключения к персональному компьютеру и обладает 91 архитектурной и инженерной функциями.

Этот прибор обрабатывает 50 англо-американских значений (футы, дюймы, и т.д.) и 41 метрическое значение, что позволяет работать с любыми картами и чертежами. Можно ввести наиболее часто используемый вид измерений, и прибор автоматически будет переводить масштабные измерения. Обладает возможностью сохранения данных. Имеет возможность подключения к компьютеру с помощью набора для подключения PC-Interface Kit. Совместим с Windows . Работает с Excel, Lotus.

Технические характеристики курвиметра Scale Master II:

Размер: 182 x 41 x 15 мм 
Вес: 54 г 
Материал колеса: цельный полимер 
Эл. питания: 2 Х 3 Volt — литиум 
Срок использования: до 400 часов 
Автоматическое выключение: 5 мин. 
Кол-во кнопок: 12 
Рабочие температуры: 0 – 55О С 
Размер дисплея: 19 x 64 мм .

Стоимость такого прибора + Набор для подключения к РС –  >11000 рублей

Обобщая информацию об электронных курвиметрах, можно сделать вывод, что их использование в полевых условиях, особенно более сложных аналогов, связано с некоторыми трудностями. Подверженность внешним воздействиям таким как холод и влага, зависимость от наличия элементов питания и значительно меньшая ударопрочность предполагают использование такого прибора в первую очередь в тепличных условиях городских помещений для предварительной разработки маршрутов. При этом, неоспоримым преимуществом электронного курвиметра будет максимальная точность измерений, и возможность немедленной их обработки, например, перевода в километры в зависимости от ранее выставленного масштаба.

http://mirage-spb.narod.ru/positiff.html

Была ли эта статья полезной?

Способы определения пройденного расстояния

Некоторое представление о глазомерной оценке расстояний может дать следующая таблица , в которой приведены предельные расстояния видимости объектов в дневное время для человека с нормальным зрением.

Наблюдаемый объект	Расстояние, км
Большие башни, маяки, элеваторы	16-20
Населенные пункты (общим контуром)	10-12
Фабричные корпуса и трубы	6
Небольшие отдельно стоящие дома, избы	4
Трубы на крышах	2-3
Отдельные высокие деревья	2-3
Стволы деревьев, телеграфные столбы, километровые столбы, фигура человека (общий контур)	1
Движения рук и ног идущего человека	0,6-0,7
Сучья и ветви на деревьях	0,4-0,6
Овал лица, цвет и части одежды человека, переплеты рам в окнах	0,3
Черепица на крыше, листья деревьев, проволока на кольях	0,2
Черты лица, глаза, кисти рук человека	0,07-0,1

Для развития глазомера необходимо иметь представление о том, как далеко лежит от наблюдателя линия горизонта. Дальность горизонта (ДГ) определяется по формуле:

Человек ростом 170 см, стоя на ровной местности, видит линию горизонта на расстоянии около 4,5 км, а поднявшись на высоту 5 м, может наблюдать местность в радиусе до 9 км.

Определение расстояний по времени и скорости движения .
В качестве вспомогательного способа для общего ориентирования можно применить расчет пройденного расстояния, зная время движения и среднюю скорость. Время движения можно определить довольно точно по часам или секундомеру. Сложнее обстоит дело с определением в походных условиях средней скорости движения группы. Причем трудности возникают как с определением абсолютной величины скорости, так и с поддержанием ее постоянства. Однако в некоторых видах путешествии (сплав по реке, движение на лыжах) все-таки возникает необходимость в определении скорости. В каждом конкретном случае надо пытаться определить скорость движения, например по известному отрезку пути, и затем, двигаясь в том же темпе, можно использовать ранее определенное значение скорости и время для расчета неизвестного отрезка пути. Более подробно о скорости движения группы будет рассказано дальше.
В авто-, мото-, а также велосипедном путешествиях пройденный путь определяет спидометр или специальный счетчик, установленный на велосипеде. Интересно, что тот же принцип определения пройденного пути можно использовать в лыжном и пешем походах. Полярные исследователи издавна пользуются для этой цели одометром — прибором, состоящим из колеса, например от детского велосипеда, с насечкой на ободе и счетчика оборотов. Колесо прикрепляется специальным кронштейном к нартам или саням. Для повышения точности измерения одометр прокатывают несколько раз по заранее отмеренному отрезку для определения поправки на проскальзывание по льду или снежному насту. Для простоты расчетов составляют таблицу пройденного расстояния.

Определение расстояний по линейным размерам предметов.

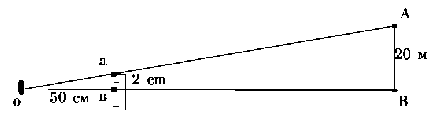
Определение расстояний по известным линейным размерам предметов, расположенных на местности. Сущность этого способа видна из рисунке. Наблюдатель держит линейку, например, плиты спортивного компаса перед собой перпендикулярно лучу зрения на расстоянии 50 см от глаз и определяет по ней величины отрезка ав, закрывающего наблюдаемый объект (дерево высотой 20 м). Из подобия треугольников Оав и ОАВ видно, что:

ОА=АВ х Оа/ав=500м.

Для точного выдерживания базы измерения — в нашем примере 50 см — удобно пользоваться следующим приемом. Длина вытянутой руки фиксируется бичевкои или ниткой с двумя узлами, удаленными друг от друга на заранее точно вымеренный отрезок (50 см). Один узелок зажимается зубами, а другой прижимается пальцем к линейке.
Карты. Основные понятия
Определение направлений и сторон горизонта

Источник

Способы определения пройденного расстояния

Глазомерно расстояние определяют путем сравнения с известным на местности отрезком. На точность глазомерного определения расстояния оказывают влияние освещенность, размеры объекта, его контраст с окружающим фоном, прозрачность атмосферы и другие факторы. Расстояния кажутся меньшими, чем в действительности, при наблюдении через водные пространства, лощины и долины, при наблюдении крупных и отдельно расположенных объектов. И наоборот, расстояния кажутся большими, чем в действительности, при наблюдении в сумерках, против света, в туман, при пасмурной и дождливой погоде. Все эти особенности следует учитывать при глазомерном определении расстояний. Точность глазомерного определения расстояний зависит также от натренированности наблюдателя. Опытным наблюдателем расстояния до 1000 м могут быть определены глазомерно с ошибкой 10-15%. При определении расстояния более 1000 м ошибки могут достигать 30%, а при недостаточной опытности наблюдателя 50%.

Определение расстояний по спидометру. Расстояние, пройденное машиной, определяется как разность показаний спидометра в начале и конце пути. При движении по дорогам с твердым покрытием оно будет на 3-5%, а по вязкому грунту на 8-12% больше действительного расстояния. Такие погрешности в определении расстояний по спидометру возникают от пробуксовки колес (проскальзывания гусениц), износа протекторов покрышек и изменения давления в шинах. Если необходимо определить пройденное машиной расстояние возможно точнее, надо в показания спидометра внести поправку. Такая необходимость возникает, например, пря движении по азимуту или при ориентировании с использованием навигационных приборов.

Величина поправки определяется перед маршем. Для этого выбирается участок дороги, который по характеру рельефа и почвенного покрова подобен предстоящему маршруту. Этот участок проезжают с маршевой скоростью в прямом и обратном направлениях, снимая показания спидометра в начале и конце участка. По полученным данным определяют среднее значение протяженности контрольного участка и вычитают из него величину этого же участка, определенную по карте или на местности лентой (рулеткой). Разделив полученный результат на длину участка, измеренного по карте (на местности), и умножив на 100, получают коэффициент поправки.

Например, если среднее значение контрольного участка равно 4,2 км, а измеренное по карте 3,8 км, то коэффициент поправки

К=((4,2-3,8)/3,8)*100 = 10%

Таким образом, если длина маршрута, измеренного по карте, составляет 50 км, то на спидометре будет отсчет 55 км, т. е. на 10% больше. Разница в 5 км и есть величина поправки. В некоторых случаях она может быть отрицательной.

Измерение расстояний шагами. Этот способ применяется обычно при движении по азимуту, составлении схем местности, нанесении на карту (схему) отдельных объектов и ориентиров и в других случаях. Счет шагов ведется, как правило, парами. При измерении расстоянии большой протяженности шаги более удобно считать тройками попеременно под левую и правую ногу. После каждой сотни пар или троек шагов делается отметка каким-нибудь способом и отсчет начинается снова. При переводе измеренного расстояния шагами в метры число пар или троек шагов умножают на длину одной пары или тройки шагов. Например, между точками поворота на маршруте пройдено 254 пары шагов. Длина одной пары шагов равна 1,6 м. Тогда Д =254Х1,6=406,4 м.

Обычно шаг человека среднего роста равен 0,7- 0,8 м. Длину своего шага достаточно точно можно определить по формуле

где Д-длина одного шага в метрах

Р — рост человека в метрах.

Например, если рост человека 1,72 м, то длина его шага

Более точно длина шага определяется промером какого-нибудь ровного линейного участка местности, например дороги, протяженностью 200-300 м, который заранее измеряется мерной лентой (рулеткой, дальномером и т. п.). При приближенном измерении расстояний длину пары шагов принимают равной 1,5 м.

Средняя ошибка измерения расстояний шагами в зависимости от условий движения составляет около 2-5% пройденного расстояния.

Счет шагов может выполняться с помощью шагомера (рис.1). Он имеет вид и размеры карманных часов. Внутри прибора помещен тяжелый молоточек, который при встряхивании опускается, а под воздействием пружины возвращается в первоначальное положение. При этом пружина перескакивает по зубцам колесика, вращение которого передается на стрелки. На большой шкале циферблата стрелка показывает число единиц и десятков шагов, на правой малой-сотни, а на левой малой-тысячи. Шагомер подвешивают отвесно к одежде. При ходьбе вследствие колебания его механизм приходит в действие и отсчитывает каждый шаг.

Определение расстоянии по времени и скорости движения. Этот способ применяется для приближенного определения величины пройденного расстояния, для чего среднюю скорость умножают на время движения. Средняя скорость пешехода около 5, а при движении на лыжах 8-10 км/ч. Например, если разведывательный дозор двигался на лыжах 3 ч, то он прошел около 30 км.

Определение расстояний по соотношению скоростей звука и света. Звук распространяется в воздухе со скоростью 330 м/с, т. е. округленно 1 км за 3 с, а свет- практически мгновенно (300000 км/ч). Таким образом, расстояние в километрах до места вспышки выстрела (взрыва) равно числу секунд, прошедших от момента вспышки до момента, когда был услышан звук выстрела (взрыва), деленному на 3. Например, наблюдатель услышал звук взрыва через 11 с после вспышки. Расстояние до места вспышки

Определение расстояний на слух. Натренированный слух-хороший помощник в определении расстояний ночью. Успешное применение этого способа во многом зависит от выбора места для прослушивания. Оно выбирается таким образом, чтобы ветер не попадал прямо в уши. Вокруг в радиусе нескольких метров устраняются причины шума, например сухая трава, ветки кустарника и т. п. В безветренную ночь при нормальном слухе различные источники шумов могут быть слышны на даль-ностях, указанных в табл. 1.

Источник

Способы определения расстояний без специальных средств

Ведёте ли вы автомобиль, путешествуете ли с рюкзаком, умение определять расстояния — это важный и полезный навык, как в городе, так и в дали от городской суеты. В данной статье, я расскажу о том, как рассчитывать расстояния и тренировать глазомер.

Варианты определения расстояний до объектов

Среди полезных умений, которые рекомендуется освоить всем, кто предпочитает спокойному отдыху активный, относится определение расстояния на местности. Ситуаций, когда этот навык может пригодиться, множество – отсутствие картографического материала или его порча, утеря, необходимость определить ширину реки на глаз, расстояние до цели, произвести расчет высоты дерева, которое нужно использовать в качестве моста и другое.

Существует не один способ определения расстояний на местности

Существующие варианты отличаются различной погрешностью измерений и инструментарием. Узнать расстояние можно:

1. Методом «на глаз». Подходит, когда на местности есть признаки цивилизации, хотя бы столбы связи.
2. С помощью собственных шагов. Это удобный способ вычисления длины маршрута. Поскольку длина шага – величина постоянная, рекомендуется заранее ее узнать и запомнить.
3. По видимости объектов. Требует навыка, дает наиболее точный результат в ясную погоду.

Определение расстояния «на глаз» или по линейным объектам

Метод измерения расстояния «на глаз» подходит, когда есть объект с известным размером (длина, ширина или высота). Такой расчет считается точным на 90%, а иногда и больше, если набраться опыта.

Линейные размеры самых часто встречающихся объектов:

• легковой автомобиль — Д*Ш*В соответствует 4м*1,5м*1,6м;
• взрослый человек – в среднем 1,7 м;
• голова человека – В*Ш соответствует 0,25м*0,20м;
• столб связи (деревянный) – 6 м;
• столб связи (бетонный) – 8 м;
• расстояние между столбами ЛЭП – 50 м;
• между столбами высоковольтных линий – 100 м;
• деревенский дом – 7 м;
• один этаж многоквартирного дома (панельного) – 3 м.

L Как определять стороны света в природе, рассказываю в статье: Как определить север и юг без компаса днем и ночью

Как определить расстояние до объекта

Возьмите линейку и расположите ее на уровне измеряемого объекта в 50 см от глаз. Размеры предмета (длину, ширину или высоту) измеряют по линейке и учитывают в миллиметрах.

Определение расстояния по линейке

Теперь воспользуйтесь формулой:

Расстояние, м =(реальный размер в см/измеренный размер по линейке в мм)*5.

Этот академический метод в туристической среде был немного упрощен. Определение расстояния туристы проводят по большому пальцу.

Рассмотрим на примере измерения расстояния до столба связи (высота 8 м). Длина большого пальца около 6 см. Вытяните руку перед собой, сожмите ладонь в кулак так, чтобы большой палец смотрел вверх. Расстояние от глаз до пальца будет около 60 см. Определите какой длине соответствует столб, к примеру трети пальца (2 см).

Далее осталось рассчитать пропорцию:

Х = (8 м * 60 см)/2 см =240 м.

Вычисление расстояния шагами

Умение определять расстояния собственными шагами может пригодиться как для любителей туризма (например, при составлении схем местности и наоборот, при поиске объекта, указанного на карте или плане), так и обычным горожанам, которые занимаются, скажем, спортивной ходьбой.

Длина шага — величина постоянная

Шаги используют в качестве мерной единицы по причине того, что человек обычно делает одинаковые по длине шаги, когда идет размеренным шагом по ровной поверхности. Именно эту длину своего шага рекомендуется вычислить и запомнить, как эталонную.

На изменение эталонной длины влияет:

• усталость человека,
• температура воздуха, в жару шаги короче и скорость движения меньше,
• движение по пересеченной местности,
• ходьба в группе, когда мы интуитивно или намеренно подстраиваемся под скорость и шаг других людей,
• тяжелый рюкзак.

Способ «Мокрые ноги »
Определить длину шага можно несколькими способами.

Способ «Мокрые ноги»

Смысл такого измерения в том, что нужно «наследить» мокрыми ногами, затем взять рулетку и узнать расстояние от одной пятки до другой. Для чистоты расчетов, следует сделать несколько шагов, померить расстояния и вычислить среднее значение.

Для метода подойдет любая лужа, если рядом есть сухой асфальт, можно пройти по снегу, грязи, песчаному пляжу, специально намочить ноги и прогуляться дома по полу. Главное, чтобы оставались следы от ступни.

Способ ходьбы на короткое расстояние
Отмерьте на ровной поверхности рулеткой расстояние 10 метров. После этого пройдите и посчитайте количество шагов. Разделите 10 метров на шаги, получите длину одного шага. Затем пройдите в обратную сторону, и снова высчитайте длину шага. Вычислите среднее значение шага.

По карте
Для данного метода подойдет карта, схема местности с объектами А и Б, находящимися в относительной близости друг от друга и расстояние между которыми легко вычислить. Идите из точки А к точке Б и считайте шаги. Разделите расстояние по полученное количество – узнаете длину собственного шага. Вместо бумажной карты можно использовать навигатор, проложив маршрут между двумя точками и затем пройдя его.

По росту
Зная рост, также можно высчитать длину шага, однако вычисление будет слишком усредненным. Для этого рост, выраженный в сантиметрах, нужно умножить на 0,413 (для женщин) или 0,415 (для мужчин).

Имея длину шага, теперь можно без труда считать расстояния в походе или на прогулке. Интересно, что если ввести такой подсчет в привычку, то скоро вы заметите, что считаете шаги уже по инерции. Есть два способа учитывать шаги.

1. Считать каждый шаг.
2. Считать через шаг, т.е. только правую ногу или только левую. Это более удобный вариант для длительных переходов.

Чтобы не сбиться при подсчете, когда количество шагов переваливает за отметку 100, можно на каждую сотню загибать палец или перекладывать спички из одного кармана в другой.

Видимость объектов – как способ узнать расстояние

По тому различимы объекты, находящиеся вдали глазом или нет, также можно достаточно точно определять расстояние. Тренировкой возможно добиться снижения погрешности в определении длины до 10-20% на 1 км.

Определение расстояния по видимым объектам

Используя этот метод, нужно учитывать, что глаз по-разному воспринимает расстояния:

• в темное время суток расстояние визуально увеличивается;
• при наличии осадков объект будет казаться дальше;
• предмет на равнине кажется ближе, чем на холмистой местности;
• водные преграды сильно скрадывают расстояния;
• темный объект будет казаться дальше, чем светлый.

Данные, приведенные ниже, рассчитаны на определение расстояния до объекта днем в ясную погоду на равнинной местности.

1. Если ваш глаз вдали смог различить деревенский дом, то расстояние до него не более 5 км. Способны рассмотреть трубу на крыше? Это уже 3 км.
2. Если возможно увидеть движение ног человека (идущего или бегущего) – до 700 м.
3. Стволы деревьев, столбы линий связи можно распознать с расстояния не более 1 км.
4. Лицо различимо с расстояния до 100 м.

L Как определить погоду в походных условиях, вы узнаете из статьи: Способы как узнать погоду по приметам на завтра

Заключение

В походе нет неважных навыков. Чем больше вы умеете, тем уверенней вы себя чувствуете, особенно в экстремальных ситуациях. Точно определять расстояния «на глаз» можно научиться, всего лишь чаще тренируйте свой глазомер, используя методы, описанные в данной статье.

Источник

Масштаб. Определение расстояний

Масштаб — это отношение длины линии на чертеже, плане или карте к длине соответствующей линии в действительности. Он показывает, во сколько раз расстояние на карте уменьшено относительно реального расстояния на местности. Если, например, масштаб географической карты 1 : 1 000 000, это значит, что 1 см на карте соответствует 1 000 000 см на местности, или 10 км.

Различают численный, линейный и именованный масштабы.

Численный масштаб изображается в виде дроби, у которой числитель равен единице, а знаменатель – число, показывающее, во сколько раз уменьшены линии на карте (плане) относительно линий на местности. Например, масштаб 1:100 000 показывает, что все линейные размеры на карте уменьшены в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем масштаб мельче, при меньшем знаменателе — крупнее. Численный масштаб – это дробь, поэтому числитель и знаменатель даются в одинаковых измерениях (сантиметрах).

Линейный масштаб представляет собой прямую линию, разделенную на равные отрезки. Эти отрезки соответствуют определенному расстоянию на изображаемой местности; деления обозначаются цифрами. Мера длины, по которой нанесены деления на масштабной линейке, называются основанием масштаба. В нашей стране основание масштаба принято равным 1 см. Количество метров или километров, соответствующее основанию масштаба, называют величиной масштаба. При построении линейного масштаба цифру 0, от которой начинается отсчет делений, обычно ставят не у самого конца масштабной линии, а отступив на одно деление (основание) вправо; на первом же отрезке налево от 0 наносят наименьшие деления линейного масштаба – миллиметры. Расстояние на местности, соответствующее одному наименьшему делению линейного масштаба, отвечает точности масштаба, а 0,1 мм – предельной точности масштаба. Линейный масштаб по сравнению с численным имеет то преимущество, что дает возможность без дополнительных вычислений определять действительное расстояние на плане и карте.

Именованный масштаб – масштаб, выраженный словами, например, в 1 см 32 км.

Измерение расстояний на карте и плане.

Измерение расстояний с помощью масштаба. Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е. на местности это расстояние составляет 1 * 5 = 5  (км). Измерять расстояние по карте можно и с помощью циркуля-измерителя. В этом случае удобно пользоваться линейным масштабом.

Измерение расстояний с помощью градусной сети. Для расчета расстояний по карте или глобусу можно использовать следующие величины: длина дуги 1° меридиана и 1° экватора равна приблизительно 111 км. Для меридианов это верно всегда, а длина дуги 1° по параллелям уменьшается к полюсам. На экваторе его можно тоже принять равному 111 км. А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.

---