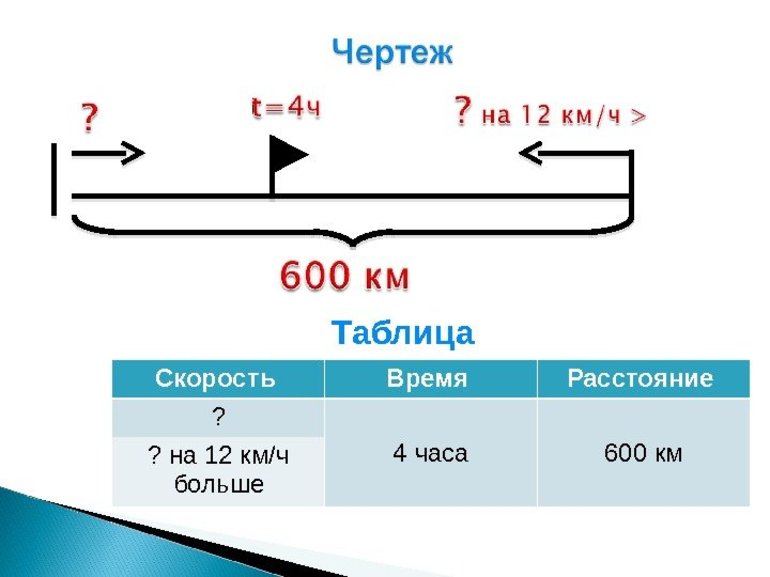
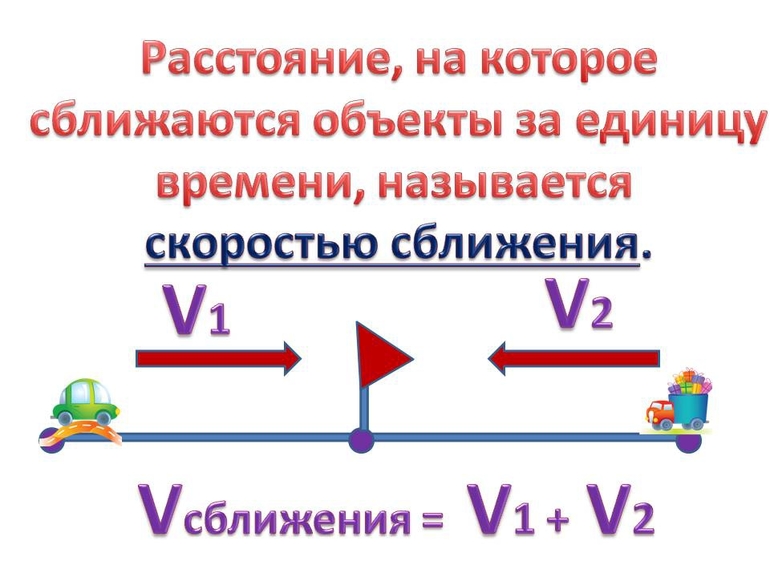
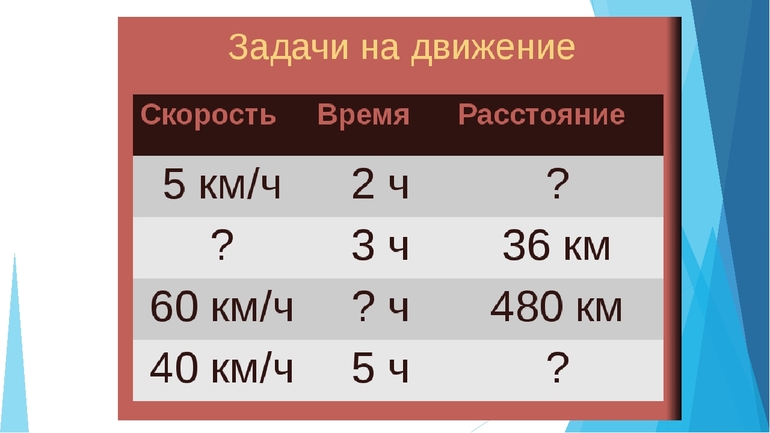
Как найти скорость время расстояние
Добавлено: 12 февраля 2023 в 16:40

Время, расстояние и скорость — три фундаментальные величины, играющие важную роль как в математике, так и в физике. Все вместе они образуют движение, которое и изучают в школе, начиная с 4-го класса.
Теория о данных факторах важна и для подготовки к ЕГЭ по физике, поэтому сегодня мы разберемся с тем, как найти скорость, время, расстояние и понять взаимодействия между указанными параметрами.
К преимуществам темы относят то, что формулы для этих величин просты в запоминании. А при возникновении трудностей в обучении поможет таблица скорости, времени и расстояния.
Скорость время расстояние в ЕГЭ по физике
Понятие о времени
Временем называют особый маркер, который и определяет то или иное событие. Мы сталкиваемся с этим явлением регулярно. Время помогает нам разобраться, где прошлое, где настоящее, а где будущее.
Невозможно рассматривать теорию движения без учета времени, т.к. оно выступает в роли одной из пространственных координат. Однако, если в случае с прочими осями мы можем двигаться в разных направлениях, в случае со временем перемещение возможно только вперед или назад.
Чтобы получше понять правило, нужно разобраться с тем, что собой представляет пространство. Потому что оно объясняет смысл указанного параметра.
Время изучают с античных времен, но с тех пор в науке осталось немало неразрешенных вопросов касающихся этой величины:
- Что является причиной течения времени;
- Почему время может двигаться только по одному направлению;
- Действительно ли время является одномерным параметром;
- Возможно ли определить кванты этого параметра и как это сделать.
Скорость время расстояние в ЕГЭ по физике
Расстояние и скорость
Если смотреть на обсуждаемые величины с точки зрения физики, то можно определить их так:
Расстояние — это размерность длинны, которую выражают в единицах длинны. В каких единицах измеряется пройденный путь? Данная величина измеряется в метрах.
В математике расстоянием называют меру пройденного пути (другими словами, длину). Для определения изменений положений используются оси координат. В чем измеряется расстояние и как обозначается в математике?
В физике путь измеряется в метрах, секундах или часах. А в математике путь измеряется в единицах длины (метрах, метрах в секунду, километрах в час).
Расстояние представляет меру пройденного пути, длину. Для определения изменений положений используют оси координат. Обычно координатная ось X направлена вдоль направления движения, а Y — перпендикулярно ей. В физике координатной осью обычно называют ось, в направлении которой изменяется физическая величина.
В процессе нахождения пройденного пути по общей формуле крайне важную роль играет еще один фактор, называемый скоростью. Она представляет собой параметр быстроты движения объектов.
Скорость время расстояние в ЕГЭ по физике
Скорость можно определить, если известны время и пройденный путь. Подставив эти величины в формулу для пройденного пути, получим формулу для нужного нам неизвестного.
Скорость — параметр скалярный, и путь измеряется в единицах расстояния, а скорость в единицах времени.
Её отмечают, как одну из важнейших математических величин. По причине этого для её определения существуют формулы, которые используются во многих смежных математических дисциплинах.
Эти формулы не только позволяют определить скорость, но и позволяют вывести новые формулы для таких величин, как ускорение, сила, вес и др. На практике для определения скорости используют две основные формулы: формулу скорости равноускоренного движения и формулу ускорения.
Скорость при равноускоренном движении – это скорость тела после истечения определенного промежутка времени.
Скорость время расстояние в ЕГЭ по физике
Общая формула
Время, расстояние и скорость — это фундаментальные, взаимосвязанные параметры. Изучая один из них, невозможно проигнорировать другие ключевые элементы.
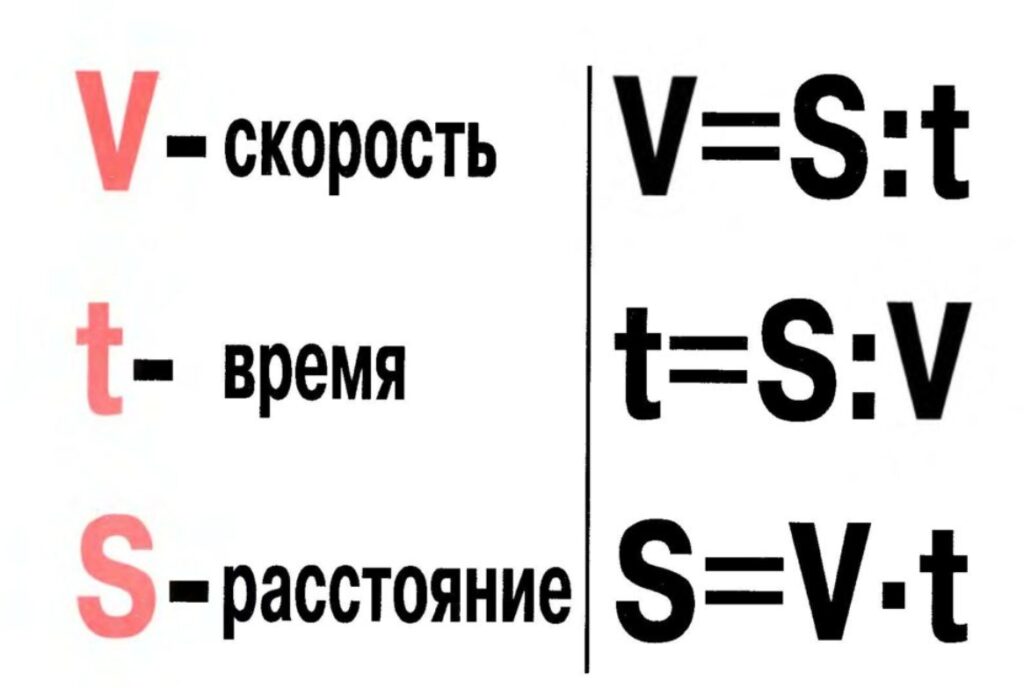
Взаимосвязь этих трех величин отображается в общей формуле S = V * t (формула пройденного пути в физике и математике).
- S — обозначает расстояние;
- V — обозначает скорость;
- t — обозначается время, что было потрачено на весь путь.
Выучив это равенство, вы сможете легко определить любой из трех параметров.
Например, S = V * t — это формула того, как найти расстояние, зная скорость и время. Зная расстояние и скорость, вы поймете, как найти время:
- t = S / V.
А параметр скорости определяется так:
- V = S / t.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Кандидат физико-математичеких наук. Преподавательский стаж более 10 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Читайте также:
Оглавление:
- Кинематика
- Динамика
- Статика
- Гидростатика
- Импульс
- Работа, мощность, энергия
- Молекулярная физика
- Термодинамика
- Электростатика
- Электрический ток
- Магнетизм
- Колебания
- Оптика
- Атомная и ядерная физика
- Основы специальной теории относительности (СТО)
- Равномерное движение по окружности
- Расширенная PDF версия документа «Все главные формулы по школьной физике»
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
К оглавлению…
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению…
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению…
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т.ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению…
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению…
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению…
Мы собрали основные формулы по физике с пояснениями в картинках. Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время — количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:
- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
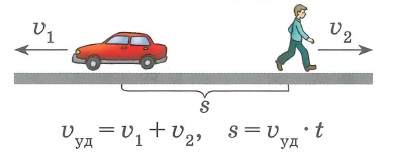
- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
Равномерное движение |
|
| S= U∙t, U= S/t, t=S/U | Уравнение движения при равномерном движении?
где U-скорость, t-время, S-расстояние |
| x=x0+U0t | Координата при равномерном прямолинейном движении |
Равномерное движение по окружности |
|
| T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a) |
T – период N – количество оборотов |
| v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t |
v – частота R – радиус окружности |
| ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R) |
ω – угловая скорость t – время |
| υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t |
U – линейная скорость тела |
|
a=υ2/R, a=ω2R, a=Uω |
a – центростремительное ускорение |
| L=φR | L – длина дуги окружности (φ – угол поворота (в радианах)) |
Равноускоренное движение |
|
| X=X0+υ0∙t+(a∙t2)/2 | Уравнение прямолинейного равноускоренного движения |
| S=U0t+a∙t2/2 S= (υ2-υ02) /2а S= (υ+υ0) ∙t /2 = Uср∙t |
Расстояние при равноускоренном движении |
| υ=υ0+a∙t | Rонечная скорость тела при равноускоренном движении |
| a=(υ-υ 0)/t | Ускорение |
| U=√(2gh) tпадения=√(2h/g) S=U∙√(2h/g) |
— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с2, t-время падения, S-расстояние) |
| hmax=U02/2g | Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U0 |
| tподъема=U0/g | Время подъема тела на максимальную высоту |
| tполета=2U0/g | Полное время полета (до возвращения в исходную точку) |
| Sторм=U02/2a | Тормозной путь тела двигавшегося до начала торможения со скоростью U0 , а затем тормозившего с ускорением а |
| U = √(U02+(gt)2) tgβ = Uy/Ux = gt/U0 |
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту |
| hmax=(U0∙sinα)2/2g tподъема=(U0∙sinα)/g |
Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и максимальная высота |
|
Sx=Ux∙tполета |
Полное время и дальность полета при броске под углом к горизонту |
Импульс |
|
|
p=mυ |
Импульс тела |
|
Ft=∆p |
Импульс силы |
|
F=∆p/∆t |
Второй закон Ньютона в импульсной форме |
|
pk=pn |
Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется |
Энергия |
|
|
A=F∙S∙cosα |
Механическая работа (F – сила, S – путь, – угол между направлением движения и силой) |
|
P=A/t=F∙υ |
Мощность (если мощность переменная, то рассчитывается средняя мощность) |
|
Eп=mgh |
Потенциальная энергия тела, поднятого над землей |
|
Eп=kx2/2 |
Потенциальная энергия упруго деформированного тела |
|
η=Aп/Аз |
Коэффициент полезного действия |
|
Ek=mυ2/2 |
Кинетическая энергия тела |
Молекулярная физика |
|
|
ρ=m/V |
Плотность (ρ – его плотность, m – масса вещества, V – объем) |
|
ν=N/ Na = m/M |
Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса) |
|
М=m/ν |
Молярная масса |
|
m0=m/N=M/Na |
Масса одной молекулы вещества |
|
P=nkT=1/3nm0υ2 |
Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость) |
|
Uкв=√(3kT/m0), Uкв=√(3RT/M) |
Cредняя квадратичная скорость |
|
Ek=3/2∙kT |
Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура) |
|
kNa=R |
Связь универсальной газовой постоянной и постоянной Авогадро |
|
PV=m/M∙RT |
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) |
|
PV=const (m=const и T= const) |
Газовые законы. Закон Бойля-Мариотта (изотермический процесс) |
|
V/T=const (m=const и p= const) |
Газовые законы. Закон Гей-Люссака (изобарный процесс) |
|
P/T =const (m=const и V= const) |
Газовые законы. Закон Шарля (изохорный процесс) |
|
PV/T=const (m=const ) |
Газовые законы. Универсальный газовый закон (Клапейрона) |
|
V=Vo(1+λt) |
Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости) |
|
l=lo(1+αt) |
Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела) |
Динамика |
|
|
Первый закон Ньютона |
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения |
|
F=ma |
Второй закон Ньютона (F – сила, m – масса, а – ускорение). |
|
F1-2 = — F2-1 |
Третий закон Ньютона (сила действия равна силе противодействия) |
|
Fупр = kx |
Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины) |
|
Fy=-kx |
Закон Гука |
|
Fтр.скольжения=Fтр.макс = μТ |
Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.) |
|
F=mg |
Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел) |
|
gh = GM/(Rn+h)2 = |
Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты) |
|
U = √(GM/(Rn+h)) |
Скорость спутника на круговой орбите радиусом r = Rn + h |
|
U=√(gRn) |
Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты) |
|
T12/T22 = R13/R23 |
Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно |
|
Р=m(g+a) |
Вес тела, движущегося с ускорением а↑ |
Термодинамика |
|
|
Q=cm(T2-T1) |
Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура) |
|
Q=λm |
Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости) |
|
Q=rm |
Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара) |
|
Q=qm |
Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива) |
|
A=P∙ΔV = m/M∙ R∙ΔT, p = const |
Работа идеального газа |
|
U=3/2∙M/µ∙RT |
Внутренняя энергия идеального одноатомного газа |
|
ΔU=A+Q |
Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом) |
|
η= (Q1 — Q2)/ Q1 |
КПД тепловых двигателей |
|
η= (Т1 — Т2)/ Т1 |
КПД идеальных двигателей (цикл Карно) |
|
ρ=pM/RT |
Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура) |
|
φ=ρ/ρ0∙100% |
Относительная влажность (ρ — абсолютная влажность, ρ0 -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре) |
|
Ep = σS |
Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости) |
|
Fн= σL |
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L |
Статика и Гидростатика |
|
|
M=F∙ℓ |
Момент силы (F – сила, ℓ – плечо силы, т.е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) |
|
Р=F/S |
Давление (F – сила, S – площадь на которую распределено действие силы) |
|
P=ρ∙g∙h |
Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости) |
|
Fa=ρж∙g∙V |
Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости) |
Электростатика |
|
|
q = Ne |
Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд) |
|
λ=q/L, σ=q/S, ρ=q/V |
Линейная, поверхностная и объемная плотность заряда |
|
F=k∙q1∙q2/R2 |
Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε): |
|
E=1/(4πεε0) |
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра |
|
E= σ/(2εε0) |
Напряженность электрического поля, которую создает заряженная плоскость |
|
ε=E0/E |
Диэлектрическая проницаемость |
|
E=F/q |
Напряженность электрического поля |
|
E=k∙q/R2 |
Напряженность электрического поля точечного заряда |
|
E=2πkσ |
Напряженность электрического поля бесконечной плоскости |
|
W= k∙q1q2/R = k∙q1q2/εr |
Потенциальная энергия взаимодействия двух электрических зарядов |
|
U=Ed, Δφ=E∙ Δl |
Cвязь между напряженностью поля и напряжением |
|
A=qU, U=A/q |
Работа электрического поля, Напряжение |
|
A= qEd, U=E∙d |
Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля |
|
φ=W/q |
Потенциал |
|
φ=k∙q/R |
Потенциал точечного заряда |
|
C=q/U |
Электроемкость |
|
C=S∙ε∙ε0/d |
Электроемкость плоского конденсатора |
|
q=CU |
Заряд конденсатора |
|
E = U/d = σ/εε0 |
Напряженность поля внутри конденсатора |
|
F=qE/2 |
Сила притяжения пластин конденсатора |
|
W=qU/2=q²/2С=CU²/2 |
Энергия заряженного конденсатора |
Электрический ток |
|
|
I=q/t |
Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t) |
|
R=ρ∙ℓ/S |
Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника) |
|
R=R0(1+αt) |
Сопротивление проводника |
|
I=U/R |
Закон Ома для участка цепи (U – электрическое напряжение) |
|
I1=I2=I, U1+U2=U, R1+R2=R |
Законы последовательного соединения |
|
U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R |
Законы параллельного соединения |
|
ε=Aст/q |
Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q) |
|
I=ε/(R+r) |
Закон Ома для полной цепи |
|
I=ε/r |
Сила тока короткого замыкания (R=0) |
|
Q=A=I2Rt |
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике |
|
P=IU=U2/R=I2R |
Мощность электрического тока |
|
m = kQ = kIt |
Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит |
Магнетизм |
|
|
Fa=IBℓsinα |
Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля) |
|
M = NBIS∙sinα |
Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции) |
|
Fл=Bqυ∙sinα |
Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля) |
|
R=mU/qB |
Радиус траектории полета заряженной частицы в магнитном поле |
|
B=Fmax/ℓ∙I |
Вектор магнитной индукции |
|
Ф=BSсos α Ф=LI |
Магнитный поток Φ через площадь S |
|
Ei=ΔФ/Δt |
Закон электромагнитной индукции |
|
Ei=Вℓυsinα |
ЭДС индукции при движении проводника |
|
Esi=-L∙ΔI/Δt |
ЭДС самоиндукции |
|
Wм=LI2/2 |
Энергия магнитного поля катушки |
Колебания |
|
|
a+ω02x=0 |
Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0 |
|
x = A cos (ωt + φ0) |
Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний). |
|
Х=Хmax∙cos ωt |
Уравнение гармонических колебаний |
|
T=t/N, v=N/t=1/T |
Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота) |
|
υ = x'(t) = –Aω sin (ωt + φ0) |
Скорость тела при колебательном движении |
|
υm = ωA |
Максимальное (амплитудное) значение скорости |
|
a = υ'(t) = x»(t) |
Ускорение тела при колебательном движении |
|
am = Aω2 |
Максимальное (амплитудное) значение ускорения |
|
ω0=√(g/ℓ) |
Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения) |
|
ω0=√(k/m) |
Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника) |
|
W=CU2/2+LI2/2 |
Электрический контур |
|
T=2π ∙√LC |
Период колебаний кол. контура и циклическая частота |
|
Iд=I0/√2, Iд=Imax/√2 |
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения |
|
P=UдIд =Iд2R=Uд2/R |
Мощность в цепи переменного тока |
|
U1/U2=n1/n2 |
Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2 |
|
λ= υТ=υ/v |
Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота) |
|
XL=ωL=2πLν |
Индуктивное сопротивление |
|
Xc=1/ωC |
Емкостное сопротивление |
|
Z=√(Xc-XL)2+R2 |
Полное сопротивление |
Оптика |
|
|
Lопт=Ln |
Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит) |
|
x=mλL/d |
Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели). |
|
d∙sin φ=k λ |
Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку) |
|
n21=n2/n1= υ 1/ υ 2 |
Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч) |
|
n21=sinα/sinβ |
Показатель преломления |
|
1/F=1/d + 1/f |
Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы) |
|
D=1/F |
Оптическая сила линзы |
|
Δd=kλ, Δd=(2k+1)λ/2 |
max интерференции, min интерференции |
Атомная и ядерная физика |
|
|
E=hv=hc/λ |
Энергия кванта света, т.е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) |
|
P=mc=h/ λ=Е/с |
Импульс фотона |
|
hν=Aвых+(mU2/2)max |
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (Авых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света) |
|
(mU2/2)max=еUз |
Максимальная кинетическая энергия вылетающих электронов |
|
νк = Aвых/h |
Красная граница фотоэффекта |
|
hνnm = |En – Em| |
Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний |
|
N=N0∙2—t/T |
Закон радиоактивного распада |
|
ECB=(Zmp+Nmn-Mя)∙c2 |
Энергия связи атомных ядер |
Основы СТО |
|
|
ℓ=ℓ0∙√1-υ2/c2 |
Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины |
|
t=t1/√(1-υ2/c2) |
Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета |
|
υ=(υ1+υ2)/1+ υ1∙υ2/c2 |
Релятивистский закон сложения скоростей |
|
Е = mс2 |
Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела) |