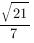Как найти расстояние в призме треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

В правильной треугольной призме , все рёбра которой равны , найдите расстояние между прямыми и

Прямые AA_1 и BC_1 — скрещивающиеся.

Расстояние между ними равно длине их общего перпендикуляра. Оно также равно расстоянию от AA_1 до параллельной ей плоскости BB_1C_1 , в которой лежит прямая BC_1 .

Проведем A_1H , где H — середина B_1C_1 . Треугольник правильный, поэтому

Также , поскольку призма прямая.

По признаку перпендикулярности прямой и плоскости, Значит, A_1H перпендикулярна любой прямой, лежащей в плоскости BB_1C_1 , в том числе прямой BC_1.

Кроме того, Получим, что A_1H — общий перпендикуляр к прямым AA_1 и BC_1 , и длина A_1H равна расстоянию между AA_1 и BC_1. Найдем A_1H как высоту правильного треугольника со стороной

$A_1H=frac{sqrt{3}cdot sqrt{3}}{2}=1,5.$

Задание 14 Профильного ЕГЭ по математике. Стереометрия

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 14 Профильного ЕГЭ по математике. Стереометрия. Задача 6» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В данной подборке из открытого банка ФИПИ
рассматриваются задачи на нахождение расстояния от вершины правильной треугольной
призмы до секущей плоскости. (Вспомним, что у правильной треугольной призмы в
основании лежит правильный треугольник, и боковые рёбра перпендикулярны
основаниям).

Некоторые факты
стереометрии, которые пригодятся при решении этих задач. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного
из этой точки на данную плоскость.

Признак
перпендикулярности плоскостей.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти
плоскости перпендикулярны.

Признак
перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым в плоскости,
то она перпендикулярна этой плоскости.

Теорема о трёх перпендикулярах. Если прямая,
проведенная на плоскости через основание наклонной, перпендикулярна ее проекции,
то она перпендикулярна наклонной.
И обратно: Если прямая на плоскости перпендикулярна наклонной, то она
перпендикулярна и проекции наклонной.

Задача 1. В правильной
треугольной призме ABCA₁B₁C₁
стороны
основания равны 1, боковые

рёбра
равны 3, точка D — середина
ребра CC₁. Найдите
расстояние от вершины C до плоскости ADB₁.

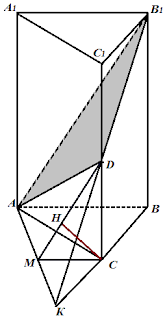
Решение. Построим сечение
данной призмы плоскостью АDВ₁. Это
треугольник АDВ₁. Секущая плоскость ADB₁
имеет с основанием общую точку А, следовательно пересекает плоскость АВС
по прямой, проходящей через точку А. Определим вторую точку этой прямой.
Продолжим сторону основания ВС до пересечения с прямой B₁D и получим
точку К – общую для плоскости АВС и секущей плоскости АDВ₁.
Следовательно, прямая, по которой пересекаются эти плоскости – это прямая АК.

Заметим, что треугольники КСD и DВ₁С₁ равны ( они
прямоугольные, С₁D = DС по условию, углы С₁DB₁и
СDК – вертикальные). Значит СК = B₁С₁ = АС. Треугольник
АСК – равнобедренный, угол САК равен углу СКА и равен 30 градусам (угол АСВ
внешний угол треугольника АСК и равен сумме углов САК и СКА). Проведём высоту СМ. В треугольнике СМК катет
МС равен половине гипотенузы КС, значит СМ = 0,5.

Соединив
точки М и D, получим прямоугольный
треугольник МDС. В нём проведём
высоту СН. Докажем, что СН и есть расстояние от точки А до плоскости АDВ₁. Так как прямая
АК перпендикулярна МС, то АК перпендикулярна и МD по теореме о трёх перпендикулярах. Значит, АК
перпендикулярна плоскости DМС
и прямой НС. Но НС перпендикулярна МD, значит и плоскости АDК (по признаку
перпендикулярности прямой и плоскости).

Задачи для самостоятельного решения.

1.
В
правильной треугольной призме ABCA₁B₁C₁
стороны
основания равны 1, боковые рёбра равны 2, точка D — середина ребра CC₁. Найдите
расстояние от вершины C до плоскости ADB₁.

2.
В
правильной треугольной призме ABCA₁B₁C₁ стороны основания
равны 2, боковые рёбра равны 3, точка D — середина ребра CC₁. Найдите
расстояние от вершины C до плоскости ADB₁.

3.
В
правильной треугольной призме ABCA₁B₁C₁ стороны
основания равны 3, боковые рёбра равны 1, точка D — середина ребра CC₁. Найдите расстояние
от вершины C до плоскости ADB₁.

4.
В
правильной треугольной призме ABCA₁B₁C₁
стороны
основания равны 2, боковые рёбра равны 1, точка D — середина ребра CC₁. Найдите
расстояние от вершины C до плоскости ADB₁.

5.
В
правильной треугольной призме ABCA₁B₁C₁
стороны
основания равны 3, боковые рёбра равны 2, точка D — середина ребра CC₁. Найдите
расстояние от вершины C до плоскости ADB₁.

Источник

12
Май 2012

13 Задание (2022) (C2)

Расстояние между скрещивающимися прямыми-2. Задание С2

В этой статье мы разберем решение такой задачи: В правильной треугольной призме , все рёбра которой равны 1, найдите расстояние между прямыми и

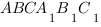
Рассмотрим чертеж задачи:

Чтобы найти расстояние между скрещивающимися прямыми, нужно, для начала, через одну из прямых провести плоскость, параллельную второй прямой. В нашем случае для этого прийдется сделать дополнительное построение:

Мы получили призму, в основании которой лежит ромб со стороной, равной 1 и углом 60°.

Теперь в плоскости грани DBB_1 проведем прямую D_1B параллельно прямой A_1C ,

и через эту прямую проведем плоскость ABD_1 , которая будет параллельна прямой A_1C :

Расстояние между прямыми и A_1C равно расстоянию от любой точки прямой A_1C до плоскости AB D_1 .

Будем искать расстояние от точки С до плоскости AB D_1 . Для этого проведем плоскость DCC_1 , перпендикулярно плоскости AB D_1 (, так как диагонали ромба перпендикулярны, $AB{ortho}DD_1$ , так как призма правильная):

KD_1 — линия пересечения плоскости AB D_1 и плоскости DCC_1 .

Рассмотрим треугольник D_1KC . Нам нужно найти расстояние от точки С до прямой D_1K , то есть высоту треугольника, проведенную из вершины С:

(из треугольника KBC ), $D_1K=sqrt{7}/2$ (из треугольника DD_1K ), D_1C=2 (из треугольника D_1CC_1 ):

Дальше поступим так:

1. Найдем cos C по теореме косинусов.

2. Найдем sin C через основное тригонометрическое тождество.

3. Найдем площадь треугольника D_1KC по формуле .

4. Из площади выразим высоту, опущенную на основание D_1K — это и есть искомое расстояние.

3. $S_{D_1KC}={1/2}2sqrt{3}/2{1/2}=sqrt{3}/4$

Ответ:

Замечание: призму можно было достроить «вверх». Попробуйте это решение самостоятельно.

И.В. Фельдман, репетитор по математике.

|
Отзывов (14)
| Метки: решение задания С2

Источник

Очень многие подобные задачи решаются дополнительным построением (достроением, пристроением.). Нужно взять ещё одну точно такую же призму, «поставить» на исходную. Верхние точки добавленной призмы обозначить теми же буквами с индексом 2, т.е. А2, В2 и С2. Сразу же становится ясно, что искомая плоскость (АКС) является частью плоскости треугольника АВ2С, и что точка Р лежит на середине А1В1.

Далее, расстояние ВН проще всего определить через объём пирамиды АВСВ2. Если рассматривать в качестве основания пирамиды плоскость треугольника АВС, (высота ВВ2=6), то объём

V=(1/3)*6*2^2*√3/4=2√3.

С другой стороны, в качестве основания пирамиды можно рассматривать плоскость треугольника АВ2С, тогда ВН — высота этой пирамиды. Осталось вычислить площадь треугольника АВ2С. Он равнобедренный. Стороны АВ2 и СВ2 легко вычисляются по Пифагору и равны √40. Высота также по Пифагору равна √39. Значит площадь треугольника АВ2С равна (1/2)*2*√39=√39. Тогда ВН=6√3/√39)=6/√13=1,664100589

Источник

На чтение 4 мин Просмотров 66.4к. Опубликовано 13 февраля, 2019

Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Содержание

Призма треугольная — определение
Элементы треугольной призмы
Виды треугольных призм
Прямая треугольная призма
Наклонная треугольная призма
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Площадь боковой поверхности призмы
Площадь полной поверхности призмы
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Пример призмы
Задачи на расчет треугольной призмы

Призма треугольная — определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы.

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы.

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

или

V=S_осн^. h

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

или

S_бок=P_осн^.h

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн^.h, то получим:

S_{полн.пов.}=P_осн^.h+2S_осн

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы:

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см², то высота должна быть выражена в сантиметрах, а объем — в см³ . Если площадь основания в мм², то высота должна быть выражена в мм, а объем в мм³ и т. д.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k² = S₁2² = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

Источник