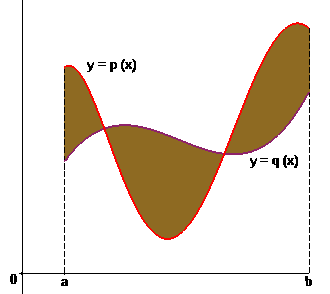
Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: 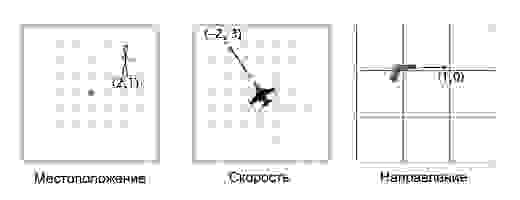
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
Расстояние
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
Важность дистанционных метрик в моделировании машинного обучения
Дата публикации Jan 13, 2019
Ряд алгоритмов машинного обучения — контролируемых или неконтролируемых — используют метрики расстояния, чтобы знать шаблон входных данных для принятия любого решения на основе данных. Хороший показатель расстояния помогает значительно повысить производительность процессов классификации, кластеризации и поиска информации. В этой статье мы обсудим различные метрики расстояния и то, как они помогают в моделировании машинного обучения.
Введение
Во многих реальных приложениях мы используем алгоритмы машинного обучения для классификации или распознавания изображений, а также для извлечения информации из содержимого изображения. Например, распознавание лиц, цензурированные изображения в Интернете, розничный каталог, системы рекомендаций и т. Д. Здесь очень важно выбрать хороший показатель расстояния. Метрика расстояния помогает алгоритмам распознавать сходства между содержимым.
Определение базовой математики (Источник Википедия),
Метрика расстояния использует функцию расстояния, которая обеспечивает метрику отношения между каждым элементом в наборе данных.
Некоторые из вас могут подумать, что это за функция расстояния? как это работает? как он решает, что определенный контент или элемент данных имеет какие-либо отношения с другим? Что ж, давайте попробуем выяснить это в следующих нескольких разделах.
Функция расстояния
Вы помните изучение теоремы Пифагора? Если вы это сделаете, то вы можете вспомнить вычисление расстояния между двумя точками данных, используя теорему.
Чтобы вычислить расстояние между точками данных A и B, в теореме Пифагора рассматривается длина осей x и y.
Многим из вас должно быть интересно, используем ли мы эту теорему в алгоритме машинного обучения, чтобы найти расстояние? Чтобы ответить на ваш вопрос, да, мы используем его. Во многих алгоритмах машинного обучения мы используем приведенную выше формулу в качестве функции расстояния. Мы поговорим об алгоритмах, где он используется.
Теперь вы, наверное, поняли, что такое функция расстояния? Вот упрощенное определение.
Основное определение от Math.net,
Функция расстояния обеспечивает расстояние между элементами набора. Если расстояние равно нулю, то элементы эквивалентны, иначе они отличаются друг от друга.
Функция расстояния — это не что иное, как математическая формула, используемая метриками расстояния. Функция расстояния может отличаться в зависимости от метрики расстояния. Давайте поговорим о различных дистанционных метриках и поймем их роль в моделировании машинного обучения.
Метрики расстояния
Существует несколько метрик расстояния, но для краткости этой статьи мы обсудим лишь несколько широко используемых метрик расстояния. Сначала мы попытаемся понять математику, стоящую за этими метриками, а затем определим алгоритмы машинного обучения, в которых мы используем эти метрики расстояния.
Ниже приведены часто используемые метрики расстояния —
Минковский Расстояние:
Расстояние Минковского является метрикой в нормированном векторном пространстве. Что такое нормированное векторное пространство? Нормированное векторное пространство — это векторное пространство, в котором определена норма. Предположим, что X — векторное пространство, тогда норма на X — вещественная функция ||Икс|| который удовлетворяет условиям ниже —
- Нулевой вектор-Нулевой вектор будет иметь нулевую длину.
- Скалярный фактор-Направление вектора не меняется, когда вы умножаете его на положительное число, хотя его длина будет изменена.
- Неравенство треугольникаЕсли расстояние является нормой, то рассчитанное расстояние между двумя точками всегда будет прямой линией.
Вам может быть интересно, зачем нам нужен нормированный вектор, не можем ли мы просто перейти к простым метрикам? Поскольку нормированный вектор обладает указанными выше свойствами, это помогает поддерживать индуцированную норму метрико-однородной и трансляционной инвариантом. Более подробную информацию можно найтиВот,
Расстояние можно рассчитать по приведенной ниже формуле —
Расстояние Минковского является обобщенной метрикой расстояния. Здесь обобщенный означает, что мы можем манипулировать приведенной выше формулой, чтобы рассчитать расстояние между двумя точками данных различными способами.
Как уже упоминалось выше, мы можем манипулировать значениемпи рассчитать расстояние тремя разными способами-
р = 2, евклидово расстояние
р = ∞, расстояние чебычева
Мы обсудим эти метрики расстояния ниже подробно.
Манхэттен Расстояние:
Мы используем Манхэттенское расстояние, если нам нужно рассчитать расстояние между двумя точками данных в виде сетки, как путь. Как уже упоминалось выше, мы используемМинковское расстояниеформула, чтобы найти расстояние Манхэттена, установивр-хзначение как1,
Допустим, мы хотим рассчитать расстояние,dмежду двумя точками данныхИкса такжеY
Расстояниеdбудет рассчитываться с использованиемабсолютная сумма разностеймежду его декартовыми координатами, как показано ниже:
где, n- количество переменных,XIа такжеугявляются переменными векторов x и y соответственно в двумерном векторном пространстве. то естьх = (х1, х2, х3, . )а такжеу = (у1, у2, у3,…),
Теперь расстояниеdбудет рассчитываться как
(x1 — y1)+(x2 — y2)+(х3 — у3)+… +(xn — yn),
Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:
Расстояние до Манхэттена также известно как геометрия такси, расстояние до городских кварталов и т.д.
Евклидово расстояние:
Евклидово расстояние — одна из наиболее часто используемых метрик расстояния. Он рассчитывается по формуле Минковского расстояния путем установкир-хзначение для2, Это обновит расстояние«D»формула как ниже:
Давай остановимся ненадолго! Эта формула выглядит знакомо? Ну да, мы только что видели эту формулу выше в этой статье при обсуждении«Теорема Пифагора».
Евклидова формула расстояния может быть использована для расчета расстояния между двумя точками данных на плоскости.
Расстояние косинуса:
В основном, метрика косинусного расстояния используется для поиска сходства между различными документами. В косинусной метрике мы измеряем степень угла между двумя документами / векторами (термин частоты в разных документах собирается как метрика). Эта конкретная метрика используется, когда величина между векторами не имеет значения, но ориентация.
Формула подобия косинуса может быть получена из уравнения точечных произведений:
Теперь вы должны подумать, какое значение угла косинуса будет полезно для определения сходства.
Теперь, когда у нас есть значения, которые будут рассматриваться для измерения сходства, нам нужно знать, что означают 1, 0 и -1.
Здесь значение косинуса 1 предназначено для векторов, указывающих в одном и том же направлении, то есть между документами / точками данных есть сходства. В нуле для ортогональных векторов, т. Е. Не связанных (найдено некоторое сходство). Значение -1 для векторов, указывающих в противоположных направлениях (без сходства).
Махаланобис Расстояние:
Расстояние Махаланобиса используется для расчета расстояния между двумя точками данных в многомерном пространстве.
Согласно определению Википедии,
Махаланобис расстояниеявляется мерой расстояния между точкой P и распределением D. Идея измерения состоит в том, сколько стандартных отклонений P от среднего значения D.
Преимущество использования расстояния по махаланобису заключается в том, что учитывается ковариация, которая помогает измерять силу / сходство между двумя различными объектами данных. Расстояние между наблюдением и средним может быть рассчитано, как показано ниже:
Здесь S — ковариационные метрики. Мы используем обратную метрику ковариации, чтобы получить нормализованное по дисперсии уравнение расстояния.
Теперь, когда у нас есть базовое представление о различных метриках расстояния, мы можем перейти к следующему шагу, а именно к методам / моделированию машинного обучения, в которых используются эти метрики различий.
Моделирование машинного обучения и дистанционные метрики
В этом разделе мы будем работать над некоторыми базовыми вариантами использования для классификации и кластеризации. Это поможет нам понять использование метрик расстояния в моделировании машинного обучения. Мы начнем с быстрого введения контролируемых и неконтролируемых алгоритмов и постепенно перейдем к примерам.
1. Классификация
K-Ближайшие соседи (KNN) —
KNN — это не вероятностный контролируемый алгоритм обучения, т.е. он не дает вероятности принадлежности к какой-либо точке данных, а KNN классифицирует данные при жестком назначении, например, точка данных будет принадлежать 0 или 1. Теперь вы должны подумать как работает KNN, если не используется уравнение вероятности. KNN использует метрики расстояния, чтобы найти сходства или различия.
Давайте возьмем набор данных iris, который имеет три класса, и посмотрим, как KNN будет определять классы для тестовых данных.
На изображении № 2 над черным квадратом находится тестовая точка данных. Теперь нам нужно найти, к какому классу относится эта контрольная точка данных, с помощью алгоритма KNN. Теперь мы подготовим набор данных для создания модели машинного обучения, чтобы предсказать класс для наших тестовых данных.
В алгоритме классификации КНН мы определяем постоянную«K».K — количество ближайших соседей контрольной точки данных. Эти K точек данных затем будут использоваться для определения класса для точки тестовых данных (обратите внимание, что это в наборе обучающих данных).
Вам интересно, как бы мы нашли ближайших соседей. Ну вот где метрика расстояния входит в картинки. Сначала мы рассчитываем расстояние между каждым поездом и контрольной точкой данных, а затем выбираем ближайшую вершину в соответствии со значением k.
Мы не будем создавать KNN с нуля, но будем использовать scikit KNN классификатор
Как видно из приведенного выше кода, мы используем метрику расстояния Минковского со значением p, равным 2, то есть в классификаторе KNN будет использоваться формула Евклидовой метрики расстояния.
По мере продвижения вперед в моделировании машинного обучения мы можем теперь обучать нашу модель и начинать предсказывать класс для тестовых данных.
Как только верхние ближайшие соседи выбраны, мы проверяем большинство проголосовавших классов в соседях —
Из приведенного выше изображения, вы можете угадать класс для контрольной точки? Это класс 1, так как он является самым популярным.
Из этого небольшого примера мы увидели, какметрика расстояниябыл важен для классификатора KNN.Это помогло нам получить самые близкие точки данных поезда, для которых были известны классы.Существует вероятность, что при использовании различных метрик расстояния мы могли бы получить лучшие результаты. Таким образом, в не вероятностном алгоритме, таком как KNN, метрики расстояния играют важную роль.
2. Кластеризация
K-нуждаемость
В алгоритмах классификации, вероятностных или не вероятностных, нам будут предоставлены помеченные данные, что упрощает прогнозирование классов. Хотя в алгоритме кластеризации у нас нет информации о том, какая точка данных принадлежит какому классу. Метрики расстояния являются важной частью этого вида алгоритма.
В K-средних мы выбираем количество центроидов, которые определяют количество кластеров.Затем каждая точка данных будет привязана к ближайшему центроиду, используя метрику расстояния (евклидово), Мы будем использовать данные радужной оболочки, чтобы понять основной процесс K-средних.
На приведенном выше изображении № 1, как вы можете видеть, мы случайно разместили центроиды, а на рисунке № 2, используя метрику расстояния, пытались найти ближайший класс кластеров.
Нам нужно будет повторять назначение центроидов до тех пор, пока у нас не будет четкой кластерной структуры.
Как мы видели в приведенном выше примере, не имея никаких знаний о метках с помощью метрики расстояния в K-средних, мы разбили данные на 3 класса.
3. Обработка естественного языка
Поиск информации
В поиске информации мы работаем с неструктурированными данными. Данные могут быть статьей, веб-сайтом, электронной почтой, текстовыми сообщениями, публикацией в социальных сетях и т. Д. С помощью методов, используемых в НЛП, мы можем создавать векторные данные таким образом, чтобы их можно было использовать для получения информации при запросе. Как только неструктурированные данные преобразуются в векторную форму, мы можем использовать метрику косинусного сходства, чтобы отфильтровать ненужные документы из корпуса.
Давайте возьмем пример и поймем использование косинусного сходства.
- Создать векторную форму для Корпуса и Query-
2. Проверьте сходства, т.е. найдите, какой документ в корпусе имеет отношение к нашему запросу.
Как видно из приведенного выше примера, мы запросили слово«Коричневый»и в корпусе есть только три документа, которые содержат слово«Коричневый».При проверке с помощью косинусной метрики сходства он дал те же результаты, имея> 0 значений для трех документов, кроме четвертого
Вывод
В этой статье мы узнали о нескольких популярных метриках расстояния / сходства и о том, как их можно использовать для решения сложных задач машинного обучения. Надеюсь, что это будет полезно для людей, которые только начинают изучать машинное обучение и науку о данных.
http://habr.com/ru/post/131931/
http://www.machinelearningmastery.ru/importance-of-distance-metrics-in-machine-learning-modelling-e51395ffe60d/
Skip to content
Длина вектора в пространстве
Длиной (или модулем) вектора называется расстояние между началом и концом вектора.
Длина вектора a{X,Y,Z} выражается через его координаты следующей формулой:
Пример
Длина вектора $aleft{ { — 2,3,sqrt 3 } right}$ равна
$left| a right| = sqrt {{X^2} + {Y^2} + {Z^2}} = $
$sqrt {{{left( { — 2} right)}^2} + {3^2} + {{left( {sqrt 3 } right)}^2}} = sqrt {16} = 4$
Расстояние между двумя точками в пространстве
Расстояние d между точками в пространстве A1{x1;y1;z1}, A2{x2;y2;z2} представляется формулой
Пример
Расстояние между точками A1{4;-6;3} и A2 {-1;5;-4}
$d = sqrt {{{left( {{x_2} — {x_1}} right)}^2} + {{left( {{y_2} — {y_1}} right)}^2} + {{left( {{z_2} — {z_1}} right)}^2}} = $
$=sqrt {{{left( { — 1 — 4} right)}^2} + {{left( {5 — left( { — 6} right)} right)}^2} + {{left( { — 4 — 3} right)}^2}} =$
$ =sqrt {25 + 121 + 49} = sqrt {195} approx 14$
12831
Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми
({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V.
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4.
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
1.6. Расстояние между двумя точками
Если
нам известны координаты точек (естественно,
в заданной системе координат), то
однозначно известно их положение.
Поэтому можно найти любые геометрические
характеристики их взаимного расположения.
Получим формулы, позволяющие по известным
координатам двух точек вычислить
расстояние между ними.
В
простейшем случае, когда две
точки А1 и А2 находятся
на одной оси, расстояние между ними
определяется формулой
s
= |x2 −
x1|,
(3)
где х1, х2 −
координаты точек А1 и А2 соответственно.
Очевидно,
что расстояние от А1 до А2 равно
расстоянию от А
2 до А1,
что и привело у к тому, что в формуле (3)
появился знак модуля числа.
Пусть
на плоскости задана система координат ХОY,
в которой координаты точки А1 равны х1 и у1,
а координаты точки А2,
соответственно, равны х2 и у2 (рис.
8).
рис.
8
В
прямоугольном треугольнике А1А2В длина
стороны А2В равна |х2 −
х1|,
а длина стороны А1В
= |у2 −
у1|,
поэтому расстояние между точками А1 и А2 можно
найти по теореме Пифагора:
s
= √{(x2
−
x1)2 +
(y2 −
y1)2}.
(4)
Сложение
векторов
Пусть
даны два вектора
и
.
Приложим вектор
к
точке
(концу
вектора
)
и получим вектор
(рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор
называется суммой
векторов
и
и
обозначается
.
Это нахождение суммы называется правилом
треугольника.
Сумму
двух неколлинеарных векторов
и
можно
найти по правилу
параллелограмма.
Для этого откладываем от любой
точки
векторы
и
,
а затем строим параллелограмм
(рис.
1.7,6). Диагональ
параллелограмма
определяет сумму:
.
Для
нахождения суммы нескольких векторов
можно построить ломаную из равных им
векторов. Тогда замыкающий
вектор,
соединяющий начало первого вектора
ломаной с концом последнего ее вектора,
равен сумме всех векторов ломаной. На
рис.1.7,в изображена сумма
четырех
векторов
.
Таким способом (
правило
ломаной)
можно сложить любое конечное число
векторов. Заметим, что сумма векторов
не зависит от точек приложения слагаемых
и от порядка суммирования.
«выстраивая цепочку» векторов для
суммы в виде
,
получим вектор, равный вектору
.
Если ломаная получилась замкнутой, то
сумма равна нулевому вектору.
Вычитание
векторов
Вектор
называется противоположным вектору
,
если их сумма равна нулевому вектору:
.
Противоположный вектор
имеет
длину
,
коллинеарен и противоположно направлен
вектору
(рис.1.8,а,б).
Нулевой вектор является противоположным
самому себе.
Разностью
векторов
и
называется
сумма вектора
с
вектором
,
противоположным вектору
:
Для
нахождения разности векторов
и
приложим
к произвольной точке
векторы
,
а также вектор
,
противоположный вектору
(рис.1.9,а).
Искомую разность находим по правилу
параллелограмма:
Для
нахождения разности проще использовать
правило треугольника (рис. 1.9,6). Для этого
прикладываем к произвольной
точке
векторы
.
Вектор
при
этом равен искомой разности
.
Вычитание
векторов — действие, обратное сложению
— можно определить также следующим
образом: разностью
векторов
и
называется
такой вектор
,
который в сумме с вектором
дает
вектор
(рис.1.9,в),
т.е. разность
—
это решение уравнения
.
Пример
1.2. Для
векторов на рис. 1.6 найти следующие суммы
и разности:
Решение. Учитывая
равенство
,
получаем по правилу треугольника
.
Поскольку
и
,
то
.
По
правилу параллелограмма
.
Так
как
и
,
находим
Умножение
вектора на число
Произведением
ненулевого вектора а на действительное
число
называется
вектор
,
удовлетворяющий условиям:
1)
длина вектора
равна
,
т.е.
;
2)
векторы
и
коллинеарные
;
3)
векторы
и
одинаково
направлены, если
,
и противоположно направлены, если
.
Произведение
нулевого вектора на любое число
считается
(по определению) нулевым вектором:
;
произведение любого вектора на число
нуль также считается нулевым вектором:
.
Из определения произведения следует,
что:
а)
при умножении на единицу
вектор
не изменяется:
;
б)
при умножении вектора на
получается
противоположный вектор:
;
в) деление
вектора на отличное от нуля число
сводится
к его умножению на число
,
обратное
.
г)
при делении ненулевого вектора
на
его длину, т.е. при умножении
на
число
получаем
единичный вектор, одинаково направленный
с вектором
.
Действительно,
длина вектора
равна
единице:
.
Вектор
коллинеарен
и одинаково направлен с вектором
,
так как
;
д)
при умножении единичного вектора на
число
получаем
коллинеарный ему вектор, длина которого
равна
.
На
рис.1.10 изображены векторы, получающиеся
в результате умножения данного
вектора
на
и
,
а также противоположный вектор
.
Свойства
линейных операций над векторами
Сложение
векторов и умножение вектора на число
называются линейными
операциями над векторами.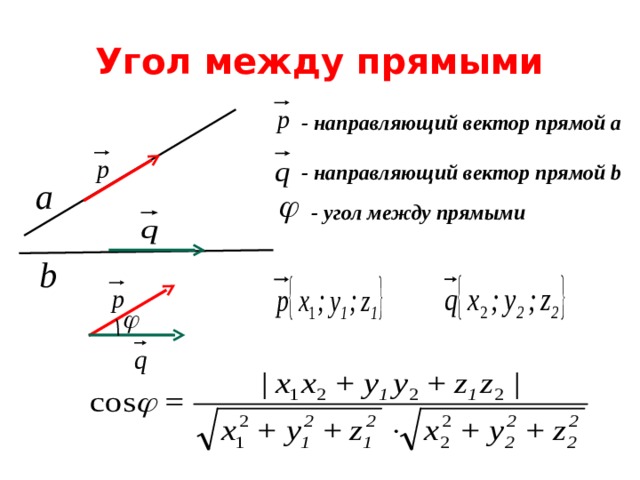
CREATE OR REPLACE FUNCTION public.euclidian(
arr1 double precision[],
arr2 double precision[])
RETURNS double precision AS
$BODY$
select sqrt(SUM(tab.v)) as euclidian from (SELECT
UNNEST(vec_sub(arr1,arr2)) as v) as tab;
$BODY$
LANGUAGE sql IMMUTABLE STRICT
Вспомогательная функция:
CREATE OR REPLACE FUNCTION public.vec_sub(
arr1 double precision[],
arr2 double precision[])
RETURNS double precision[] AS
$BODY$
SELECT array_agg(result)
FROM (SELECT (tuple.val1 - tuple.val2)*(tuple.val1 - tuple.val2)
AS result
FROM (SELECT UNNEST($1) AS val1
,UNNEST($2) AS val2
,generate_subscripts($1, 1) AS ix) tuple
ORDER BY ix) inn;
$BODY$
LANGUAGE sql IMMUTABLE STRICT
Запрос :
select tab.id as tabid, tab.name as tabname,
euclidian(target_vector,tab.vector) as eucl from tab
order by eulc ASC
limit 1
Пока всё отлично работает.
Но нетрудно заметить, что запрос может быть выполнен не иначе как полным перебором всех записей в таблице tab.
Вопрос — как можно изловчиться и обеспечить индексный поиск в таблице tab при выполнении запроса? Чтобы хотя бы 90% ненужных записей отбрасывалось по индексу, а в оставшихся 10% уже допустимо полным перебором пройти.
P.S. одно из текущих направлений поиска решения: расширение PostGIS позволяет вести поиск и сортировку по расстоянию (ST_3DDistance), фильтр по удаленности (ST_3DWithin) и пр. в 3-х мерном пространстве — делается это быстро по индексам. Может быть как-то кто-то это абстрагировал на случай N-мерного пространства?
P.S.2. данные метеорологических наблюдений:
- сделал запрос select max(val), min(val) from (select unnest(vector)
as val from tab) as tab1 — 0.485470712185 -0.41735497117 — я точно не
знаю, думаю значения координат в теории не превышают 1.0 по модулю - при этом векторы не нормализованы, расстояние от (0,0,…0) лежит в
пределах от 1.2 до 1.6.
P.S.3. Подобную задачу не первый раз решаю — предыдущий раз это было связано с поиском ближайшей точки в облаке точек (3D), но там у меня было все локально в памяти (база данных iBoxDB), там даже и не рыпался от полного перебора уйти… а тут вся мощь сервера postgresql — из принципа хочется решить).
P.S.4. Исходя из данных наблюдений, максимальное расстояние между точками (на основании имеющейся статистики) составляет примерно 3.2 — расширим на всякий случай до 5, ну или до 10. Мне точно не интересны точки, отдаленные друг от друга более чем на 1.0. Выделим из 128-мерного пространства несколько (сколько не жалко, скажем 10,20) трехмерных проекций — наборов координат (v1,v2,v3), (v4,v5,v6), и т.д. Очевидно, если в одной из трехмерных проекций расстояние превысило лимит (1.0) — то меньшим на полном наборе координат оно точно уже не станет.
P.S.5. В сторону buckets предлагаю больше не копать — во первых их ну ооочень много получится, как не раскидывай — даже если строить на проекции а не на полной размерности, скажем взять первых 64 координаты и раскидать по букетам (<0,>=0) — получится 18446744073709551616 возможных букетов — куда тут… Во вторых, есть проблема границ букетов — точки могут находиться на минимальном расстоянии но попасть в соседние букеты, это нада учитывать в запросах, для этого нужно держать диаграмму соседей для каждого букета… если же применять простейшее разбиение (<0,>=0) — оно в принципе теряет всякий смысл, потому что для одной оси граница только одна и нужно все равно искать и там и там.
Расстояние между векторами — исчисление 3
Все ресурсы исчисления 3
6 Диагностические тесты
373 практических теста
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Исчисление 3 Помощь »
Векторы и векторные операции »
Расстояние между векторами
По векторам
найти расстояние между ними, .
Возможные ответы:
Правильный ответ:
Объяснение:
, чтобы найти расстояние между векторами
Мы делаем следующий расчет:
Отчет о ошибке
Найдите расстояние между двумя векторами
33.
Правильный ответ:
Объяснение:
, чтобы найти расстояние между двумя векторами
Мы делаем следующий расчет
Отчет о ошибке
.
Правильный ответ:
Объяснение:
Евклидово расстояние между двумя векторами:
Подставив указанные числа, мы получим:
Сообщить об ошибке
Найдите расстояние между если и .
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для нахождения модуля вектора .
Подставьте точки в уравнение, предполагая и .
Ответ:
Сообщить об ошибке Возможные ответы:
Ничего из вышеперечисленного
Правильный ответ:
5
Объяснение:
Сначала нам нужно найти
, поэтому
Сообщить об ошибке
Вычислить расстояние между векторами и .
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для расстояния между двумя векторами
и
равна
.
Используя заданные векторы, получаем
Сообщить об ошибке
Найти расстояние между векторами и .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти расстояние между векторами, мы используем формулу
,
, где один вектор
, а другой
.
Используя заданные нам векторы, получаем
.
Сообщить об ошибке
Найти расстояние между векторами и .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти расстояние между векторами, мы используем формулу
,
, где один вектор
, а другой
.
Используя заданные векторы, мы получаем
.
Сообщить об ошибке
Расстояние между (1, 3, -10) и (2, 5, 4) равно
Возможные ответы:
Ничего из перечисленного
Правильный ответ:
Объяснение:
Мы используем формулу расстояния:
Сообщить об ошибке
Учитывая точки P :(2,−1,5) и Q :(−2,0,3).
Возможные ответы:
Ничего из вышеперечисленного
Правильный ответ:
Объяснение:
Сначала нам нужно найти:
Следовательно,
Отчет о ошибке
← Предыдущий 1 2 3 4 5 Следующий →
Уведомление об авторских правах
Все расчет 3 Ресурсы
660004. Тесты
373 практических теста
Вопрос дня
Карточки
Учитесь по концепции
scipy.spatial.distance.cdist — Руководство по SciPy v1.9.3
- scipy.spatial.distance.cdist( XA , XB , metric=’евклидов’ , * , out=None , **kwargs 3)[68]
-
Вычислить расстояние между каждой парой двух наборов входных данных.
Общие соглашения о вызовах см. в примечаниях.
- Параметры
-
- XA массив_подобный
-
Массив (m_A) по (n) из (m_A)
оригинальные наблюдения в (n)-мерном пространстве.
Входы преобразуются в тип с плавающей запятой. - XB array_like
-
Массив (m_B) на (n) из (m_B)
оригинальные наблюдения в (n)-мерном пространстве.
Входы преобразуются в тип с плавающей запятой. - метрика str или вызываемая, необязательная
-
Используемая метрика расстояния. Если строка, функция расстояния может быть
«брейкертис», «канберра», «чебышев», «городской квартал», «корреляция»,
«косинус», «игральные кости», «евклидово», «хамминг», «жаккард», «дженсеншаннон»,
«kulczynski1», «mahalanobis», «matching», «minkowski»,
«Рогерстанимото», «Расселрао», «Севклидов», «Сокалмихенер»,
‘sokalsneath’, ‘sqeuclidean’, ‘yule’. - **kwargs dict, необязательный
-
Дополнительные аргументы для метрики : см.
документацию по каждой метрике для
список всех возможных аргументов.Некоторые возможные аргументы:
p : скаляр
P-норма для Минковского, взвешенная и невзвешенная.
По умолчанию: 2.w : массив_подобный
Весовой вектор для метрик, поддерживающих веса (например, Минковского).В : массив_подобный
Вектор дисперсии для стандартизированного евклидова.
По умолчанию: var(vstack([XA, XB]), ось=0, ddof=1)VI : array_like
Обратная ковариационная матрица для Махаланобиса.
По умолчанию: inv(cov(vstack([XA, XB].T))).Tвыход: ndarray
Выходной массив
Если не None, матрица расстояний Y хранится в этом массиве.
- Возвращает
-
- Y ndarray
-
Возвращается матрица расстояний (m_A) на (m_B).
Для каждого (i) и (j) метрика
dist(u=XA[i], v=XB[j])вычисляется и сохраняется в
(ij)-я запись.
- Поднимает
-
- ValueError
-
Исключение выдается, если XA и XB не имеют
одинаковое количество столбцов.
Примечания
Ниже приведены общепринятые соглашения о вызовах:
-
Y = cdist(XA, XB, "евклидово")Вычисляет расстояние между (m) точками, используя
Евклидово расстояние (2-норма) как метрика расстояния между
точки. Точки расположены как (m)
(n)-мерные векторы-строки в матрице X. -
Y = cdist(XA, XB, 'Минковский', p=2.)Вычисляет расстояния, используя расстояние Минковского
(|u-v|_p) ((p)-норма), где (p > 0) (примечание
что это квазиметрика только в том случае, если (0 < p < 1 )). -
Y = cdist(XA, XB, 'городской квартал')Вычисляет расстояние в квартале или на Манхэттене между
точки. -
Y = cdist(XA, XB, 'севклидово', V=нет)92) между
векторы. -
Y = cdist(XA, XB, 'косинус')Вычисляет косинусное расстояние между векторами u и v,
[1 — frac{u cdot v}
{{|и|}_2 {|v|}_2}], где (|*|_2) — 2-норма его аргумента
*, и
(u cdot v) является скалярным произведением (u) и (v). -
Y = cdist(XA, XB, «корреляция»)Вычисляет корреляционное расстояние между векторами u и v. Это
[1 — frac{(u — bar{u}) cdot (v — bar{v})}
{{|(u — bar{u})|}_2 {|(v — bar{v})|}_2}], где (bar{v}) — среднее значение элементов вектора v,
и (x cdot y) является скалярным произведением (x) и (y). -
Y = cdist(XA, XB, 'Хэмминг')Вычисляет нормализованное расстояние Хэмминга или пропорцию
эти элементы вектора между двумя n-векторамиuиv
что не согласен. Для экономии памяти матрицаXможет быть типа
логический. -
Y = cdist(XA, XB, 'жаккард')Вычисляет расстояние Жаккара между точками. Учитывая два
векторов,uиv, расстояние Жаккара равно
доля тех элементовu[i]иv[i], что
не согласен, где хотя бы один из них отличен от нуля. -
Y = cdist(XA, XB, 'дженсеншаннон')Вычисляет расстояние Дженсена-Шеннона между двумя массивами вероятностей.
Учитывая два вектора вероятности, (p) и (q),
Расстояние Дженсена-Шеннона равно 9.0005[sqrt{frac{D(pпараллельный m) + D(qпараллельный m)}{2}}]
, где (m) — среднее поточечное между (p) и (q)
а (D) — дивергенция Кульбака — Лейблера. -
Y = cdist(XA, XB, "чебышев")Вычисляет расстояние Чебышева между точками.
Расстояние Чебышева между двумя n-векторамииииравно
максимальное расстояние по норме-1 между их соответствующими элементами. Более
точно, расстояние равно[d(u,v) = max_i {|u_i-v_i|}.]
-
Y = cdist(XA, XB, 'канберра')Вычисляет канберрское расстояние между точками.
Расстояние в Канберре между двумя точкамииииравно.
[d(u,v) = sum_i frac{|u_i-v_i|}
{|u_i|+|v_i|}.]
-
Y = cdist(XA, XB, 'брейкертис')Вычисляет расстояние Брея-Кертиса между точками.
Расстояние Брея-Кертиса между двумя точками 9T}) где ((1/V)) (VI
переменная) — обратная ковариация. ЕслиVIне None,
VIбудет использоваться как обратная ковариационная матрица. -
Y = cdist(XA, XB, 'юл')Вычисляет Йольское расстояние между логическими
векторы. (см. документацию по функциямyule) -
Y = cdist(XA, XB, «совпадение»)Синоним слова «хамминг».
-
Y = cdist(XA, XB, 'кости')Вычисляет расстояние Dice между булевыми векторами. (видеть
костидокументация по функциям) -
Y = cdist(XA, XB, 'Кульчинский1')Вычисляет расстояние по Кульчинскому между логическими
векторы. (см. документацию по функциямkulczynski1) -
Y = cdist(XA, XB, 'Рогерстанимото')Вычисляет расстояние Роджерса-Танимото между логическими
векторы.(см.
rogerstanimotoдокументация по функциям) -
Y = cdist(XA, XB, 'расселрао')Вычисляет расстояние Рассела-Рао между логическими
векторы. (см. документацию по функциямrussellrao) -
Y = cdist(XA, XB, 'сокалмиченер')Вычисляет расстояние Сокаля-Михенера между логическими
векторы. (см. функциональную документациюsokalmichener) -
Y = cdist(XA, XB, 'sokalsneath')Вычисляет расстояние Сокала-Снита между векторами. (видеть
sokalsneathдокументация по функциям) -
Y = cрасст(XA, XB, f)Вычисляет расстояние между всеми парами векторов в X
используя предоставленную пользователем функцию 2-арности f. Например,
Евклидово расстояние между векторами можно вычислить
следующим образом:dm = cdist(XA, XB, lambda u, v: np.sqrt(((u-v)**2).sum()))
Обратите внимание, что вам следует избегать передачи ссылки на один из
функции расстояния, определенные в этой библиотеке.Например:
dm = cdist(XA, XB, sokalsneath)
будет вычислять попарные расстояния между векторами в
X с использованием функции Pythonsokalsneath. Это приведет к
sokalsneath вызывается ({n choose 2}) раз, что
неэффективен. Вместо этого оптимизированная версия C более
эффективным, и мы вызываем его, используя следующий синтаксис:dm = cdist(XA, XB, 'sokalsneath')
Примеры
Найдите евклидовы расстояния между четырьмя двумерными координатами:
>>> из scipy.spatial расстояние импорта >>> координаты = [(35.0456, -85.2672), ... (35.1174, -89.9711), ... (35,9728, -83,9422), ... (36.1667, -86.7833)] >>> Distance.cdist(координаты, координаты, 'евклидово') массив([[ 0. , 4,7044, 1,6172, 1,8856], [ 4,7044, 0, , 6,0893, 3,3561], [ 1,6172, 6,0893, 0. , 2,8477], [ 1,8856, 3,3561, 2,8477, 0. ]])Найдите манхэттенское расстояние от трехмерной точки до углов объекта
куб:>>> a = np.
array([[0, 0, 0], ... [0, 0, 1], ... [0, 1, 0], ... [0, 1, 1], ... [1, 0, 0], ... [1, 0, 1], ... [1, 1, 0], ... [1, 1, 1]]) >>> b = np.array([[ 0,1, 0,2, 0,4]]) >>> Distance.cdist(a, b, 'городской квартал') массив([[ 0,7], [ 0,9], [1.3], [ 1,5], [ 1,5], [1,7], [ 2.1], [ 2.3]])
5.3.1: Расстояние между точкой и плоскостью
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14667
Расстояние между точкой и плоскостью
Расстояние между конкретной точкой и плоскостью важно для ряда различных действий.
Например, вышка для прыжков с тарзанки не была бы очень безопасной, если бы расстояние до земли не измерялось в точке непосредственно под башней, поскольку любой угол, отклоняющийся от прямой линии вниз, увеличил бы расстояние и привел бы к веревке.
Программист компьютерных игр должен знать, как рассчитать расстояние между местоположением персонажа на экране и стенами вокруг него, чтобы сообщить игре, как определить, когда снаряд попадает в цель или когда персонаж попадает в стену.
Расстояние между точкой и плоскостью
Определение точки, ближайшей к началу координат
Независимо от ориентации плоскости всегда будет одна точка, расположенная ближе к началу координат, чем любая другая точка на плоскости. Это означает, что вектор положения для этой точки короче, чем для любой другой точки на плоскости. На приведенной ниже диаграмме показана двухмерная проекция плоскости, выделенная серым цветом, рядом с точкой, находящейся не на плоскости, черным цветом. Векторы положения в различные точки показаны на диаграмме. Вектор положения, отмеченный синим цветом, короче, чем векторы положения для других точек. Этот кратчайший вектор равен перпендикулярно плоскости.
Эта ортогональность (то есть перпендикулярность) полезна для нас, потому что это означает, что вектор положения для этой специальной точки параллелен вектору нормали. Следовательно, если мы знаем уравнение для вектора нормали и вектор положения для любой точки на плоскости, мы можем определить положение ближайшей к началу координат точки на плоскости, найдя проекцию вектора положения данной точки на нормаль направление.
Двугранный угол
Угол между двумя плоскостями называется двугранным углом . Угол между двумя плоскостями равен углу между их векторами нормали. Если мы хотим определить двугранный угол между двумя плоскостями, мы идентифицируем векторы нормалей к двум плоскостям, тогда мы можем использовать скалярное произведение двух векторов нормалей, чтобы определить угол между двумя нормалями, который также является двумя плоскостями.
Примеры
Пример 1
Три точки ( P=(3,7,2), Q=(1,4,3)) и ( R=(2 ,3,4)) определяют плоскость. Определить точку на плоскости, ближайшую к началу координат.
Решение
Сначала найдите векторы между двумя парами точек.
( begin{array}{l}
overrightarrow{P Q}=leftlangleleft(Q_{x}-P_{x}right),left(Q_{y}-P_{ y}right),left(Q_{z}-P_{z}right)rightrangle=langle(1-3),(4-7),(3-2)rangle=langle -2,-3,1угол
overrightarrow{PR}=leftlangleleft(R_{x}-P_{x}right),left(R_{y}-P_{y}right),left(R_{z} -P_{z}right)rightrangle=langle(2-3),(3-7),(4-2)rangle=langle-1,-4,2rangle
end{ array})
Произведение этих двух векторов перпендикулярно плоскости.
( begin{array}{l}
overrightarrow{P Q} times overrightarrow{PR}=leftlangleleft(P Q_{y} P R_{z}-P Q_{z} P R_{y}right),left(P Q_{z} P R_{x}-P Q_{x} P R_{z}right),left(P Q_{x} P R_{y} -P Q_{y} P R_{x}right)rightrangle \
overrightarrow{P Q} times overrightarrow{P R}=langle[(-3 cdot 2)-(1 cdot-4)],[(1 cdot-1)-(-2 cdot 2) ],[(-2 cdot-4)-(-1 cdot-3)]rangle \
vec{n}=overrightarrow{P Q} times overrightarrow{P R}=langle[(- 6)-(-4)],[(-1)-(-4)],[(8)-(3)]rangle=langle-2,3,5rangle
end{массив} )
Точку на плоскости, ближайшую к началу координат, можно найти, определив проекцию вектора положения любой из этих трех точек на вектор нормали. Помните, что векторная проекция одного вектора на направление другого задается скалярным произведением первого вектора на единичный вектор, определяющий направление второго вектора: ( (vec{A} times vec {B}) vec{B}). 9{2}}}=frac{langle-2,3,5rangle}{sqrt{38}}=langle-0.32,0.49,0.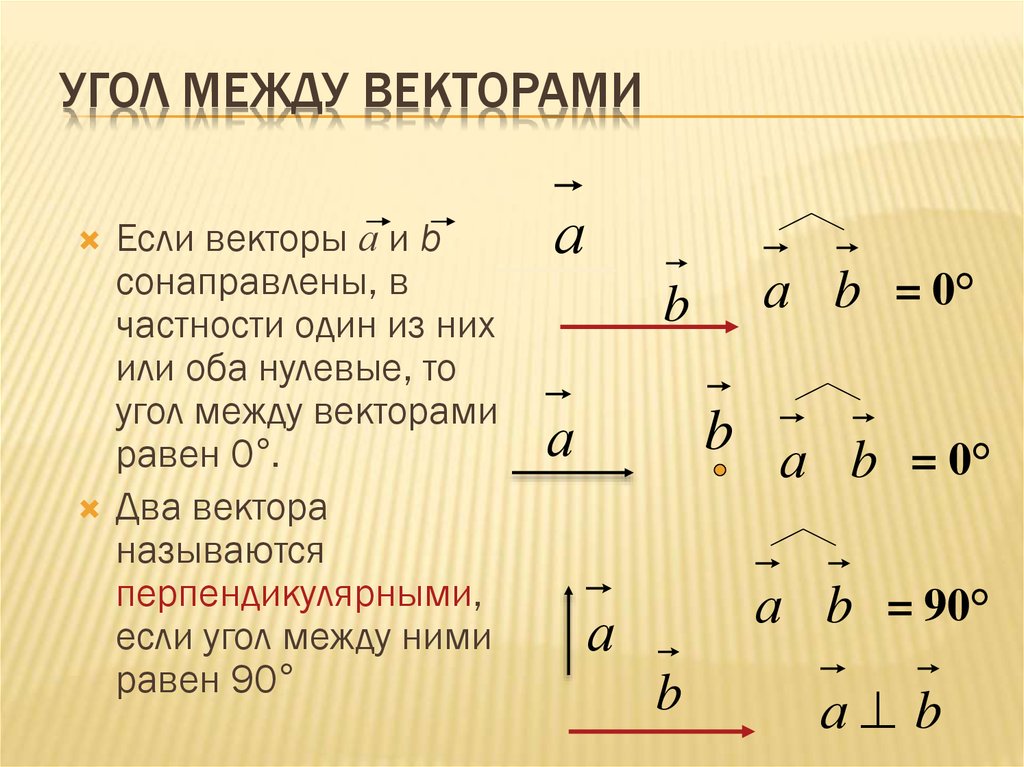
vec{P} timeshat {n}=P_{x} шляпа{n}_{x}+P_{y} шляпа{n}_{y}+P_{z} шляпа{n}_{z}=(3)( -0,32)+(7)(0,49)+(2)(0,81)= \
-0,96+3,43+1,62=4,09 \
(vec{P} times шляпа{n}) шляпа{n }=(4.09)langle-0.32,0.49,0.81rangle=langle-1.3088,2.0041,3.3129rangle
end{массив})
Следовательно, ближайшая к началу координат точка на плоскости (- 1,3088, 2,0041, 3,3129).
Пример 2
Три точки ( P=(3,7,2), Q=(1,4,3)) и ( R=(2,3,4)) определяют самолет. Определите двугранный угол между этой плоскостью и плоскостью x-y.
Решение
Как мы видели в примере выше, эти три точки определяют плоскость с вектором нормали ( vec{n}=langle-2,3,5rangle)
нормаль к плоскости xy представляет собой единичный вектор ( hat{z}=langle 0,0,1rangle). Чтобы найти угол между этими двумя векторами, мы используем тот факт, что ( vec{A} times vec{B}=|vec{A}||vec{B}|) и что ( vec{A} times vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z})
Сначала найдите числовое значение для скалярный продукт: 9{ circ}
end {Array} )
Пример 3
Определите дихедральный угол между двумя плоскостями 12 x + 23 y + 14 0007 Z — 5 = 00008 + 140007 Z — 00007 y + 14 0007 .
Решение
Этот угол также равен углу между нормалями к двум плоскостям. В двух предыдущих задачах мы определили единичные векторы, перпендикулярные этим двум плоскостям ( overrightarrow{n_{1}}=leftlanglefrac{12}{29.5}, frac{23}{29.5}, frac{14}{29.5}rightrangle) и ( overrightarrow{n_{2}}=leftlanglefrac{7}{ sqrt{59}}, frac{3}{sqrt{59}}, frac{1}{sqrt{59}},rightrangle). Затем мы можем использовать скалярное произведение этих двух векторов нормалей, чтобы определить угол между ними. Скалярное произведение определяется как ( vec{A} times vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}+ ldots) и как ( vec{A} times vec{B}=|A||B| cos theta). Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.
( begin{array}{l}
overrightarrow{n_{1}} times overrightarrow{n_{2}}=overrightarrow{n_{1 x} n_{2 x}}+overrightarrow {n_{1 y} n_{2 y}}+overrightarrow{n_{1 z} n_{2 z}}=frac{12 cdot 7}{29,5 sqrt{59}}+frac{23 cdot 3}{29 cdot 5 sqrt{59}}+frac{14 cdot 1}{29,5 sqrt{59}} \
overrightarrow{n_{1}} times overrightarrow{n_{2 }}=frac{12 cdot 7}{29,5 sqrt{59}}+frac{23 cdot 3}{29,5 sqrt{59}}+frac{14 cdot 1}{29,5 sqrt{ 59}}=frac{119}{226,6}+frac{69}{226,6}+frac{14}{226,6}=frac{202}{226,6}=0,89{circ}
end{array})
Пример 4
Определить угол между плоскостью 2 x — 5 y + 8 — 907 08 08 0 и
7 0 —
z самолет.
Решение
Двугранный угол определяется как угол между двумя плоскостями, а также равен углу между двумя единичными векторами нормали. В этом случае мы уже знаем единичный вектор нормали для плоскости y-z, ( hat{x}=langle 1,0,0rangle). Однако нам еще нужно определить единичный вектор для плоскости 2 9{2}}}=frac{langle 2,-5,8rangle}{sqrt{4+25+64}}=frac{langle 2,-5,8rangle}{9,64} = leftlanglefrac{2}{9.64}, frac{-5}{9.64}, frac{8}{9.64}rightrangle)
Угол между двумя плоскостями равен углу между двумя нормальными векторами.
Затем мы можем использовать скалярное произведение этих двух векторов нормалей, чтобы определить угол между ними. Скалярное произведение определяется как ( vec{A} times vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}+ ldots) и как ( vec{A} times vec{B}=|A||B| cos theta). Во-первых, нам нужно найти компонентную версию скалярного произведения и величины двух векторов нормалей.
( overrightarrow{n_{1}} times overrightarrow{n_{2}}=overrightarrow{n_{1 x}} overrightarrow {n_{2 x}}+overrightarrow{n_{1 y }} overrightarrow{n_{2 y}}+overrightarrow{n_{1 z}}overrightarrow {n_{2 z}}=frac{2 cdot 1}{9,64}+frac{-5 cdot 0}{9,64}+frac{8 cdot 0}{9,64}=frac{2}{9,64}=0,2074)
Поскольку эти два вектора являются единичными, их величины равны 1,
.
( begin{array}{l}
cos theta=frac{overrightarrow{n_{1}} times overrightarrow{n_{2}}}{left|overrightarrow{n_{1 }}right|left|overrightarrow{n_{2}}right|}=frac{0,2074}{(1)(1)}=0,2074 \ 9{circ}
end{array})
Пример 5
Три точки ( vec{P}=langle-2,3,4rangle, vec{Q}=langle 5 ,-6,7rangle) и ( vec{R}=langle 8,9,-1rangle) определяют плоскость. Определить точку на плоскости, ближайшую к началу координат.
Решение
Ближайшую к началу координат точку на плоскости можно найти, определив проекцию вектора положения одной из этих трех точек на вектор нормали. Помните, что векторная проекция одного вектора на направление другого задается скалярным произведением первого вектора на единичный вектор, определяющий направление второго вектора: ( (vec{P} times hat{ п}) шляпа{п}).
Мы можем использовать векторы положения трех точек, чтобы определить два вектора внутри плоскости. Когда у нас есть эти два вектора, их векторное произведение будет определять направление нормали к плоскости.
( begin{array}{l}
vec{A}=vec{Q}-vec{P}=langle 5,-6,7 rangle-langle-2,3,4rangle=langle 7,-9,3rangle \
vec{B}=vec{R}-vec{P}=langle 8,9, -1rangle-langle-2,3,4rangle=langle 10,6,-5rangle
end{массив})
Теперь определите векторное произведение двух векторов
( begin{array}{l}
vec{n}=vec{A} times vec{B}=leftlangleleft( A_{y} B_{z}-A_{z} B_{y}right),left(A_{z} B_{x}-A_{x} B_{z}right),left(A_{ x} B_{y}-A_{y} B_{x}right)rightrangle \
vec{n}=vec{A} times vec{B}=langle(45-18 ),(30-(-35)),(42+90)rangle \
vec{n}=vec{A} times vec{B}=langle 27,65,132rangle
end {массив})
Теперь нам нужно определить единичный вектор, связанный с этим вектором нормали 9{2}}}=frac{langle 27,65,132rangle}{sqrt{22378}} \
шляпа{n}=frac{vec{n}}{|vec{n}| }=langle 0.181,0.435,0.882rangle
end{array})
Теперь мы определяем векторную прогрессию одного из трех векторов начального положения в направлении этого единичного вектора нормали: ( ( vec{P} times hat{n}) hat{n}).
( begin{array}{l}
vec{A} times vec{B}=A_{x} B_{x}+A_{y} B_{ y}+A_{z} B_{z}+ldots \
(vec{P} times hat{n}) hat{n}=(-2(0,181)+3(0,435)+4 (0,882))угол 0,181,0,435,0,882угол
(vec{P} times шляпа{n}) шляпа{n}=(4,471)langle 0,181,0,435,0,882rangle \
(vec{P} times шляпа{n}) hat{n}=(4.471)langle 0.181,0.435,0.882rangle=langle 0.809,1.945,3.943rangle
end{массив})
Пример 7
Определение точки на плоскости 7 x + 3 y + z + 12 = 0, что ближе всего к началу координат.
Решение
Ближайшую к началу координат точку на плоскости можно найти, определив проекцию вектора положения любой точки на плоскости на вектор нормали. Векторная проекция одного вектора на направление другого задается скалярным произведением первого вектора на единичный вектор, определяющий направление второго вектора: ( (vec{P} times hat{n} ) шляпа{п}).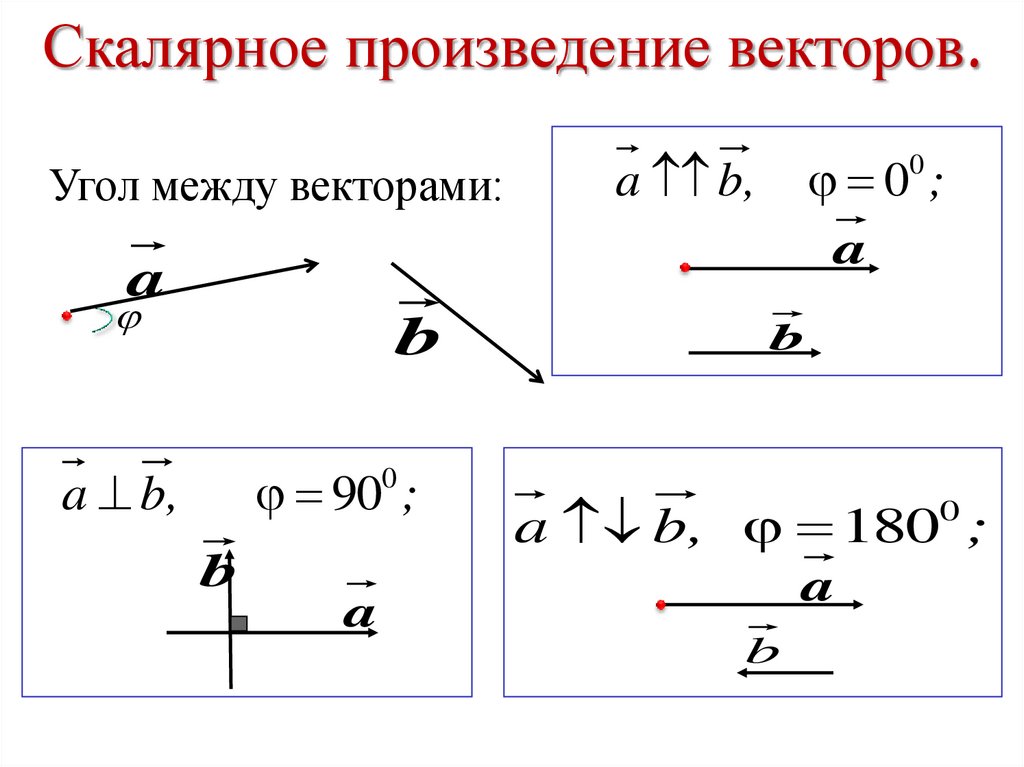
Нам также нужно знать положение точки на плоскости. Если мы запишем уравнение плоскости в форме точки пересечения, мы сможем определить вектор положения для осей x, y и z плоскости.
Уравнение ( 1=frac{x}{a}+frac{y}{b}+frac{z}{c}) должно выполняться для всех точек на плоскости. Следовательно, мы должны сначала переставить 7 x +3 y + z + 12 = 0 в виде ( 1=frac{x}{a}+frac{y}{b}+frac {г}{с}).
( 7 x+3 y+z=-12 text { становится } frac{7}{-12} x+frac{3}{-12} y+frac{1}{-12} z =1)
Следовательно, ( a=frac{-12}{7}, b=frac{-12}{3}=-4) и ( c=frac{- 12}{1}=-12), а векторы положения трех точек пересечения равны ( vec{A}=langle-1.714,0,0rangle, vec{B}=langle 0,- 4,0rangle) и ( vec{C}=langle 0,0,-12rangle).
Чтобы решить задачу, вычислите скалярное произведение.
( (vec{B} times шляпа{n}) шляпа{n}=left(B_{x} шляпа{n}_{x}+B_{y} шляпа{n }_{y}+B_{z} hat{n}_{z}right) hat{n} = left(0left(frac{7}{sqrt{59}}right) -4влево(frac{3}{sqrt{59}}right)+0влево(frac{1}{sqrt{59}}right)right)leftlanglefrac{ 7}{sqrt{59}}, frac{3}{sqrt{59}}, frac{1}{sqrt{59}}rightrangle)
( (vec{ B} times hat{n}) hat{n}=frac{-12}{sqrt{59}}leftlanglefrac{7}{sqrt{59}}, frac{3 }{sqrt{59}}, frac{1}{sqrt{59}}rightrangle=leftlanglefrac{-84}{59}, frac{-36}{59}, frac{-12} {59}rightrangle=langle-1.424,-0.610,-0.203rangle)
Обзор
Три точки определяют плоскость. Определить точку на плоскости, ближайшую к началу координат.
- ( P=(3,6,9), Q=(9,6,3) text { и } R=(6,-9,9))
- ( P=(1,-7,2), Q=(4,2,9) text { и } R=(3,-5,1))
- ( P=(3,8,10), Q=(-2,5,8) text { и } R=(7,4,8))
- ( P=(9,-1,4), Q=(6,2,-8) text { и } R=(12,9,10))
- ( P=(5,8,-9), Q=(-5,3,9) text { и } R=(10,4,-6))
Определите двугранный угол между каждой из плоскостей в вопросах 1-5 и плоскостью x-y.
- ( P=(3,6,9), Q=(9,6,3) text { и } R=(6,-9,9))
- ( P=(1,-7,2), Q=(4,2,9) text { и } R=(3,-5,1))
- ( P=(3,8,10), Q=(-2,5,8) text { и } R=(7,4,8))
- ( P=(9,-1,4), Q=(6,2,-8) text { и } R=(12,9,10))
- ( P=(5,8,-9), Q=(-5,3,9) text { и } R=(10,4,-6))
Определите двугранный угол между двумя плоскостями.
- ( 9 x+17 y-4 z-7=0 text { и }-17 x+24 y+14 z+2=0)
- ( 2 x-4 y+10 z-11=0 text { и } 2 x-9 y+4 z+12=0)
- ( -7 х+20 у+6 г+4=0 текст { и }-19х-3 у+г+5=0)
- ( 5 x-8 y+20 z-5=0 text { и } 6 x+y+19 z-7=0)
- ( 14 x+11 y-5 z-16=0 text { и } 11 x-13 y+8 z+4=0)
- ( -10 х+9 у+2 г+8=0 текст { и } 21 х+7 у-4 г+15=0)
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 5.
Словарь
| Срок | Определение |
|---|---|
| Двугранный угол | Двугранный угол — это угол между двумя плоскостями в трехмерном пространстве. |
| Происхождение | Начало координат — это точка пересечения осей x и y на декартовой плоскости. Координаты начала координат (0, 0). |
| ортогональность | Быть ортогональным значит быть перпендикулярным. |
| Перпендикулярный | Перпендикулярные прямые — это прямые, пересекающиеся под углом 90 o . Произведение наклонов двух перпендикулярных прямых равно -1. |
| самолет | Плоскость — это плоская двумерная поверхность. Его можно представить как лист бумаги бесконечной площади.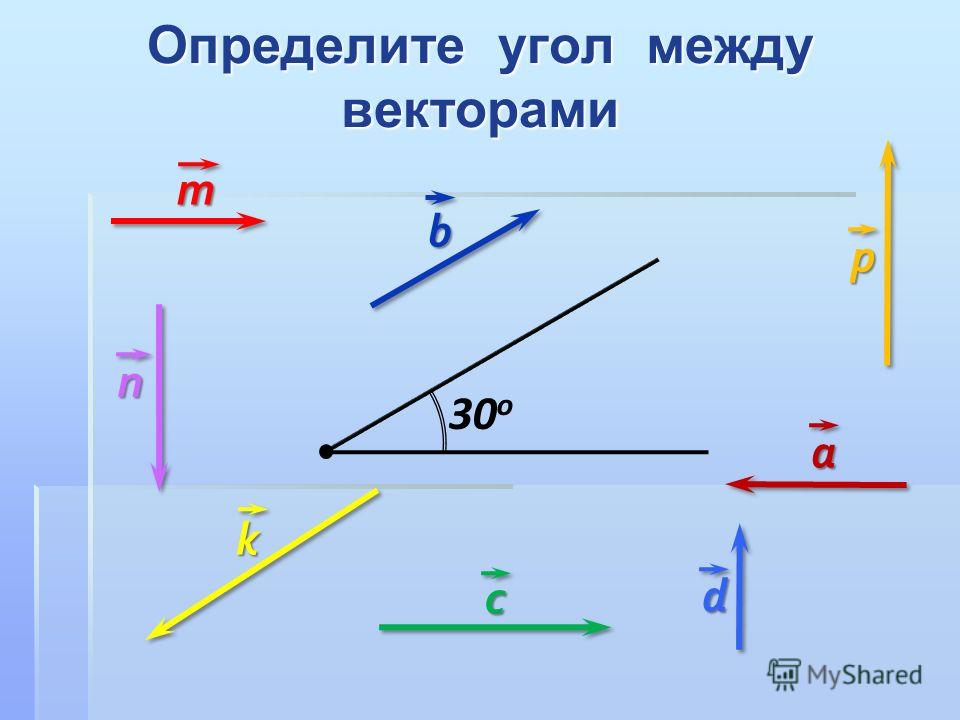
No related posts. |
Содержание
Для понимания материалов настоящего раздела рекомендуется ознакомиться с разделом ЛИНЕЙНОЕ ПРОСТРАНСТВО
.
Евклидово пространство
Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты.
В настоящем разделе понятие расстояния между двумя векторами — элементами
линейного пространства — будет вводиться посредством скалярного произведения
векторов. Насколько обоснован такой порядок введения понятий:
$ mbox{} qquad $ скалярное произведение $ to $ длина ?
Ведь в аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов $ X_{} $ и $ Y_{} $ определялось как произведение длин этих векторов
на косинус угла между ними:
$ langle X,Y rangle = |X| cdot |Y| cdot cos (widehat{X,Y}) $. Тем не менее,
формально непротиворечива и обратная схема: если допустить, что
скалярное произведение любых двух векторов может быть как-то
вычислено (например, в $ mathbb R^{3} $ по формуле $ langle X,Y rangle = x_1y_1+x_2y_2+x_3y_3 $
при заданных прямоугольных координатах $ (x_1,x_2,x_3) $ и
$ (y_1,y_2,y_3) $ векторов $ X_{} $ и $ Y_{} $), то и длину векторов и угол между
ними можно выразить через подходящие скалярные произведения:
$$ |X|=sqrt{ langle X,X rangle},qquad widehat{X,Y}=arccos frac{ langle X,Y rangle}{sqrt{langle X,X rangle langle Y,Y rangle}} .$$
Определения
Вещественное линейное пространство $ mathbb E_{} $ называется евклидовым1),
если в этом пространстве определена функция, ставящая в соответствие паре
векторов $ {X,Y}subset mathbb E $ вещественное число, называемое скалярным
произведением векторов2) $ X_{} $ и $ Y_{} $, и обозначаемое $ langle X,Y rangle_{} $ или $ (X,Y)_{} $; при этом фцнкция
подчиняется аксиомам:
1.
$ langle X,Y rangle= langle Y,X rangle $ для $ { X,, Y} subset mathbb E $;
2.
$ langle X_1+X_2,Y rangle = langle X_1,Y rangle + langle X_2,Y rangle $ для $ { X_1,, X_2,, Y } subset mathbb E $;
3.
$ langle lambda, X,Yrangle=lambda, langle X,Yrangle $ для $ { X,Y}subset mathbb E, lambda in mathbb R $;
4.
$ langle X,X rangle>0 $ для $ forall Xne mathbb O $, $ langle mathbb O,mathbb O rangle =0 $.
Из аксиом
1
и
2
вытекает свойство линейности скалярного произведения и по второму вектору:
2′.
$ langle X,Y_1+Y_2 rangle = langle X,Y_1 rangle + langle X,Y_2 rangle $ для $ {X, Y_1,, Y_2 } subset mathbb E $
.
П
Пример 1. Пространство $ mathbb R_{}^{n} $, рассматриваемое как пространство вещественных векторов-столбцов.
Для векторов
$$ X=left[begin{array}{l} x_1 \ vdots \ x_n end{array} right] quad mbox{ и } quad
Y=left[begin{array}{l} y_1 \ vdots \ y_n end{array} right]
$$
их скалярное произведение определим обобщением привычной из геометрии формулы
$$
langle X,Y rangle = sum_{j=1}^n x_jy_j = X^{top}Y ;
$$
в последней формуле $ {}^{top} $ означает транспонирование.
Будем называть это скалярное произведение стандартным. Легко проверить выполнимость аксиом
1
—
4
.
Однако стандартное определение скалярного произведения вовсе не является
единственно допустимым; формально скалярное произведение можно ввести и другим способом.
Рассмотрим (пока произвольную) вещественную квадратную матрицу $ A_{} $ порядка $ n_{} $ и положим
$$
begin{array}{cccr}
langle X,Y rangle = X^{top} A Y & = &
a_{11}x_1y_1+a_{12}x_1y_2+ dots + a_{1n}x_1y_n &+ \
&+&a_{21}x_2y_1+a_{22}x_2y_2+ dots + a_{2n}x_2y_n &+ \
&+& dots &+ \
&+&a_{n1}x_ny_1+a_{n2}x_ny_2+ dots + a_{nn}x_ny_n & .
end{array}
$$
(Здесь векторы $ X_{} $ и $ Y_{} $ из $ mathbb R_{}^{n} $ снова рассматриваются как столбцы.) Если матрица $ A_{} $ является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.
Зачем нужна такая возможность в неоднозначности определения скалярного произведения в одном и том же пространстве? — Ответ на этот вопрос откладывается до следующего пункта. А пока приведу одно замечание3).
Введенное — по любому из допустимых алгоритмов — скалярное произведение в $ mathbb R^{n}_{} $ является функцией от $ 2,n $ аргументов — координат векторов $ X_{} $ и $ Y_{} $:
$$ langle X,Y rangle = F(x_1,dots,x_n,y_1,dots,y_n) . $$
Что это за функция? — Очевидно, это — полином, причем однородный второй степени.
Однако по каждой переменной из набора $ x_{1},dots,x_n $ он является линейным. Именно, аксиомы
2
и
3
можно объединить в одно свойство линейности:
$$
F(lambda_1X_1+ lambda_2X_2,Y)=lambda_1 F(X_1,Y)+ lambda_2 F(X_2,Y) mbox{ при } {lambda_1,lambda_2 } subset mathbb R,
{X_1,X_2 } subset mathbb R^n .
$$
Аналогичное утверждение справедливо и относительно координат вектора $ Y_{} $. Наличие подобных свойств позволяет выделить во множестве произвольных однородных полиномов второй степени (квадратичных форм) от $ 2, n $ переменных подмножество билинейных форм. Это определение допускает обобщение на произвольное количество наборов переменных из $ mathbb R^{n}_{} $: полилинейная форма. В частности, полилинейной формой является определитель матрицы порядка $ n_{} $ как функция от $ n^{2} $ элементов этой матрицы, объединенных в наборы строк или столбцов (см.
☞
ЗДЕСЬ ).
П
Пример 2. Пространство $ mathbb P_{n} $ полиномов одной переменной степеней $ le n_{} $ с вещественными коэффициентами.
Скалярное произведение полиномов
$$ p(x)=a_{0}x^n+a_1x^{n-1}+dots + a_n quad mbox{ и } quad
q(x)=b_{0}x^n+b_1x^{n-1}+dots + b_n $$
введем формулой
$$
langle p(x), q(x) rangle = sum_{j=0}^n a_j b_j.
$$
Легко проверить справедливость всех аксиом.
В том же пространстве укажем еще один способ задания скалярного произведения
$$
langle p(x), q(x) rangle = int_{a}^b p(t)q(t) d,t
$$
при некоторых фиксированных вещественных константах $ a_{} $ и $ b_{} $, $ a_{}<b $.
Аксиомы
1
—
3
следуют из свойств определенного интеграла.
Проверка выполнения аксиомы
4
более кропотлива и проводится
☞
ЗДЕСЬ.
?
В том же пространстве $ mathbb P_{n} $ можно ли определить скалярное произведение формулой
$$ langle p(x),q(x) rangle = sum_{k=1}^m p(x_k) q(x_k) quad npu {x_k}_{k=1}^m subset mathbb R ? $$
П
Пример 3. Линейное пространство $ mathbb R^{ntimes n} $ вещественных квадратных матриц порядка $ n_{} $. Скалярное произведение введем формулой
$$
langle A,B rangle = sum_{j,k=1}^n a_{jk}b_{jk} , .
$$
В связи с последней формулой, упомянем две ее интерпретации. Первая из них связана с операцией векторизации матрицы:
$$
langle A,B rangle=operatorname{Vec}(A)^{top} operatorname{Vec}(B) , .
$$
Тем самым введенное скалярное произведение в пространстве $ mathbb R^{ntimes n} $ матриц эквивалентно стандартному скалярному произведению векторов в $ mathbb R^{n^2} $.
Вторая интерпретация формулы связана с операцией
$ operatorname{Sp} $ нахождения следа матрицы, т.е. суммы элементов ее главной диагонали:
$$
langle A,B rangle = operatorname{Sp} left(Acdot B^{top} right) , .
$$
Эквивалентность последнего представления определению устанавливается непосредственной проверкой.
На основании аксиом скалярного произведения, его вычисление для произвольных векторов $ X_{} $ и $ Y_{} $ может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система $ {X_1,dots,X_{n}} $ составляет базис пространства $ mathbb E $, то, разложив
оба вектора по этому базису
$$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n ,
$$
получаем:
$$langle X,Y rangle=langle x_1X_1+ dots +x_nX_n , y_1X_1+ dots +y_nX_n rangle=$$
$$
=
left{
begin{array}{ccc}
&&x_1y_1 langle X_1,X_1 rangle + x_1y_2 langle X_1,X_2 rangle + dots + x_1y_n langle X_1,X_n rangle + \
&+&x_2y_1 langle X_2,X_1 rangle + x_2y_2 langle X_2,X_2 rangle + dots + x_2y_n langle X_2,X_n rangle+ \
&+ & dots qquad + \
&+&x_ny_1 langle X_n,X_1 rangle + x_ny_2 langle X_n,X_2 rangle + dots + x_ny_n langle X_n,X_n rangle
end{array} right} =
$$
$$
=(x_1,x_2,dots,x_n)left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \
dots & & & dots \
langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle
end{array}
right) left(begin{array}{c}
y_1 \ y_2 \ vdots \ y_n
end{array}right) .
$$
Итак, при изменении векторов $ X_{} $ и $ Y_{} $ в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в $ mathbb E_{} $. Фактически задание
скалярного произведения в разобранном выше примере пространства $ mathbb R^{n} $ по формуле $ langle X,Y rangle=X^{top}AY $ можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера $ 1_{} $, матрица
$$
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \
dots & & & dots \
langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle
end{array}
right)
$$
должна обладать некоторыми принципиальными свойствами. Так оно и окажется, см.
☟
НИЖЕ.
Матрицей Грама системы векторов4) $ {X_1,dots,X_{m} } $ называется квадратная матрица
$$
G(X_1,dots,X_m)=left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right) = left[ langle X_j,X_k rangle right]_{j,k=1}^m .
$$
Ее определитель называется определителем Грама5) (или грамианом) системы векторов $ {X_1,dots,X_{m} } $:
$$
{mathfrak G}(X_1,dots,X_m)=left|
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right| = det left[ langle X_j,X_k rangle right]_{j,k=1}^m .
$$
С помощью матрицы Грама формула скалярного произведения записывается в виде
$$
langle X,Y rangle =[x_1,dots,x_n] G(X_1,dots,X_n)
left[ begin{array}{c}
y_1 \ vdots \ y_n
end{array}
right] .
$$
П
Пример 4. В пространстве $ mathbb R^{n} $ столбцов из $ n_{} $ элементов при стандартном способе задания скалярного произведения
$$
langle X,Y rangle = sum_{j=1}^n x_jy_j quad npu quad X=[x_1,dots,x_n]{^{top}},
Y=[y_1,dots,y_n]{^{top}}
$$
матрицу Грама системы векторов $ {X_j=[x_{j1},x_{j2},dots,x_{jn}]^{top} }_{j=1}^m $ можно представить в виде произведения матриц
$$
G(X_1,dots,X_{m})=left(
begin{array}{llll}
x_{11} & x_{12} & dots & x_{1n} \
x_{21} & x_{22} & dots & x_{2n} \
dots & & & dots \
x_{m1} & x_{m2} & dots & x_{mn}
end{array}
right)
left(
begin{array}{llll}
x_{11} & x_{21} & dots & x_{m1} \
x_{12} & x_{22} & dots & x_{m2} \
vdots & & & vdots \
x_{1n} & x_{2n} & dots & x_{mn}
end{array}
right) .
$$
Произведение имеет вид $ Mcdot M^{top} $ и, согласно теореме Бине-Коши, определитель этого произведения равен $ 0_{} $ при $ m>n_{} $ и неотрицателен при $ m le n $. НИЖЕ будет установлено, что обнаруженные свойства определителя Грама являются универсальными: они выполняются в произвольном евклидовом пространстве. См. также, «обращение» этого результата — задача
4
☞
ЗДЕСЬ.
Свойства
Т
Теорема. Имеет место неравенство Коши–Буняковского:
$$
langle X,Y rangle ^2 le langle X,X rangle langle Y,Y rangle quad npu forall {X,Y }subset mathbb E .
$$
Доказательство для случая $ mathbb R^{n}_{} $ приведено
☞
ЗДЕСЬ. Для доказательства общего случая используем одну вспомогательную конструкцию. Из аксиомы
4
следует, что для $ forall lambda in mathbb R $ будет выполнено
$ langle lambda, X — Y,, lambda, X — Y rangle ge 0 $. Имеем:
$$
0 le langle lambda, X — Y,, lambda, X — Y rangle le lambda^2 langle X,X rangle — 2,lambda langle X,Y rangle
+langle Y,Y rangle .
$$
Квадратное относительно $ lambda_{} $ неравенство будет выполнено при всех вещественных значениях этого параметра тогда и только тогда, когда дискриминант квадратного трехчлена будет отрицателен:
$$
mathcal D=langle X,Y rangle^2 — langle X,X rangle langle Y,Y rangle le 0 .
$$
♦
=>
С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:
$$ left( int_a^b p(t)q(t) d,t right)^2 le int_a^b p^2(t) d,t cdot int_a^b q^2(t) d,t $$
для произвольных полиномов6) $ {p(x),q(x) } subset mathbb R [x] $.
Длиною вектора $ X_{} $ в евклидовом пространстве $ mathbb E_{} $ называется число
$$ |X| = sqrt{langle X,X rangle} ; $$
здесь квадратный корень понимается как корень арифметический: $ |X| ge 0 $. Расстоянием между векторами $ X_{} $ и $ Y_{} $ называется число $ |X-Y| $.
Это формальное определение немедленно входит в противоречие со здравым смыслом: длина вектора в линейном пространстве оказывается не фиксированной, раз и навсегда, величиной — как мы привыкли в геометрии, — но зависящей от способа задания скалярного произведения в этом пространстве. На самом деле это противоречие не мешает нам даже в повседневной жизни. Так, никому и в голову не приходит, что расстояние между двумя городами фактически вычисляется «нечестно»: не по прямой, их соединяющей (и, следовательно, проходящей сквозь Землю), а по дуге, проходящей по поверхности земного эллипсоида… Вопрос о том, какое расстояние является более истинным подменяется другим: какое из расстояний позволяет решить ту или иную практическую задачу.
П
См. по этому поводу
☞
Расстояние Махаланобиса.
П
В $ mathbb R^{n}_{} $ при скалярном произведении, заданном стандартным способом
формулой
$$
langle X,Y rangle
= sum_{j=1}^n x_jy_j quad npu quad X=[x_1,dots,x_n]{^{top}},
Y=[y_1,dots,y_n]{^{top}} ,
$$
длина вектора $ X_{} $ определяется естественным (с точки зрения геометрии) способом: $ |X|=sqrt{x_1^2+dots+x_n^2} $.
В пространстве полиномов со скалярным произведением
$$
langle p(x), q(x) rangle = int_{a}^b p(t)q(t) d,t
$$
для избежания путаницы не используют словосочетание
«длина полинома $ p_{}(x) $»; вместо этого величину
$$ sqrt{int_a^b p^2(t) d,t} $$
называют нормой этого полинома и обозначают $ | p(x) | $. Это же название
распространяется и в линейное пространство квадратных матриц со скалярным
произведением заданным формулой $ langle A,B rangle = operatorname{Sp} left(Acdot B^{top} right) = sum_{j,k=1}^n a_{jk}b_{jk} $: величина
$$|A| = sqrt{operatorname{Sp} left(Acdot A^{top} right)}=sqrt{sum_{j,k=1}^n a_{jk}^2}$$
называется (евклидовой) нормой матрицы7) $ A=left[a_{jk} right]_{j,k=1}^n $. Это же определение распространяется и на векторы пространства $ mathbb R^{n} $, как частный случай матриц: говорят о норме вектора $ X_{} $, имея в виду его длину: $ |X| = sqrt{langle X,X rangle} $. Нигде далее в настоящем разделе я не буду использовать этот термин.
С помощью введенного определения неравенство Коши-Буняковского можно переписать
в виде
$$
|langle X,Y rangle| le |X| cdot |Y| quad npu forall {X,Y }subset mathbb E ,
$$
где $ | cdot | $ в левой части означает модуль, а в правой части — длину.
Т
Теорема. Имеет место неравенство треугольника
$$
|X+Y| le |X|+|Y| quad npu forall {X,Y }subset mathbb E .
$$
Доказательство. На основании неравенства Коши-Буняковского, имеем:
$$
0 le langle X+Y,, X+Y rangle=langle X,X rangle+2langle X,Y rangle+langle Y,Y rangle le |X|^2+2, |X| cdot |Y| +|Y|^2=left(|X|+|Y| right)^2 .
$$
♦
Углом между векторами $ X_{} $ и $ Y_{} $ называется угол
$$varphi = widehat{X,Y} = arccos frac{langle X,Y rangle}{|X|cdot |Y|} .$$
Ввиду неравенства Коши-Буняковского это определение непротиворечиво: дробь под знаком арккосинуса не превосходит 1 по абсолютной величине. Векторы $ X_{} $ и $ Y_{} $ называются ортогональными: $ X bot Y $ если угол между ними равен $ pi/2 $, или, что то же, $ langle X,Y rangle=0 $.
Введенное таким определением понятие является естественным обобщением понятия угла на плоскости и в трехмерном пространстве. Хотя в пространствах размерностей больших $ 3_{} $ человеческие мозги думать не приучены, тем не менее, абстракция находит практическое применение в задаче информационного поиска.
Косинусное расстояние
Пусть задача заключается в сравнении двух текстовых документов «на похожесть». Имеются некоторые наборы ключевых слов, описывающих каждый из этих документов. Составим объединение этих наборов, упорядочим получившийся набор (пронумеруем слова), посчитаем частоты вхождений каждого из слов в каждый из документов.
Получим два вектора:
$$ X_1=(f_{11},f_{12},dots), X_2=(f_{21},f_{22},dots) , $$
описывающие каждый из документов. Здесь $ f_{jk} in {0,1,2,dots, } $ — количество вхождений $ k_{} $-го слова в $ j_{} $-й документ. Для оценки близости векторов, на первый взгляд, кажется естественным вычислить расстояние между ними стандартным способом:
$$ |X_1-X_2| = sqrt{ sum_{k} (f_{1k}-f_{2k})^2} . $$
Однако, по здравому размышлению, понимаем, что при таком способе, документы различные по объему (общему количеству слов) будут слишком сильно отличаться друг от друга, при том, что могут оказаться близкими по сути (как будет отличаться большая статья от собственного реферата). Поэтому имеет смысл усреднить частоты в обоих текстах, т.е. рассматривать расстояние между векторами $ X_1/|X_1| $ и $ X_2/|X_2| $ единичной длины:
$$ left|frac{X_1}{|X_1|}-frac{X_2}{|X_2|}right| = sqrt{2left( 1- frac{langle X_1,X_2 rangle}{|X_1|cdot |X_2|} right)} ; $$
скалярное произведение под знаком корня вычисляется стандартным способом: $ langle X_1,X_2 rangle=sum_{k} f_{1k}f_{2k} $. Отсюда и возникает понятие косинусного расстояния: величина
$$
frac{langle X_1,X_2 rangle}{|X_1|cdot |X_2|}
$$
неотрицательна (поскольку компоненты векторов $ X_1,X_2 $ неотрицательны), и чем ближе она к $ 1_{} $ тем меньше расстояние между между нормированными векторами. Эта величина называется также похожестью
или cходством 
Т
Теорема [Пифагор]. Если $ X bot Y $, то $ |X+Y|^2=|X|^2+|Y|^2 $.
=>
Если векторы $ X_1,dots,X_k $ попарно взаимно ортогональны, то
$$|X_1+dots +X_k|^2=|X_1|^2+dots +|X_k|^2 . $$
П
Пример. Найти расстояние между полиномами
$$p(x)=x^{100}-1/2,x^{85}-1/2,x^{64}+5,x^{34}-5,x^{32}+5,x^2+1
quad u quad q(x)=5,x^2+1
$$
если скалярное произведение задается формулой
а) $ displaystyle langle p(x), q(x) rangle = sum_{j=0}^{100} a_j b_j $ ;
б) $ displaystyle langle p(x), q(x) rangle = int_{-1}^1 p(t)q(t) d, t $.
Решение. Для случая а) нам достаточно просто вычислить сумму квадратов коэффициентов разности $ p(x)-q(x) $: расстояние равно $ sqrt{103/2} $.
Для случая б) нам придется иметь дело с интегралом
$$
int_{-1}^1 left(p(t)-q(t) right)^2 d, t =
int_{-1}^1 left(t^{100}-1/2,t^{85}-1/2,t^{64}+5,t^{34}-5,t^{32} right)^2 d, t
,
$$
который, несмотря на свой громоздкий вид, может быть вычислен элементарными приемами математического анализа. В этом случае расстояние будет равно
$ sqrt{95965413818,big/ 16503052280715} $.
Ответ. а) $ approx 7.176 $ ; б) $ approx 0.076 $.
§
Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной,
имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если
коэффициенты полиномов
$$f(x)=x^n+a_1x^{n-1}+dots+a_n quad u quad
{tilde f}(x)=x^n+{tilde a}_1x^{n-1}+dots+{tilde a}_n$$
из $ mathbb C[x] $ близки, то и корни этих полиномов (при соответствующей нумерации)
будут близки на комплексной плоскости. В этой теореме мера близости полиномов оценивается по формуле
$$ sqrt[n]{sum_{k=1}^n|a_k-{tilde a}_k| gamma^{n-k} } quad
npu quad gamma = max_{jin {1,dots,n}}
left( sqrt[j]{|a_j|} ,
sqrt[j]{|{tilde a}_j|} right) , $$
которая, хоть и не совпадает с формулой
$$
sqrt{sum_{k=1}^n left(a_k-{tilde a}_k right)^2} ,
$$
определяющей расстояние в пространстве полиномов, но идейно ей близка. Вычисленное в предыдущем примере расстояние между полиномами $ p_{}(x) $ и $ q_{}(x) $ по формуле а) оказывается достаточно большим в том смысле, что если для полинома $ p_{}(x) $ искать полином, имеющий
почти такое же расположение корней на $ mathbb C_{} $, то полином $ q_{}(x) $ окажется
неподходящим кандидатом.9)
Другое дело, если ставится задача приближения полинома $ p_{}(x) $ только на интервале
$ [-1,1] $ — тогда полином $ q_{}(x) $ может оказаться вполне полезным. Выясним сначала
природу интеграла, возникшего при решении. Пусть сначала $ p_{}(x) $ и $ q_{}(x) $
— произвольные, но (для простоты рассуждений) неотрицательные на интервале $ [a_{},b] $ полиномы. Геометрический смысл интеграла $ int_a^b p(t) d, t $ — площадь криволинейной трапеции на плоскости $ (x_{},y) $, ограниченной прямыми $ x=a_{},,x=b,,y=0 $ и графиком $ y=p(x) $.
Следовательно, геометрический смысл интеграла
$$
int_a^b left| p(t)-q(t) right| d, t
$$
— площадь фигуры, ограниченной прямыми $ x=a,,x=b_{} $ и графиками $ y=p(x), y=q(x) $
(заштрихована коричневым на рисунке). Чем меньше эта площадь, тем «теснее» друг к другу на отрезке
$ [a_{},b] $ расположены графики $ y=p(x) $ и $ y=q(x) $. Величина
$$
sqrt{int_a^b left( p(t)-q(t) right)^2 d, t} ,
$$
вообще говоря, не совпадает с предыдущей, но смысл ее тот же:
она позволяет оценивать близость графиков на всем отрезке
$ [a_{},b] $. Ответ в примере для варианта б) позволяет заключить, что на отрезке $ [-1,1] $ полином $ p_{}(x) $ неплохо приближается своими младшими одночленами, т.е. на указанном отрезке график $ y=p(x) $ не должен слишком сильно отличаться от параболы $ y=5,x^2+1 $.
Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден
для наблюдения за большими объектами, а телескоп — за малыми.
Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.
Т
Теорема. В евклидовом пространстве имеет место равенство параллелограмма
$$
|X+Y|^2+|X-Y|^2 =2(|X|^2+|Y|^2) quad npu forall {X,Y }subset mathbb E .
$$
Ортогонализация
Пусть $ dim mathbb E=n $ и векторы $ {X_1,dots,X_n} $ составляют базис $ mathbb E_{} $.
Этот базис называется ортогональным если векторы попарно ортогональны: $ X_jbot X_k $; базис называется нормированным если каждый его вектор имеет единичную длину: $ |X_j|=1 $; базис называется ортонормированным если он ортогонален и нормирован, т.е.
$$langle X_j,X_k rangle=delta_{jk} ,quad npu quad {j,k} subset {1,dots,n } .$$
Здесь $ delta_{jk}^{} $ — символ Кронекера.
Ортогональный базис будем обозначать $ {mathfrak E}_1,dots, {mathfrak E}_n $.
?
Чему равно расстояние между двумя векторами ортонормированного базиса?
В пространстве $ mathbb R_{}^{n} $ стандартным ортогональным базисом является базис, состоящий из векторов
$$
{mathfrak e}_j = big[underbrace{0,dots,0,1}_{j},0,dots,0big]^{top} quad npu quad
j in {1,dots,n} .
$$
Существование же ортогонального базиса в произвольном евклидовом пространстве
еще требует доказательства. Предварительно установим следующий результат.
Т
Теорема. Если ненулевые векторы $ X_1,dots, X_{n} $ попарно ортогональны, то они линейно независимы.
Доказательство. В самом деле, если
$$ lambda_1 X_1 + dots + lambda_n X_n = mathbb O , $$
то, домножив это равенство скалярно на $ X_{1} $, получим
$$ lambda_1 langle X_1,X_1 rangle + dots + lambda_n langle X_1,X_n rangle = 0 . $$
Поскольку $ langle X_1,X_j rangle=0 $ для $ jin {2,dots,n} $, то $ lambda_1 langle X_1,X_1 rangle=0 $,
откуда $ lambda_1=0 $. Аналогично показывается, что и все остальные $ lambda_j $ равны 0.
♦
Задача. Пусть имеется произвольная система $ {X_1,dots,X_k} $ линейно независимых
векторов. Требуется построить систему ортогональных векторов
$ left{{mathfrak E}_1,dots, {mathfrak E}_k right} $ такую, чтобы линейные оболочки любых подсистем совпадали:
$$
{mathcal L}left(X_1,dots,X_m right) ={mathcal L}left({mathfrak E}_1,dots, {mathfrak E}_m right) quad npu quad
min {1,dots,k} .
$$
Иными словами, вектор $ {mathfrak E}_1 $ должен линейно зависеть от $ X_{1} $, вектор $ {mathfrak E}_2 $ должен линейно выражаться через $ X_1,X_2 $, $ {mathfrak E}_3 $ — через $ X_1,X_2,X_3 $ и т.д.
Алгоритм ортогонализации Грама — Шмидта
10)
В случае $ m_{}=1 $ возьмем $ {mathfrak E}_1=X_1 $: поскольку вектор $ X_{1} $ входит в линейно независимую систему , то $ {mathfrak E}_1 ne mathbb O $. Далее, будем искать $ {mathfrak E}_2 $ в виде
$${mathfrak E}_2=X_2 + alpha_{21} {mathfrak E}_1 $$
при пока неопределенном коэффициенте $ alpha_{21} $. Очевидно, что при таком выборе $ {mathfrak E}_2 $
условие $ {mathcal L}(X_1,X_2)={mathcal L}({mathfrak E}_1,{mathfrak E}_2) $ будет выполнено. Подберем $ alpha_{21} $ так, чтобы выполнялось $ {mathfrak E}_2 bot {mathfrak E}_1 $.
$$0=langle {mathfrak E}_1,{mathfrak E}_2 rangle=langle {mathfrak E}_1,X_2 rangle+alpha_{21} langle {mathfrak E}_1,{mathfrak E}_1 rangle
Rightarrow alpha_{21}=-langle {mathfrak E}_1,X_2 rangle big/ langle {mathfrak E}_1,{mathfrak E}_1 rangle
.
$$
Таким образом, коэффициент $ alpha_{21} $, а вместе с ним и вектор $ {mathfrak E}_2 $
определяются единственным образом. При этом $ {mathfrak E}_2ne mathbb O $, ибо, в
противном случае, векторы $ X_2 $ и $ {mathfrak E}_1=X_1 $ были бы л.з.,
что противоречит предположению о линейной независимости системы $ {X_1,dots,X_k} $.
Продолжаем процесс далее: вектор $ {mathfrak E}_3 $
ищем в виде
$${mathfrak E}_3=X_3 + alpha_{31} {mathfrak E}_1 + alpha_{32} {mathfrak E}_2 $$
при пока неопределенных коэффициентах $ alpha_{31} $ и $ alpha_{32} $.
Условие $ {mathcal L}(X_1,X_2,X_3)={mathcal L}({mathfrak E}_1,{mathfrak E}_2,{mathfrak E}_3) $ выполняется поскольку
$$alpha_{31} {mathfrak E}_1 + alpha_{32} {mathfrak E}_2 in {mathcal L}(X_1,X_2)
subset {mathcal L}(X_1,X_2,X_3) .$$
Подберем скаляры $ alpha_{31} $ и $ alpha_{32} $ так,
чтобы выполнялось $ {mathfrak E}_3 bot {mathfrak E}_1 $ и $ {mathfrak E}_3 bot {mathfrak E}_2 $. Два этих условия задают систему линейных уравнений
$$left{
begin{array}{cc}
langle X_3,{mathfrak E}_1 rangle + alpha_{31} langle {mathfrak E}_1, {mathfrak E}_1 rangle + alpha_{32}
langle {mathfrak E}_2 , {mathfrak E}_1 rangle &=0 ,\
langle X_3,{mathfrak E}_2 rangle + alpha_{31} langle {mathfrak E}_1, {mathfrak E}_2 rangle + alpha_{32}
langle {mathfrak E}_2 , {mathfrak E}_2 rangle &=0 ,
end{array}
right.
iff
begin{array}{c}
alpha_{31}=-langle X_3,{mathfrak E}_1 rangle big/ |{mathfrak E}_1|^2 \
alpha_{32}=-langle X_3,{mathfrak E}_2 rangle big/ |{mathfrak E}_2|^2
end{array}
$$
Процесс продолжается далее аналогично. Допустим, что векторы $ {mathfrak E}_1,dots,{mathfrak E}_{k-1} $ уже построены, они ненулевые, попарно ортогональные и
$$ {mathcal L}left(X_1,dots,X_{k-1} right)=
{mathcal L}left({mathfrak E}_1,dots, {mathfrak E}_{k-1} right) .$$
Вектор $ {mathfrak E}_{k} $ ищем в виде:
$$
{mathfrak E}_{k} =X_k+alpha_{k1} {mathfrak E}_1 + alpha_{k2} {mathfrak E}_2 +dots + alpha_{k,k-1} {mathfrak E}_{k-1}
$$
при пока неопределенных коэффициентах $ alpha_{k1},dots ,alpha_{k,k-1} $.
Условие $ {mathcal L}left(X_1,dots,X_{k-1},X_k right)=
{mathcal L}left({mathfrak E}_1,dots, {mathfrak E}_{k-1},{mathfrak E}_{k} right) $ выполнено и, кроме того, $ {mathfrak E}_{k}ne mathbb O $
(в противном случае $ X_k in {mathcal L}left({mathfrak E}_1,dots, {mathfrak E}_{k-1} right)
={mathcal L}left(X_1,dots,X_{k-1} right) $, т.е. система $ {X_1,dots,X_{k-1},X_k } $
линейно зависима. Коэффициенты $ alpha_{k1}, dots ,alpha_{k,k-1} $
подбираются из условий $ {mathfrak E}_{k} bot {mathfrak E}_1,dots,
{mathfrak E}_{k} bot {mathfrak E}_{k-1} $. Получающаяся система линейных уравнений
имеет единственное решение
$$alpha_{k1}=- langle X_k,{mathfrak E}_1 rangle big/ |{mathfrak E}_1|^2 ,dots,
alpha_{k,k-1}=-langle X_k,{mathfrak E}_{k-1} rangle big/ |{mathfrak E}_{k-1}|^2
,
$$
и это решение определяет единственный вектор $ {mathfrak E}_{k} $.
♦
П
Пример. Ортогонализовать систему векторов
$$ X_1=left[1,0,0,0,1 right], X_2=left[1,1,0,1,1 right],
X_3=left[1,1,1,1,1 right]
$$
при стандартном способе задания скалярного произведения в $ mathbb R^5 $.
Решение. Имеем:
$$
begin{array}{lcll}
{mathfrak E}_{1}&=&X_1,, & Rightarrow {mathfrak E}_{1} =left[1,0,0,0,1 right] , \
{mathfrak E}_{2}&=&X_2+alpha_{21} {mathfrak E}_{1}, & \
& &qquad alpha_{21}=-langle X_2,{mathfrak E}_{1} rangle/|{mathfrak E}_{1}|^2=-1 &
Rightarrow {mathfrak E}_{2}= left[0,1,0,1,0 right] , \
{mathfrak E}_{3}&=&X_3+alpha_{31} {mathfrak E}_{1} +alpha_{32} {mathfrak E}_{2}, & \
& & qquad alpha_{31}=- langle X_3,{mathfrak E}_{1} rangle/|{mathfrak E}_{1}|^2=-1, & \
& & qquad alpha_{32}=- langle X_3,{mathfrak E}_{2} rangle/|{mathfrak E}_{2}|^2=-1 &
Rightarrow {mathfrak E}_{3}= left[0,0,1,0,0 right] .
end{array}
$$
Ответ. $ {mathfrak E}_{1}=left[1,0,0,0,1 right], {mathfrak E}_{2}=left[0,1,0,1,0 right], {mathfrak E}_{3}=left[0,0,1,0,0 right] $.
П
Пример. Пусть в пространстве полиномов скалярное произведение
задается формулой
$$ langle p(x),q(x) rangle=int_{-1}^{1} p(t)q(t) d, t .$$
Построить ортогональный базис этого пространства.
Решение. Искомый базис строится ортогонализацией канонического базиса $ 1,x,x^2,dots, x^n $. В результате получаем систему полиномов:
$$1, x, x^2-frac{1}{3}, x^3-frac{3}{5}, x, x^4-frac{6}{7}, x^2+frac{3}{35},dots $$
Полиномы, получающиеся из этих нормированием:
$$P_0(x)=1, P_1(x)= x, P_2(x)=frac{1}{2}(3,x^2-1),
P_3(x)= frac{1}{2}( 5,x^3-3, x), $$
$$
P_4(x)= frac{1}{8}(35,x^4-30, x^2+3),dots
$$
$$
P_n(x)=frac{1}{2^n} sum_{k=0}^{lfloor n/2 rfloor}
frac{(-1)^k(2n-2k)!}{k!(n-k)!(n-2k)!} x^{n-2k}
$$
известны как полиномы Лежандра.
Здесь $ lfloor mbox{ } rfloor $ означает целую часть числа. Рекуррентное соотношение
$$kP_{k}(x)-(2k-1),xP_{k-1}(x)+(k-1),P_{k-2}(x) equiv 0, quad kge 2
;$$
позволяет найти полином $ P_{k}(x) $ если уже вычислены $ P_{k-1}(x) $ и $ P_{k-2}(x) $.
♦
В ортонормированном базисе пространства $ mathbb E_{} $ матрица Грама из формулы скалярного произведения
$$
langle X,Y rangle=(x_1,dots,x_n) G(X_1,dots,X_n)
left( begin{array}{c}
y_1 \ vdots \ y_n
end{array}
right)
$$
становится единичной и в таком базисе скалярное произведение становится стандартным :
$$ langle X,Y rangle=sum_{j=1}^n x_jy_j .$$
Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.
Т
Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.
=>
В пространстве $ mathbb R^{n}_{} $ матрица, составленная из столбцов произвольного ортонормированного базиса, является ортогональной.
Матричный формализм алгоритма Грама-Шмидта: QR-разложение
Материал настоящего пункта может быть пропущен при первоначальном чтении.
Рассмотрим пример из предыдущего пункта об ортогонализации системы векторов в $ mathbb R^5 $; только векторы будем рассматривать столбцами:
$$ X_1=left[begin{array}{c} 1 \ 0 \ 0 \ 0 \ 1 end{array} right], X_2=left[ begin{array}{c} 1 \ 1 \ 0 \ 1 \ 1 end{array} right],
X_3=left[ begin{array}{c} 1 \ 1 \ 1 \ 1 \ 1 end{array} right] , .
$$
Составим из них матрицу
$$ A_{5times 3} = left[ X_1,X_2,X_3 right] , . $$
Алгоритм Грама-Шмидта означает некоторые действия со столбцами этой матрицы, и эти действия могут быть записаны на языке матричного формализма, а именно — с помощью операции умножения этой матрицы на последовательность матриц определенного вида. В самом деле, на первом шаге алгоритма, «все остается на месте»: столбец $ {mathfrak E}_1 $ совпадает с $ X_{1} $, а оставшиеся столбцы мы пока не трогаем. Формально это «бездействие» можно записать с помощью умножения матрицы $ A_{} $ на единичную матрицу порядка $ 3_{} $.
$$ Acdot E_{3} = left[{mathfrak E}_1,X_2,X_3 right] , . $$
Следующий шаг алгоритма уже менее тривиален: в получившейся матрице производятся действия над первыми двумя столбцами. При этом первый столбец остается неизменным, последний — тоже, а изменяется лишь второй:
$$ {mathfrak E}_2 = X_2 + alpha_{21} {mathfrak E}_1 , . $$
Для получившейся на первом шаге матрицы, это действие эквивалентно домножению ее справа на матрицу
$$ R_2 = left(
begin{array}{ccc} 1 & alpha_{21} & 0 \
0 & 1 & 0 \
0 & 0 & 1
end{array} right) , .
$$
Если значение $ alpha_{21} $ вычисляется как указано в алгоритме:
$$alpha_{21}=- langle {mathfrak E}_1,X_2 rangle big/ langle {mathfrak E}_1,{mathfrak E}_1 rangle =- langle X_1,X_2 rangle big/ langle X_1,X_1 rangle , , $$
то получившаяся матрица
$$ Acdot E_{3} R_2 = left[{mathfrak E}_1,{mathfrak E}_2,X_3 right] $$
имеет первые два столбца ортогональными. Следующее преобразование получившейся системы столбцов равносильно домножению получившейся матрицы справа на матрицу вида
$$ R_3 = left(
begin{array}{ccc} 1 & 0 & alpha_{31} \
0 & 1 & alpha_{32} \
0 & 0 & 1
end{array} right) , .
$$
Если значения $ alpha_{31} $ и $ alpha_{32} $ вычисляются как указано в алгоритме, то
получившаяся матрица
$$ Acdot E_{3} R_2 R_3 = left[{mathfrak E}_1,{mathfrak E}_2,{mathfrak E}_3 right] $$
имеет систему своих столбцов ортогональной. Можно произвести еще одно дополнительное домножение
$$ Acdot E_{3} R_2 R_3 cdot left( begin{array}{ccc} 1/langle {mathfrak E}_1,{mathfrak E}_1 rangle & 0 & 0 \ 0 & 1/langle {mathfrak E}_2,{mathfrak E}_2 rangle & 0 \ & 0 & 1/ langle {mathfrak E}_3,{mathfrak E}_3 rangle end{array} right) , ,
$$
превратив полученную матрицу в матрицу с ортонормированной системой столбцов.
Теперь обдумаем полученный результат. Матрицы, на которые производились домножения матрицы $ A_{} $ имеют довольно специфическую форму: они — либо диагональные, либо же отличаются от единичной матрицы в одном их своих столбцов. Эти матрицы могут быть отнесены к типу матриц элементарных преобразований системы столбцов произвольной матрицы $ A_{} $. Все они являются верхнетреугольными, и их произведение $ R_{} $ относится к тому же типу. Обратная к верхнетреугольной также является верхнетреугольной. В результате, можно получить разложение матрицы $ A_{} $ в произведение
$$ A=Q_{5times 3}R^{-1} , , $$
где вторая матрица в произведении является верхнетреугольной, а первая имеет свои столбцы ортонормированными.
Т
Теорема [о QR-разложении]. Для любой вещественной матрицы $ A_{mtimes n}^{} $ ранга $ n< m $ существует вещественная матрица $ Q_{mtimes n} $ c ортонормированными столбцами и верхнетреугольная вещественная матрица11) $ tilde R_{ntimes n} $, такие, что
$$ A=Q tilde R , . $$
П
Пример. Для матрицы из предыдущего примера имеем:
$$
left(
begin{array}{ccc} 1 & 1 & 1 \
0 & 1 & 1 \
0 & 0 & 1 \
0 & 1 & 1 \
1 & 1 & 1
end{array} right)
=
$$
$$
=left(
begin{array}{ccc}
1/sqrt{2} & 0 & 0 \
0 & 1/sqrt{2} & 0 \
0 & 0 & 1 \
0 & 1/sqrt{2} & 0 \
1/sqrt{2} & 0 & 0
end{array} right) left{
left(
begin{array}{rrr}
1 & -1 & 0 \
0 & 1 & 0 \
0 & 0 & 1
end{array} right)
left(
begin{array}{rrr}
1 & 0 & -1 \
0 & 1 & -1 \
0 & 0 & 1
end{array} right)
left(
begin{array}{ccc}
1/sqrt{2} & 0 & 0 \
0 & 1/sqrt{2} & 0 \
0 & 0 & 1
end{array} right)
right}^{-1}
$$
$$
= left(
begin{array}{ccc}
1/sqrt{2} & 0 & 0 \
0 & 1/sqrt{2} & 0 \
0 & 0 & 1 \
0 & 1/sqrt{2} & 0 \
1/sqrt{2} & 0 & 0
end{array} right)left(
begin{array}{rrr}
sqrt{2} & sqrt{2} & sqrt{2} \
0 & sqrt{2} & sqrt{2} \
0 & 0 & 1
end{array} right)
, .
$$
♦
=>
Для квадратной неособенной вещественной матрицы $ A_{} $ матрица $ Q_{} $ в QR-разложении будет ортогональной.
Последний результат имеет уже самостоятельное значение, не относящееся к материалам настоящего раздела. Например, его можно использовать для обращения матрицы $ A_{} $. Дело в том, что ортогональная матрица обращается достаточно просто: $ Q^{-1} = Q^{top} $.
Расстояние от точки до многообразия
Задача. Найти расстояние от заданного вектора $ X_{} $ до заданного множества $ mathbb Ssubset mathbb E $.

Такая постановка требует немедленного уточнения: что такое расстояние от вектора до множества?
Обратясь за помощью к геометрии, мы можем ввести это понятие, основываясь на понятии расстояния между точками: например, расстояние от точки $ Xin mathbb R^2 $ до множества $ mathbb S subset mathbb R^2 $ определить как минимальное из возможных расстояний между точками $ X_{} $ и $ Y_{} $, где $ Yin mathbb S $. Следующий пример показывает, что наше определение оказывается ущербным.
П
Пример. Множество
$$ mathbb S={(x,y)in mathbb R^2 mid x^2+y^2<1 } $$
не содержит своих граничных точек; требуемый минимум расстояний от точки $ X=(2,0) $ до точек круга не достигается так как при любом выборе
точки $ Y_1 in mathbb S $ найдется более близкая к точке $ X_{} $ точка $ Y_2 in mathbb S $.
Расстоянием от вектора $ Xin mathbb E $ до множества $ mathbb Ssubset mathbb E $ назовем число
$$inf_{Yin mathbb S} |X-Y| . $$
По традиции, идущей из геометрии, в алгебре также говорят о «расстоянии от конца вектора $ X_{} $…» или о «расстоянии от точки $ X_{} $…» Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие конец вектора
отсутствует в аксиоматике евклидова пространства.
В случае произвольного множества $ mathbb S $ поставленная задача весьма сложна. В настоящем пункте мы будем решать ее только для частного случая расстояния от точки до плоскости, т.е. от вектора $ Xin mathbb E $ до линейного многообразия $ mathbb M subset mathbb E $.
Ортогональное дополнение
Говорят, что вектор $ X_{} $ ортогонален множеству $ mathbb S subset mathbb E $, если $ X_{} $ ортогонален любому вектору $ Y_{} $ из $ mathbb S $.
Т
Теорема 1. Для того, чтобы вектор $ X_{} $ был ортогонален линейному подпространству $ mathbb E_1 $ необходимо и достаточно, чтобы $ X_{} $ был ортогонален
произвольному базису этого подпространства.
Т
Теорема 2. Множество векторов $ X_{} $ ортогональных подпространству $ mathbb E_{1} subset mathbb E $ образует подпространство. Оно называется ортогональным дополнением подпространства $ mathbb E_1 $ в $ mathbb E_{ } $ и обозначается $ mathbb E_1^{^{bot}} $. Справедливо равенство
$$
mathbb E=mathbb E_1 oplus mathbb E_1^{^{bot}} ,
$$
т.е. пространство $ mathbb E_{ } $ раскладывается в прямую сумму своего произвольного подпространства $ mathbb E_1 $ и ортогонального дополнения $ mathbb E_1^{^{bot}} $ этого подпространства.
П
Пример. Построить $ mathbb E_1^{^{bot}} $ для
$$
mathbb E_1 ={mathcal L} left(
left[
begin{array}{r}
1 \ 0 \ 1 \ 0
end{array}
right],
left[
begin{array}{r}
0 \ 1 \ 1 \ -2
end{array}
right],
left[
begin{array}{r}
2 \ -1 \ 1 \ 2
end{array}
right]
right)
$$
и скалярного произведения заданного стандартным способом: $ langle X,Y rangle = x_1y_1+dots+x_4y_4 $.
Решение. Будем искать произвольный — т.е. не обязательно ортогональный — базис $ mathbb E_1^{^{bot}} $. Вектор $ X=[x_1,x_2,x_3,x_4]^{^{top}} $,
принадлежащий $ mathbb E_1^{^{bot}} $, должен
быть ортогонален всем векторам из $ mathbb E_1 $, и, в частности, тем, на которые
натянуто это подпространство. Из полученных равенств составляем систему
$$
left{
begin{array}{rrrrl}
x_1&&+x_3&&= 0, \
&x_2&+x_3&-2,x_4 &=0, \
2,x_1&-x_2&+x_3&+2,x_4 &=0,
end{array}
right.
$$
не заботясь о том, что некоторые уравнения могут оказаться зависимыми от других.
Множество решений этой системы как раз и будет совпадать с $ mathbb E_1^{^{bot}} $.
Нам остается лишь найти базис этого множества, т.е. фудаментальную систему решений:
$$
iff
left{
begin{array}{rrrrl}
x_1&&+x_3&&= 0, \
&x_2&+x_3&-2,x_4 &=0
end{array}
right. Rightarrow
begin{array}{cc|cc}
x_1 & x_2 & x_3 & x_4 \ hline
-1 & -1 & 1 & 0 \
0 & 2 & 0 & 1
end{array}
$$
Ответ.
$ mathbb E_1^{^{bot}}={mathcal L}left([-1,-1,1,0]^{top},[0,2,0,1]^{top} right) $.
П
Пример. Построить $ mathbb E_1^{^{bot}} $ для
$$
mathbb E_1=
left{
Xin mathbb R^4 left|
begin{array}{rrrrl}
3,x_1&+2,x_2&-x_3&-x_4 &= 0, \
x_1&+x_2&-3,x_3&-2,x_4 &=0, \
2,x_1&+x_2&+2,x_3&+x_4 &=0
end{array}
right.
right}
$$
и скалярного произведения заданного стандартным способом: $ langle X,Y rangle = x_1y_1+dots+x_4y_4 $.
Решение этого примера можно было бы провести сведением к предыдущему случаю. Однако
базисные векторы $ mathbb E_1^{^{bot}} $ легко определяются из следующих соображений.
Заметим, что каждое из уравнений системы, задающей $ mathbb E_1 $, можно «перевести на язык» скалярного произведения
$$
3,x_1+2,x_2-x_3-x_4=0 iff left([3,2,-1,-1]^{^{top}}, [x_1,x_2,x_3,x_4]^{^{top}} right)=0
.
$$
Формально это соотношение означает, что произвольный вектор $ X_{} $ из $ mathbb E_1 $
должен быть ортогонален вектору $ [3,2,-1,-1]^{^{top}} $. Но последний факт как раз и означает, что $ [3,2,-1,-1]^{^{top}}in mathbb E_1^{^{bot}} $. Аналогичные рассуждения справедливы и для других уравнений системы. Имеем:
$$
mathbb E_1^{^{bot}}=
{mathcal L} left(
left[
begin{array}{r}
3 \ 2 \ -1 \ -1
end{array}
right],
left[
begin{array}{r}
1 \ 1 \ -3 \ -2
end{array}
right],
left[
begin{array}{r}
2 \ 1 \ 2 \ 1
end{array}
right]
right)=
{mathcal L} left(
left[
begin{array}{r}
3 \ 2 \ -1 \ -1
end{array}
right],
left[
begin{array}{r}
1 \ 1 \ -3 \ -2
end{array}
right]
right)
$$
♦
?
Доказать следующие свойства операции $ perp $:
а) $ left(mathbb E_1^{^{bot}} right)^{^{bot}}=mathbb E_1 $;
б) $ left(mathbb E_1 +mathbb E_2 right)^{^{bot}}=mathbb E_1^{^{bot}} cap mathbb E_2^{^{bot}} $;
в) $ left(mathbb E_1 cap mathbb E_2 right)^{^{bot}}=mathbb E_1^{^{bot}}+mathbb E_2^{^{bot}} $.
?
Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой
$$
langle A,B rangle = operatorname{Sp} left(Acdot B^{top} right) = sum_{j,k=1}^n a_{jk}b_{jk} ,
$$
подпространство кососимметричных матриц является ортогональным дополнением подпространства симметричных матриц.
Вычисление расстояния
Теорема $ 2 $ из предыдущего пункта позволяет сформулировать результат, на котором и будет основано решение задачи вычисления расстояния.
Т
Теорема 3. Для любого вектора $ Xin mathbb E $ существует единственное представление его в виде
$$
X=X^{^{parallel}}+X^{^{bot}} quad npu X^{^{parallel}}in mathbb E_1,
X^{^{bot}} in mathbb E_1^{^{bot}} .
$$
В этом разложении вектор $ X^{^{parallel}} $ называется ортогональной проекцией вектора $ X_{} $ на $ mathbb E_1 $, а вектор $ X^{^{bot}} $ — ортогональной составляющей вектора $ X_{} $ относительно $ mathbb E_1 $ или же перпендикуляром, опущенным из точки $ X_{} $ на подпространство $ mathbb E_1 $.
Используемые обозначения $ X^{^{parallel}} $ и $ X^{^{bot}} $ не являются общеупотребительными. Я их придумал сам — показались наглядными, но впоследствии встретил
☞
в одной статье Википедии; только там они записаны в вариантах $ X_{parallel} $ и $ X_{bot} $.
Т
Теорема 4. Длина перпендикуляра, опущенного из точки $ X_{} $ на подпространство $ mathbb E_1 $ , равна расстоянию от этой точки до подпространства:
$$left|X^{^{bot}}right|=min_{Yin mathbb E_1} |X-Y| . $$
Доказательство.
$$
X^{^{bot}}=left( X-X^{^{parallel}} right) perp mathbb E_1 Rightarrow
X^{^{bot}} perp left( -Y+X^{^{parallel}} right) quad
npu forall Y in mathbb E_1 .
$$
По теореме Пифагора:
$$
left|X^{^{bot}} right|^2+ left|X^{^{parallel}} -Y right|^2
=left|X^{^{bot}}+ X^{^{parallel}} -Y right|^2 =
|X-Y|^2 Rightarrow
$$
$$
Rightarrow left|X^{^{bot}} right|^2le |X-Y|^2
Rightarrow left|X^{^{bot}} right|le min_{Yin mathbb E_1} |X-Y|
.
$$
С другой стороны, указанный минимум достигается при $ Y=X^{^{parallel}} $ поскольку
$ left|X^{^{bot}} right|=left|X-X^{^{parallel}}right| $.
♦
Итак, задача, поставленная в начале
☞
ПУНКТА, решается вычислением $ left|X^{^{bot}} right| $. Для нахождения последнего числа сначала найдем базис $ {X_1,dots,X_k } $ подпространства $ mathbb E_1 $.
Далее, ищем $ X^{^{parallel}} $, принадлежащий $ mathbb E_1 $, в виде
линейной комбинации базисных векторов:
$$
X^{^{parallel}}=alpha_1 X_1 + dots + alpha_k X_k .
$$
Для нахождения скаляров $ alpha_1,dots , alpha_k $ используем тот факт, что вектор $ X^{^{bot}}=X-X^{^{parallel}} $ должен быть ортогонален
$ mathbb E_1 $, а значит, ортогонален каждому $ X_j $:
$$langle X-X^{^{parallel}}, X_j rangle =0 iff langle X^{^{parallel}}, X_j rangle=langle X,X_j rangle
. $$
Получаем систему линейных уравнений:
$$
left{
begin{array}{ccccc}
alpha_1 langle X_1,X_1 rangle &+ alpha_2 langle X_1,X_2 rangle &+ dots &+ alpha_k langle X_1,X_k rangle &= langle X,X_1 rangle, \
alpha_1 langle X_2,X_1 rangle & + alpha_2 langle X_2,X_2 rangle &+ dots &+ alpha_k langle X_2,X_k rangle &= langle X,X_2 rangle, \
dots & & & & dots \
alpha_1 langle X_k,X_1 rangle & + alpha_2 langle X_k,X_2 rangle &+ dots &+ alpha_k langle X_k,X_k rangle &= langle X,X_k rangle.
end{array}
right.
$$
с матрицей, которая нам уже известна как матрица Грама системы векторов:
$ G(X_1,dots,X_k) $.
Для однозначной разрешимости относительно $ alpha_1,dots , alpha_k $ необходимо и достаточно (см.
☞
теорема Кронекера-Капелли ), чтобы определитель этой матрицы — т.е. определитель Грама $ mathfrak G(X_1,dots,X_k) $ — был отличен от нуля.
Матрица Грама обращается в единичную если векторы $ X_1,dots,X_k $ входят в состав ортонормированного базиса пространства $ mathbb E_{} $. Следовательно, по крайней мере в этом частном случае, система уравнений будет иметь единственное решение. В одном из последующих
☟
ПУНКТОВ будет установлен и более общий факт:
$$
mathfrak{G}(Y_1,dots,Y_k)=0 iff quad mbox{ система векторов } quad {Y_1,dots,Y_k} quad
mbox{ линейно зависима. }
$$
Этот факт позволяет нам заключить, что, поскольку векторы $ {X_1,dots,X_k} $ — базисные для подпространства $ mathbb E_1 $, то система уравнений имеет единственное решение относительно $ alpha_1,dots , alpha_k $:
$$alpha_1=alpha_1^{*},dots , alpha_k=alpha_k^{*} .$$
Теперь может быть найдена проекция вектора $ X_{} $ на $ mathbb E_1 $:
$$
X^{^{parallel}}=alpha_1^{*} X_1 + dots + alpha_k^{*} X_k ,
$$
а затем и составляющая: $ X^{^{bot}}=X-X^{^{parallel}} $.
П
Пример. Найти расстояние от точки $ X=[1,1,2,2,2] $ до подпространства
$$
mathbb E_1=
left{
Xin mathbb R^5 left|
begin{array}{rrrrrl}
x_1&-x_2&-x_3&+x_4 & &= 0, \
2,x_1&-x_2&-x_3&+2,x_4 &-x_5 &=0
end{array}
right.
right} ,
$$
если скалярное произведение определяется стандартно: $ langle X,Y rangle=sum_{j=1}^5 x_jy_j $.
Решение. Базис $ mathbb E_1 $ составляет фундаментальная система решений системы линейных уравнений, например:
$$X_1=[0,-1,1,0,0], X_2=[-1,0,0,1,0], X_3=[1,1,0,0,1] .$$
Составляем матрицу Грама этой системы векторов и выписываем систему уравнений:
$$
left(
begin{array}{rrr}
2 & 0 & -1 \
0 & 2 & -1 \
-1 & -1 & 3
end{array}
right)
left(
begin{array}{r}
alpha_1 \
alpha_2 \
alpha_3
end{array}
right)
=
left(
begin{array}{r}
1 \
1 \
4
end{array}
right) Rightarrow alpha_1=frac{7}{4},, alpha_2=frac{7}{4},, alpha_3=frac{5}{2} .
$$
Ортогональная проекция вектора $ X_{} $ на $ mathbb E_1 $:
$$
X^{^{parallel}}= frac{7}{4} X_1 + frac{7}{4} X_2 + frac{5}{2} X_3=left[frac{3}{4},, frac{3}{4},, frac{7}{4},, frac{7}{4},, frac{5}{2} right] ,
$$
а ортогональная составляющая вектора $ X_{} $ относительно $ mathbb E_1 $:
$$
X^{^{bot}}=X-X^{^{parallel}}=
left[frac{1}{4},, frac{1}{4},, frac{1}{4},, frac{1}{4},, — frac{1}{2} right] quad Rightarrow left|X^{^{bot}}right| =frac{1}{sqrt{2}} .
$$
Ответ. $ 1/sqrt{2} $.
§
Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений
☞
ЗДЕСЬ.
=>
Расстояние от точки $ X_{} $ до линейного подпространства, базисными векторами которого являются $ X_1,dots,X_k $, вычисляется по формуле:
$$
d=sqrt{frac{{mathfrak G}(X_1,dots,X_k, X)}{{mathfrak G}(X_1,dots,X_k)}} .
$$
Доказательство
☞
ЗДЕСЬ.
П
Пример. В пространстве полиномов с вещественными коэффициентами степеней не выше $ 5_{} $ со скалярным произведением, заданным формулой
$$langle p(x),q(x) rangle = int_{-1}^1 p(t)q(t) d,t $$
найти расстояние от полинома $ p(x)= -x^5+x^3-3,x+1 $ до линейного подпространства четных полиномов.
Решение. Базис подпространства четных полиномов состоит, например, из $ 1,x^2,x^4 $. Имеем:
$$
{mathfrak G}(1,x^2,x^4)=left|
begin{array}{ccc}
int_{-1}^1 1 cdot 1 d,t & int_{-1}^1 1 cdot t^2 d,t & int_{-1}^1 1 cdot t^4 d,t \
int_{-1}^1 1 cdot t^2 d,t & int_{-1}^1 t^2 cdot t^2 d,t & int_{-1}^1 t^2cdot t^4 d,t \
int_{-1}^1 1 cdot t^4 d,t & int_{-1}^1 t^2 cdot t^4 d,t & int_{-1}^1 t^4 cdot t^4 d,t
end{array}
right|=left|
begin{array}{ccc}
2 & 2/3 & 2/5 \
2/3 & 2/5 & 2/7 \
2/5 & 2/7 & 2/9
end{array}
right|=frac{2048}{496125} ;
$$
$$
{mathfrak G}(1,x^2,x^4,p(x))=left|
begin{array}{cccc}
2 & 2/3 & 2/5 & 2 \
2/3 & 2/5 & 2/7 & 2/3 \
2/5 & 2/7 & 2/9 & 2/5 \
2 & 2/3 & 2/5 & 3632/495
end{array}
right|=frac{5410816}{245581875} .
$$
Отношение полученных определителей даст квадрат расстояния:
$$ d^2=2642/495 . $$
К этому же ответу можно было прийти и быстрее если заметить, что при заданном скалярном произведении любой четный полином ортогонален любому нечетному полиному. Следовательно для выделения у $ p(x) $ ортогональной составляющей относительно подпространства четных полиномов достаточно оставить в его каноническом виде только нечетные одночлены. Расстояние равно норме полинома $ p(x)-1 $.
♦
Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.
Т
Теорема 5. Расстояние от точки $ X_{} $ до линейного многообразия $ mathbb M=X_0+mathbb E_1 $ равно длине ортогональной составляющей вектора $ X-X_0 $
относительно подпространства $ mathbb E_1 $.
Доказательство. Геометрический смысл понятен из рисунков, иллюстрирующих решение проблемы в $ mathbb R^{3} $: надо свести задачу к случаю из предыдущей теоремы с помощью сдвига всей конструкции на вектор $ (-X_0) $.
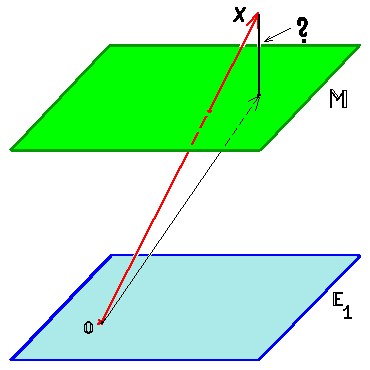
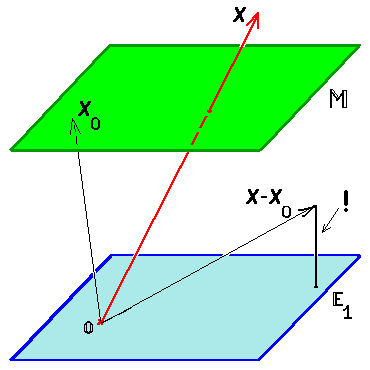
Формальности:
$$
min_{Yin mathbb M} |X-Y| =min_{Zin mathbb E_1} |X-(X_0+Z)|= min_{Zin mathbb E_1} |(X-X_0)-Z)| .
$$
Последняя величина — это расстояние от точки $ X-X_0 $ до $ mathbb E_1 $ ;
согласно теореме $ 4 $ оно равно длине ортогональной составляющей вектора $ X-X_0 $ относительно $ mathbb E_1 $.
♦
=>
Расстояние от точки $ X_{} $ до линейного многообразия, заданного параметрически
$$
mathbb M=left{X_0+lambda_1 X_1+dots+lambda_k X_k quad mid quad
(lambda_1,dots,lambda_k) in {mathbb R}^k right}
$$
при фиксированных линейно независимых
$ {X_0,X_1,dots,X_k }subset {mathbb E} $
вычисляется по формуле:
$$
d=sqrt{frac{{mathfrak G}(X_1,dots,X_k, X-X_0)}{{mathfrak G}(X_1,dots,X_k)}} .
$$
§
Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями)
☞
ЗДЕСЬ.
Угол между вектором и линейным многообразием
Материал настоящего пункта может быть пропущен при первоначальном чтении.
Углом между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ назовем число — точную нижнюю грань множества углов между $ X_{} $ и всевозможными векторами $ Y in mathbb E_1 $. Углом между вектором $ Xin mathbb E $ и линейным многообразием $ mathbb M=X_0+mathbb E_1 $ называется угол между $ X_{} $ и $ mathbb E_1 $.
Т
Теорема. Угол между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ равен углу между этим вектором и его ортогональной проекцией $ X^{^{parallel}} $ на $ mathbb E_1 $.
Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.
П
Пример. Определить угол между вектором $ X_0=[1,0,3,0] $ и линейной оболочкой
$$ mathcal L([5,3,4,-3],[1,1,4,5],[2,-1,1,2]) . $$
Решение. Воспользуемся результатом, приведенным
☞
ЗДЕСЬ (для правильной стыковки рассматриваем все векторы как столбцы):
$$ X_{ast}=L(L^{top} L_{})^{-1} L^{top} X_0 , . $$
Здесь
$$
L=left(begin{array}{rrr}
5 & 1 & 2 \
3 & 1 & -1 \
4 & 4 & 1 \
-3 & 5 & 2
end{array}
right), qquad L^{top} L =
left(begin{array}{rrr}
59 & 9 & 5 \
9 & 43 & 15 \
5 & 15 & 10
end{array}
right),
$$
$$
(L^{top} L )^{-1} =
left(begin{array}{rrr}
41/2312 & -3/2312 & -2/289\
-3/2312 & 113/2312 & -21/289\
-2/289 & -21/289 & 307/1445
end{array}
right)
$$
$$
L(L^{top} L_{})^{-1} L^{top}=
left(begin{array}{rrrr}
9/10 & -1/5 & 1/5 & -1/10 \
-1/5 & 3/5 & 2/5 & -1/5 \
1/5 & 2/5 & 3/5 & 1/5\
-1/10 & -1/5 & 1/5 & 9/10
end{array}
right), quad
X_{ast}= left(begin{array}{r}
3/2 \ 1 \ 2 \ 1/2
end{array}
right) , .
$$
$$
widehat{X_0,X_{ast}}=arccos frac{langle X_0,X_{ast} rangle }{sqrt{ langle X_0,X_0rangle langle X_{ast},X_{ast} rangle}}= arccos frac{sqrt{3}}{2}= frac{pi}{6} , .
$$
♦
Свойства матрицы Грама
Т
Теорема. $ {mathfrak G}(X_{1},dots,X_m)=0 $ тогда и только тогда, когда система векторов $ {X_{1},dots,X_m } $ линейно зависима.
Доказательство. Если система векторов $ {X_{1},dots,X_m} $ линейно зависима, то имеет место равенство
$$alpha_1 X_1+alpha_2 X_2+dots+alpha_{m} X_{m}=mathbb O$$
при некотором нетривиальном наборе скаляров $ alpha_1=alpha_1^{*},dots,alpha_m=alpha_m^{*} $. Домножим это соотношение (скалярно) на векторы $ X_1,X_2,dots,X_m $, получим систему уравнений, которую перепишем в матричном виде:
$$
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
left(
begin{array}{c} alpha_1 \ alpha_2 \ vdots \ alpha_m
end{array}
right)=
left(
begin{array}{c}
0 \ 0 \ vdots \ 0
end{array}
right) .
$$
Если рассмотреть эту систему относительно переменных $ alpha_{1},dots,alpha_m $, то она оказывается однородной и, по предположенному, будет иметь нетривиальное решение $ alpha_1=alpha_1^{*},dots,alpha_m=alpha_m^{*} $ . Следовательно (см.
☞
ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛИ ) ее определитель равен нулю: $ {mathfrak G}(X_{1},dots,X_m)=0 $.
Обратно, если определитель Грама равен нулю, то предыдущая система имеет нетривиальное решение относительно $ alpha_{1},dots,alpha_m $. Пусть $ alpha_1=alpha_1^{star},dots,alpha_m=alpha_m^{star} $ — какое-то из этих решений. Составим вектор
$$X^{star}= alpha_1^{star} X_1+alpha_2^{star} X_2+dots+alpha_{m}^{star} X_{m} $$
и вычислим скалярное произведение его на самого себя:
$$ langle X^{star},X^{star} rangle = $$
$$ = (alpha_1^{star} ,alpha_2^{star} ,dots,alpha_m^{star} )
underbrace{left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
left(begin{array}{c}
alpha_1^{star} \ alpha_2^{star} \ vdots \ alpha_m^{star}
end{array}right)}_{=mathbb O_{mtimes 1}}=0 . $$
Таким образом длина вектора $ X^{star} $ равна нулю, и, следовательно, по аксиоме
4
, сам вектор $ X^{star} $ — нулевой. Но тогда система векторов $ {X_{1},dots,X_m} $ линейно зависима.
♦
=>
Ранг матрицы Грама совпадает с рангом системы порождающих ее векторов:
$$ operatorname{rank} (G(X_1,dots,X_m))= operatorname{rank} {X_1,dots,X_m } . $$
=>
Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.
Т
Теорема. $ {mathfrak G}(X_{1},dots,X_m) ge 0 $ для любого набора векторов $ {X_{1},dots,X_m } $.
Доказательство
☞
ЗДЕСЬ
=>
Матрица Грама линейно независимой системы векторов является положительно определенной.
Матрица Грама произвольной системы векторов является положительно полуопределенной.
§
Дальнейшие свойства матрицы и определителя Грама
☞
ЗДЕСЬ
Задачи
Источник
Материалы этого раздела составлены на основе книги
Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969
The Euclidean distance formula finds the distance between any two points in Euclidean space.
A point in Euclidean space is also called a Euclidean vector.
You can use the Euclidean distance formula to calculate the distance between vectors of two different lengths.
For vectors of different dimension, the same principle applies.
Suppose a vector of lower dimension also exists in the higher dimensional space. You can then set all of the missing components in the lower dimensional vector to 0 so that both vectors have the same dimension. You would then use any of the mentioned distance formulas for computing the distance.
For example, consider a 2-dimensional vector A in R² with components (a1,a2), and a 3-dimensional vector B in R³ with components (b1,b2,b3).
To express A in R³, you would set its components to (a1,a2,0). Then, the Euclidean distance d between A and B can be found using the formula:
d² = (b1 - a1)² + (b2 - a2)² + (b3 - 0)²
d = sqrt((b1 - a1)² + (b2 - a2)² + b3²)
For your particular case, the components will be either 0 or 1, so all differences will be -1, 0, or 1. The squared differences will then only be 0 or 1.
If you’re using integers or individual bits to represent the components, you can use simple bitwise operations instead of some arithmetic (^ means XOR or exclusive or):
d = sqrt(b1 ^ a1 + b2 ^ a2 + ... + b(n-1) ^ a(n-1) + b(n) ^ a(n))
And we’re assuming the trailing components of A are 0, so the final formula will be:
d = sqrt(b1 ^ a1 + b2 ^ a2 + ... + b(n-1) + b(n))

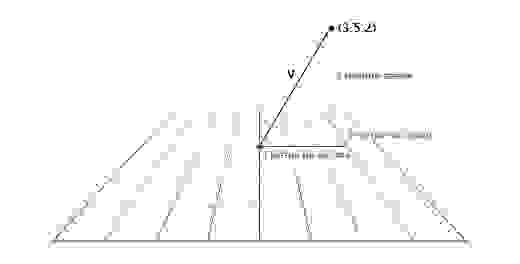
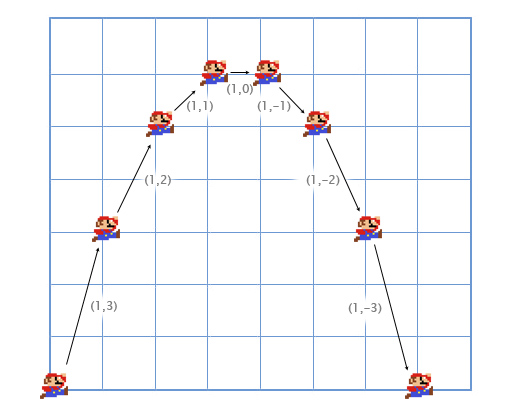
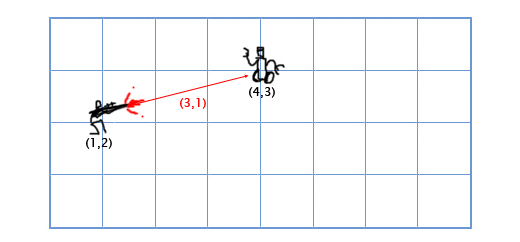
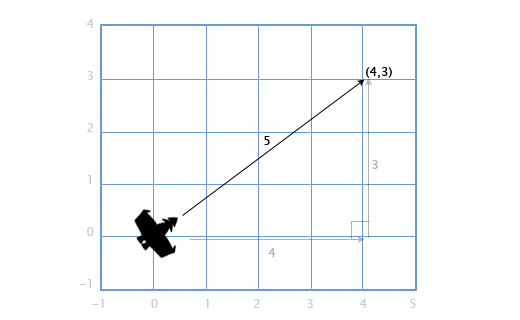
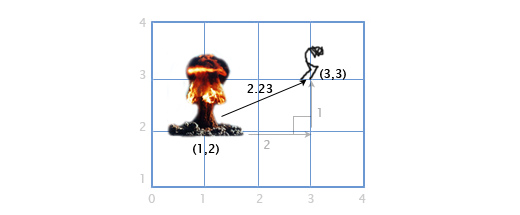
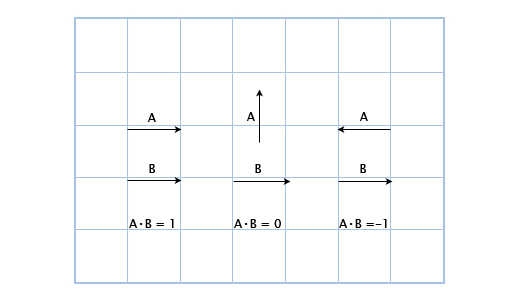
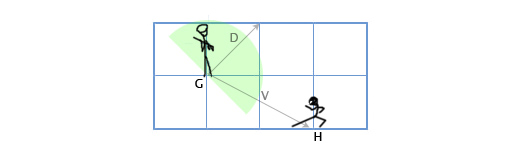
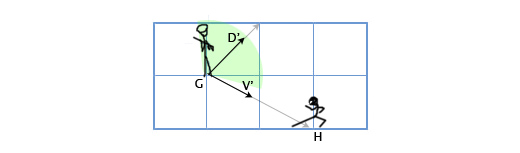
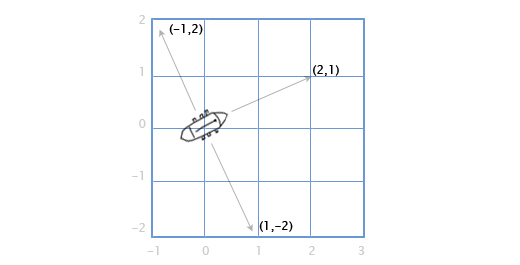
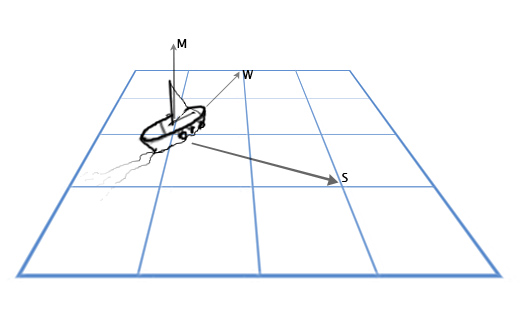
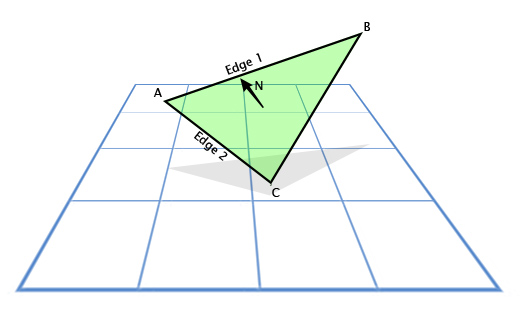
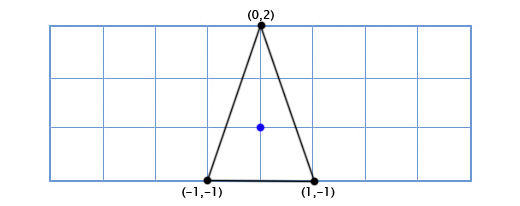
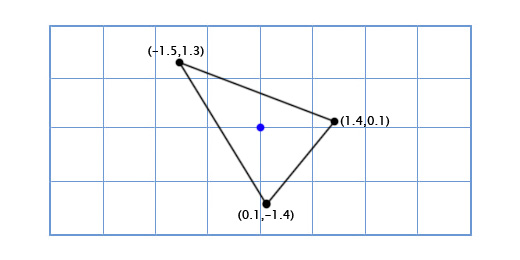
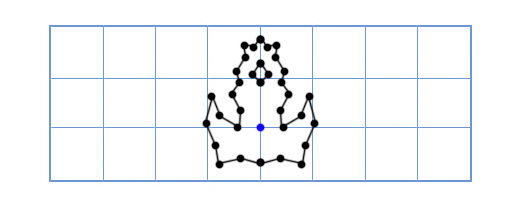
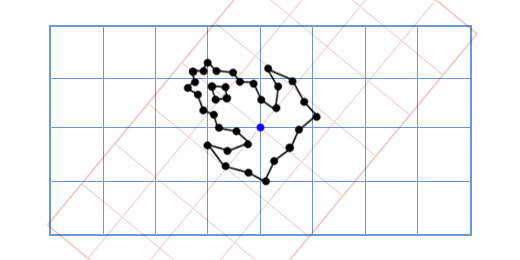
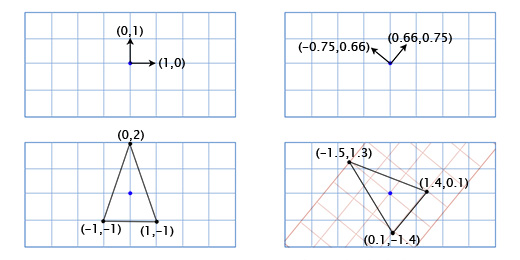
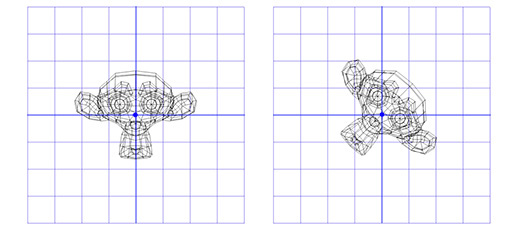
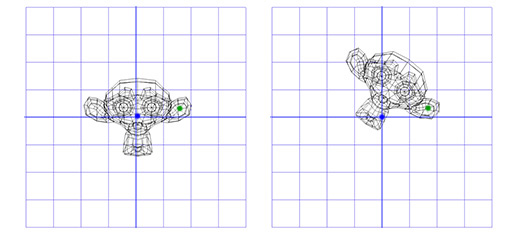
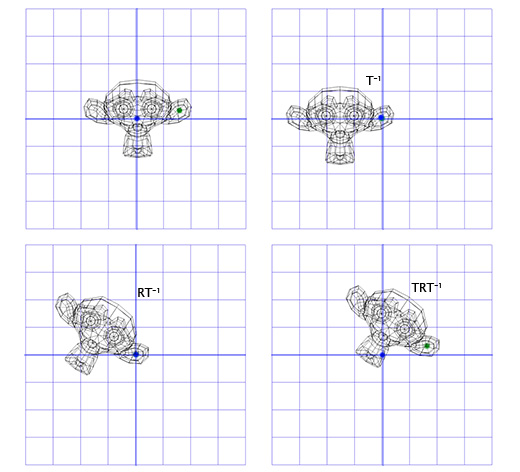
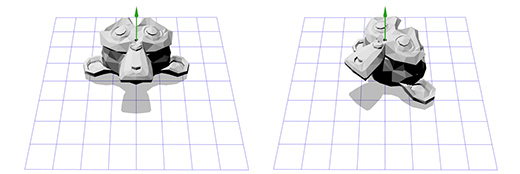
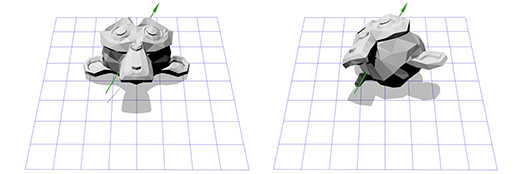
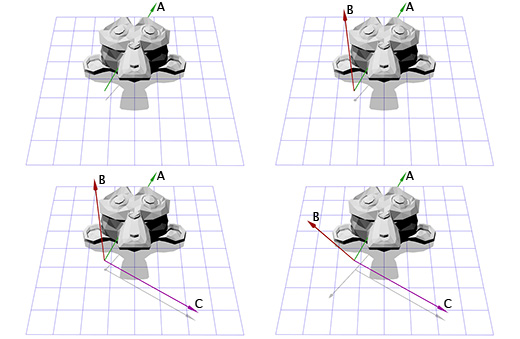
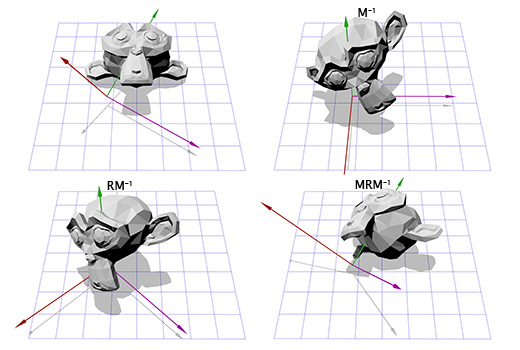
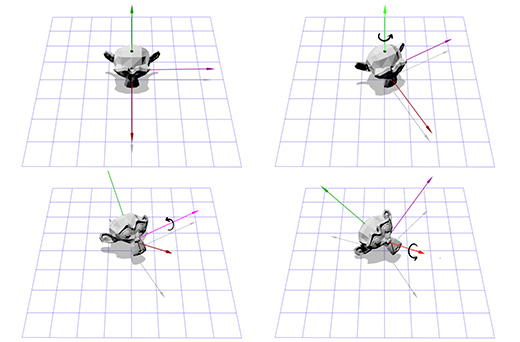

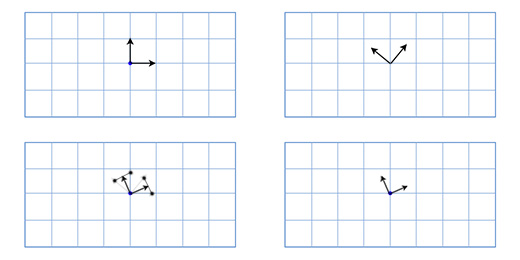

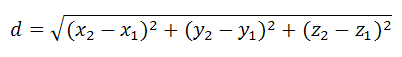
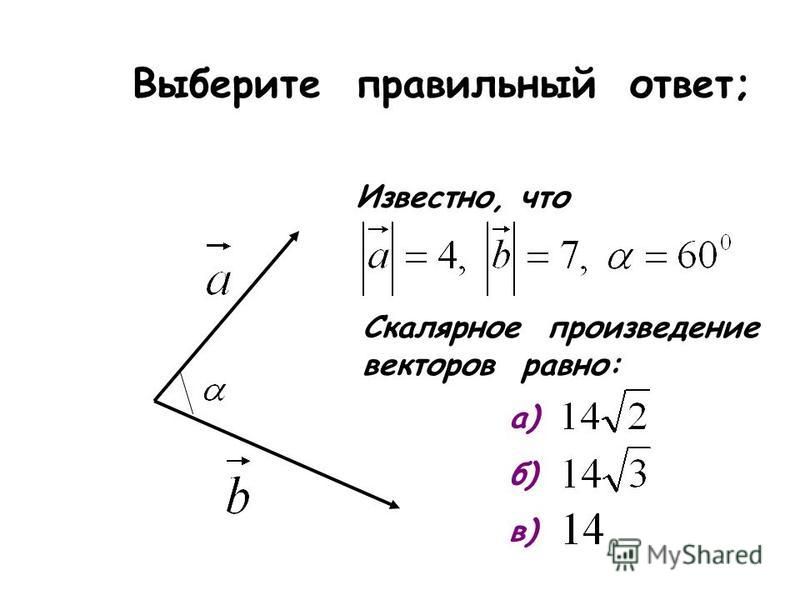


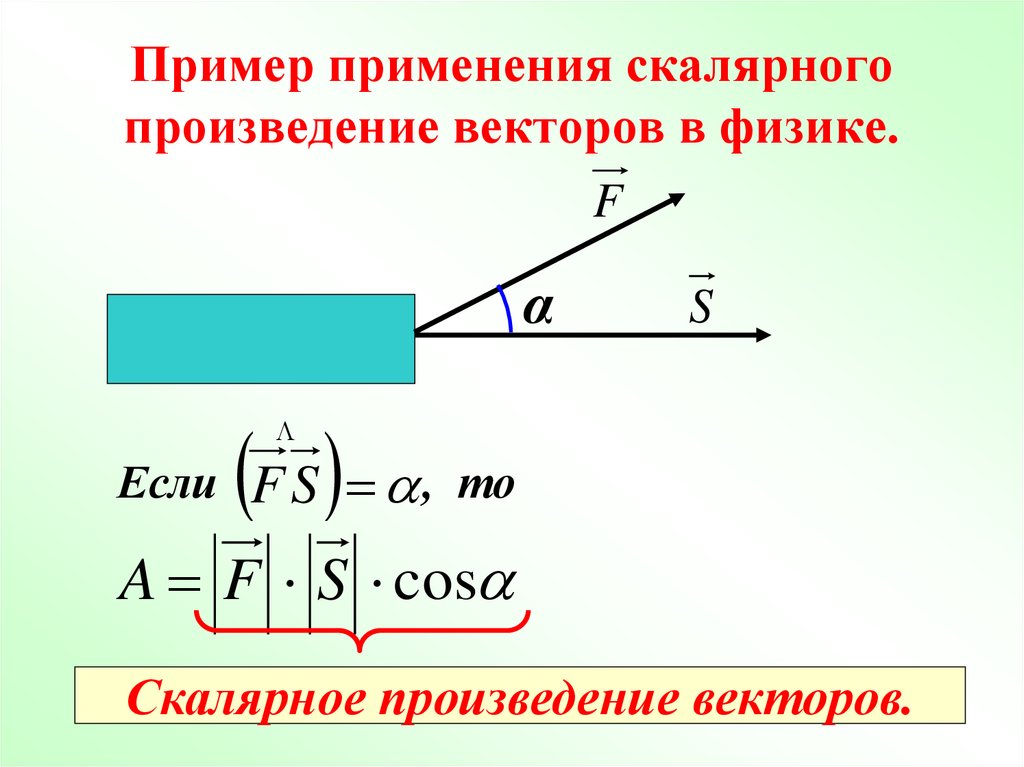 41735497117 — я точно не
41735497117 — я точно не
 документацию по каждой метрике для
документацию по каждой метрике для


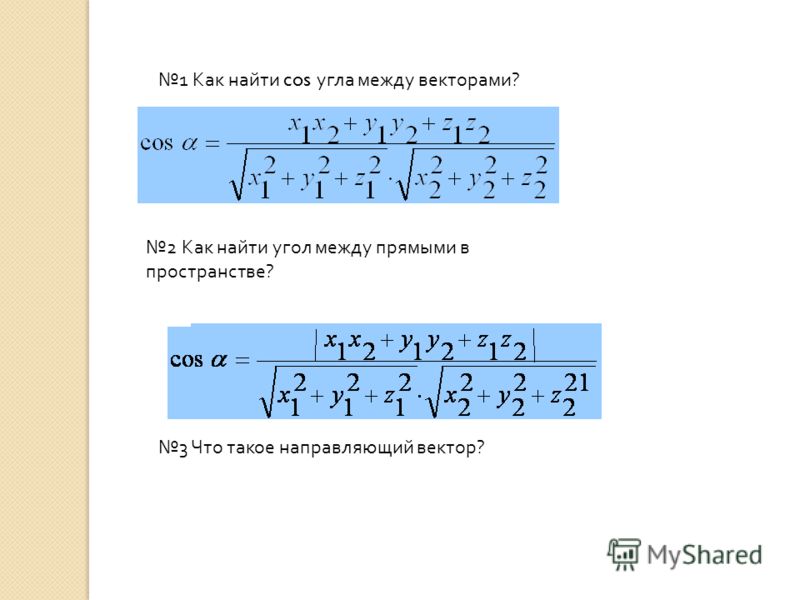 ]
]  (см.
(см. 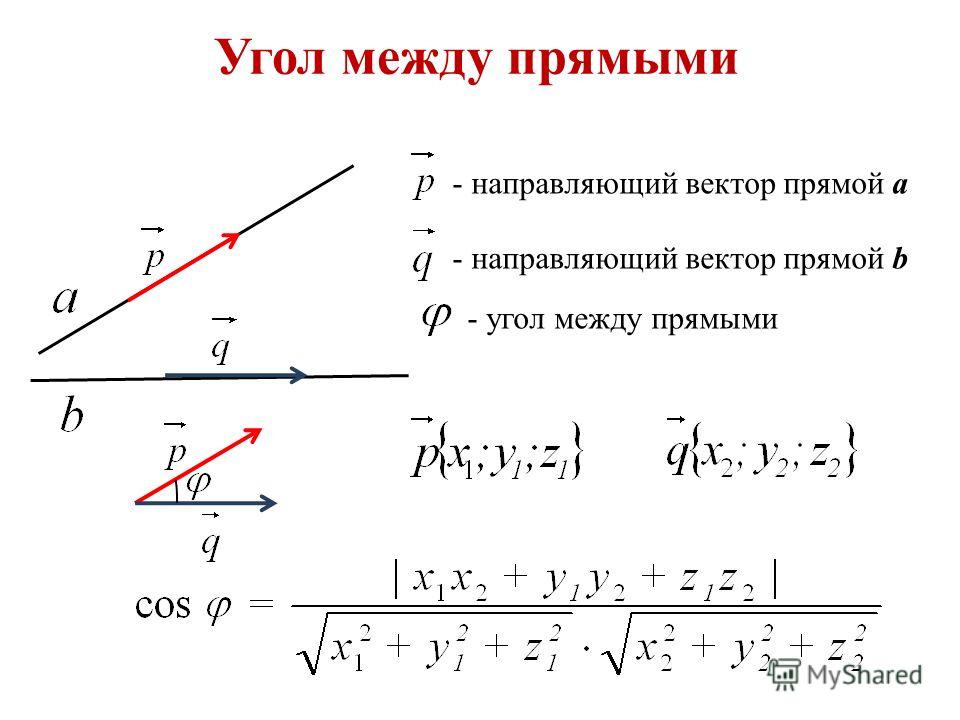 Например:
Например:  array([[0, 0, 0],
... [0, 0, 1],
... [0, 1, 0],
... [0, 1, 1],
... [1, 0, 0],
... [1, 0, 1],
... [1, 1, 0],
... [1, 1, 1]])
>>> b = np.array([[ 0,1, 0,2, 0,4]])
>>> Distance.cdist(a, b, 'городской квартал')
массив([[ 0,7],
[ 0,9],
[1.3],
[ 1,5],
[ 1,5],
[1,7],
[ 2.1],
[ 2.3]])
array([[0, 0, 0],
... [0, 0, 1],
... [0, 1, 0],
... [0, 1, 1],
... [1, 0, 0],
... [1, 0, 1],
... [1, 1, 0],
... [1, 1, 1]])
>>> b = np.array([[ 0,1, 0,2, 0,4]])
>>> Distance.cdist(a, b, 'городской квартал')
массив([[ 0,7],
[ 0,9],
[1.3],
[ 1,5],
[ 1,5],
[1,7],
[ 2.1],
[ 2.3]])