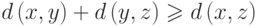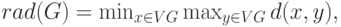From Wikipedia, the free encyclopedia
«Geodesic distance» redirects here. For distances on the surface of a sphere, see Great-circle distance. For distances on the surface of the Earth, see Geodesics on an ellipsoid. For geodesics in differential geometry, see Geodesic.
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path (also called a graph geodesic) connecting them. This is also known as the geodesic distance or shortest-path distance.[1] Notice that there may be more than one shortest path between two vertices.[2] If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.
In the case of a directed graph the distance d(u,v) between two vertices u and v is defined as the length of a shortest directed path from u to v consisting of arcs, provided at least one such path exists.[3] Notice that, in contrast with the case of undirected graphs, d(u,v) does not necessarily coincide with d(v,u)—so it is just a quasi-metric, and it might be the case that one is defined while the other is not.
[edit]
A metric space defined over a set of points in terms of distances in a graph defined over the set is called a graph metric.
The vertex set (of an undirected graph) and the distance function form a metric space, if and only if the graph is connected.
The eccentricity ϵ(v) of a vertex v is the greatest distance between v and any other vertex; in symbols,
It can be thought of as how far a node is from the node most distant from it in the graph.
The radius r of a graph is the minimum eccentricity of any vertex or, in symbols,
The diameter d of a graph is the maximum eccentricity of any vertex in the graph. That is, d is the greatest distance between any pair of vertices or, alternatively,
To find the diameter of a graph, first find the shortest path between each pair of vertices. The greatest length of any of these paths is the diameter of the graph.
A central vertex in a graph of radius r is one whose eccentricity is r—that is, a vertex whose distance from its furthest vertex is equal to the radius, equivalently, a vertex v such that ϵ(v) = r.
A peripheral vertex in a graph of diameter d is one whose eccentricity is d—that is, a vertex whose distance from its furthest vertex is equal to the diameter. Formally, v is peripheral if ϵ(v) = d.
A pseudo-peripheral vertex v has the property that, for any vertex u, if u is as far away from v as possible, then v is as far away from u as possible. Formally, a vertex v is pseudo-peripheral if, for each vertex u with d(u,v) = ϵ(v), it holds that ϵ(u) = ϵ(v).
A level structure of the graph, given a starting vertex, is a partition of the graph’s vertices into subsets by their distances from the starting vertex.
A geodetic graph is one for which every pair of vertices has a unique shortest path connecting them. For example, all trees are geodetic.[4]
The weighted shortest-path distance generalises the geodesic distance to weighted graphs. In this case it is assumed that the weight of an edge represents its length or, for complex networks the cost of the interaction, and the weighted shortest-path distance dW(u, v) is the minimum sum of weights across all the paths connecting u and v. See the shortest path problem for more details and algorithms.
Algorithm for finding pseudo-peripheral vertices[edit]
Often peripheral sparse matrix algorithms need a starting vertex with a high eccentricity. A peripheral vertex would be perfect, but is often hard to calculate. In most circumstances a pseudo-peripheral vertex can be used. A pseudo-peripheral vertex can easily be found with the following algorithm:
- Choose a vertex
.
- Among all the vertices that are as far from
as possible, let
be one with minimal degree.
- If
then set
and repeat with step 2, else
is a pseudo-peripheral vertex.
See also[edit]
- Distance matrix
- Resistance distance
- Betweenness centrality
- Centrality
- Closeness
- Degree diameter problem for graphs and digraphs
- Metric graph
Notes[edit]
- ^ Bouttier, Jérémie; Di Francesco,P.; Guitter, E. (July 2003). «Geodesic distance in planar graphs». Nuclear Physics B. 663 (3): 535–567. arXiv:cond-mat/0303272. doi:10.1016/S0550-3213(03)00355-9.
By distance we mean here geodesic distance along the graph, namely the length of any shortest path between say two given faces
- ^ Weisstein, Eric W. «Graph Geodesic». MathWorld—A Wolfram Web Resource. Wolfram Research. Archived from the original on 2008-04-23. Retrieved 2008-04-23.
The length of the graph geodesic between these points d(u,v) is called the graph distance between u and v
- ^ F. Harary, Graph Theory, Addison-Wesley, 1969, p.199.
- ^ Øystein Ore, Theory of graphs [3rd ed., 1967], Colloquium Publications, American Mathematical Society, p. 104
Пусть
—
граф (или псевдограф).
Расстояние в графе удовлетворяют
аксиомам метрики
1)
,
2)
(не
в ориентированном графе)
3)
4)
в
связном графе (не в ориентированном
графе).
Пусть
связный
граф (или псевдограф).
-
Определение
Диаметром графа G
называется величина
.
Пусть
.
-
Определение
Максимальным удалением (эксцентриситетом)
в графе G
от вершины
называется
величина
.
-
Определение
Радиусом графа G
называется величина
-
Определение
Центром графа Gназывается
любая вершина
такая,
что
.
Алгоритм фронта волны
Пусть
ориентированный
граф с n³2 вершинами и v,w
(v¹w)
– заданные вершины из V.
Алгоритм поиска
минимального пути из
в
в
ориентированном графе
(алгоритм
фронта волны).
1) Помечаем
вершину
индексом
0, затем помечаем вершины Î образу вершины
индексом
1. Обозначаем их FW1
(v).
Полагаем k=1.
2)
Если
или
k=n-1,
и одновременно
то вершина
не
достижима из
.
Работа алгоритма заканчивается.
В противном случае продолжаем:
3)
Если
,
то переходим к шагу 4.
В противном случае мы нашли
минимальный путь из
в
и
его длина равна k.
Последовательность вершин
есть этот минимальный путь. Работа
завершается.
4)
Помечаем индексом k+1
все непомеченные вершины, которые
принадлежат образу множества вершин c
индексом k.
Множество вершин с индексом k+1
обозначаем
.
Присваиваем k:=k+1
и переходим к 2).
-
Замечания
Множество
называется
фронтом волны kго
уровня.
·
Вершины
могут
быть выделены неоднозначно, что
соответствует случаю, если
несколько
минимальных путей из
в
.
Чтобы найти расстояния в
ориентированном графе, необходимо
составить матрицу минимальных расстояний
R(D)между
его вершинами. Это квадратная матрица
размерности
,
элементы главной диагонали которой
равны нулю (,
i=1,..,n).
Сначала составляем матрицу
смежности. Затем переносим единицы из
матрицы смежности в матрицу минимальных
расстояний (,
если
).
Далее построчно заполняем матрицу
следующим образом.
Рассматриваем первую строку,
в которой есть единицы. Пусть это строка
− i-тая
и на пересечении с j-тым
столбцом стоит единица (то есть
).
Это значит, что из вершины
можно
попасть в вершину
за
один шаг. Рассматриваем j-тую
сроку (строку стоит вводить в рассмотрение,
если она содержит хотя бы одну единицу).
Пусть элемент
.
Тогда из вершины
в
вершину
можно
попасть за два шага.
Таким образом, можно записать
.
Следует заметить, что если в рассматриваемых
строках две или более единиц, то следует
прорабатывать все возможные варианты
попадания из одной вершины в другую,
записывая в матрицу длину наикратчайшего
из них.
-
Пример Найдем
расстояния в ориентированном графе D,
изображенном на рис. 7. В данной задаче
количество вершин n=7,
следовательно, матрицы смежности
и минимальных расстояний между вершинами
ориентированного графа Dбудут
иметь размерность 7×7.

Матрица смежности:

Начинаем заполнять матрицу
R(D)
минимальных расстояний: сначала ставим
нули по главной диагоналии rij=aij,
если aij=1,
(т.е. переносим единицы из матрицы
смежности). Рассматриваем первую строку.
Здесь есть две единицы, то есть из первой
вершины за один шаг можно попасть во
вторую и шестую. Из второй вершины можно
попасть за один шаг в третью (путь в
первую вершину нас не интересует),
следовательно, можно записать
.
Из шестой вершины можем добраться за
один шаг в пятую и седьмую, а значит,
,
.
Теперь ищем маршруты, исходящие из
первой вершины, состоящие из 3 шагов: за
2 шага идем в третью вершину, оттуда за
один шаг попадаем в четвертую, поэтому
.
В итоге получаем следующую матрицу:
Таким образом, диаметром
исследуемого ориентированного графа
будет
.
Для каждой вершины заданного
ориентированного графа найдем максимальное
удаление (эксцентриситет) в графе G от
вершины нее по формуле, которая была
приведена выше
:
r(vi)
− максимальное из расстояний, стоящих
в i-той
строке. Таким образом,
r(v1)=3,
r(v2)=3,
r(v3)=5,
r(v4)=4,
r(v5)=2,
r(v6)=2,
r(v7)=3.
Значит, радиусом графа G
будет
Соответственно, центрами
графа G будут
вершины v5
иv6
, так как величины их эксцентриситетов
совпадают с величиной радиуса.
Опишем теперь нахождение
минимального пути из вершины v3
в вершинуv6
по алгоритму фронта волны. Обозначим
вершину v3
как V0,
а вершину v6—
как W
(см. рис. 8). Множество вершин, принадлежащих
образу V0,
состоит из одного элемента — это вершина
v4,
которую, согласно алгоритму, обозначаем
как V1:
FW1(v3)={v4}.
Поскольку искомая вершина
не принадлежит фронту волны первого
уровня
,
продолжаем работу алгоритма. Строим
фронт волны второго уровня — это множество
вершин, принадлежащих образу вершиныV1:
FW2(v3)={v7},
обозначаем v7≡V2.
В образ вершины V2
входят две вершины —v5
и v4,
но, так как v4
уже была помечена как V0,
то фронт волны третьего уровня состоит
из одного элемента: FW3(v3)={v5},
v5≡V3.
Из непомеченных вершин в образ вершины
V3
входят v1
и v2,
соответственно, FW4(v3)={v1,
v2},
v1≡V4,
v2≡V4.
Теперь помечены все вершины, кроме v6,
которая входит в образ вершины
,
то есть FW5(v3)={v6≡W},
работа алгоритма закончена. Минимальный
путь (5 шагов) из вершины v3
в вершинуv6
выглядит так: v3v4v7v5v1v6.

Минимальный путь в
нагруженном ориентированном графе по
методу Форда-Беллмана
Найти минимальный путь в
нагруженном ориентированном графе из
вершины
в
вершину
по
методу Форда-Беллмана.
Рассмотрим сначала общую
задачу – нахождения минимального пути
из вершины vнач
в vкон.
Пусть D=(V,X)
– нагруженный ориентированный граф,
V={v1,…,vn},
n>1.
Введем величины
,
где i=1,…,n,
k=0,1,2,…,n–1.
Для каждого фиксированного
i и
k
величина
равна
длине минимального пути среди путей из
vнач
в vi
содержащих не более k
дуг. Если путей нет, то
.
Положим также
.
Составляем матрицу длин
дуг C(D)=[cij]
порядка n:
Утверждение.
При i=2,…,n,
k³0
выполняется равенство
.
(3.1)
Алгоритм Форда-Беллмана
нахождения минимального пути в нагруженном
ориентированном графе D из vнач
в vкон.(
vнач
≠ vкон).
(
записываем в виде матрицы, i—
строка, k-столбец).
1) Составляем
таблицу
,
i=1,…,n,
k=0,…,n-1.
Если
,
то пути из vнач
в vкон
нет. Конец алгоритма.
2) Если
то
это число выражает длину любого
минимального пути из vнач
в vкон.
Найдем минимальное k1³1,
при котором
.
По определению
получим,
что k1—
минимальное число дуг в пути среди всех
минимальных путей из vначв
vкон.
3) Затем
определяем номера i2,…,
такие,
что
,
,
,
то есть восстанавливаем по
составленной таблице и матрице стоимости
искомый минимальный путь из vнач
в vкон.
-
Пример
Найдем минимальный путь из
вершины v2
в v6
в ориентированном нагруженном графе
D,
изображенном на рис. 9. В рассматриваемом
графе количество вершин n=7,
следовательно, матрица длин дуг
ориентированного графа Dбудет
иметь размерность 7×7.

9.
Матрица длин дуг для рассматриваемого
графа будет выглядеть следующим образом:
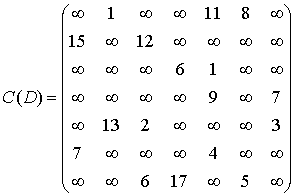
Согласно алгоритму, составляем
таблицу стоимости минимальных путей
из вершины v2
в вершину vi
не более, чем за k
шагов, k=0,…n-1
(n=7,
следовательно, k=0,…6).
Как было определено выше,
,
и
для
всех остальных вершин vi≠
v2,
то есть первый столбец таблицы состоит
из элементов, равных
,
кроме элемента
.
Второй столбец таблицы повторяет вторую
строку матрицы стоимости, поскольку
представляет собой стоимость возможных
путей из вершины v2
за один шаг. Далее по формуле (3.1) находим
по столбцам все оставшиеся элементы
таблицы. Например, чтобы найти элемент
,
складываем элементы столбца
и
первого столбца матрицы стоимости и
выбираем минимальное из получившихся
чисел:
.
В конечном итоге получаем следующую
таблицу:
Теперь необходимо по
построенной таблице и по матрице C(D)
восстановить минимальный путь из вершины
v2
в v6,
который будет строиться с конца, то
есть, начиная с вершины v6.
Для этого выбираем минимальное из чисел,
стоящих в строке, соответствующей v6
в таблице. Это число – 21 – длина
минимального искомого пути. В первый
раз такая длина была получена при
количестве шагов, равном 4. В вершину v6
мы можем попасть за один шаг из вершин
v1
и v7
(длина соответствующих дуг 8 и 5
соответственно – данные из матрицы
C(D)).
Выбираем минимальную по длине из этих
дуг. Далее, в вершину v7
можно попасть из v4
и v5(длина
соответствующих дуг 7 и 3 соответственно).
Продолжая аналогичным образом, найдем
искомый путь за 4 шага минимальной длины
из вершины v2
в v6:
v2v3v5v7v6.
78
Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
2) d(v, w) = d(w, v);
3) d(v, w) d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
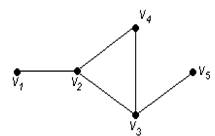
Пример 82.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.
Расстояние между двумя вершинами
Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.
Обозначение – d (U, V)
Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.
пример
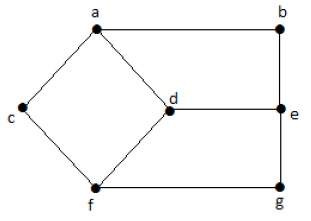
Посмотрите на следующий график –
Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ –
- да, а, бе
- дф, фг, гэ
- де (считается для расстояния между вершинами)
- дф, фц, ca, ab, be
- да, ac, cf, fg, ge
Эксцентриситет вершины
Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.
Обозначение – e (V)
Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.
пример
На приведенном выше графике эксцентриситет «а» равен 3.
Расстояние от «a» до «b» равно 1 («ab»),
от ‘a’ до ‘c’ равно 1 (‘ac’),
от «а» до «d» равно 1 («объявление»),
от ‘a’ до ‘e’ равно 2 (‘ab’ – ‘be’) или (‘ad’ – ‘de’),
от ‘a’ до ‘f’ равно 2 (‘ac’ – ‘cf’) или (‘ad’ – ‘df’),
от ‘a’ до ‘g’ равно 3 (‘ac’ – ‘cf’ – ‘fg’) или (‘ad’ – ‘df’ – ‘fg’).
Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.
Другими словами,
е (б) = 3
е (с) = 3
е (д) = 2
е (е) = 3
е (е) = 3
е (г) = 3
Радиус связного графа
Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.
Обозначение – r (G)
Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.
Пример – На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».
Диаметр графика
Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.
Обозначение – d (G)
Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.
Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.
Центральная точка
Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если
e (V) = r (V),
тогда «V» является центральной точкой графа «G».
Пример – в примере графика ‘d’ является центральной точкой графика.
e (d) = r (d) = 2
Центр
Множество всех центральных точек «G» называется центром графа.
Пример. В примере графика {‘d’} является центром графика.
Длина окружности
Число ребер в самом длинном цикле «G» называется окружностью «G».
Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.
обхват
Число ребер в кратчайшем цикле G называется его обхват.
Обозначения – g (G).
Пример – в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.
Теорема о сумме степеней вершин
Если G = (V, E) ненаправленный граф с вершинами V = {V 1 , V 2 ,… V n }, то
n ∑ i = 1 градус (V i ) = 2 | E |
Следствие 1
Если G = (V, E) ориентированный граф с вершинами V = {V 1 , V 2 ,… V n }, то
n ∑ i = 1 градус + (V i ) = | E | = n ∑ i = 1 град – (V i )
Следствие 2
В любом неориентированном графе число вершин с нечетной степенью является четным.
Следствие 3
В неориентированном графе, если степень каждой вершины равна k, то
к | V | = 2 | E |
Следствие 4
В неориентированном графе, если степень каждой вершины не меньше k, то
к | V | ≤ 2 | E |
Следствие 5
В неориентированном графе, если степень каждой вершины не более k, то
к | V | ≥ 2 | E |
Связность и компоненты
Граф называется связным, если
в нем для любых двух вершин имеется
маршрут, соединяющий эти вершины. Заметим, что ввиду теоремы 1 можно
в этом определении заменить слово «маршрут» словами «простой
путь«.
Для произвольного графа определим на множестве вершин отношение
соединимости: вершина 

если существует соединяющий их маршрут.
Легко видеть, что это отношение
рефлексивно, симметрично и транзитивно, то есть является отношением
эквивалентности. Классы эквивалентности называются областями
связности, а порождаемые ими подграфы — компонентами связности
графа. В связном графе имеется только одна компонента связности —
весь граф. Компоненты связности можно определить также
как максимальные по включению связные подграфы данного графа.
У графа на рис. 2.2 имеется
четыре области
связности — 
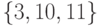
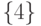
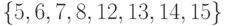
Рис.
2.2.
Вершина называется шарниром
(или точкой
сочленения ), если при
ее удалении число компонент связности увеличивается. У графа
на рис. 2.2 имеется четыре шарнира — это вершины 

Ребро, при удалении которого увеличивается число компонент связности,
называется перешейком.
Перешейками графа, изображенного
на рис. 2.2, являются ребра 

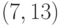
Легко доказываются следующие свойства шарниров и перешейков:
Теорема 4. Ребро является перешейком в том и только том случае,
если в графе нет простого цикла, содержащего это ребро.
Метрические характеристики графов
Расстоянием между двумя
вершинами графа называется наименьшая длина
пути, соединяющего эти вершины. Расстояние между вершинами
и 
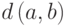
графе нет пути,
соединяющего 

разным
компонентам связности, то расстояние между ними считается бесконечным.
Функция 
-
, причем
тогда
и только тогда, когда;
-
;
-
(неравенство треугольника).
В математике функцию двух переменных, определенную на некотором множестве
и удовлетворяющую условиям 1 — 3, называют метрикой, а множество, на
котором задана метрика, — метрическим пространством. Таким образом,
множество вершин любого графа можно рассматривать как метрическое
пространство.
Расстояние от данной вершины 
вершины
называется эксцентриситетом вершины 
через 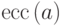
Вершину с наименьшим эксцентриситетом называют центральной,
а вершину с наибольшим эксцентриситетом — периферийной.
Множество всех центральных вершин называется центром графа.
Сама величина наименьшего эксцентриситета
называется радиусом графа и
обозначается
через 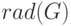
и обозначается 
Наименьший диаметр имеет полный граф — его диаметр равен 1. Среди
связных
графов с 

имеет
цепь 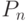
Если расстояние между двумя вершинами равно диаметру графа, то кратчайший
путь, соединяющий эти вершины, называется диаметральным путем,
а подграф, образованный вершинами и ребрами этого пути, — диаметральной
цепью.
Для графа, изображенного на рис. 2.3, эксцентриситеты вершин приведены в следующей таблице:
Центр этого графа составляют вершины 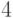
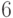
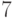
периферийные вершины — 
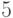
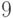
радиус его
равен 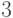
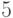
порождается множеством вершин 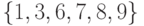
Рис.
2.3.












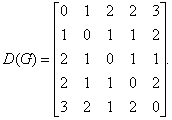

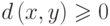 , причем
, причем 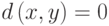 тогда
тогда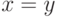 ;
; ;
;