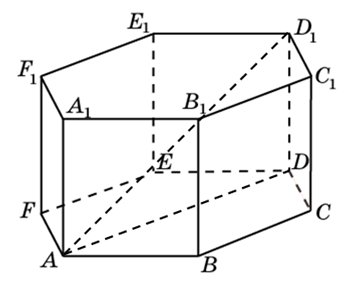
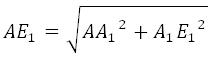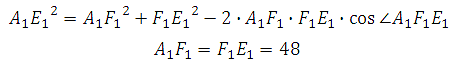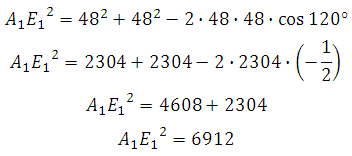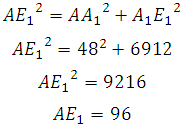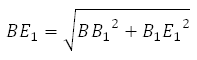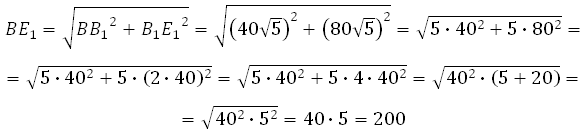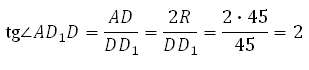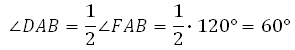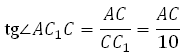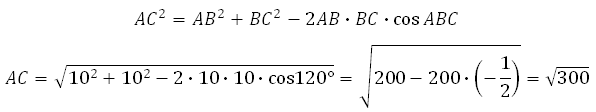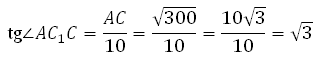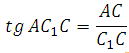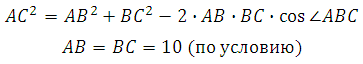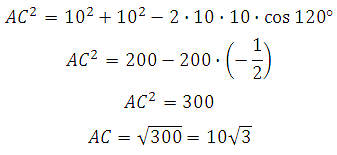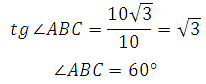Как найти растояние в шестиугольной призме - Исправление недочетов и поиск решений вместе с Examum.ru

На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.

Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

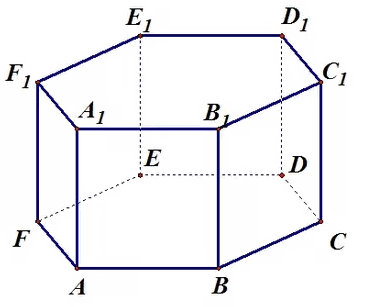
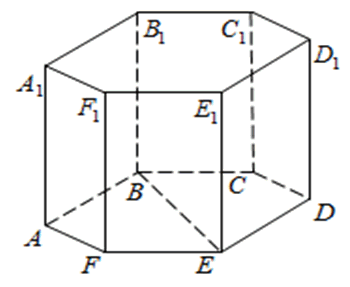
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник. Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.

Используется теорема Пифагора и теорема косинусов. Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.

Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6). Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.

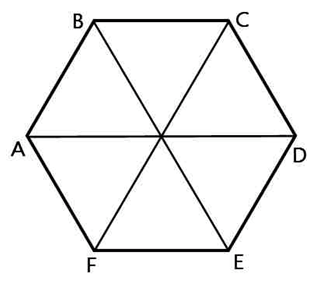
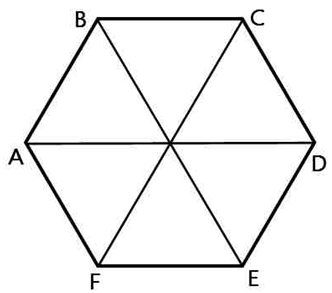
Кратко: что представляет собой правильный шестиугольник?

Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны.

*Противолежащие стороны параллельны.

Дополнительная информация

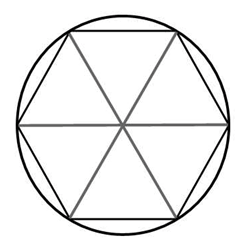
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?

У каждого треугольника угол при его вершине лежащей в центре равен 60⁰ (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.

То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.

Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.

*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.

Рассмотрим задачи:

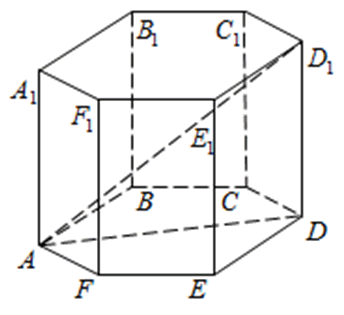
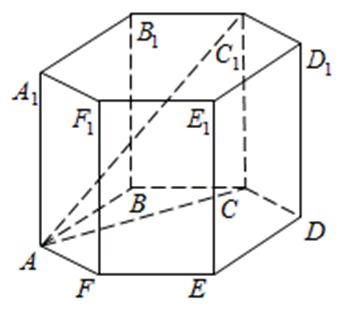
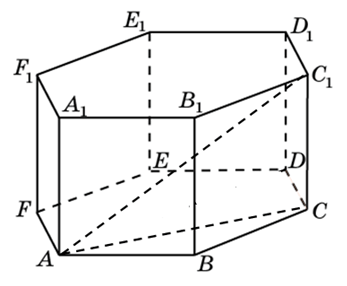
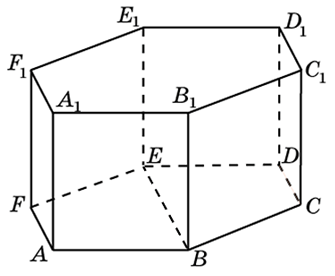
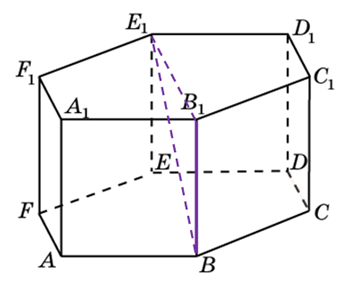
272533. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 48. Найдите расстояние между точками A и E₁.

Рассмотрим прямоугольный треугольник AA₁E₁. По теореме Пифагора:

*Угол между сторонами правильного шестиугольника равен 120 градусам.

Отрезок АЕ₁является гипотенузой, АА₁и А₁Е₁ катеты. Ребро АА₁ нам известно. Катет А₁Е₁ мы можем найти используя используя теорему косинусов.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

Следовательно

По теореме Пифагора:

Ответ: 96

*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 35. Найдите расстояние между точками B и E.

Рассмотрим правильный шестиугольник:

Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.

Таким образом,

Ответ: 70

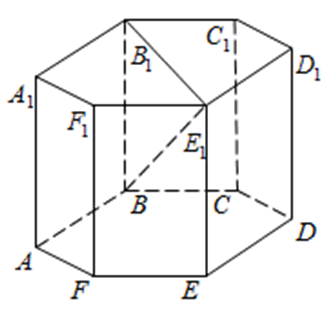
273353. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E₁.

Рассмотрим прямоугольный треугольник BB₁E₁. По теореме Пифагора:

Отрезок B₁E₁ равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть

Таким образом,

Ответ: 200

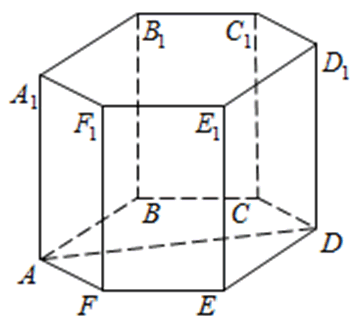
273683. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 45. Найдите тангенс угла AD₁D.

Рассмотрим прямоугольный треугольник ADD₁, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.

Таким образом,

Ответ: 2

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.

Рассмотрим правильный шестиугольник:

В нём углы между сторонами равны 120°. Значит,

Сама длина ребра не имеет значения, на величину угла она не влияет.

Ответ: 60

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим прямоугольный треугольник AC₁C:

Найдём AC. В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :

Таким образом,

Значит, угол AC₁C равен 60 градусам.

Ответ: 60

274453. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 10. Найдите угол AC₁C. Ответ дайте в градусах.

Рассмотрим треугольник AС₁С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть

Катет С₁С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):

В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть

Следовательно

Таким образом:

Ответ: 60

245364. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками А и Е₁.

Посмотреть решение

245365. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите расстояние между точками В и Е.

Посмотреть решение

245366. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁все ребра равны корню из пяти. Найдите расстояние между точками В и Е₁.

Посмотреть решение

245367. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите тангенс угла AD₁D.

Посмотреть решение

245368. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.

Посмотреть решение

245369. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все ребра равны 1. Найдите угол AC₁C. Ответ дайте в градусах.

Посмотреть решение

На этом всё! Успеха Вам!

В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Как найти расстояние между точками в правильной шестиугольной призме?

ksandr97
[2.1K]

7 лет назад

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.

Rafail
[136K]

7 лет назад

Вокруг правильного шестиугольника ABCDEF со сторонами, равными 1 можно описать окружность радиусом 1. Соединим точки ACE. Получился равносторонний треугольник, вписанный в окружность радиуса 1. Сторона такого треугольника √(3). Итак AE=√(3), EE=1. Пифагор нам подсказывает, что AE1=2.

автор вопроса выбрал этот ответ лучшим

в избранное

ссылка

отблагодарить

ksandr97
[2.1K]

Благодарю!
— 7 лет назад

Знаете ответ?

Источник

В правильной шестиугольной призме все рёбра равны 1. Найдите расстояние от точки В до плоскости

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость.

По свойству правильного шестиугольника Значит,, поскольку и B_1C_1 параллельны.

, т.к. призма прямая.

Получим, что по признаку перпендикулярности прямой и плоскости.

Это значит, что любая прямая, лежащая в плоскости W, перпендикулярна прямой BC_1 .

Проведем

Тогда По признаку перпендикулярности прямой и плоскости,

Тогда BH — расстояние от точки B до плоскости

Перейдем к плоскому чертежу — сечению призмы плоскостью FBB_1. Это сечение — прямоугольник.

$FF_1= BB_1= 1, FB = sqrt{3},$ тогда

Запишем площадь прямоугольного треугольника FBB_1 двумя способами.

$S_{vartriangle }=frac{1}{2}acdot h,$

$S_{vartriangle FBB_1}=frac{1}{2}cdot FBcdot BB_1=frac{1}{2}cdot FB_1cdot BH.$

Отсюда $BH=frac{sqrt{3}}{2}.$

Задание 14 Профильного ЕГЭ по математике. Стереометрия

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 14 Профильного ЕГЭ по математике. Стереометрия. Задача 3» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Задание

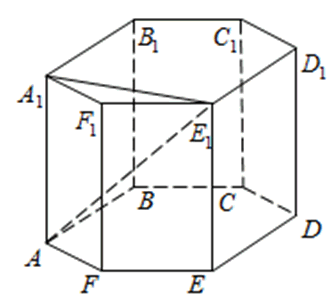
В правильной шестиугольной призме $A…F_1$ все ребра которой равны 1, найдите расстояние между прямыми $BB_1$ и $EF_1$.

Дано

$A…F_1$ — правильная шестиугольная призма все ребра которой равны 1
$BB_1$ и $EF_1$ — прямые
расстояние между $BB_1$ и $EF_1$ — ?

Решение

1) Выясняем, какое, собственно, расстояние нам нужно искать:

Нам нужно найти расстояние между прямыми $BB_1$ и $EF_1$.
Прямая $BB_1$ лежит в плоскости $BB_1C_1$.
Прямая $EF_1$ лежит в плоскости $EFF_1$.
Плоскости $BB_1C_1$ и $EFF_1$ параллельны.
Строим прямую $BF$ так, чтобы она была одновременно перпендикулярна обеим плоскостям $BB_1$ и $EF_1$.
Расстояние $BF$ является расстоянием между прямыми $BB_1$ и $EF_1$.

2) Находим расстояние $BF$:

По свойствам правильной шестиугольной призмы $$ BF=sqrt{3}cdot1=sqrt{3} $$

Ответ: $sqrt{3}$.

См. также

Расстояние между скрещивающимися прямыми в пространстве
Правильная шестиугольная призма

Категория:

С2 (стереометрия)

Источник

Видеокурсы Инны Фельдман
Рубрики
- 01 Задание (2022)
- 02 Задание (2022)
- 03 Задание (2022)
- 04 Задание (2016)
- 05 Задание (2022)
- 06 Задание (2022)
- 07 Задание (2022)
- 08 Задание (2022)
- 11 Задание (2022)
- 12 Задание (2022) (C1)
- 13 Задание (2022) (C2)
- 14 Задание (2022) (C3)
- 15 Задание (2022) (C4)
- 16 Задание (2022)
- 17 Задание (2022) (C6)
- 18 Задание (2022) (С7)
- АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
- База ЕГЭ Задание 19
- База ЕГЭ Задание 20
- БЕЗ РУБРИКИ
- ВИДЕОЛЕКЦИИ
- ВИДЕОТЕКА
- ВИДЕОУРОКИ
- Вопросы для повторения
- Диагностические работы
- Задание 01 (2016)
- Задание 02 (2016)
- Задание 03 (2016)
- ЗАДАЧИ С ПАРАМЕТРОМ
- Задачи с практическим содержанием
- ИНТЕГРАЛ
- Интерактивные модели
- ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- Комбинаторика
- ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- МГУ, ДВИ
- НОВОСТИ
- ОГЭ (ГИА) Задание 11
- ОГЭ (ГИА) Задание 15
- ОГЭ (ГИА) Задание 15
- ОГЭ (ГИА) Задание 24
- ОГЭ (ГИА) Задание 25
- ОНЛАЙН КУРСЫ
- Оплата
- ПЛАНИМЕТРИЯ
- ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- ПОЛЕЗНЫЕ СОВЕТЫ
- ПРЕЗЕНТАЦИИ
- ПРОГРЕССИИ
- ПРОИЗВОДНАЯ
- РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ
- СТЕРЕОМЕТРИЯ
- ТЕКСТОВЫЕ ЗАДАЧИ
- Теория вероятностей
- ТЕОРИЯ ЧИСЕЛ
- Тесты
- Тренировочные варианты
- ТРИГОНОМЕТРИЯ
- УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
- ФУНКЦИИ И ГРАФИКИ

Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.

2014-11-15

Главная » СТАТЬИ » 13 Задание (2022) (C2) » Видеотека. Стереометрия. Расстояние от точки до плоскости.

15
Ноя 2014

13 Задание (2022) (C2)ВИДЕОТЕКАВИДЕОУРОКИ

Видеотека. Стереометрия. Расстояние от точки до плоскости.

1. В правильной шестиугольной призме все ребра равны 1. Найти расстояние от точки до плоскости .

Инна |
Отзывов нет

Добавить комментарий

ПАРОЛЬ ДЛЯ БИБЛИОТЕКИ 010101
Подпишитесь на рассылку сайта и ВЫБЕРИТЕ В ПОДАРОК ЛЮБУЮ ВИДЕОЛЕКЦИЮ!
репетитор по информатике
Видеокурсы Анны Малковой.
Рекомендую:
ЕГЭ-ТРЕНЕР, видеоуроки по математике Ольги Себедаш
ЕГЭ-Студия: подготовка к ЕГЭ и олимпиадам
Репетитор по математике. Подготовка к ЕГЭ и ДВИ в МГУ.
Простая физика — сайт Анны Денисовой
EgeMaximum — сайт Елены Репиной
ЕГЭ-ШАНС — сайт Ларисы Гайковой
Последние записи
- Условная вероятность. Формула Байеса
- Новые задачи по теории вероятностей
- Видеолекция «Решение задач на оптимизацию на ЕГЭ по математике»
- Тренировочный вариант №51
- Тренировочный вариант №50
архив записей

архив записей

2023

Сайт репетитора по математике Фельдман Инны Владимировны.
Индивидуальная подготовка к ОГЭ и ЕГЭ по математике. Справочные материалы, видеолекции и видеоуроки по математике.
© Все права сохранены. 2012-2021

Источник

Как найти расстояние между точками в правильной шестиугольной призме?

Задание

Дано

Решение

См. также

Категория:

Видеокурсы Инны Фельдман

Рубрики

Видеотека. Стереометрия. Расстояние от точки до плоскости.

Добавить комментарий

ПАРОЛЬ ДЛЯ БИБЛИОТЕКИ 010101

Подпишитесь на рассылку сайта и ВЫБЕРИТЕ В ПОДАРОК ЛЮБУЮ ВИДЕОЛЕКЦИЮ!

репетитор по информатике

Видеокурсы Анны Малковой.

Рекомендую:

Последние записи

архив записей