Как проверить, верно ли решено уравнение?
Подставить полученное решение вместо неизвестного. Если обе части уравнения равны, значит решено правильно. Если нет — просмотреть внимательно своё решение.
Например было такое уравнение
2х^2 — 2х + 20 = 0
Вы решили это квадратное уравнение и узнали, что х = 5
Проверяем, подставляя вместо х значение 5
2*5*5 — 2*5 + 20 = 0
50 — 10 + 20 = 0
60 = 0
не верно
А вот если бы
0 = 0
тогда верно
если у тебя уравнение с иксом, то найденный икс подставляешь в изначальное уравнение. если левая часть равна правой, то все верной. а если при подстановки икса левая часть не равна правой, значит корень уравнения найден не верно.
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x= 2x -5
4+3x -2x =-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4 +3x-2x=-5
3x-2x=-5 -4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅ (-9) =2⋅ (-9) -5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
Далее делим все уравнение на 3.
3x :3 =45 :3
(3:3)x=15
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Как проверить, верно ли решено уравнение?
Математика | 5 — 9 классы
Как проверить, верно ли решено уравнение?
Подставить получившиеся значения в уравнение, если ответы совпадают, значит ты решила все верно.
Проверь и реши, верно ли найден результат?
Проверь и реши, верно ли найден результат.
Если нет, исправь.
Какое равенство называют уравнением?
Какое равенство называют уравнением?
Какое число называют корнем уравнения?
Что значить решить уравнение?
Как проверить, верно ли решено уравнение?
Как найти неизвестное слагаемое ; вычитаемое ; уменьшаемое.
Как проверить, верно ли решено уравнение?
Как проверить, верно ли решено уравнение?
Реши уравнения и письменно проверь?
Реши уравнения и письменно проверь.
Проверь , верно ли найдено значение выражения?
Проверь , верно ли найдено значение выражения.
И я решила))) удачи.
Проверь, верны ли равенства?
Проверь, верны ли равенства.
Как проверить, верно ли решено уравнение?
Как проверить, верно ли решено уравнение?
Проверь верны ли равенства?
Проверь верны ли равенства.
Проверь, какие записи верные, а какие неверные?
Проверь, какие записи верные, а какие неверные.
Проверь, верны ли равенства ?
Проверь, верны ли равенства :
На этой странице сайта вы найдете ответы на вопрос Как проверить, верно ли решено уравнение?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
0. 4 * 1000 = 400. Т. к. В 1 километре содержится 1000 метров.
1 км = 1000 м 1000 м : 5·2 = 200·2 = 400 м или 1000 м · ² / ₅ = 400 м.
Условие 1ширина — 8 см 1длина — ? На1 см меньше 2ширина — ? 2 длина — ? S1 — ? S2 — ? P1 = p2 решение 8 — 1 = 7 см длина 1 (8 + 7) * 2 = 30 см p1 = p2 30 : 4 = 7, 2 см стороны 2 30 * 30 = 900 см s1 7, 2 * 7, 2 = 5184 см s2.
1 дм = 10 см. Длина прямоугольника — 10 + 8 = 18(см) Перимети прямоугольника — (18 + 8)×2 = 52(см) Сторона квадрата — 52 : 4 = 13(см) Площадь прямоугольника — 18×8 = 144(см2) Площадь квадрата — 13×13 = 169(см2) Если удовлетворил ответ, прошу постави..
Мода = 2. 1 мода = 3, 5 мода = НИЧЕГО мода = 6. 1 и 7. 5 мода 0. 6.
1) 1. 7 — 1 = 6 2. 3 1 / 5 — 1 / 5 = 3 3. 15. 9 — 0. 6 = 15. 3 4. 20 — 0. 4 = 19. 6 2) 1. Мода = 2. 1 ; 2. Мода = 3. 5 ; 3. Моды нет ; 4. Мода = 7. 5 ; 5. Мода = 0. 6 ;..
57 : 3 • 4 = 76 1. 57 : 3 = 19 ; 2. 19 • 4 = 76 Ответ : 76 24 • 3 : 6 = 12 1. 24 • 3 = 72 ; 2. 72 : 6 = 12 Ответ : 12.
57 : 3 * 4 = 76 ; 24 * 3 : 6 = 12 ;..
S = ab 2дм = 40см. 4дм = 40 см. S = 20 * 40 = 800.
источники:
http://tutomath.ru/6-klass/chto-takoe-uravnenie-i-korni-uravneniya-kak-reshit-uravnenie.html
http://matematika.my-dict.ru/q/1795123_kak-proverit-verno-li-reseno-uravnenie/
«Равенство» — это тема, которую ученики проходят еще в начальной школе. Сопутствует ей также ей «Неравенства». Эти два понятия тесно взаимосвязаны. Кроме того, с ними связывают такие термины, как уравнения, тождества. Итак, что такое равенство?
Понятие равенства
Под этим термином понимают высказывания, в записи которых есть знак «=». Равенства разделяются на верные и неверные. Если в записи вместо = стоит <, >, тогда речь идет о неравенствах. Кстати, первый признак равенства говорит о том, что обе части выражения идентичны по своему результату или записи.
Кроме понятия равенства, в школе изучают также тему «Числовое равенство». Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака =. К примеру, 2*5+7=17. Обе части записи равны между собой.
В числовых выражениях подобного типа могут использоваться скобки, влияющие на порядок действий. Итак, существует 4 правила, которые следует учесть при вычислении результатов числовых выражений.
- Если в записи нет скобок, тогда действия выполняются с высшей ступени: III→II→I. Если есть несколько действий одной категории, тогда они выполняются слева направо.
- Если в записи есть скобки, тогда действие выполняется в скобках, а затем с учетом ступеней. Возможно, в скобках будет несколько действий.
- Если выражение представлено в виде дроби, тогда вычислять нужно сначала числитель, потом знаменатель, затем числитель делится на знаменатель.
- Если в записи есть вложенные скобки, тогда вычисляется сначала выражение во внутренних скобках.
Итак, теперь понятно, что такое равенство. В дальнейшем будут рассмотрены понятия уравнения, тождества и способы их вычисления.
Свойства числовых равенств
Что такое равенство? Изучение этого понятия требует знания свойств числовых тождеств. Приведенные ниже текстовые формулы позволяют лучше изучить данную тему. Конечно, эти свойства больше подходят для изучения математики в старших классах.
1. Числовое равенство не будет нарушено, если в обеих его частях прибавить одно и то же число к существующему выражению.
А = В ↔ А + 5 = В + 5
2. Не будет нарушено уравнение, если обе его части умножить или разделить на одно и то же число или выражение, которые отличны от нуля.
Р = О ↔ Р ∙ 5 = О ∙ 5
Р = О ↔ Р : 5 = О : 5
3. Прибавив к обеим частям тождества одинаковую функцию, которая имеет смысл при любых допустимых значениях переменной, мы получим новое равенство, равносильное первоначальному.
F(X) = Ψ(X) ↔ F(X) + R(X) = Ψ(X) + R(X)
4. Любое слагаемое или выражение можно перенести по другую сторону знака равенства, при этом нужно поменять знаки на противоположные.
Х + 5 = У – 20 ↔ Х = У – 20 – 5 ↔ Х = У – 25
5. Умножив или разделив обе части уравнения на одну и ту же функцию, отличную от нуля и имеющую смысл для каждого значения Х из ОДЗ, мы получим новое уравнение, равносильное первоначальному.
F(X) = Ψ(X) ↔ F(X) ∙ R(X) = Ψ(X) ∙ R(X)
F(X) = Ψ(X) ↔ F(X) : G(X) = Ψ(X) : G(X)
Приведенные правила в явной степени указывают на принцип равенства, который существует при определенных условиях.
Понятие пропорции
В математике существует такое понятие, как равенство отношений. В этом случае подразумевается определение пропорции. Если разделить А на В, то результатом будет отношение числа А к числу В. Пропорцией называют равенство двух отношений:
Иногда пропорция записывается следующим образом: A : B = C : D. Отсюда вытекает основное свойство пропорции: A * D = D * C, где A и D – крайние члены пропорции, а В и С – средние.
Тождества
Тождеством называют равенство, которое будет верно при всех допустимых значениях тех переменных, которые входят в задание. Тождества могут быть представлены как буквенные или числовые равенства.
Тождественно равными называются выражения, содержащие в обеих частях равенства неизвестную переменную, которая способна приравнять две части одного целого.
Если проводить замены одного выражения другим, которое будет равно ему, тогда речь идет о тождественном преобразовании. В этом случае можно воспользоваться формулами сокращенного умножения, законами арифметики и прочими тождествами.
Чтобы сократить дробь, нужно провести тождественные преобразования. К примеру, дана дробь. Чтобы получить результат, следует воспользоваться формулами сокращенного умножения, разложением на множители, упрощением выражений и сокращением дробей.
При этом стоит учесть, что данное выражение будет тождественным тогда, когда знаменатель не будет равен 3.
5 способов доказать тождество
Чтобы доказать равенство тождественное, нужно провести преобразование выражений.
I способ
Необходимо провести равносильные преобразования в левой части. В результате получается правая часть, и можно говорить о том, что тождество доказано.
II способ
Все действия по преобразованию выражения происходят в правой части. Итогом проделанных манипуляций является левая часть. Если обе части идентичны, то тождество доказано.
III способ
«Трансформации» происходят в обеих частях выражения. Если в результате получатся две идентичные части, тождество доказано.
IV способ
Из левой части вычитается правая. В результате равносильных преобразований должен получиться нуль. Тогда можно говорить о тождественности выражения.
V способ
Из правой части вычитается левая. Все равносильные преобразования сводятся к тому, чтобы в ответе стоял нуль. Только в таком случае можно говорить о тождественности равенства.
Основные свойства тождеств
В математике зачастую используют свойства равенств, чтобы ускорить процесс вычисления. Благодаря основным алгебраическим тождествам процесс вычисления некоторых выражений займет считанные минуты вместо долгих часов.
- Х + У = У + Х
- Х + (У + С) = (Х + У) + С
- Х + 0 = Х
- Х + (-Х) = 0
- Х ∙ (У + С) = Х∙У + Х∙С
- Х ∙ (У – С) = Х∙У – Х∙С
- (Х + У) ∙ (С + Е) = Х∙С + Х∙Е + У∙С + У∙Е
- Х + (У + С) = Х + У + С
- Х + (У – С) = Х + У – С
- Х – (У + С) = Х – У – С
- Х – (У – С) = Х – У + С
- Х ∙ У = У ∙ Х
- Х ∙ (У ∙ С) = (Х ∙ У) ∙ С
- Х ∙ 1 = Х
- Х ∙ 1/Х = 1, где Х ≠ 0
Формулы сокращенного умножения
По своей сути формулы сокращенного умножения являются равенствами. Они помогают решить множество задач в математике благодаря своей простоте и легкости в обращении.
- (А + В)2 = А2 + 2∙А∙В + В2 – квадрат суммы пары чисел;
- (А – В)2 = А2 – 2∙А∙В + В2 – квадрат разности пары чисел;
- (С + В) ∙ (С – В) = С2 – В2 – разность квадратов;
- (А + В)3 = А3 + 3∙А2∙В + 3∙А∙В2 + В3 – куб суммы;
- (А – В)3 = А3 – 3∙А2∙В + 3∙А∙В2 – В3 – куб разности;
- (Р + В) ∙ (Р2 – Р∙В + В2) = Р3 + В3 – сумма кубов;
- (Р – В) ∙ (Р2 + Р∙В + В2) = Р3 – В3 – разность кубов.
Формулы сокращенного умножения зачастую применяются, если необходимо привести многочлен к привычному виду, упростив его всеми возможными способами. Представленные формулы доказываются просто: достаточно раскрыть скобки и привести подобные слагаемые.
Уравнения
После изучения вопроса, что такое равенство, можно приступать к следующему пункту: что такое уравнение. Под уравнением понимается равенство, в котором присутствуют неизвестные величины. Решением уравнения называют нахождение всех значений переменной, при которых обе части всего выражения будут равны. Также встречаются задания, в которых нахождение решений уравнения невозможно. В таком случае говорят, что корней нет.
Как правило, равенства с неизвестными в качестве решения выдают целые числа. Однако возможны случаи, когда корнем являются вектор, функция и другие объекты.
Уравнение является одним из важнейших понятий в математике. Большинство научных и практических задач не позволяют измерить или вычислить какую-либо величину. Поэтому необходимо составлять соотношение, которое удовлетворит все условия поставленной задачи. В процессе составления такого соотношения появляется уравнение или система уравнений.
Обычно решение равенства с неизвестным сводится к преобразованию сложного уравнения и сведению его к простым формам. Необходимо помнить, что преобразования нужно проводить относительно обеих частей, в противном случае на выходе получится неверный результат.
4 способа решить уравнение
Под решением уравнения понимают замену заданного равенства другим, которое равносильно первому. Подобная подмена известна как тождественное преобразование. Чтобы решить уравнение, необходимо воспользоваться одним из способов.
1. Одно выражение заменяется другим, которое в обязательном порядке будет тождественно первому. Пример: (3∙х+3)2=15∙х+10. Это выражение можно преобразовать в 9∙х2+18∙х+9=15∙х+10.
2. Перенесение членов равенства с неизвестным из одной стороны в другую. В таком случае необходимо правильно менять знаки. Малейшая ошибка сгубит всю проделанную работу. В качестве примера возьмем предыдущий «образец».
9∙х2 + 12∙х + 4 = 15∙х + 10
9∙х2 + 12∙х + 4 – 15∙х – 10 = 0
9∙х2 – 3∙х – 6 = 0
Дальше уравнение решается с помощью дискриминанта.
3. Перемножение обеих частей равенства на равное число или выражение, которые не равняются 0. Однако стоит напомнить, что если новое уравнение не будет равносильным равенству до преобразований, тогда количество корней может существенно измениться.
4. Возведение в квадрат обеих частей уравнения. Этот способ просто замечательный, особенно когда в равенстве есть иррациональные выражения, то есть квадратный корень и выражение под ним. Тут есть один нюанс: если возвести уравнение в четную степень, тогда могут появиться посторонние корни, которые исказят суть задания. И если неправильно извлечь корень, тогда смысл вопроса в задаче будет неясен. Пример: │7∙х│=35 → 1) 7∙х = 35 и 2) – 7∙х = 35 → уравнение будет решено верно.
Итак, в этой статье упоминаются такие термины, как то уравнения и тождества. Все они происходят от понятия «равенство». Благодаря различного рода равносильным выражениям решение некоторых задач в значительной мере облегчено.
Признаки равенства треугольников
О чем эта статья:
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
- Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
- Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
- Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
- Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
- Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Треугольники. Признаки равенства треугольников
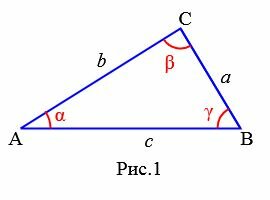
Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .
Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.
Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.
Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.
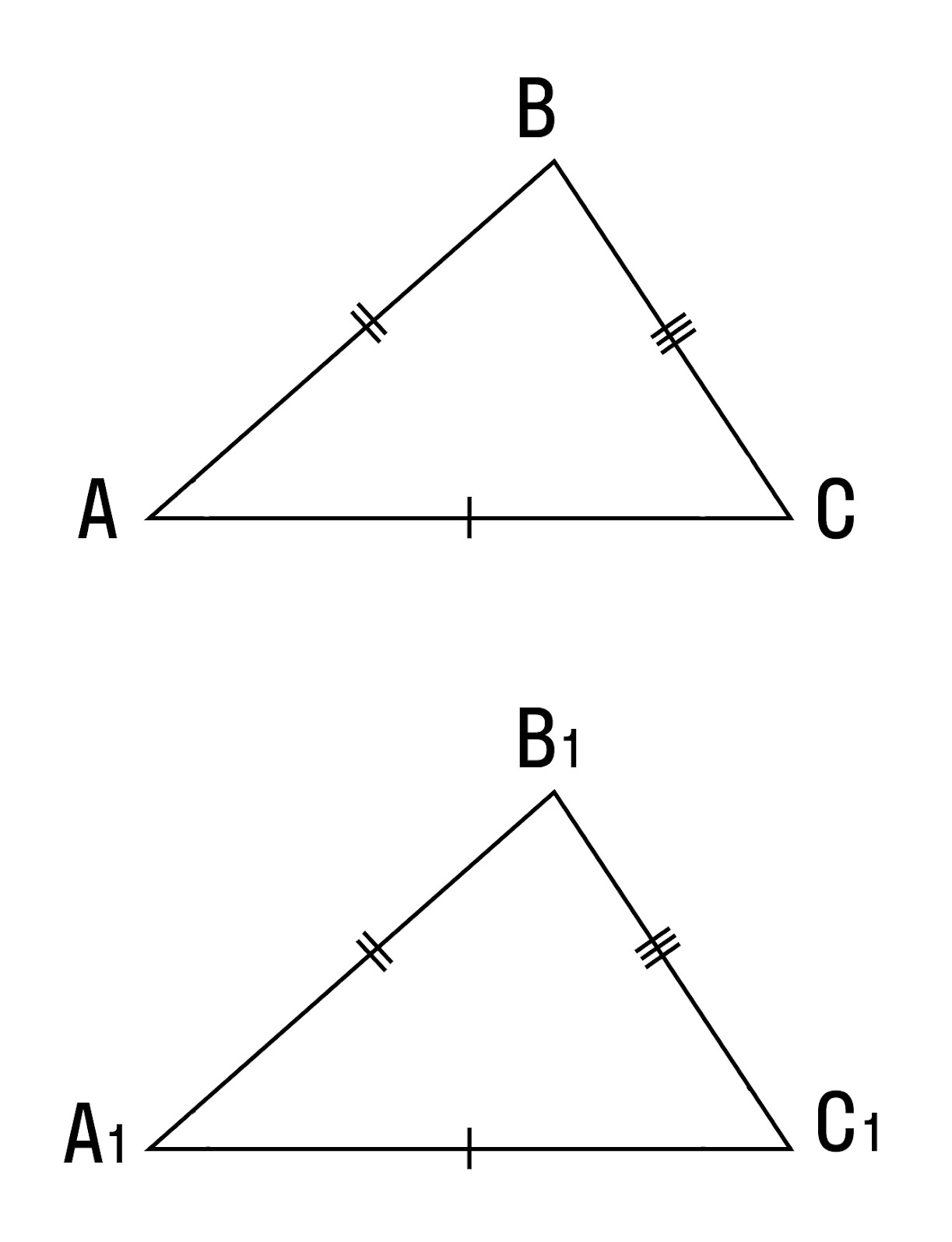
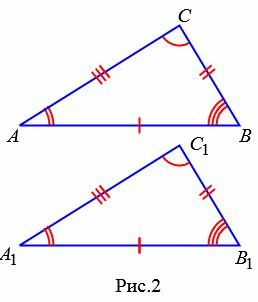
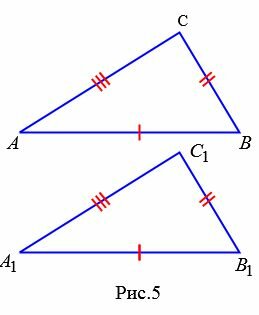
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A1B1C1. Треугольник ABC можно наложить на треугольник A1B1C1 так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.
Вышеизложенное можно сформулировать так:
Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A1B1C1 обозначается так:
Первый признак равенства треугольников
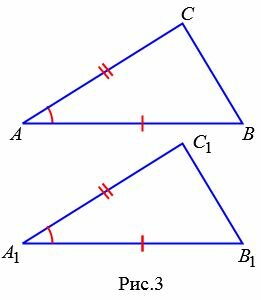
Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1C1 (Рис.3). Пусть AB=A1B1, AС=A1С1 и ∠A=∠A1. Докажем, что 
Второй признак равенства треугольников
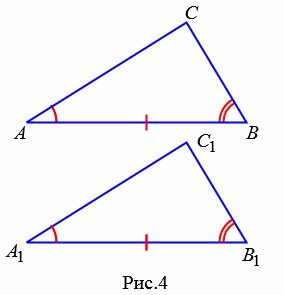
Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1С1 (Рис.4). Пусть AB=A1B1, ∠A=∠A1, ∠B=∠B1. Докажем, что 
Третий признак равенства треугольников
Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.
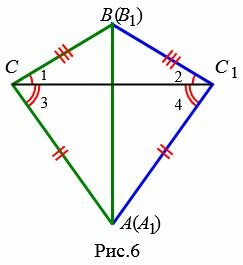
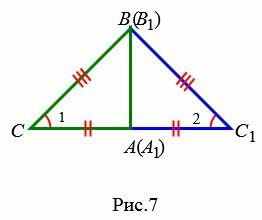
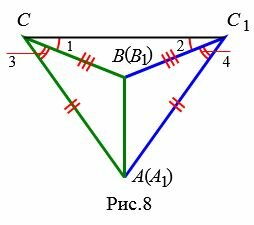
Доказательство. Рассмотрим треугольники ABC и A1B1С1. Пусть AB=A1B1, AC=A1C1 и BC=B1C1. Докажем, что 
Возможны три варианта: луч CC1 проходит внутри угла ACB(Рис.6); луч CC1 совпадает с одной из сторон угла ACB (Рис.7); луч CC1 проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.
Имеем AC=A1C1, BC=B1C1 ∠ACB=∠A1C1B1 и по первому признаку равенства треугольников 
Вариант 2 (Рис.7). Так как по условию теоремы AC=A1C1 и BC=B1C1, то треугольник BСС1 равнобедренный. Тогда ∠1=∠2. Имеем: AC=A1C1, BC=B1C1, ∠1=∠2 и по первому признаку равенства треугольников 
Вариант 3 (Рис.8). Так как по условию теоремы AC=A1C1 и BC=B1C1, то треугольники AСС1 и BСС1 равнобедренные. Тогда ∠1=∠2 и 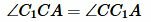
Имеем AC=A1C1, BC=B1C1 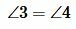

Задачи и решения
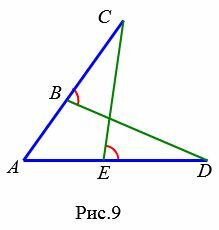
Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).
Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .
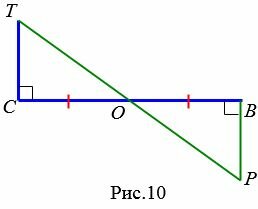
Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T
Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .
Равные треугольники

Средняя оценка: 4.5
Всего получено оценок: 313.
Средняя оценка: 4.5
Всего получено оценок: 313.
Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.
Определение
Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.
Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.
Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$
Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.
Признаки равенства
Выделяют три признака равенства треугольников:
1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.
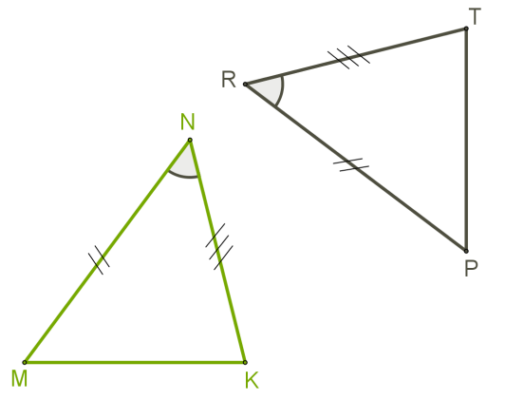
2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.
3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.
Кроме того, стоит выделить некоторые свойства:
- Сумма двух внутренних углов треугольника будет всегда меньше 180 0 .
- Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Алгоритм доказательства равенства фигур
- Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
- На рисунке отметить, все необходимые данные в условии задания.
- Проверить есть ли у двух треугольников общая сторона либо угол.
- Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
- При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
- При необходимости, можно сделать дополнительное построение.
Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.
Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.
Пример
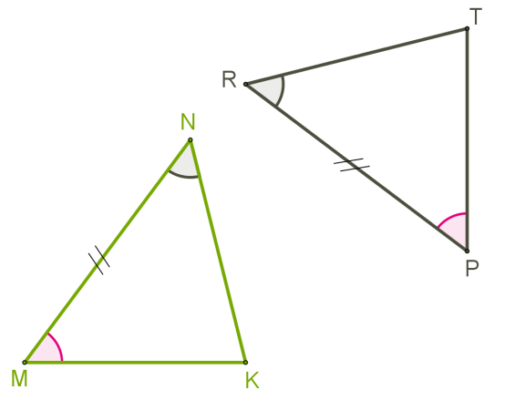
Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.
Решение:
Стоит обратить внимание на рисунок
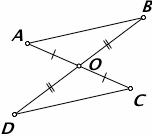
В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.
Что мы узнали?
Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.
http://matworld.ru/geometry/treugolniki.php
http://obrazovaka.ru/matematika/ravnye-treugolniki-opredelenie-svoystva.html
Равенства
(знак (=))
(6=6) — это верное равенство;
(6=7) — неверное равенство, так как (6) не равно (7).
Неравенства
(знаки (<) и (>))
(8>6) и (4<10) — это верные неравенства.
(8) больше (6), (4) меньше (10).
(8<7) — неверное неравенство,
так как (8) больше (7), а знак стоит — «меньше».
В данной публикации мы рассмотрим, что такое арифметическое (математическое) равенство, а также перечислим его основные свойства с примерами.
- Определение равенства
-
Свойства равенств
- Свойство 1
- Свойство 2
- Свойство 3
Определение равенства
Математическое выражение, которое содержит числа (и/или буквы) и знак “равно”, разделяющий его на две части, называется арифметическим равенством.
Выделяют 2 типа равенств:
- Тождество – обе части тождественно равны. Например:
- 5 + 12 = 13 + 4
- 3x + 9 = 3 ⋅ (x + 3)
- Уравнение – равенство верно при определенных значениях содержащихся в нем букв. Например:
- 10x + 20 = 43 + 37
- 15x + 10 = 65 + 5
Свойства равенств
Свойство 1
Части равенства можно менять местами, при этом оно останется верным.
Например, если:
12x + 36 = 24 + 8x
Следовательно:
24 + 8x = 12x + 36
Свойство 2
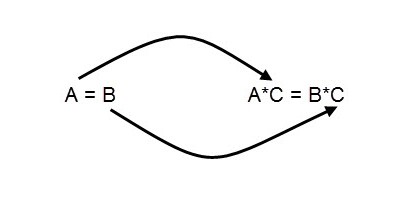
К обеим частям равенства можно прибавить или отнять одно и то же число (или математическое выражение). Равенство при этом не будет нарушено.
То есть, если:
a = b
Значит:
- a + x = b + x
- a – y = b – y
Примеры:
- 16 – 4 = 10 + 2 ⇒ 16 – 4 + 5 = 10 + 2 + 5
- 13x + 30 = 7x + 6x + 30 ⇒ 13x + 30 – y = 7x + 6x + 30 – y
Свойство 3
Если обе части равенства умножить или разделить на одно и то же число (или математическое выражение), оно не будет нарушено.
То есть, если:
a = b
Значит:
- a ⋅ x = b ⋅ x
- a : y = b : y
Примеры:
- 29 + 11 = 32 + 8 ⇒ (29 + 11) ⋅ 3 = (32 +
⋅ 3
- 23x + 46 = 20 – 2 ⇒ (23x + 46) : y = (20 – 2) : y
















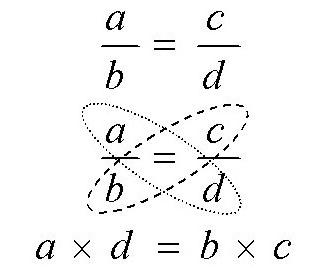





 ⋅ 3
⋅ 3