Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
Пусть дана плоская система трех сил F1, F2 и F3, линии действия которых сходятся в точке А (см. рисунок а).
На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А. Сложив первые две силы F1 и F2 по правилу параллелограмма, получим их равнодействующую R (см. рисунок а):
R = F1 + F2.
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3:
FΣ = R + F3 = F1 + F2 + F3,
где FΣ – равнодействующая данной системы трех сил.
Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
FΣ = F1 + F2 + F3 +…+ Fn.
Сокращенно это равенство можно записать так:
FΣ = ΣFi, где i – все целые числа от единицы до n.
Очевидно, что построения, выполненные на рисунке a, можно заменить более простым, как показано на рисунке b. Многоугольник АВСD называют силовым многоугольником. Сторона AD, соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b).
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.
***
Геометрическое условие равновесия плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая FΣ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:
FΣ = F1 + F2 + F3 +…+ Fn = ΣFi = 0
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.
При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Пример решения задачи
В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G.
Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:
ΣFi = 0, или G + N + R = 0.
Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок). Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:
N = G tg α; R = G/cos α
Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R.
Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки), причем согласно аксиоме взаимодействия:
F = R, P = N.
Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.
***
Проекция силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.
Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
Px = Pcos α, Py = Psin α.
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции — проекция, направленная в положительном направлении оси считается положительной, в противном случае — отрицательной.
Возможны два частных случая:
— если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку);
— если сила параллельна оси, то она проецируется на ось в натуральную величину.
Зная проекции силы на координатные оси, можно определить ее величину (модуль), используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила — гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = Py/Px.
Отметим, что силу P можно представить, как равнодействующую двух составляющих сил Px и Py, параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция — алгебраическая.
***
Аналитический способ определения равнодействующей плоской системы сил
Пусть дана плоская система сходящихся сил F1, F2, F3, F4….Fn.
Равнодействующая этой системы FΣ = ΣFi.
В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. FΣx = ΣFix.
Правую часть этого равенства можно представить упрощенно: FΣx = ΣX.
Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y, алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:
FΣx = ΣX; FΣy = ΣY.
Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:
FΣ = √(FΣx2+ FΣy2) (здесь и далее √ — знак корня);
Направляющий тангенс угла между вектором FΣ и осью x:
tg (FΣ, x) = FΣy / FΣx.
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
***
Аналитические условия равновесия плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:
FΣ = 0; Fx = 0; Fy= 0.
Учитывая, что FΣx = ΣX; FΣy = ΣY, получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:
ΣX = 0; ΣY = 0.
Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.
Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.
***
Сложение параллельных сил
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
§1. Геометрический способ сложения сил
Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил
(рис. 1, a), откладываем от произвольной точки О (рис. 1, б) вектор Oa, изображающий в выбранном масштабе cилу F1, от точки a откладываем вектор
, изображающий силу F2, от точки b откладываем вектор bc, изображающий силу F3 и т. д.; от конца m предпоследнего вектора откладываем вектор mn, изображающий силу Fn. Соединяя начало первого вектора с концом последнего, получаем вектор
, изображающий геометрическую сумму или главный вектор слагаемых сил:
или
От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное построение представляет собою результат последовательного применения правила силового треугольника.
Рис.1. Система сил
Фигура, построенная на рис. 1,б, называется силовым (в общем случае векторным) многоугольником. Таким образом, геометрическая сумма или главный вектор нескольких сил изображается замыкающей стороной силового многоугольника, построенного из этих сил (правило силового многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора
— в сторону противоположную.
Сходящимися называются силы, линии действия которых пересекаются в одной точке, называемой центром системы (см. рис. 1, а).
По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 1, а в точке А).
Последовательно применяя аксиому параллелограмма сил, приходим к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы
сходятся в точке A (рис. 1, а), то сила, равная главному вектору , найденному построением силового многоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.
Примечания.
1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник — отличный от первого.
2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.
3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
§2.Равновесие системы сходящихся сил
Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.
Отсюда получаем два важных вывода:
1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».
2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил.
Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.
1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то
может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда многоугольник замкнется.
Следовательно, для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут.
2. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой: .
Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно , т. е. когда действующие на тело силы будут удовлетворять равенствам:
Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия
Равенства выражают также необходимые условия (или уравнения) равновесия свободного твердого тела, находящегося под действием сходящихся сил.
Видео-урок «Сила-вектор. Система сил»
Вопросы для самопроверки:
— Какая система сил называется сходящейся?
— Как определить равнодействующую системы сходящихся сил путем построения силового многоугольника?
— Какие силы называются сходящимися? Как определить их равнодействующую?
— Что называется главным вектором плоской системы сил?
— Что называется главным моментом плоской системы сил относительно какого-нибудь центра?
— Составьте условие равновесия для произвольной плоской системы сил.
— Составьте условие равновесия для системы сходящихся сил.
— Составьте условие равновесия для плоской системы параллельных сил.
— Сформулируйте геометрическое условие равновесия системы сходящихся сил.
— Что называется главным вектором системы сил?
— В чем различие между главным вектором и равнодействующей системы сил?
— Для какой системы сил равнодействующая и главный вектор совпадают?
— Назовите методы определения равнодействующей системы сходящихся сил.
— Как выражаются проекции равнодействующей системы сходящихся сил через проекции сил этой системы?
— Определите величину силы по известным проекциям
=3кН; 4кН.
— Определить модуль и направления силы, если известны ее проекции
=30H; =40H.
— Назовите необходимое и достаточное условие равновесия системы сходящихся сил.
— Что такое силовой многоугольник?
— Запишите условие равновесия системы сходящихся сил в векторной форме.
— Сформулируйте условия равновесия системы сходящихся сил в координатной форме.
— Какой из силовых многоугольников на рисунке относится к уравновешенной системе сходящихся сил?
— Как определяется направление равнодействующей системы сходящихся сил при построении силового многоугольника?
— Каковы условия и каковы уравнения равновесия системы сходящихся сил, расположенных в пространстве и плоскости?
— Как сложить силы:
а) геометрически,
б) аналитически?
— Как разложить силу по двум заданным направлениям?
Скачать материал

Скачать материал


- Сейчас обучается 267 человек из 65 регионов




- Сейчас обучается 387 человек из 62 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ТЕМА УРОКА:
«Плоская система сходящихся сил. Определение равнодействующей геометрическим способом» -
2 слайд
Плоская система сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис. 2.1).
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;… …; Fn), п — число сил, входящих в систему.
По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке. -
3 слайд
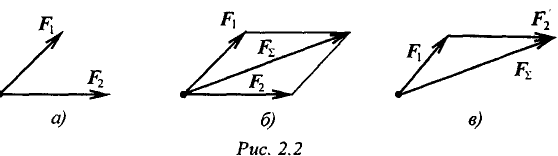
Равнодействующая сходящихся сил.
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
-
4 слайд
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
При графическом способе определения равнодействующей век-торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующем векторам сил. -
5 слайд
Порядок построения многоугольника сил:
Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего.
Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет. -
6 слайд
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил. -
7 слайд
Решение задач на равновесие геометрическим способом
Порядок решения задач:
Определить возможное направление реакций связей.
Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
Для уточнения решения рекомендуется определить величины, векторов (сторон многоугольника) с помощью геометрических зависимостей. -
8 слайд
Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5, а).
Решение
1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5, а).
Определяем возможные направления реакций связей «жесткие стержни».
γ = 1800 – 600 – 450
Усилия направлены вдоль стержней. -
9 слайд
2. Освободим точку А от связей, заменив действие связей их реакциями (рис. 2.5, б).
3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в некотором масштабе.
Из концов вектора F проводим линии, параллельные реакциям и R1 и R2.
Пересекаясь, линии создадут треугольник (рис. 2.5, в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях. -
-
11 слайд
Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная:
Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону. -
12 слайд
Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6, а).
Решение
1.Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки А к точке В.
2.Груз находится в равновесии, следовательно, в равновесии находится точка А, в которой пересекаются три силы. Освободим точку А от связей и рассмотрим ее равновесие (рис. 2.6, б).
Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН. -
13 слайд
3.Строим треугольник для сил, приложенных в точке А, начиная с известной силы Т3. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А.
Образовался прямоугольный треугольник (рис. 2.6, е).
4. Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике: -
14 слайд
Замечание. При равновесии векторы сил в треугольнике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 2.6, а. Направления совпали, следовательно, направления реакций определены верно.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 946 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
3 из 5
- 18.03.2017
- 3817
- 50
- 18.03.2017
- 1868
- 2
- 18.03.2017
- 348
- 1
- 18.03.2017
- 555
- 1
- 18.03.2017
- 381
- 1
- 18.03.2017
- 1097
- 3
- 18.03.2017
- 550
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Основы менеджмента в туризме»
-
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Равнодействующая сходящихся сил
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
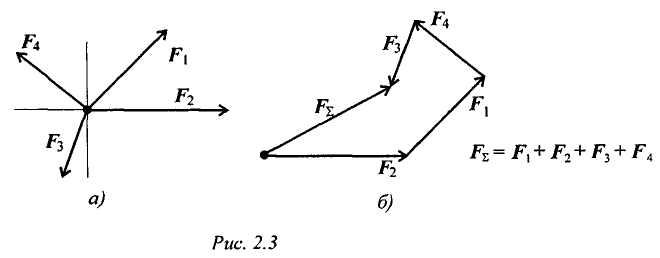
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:


















