Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
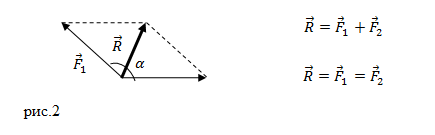
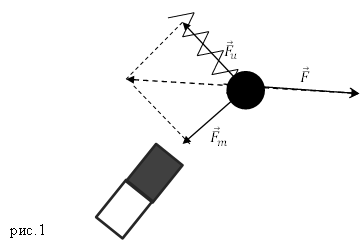
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
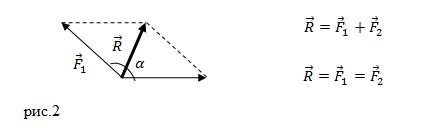
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60<>^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline$ можно найти, используя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<20>^2+<10>^2+2cdot 20cdot 10<cos (60<>^circ ) >>approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
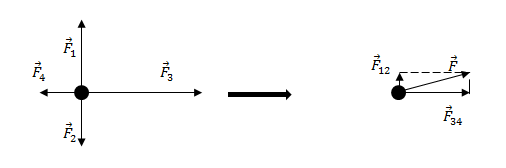
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
Найдем равнодействующую сил $<overline>_1$ и $<overline>_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
Так как $F_1>F_2$, то сила $<overline>_<12>$ направлена в туже сторону, что и сила $<overline>_1$.
Найдем равнодействующую сил $<overline>_3$ и $<overline>_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
Направление силы $<overline>_<34>$ совпадает с направлением вектора $<overline>_3$, так как $<overline>_3><overline>_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
Силы $<overline>_<12>$ и $<overline>_<34>$ взаимно перпендикулярны. Найдем длину вектора $overline$ по теореме Пифагора:
http://kartaslov.ru/%D0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%90%D1%83%D1%80%D0%B8%D0%BA%D0%B0_%D0%9B%D1%83%D0%BA%D0%BE%D0%B2%D0%BA%D0%B8%D0%BD%D0%B0_%D0%A2%D0%B5%D1%85%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0_%D0%A8%D0%BF%D0%B0%D1%80%D0%B3%D0%B0%D0%BB%D0%BA%D0%B0/3
http://www.webmath.ru/poleznoe/fizika/fizika_139_formula_ravnodejstvujushhej_vseh_sil.php
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
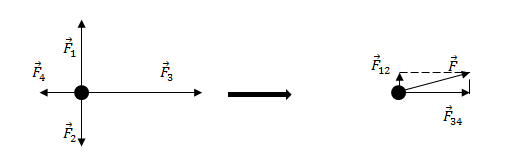
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
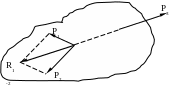
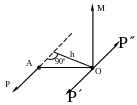
Если к телу
приложены три непараллельные взаимно
уравновешивающиеся силы, то они образуют
систему сходящихся сил (линии
действия этих сил пересекаются в одной
точке).
Д
ве
силы
и
(рис.2.5) образуют равнодействующую
,
которая при равновесии сил (что считается
известным) равна силе
по модулю, лежит на одной прямой и
направлена в противоположную сторону.
Рис.2.5
Следовательно,
три силы пересекаются в одной точке (и
лежат в одной плоскости).
Эта теорема
часто используется при поиске величины
и направления одной из реакций опор
конструкции, к которой приложены 3 силы.
Лекция 3 Произвольная система сил в пространстве и на плоскости
Система
пар сил. Сложение пар сил Условие
равновесия пар сил. Уравнения равновесия.
Система сил, произвольно расположенных
в пространстве. Приведение силы к центру
(метод Пуансо). Сложение сил
Сложение пар
сил
Е
сли
к телу приложить пары сил, то можно
использовать для их сложения векторы
– моменты пар сил. Так как момент пары
сил не изменяется при переносе пары сил
в параллельную плоскость и не изменяется
при перемещении пары сил в плоскости
ее действия, то момент пары сил считается
свободным вектором (в отличие от силы
– скользящего вектора). А это означает,
что векторы – моменты пар сил можно
приложить к одной точке тела и сложить
их по правилу сложения сходящихся
векторов – построить векторный
многоугольник, замыкающая которого
определяет момент пары сил, эквивалентной
заданной системе пар сил (см. рис.3.1).
Рис.3.1
Таким образом,
,
что означает, что в результате сложения
пар сил получается одна пара сил, момент
которой равен геометрической сумме
моментов пар сил. Эту пару сил можно
представить расположенной в плоскости,
перпендикулярной к вектору
и
стремящейся повернуть тело вокруг оси,
совпадающей с вектором
против хода часовой стрелки, если
смотреть вдоль вектора
к его основанию. При этом пару сил могут
образовывать любые две силы
и
(
)
так, чтобы произведение одной из сил
пары на плечо пары сил было равно моменту
М.
Условие
равновесия пар сил. Уравнения равновесия
Пары сил,
приложенные к твердому телу, взаимно
уравновешиваются, если векторный
многоугольник моментов пар сил замкнут,
т.е. если
.
Так как вектор
можно определить аналитическим способом,
зная моменты заданных пар сил (по аналогии
с аналитическим методом определения
равнодействующей сходящихся сил), т.е.
,
где
;
;
,
то при равновесии пар сил
моменты пар сил должна удовлетворять
трем уравнениям равновесия
;
;
(алгебраическая сумма проекций
моментов пар сил на каждую из прямоугольных
координатных осей должна равняться
нулю).
Если пары сил
лежат в одной плоскости, то следует
использовать одно уравнение равновесия
пар сил:
.
Система сил, произвольно расположенных в пространстве
Приведение
силы к центру (метод Пуансо). Сложение
сил
Для сложения
сил в самом общем случае широко
используется метод Пуансо – приведение
каждой силы к центру.
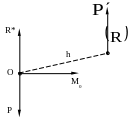
В результате
приведения силы
к центру О (рис.3.2) получаются вместо
одной три силы, из которых можно выделить
силу
,
геометрически равную заданной силе
,
приложенную к центру, и пару сил
,
момент которой
равен моменту
заданной силы
относительно центра О.
~
~
,
при этом
,
(имеется в виду, что к центру О
приложены две взаимоуравновешивающиеся
силы
и
,
параллельные и равные силе Р по
модулю, но направленные в противоположные
стороны, так что
).
Рис.3.2
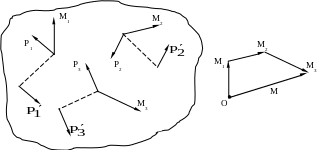
Р
ассмотрим
последовательность операций при сложении
нескольких сил, линии действия которых
не пересекаются в одной точке и не лежат
в одной плоскости (самый общий случай).
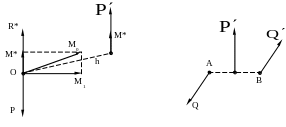
Силы
;
и
(для примера достаточно трех сил) приводим
к центру (рис.3.2) и получаем три сходящиеся
силы
;
;
и три пары сил
;
и
,
моменты которых
;
и
. Рис.3.3
Складывая
сходящиеся силы построением силового
многоугольника, получаем силу
,
приложенную к центру. Складывая моменты
пар сил построением многоугольника
моментов, получаем момент
той пары сил, которая эквивалентна трем
парам сил.
Так как момент
каждой пары сил геометрически равен
моменту заданной силы относительно
центра, следует записать
,
отсюда следует, что
,
т.е. момент пары сил, эквивалентной трем
парам сил, равен геометрической сумме
моментов заданных сил
,
и
относительно центра О. Эта сумма
моментов получила название главного
момента заданных сил относительно
центра. А сила
получила название главного вектора
заданных сил (Главный вектор нельзя
назвать равнодействующей заданной
системы сил, хотя
,
так как он один не эквивалентен заданной
системе сил; эквивалентна заданной
системе сил – совокупность силы
и пары сил, момент которой
).
Итак, в результате
сложения сил, произвольно расположенных
в пространстве, методом приведения их
к центру получаются сила и пара сил.
Сила
,
приложенная к центру, называется главным
вектором; он равен геометрической
сумме заданных сил. Момент пары сил
равен геометрической сумме моментов
заданных сил относительно центра,
которая образует главный момент
заданных сил относительно центра
.
Нетрудно
сообразить, что главный вектор
не зависит от выбора центра приведения,
а главный момент
изменяет свою величину и направление
при изменении положения центра приведения.
Возможные
случаи приведения сил к центру
Сложение сил,
произвольно расположенных в пространстве,
методом приведения их к центру, дает
различные результаты при разных значениях
и
.
1
)
,
а
.
Силы приводятся к одной силе, следовательно,
заданные силы можно заменить их
равнодействующей (главный вектор
превращается в равнодействующую).
2)
,
а
.
Силы приводятся к одной паре сил, она
эквивалентна заданной системе сил. (В
этом случае вектор
не изменяет свою величину и свое
направление при изменении положения
центра приведения).
3)
и
,
но
.
Рис.3.4
В этом случае (см. рис.3.4) следует
показать пару сил, соответствующую
моменту
,
выбрав силу этой пары сил
равной величине главного вектора
и направив ее в сторону, противоположную
главному вектору (приложив эту силу к
центру приведения).
Тогда две силы
и
можно отбросить как две взаимно
уравновешивающиеся силы и останется
только одна сила
,
равная главному вектору, т.е. геометрической
сумме заданных сил. Эта сила –
равнодействующая заданных сил. Ее линия
действия отстоит от центра приведения
на расстоянии, равном плечу пары сил
,
т.е
.
4
)
и
,
но
(самый общий случай). Можно в этом случае
получить новую картину сил, если пару
сил, момент которой
,
заменить двумя парами сил, моменты
которых
и
(см. рис.3..5), причем
.
Рис.35
Покажем пару
сил, соответствующую моменту
,
выбрав силы этой пары равными главному
вектору, приложив одну из сил (
)
к центру приведения и направив ее
противоположно главному вектору.
Тогда две силы
и
можно отбросить (см. случай 3). Остаются
сила
и пара сил, соответствующая моменту
,
расположенная в плоскости, перпендикулярной
силе. Такая совокупность силы и пары
сил получила название: «силовой винт»
или «динама».
Определение
главного вектора и главного момента
системы сил относительно центра
аналитическим способом
Зная силы
,
,
…
,
приложенные к твердому телу (зная их
величину и углы между силой и осями
координат), можно определить модуль и
направление главного вектора заданных
сил по способу проекций:
,
;
;
(аналогично определению
аналитическим способом равнодействующей).
Главный момент
системы сил относительно центра (его
величину и направление) также можно
определить по способу проекций:
,
где
— алгебраическая сумма моментов сил
относительно координатной оси Ox,
определяющая проекцию вектора
на ось Ox, которая
получила название главного момента
системы сил относительно оси —
;
(главный момент системы сил относительно
оси Oy);
(главный
момент системы сил относительно оси
Oz).
Условия
равновесия сил. Уравнения равновесия
Если при сложении
сил, произвольно расположенных в
пространстве, силовой многоугольник
получается замкнутым и векторный
многоугольник моментов также получится
замкнутым, то силы взаимно уравновешиваются.
Следовательно, условие равновесия сил
получают вид:
и
.
Это позволяет записать условия равновесия
сил в аналитической форме – уравнения
равновесия:
1.
; 2.
; 3.
;
4.
; 5.
; 6.
.
Получаем 6
уравнений равновесия пространственной
системы сил.
Соседние файлы в папке Первый курс Летняя сессия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.07.20214.74 Mб4Статика.docx
- #