Как найти равнодействующую сил действующих на автомобиль

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

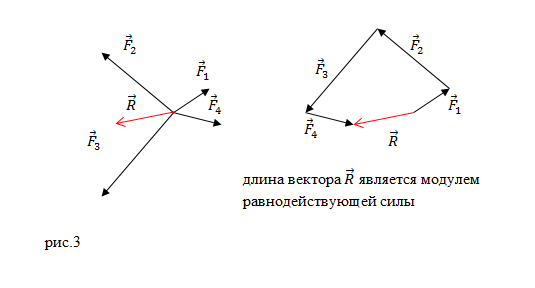
Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

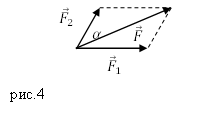
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Как найти равнодействующую трех векторов

Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)

Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:

Таким образом, равнодействующая всех сил равна

а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?

Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.

«Систему отсчета считать инерциальной.» Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.

ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.

Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.

т.е. в инерциальной системе отсчёта нет силы трения?

и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?

Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.

Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.

Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол — 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.

Подскажите пожалуйста, где в моих рассуждениях ошибка?

Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.

Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.

а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!

Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с

На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)

На рисунке обозначена равнодействующая векторов и

Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора

А как определили эту равнодействующую трёх сил, я понять не могу?!

Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).

Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.

векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!

Когда Вы складываете параллельные вектора, у Вас просто получается «вырожденный треугольник». Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.

Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)

Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен

Под действием одной силы F₁ тело движется с ускорением 4 м/с 2 . Под действием другой силы F₂, направленной противоположно силе F₁, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F₁ и F₂? Ответ дайте в метрах на секунду в квадрате.

Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением

Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)

Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен

в условии написано,что нужно найти вес тела.

а в решении модуль силы тяжести.

Как вес может измеряться в Ньютонах.

В условии ошибка(

Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.

Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.

Понятие «вес тела» введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.

Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?

Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.

Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.

Здесь сразу вспоминается детская задачка: «Что весит больше: килограмм пуха или килограмм свинца?» Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.

С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?

В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.

Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства

Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.

Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне «Ваш e-mail» должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.

Формула модуля равнодействующей силы

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

Складывают векторы, используя правило треугольника (рис.1)

правило параллелограмма (рис.2).

или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?

Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]

Ответ. $F=52,92$ Н

Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?

Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:

Следовательно, модуль силы можно найти как:

Ускорение точки будем искать, используя связь между ним и перемещением точки:

Первая производная от $s$ по времени равна:

Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:

Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:

В механике чаще всего приходится иметь дело с силами различной величины, действующими в различных направлениях. Силы принято обозначать на схемах стрелками и буквами, причем направление стрелок должно совпадать с направлением действия силы, а длины всех стрелок должны быть выдержаны в одном масштабе пропорционально величинам сил. Начало («хвост») стрелки устанавливают в точке приложения силы.

Рис. Силы, действующие на автомобиль, изображают стрелками.

Приведем простой пример: на кузов автомобиля действуют две силы — сила сопротивления воздуха и сила ветра, дующего под углом 90° к продольной оси (и направлению движения) автомобиля. Скорость автомобиля (т. е. встречного движения воздуха) 30 метров в секунду (30 м/сек), или 108 километров в час (км/час), скорость ветра 10 м/сек, или 36 км/час. Величины сил лобового сопротивления и бокового ветра примерно пропорциональны квадратам скорости, так что можно изобразить стрелки длиной 30^2 = 900 или 90 мм и 10^2 = 100 или 10 мм, приложенные в точке центра тяжести автомобиля.

Вообще же величины сил измеряют в килограммах (сокращенно кг).

Практически, действие силы или нескольких сил на тело приводит к началу движения (перемещения) неподвижного тела, к изменению направления и скорости движения тела или к давлению одного тела на другое, если одно из них препятствует перемещению другого.

Попутно отметим, что давление измеряют в килограммах (кг), приходящихся на 1 квадратный сантиметр (см2). Если нагрузка, действующая на одно колесо автомобиля, равна 300 кг, а поверхность соприкасающейся с дорогой части шины (отпечатка шины) равна 150 см2, то давление составляет 300:150 = 2 кг/см2 (удельное давление шины на грунт).

Рис. Нагрузка, приходящаяся на колесо, распределяется по поверхности отпечатки шины.

На тело, например на автомобиль, могут действовать несколько сил. Совокупность нескольких сил, одновременно действующих на тело, называется системой сил. Эти несколько сил можно суммировать (сложить), чтобы выявить равнодействующую (или результирующую) силу. Если силы действуют в одном направлении и приложены в одной точке, их равнодействующая приложена в той же точке, направлена в ту же сторону и равна по величине сумме составляющих сил.

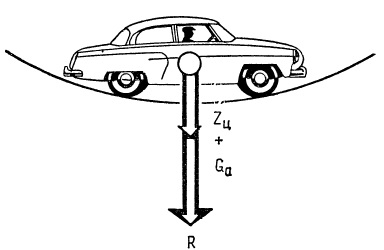
Рис. Впадина дороги. Сила тяжести и центробежная сила действуют в одном направлении и складываются.

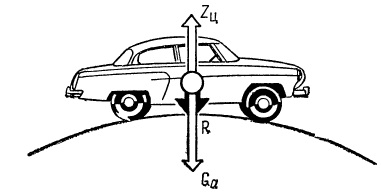
Рис. Перекат дороги. Центробежная сила противодействует силе тяжести.

Например, при прохождении автомобилем впадины дороги сила тяжести Ga и центробежная сила Zц, приложенные в точке центра тяжести, дают равнодействующую R = Ga + Zц. Если силы направлены в противоположные стороны (прохождение выпуклого места дороги), равнодействующая равна их разности, приложена опять в точке центра тяжести и направлена в сторону большей силы. Если противодействующие силы равны, тело находится в покое или в установившемся движении, так как равнодействующая равна нулю.

Рис. При сложении сил ветра и давления встречного воздуха равнодействующая направлена по диагонали параллелограмма этих сил.

Возвратимся к примеру с боковым ветром. Здесь действуют две силы в разных направлениях, приложенные к одной точке. Сложение таких сил отличается от сложения сил, направленных в одну или в противоположные стороны. Равнодействующая сил встречного воздуха и бокового ветра направлена по диагонали параллелограмма, сторонами которого являются составляющие силы, и равна длине этой диагонали (т. е. в данном примере R = корень_из_(10:2 + 90:2) = 90,5).

Можно складывать силы встречного воздуха и бокового ветра, дующего под различными углами к продольной оси автомобиля.

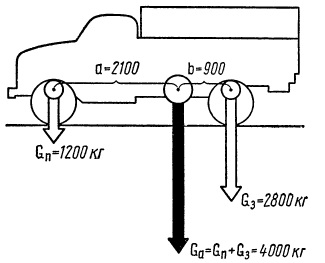
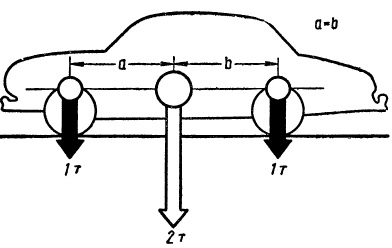
Рис. Складывая веса, приходящиеся на передние и задние колеса, можно получить вес автомобиля.

Бывают случаи, когда на тело (автомобиль) действуют две параллельные силы, приложенные в разных точках (например, нагрузка на передние и задние колеса автомобиля). Равнодействующая равна их сумме, направлена параллельно в ту же сторону, а точка приложения ее находится на линии, соединяющей точки приложения двух составляющих сил, причем расстояния от точки приложения равнодействующей силы до точек приложения составляющих обратно пропорциональны величинам составляющих сил. Приведем пример: база автомобиля равна 3000 мм, на передние колеса приходится 1200 кг, или 30% нагрузки, на задние — 2800 кг, или 70%; отсюда найдем, что величина равнодействующей силы составляет 4000 кг и эта сила приложена в точке, находящейся на расстоянии (70*3000)/100 = 2100 мм от передней оси и (30*3000)/100 = 900 мм от задней. Отметим, что в данном случае равнодействующая сила является пол-
ным весом автомобиля.

Если приложенные к телу силы направлены в разные стороны, равнодействующая равна разности этих сил и направлена в сторону большей силы, а точка ее приложения лежит на продолжении прямой, проходящей через точки приложения составляющих сил, за большей силой. Расстояния от равнодействующей до составляющих сил обратно пропорцион-альны величинам этих сил.

Рис. На концы оси действуют силы, направленные в разные стороны. Их равнодействующая показана справа (слева по ходу автомобиля).

Возьмем в качестве примера такой случай: левое колесо во время движения автомобиля попадает на бугор, а правое — в выбоину. На концы оси действуют противоположно направленные силы; в зависимости от величины неровностей, скорости движения и т. д., силы могут быть разными. Допустим, что действующая на левое колесо сила в 10 раз больше действующей на правое (В = А:10); колея автомобиля равна 1400 мм. Равнодействующая сила равна А — 1/10А = 9/10А. Расстояние Х от этой силы до большей силы вычисляем из пропорции:

Х / (Х + 1400) = А/10А;
10х = х + 1400,
х = 155 мм.

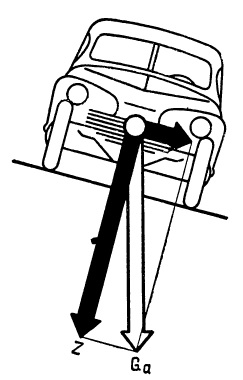
Рис. Силу тяжести автомобиля на косогоре можно разложить на две, направленные параллельно и перпендикулярно поверхности дороги.

Отсюда расстояние от равнодействующей до меньшей силы равно 1555 мм.

Силы можно (и бывает нужно) не только складывать, но и раскладывать. Разложение одной силы на две обычно приходится производить в том случае, когда нужно узнать, какие части известной силы действуют в заданных направлениях.

Рис. Сила тяжести (вес автомобиля) раскладывается на две силы, действующие на передние и задние колеса.

Например, нужно узнать, какая часть силы тяжести, приложенной к центру тяжести находящегося на косогоре автомобиля, направлена вбок и какая перпендикулярно поверхности дороги. Поскольку разложение силы является действием, обратным сложению, принимаем данную силу за диагональ параллелограмма и из точки приложения силы проводим две линии в заданных направлениях, а из вершины силы проводим линии, параллельные проведенным ранее. В результате получаем параллелограмм, стороны которого и являются искомыми силами.

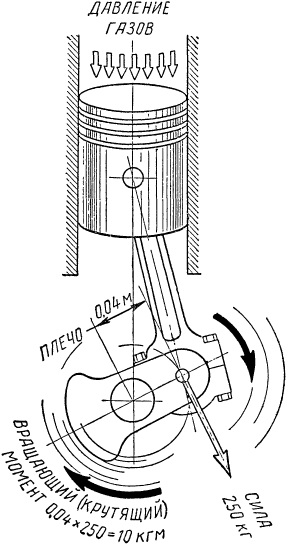
Рис. Крутящий момент возникает от силы давления газов, переданной через поршень и шатун и приложенной на плече, равном радиусу кривошипа.

Разложение силы на параллельные также происходит в порядке, обратном сложению. Нужно лишь знать расстояние отданной силы до ее предполагаемых составляющих (или задаться этими расстояниями). Если вес автомобиля равен 2 т, а центр тяжести расположен посередине базы, т. е. расстояния от заданной силы тяжести (2 т) до передней и задней осей автомобиля равны, то на каждую ось приходится половина веса автомобиля — 1 т. Каждая составляющая сила равна половине данной силы. Если центр тяжести сдвинут от середины базы и расположен, например, на расстоянии 1/3 базы от задней оси, составляющие силы, равные в сумме данной, обратно пропорциональны расстояниям от осей до центра тяжести, т. е. на задние колеса придется 2/3 веса автомобиля, на передние — 1/3.

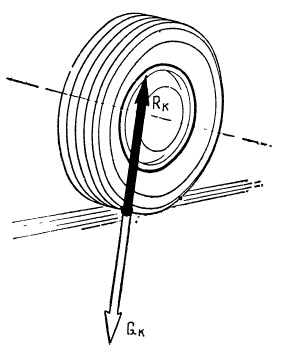
Рис. Реакция дороги равна силе тяжести (весу), приходящейся на колесо.

Но возможны положения, когда силы или сила вызывают поворот или вращение тела. Такое положение возникает, например, когда противодействующие параллельные силы равны, а их равнодействующей не существует — она равна нулю. Систему таких сил называют парой сил, расстояние между ними — плечом пары, а произведение одной из сил на плечо — моментом пары. Момент измеряют в килограммометрах (кгм), так как в произведение входит сила, измеренная в кг, и плечо, измеренное в м. Подобное положение имеется и в случае, когда одна сила действует на тело, закрепленное в какой-либо точке. Момент силы тогда является произведением силы на кратчайшее расстояние (плечо) от линии действия силы до неподвижной точки. Этот момент вызывает вращение тела или его скручивание, поэтому его называют крутящим моментом или вращающим моментом.

Действию всегда соответствует равное ему и противоположно направленное противодействие. Сила тяжести автомобиля давит через колесо на дорогу; если асфальт размягчен в жаркую погоду, шина вдавливается в асфальт. Но и дорога с той же силой давит на шину. Эта последняя сила называется реакцией дороги. Точно так же ноги спортсмена при прыжке давят на песчаную площадку, оставляя в ней след, а площадка как бы подбрасывает спортсмена; в момент приземления спортсмен ощущает удар — давление площадки на ступню и одновременно вдавливает с той же силой песок.

Предлагаем вам продолжить подготовку к ЕГЭ по физике и порешать задачи вместе с нами. Сегодня рассмотрим задание №2 из ЕГЭ прошлых лет.

Задача № 1

Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (Рис. 1). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? Ответ дайте в ньютонах.

Рис. 1

Решение

Известно, что, согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением:

F = ma

Ускорение при равноускоренном движении можно определить по формуле:

a =

Из графика (Рис. 1) видно, что ускорение удобно определить при:

t₁ = 8 с, когда V₁ = 4 м/с

и

t₀ = 0 с, когда V₁ = 0 м/с

Подставим в формулу числовые значения и найдем «а»:

a =  = 0,5 м/с

Тогда, равнодействующая всех сил будет равна:

F = 1000 · 0,5 = 500 Н

Ответ: 500.

---

Задача № 2

На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (Рис. 2), вид сверху. Каков модуль равнодействующей этих сил, если F₁ = 1 Н? Ответ дайте в ньютонах и округлите до десятых.

Рис. 2

Решение

Так как на (Рис. 2) вектор силы F₁ равен одной клетке, то делаем вывод, что масштаб одной клетки равен 1Н.

Используя правило треугольника, найдем равнодействующую F_р

векторов F_1, F_2, и F₃. Результат покажем на (Рис. 3):

 Рис. 3

Модуль равнодействующей F_р найдем по теореме Пифагора, используя (Рис. 3):

Fр = √(+ ) = √10 ≈ 3,2 Н

Ответ: 3,2

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Силы, действующие на автомобиль.

Для правильного и безопасного управления автомобилем водители должны знать физические законы его поведения на дороге. Эти знания помогают при правильной оценке конкретной дорожной ситуации выбрать оптимальное решение и, воздействуя на органы управления автомобиля, совершать безопасные маневрирования. Различные силы, воздействующие на автомобиль, заставляют его двигаться и останавливаться. Каждому водителю необходимо знать законы движения автомобиля, понимать их природу, учитывать и использовать их при управлении своим транспортным средством.

Силы, действующие на автомобиль, делятся на две группы. Первая группа оказывает сопротивление движению, вторая — заставляет его двигаться.

1. Сила тяжести — возникает под воздействием силы притяжения Земли и направлена вертикально вниз, распределяясь по всем осям и колесам автомобиля. Фактический вес транспортного средства оказывает давление на дорожное покрытие, и чем он больше, тем больше становится величина силы сцепления колес с дорогой. Эта сила оказывает существенное влияние вначале движения и в дальнейшем его процессе на ведущие колеса автомобиля.

2. Силы реакции дорожного полотна — возникает из-за сил, действующих со стороны транспортного средства в местах соприкосновения колес с дорогой. Чем больше сила тяжести, действующая со стороны колеса автомобиля на дорожное полотно, тем больше сила ответной реакции со сторноы дороги.

3. Сила тяги всегда направлена в сторону движения автомобиля. Она возникает при передаче крутащего момента от двигателя к ведущим колесам, где они в свою очередь стараются переместить слои дорожного полотна назад. Чем больше крутящий момент двигателя и выше передаточное число коробки передач и главной передачи, чем меньше радиус колеса с учетом деформации шины, тем больше становится тяговая сила. Если величина тяговой силы превышает силы сцепления колес с дорогой, возникает пробуксовка ведущих колес. Поэтому начинать движение на скользкой дороге или по бездорожью, а так же с перевозимым грузом необходимо с включением низшей передачи, когда сила тяги достигает наибольшей велечины.

4. Центробежная сила возникает в момент прохождения поворотов или смещения транспортного средства влево или вправо относительно проезжей части. В эти моменты автомобиль стремиться сохранить первоначально заданное направление движения. Величина этой силы прямо пропорциональна радиусу вхождения в поворот. Направление ее действия — от центра тяжести в противоположную сторону поворота. Так, при вхождении в правый поворот центробежная сила старается отклонить автомобиль влево на встречную полосу, а при прохождении левого поворота — вправо, в сторону обочины. Уменьшить ее значение можно только снижением скорости движения и увеличением радиуса траектории входа в поворот. При неправильной выбранной скорости и радиусе поворота центробежная сила может развернуть автомобиль вокруг его оси, что приведет к заносу, отбросить в сторону и, наконец, перевернуть.

5. Сила сцепления шины с дорожным полотном возникает в процессе движения и зависит от многих факторов:

Водителю необходимо учитывать все эти факторы, так как когда сила тяги на колеса автомобиля превышает силу сцепления с дорожным полотном, может произойти пробуксовка колес, а на скользкой дороге возможны заносы и выход из-под контроля управления автомобиля.

6. Сила сопротивления воздуха направлена в сторону, противоположную движению транспортного средства. Она возникает в процессе движения за счет давления на воздух поверхностями автомобиля, поэтому многое зависит от аэродинамической конструкции формы кузова автомобиля. Эта сила возрастает с увеличением скорости движения.

7.Сила сопротивления каченю возникает в процессе движения при трении шин автомобиля о поверхность дороги, вследствие чего возникают трения в передаточном механизме (в подшипниках колес). Эта сила прямо пропорциональна массе транспортного средства и коэффициенту сопротивления качению. Коэффициент сопротивления качению зависит от состояния дороги и определяется опытным путем. Сила сопротивления качению направлена в сторону, противоположную движению.

Источник

Силы действующие на автомобиль при движении

Схема сил действующих на ведущее колесо

На движущийся автомобиль действует ряд сил, часть из которых направлена по оси движения автомобиля, а часть — под углом к этой оси. Условимся называть первые из этих сил продольными, а вторые боковыми.

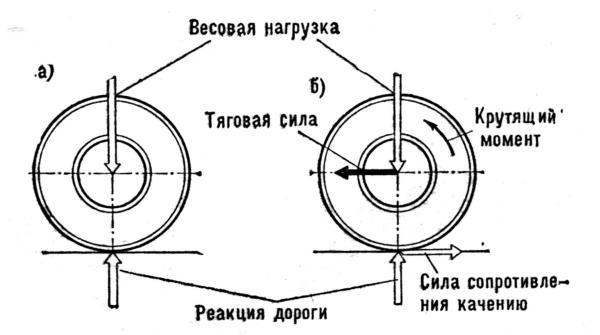
Рис. Схема сил действующих на ведущее колесо.
а — состояние неподвижности; б — состояние движения

Продольные силы могут быть направлены как по ходу, так и против хода движения автомобиля. Силы, направленные по ходу движения, являются движущимися и стремятся продолжить движение. Силы, направленные против хода движения, являются силами сопротивления и стремятся остановить автомобиль.

На автомобиль, движущийся по горизонтальному и прямому участку дороги, действуют следующие продольные силы:

При движении автомобиля в гору возникает сила сопротивления подъему, а при разгоне автомобиля—сила сопро­тивления разгону (сила инерции).

Тяговая сила

Сила сцепления колес с дорогой

У легковых автомобилей полный вес рас­пределяется по осям примерно поровну. Поэтому сцепной вес его можно принять равным 50% полного веса. У грузовых автомоби­лей при полной их на­грузке сцепной вес (вес, приходящийся на заднюю ось) составляет примерно 60—70% полного веса.

Величина коэффициента сцепления имеет большое значение для эксплуатации автомобиля и безопасности движения, так как от него зависят проходимость автомобиля, тормозные качества, возможность, пробуксовки и заноса ведущих колес. При незначи­тельном коэффициенте сцепления трогание автомобиля с места со­провождается пробуксовкой, а торможение — скольжением колес. В результате автомобиль иногда не удается тронуть с места, а при торможении происходит резкое увеличение тормозного пути и возникновение заноса.

На асфальтобетонных покрытиях в жаркую погоду на поверх­ность выступает битум, делая дорогу маслянистой и более скольз­кой, что снижает коэффициент сцепления. Особенно сильно снижается коэффициент сцепления при смачивании дороги первым дождем, когда образуется еще не смытая пленка жидкой грязи. Заснежённая или обледенелая дорога особенно опасна в теплую погоду, когда поверхность подтаивает.

При увеличении скорости движения коэффициент сцепления снижается, в особенности на мокрой дороге, так как выступы ри­сунка протектора шины не успевают продавливать пленку влаги.

Исправное состояние рисунка протектора шины имеет большое значение при движении по грунтовым дорогам, снегу, песку, а также по дорогам с твердым покрытием, по покрытым пленкой грязи или воды. Благодаря наличию выступов рисунка опорная площадь шины уменьшается и, следовательно, возрастает удельное давление на поверхность дороги. При этом легче продавливается грязевая пленка и восстанавливается контакт с дорожным покрытием, а на легком грунте происходит непосредственное зацепление выступов рисунка за грунт.

Повышенное давление воздуха в шине уменьшает ее опорную поверхность, вследствие чего удельное давление возрастает на­столько, что при трогании с места и при торможении может произойти разрушение резины и сцепление колес с дорогой уменьшается.

Таким образом, величина коэффициента сцепления зависит от многих условий и может изменяться в довольно значительных пределах. Так как много дорожно-транспортных происшествий происходит из-за плохого сцепления, то водители должны уметь приблизительно оценивать величину коэффициента сцепления и выбирать скорость движения и приемы управления в соответствии с ним.

Сила сопротивления воздуха

Передней частью автомобиля воздух сжимается и раздвигает­ся, в то время как в задней части автомобиля создается разреже­ние, которое вызывает образование завихрений.

Сила сопротивления воздуха зависит от величины лобовой, поверхности автомобиля, его формы, а также от скорости движе­ния. Лобовую площадь грузового автомобиля определяют как произведение колеи (расстояние между шинами) на высоту авто­мобиля. Сила сопротивления воздуха возрастает пропорционально квадрату скорости движения автомобиля (если скорость возра­стает в 2 раза, то сопротивление воздуха увеличивается в 4 раза).

Для улучшения обтекаемости и уменьшения сопротивления воздуха ветровое стекло автомобиля располагают наклонно, а вы­ступающие детали (фары, крылья, ручки дверей) устанавливают заподлицо с внешними очертаниями кузова. У грузовых автомоби­лей можно уменьшить силу сопротивления воздуха, закрыв грузо­вую платформу брезентом, натянутым между крышей кабины и задним бортом.

Сила сопротивления качению

Сила сопротивления качению равна произведению полного веса автомобиля на коэффициент сопротивления качению шин, который зависит от давления воздуха в шинах и качества дорожного покрытия. Вот- некоторые значения коэффициента сопротивления качению шин:

Сила сопротивления подъему

При движении на подъем автомобиль испытывает дополнитель­ное сопротивление, которое зависит от угла наклона дороги к гори­зонту. Сопротивление подъему тем больше, чем больше вес автомобиля и угол наклона дороги. При подъезде к подъему необходимо правильно оценить возможности преодоления подъема. Если подъем непродолжительный, его преодолевают с разгоном автомобиля перед подъемом. Если подъем продолжительный, его преодолевают на пониженной передаче, переключившись на нее у начала подъема.

При движении автомобиля на спуске сила сопротивления подъему направлена в сторону движения и является движущей силой.

Источник

Теория движения автомобиля: основные элементы

Силы, действующие на автомобиль

На автомобиль, независимо от того, движется он или неподвижен, действует сила тяжести (вес), направленная отвесно вниз.

Сила тяжести прижимает колеса автомобиля к дороге. Равнодействующая этой силы, размещена в центре тяжести. Распределение веса автомобиля по осям зависит от расположения центра тяжести. Чем ближе к одной из осей расположен центр тяжести, тем больше будет нагрузка на эту ось. На легковых автомобилях нагрузка на оси распределяется примерно поровну.

Большое значение на устойчивость и управляемость автомобиля имеет расположение центра тяжести не только в отношении продольной оси, но и по высоте. Чем выше центр тяжести, тем менее устойчивым будет автомобиль. Если автомобиль находится на горизонтальной поверхности, то сила тяжести направлена отвесно вниз. На наклонной поверхности она раскладывается на две силы (см. рисунок): одна из них прижимает колеса к поверхности дороги, а другая стремится опрокинуть автомобиль. Чем выше центр тяжести и чем больше угол наклона автомобиля, тем скорее нарушится устойчивость и автомобиль может опрокинуться.

Во время движения, кроме силы тяжести, на автомобиль действует и ряд других сил, на преодоление которых затрачивается мощность двигателя.

На рисунке показана схема сил, действующих на автомобиль во время движения. К ним относятся:

Движение автомобиля возможно только при условии, что его колеса будут иметь достаточное сцепление с поверхностью дороги.

Если сила сцепления будет недостаточной (меньше величины силы тяги на ведущих колесах), то колеса пробуксовывают.

Сила сцепления с дорогой зависит от веса, приходящегося на колесо, от состояния покрытия дороги, давления воздуха в шинах и рисунка протектора.

Для определения влияния состояния дороги на силу сцепления служит коэффициент сцепления, который определяют делением силы сцепления ведущих колес автомобиля на вес автомобиля, приходящийся на эти колеса.

Коэффициент сцепления зависит от вида покрытия дороги и от его состояния (наличия влаги, грязи, снега, льда); величина его приведена в таблице (см. рисунок).

На дорогах с асфальтобетонным покрытием коэффициент сцепления резко уменьшается, если на поверхности имеется влажная грязь и пыль. В этом случае грязь образует пленку, резко уменьшающую коэффициент сцепления.

На дорогах с асфальтобетонным покрытием в жаркую погоду появляется на поверхности маслянистая пленка из выступающего битума, снижающая коэффициент сцепления.

Уменьшение коэффициента сцепления колес с дорогой наблюдается также при увеличении скорости движения. Так, при возрастании скорости движения на сухой дороге с асфальтобетонным покрытием с 30 до 60 км/ч коэффициент сцепления уменьшается на 0,15.

Разгон, ускорение, накат

Мощность двигателя затрачивается на приведение во вращение ведущих колес автомобиля и преодоление сил трения в механизмах трансмиссии.

Если величина усилия, с которым вращаются ведущие колеса, создавая тяговую силу, будет больше чем суммарная сила сопротивления движению, то автомобиль будет двигаться с ускорением, т.е. с разгоном.

Ускорением называется прирост скорости за единицу времени. Если тяговое усилие равно силам сопротивления движению, то автомобиль будет двигаться без ускорения с равномерной скоростью. Чем выше максимальная мощность двигателя и меньше величина суммарных сил сопротивления, тем быстрее автомобиль достигнет заданной скорости.

Кроме того, на величину ускорения влияет вес автомобиля, передаточное число коробки передач, главной передачи, количество передач и обтекаемость автомобиля.

Во время движения накапливается определенный запас кинетической энергии, и автомобиль приобретает инерцию. Благодаря инерции автомобиль может двигаться некоторое время с отключенным двигателем – накатом. Движение накатом используют для экономии топлива.

Торможение автомобиля

Торможение автомобиля имеет большое значение для безопасности движения и зависит от его тормозных качеств. Чем лучше и надежнее тормоза, тем быстрее можно остановить движущийся автомобиль и тем с большей скоростью можно двигаться, а следовательно, и больше будет его средняя скорость.

Во время движения автомобиля накопленная кинетическая энергия поглощается при торможении. Торможению помогают силы сопротивления воздуха, сопротивления качению и сопротивления подъему. На уклоне силы сопротивления подъему отсутствуют, а к инерции автомобиля добавляется составляющая сила тяжести, которая затрудняет торможение.

При торможении между колесами и дорогой возникает тормозная сила, противоположная направлению силы тяги. Торможение зависит от соотношения между тормозной силой и силой сцепления. Если сила сцепления колес с дорогой будет больше тормозной силы, то автомобиль затормаживается. Если тормозная сила будет больше силы сцепления, то при заторможенных колесах произойдет их скольжение относительно дороги. В первом случае при торможении колеса катятся, постепенно замедляя вращение, а кинетическая энергия автомобиля превращается в тепловую энергию, нагревающую тормозные колодки и диски (барабаны). Во втором случае колеса перестают вращаться и будут скользить по дороге, поэтому большая часть кинетической энергии будет превращаться в тепло трения шин о дорогу. Торможение с остановившимися колесами ухудшает управляемость автомобиля, особенно на скользкой дороге, и приводит к ускоренному износу шин.

Наибольшую тормозную силу можно получить только тогда, когда тормозные моменты на колесах будут пропорциональны нагрузкам, приходящимся на них. Если такая пропорциональность не будет соблюдена, то тормозная сила на одном из колес не будет полностью использована.

Эффективность торможения оценивается по тормозному пути и величине замедления.

Тормозной путь – это расстояние, которое проходит автомобиль от начала торможения до полной остановки. Замедление автомобиля – это величина, на которую уменьшается скорость автомобиля за единицу времени.

Управляемость автомобиля

Под управляемостью автомобиля понимают его способность изменять направление движения.

Во время движения автомобиля по прямой очень важно, чтобы управляемые колеса не поворачивались произвольно и водителю не нужно было бы затрачивать усилия для удержания колес в нужном направлении. На автомобиле предусмотрена стабилизация управляемых колес в положении движения в прямом направлении, которая достигается продольным углом наклона оси поворота и углом между плоскостью вращения колеса и вертикалью. Благодаря продольному наклону колесо устанавливается так, что его точка опоры по отношению оси поворота снесена назад на величину а и его работа подобна ролику (см. рисунок).

При поперечном наклоне повернуть колесо всегда труднее, чем вернуть его в исходное положение – движения по прямой. Это объясняется тем, что при повороте колеса передняя часть автомобиля приподнимается на величину б (водитель прилагает сравнительно большее усилие к рулевому колесу).

Для возвращения управляемых колес в положение, соответствующее движению по прямой, вес автомобиля помогает поворачиванию колес и водитель прикладывает к рулевому колесу небольшое усилие.

На автомобилях, особенно у тех, где давление воздуха в шинах невелико, возникает боковой увод. Боковой увод возникает в основном под действием поперечной силы, вызывающей боковой прогиб шины; при этом колеса катятся не по прямой, а смещаются в сторону под действием поперечной силы (см. рисунок).

Оба колеса передней оси имеют одинаковый угол увода. При уводе колес меняется радиус поворота, который увеличивается, уменьшая поворачиваемость автомобиля, а устойчивость движения при этом не изменяется.

При уводе колес задней оси радиус поворота уменьшается, особенно это заметно, если угол увода задних колес больше, чем у передних, стабильность движения нарушается, автомобиль начинает «рыскать» и водителю все время приходится подправлять направление движения. Для уменьшения влияния увода на управляемость автомобиля давление воздуха в шинах передних колес должно быть несколько меньше, чем у задних. Увод колес будет тем больше, чем большей будет боковая сила, действующая на автомобиль, например, на крутом повороте, где возникают большие центробежные силы.

Занос автомобиля

Заносом называется боковое скольжение задних колес при продолжающемся поступательном движении автомобиля. Иногда занос может привести к повороту автомобиля вокруг своей вертикальной оси.

Занос может возникать в результате ряда причин. Если резко повернуть управляемые колеса, то может оказаться, что инерционные силы станут больше, чем сила сцепления колес с дорогой, особенно часто это случается на скользких дорогах.

При неодинаковых тяговых или тормозных силах, приложенных на колеса правой и левой сторон, действующих в продольном направлении, возникает поворачивающий момент, приводящий к заносу. Непосредственной причиной заноса при торможении являются неодинаковые тормозные силы на колесах одной оси, неодинаковое сцепление колес правой или левой стороны с дорогой или неправильное размещение груза относительно продольной оси автомобиля. Причиной заноса автомобиля на повороте может быть также торможение его, так как при этом к поперечной силе добавляется продольная сила и их сумма может превысить силу сцепления, препятствующую заносу (см. рисунок).

Чтобы предотвратить начавшийся занос автомобиля, необходимо: прекратить торможение, не выключая сцепление (на автомобилях с МКПП); повернуть колеса в сторону заноса.

Эти приемы выполняют сразу же, как только начался занос. После прекращения заноса нужно выровнять колеса, чтобы занос не начался в другом направлении.

Чаще всего занос получается при резком торможении на мокрой или обледенелой дороге, особенно быстро нарастает занос на большой скорости, поэтому при скользкой или обледенелой дороге и на поворотах нужно уменьшать скорость, не применяя торможение.

Проходимость автомобиля

Проходимостью автомобиля называется его способность двигаться по плохим дорогам и в условиях бездорожья, а также преодолевать различные препятствия, встречающиеся на пути. Проходимость определяется:

Основным фактором, характеризующим проходимость, является соотношение между наибольшей тяговой силой, используемой на ведущих колесах, и силой сопротивления движению. В большинстве случаев проходимость автомобиля ограничивается недостаточной силой сцепления колес с дорогой и в связи с этим невозможностью использовать максимальную тяговую силу. Для оценки проходимости автомобиля по грунту пользуются коэффициентом сцепного веса, определяемым делением веса, приходящегося на ведущие колеса, на общий вес автомобиля. Наибольшую проходимость имеют автомобили, у которых все колеса являются ведущими. В случае применения прицепов, увеличивающих общий вес, но не изменяющих сцепной вес, проходимость резко снижается.

На величину сцепления ведущих колес с дорогой значительное влияние оказывает удельное давление шин на дорогу и рисунок протектора. Удельное давление определяется давлением веса, приходящегося на колесо, на площадь отпечатка шины. На рыхлых грунтах проходимость автомобиля будет лучше, если удельное давление будет меньше. На твердых и скользких дорогах проходимость улучшается при большем удельном давлении. Шина с крупным рисунком протектора на мягких грунтах будет иметь отпечаток большей площади и имеет меньшее удельное давление, а на твердых грунтах отпечаток этой шины будет меньшей площади и удельное давление увеличивается.

Проходимость автомобиля по габаритным размерам определяется по:

Источник

Силы действующие на автомобиль

В механике чаще всего приходится иметь дело с силами различной величины, действующими в различных направлениях. Силы принято обозначать на схемах стрелками и буквами, причем направление стрелок должно совпадать с направлением действия силы, а длины всех стрелок должны быть выдержаны в одном масштабе пропорционально величинам сил. Начало («хвост») стрелки устанавливают в точке приложения силы.

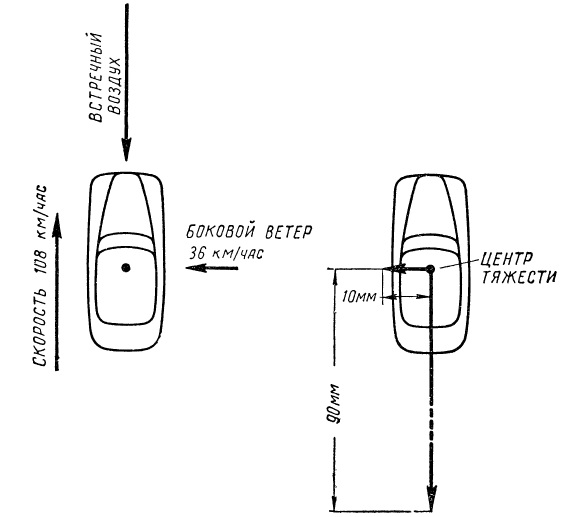
Рис. Силы, действующие на автомобиль, изображают стрелками.

Приведем простой пример: на кузов автомобиля действуют две силы — сила сопротивления воздуха и сила ветра, дующего под углом 90° к продольной оси (и направлению движения) автомобиля. Скорость автомобиля (т. е. встречного движения воздуха) 30 метров в секунду (30 м/сек), или 108 километров в час (км/час), скорость ветра 10 м/сек, или 36 км/час. Величины сил лобового сопротивления и бокового ветра примерно пропорциональны квадратам скорости, так что можно изобразить стрелки длиной 30^2 = 900 или 90 мм и 10^2 = 100 или 10 мм, приложенные в точке центра тяжести автомобиля.

Вообще же величины сил измеряют в килограммах (сокращенно кг).

Практически, действие силы или нескольких сил на тело приводит к началу движения (перемещения) неподвижного тела, к изменению направления и скорости движения тела или к давлению одного тела на другое, если одно из них препятствует перемещению другого.

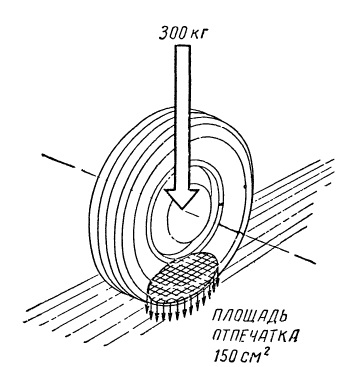
Попутно отметим, что давление измеряют в килограммах (кг), приходящихся на 1 квадратный сантиметр (см2). Если нагрузка, действующая на одно колесо автомобиля, равна 300 кг, а поверхность соприкасающейся с дорогой части шины (отпечатка шины) равна 150 см2, то давление составляет 300:150 = 2 кг/см2 (удельное давление шины на грунт).

Рис. Нагрузка, приходящаяся на колесо, распределяется по поверхности отпечатки шины.

На тело, например на автомобиль, могут действовать несколько сил. Совокупность нескольких сил, одновременно действующих на тело, называется системой сил. Эти несколько сил можно суммировать (сложить), чтобы выявить равнодействующую (или результирующую) силу. Если силы действуют в одном направлении и приложены в одной точке, их равнодействующая приложена в той же точке, направлена в ту же сторону и равна по величине сумме составляющих сил.

Рис. Впадина дороги. Сила тяжести и центробежная сила действуют в одном направлении и складываются.

Рис. Перекат дороги. Центробежная сила противодействует силе тяжести.

Например, при прохождении автомобилем впадины дороги сила тяжести Ga и центробежная сила Zц, приложенные в точке центра тяжести, дают равнодействующую R = Ga + Zц. Если силы направлены в противоположные стороны (прохождение выпуклого места дороги), равнодействующая равна их разности, приложена опять в точке центра тяжести и направлена в сторону большей силы. Если противодействующие силы равны, тело находится в покое или в установившемся движении, так как равнодействующая равна нулю.

Рис. При сложении сил ветра и давления встречного воздуха равнодействующая направлена по диагонали параллелограмма этих сил.

Возвратимся к примеру с боковым ветром. Здесь действуют две силы в разных направлениях, приложенные к одной точке. Сложение таких сил отличается от сложения сил, направленных в одну или в противоположные стороны. Равнодействующая сил встречного воздуха и бокового ветра направлена по диагонали параллелограмма, сторонами которого являются составляющие силы, и равна длине этой диагонали (т. е. в данном примере R = корень_из_(10:2 + 90:2) = 90,5).

Можно складывать силы встречного воздуха и бокового ветра, дующего под различными углами к продольной оси автомобиля.

Рис. Складывая веса, приходящиеся на передние и задние колеса, можно получить вес автомобиля.

Бывают случаи, когда на тело (автомобиль) действуют две параллельные силы, приложенные в разных точках (например, нагрузка на передние и задние колеса автомобиля). Равнодействующая равна их сумме, направлена параллельно в ту же сторону, а точка приложения ее находится на линии, соединяющей точки приложения двух составляющих сил, причем расстояния от точки приложения равнодействующей силы до точек приложения составляющих обратно пропорциональны величинам составляющих сил. Приведем пример: база автомобиля равна 3000 мм, на передние колеса приходится 1200 кг, или 30% нагрузки, на задние — 2800 кг, или 70%; отсюда найдем, что величина равнодействующей силы составляет 4000 кг и эта сила приложена в точке, находящейся на расстоянии (70*3000)/100 = 2100 мм от передней оси и (30*3000)/100 = 900 мм от задней. Отметим, что в данном случае равнодействующая сила является пол-
ным весом автомобиля.

Если приложенные к телу силы направлены в разные стороны, равнодействующая равна разности этих сил и направлена в сторону большей силы, а точка ее приложения лежит на продолжении прямой, проходящей через точки приложения составляющих сил, за большей силой. Расстояния от равнодействующей до составляющих сил обратно пропорцион-альны величинам этих сил.

Рис. На концы оси действуют силы, направленные в разные стороны. Их равнодействующая показана справа (слева по ходу автомобиля).

Возьмем в качестве примера такой случай: левое колесо во время движения автомобиля попадает на бугор, а правое — в выбоину. На концы оси действуют противоположно направленные силы; в зависимости от величины неровностей, скорости движения и т. д., силы могут быть разными. Допустим, что действующая на левое колесо сила в 10 раз больше действующей на правое (В = А:10); колея автомобиля равна 1400 мм. Равнодействующая сила равна А — 1/10А = 9/10А. Расстояние Х от этой силы до большей силы вычисляем из пропорции:

Х / (Х + 1400) = А/10А;
10х = х + 1400,
х = 155 мм.

Рис. Силу тяжести автомобиля на косогоре можно разложить на две, направленные параллельно и перпендикулярно поверхности дороги.

Отсюда расстояние от равнодействующей до меньшей силы равно 1555 мм.

Силы можно (и бывает нужно) не только складывать, но и раскладывать. Разложение одной силы на две обычно приходится производить в том случае, когда нужно узнать, какие части известной силы действуют в заданных направлениях.

Рис. Сила тяжести (вес автомобиля) раскладывается на две силы, действующие на передние и задние колеса.

Например, нужно узнать, какая часть силы тяжести, приложенной к центру тяжести находящегося на косогоре автомобиля, направлена вбок и какая перпендикулярно поверхности дороги. Поскольку разложение силы является действием, обратным сложению, принимаем данную силу за диагональ параллелограмма и из точки приложения силы проводим две линии в заданных направлениях, а из вершины силы проводим линии, параллельные проведенным ранее. В результате получаем параллелограмм, стороны которого и являются искомыми силами.

Рис. Крутящий момент возникает от силы давления газов, переданной через поршень и шатун и приложенной на плече, равном радиусу кривошипа.

Разложение силы на параллельные также происходит в порядке, обратном сложению. Нужно лишь знать расстояние отданной силы до ее предполагаемых составляющих (или задаться этими расстояниями). Если вес автомобиля равен 2 т, а центр тяжести расположен посередине базы, т. е. расстояния от заданной силы тяжести (2 т) до передней и задней осей автомобиля равны, то на каждую ось приходится половина веса автомобиля — 1 т. Каждая составляющая сила равна половине данной силы. Если центр тяжести сдвинут от середины базы и расположен, например, на расстоянии 1/3 базы от задней оси, составляющие силы, равные в сумме данной, обратно пропорциональны расстояниям от осей до центра тяжести, т. е. на задние колеса придется 2/3 веса автомобиля, на передние — 1/3.

Рис. Реакция дороги равна силе тяжести (весу), приходящейся на колесо.

Но возможны положения, когда силы или сила вызывают поворот или вращение тела. Такое положение возникает, например, когда противодействующие параллельные силы равны, а их равнодействующей не существует — она равна нулю. Систему таких сил называют парой сил, расстояние между ними — плечом пары, а произведение одной из сил на плечо — моментом пары. Момент измеряют в килограммометрах (кгм), так как в произведение входит сила, измеренная в кг, и плечо, измеренное в м. Подобное положение имеется и в случае, когда одна сила действует на тело, закрепленное в какой-либо точке. Момент силы тогда является произведением силы на кратчайшее расстояние (плечо) от линии действия силы до неподвижной точки. Этот момент вызывает вращение тела или его скручивание, поэтому его называют крутящим моментом или вращающим моментом.

Источник