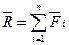Содержание
- wiki.eduVdom.com
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Графическое определение равнодействующей сходящихся сил
- Техническая механика. Шпаргалка
- Оглавление
- Равнодействующая сходящихся сил
- Графический способ определения равнодействующей сходящихся сил на плоскости.
- Определение равнодействующей геометрическим способом
wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Теория вероятностей и математическая статистика 
Строительная механика для строительных специальностей 
Матанализ. Дифференциальное и интегральное исчисление 
economics
Теоретическая механика. Статика:
Контакты
Графическое определение равнодействующей сходящихся сил
Теорема 1. Равнодействующая системы сходящихся сил существует, приложена в центре системы, равна их геометрической (векторной) сумме и изображается замыкающей стороной силового многоугольника.
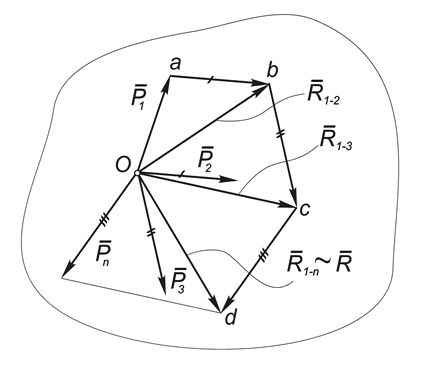
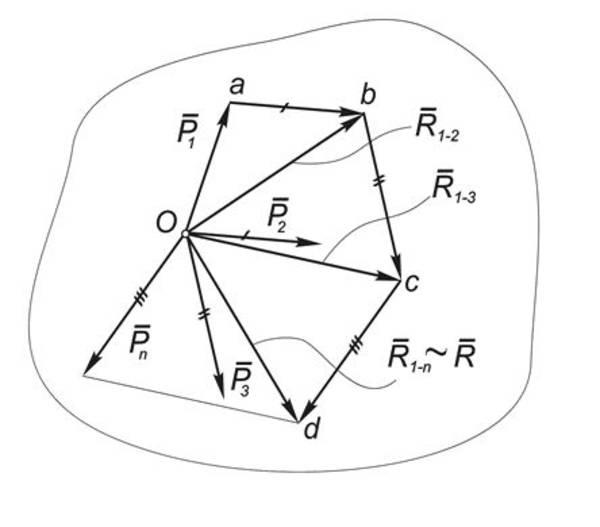
Для доказательства рассмотрим систему сходящихся сил, приложенных в центре О : (Рис.1).
По аксиоме параллелограмма две первых силы этой системы можно заменить равнодействующей $vec>$, которая изображается замыкающей стороной силового треугольника Oab и как вектор равна сумме векторов $vec<Р_1>$ и $vec<Р_2>$:
Затем точно так же можно найти равнодействующую силы $vec>$ и силы $vec<Р_3>$, откладывая от точки b вектор $bc = vec<Р_3>$:
Продолжая эту процедуру, мы найдем равнодействующую всей системы:
, которая изображается замыкающей стороной силового многоугольника Oabcd.
Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
Универсальным для определения равнодействующей системы сходящихся сил является аналитический метод, к рассмотрению которого мы и переходим.
Источник
Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Источник
Равнодействующая сходящихся сил
Равнодействующая сходящихся сил
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
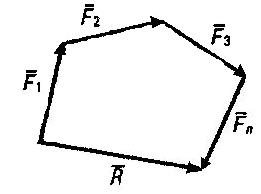
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Возможно эти страницы вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Графический способ определения равнодействующей сходящихся сил на плоскости.
Пусть задана произвольная система сходящихся сил 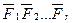
Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействующую этих сил. Равнодействующая такой системы может быть определена графически и аналитически.
Графически сложение двух сходящихся сил производится по правилу параллелограмма, причем 
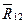
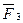
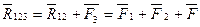
Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой. Равнодействующая сила 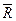
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской — плоской.
Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпадать с началом первой силы.
Такой силовой многоугольник называют замкнутым.
Получено условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равнялась нулю 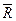
Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.
Источник
Определение равнодействующей геометрическим способом
Геометрический способ заключается в построение силового многоугольника, аналитический – в определении суммы проекций всех действующих сил на две взаимноперпендикулярные оси.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых.
Порядок построения силового многоугольника
1. Выбираем полюс построения.
2. Помещаем в полюс начало первого вектора F2 (векторы сил можно вычерчивать в любом порядке) переместив его параллельно самому себе, сохранив его величину.
3. Помещаем в конец первого вектора начало второго F1 . Вычерчиваем один за другим в аналогичном порядке векторы остальных сил F4 , F3.
4. Вектор равнодействующей замыкает полученную ломаную линию;он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Рекомендация. Обратить внимание на направление векторов.
Геометрическое условие равновесия ПССС: силовой многоугольник должен быть замкнут.
Определение равнодействующей аналитическим способом
Модуль (величину) равнодействующей определяют по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
Проекция силы на ось
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).
Аналитическое условие равновесия ПССС: суммы проекций всех сил на две взаимноперпендикулярные оси должны быть равны нулю.
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Тема 1.3. Плоская система произвольно расположенных сил
Момент силы относительно точки
Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на плечо.
Плечо – кратчайшее расстояние от точки до линия действия силы (перпендикуляр, опущенный из точки на линию действия силы) (рис. 4.4).
Обозначение момента Mо(F) или mо(F); m0(F) = Fa.
Единица измерения mo(F) = Н·м.
Момент считается положительным, если сила пытается развернуть тело по часовой стрелке.
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку, т. к. в этом случае расстояние от точки до силы равно нулю.
Плоская система произвольно расположенных сил
Главный вектор равен геометрической суммевекторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.
По величине проекций главного вектора на оси координат находим модуль главного вектора:
Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.
Таким образом, ПСПРС приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).
Три формы условия равновесия ПСПРС
Для разных случаев используются три группы уравнений равновесия.
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Балочные системы. Определение реакций опор и моментов защемления
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
q

q — интенсивность нагрузки, Н/м;
l— линия действия распределенной нагрузки, м;
Q = ql — равнодействующая распределенной нагрузки.
Разновидности опор балочных систем (см. реакции и их связи)Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силами RaxиRAy и парой с моментом MrА.
Для определения этих неизвестных удобно использовать систему уравнений в виде
Каждое уравнение имеет одну неизвестную величину и решается без подстановок. Для контроля правильности решений используют дополнительное равнение моментов относительно любой точки на балке, например В:
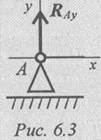
Шарнирно-подвижная опора (рис. 6.3).
Опора допускает поворот вокруг шарнира и перемещениевдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
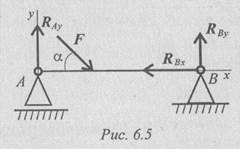
Балка на двух шарнирных опорах (рис. 6.5)
Тема 1.4. Центр тяжести
Сила тяжести — это сила, с которой тело притягивается к Земле, она распределена по всему объему тела.
Цент тяжести –это точка приложения силы тяжести.
Формулы для определения центра тяжести плоских фигур:
где Аn — площадь простейшей (элементарной) фигуры;
xn, yn — координаты центра тяжести простейшей (элементарной) фигуры.
Выражение 
Координаты центра тяжести сечения можно выразить через статический момент:
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Источник
Графическое определение равнодействующей сходящихся сил
Теорема 1. Равнодействующая системы сходящихся сил существует,
приложена в центре системы, равна их геометрической (векторной) сумме и
изображается замыкающей стороной силового многоугольника.
Для доказательства рассмотрим систему сходящихся сил, приложенных в
центре О : (Рис.1).
Рис.1
По аксиоме параллелограмма две первых силы этой системы можно
заменить равнодействующей $vec{R_{1-2}}$, которая изображается замыкающей стороной
силового треугольника Oab и как вектор равна сумме векторов $vec{Р_1}$ и $vec{Р_2}$:
$$(vec{Р_1}, vec{Р_2}) sim ( vec{R_{1-2}} = vec{Р_1} + vec{Р_2}$$
Затем точно так же можно найти равнодействующую силы $vec{R_{1-2}}$ и силы $vec{Р_3}$,
откладывая от точки b вектор $bc = vec{Р_3}$:
$$(vec{Р_1}, vec{Р_2}, vec{Р_3}) sim (vec{R_{1-2}}, vec{Р_3}) sim vec{R_{1-3}} = vec{Р_1} + vec{Р_2} + vec{Р_3}$$
Продолжая эту процедуру, мы найдем равнодействующую всей системы:
$$(vec{Р_1}, vec{Р_2}, dots, vec{Р_n}) sim (vec{R_{1-(n-1)}} , vec{Рn}) sim (vec{R_{1-n}}) sim vec{R} = sum_{i=1}^{i=n} vec{Р_i}$$
, которая изображается замыкающей стороной силового многоугольника Oabcd.
Отметим, что в общем случае этот многоугольник будет пространственной
фигурой, поэтому графический метод определения равнодействующей удобен
только для плоской системы сил.
Универсальным для определения равнодействующей системы сходящихся сил
является аналитический метод, к рассмотрению которого мы и переходим.
Примечания:
-
Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, хотя при этом мы получим другой силовой многоугольник – отличный от первого.
-
Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.
Равнодействующая сходящихся сил
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).
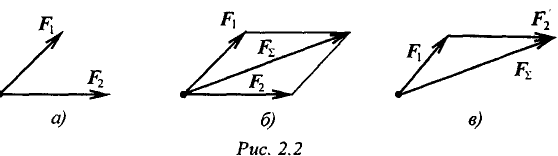
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
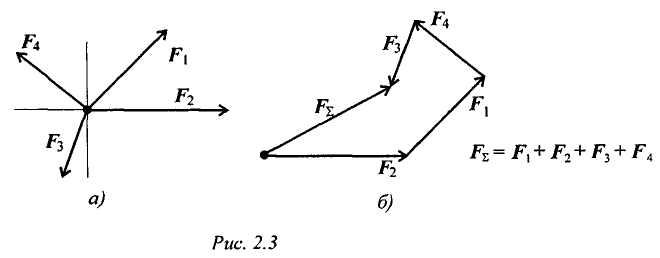
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
3. Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n — число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Положение вектора
силы
в
плоской декартовой системе координат
ХОУ задано точками: А – начало вектора
с координатами ()
и В – конец вектора с координатами (),
которые указаны в таблице С1-1. К точке
А также приложена сила,
проекции которой на оси координат равныи
и представлены в таблице С1-2.
Требуется: 1)
построить в выбранном масштабе векторы
сил
и
;
2) вычислить модули
сил
и
;
3) построить
равнодействующую
этих сил, определить ее модуль и угол
наклона к оси абсцисс;
4) найти по модулю
и направлению силу
.
Таблица С1-1
|
Цифра |
ХА, |
УА, |
ХВ, |
УВ, |
|
0 |
-2 |
6 |
4 |
4 |
|
1 |
3 |
-4 |
3 |
3 |
|
2 |
7 |
2 |
5 |
6 |
|
3 |
-3 |
5 |
2 |
7 |
|
4 |
-4 |
-5 |
1 |
8 |
|
5 |
6 |
-1 |
7 |
2 |
|
6 |
5 |
-7 |
6 |
3 |
|
7 |
3 |
-4 |
5 |
4 |
|
8 |
-1 |
8 |
4 |
3 |
|
9 |
-4 |
3 |
3 |
5 |
Таблица С1-2
|
Цифра |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
F2x, |
-5 |
-4 |
6 |
7 |
-3 |
-4 |
7 |
6 |
-4 |
5 |
|
F2y, |
5 |
6 |
-4 |
-3 |
4 |
5 |
-3 |
-2 |
5 |
-3 |
Методические указания к решению задачи
Для решения задачи
С1 студент должен знать и уметь:
-
Построить плоскую
систему координат в соответствующем
масштабе. Масштаб выбирается таким,
чтобы на рисунке были четко изображены
все силы, как заданные (и
),
так и искомые (и
).
-
Определять длину
вектора, т.е. его модуль, как длину
отрезка по известным координатам его
начала и конца по формуле:
.
-
Находить проекции
силы на координатные оси и находить
силу через ее проекции. Знать, чтобы
найти, например, абсциссу вектора (или
проекцию вектора на ось абсцисс), надо
из абсциссы конца вычесть абсциссу
начала вектора. Вычислять модуль силы,
зная проекции силы на координатные оси
по формуле:
-
Вычислять углы α
и β между положительными направлениями
оси абсцисс и оси ординат с вектором
силы. Для этого нужно воспользоваться
формулами:
.
Естественно:
.
Эти
косинусы называются направляющими
косинусами вектора
силы
.
-
Находить угол φ
между векторами
и
по формуле:
-
Определять модуль
искомого вектора силы
по теореме косинусов, т.е.:
.
Пример решения
задачи С1. Дано:
Решение
-
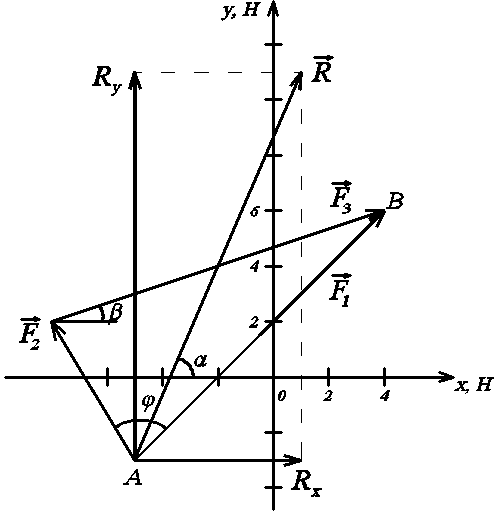
Изображаем плоскую
систему координат ХОУ (рис. С1а). Выбираем
масштаб: в 1см 2Н. Показываем точки А и
В. Строим вектор силы
.
Из точки А откладываем проекциисилы
.
Строим вектор сил.
Рис. С1а
-
Находим модуль
силы
-
Находим модуль
силы
-
Равнодействующая
равна геометрической сумме сил:
.
4.1) Первый способ
нахождения равнодействующей через ее
проекции, т.е.:
.
Проекции
равнодействующей на ось х и у равны:
.
Проекции на оси
координат силы
известны по условию задачи. Найдем
проекции силына оси х и у:
Таким образом (с
учетом знаков проекций):
На рис. С1б показываем
проекции равнодействующей
,
а затем и равнодействующую,
модуль которой равен:
Рис. С1б
4.2) Второй способ.
Находим R
как диагональ ромба, стороны которого
.
Для этого прежде определим косинус угла
φ между векторамии
:
Равнодействующую
найдем по формуле:
-
На рисунке
показываем вектор
(учитывая, что по условию задачи
).
Начало этого вектора необходимо отложить
из конца вектора,
а конец векторасовмещаем с концом вектора
(рис. С1б).
Модуль силы
находим по теореме косинусов:
Ответ:
Примечание: При
необходимости направляющие косинусы
углов наклона α и β равнодействующей
и силы
к оси абсцисс находим следующим образом:
Зная
угол α = 66°38/.
и
Угол β = 17°50/.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #