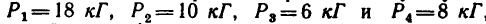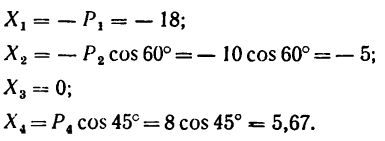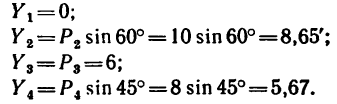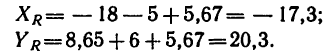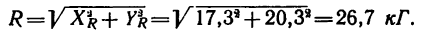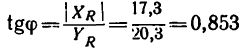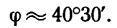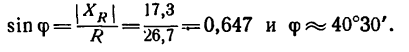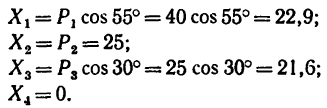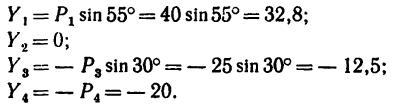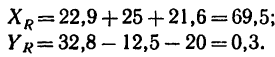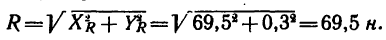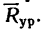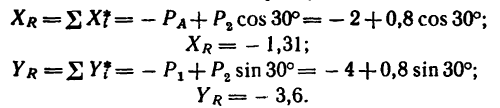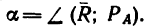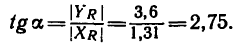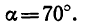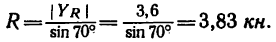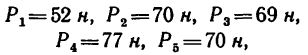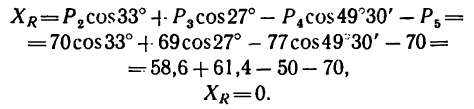Как найти равнодействующую всех сил под углом

Перейти к контенту

2010-03-23 20:42

Решение задачи о сложении нескольких сил, направленных под углом друг к другу, начнем со случая, когда на тело действуют только две силы, не лежащие на одной прямой. В этом случае, как показывает опыт, равновесие тела невозможно; значит, равнодействующая таких сил не может равняться нулю. Например, на тело, подвешенное на нити, действует вертикально сила тяжести, и если нить (а значит, и сила натяжения нити) расположена наклонно к вертикали, то тело не остается в покое. На этом основано устройство отвеса.

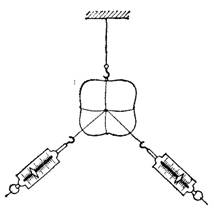
Рис. 64. Если динамометры растянуты, то равновесие груза при вертикальном положении нити невозможно

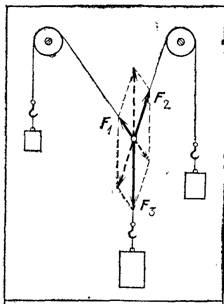
Рис. 65. Условия равновесия трех сил, действующих под углом друг к другу

Другой пример: к телу, подвешенному на нити, прикрепим два динамометра, расположенных горизонтально под углом друг к другу (рис. 64). Легко проверить на опыте, что и в этом случае тело не останется в покое и нить не будет вертикальной ни при каком растяжении динамометров.

Найдем равнодействующую двух сил, направленных под углом друг к другу. Так как равнодействующая равна по модулю и противоположна по направлению уравновешивающей силе (§ 39), то для решения задачи достаточно найти условия равновесия тела под действием трех сил (двух данных и третьей уравновешивающей). Для нахождения этих условий поставим опыт, в котором модули и направления всех сил легко определить. Свяжем три нити, привяжем к ним разные грузы и перекинем две из нитей через блоки (рис. 65). Если масса каждого из грузов меньше суммы масс двух других, то узел займет некоторое положение и будет оставаться в покое; значит, это положение будет положением равновесия. При этом все нити расположатся в одной вертикальной плоскости. На узел действуют силы,  и, равные по модулю силам тяжести, действующим на грузы, и направленные вдоль нитей. Каждая из этих сил уравновешивает две остальные. Изобразим силы, приложенные к узлу, отрезками, отложенными от узла, направленными вдоль нитей и равными, в выбранном масштабе, модулям сил. Оказывается, что при равновесии отрезок, изображающий любую из этих сил, совпадает с диагональю параллелограмма, построенного на отрезках, изображающих две другие силы. Эти параллелограммы показаны на рисунке штриховыми линиями. Значит, диагональ параллелограмма изображает равнодействующую двух сил, изображаемых его сторонами, причем равнодействующая направлена в сторону, противоположную третьей силе. Таким образом, силы складываются (как и перемещения) по правилу параллелограмма, т. е. по правилу векторного сложения.

Из правила параллелограмма сил следует, что модуль равнодействующей силы зависит не только от модулей слагаемых сил, но также и от угла между их направлениями. При изменении угла модель равнодействующей изменяется в пределах от суммы модулей сил (если угол равен нулю) до разности модулей большей и меньшей сил (если угол равен 180°).
В частном случае сложения двух равных по модулю сил можно, в зависимости от угла между силами, получить любое значение модуля равнодействующей в пределах от удвоенного модуля одной из сил до нуля.

Вместо правила параллелограмма можно применять правило треугольника, как мы это делали для перемещений. При сложении более чем двух сил можно либо прибавлять их векторно одну за другой, либо строить из векторов ломаную; тогда равнодействующая изобразится звеном, замыкающим ломаную. При равновесии ломаная замкнется: равнодействующая будет равна нулю. Например, ломаная из трех уравновешивающихся сил образует треугольник.

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее.

Нахождение равнодействующей силы

Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.

Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Примеры

На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.

Обозначим силы, выберем координатные оси

Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Системы и блоки*

Блок — механическое устройство, колесо, вращающееся вокруг своей оси. Блоки могут быть подвижными и неподвижными.

Неподвижный блок используется лишь для изменения направления силы.

Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.

Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.

Ускорение тела А в два раза меньше ускорения тела В.

Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии

Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.

Формула равнодействующей всех сил

Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.

Определение и формула равнодействующей всех сил

В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:

На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.

Основной закон динамики поступательного движения при наличии нескольких сил

Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач на равнодействующую сил

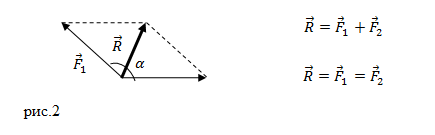
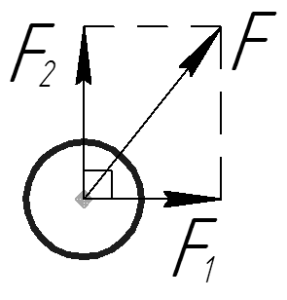
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60<>^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?

Решение. Сделаем рисунок.

Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline$ можно найти, используя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<20>^2+<10>^2+2cdot 20cdot 10<cos (60<>^circ ) >>approx 26,5 left(Нright).]

Ответ. $F=26,5$ Н

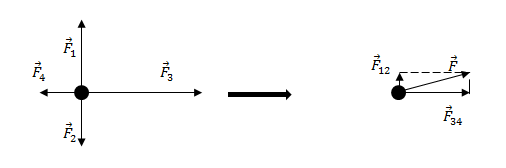
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?

Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:

Найдем равнодействующую сил $<overline>_1$ и $<overline>_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:

Так как $F_1>F_2$, то сила $<overline>_<12>$ направлена в туже сторону, что и сила $<overline>_1$.

Найдем равнодействующую сил $<overline>_3$ и $<overline>_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:

Направление силы $<overline>_<34>$ совпадает с направлением вектора $<overline>_3$, так как $<overline>_3><overline>_4$.

Равнодействующую, которая действует на материальную точку, найдем как:

Силы $<overline>_<12>$ и $<overline>_<34>$ взаимно перпендикулярны. Найдем длину вектора $overline$ по теореме Пифагора:

Законы Ньютона. Динамика.

теория по физике 🧲 динамика

Три закона Ньютона

Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.

Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.

Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.

Основное утверждение механики

Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:

Основное утверждение механики

Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.

Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).

Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.

Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.

Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.

Первый закон Ньютона

Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.

Первый закон Ньютона

Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.

Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).

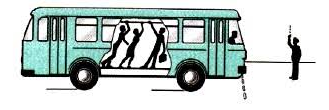
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.

Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.

Второй закон Ньютона

В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.

Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.

Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).

Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.

Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.

Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.

Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.

Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.

Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.

Второй закон Ньютона

Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.

где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела

Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.

Сила — векторная физическая величина. Обозначается F . Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.

Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с 2 . Масса яблока равна 200 г.

Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:

F = ma = 0,2 ∙ 9,8 = 1,96 (Н)

Равнодействующая сила

Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.

Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.

В этом случае второй закон Ньютона формулируется так:

Второй закон Ньютона через равнодействующие силы

Если на тело действует несколько сил, но их равнодействующая R будет равна произведению массы на ускорение этого тела.

Правила сложения сил и их проекций

Сложение двух сил, направленных вдоль одной прямой в одну сторону

Определение равнодействующей сходящихся сил:

Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом  либо методом проекций.

Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.

Задача №1

Определить равнодействующую четырех сил:

Решение — методом проекций.

1.    Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами (рис. 42, а).

2.    Находим проекции данных сил на ось х:

3.    Находим проекции данных сил на ось у:

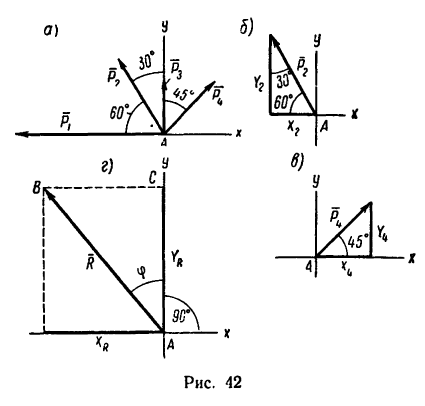
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы и на рис. 42, в для силы . Эти рисунки облегчают правильное определение проекций.

Для сил такие рисунки не нужны, так как сила лежит на оси х и, следовательно, проектируется на эту ось в натуральную величину, но зато на ось у проекция этой силы равна нулю. Сила проектируется в натуральную величину на ось у, а ее проекция на ось х равна нулю.

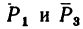
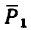
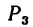
4.    Находим проекции искомой равнодействующей 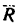на оси хну:

Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор 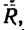заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х — влево. Положение равнодействующей R показано отдельно на рис. 42, г.

5.    Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):

6.    Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):

и, следовательно,

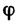
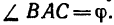
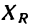
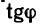
Для определения угла использован АВС (см. рис. 42, г), в котором Поэтому не имеет значения и в выражение подставлена его абсолютная величина.

Угол 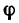можно найти при помощи синуса:

Для определения угла 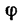можно воспользоваться и косинусом, но при работе с логарифмической счетной линейкой эта функция менее удобна.

Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом 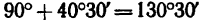к положительному направлению оси х.

Задача №2

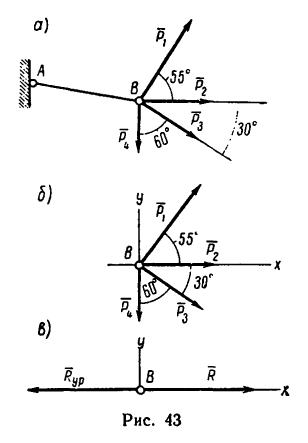
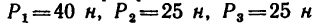
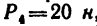
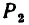
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: , направленные, как показано на рис. 43, а (сила горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.

Решение — методом проекций.

1.    Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.

2.    Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами

3.    Найдем проекции заданных сил на ось х:

4.    Найдем проекции заданных сил на ось у:

5.    Найдем проекции равнодействующей R на оси х и у:

6.    Найдем модуль равнодействующей:

Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.

Таким образом, четыре заданные силы натягивают веревку равнодействующей силой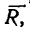 приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.

Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.

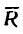
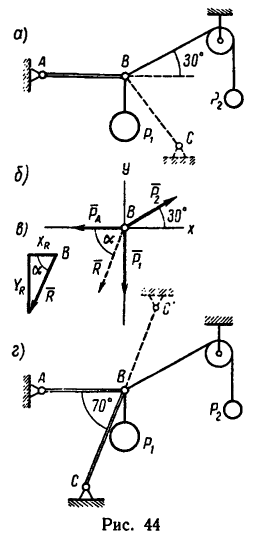
На  рис. 43, в показаны равнодействующая и уравновешивающая

Задача №3

На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами 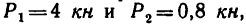, как показано на рис. 44, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой 2 кн? Какое усилие при этом будет испытывать стержень ВС?

Соединения стержней между собой и с опорами шарнирные.

Решение — методом проекций.

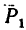
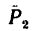
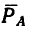
1.    На точку В действуют три силы: — вертикально вниз, — вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 44,6 и найдем их равнодействующую, вдоль направления действия которой необходимо установить стержень ВС.

2.    Оси проекций совместим с силами 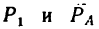и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:

3.    Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым 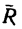на рис. 44,6, и положение стержня ВС определится углом

4.    Определим значение угла а из треугольника, образуемого 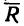и его проекциями (рис. 44,в):

Этому значению соответствует угол
5.    Стержень ВС необходимо установить под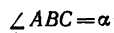= 70° к стержню АВ., и тогда он будет сжиматься силой, равной

Описанное положение стержня показано на рис. 44, г.

Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.

Задача №4

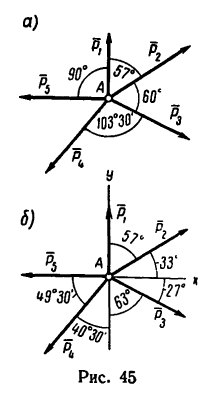
Определить равнодействующую пяти сил:

действующих на точку А, как показано на рис. 45,а.

Решение — методом проекций.

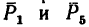
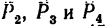
1.    Так как силы направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы будут образовывать с осями проекций углы, показанные на рис. 45.б

2. Найдем проекцию равнодействующей на ось х:

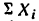
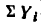
* Здесь — обозначена алгебраическая сумма проекций всех сил на ось х, а — алгебраическая сумма проекций тех же сил на ось у.

3. Найдем проекцию равнодействующей на ось у:

4.    Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.

Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.