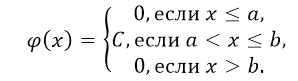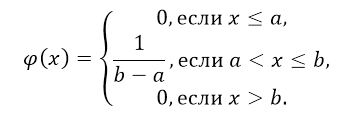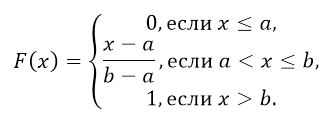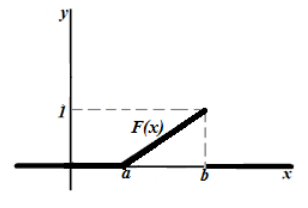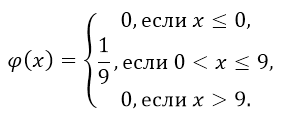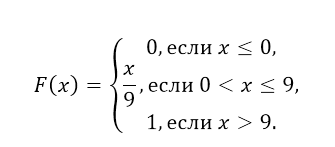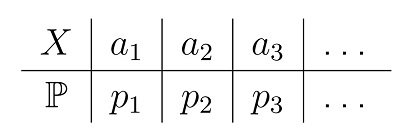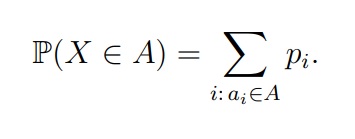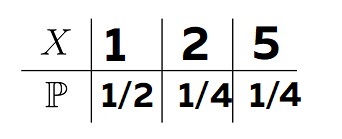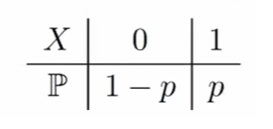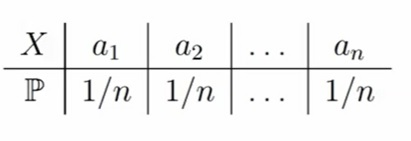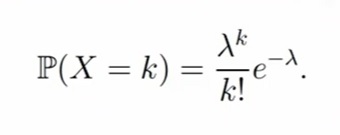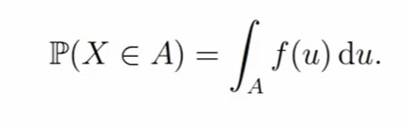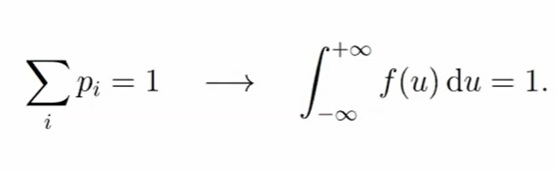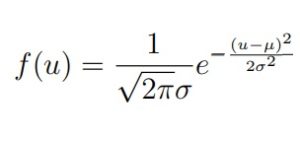Равномерное случайное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
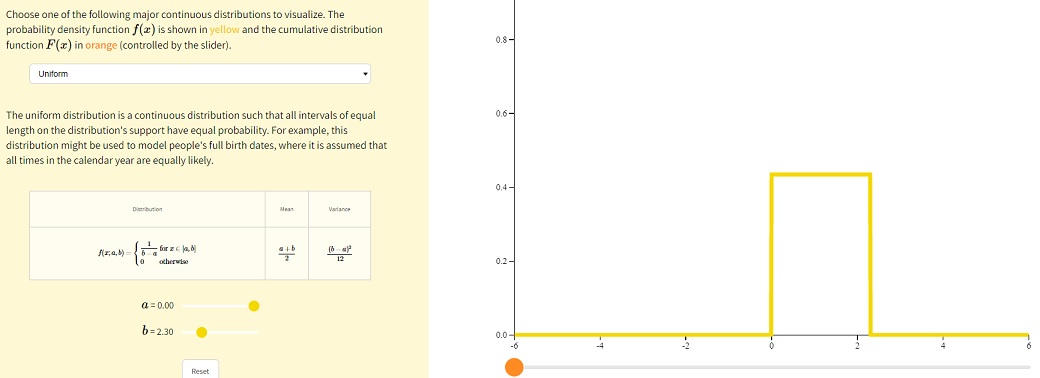
Равномерным называют распределение вероятностей непрерывной случайной величины
, если на интервале
, которому принадлежат все возможные
значения
, плотность сохраняет постоянное значение.
Функция распределения
равномерного закона:
Числовые характеристики равномерного распределения
Математическое ожидание равномерно распределенной случайной величины:
Дисперсия
равномерного случайного
распределения:
Среднее квадратическое отклонение случайной величины, распределенной равномерно:
Для равномерного распределения коэффициент асимметрии:
Коэффициент эксцесса
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Кроме равномерного, основные законы распределения непрерывных случайных величин:
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Экспоненциальный (показательный) закон распределения случайной величины
Примеры решения задач
Пример 1
Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность вероятности
равномерного распределения на интервале
:
Искомая вероятность:
Ответ:
.
Пример 2
Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).
Решение
Плотность
вероятности случайной величины, распределенной равномерно на интервале
В нашем
случае
Получаем:
Функцию
распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
Построим
графики:
График плотности распределения
График функции распределения
Математическое
ожидание величины, распределенной равномерно:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
равномерного распределения:
Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:
Ответ:
Пример 4
Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.
Решение
Дисперсия
равномерного распределения:
при
начале интервала
:
Искомый
интервал времени:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Случайные
величины X2, X3, X4 имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<Xi<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.
Задача 2
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, xmod, xmed, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.
Задача 3
Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].
Найти:
1) дифференциальную и интегральную
функцию распределения, а также построить их графики.
2) математическое ожидание и
дисперсию;
2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).
Задача 5
Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.
Задача 6
Равномерно распределенная случайная
величина
задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).
Задача 7
Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x0.2.
Задача 8
Случайная
величина
равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).
Задача 9
Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].
Задача 10
Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?
Задача 11
Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].
Задача 12
Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.
Задача 13
СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.
Задача 15
Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.
Задача 16
Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].
Задача 17
Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).
Задача 18
По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.
Задача 19
Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.
Задача 20
Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Равномерное распределение
Перейдем теперь
к часто используемым на практике
распределениям непрерывной случайной
величины.
Непрерывная с.в.
Х
называется равномерно
распределенной
на отрезке [a,b],
если плотность ее вероятности постоянна
на этом отрезке, а вне его равна 0 (т.е.
случайная величина Х
сосредоточена на отрезке [a,b],
на котором имеет постоянную плотность).
По данному определению плотность
равномерно распределенной на отрезке
[a,b]
случайной величины Х
имеет вид:
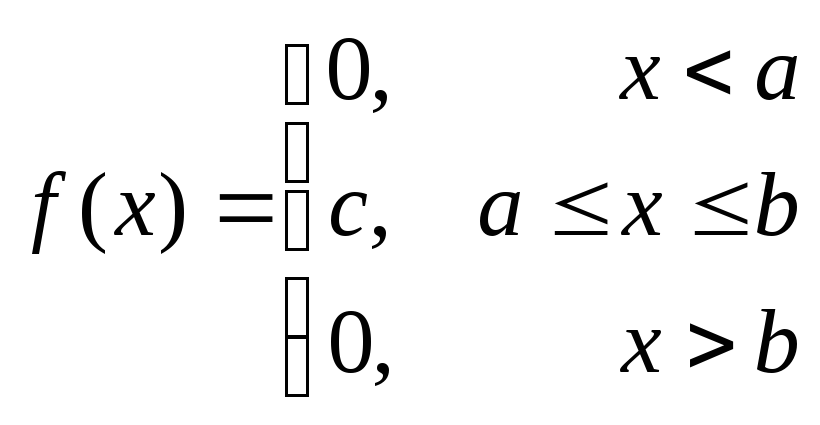
где с
есть некоторое число. Впрочем, его легко
найти, используя свойство плотности
вероятности для с.в., сосредоточенных
на отрезке
[a,b]:
.
Отсюда следует, что,
откуда.
Поэтомуплотность
равномерно распределенной на отрезке
[a,b]
случайной величины Х
имеет вид:

Судить о равномерности
распределения н.с.в. Х
можно из следующего соображения.
Непрерывная случайная величина имеет
равномерное распределение на отрезке
[a,b],
если она принимает значения только из
этого отрезка, и любое число из этого
отрезка не имеет преимущества перед
другими числами этого отрезка в смысле
возможности быть значением этой случайной
величины.
К случайным
величинам, имеющим равномерное
распределение относятся такие величины,
как время ожидания транспорта на
остановке (при постоянном интервале
движения длительность ожидания равномерно
распределена на этом интервале), ошибка
округления числа до целого (равномерно
распределена на [−0.5,
0.5]) и другие.
Вид функции
распределения F(x)
равномерно распределенной отрезке
[a,b]
случайной величины Х
ищется по известной плотности вероятности
f(x)
c
помощью формулы их связи
.
В результате соответствующих вычислений
получаем следующую формулу для функции
распределенияF(x)
равномерно распределенной отрезке
[a,b]
случайной величины Х
:

На рисунках
приведены графики плотности вероятности
f(x)
и функции распределения f(x)
равномерно
распределенной отрезке [a,b]
случайной величины Х
:
Математическое
ожидание, дисперсия, среднее квадратическое
отклонение, мода и медиана равномерно
распределенной отрезке [a,b]
случайной величины Х
вычисляются по плотности вероятности
f(x)
обычным образом (и достаточно просто
из-за простого вида f(x)).
В результате получаются следующие
формулы:
,
а модой d(X)
является любое число отрезка [a,b].
Найдем вероятность
попадания равномерно распределенной
отрезке [a,b]
случайной величины Х
в интервал
,
полностью лежащий внутри [a,b].
Учитывая известный вид функции
распределения, получаем:
.
Таким образом,
вероятность попадания равномерно
распределенной отрезке [a,b]
случайной величины Х
в интервал
,
полностью лежащий внутри [a,b],
не зависит от положения этого интервала,
а зависит только от его длины и прямо
пропорциональна этой длине.
Пример.
Интервал движения автобуса составляет
10 минут. Какова вероятность того, что
пассажир, подошедший к остановке, прождет
автобус менее 3 минут? Каково среднее
время ожидания автобуса?
Нормальное распределение
Это распределение
наиболее часто встречается на практике
и играет исключительную роль в теории
вероятностей и математической статистике
и их приложениях, поскольку такое
распределение имеют очень многие
случайные величины в естествознании,
экономике, психологии, социологии,
военных науках и так далее. Данное
распределение является предельным
законом, к которому приближаются (при
определенных естественных условиях)
многие другие законы распределения. С
помощью нормального закона распределения
описываются также явления, подверженные
действию многих независимых случайных
факторов любой природы и любого закона
их распределения. Перейдем к определениям.
Непрерывная
случайная величина называется
распределенной по нормальному
закону (или закону Гаусса),
если ее плотность вероятности имеет
вид:

где числа а
и σ
(σ>0)
являются параметрами этого распределения.
Как уже было
сказано, закон Гаусса распределения
случайных величин имеет многочисленные
приложения. По этому закону распределены
ошибки измерений приборами, отклонение
от центра мишени при стрельбе, размеры
изготовленных деталей, вес и рост людей,
годовое количество осадков, количество
новорожденных и многое другое.
Приведенная
формула плотности вероятности нормально
распределенной случайной величины
содержит, как было сказано, два параметра
а
и σ
, а потому задает семейство функций,
меняющихся в зависимости от значений
этих параметров. Если применить обычные
методы математического анализа
исследования функций и построения
графиков к плотности вероятности
нормального распределения, то можно
сделать следующие выводы.
-
Плотность
вероятности f(x)>0
для всех значений х,
а потому график функции расположен над
осью х. -
Ось х
является асимптотой графика при х
→ ± ∞,
поскольку
.
Поэтому на бесконечности график
«прижимается» к осих. -
Функция f(х)
имеет единственную точку максимума
х=а,
а максимальное значение
.
-
График функции
симметричен относительно вертикальной
прямой с уравнением х=а. -
С помощью второй
производной можно убедиться, что точки
графика
являются точками
его перегиба.
Исходя из полученной
информации, строим график плотности
вероятности f(x)
нормального распределения (он называется
кривой Гаусса − рисунок).
Выясним, как влияет
изменение параметров а
и σ
на форму кривой Гаусса. Очевидно (это
видно из формулы для плотности нормального
распределения), что изменение параметра
а
не меняет форму кривой, а приводит лишь
к ее сдвигу вправо или влево вдоль оси
х.
Зависимость от σ
сложнее. Из проведенного выше исследования
видно, как зависит величина максимуму
и координаты точек перегиба от параметра
σ
. К тому же надо учесть, что при любых
параметрах а
и σ
площадь под кривой Гаусса остается
равной 1 (это общее свойство плотности
вероятности). Из сказанного следует,
что с ростом параметра σ
кривая становится более пологой и
вытягивается вдоль оси х.
На рисунке изображены кривые Гаусса
при различных значениях параметра σ
( σ1<
σ< σ2
) и одном и
том же значении параметра а.
Выясним вероятностный
смысл параметров а
и σ
нормального распределения. Уже из
симметричности кривой Гаусса относительно
вертикальной прямой, проходящей через
число а
на оси х
понятно, что среднее значение (т.е.
математическое ожидание М(Х))
нормально распределенной случайной
величины равно а.
Из этих же соображений мода и медиана
тоже должны быть равны числу а. Точные
расчеты по соответствующим формулам
это подтверждают. Если же мы выписанное
выше выражение для f(x)
подставим в формулу для дисперсии
,
то после (достаточно непростого)
вычисления интеграла получим в ответе
числоσ2.
Таким образом, для случайной величины
Х,
распределенной по нормальному закону,
получились следующие основные ее
числовые характеристики:
.
Поэтому вероятностный
смысл параметров нормального распределения
а
и σ
следующий. Если с.в. Х
распределена нормально с параметрами
а
и σ,
то ее среднее значение равно а,
а среднее квадратическое отклонение
равно σ.
Найдем теперь
функцию распределения F(x)
для случайной величины Х,
распределенной по нормальному закону,
используя выписанное выше выражение
для плотности вероятности f(x)
и формулу
.
При подстановкеf(x)
получается «неберущийся» интеграл.
Все, что удается сделать для упрощения
выражения для F(x),
это представление этой функции в виде:
,
где Ф(х)
− так называемая функция
Лапласа,
которая имеет вид

Интеграл, через
который выражается функция Лапласа,
тоже является неберущимися (но при
каждом х
этот интеграл может быть вычислен
приближенно с любой наперед заданной
точностью). Однако вычислять его и не
потребуется, так как в конце любого
учебника по теории вероятностей есть
таблица для определения значений функции
Ф(х)
при заданном значении х.
В дальнейшем нам понадобится свойство
нечетности функции Лапласа: Ф(−х)=
−Ф(х)
для всех
чисел х.
Найдем теперь
вероятность того, что нормально
распределенная с.в. Х
примет значение из заданного числового
интервала (α,
β). Из общих
свойств функции распределения Р(α<X<
β)=F(β)
−
F(α).
Подставляя α
и
β в выписанное
выше выражение для F(x),
получим
.
Как сказано выше,
если с.в. Х
распределена нормально с параметрами
а
и σ,
то ее среднее значение равно а,
а среднее квадратическое отклонение
равно σ.
Поэтому среднее
отклонение значений этой с.в. при
испытании от числа а
равно σ. Но
это среднее отклонение. Поэтому возможны
и бо´льшие отклонения. Узнаем, насколько
возможны те или иные отклонения от
среднего значения. Найдем вероятность
того, что значение распределенной по
нормальному закону случайной величины
Х
отклониться от ее среднего значения
М(Х)=а
менее, чем на некоторое число δ, т.е.
Р(|X−a|<δ
) :
.
Таким образом,
.
Подставляя в это
равенство δ=3σ,
получим вероятность того, что значение
с.в. Х
(при одном испытании) отклонится от
среднего значения менее чем на утроенное
значение σ
(при среднем отклонении, как мы помним,
равном σ):
(значениеФ(3)
взято из таблицы значений функции
Лапласа). Это почти 1
! Тогда
вероятность противоположного события
(что значение отклонится не менее, чем
на 3σ)
равна 1−0.997=0.003,
что очень близко к 0.
Поэтому это событие «почти невозможно»
−
случается крайне редко (в среднем 3
раза из 1000).
Это рассуждение является обоснованием
широко известного «правила трех сигм».
Правило трех
сигм. Нормально
распределенная случайная величина при
единичном испытании
практически не отклоняется от своего
среднего далее, чем на 3σ.
Еще раз подчеркнем,
что речь идет об одном испытании . Если
испытаний случайной величины много, то
вполне возможно, что какое-либо ее
значение и удалится от среднего далее,
чем 3σ.
Это подтверждает следующий
Пример.
Какова вероятность, что при 100 испытаниях
нормально распределенной случайной
величины Х
хотя бы одно ее значение отклонится от
среднего более, чем на утроенное среднее
квадратическое отклонение? А при 1000
испытаниях?
Решение. Пусть
событие А
означает, что при испытании случайной
величины Х
ее значение отклонилось от среднего
более, чем на 3σ.
Как только
что было выяснено, вероятность этого
события
р=Р(А)=0.003 . Проведено
100 таких испытаний. Надо узнать вероятность
того, что событие А
произошло хотя
бы раз, т.е.
произошло от 1
до 100
раз. Это типичная задача схемы Бернулли
с параметрами n=100
(число независимых испытаний), р=0.003
(вероятность события А
в одном испытании), q=1−p=0.997.
Требуется найти Р100(1≤k≤100).
В данном случае, конечно, проще найти
сначала вероятность противоположного
события Р100(0)
− вероятность того, что событие А
не произошло ни разу ( т.е. произошло 0
раз) . Учитывая связь вероятностей самого
события и ему противоположного, получим:
.
Не так уж мало.
Вполне может произойти (происходит в
среднем в каждой четвертой такой серии
испытаний). При 1000
испытаний по такой же схеме можно
получить, что вероятность хотя бы одного
отклонения далее, чем на 3σ,
равно:
. Так что можно с большой уверенностью
дождаться хотя бы одного такого
отклонения.
Пример.
Рост
мужчин определенной возрастной группы
распределен нормально с математическим
ожиданием a,
и среднеквадратическим отклонением σ.
Какую долю костюмов k-го
роста следует предусмотреть в общем
объеме производства для данной возрастной
группы, если k-ый
рост определяется следующими пределами:
1
рост:
158 −
164см
2 рост:
164 − 170см
3 рост:
170 − 176см
4 рост:
176 − 182см
Решение.
Решим задачу при следующих значениях
параметров: а=178,
σ=6, k=3.
Пусть
с.в. Х
−
рост случайно выбранного мужчины (она
распределена по условию нормально с
заданными параметрами). Найдем вероятность
того, что наугад выбранному мужчине
понадобится 3-й
рост. Пользуясь нечетностью функции
Лапласа Ф(х)
и таблицей ее значений:
P(170<X<176)
=Ф((176−178)/6) − Ф((170−178)/6) = Ф(−0.3333)
−Ф(−1.3333)=
Ф(1.3333) −Ф(0.3333)=0.4082−0.1293=0.2789.
Поэтому в общем объеме производства
надо предусмотреть 0.2789*100%=27.89%
костюмов 3-го
роста.
Содержание:
- Примеры с решением
- Задачи с решением
Распределение вероятностей случайной величины 

С равномерным распределением встречаются всякий раз, когда по условиям опыта величина 

Вот примеры такого рода:
1) 



2) 

Двумерная случайная величина 

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1.
Найти значение 
Решение:
Поскольку для плотности распределения 
Следовательно, формула (3.4.1) принимает вид
Пример 2.
Случайная величина 



Решение:
Пользуясь формулой (2.3.3), находим 





Замечание 1.
Выражение «выберем наудачу точку
на отрезке
» означает, что координата точки
представляет случайную величину с равномерным распределением вероятностей на этом отрезке.
Возможно вам будут полезны данные страницы:
Пример 3.
Найти значение 


Решение:
Вероятность попадания точки 




Поскольку попадание в область 
откуда 
Сравнивая эту формулу с формулой (1.5.1), заключаем, что получено геометрическое определение вероятности.
Замечание 2. Двумерная случайная величина 


Пример 4.
Найти функцию распределения 

Решение:
Принимая во внимание формулу (2.3.2) и формулу (3.4.3) получаем: при
при
при



Пример 5.
Найти математическое ожидание случайной величины 

Решение:
Пользуясь формулой (2.4.8) и принимая во внимание формулу (3.4.3), находим
Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке, есть середина этого отрезка.
Пример 6.
Найти дисперсию случайной величины 

Решение:
Пользуясь формулой (2.5.15) и принимая во внимание формулы (3.4.3) и (3.4.7), находим







где 



Термин «равномерно распределенный» здесь ключевой; как показывает приведенная ниже задача 2.1.2, нужно тщательно разобраться, что это в точности значит в контексте данного примера.
Полезное наблюдение состоит в том, что можно работать с плотностью равномерного распределения, которая приписывает точке 
а тогда вероятность события 
и мы приходим к тому же ответу, что и в формуле (2.1.1). Поскольку 


Заметим, что масса, приписываемая единичному исходу 


Задача 2.1.1.
Алиса и Боб условились встретиться в «Медном чайнике» после своих субботних лекций. Каждый из них появляется там в некий момент времени независимо друг от друга, и это время равномерно распределено между 12 и 13 часами. Каждый ожидает другого в течение 

Решение:
Множество 






Дополнение этого множества состоит из двух треугольников площадью 
Поэтому площадь 
и мы хотим, чтобы эта вероятность была не меньше 1/2. Отсюда получаем
Задача 2.1.2.
Следующая задача известна как парадокс Бертрана. На круге радиуса 
а) середина хорды равномерно распределена внутри круга,
б) один конец хорды фиксирован, а второй равномерно распределен по окружности,
в) расстояние между серединой хорды и центром круга равномерно распределено на отрезке 
Решение:
В случае а) середина хорды должна находиться внутри круга, вписанного в треугольник. Поэтому
В случае б) второй конец окружности должен находиться на противоположной трети окружности. Поэтому
Наконец, в случае в) середина хорды должна находиться на расстоянии не больше 
Лекции:
- Признак Даламбера: пример решения
- Производящие функции
- Сложение и вычитание пределов
- Логарифмические неравенства
- Ломаная
- Элементы векторной алгебры
- Асимптоты графика функции
- Разложение в ряд маклорена
- Частные производные второго порядка
- Тройной интеграл
Равномерное распределение вероятностей
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Напомним определение плотности вероятности.
Введем теперь понятие равномерного распределения вероятностей:
Определение 2
Распределение называется равномерным, если на интервале, содержащем все возможные значения случайной величины, плотность распределения постоянна, то есть:
Рисунок 1.
Найдем значение константы $ C$, используя следующее свойство плотности распределения: $intlimits^{+infty }_{-infty }{varphi left(xright)dx}=1$
Получим:
[intlimits^{+infty }_{-infty }{varphi left(xright)dx}=intlimits^a_{-infty }{0dx}+intlimits^b_a{Cdx}+intlimits^{+infty }_b{0dx}=0+Cb-Ca+0=C(b-a)] [Cleft(b-aright)=1] [C=frac{1}{b-a}]
Таким образом, функция плотности равномерного распределения имеет вид:
Рисунок 2.
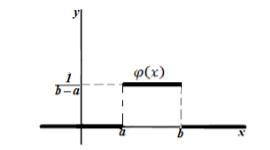
График имеет следующий вид (рис. 1):
Рисунок 3. Плотность равномерного распределения вероятности
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
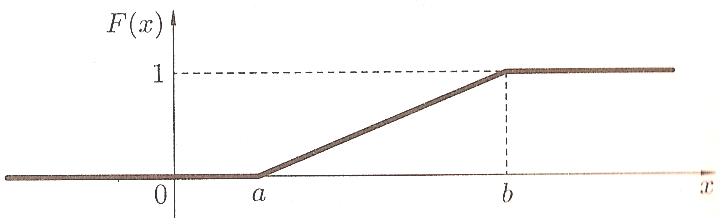
Функция равномерного распределения вероятностей
Найдем теперь функцию распределения при равномерном распределении.
Для этого будем использовать следующую формулу: $Fleft(xright)=intlimits^x_{-infty }{varphi (x)dx}$
- При $x ≤ a$, по формуле, получим:
- При $a
- При $x> 2$, по формуле, получим:
Таким образом, функция распределения имеет вид:
Рисунок 4.
График имеет следующий вид (рис. 2):
Рисунок 5. Функция равномерного распределения вероятности.
«Равномерное распределение вероятностей» 👇
Вероятность попадания случайной величины в интервал $({mathbf alpha },{mathbf beta })$ при равномерном распределении вероятностей
Для нахождения вероятности попадания случайной величины в интервал $(alpha ,beta )$ при равномерном распределении вероятностей будем пользоваться следующей формулой:
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение:
Примеры решения задачи на равномерное распределение вероятностей
Пример 1
Интервал движения между троллейбусами составляет 9 минут.
-
Составить функцию распределения и плотность распределения случайной величины $X$ ожидания пассажирами троллейбуса.
-
Найти вероятность того, что пассажир дождется троллейбус меньше чем через три минуты.
-
Найти вероятность того, что пассажир дождется троллейбус не менее чем через 4 минуты.
-
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение
Решение.
- Так как непрерывная случайная величина ожидания троллейбуса $X$ равномерно распределена, то $a=0, b=9$.
Таким образом, плотность распределения, по формуле функции плотности равномерного распределения вероятности, имеет вид:
Рисунок 6.
По формуле функции равномерного распределения вероятности, нашем случае функция распределения имеет вид:
Рисунок 7.
- Данный вопрос можно переформулировать следующим образом: найдем вероятность попадания случайной величины равномерного распределения в интервал $left(6,9right).$
Получаем:
[Pleft(6
Получаем: $Pleft(0
- Математическое ожидание: $Mleft(Xright)=frac{a+b}{2}=frac{9}{2}=4,5$.
Дисперсия: $Dleft(Xright)=frac{{(b-a)}^2}{12}=frac{81}{12}=frac{27}{4}$.
Среднее квадратическое отклонение: $sigma left(Xright)=frac{b-a}{2sqrt{3}}=frac{9}{2sqrt{3}}=frac{3sqrt{3}}{2}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 20.02.2023
Теория вероятностей изучает закономерности, возникающие в случайных
экспериментах (точнее, в их математических моделях). Случайные эксперименты в теории вероятностей моделируются с помощью объекта «случайная величина«. Это вообще центральный объект в теории вероятности. И это немного сложнее, чем подбрасывание монетки. Орёл или решка?
Случайные величины
Случайная величина — это функция, которая каждому возможному исходу в эксперименте ставит в соответствие действительное число. Можно понимать случайную величину как «кодирование» исходов эксперимента. Иными словами, с помощью случайной величины мы моделируем случайный эксперимент, ведь логично, что в теории вероятностей мы изучаем вероятность наступления какого-либо события
Нас будет интересовать множество значений случайной величины и с какими вероятностями она принимает возможные значения, т.е. мы будем говорить о вероятности событий, которые связаны со случайными величинами. Например, если X — случайная величина (будем обозначать большими латинскими буквами), то нас могут интересовать вероятности событий.
Как записывается событие
- {X = a} для некоторого a ∈ R — (в фигурных скобках записано, что случайная величина принимает какое-то значение), a — любое произвольное действительное число, ∈ — принадлежит, R — множество действительных чисел (дробные, иррациональные в т.ч.)
- {X < a} для некоторого a ∈ R
- {a ≤ X < b} для некоторых a, b ∈ R, a < b (из промежутка для каких-то чисел a и b)
В самом общем виде любое событие можно записать так: {X ∈ A} для некоторого подмножества A ⊂ R
Классификация случайных величин
Можно (нужно!) классифицировать случайные величины по мощности их множества значений
Дискретные случайные величины имеют конечное или счетное
множество значений. Примеры: {1, . . . , n}, N, Z. Это в случае, если бесконечность счетная, т.е. мы можем пересчитать элементы этой бесконечности. Это счетное множество. Например, N — все натуральные числа (от 1 до бесконечности). Z — все целые числа и так далее
Непрерывные случайные величины имеют несчетное множество
значений. Примеры: [0, 1], R. Это бесконечность на стероидах, т.е. еще «большая» бесконечность, чем обычная бесконечность, т.к. мы не можем пересчитать её элементы. Например, любой отрезок, скажем от 0 до 1, т.к. в нём присутствуют иррациональные числа (дроби, корни), которых очень много. И процесса пересчёта не существует — их будет бесконечно много
Дискретные случайные величины
Исходы дискретной случайной величины мы можем посчитать — мы можем приписать вероятности всем возможным значениям случайной величины. На примере монетки: значение ноль (решка) принимается с вероятностью 1/2, соответственно значение единица (орёл) принимается так же с вероятностью 1/2.
Чтобы задать распределение дискретной случайной величины, необходимо всем возможным значениям этой случайной величины приписать вероятности. Например:
- Перечислить возможные значения a1, a2, a3, . . .;
- Задать действительные числа p1, p2, p3 при условии
1) Вероятности не могут быть отрицательными (неотрицательность)
pi ≥ 0
2) Сумма всех значений вероятностей должна быть равна единице (нормировка)
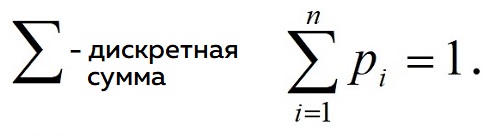
Это удобно делать с помощью таблицы распределения вероятностей X, где X — возможные значения случайной величины, P — вероятность каждого значения
Если задано распределение дискретной величины, то вероятность любых событий можно посчитать по формуле:
Читается это так: чтобы просчитать вероятность (P) любого произвольного события (X∈ A), нужно взять исходы, которые входят в множество А (ai ∈ A) и для этих индексов (i) просуммировать соответствующие вероятности Pi. Звучит не очень, но на практике это куда проще.
Например, у нас есть некоторая величина X, которая принимает значения 1, 2, 5 с вероятностью 1/2, 1/4 и 1/4
Соответственно, вероятность, что X=1 у нас будет 1/2
P(X=0) = 1/2
А вероятность, что X=10 будет 0
P(X=10) = 0
Если мы напишем в условиях x<5, то результат будет 3/4, т.к. под такое условие у нас попадает два значения
P(X<5) = 0 = 1/2 + 1/4 = 3/4
Примеры дискретных распределений
Константа. Да, это тоже случайная величина в теории вероятностей. Случайная величина X называется константой, если она принимает лишь одно значение c ∈ R с вероятностью 1
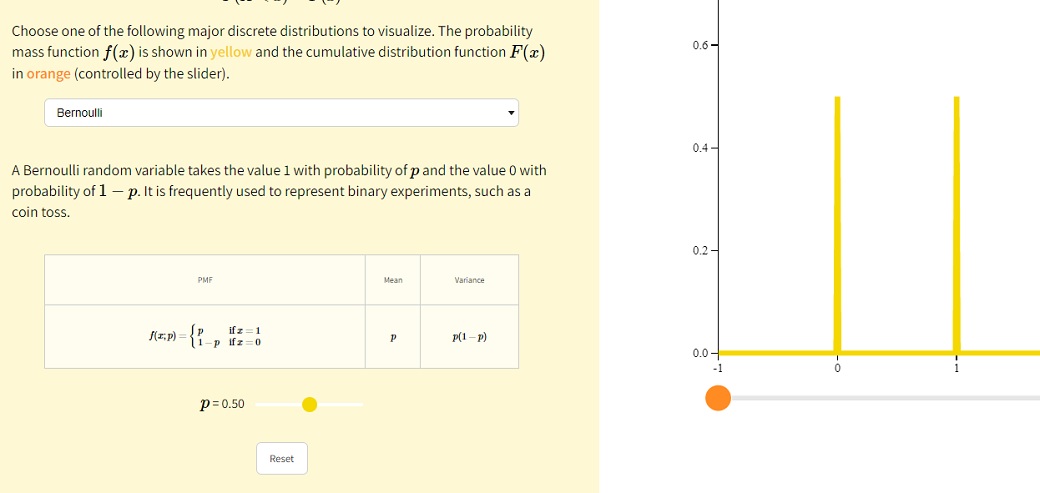
Распределение Бернулли, p ∈ [0, 1]
Самое простое распределение. То самое подбрасывание монетки, где у нас есть всего два исхода (то, что монетка может упасть ребром, мы не рассматриваем). Обозначается Ber(p). Имеет параметр p ∈ [0, 1], где p — вероятность успеха.
Случайная величина X имеет распределение Бернулли с параметром p ∈ [0, 1], если X принимает значение 1 с вероятностью p и значение 0 с вероятностью 1 − p. Параметр p называется вероятностью успеха
Таблица распределения:
Пишется как: X ∼ Ber(0.5) — это как раз про монетку, X ∼ Ber(1).
Примеры распределения Бернулли в реальной жизни: пол сотрудника, победа спортивной команды, бумага в общественном туалете (либо она есть, либо её нет).
Равномерное распределение на конечном множестве
Случайная величина X имеет равномерное распределение на множестве {a1, a2, . . . , an}, если X принимает каждое значение ai с вероятностью 1/n. Т.е. конечное количество исходов, где каждый из них принимается с одинаковой вероятностью. Таблица распределения имеет следующий вид:
Примеры равномерного распределения в реальной жизни: игральная кость, рулетка
Биномиальное распределение Bin(n, p), n ∈ N, p ∈ [0, 1]
Здесь у нас уже два параметра. Случайная величина Y имеет биномиальное распределение с параметрами n ∈ N и p ∈ [0, 1], если Y = X1 + X2 + . . . + Xn, где X1, X2, . . . , Xn ∼ Ber(p) независимые, т.е. сумма независимых случайных величин с равностью успеха p (с одной и той же вероятностью успеха). Фактически, Y — это количество «успехов» в n независимых испытания Бернулли, от нуля до n
Примеры биномиальное распределения в реальной жизни: количество студентов, которые сдали экзамен, количество орлов в n-бросании монеты, количество кликов по ссылке у n-посетителей сайтов, количество девочек, среди n-новорожденных.
Распределение Пуассона Pois(λ), λ > 0
Параметр лямбда (λ) — это интенсивность (число больше нуля). Чем больше значение λ, тем будет больше вероятность успеха за фиксированный временной интервал (характеризует интенсивность процесса, как часто встречаются успехи в нём)
Случайная величина X имеет распределение Пуассона с параметром λ > 0, если X принимает значения k = 0, 1, 2, . . . с вероятностями:
k! — факториал числа k (произведение всех натуральных чисел от 1 до k включительно)
Является предельным распределением для Bin(n, p) при p → 0, np → λ. Параметр p зависит от n. При n стремящемся к бесконечности (n -> ∞), р будет стремиться к нулю (p -> 0), но при этом np -> λ. Например, у нас есть игра «Морской бой»
Где n- количество ходов (снарядов), а m — количество блоков. Вероятность попасть в один блок (p) будет равна 1/m. Получается биноминальное распределение с такими параметрами можно попытаться аппроксимировать с помощью распределения Пуассона
Примеры распределения Пуассона в реальной жизни: По сути, это будет количество событий, которые произошли за какой-либо временной промежуток, например: количество звонков в call-центре за час, количество рожденных детей за год
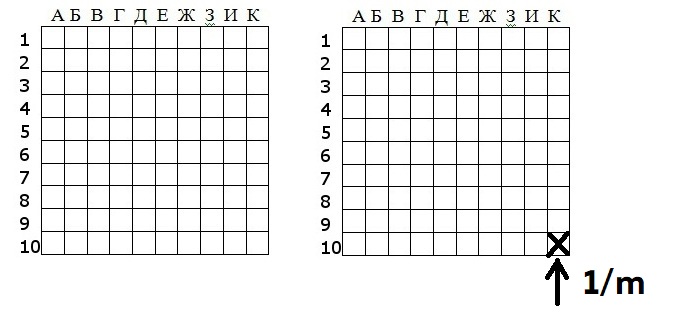
Небольшая задачка
На пустынном шоссе вероятность появления автомобиля за
30-минутный период составляет 0.95. Какова вероятность его появления
за 10 минут?
Решить её в лоб не получится, т.к.0.95 нельзя просто поделить на три — вероятность встретить автомобиль даже в случае 30 минут не равна единице, но при этом, мы можем встретить не один автомобиль, а два. Или даже три — есть множество комбинаций вероятностей.
Данная задача часто встречается на собеседованиях и интервьюеров больше интересуют ваши рассуждения о процессе решения, будете ли вы усложнять или упрощать решение.
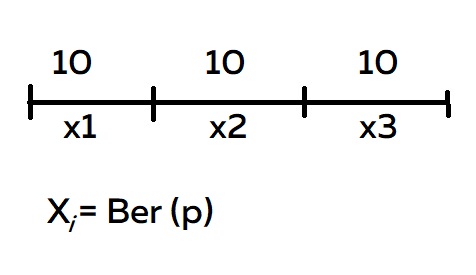
Что сюда можно прикрутить? Условия задачи отлично подходят для распределения Бернулли. Мы можем разделить отрезок 30 минут на три равных, по 10 минут. У каждого отрезка есть случайная величина. Каждая Xi — это бернуллиевская случайная величина с вероятностью наступления успеха p
Вспоминаем таблицу распределения:
Задача сводится к том, что нам нужно найти вероятность успеха р. Получается, что нашу вероятность можно записать так:
P (Xi =1 хотя бы для одного i = 1,2,3) = 0.95
Вероятность того, что мы встретим хотя бы один автомобиль равна единице. НО! Если в событие встроено условие «хотя бы один», будет правильным перейти к дополнительному событию. Здесь мы перемножаем вероятность для xi = 0, которая равняется 1-p.
1 − P(все Xi = 0 для всех i=1,2,3) или же 1- (1-p)3
Таким образом мы получаем:
1- (1-p)3 = 0.95
В итоге, чтобы посчитать вероятность события (р), нам нужно привести формулу к такому виду:
p = 1 − 3√ 1 − 0.95
Кубический корень из 0,05 ≈ 0.37, соответственно, 1 — 0,37 = 0,67
Непрерывные случайные величины
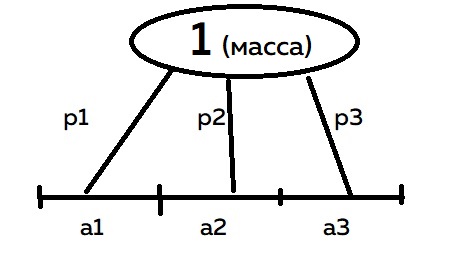
Распределение случайных величин можно представить как распределение массы по бесконечному отрезку. При дискретном распределении мы помещали точки с какой-либо частью массы (a1, a2, a3), а саму массу делили на количество этих точек (p1,p2,p3). В общем, дискретно распределили массу в точках a1, a2, a3
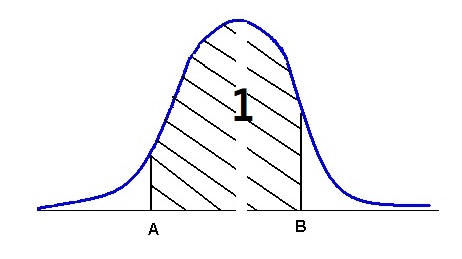
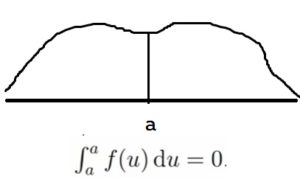
При непрерывном распределении масса будет распределяться с помощью функции плотности, которая пришла к нам из физики. Интеграл от функции плотности — это площадь под графиком. Будет это выглядеть так:
Плотность f(u) — это функция удовлетворяющая двум условиям: неотрицательность и нормировка (интеграл должен равняться единице)
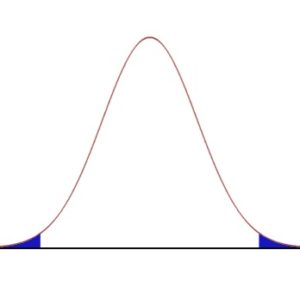
Помимо этого, функция должна затухать в конце, иначе плотность будет бесконечна, а не равна единице, хвосты должны убывать
Как считать непрерывную вероятность?
Чтобы задать распределение непрерывной случайной величины X, необходимо задать функцию плотности. Если случайная величина X имеет плотность распределения f(u), то для подмножества A ⊂ R (читается как множество A является подмножеством множества R) вероятность события {X ∈ A} считается по формуле
Существуют правила перехода от дискретного распределения к непрерывному: сумма по всем индексам дискретной суммы перетекает в интеграл, где ai равняется аргументу функции плотности (u), вероятности (pi) переходят в функцию плотности, умноженную на du. Например:
Есть нюанc: по свойствам определенного интеграла непрерывная случайная величина X с плотностью f всегда принимает наперед заданное значение a ∈ R с вероятностью 0
P(X = a) = 0
Пруф: Площадь графика от точки а до точки а будет равняться нулю, просто потому, что никакой ширины нет, то и плотности там нет никакой
Примеры непрерывных распределений
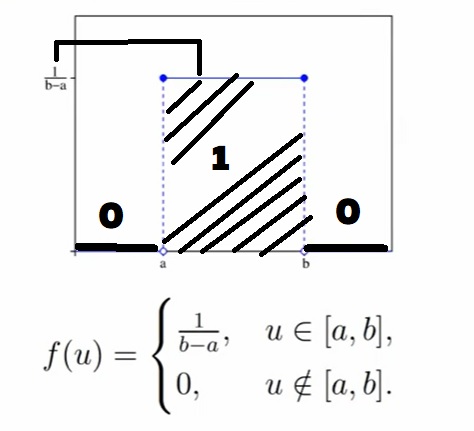
Равномерное распределение на отрезке Unif[a, b], a < b.
Равномерное распределение обозначается словом Unif (от слова uniform). По сути, это означает, что вы (по аналогии с отрезком в начале блока про непрерывные распределения) равномерно распределили массу.
Случайная величина X имеет равномерное распределение на отрезке [a, b], если её плотность f(u) имеет вид:
Примеры равномерного распределения из реальной жизни: Угол поворота стрелки в «Поле Чудес», генераторы (псевдо)случайных чисел, угол выстрела теннисной пушки
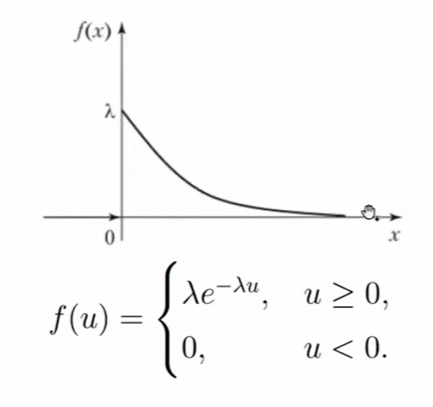
Экспоненциальное распределение Exp(λ), λ > 0
Случайная величина X имеет экспоненциальное (показательное) распределение с параметром λ > 0, если её плотность имеет вид:
До нуля у нас будет значение 0, а уже от 0 — экспоненциальное убывание. Чем больше параметр λ, тем функция плотности убывает быстрее.
Примеры экспоненциального распределения в реальной жизни: время до приезда метро, время между покупками в «Пятерочке», срок эксплуатации какой-либо техники, время работы лампочки до перегорания.
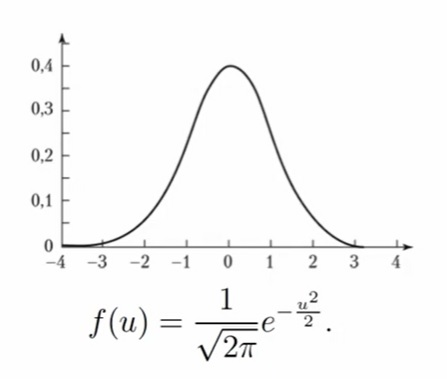
Нормальное распределение N (µ, σ2), µ ∈ R, σ > 0
Буквы в параметрах следует читать так: µ — мю, σ — сигма. Случайная величина X имеет стандартное нормальное распределение (или стандартное гауссовское), если её плотность имеет вид:
Её можно привести к такому виду:
Обозначение: X ∼ N (0, 1)
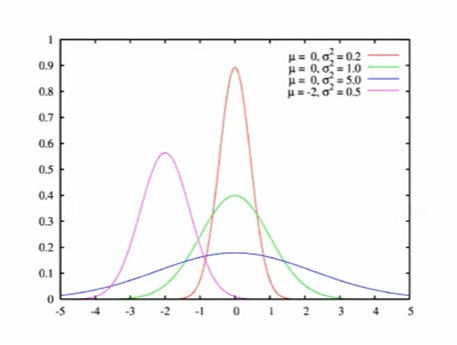
В общем случае Y имеет нормальное распределение (или гауссовское) c параметрами µ ∈ R и σ > 0, если Y = µ + σX, где X ∼ N (0, 1). Изменение параметра X растягивает, либо сжимает функцию плотности. Салатовым, по центру, мы видим стандартное нормальное распределение
Примеры нормального распределения в реальной жизни: отклонение от среднего роста призывников, отклонения от удара футболиста при пенальти (в ворота будет приходить основная часть ударов, но будут и удары мимо — там функция будет затухать)
Визуализация дискретных и непрерывных распределений
В сети есть прекрасный сайт для визуализации распределений с подстановкой параметров. С его помощью принцип распределения становится чуть более понятным — https://seeing-theory.brown.edu/
Заходим в «Probability Distributions» и выбираем «Discrete and Continuous»
Далее можно выбрать нужное распределение и подставить параметры.
Дискретное, Бернуллевское:
Равномерное, непрерывное:

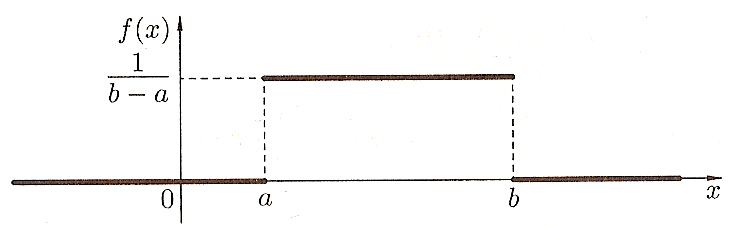







 на отрезке
на отрезке