-
Предмет и задачи
информатики. Структура современной
информатики. Понятие информации.
Информационные процессы. Непрерывная
и дискретная информация. Дискретизация.
Различные подходы к измерению количества
информации. Формулы Хартли и Шеннона.
Информатика –
наука, изучающая закономерности
получения, хранения, передачи и обработки
информации в природе и человеческом
обществе.
Предмет информатики
составляют следующие понятия:
-
аппаратное обеспечение
средств вычислительной техники; -
программное
обеспечение средств вычислительной
техники; -
средства взаимодействия
аппаратного и программного обеспечения.
Основной задачей
информатики является систематизация
приёмов и методов работы с аппаратными
программными средствами вычислительной
техники.
Задачи информатики состоят
в следующем:
1. Исследование
информационных процессов любой природы.
2. Разработка
информационной техники и создание
новейшей технологии переработки
информации на базе полученных результатов
исследования информационных процессов.
3. Решение
научных и инженерных проблем создания,
внедрения и обеспечения эффективного
использования компьютерной техники и
технологии во всех сферах общественной
жизни.
Структура информатики
:
Теоретическая
информатика—
часть информатики, включающая ряд
математических разделов. Она опирается
на математическую логику и включает
такие разделы, как теория алгоритмов и
автоматов, теория информации и теория
кодирования, теория формальных языков
и грамматик, исследование операций и
другие. Этот раздел информатики использует
математические методы для общего
изучения процессов обработки информации.
Вычислительная
техника—
раздел, в котором разрабатываются
общие принципы построения вычислительных
систем. Речь идет не о технических
деталях и электронных схемах, а о
принципиальных решениях на уровне так
называемой архитектуры вычислительных
систем, определяющей состав, назначение,
функциональные возможности и принципы
взаимодействия устройств. Примеры
принципиальных, ставших классическими
решениями в этой области-неймановская
архитектура компьютеров первых поколений,
шинная архитектура ЭВМ старших поколений,
архитектура параллельной(многопроцессорной)
обработки информации.
Программирование—
деятельность, связанная с разработкой
систем программного обеспечения. Здесь
отметим лишь основные разделы современного
программирования: создание системного
программного обеспечения и создание
прикладного программного обеспечения
Информационные
системы— раздел
информатики, связанный с решением
вопросов по анализу потоков информации
в различных сложных системах, их
оптимизации, структурировании, принципах
хранения и поиска информации. Известным
примером решения проблемы на глобальном
уровне может служить гипертекстовая
поисковая система WWW.
Искусственный
интеллект—
область информатики, в которой решаются
сложные проблемы находящиеся на
пересечении с психологией лингвистикой
и другими науками.
Термин информация происходит
от латинского informatio, что означает
разъяснение, изложение. Понятие
«информация» многогранно, и поэтому
строгого общепринятого определения
нет. В широком смысле информация –
это отражение реального мира в виде
сигналов и знаков.
В информатике
понятие «информация»
означает сведения об объектах и явлениях
окружающей среды, которые уменьшают
имеющуюся неопределенность, неполноту
знаний о них.
С понятием информации
связаны такие понятия,
как сигнал, сообщение и данные.
Сигнал – физический
процесс, параметры которого содержат
информацию о том или ином объекте,
явлении. Посредством сигналов осуществляется
перенос информации в пространстве и во
времени (например, электрический,
световой, звуковой сигналы и т.д.).
Сообщение –
информация, представленная в определенной
форме и предназначенная для приема-передачи.
Данные – информация,
представленная в форме, позволяющей ее
дальнейшую обработку в том числе и
техническими средствами, например,
компьютером.
Под информационным
процессом понимается
процесс передачи, обработки (преобразования),
восприятия и использования информации.
Для обмена
информацией, ее преобразования и передачи
необходимо наличие источника (носителя)
сообщений, передатчика (кодера), канала
связи, приемника (декодера) и
получателя сообщений
Информация может
поступать как непрерывно во времени,
так и дискретно.
Дискретность (от
лат. discretus — разделённый, прерывистый) —
означает прерывность и противопоставляется
непрерывности. Дискретные величины
принимают не все возможные значения, а
только определённые, и их можно пересчитать.
Дискретное изменение величины происходит
скачками, через определённые промежутки
времени.
Непрерывная величина
может принимать любые значения в
некотором диапазоне, которые могут быть
сколь угодно близки, но всё-таки отличаться
друг от друга. Количество таких значений
бесконечно велико.
В технике непрерывная
информация называется аналоговой,
дискретная — цифровой.
Дискретизация —
это процесс перевода непрерывного аналогового
сигнала в дискретный (обратный процесс
называется восстановлением).
Непрерывный аналоговый сигнал заменяется
последовательностью коротких импульсов
(отсчётов),
величина которых равна значению сигнала
в данный момент времени. Возможность
точного воспроизведения такого
представления зависит от интервала
времени между отсчётами.
Чаще всего применяются
два подхода к измерению информации:
-
алфавитный (т.е.
количество информации зависит от
последовательности знаков); -
содержательный или вероятностный (т.е.
количество информации зависит от ее
содержания).
Алфавитный (объемный)
подход применяется в технике, где
информацией считается любая хранящаяся,
обрабатываемая или передаваемая
последовательность знаков, сигналов.
Этот подход основан
на подсчете числа символов в
сообщении, то есть связан только с
длиной сообщения и не учитывает его
содержания. Но длина сообщения зависит
не только от содержащейся в нем информации.
На нее влияет мощность алфавита
используемого языка.
Множество используемых
в тексте символов называется алфавитом.
Полное количество
символов алфавита называется
мощностью
алфавита.
Чем меньше знаков
в используемом алфавите, тем длиннее
сообщение. Так, например, в алфавите
азбуки Морзе всего три знака (точка,
тире, пауза), поэтому для кодирования
каждой русской или латинской буквы
нужно использовать несколько знаков,
и текст, закодированный по Морзе, будет
намного длиннее, чем при обычной записи.
В вычислительной
технике наименьшей единицей измерения
информации является 1
бит (binary
digit). Один бит соответствует одному знаку
двоичного алфавита, т.е. 0 или 1.
Таким образом, 1бит
= 0 или 1.
Единицы измерения
информации
Для удобства помимо
бита применяются более крупные единицы
измерения информации.
1байт = 8 бит
1Кб (килобайт) = 1024
байт
1Мб (мегабайт) = 1024
Кб
1Гб (гигабайт) = 1024
Мб
1Тб(терабайт)=1024 Гб.
Для того чтобы
подсчитать количество информации в
сообщении необходимо умножить количество
информации, которое несет 1 символ, на
количество символов.
Информационный
объем сообщения (информационная емкость
сообщения) —
количество информации в сообщении,
измеренное в битах, байтах или производных
единицах (Кбайтах, Мбайтах и т.д.).
Формулы Хартли
и Шеннона.
Американский
инженер Р. Хартли в 1928 г. процесс
получения информации рассматривал как
выбор одного сообщения из конечного
наперёд заданного множества из N
равновероятных сообщений, а количество
информации I, содержащееся в выбранном
сообщении, определял как двоичный
логарифм N.
|
Формула |
Допустим, нужно
угадать одно число из набора чисел от
единицы до ста. По формуле Хартли можно
вычислить, какое количество информации
для этого требуется: I = log2100 > 6,644.
Таким образом, сообщение о верно угаданном
числе содержит количество информации,
приблизительно равное 6,644 единицы
информации.
Американский
учёный Клод
Шеннон предложил в 1948 г. другую формулу
определения количества информации,
учитывающую возможную неодинаковую
вероятность сообщений в наборе.
|
|
Легко заметить, что
если вероятности p1, …, pN равны, то
каждая из них равна 1 / N, и формула
Шеннона превращается в формулу Хартли.
Важно помнить, что
любые теоретические результаты применимы
лишь к определённому кругу случаев,
очерченному первоначальными допущениями.
-
Кодирование информации. Равномерные и неравномерные коды. Условие Фано. Задача построения эффективных кодов. Первая теорема Шеннона. Построение кода Шеннона-Фано. Кодирование Хаффмана.
Закодировать текст
– значит сопоставить ему другой
текст. Кодирование применяется
при передаче данных – для того, чтобы
зашифровать текст от посторонних, чтобы
сделать передачу данных более надежной,
потому что канал передачи данных может
передавать только ограниченный набор
символов (например, — только два символа,
0 и 1) и по другим причинам.
При кодировании
заранее определяют алфавит, в котором
записаны исходные тексты (исходный
алфавит) и алфавит, в котором записаны
закодированные тексты (коды), этот
алфавит называетсякодовым алфавитом.
В качестве кодового алфавита часто
используют двоичный алфавит,
состоящий из двух символов (битов) 0 и
1. Слова в двоичном алфавите иногда
называют битовыми последовательностями.
Равномерное кодирование
Наиболее простой
способ кодирования – побуквенный. При
побуквенном кодировании каждому символу
из исходного алфавита сопоставляется кодовое
слово – слово в кодовом алфавите.
Иногда вместо «кодовое слово буквы»
говорят просто «код буквы». При
побуквенном кодировании текста коды
всех символов записываются подряд, без
разделителей.
Пример 1. Исходный
алфавит – алфавит русских букв, строчные
и прописные буквы не различаются. Размер
алфавита – 33 символа.
Кодовый алфавит –
алфавит десятичных цифр. Размер алфавита
— 10 символов.
Применяется
побуквенное кодирование по следующему
правилу: буква кодируется ее номером в
алфавите: код буквы А – 1; буквы Я – 33 и
т.д.
Тогда код слова АББА
– это 1221.
Внимание: Последовательность
1221 может означать не только АББА, но и
КУ (К – 12-я буква в алфавите, а У – 21-я
буква). Про такой код говорят, что он НЕ
допускает однозначного декодирования
Неравномерное кодирование
Равномерное
кодирование удобно для декодирования.
Однако часто применяют и неравномерные
коды, т.е. коды с различной длиной кодовых
слов. Это полезно, когда в исходном
тексте разные буквы встречаются с разной
частотой. Тогда часто встречающиеся
символы стоит кодировать более короткими
словами, а редкие – более длинными. Из
примера 1 видно, что (в отличие от
равномерных кодов!) не все неравномерные
коды допускают однозначное декодирование.
Есть простое условие,
при выполнении которого неравномерный
код допускает однозначное декодирование.
Код
называется префиксным, если в
нем нет ни одного кодового слова, которое
было бы началом (по-научному, — префиксом)
другого кодового слова.
Код из примера 1 –
НЕ префиксный, так как, например, код
буквы А (т.е. кодовое слово 1) – префикс
кода буквы К (т.е. кодового слова 12,
префикс выделен жирным шрифтом).
Код из примера 2 (и
любой другой равномерный код) –
префиксный: никакое слово не может быть
началом слова той же длины.
Пример Пусть
исходный алфавит включает 9 символов:
А, Л, М, О, П, Р, У, Ы, -. Кодовый алфавит
– двоичный. Кодовые слова:
А: 00
М: 01
-: 100
Л: 101
У: 1100
Ы: 1101
Р: 1110
О: 11110
П: 11111
Кодовые слова
выписаны в алфавитном порядке. Видно,
что ни одно из них не является началом
другого. Это можно проиллюстрировать
рисунком
На рисунке
изображено бинарное дерево. Его
корень расположен слева. Из каждого
внутреннего узла выходит два ребра.
Верхнее ребро имеет пометку 0, нижнее –
пометку 1. Таким образом, каждому узлу
соответствует слова в двоичном алфавите.
Если слово X является началом (префиксом)
слова Y, то узел, соответствующий слову
X, находится на пути из корня в узел,
соответствующий слову Y. Наши кодовые
слова находятся в листьях дерева.
Поэтому ни одно из них не является
началом другого.
Теорема (условие
Фано). Любой
префиксный код (а не только равномерный)
допускает однозначное декодирование.
Разбор примера (вместо
доказательства). Рассмотрим закодированный
текст, полученный с помощью кода из
примера 3:
0100010010001110110100100111000011100
Будем его
декодировать таким способом. Двигаемся
слева направо, пока не обнаружим код
какой-то буквы. 0 – не кодовое слово, а
01 – код буквы М.
0100010010001110110100100111000011100
Значит, исходный
текст начинается с буквы М: код никакой
другой буквы не начинается с 01! «Отложим»
начальные 01 в сторону и продолжим.
01 00010010001110110100100111000011100
М
Далее таким же
образом находим следующее кодовое слово
00 – код буквы А.
01
00010010001110110100100111000011100
М А
И т. д.
Замечание. В
расшифрованном тексте 14 букв. Т.к. в
алфавите 9 букв, то при равномерном
двоичном кодировании пришлось бы
использовать кодовые слова длины 4.
Таким образом, при равномерном кодировании
закодированный текст имел бы длину 56
символов – в полтора раза больше, чем
в нашем примере (у нас 37 символов).
Учитывая
статистические свойства источника
сообщения, можно минимизировать среднее
число двоичных символов, требующихся
для выражения одной буквы сообщения,
что при отсутствии шума позволяет
уменьшить время передачи или объем
запоминающего устройства.
Такое эффективное
кодирование базируется на основной
теореме Шеннона для каналов без шума.
Первая теорема
Шеннона: если
пропускная способность канала без помех
превышает производительность источника
сообщений, т.е. удовлетворяется
условие Ck >Vu, то существует способ
кодирования и декодирования сообщений
источника, обеспечивающий сколь угодно
высокую надежность передачи сообщений.
В противном случае, т.е. если Ck <Vu
Такого способа нет. Таким образом,
идеальное кодирование по Шеннону по
существу представляет собой экономное
кодирование последовательности сообщений
при безграничном укрупнении сообщений.
Такой способ кодирования характеризуется
задержкой сообщений поскольку кодирование
очередной типичной последовательности
может начаться только после получения
последовательности источника
длительностью T, а декодирование —
только когда принята последовательность
из канала той же длительности T. Поскольку
требуется , то идеальное кодирование
требует бесконечной задержки передачи
информации. В этом причина технической
нереализуемости идеального кодирования
по Шеннону. Тем не менее, значение этого
результата, устанавливающего предельные
соотношения информационных характеристик
источника и канала для безошибочной
передачи сообщений, весьма велико.
Исторически именно теорема Шеннона
инициировала и определила развитие
практических методов экономного
кодирования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.03.2016138.75 Кб1081.doc
- #
- #
Равномерное алфавитное двоичное кодирование. Байтовый код
В этом случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано одинаковое количество информации равное %%I(А) = log_2 N%%. Формировать признак конца знака не требуется, поэтому для определения длины кода можно воспользоваться формулой %%K(A,2) > log_2 N%%. Приемное устройство просто отсчитывает оговоренное заранее количество элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при этом недопустимы сбои, например, пропуск (непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой последовательности и неправильной ее интерпретации; решается проблема путем синхронизации передачи или иными способами, о которых пойдет речь далее. С другой стороны, применение равномерного кода оказывается одним из средств контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу интерпретируется как ошибка.
Примером равномерного алфавитного кодирования является телеграфный код Бодо, пришедший на смену азбуке Морзе. Исходный алфавит должен содержать не более 32-х символов; тогда %%К(А,2) = log_2 32 = 5%%, т.е. каждый знак первичного алфавита содержит 5 бит информации и кодируется цепочкой из 5 двоичных знаков. Условие %%N ≤ 32%%, очевидно, выполняется для языков, основанных на латинском алфавите (%%T = 27 = 26 + «пробел»%%), однако в русском алфавите 34 буквы (с пробелом) — именно по этой причине пришлось «сжать» алфавит (как в коде Хаффмана) и объединить в один знак «е» и «ё», а также «ь» и «ъ», что видно из табл. 3.1. После такого сжатия %%N = 32%%, однако, не остается свободных кодов для знаков препинания, поэтому в телеграммах они отсутствуют или заменяются буквенными аббревиатурами; это не является заметным ограничением, поскольку, как указывалось выше, избыточность языка позволяет легко восстановить информационное содержание сообщения. Избыточность кода Бодо для русского языка %%Q(r,2) = 0,148%%, для английского %%Q(e,2) = 0,239%%.
Другим важным для нас примером использования равномерного алфавитного кодирования является представление символьной (знаковой) информации в компьютере. Чтобы определить длину кода, необходимо начать с установления количество знаков в первичном алфавите. Компьютерный алфавит должен включать:
- 26 х 2 = 52 букв латинского алфавита (с учетом прописных и строчных);
- 33 х 2 = 66 букв русского алфавита;
- цифры 0.. .9 — всего 10;
- знаки математических операций, знаки препинания, спецсимволы %%≈ 20%.
Получаем, что общее число символов %%N ≈ 148%%. Теперь можно оценить длину кодовой цепочки: %%K(c,2) ≥ log_2 148 ≥ 7,21%%. Поскольку длина кода выражается целым числом, очевидно, К(с,2) = 8. Именно такой способ кодирования принят в компьютерных системах: любому символу ставится в соответствие код из 8 двоичных разрядов (8 бит). Эта последовательность сохраняется и обрабатывается как единое целое (т.е. отсутствует доступ к отдельному биту) — по этой причине разрядность устройств компьютера, предназначенных для хранения или обработки информации, кратна 8. Совокупность восьми связанных бит получила название байт, а представление таким образом символов — байтовым кодированием.
Байт наряду с битом может использоваться как единица измерения количества информации в сообщении. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным. Пусть имеется некоторое сообщение (последовательность знаков); оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона (2.17)) дает %%I_{вер}%%, а объемная мера пусть равна %%I_{об}%%; соотношение между этими величинами вытекает из (2.7):
%%I_{вер} leqslant I_{об}%%;
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:
- 1 Кбайт = %%2^{10}%% байт = 1024 байт
- 1 Мбайт = %%2^{20}%% байт = 1024 Кбайт
- 1 Гбайт = %%2^{30}%% байт = 1024 Мбайт
- 1 Тбайт = %%2^{40}%% байт = 1024 Гбайт
Использование 8-битных цепочек позволяет закодировать %%2^8=256%% символов, что превышает оцененное выше %%N%% и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Однако недостаточно только условиться об определенной длине кода. Ясно, что способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьмибитных цепочек, очень много. По этой причине для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов. Подобное согласование осуществляется в форме стандартизации кодовых таблиц.
Первым таким международным стандартом, который применялся на больших вычислительных машинах, был EBCDIC (Extended Binary Coded Decimal Interchange Code) — «расширенная двоичная кодировка десятичного кода обмена». В персональных компьютерах и телекоммуникационных системах применяется международный байтовый код ASCII (American Standard Code for Information Interchange — «американский стандартный код обмена информацией»).
Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0). В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31), вырабатываемые при использовании клавиатуры. Ниже приведены некоторые ASC-коды:
| Клавиша | Двоичный код | Десятичный код |
|---|---|---|
| A(лат) | 01000001 | 65 |
| Z | 01011010 | 90 |
| [Esc] | 00011011 | 27 |
Вторая часть кодовой таблицы — она считается расширением основной — охватывает коды в интервале от 128 до 255 (первый бит всех кодов 1). Она используется для представления символов национальных алфавитов (например, русского), а также символов псевдографики. Для этой части также имеются стандарты, например, для символов русского языка это КОИ-8, КОИ-7 и др.
Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их лексикографическому порядку (т.е. порядку следования в алфавите) — это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.
В настоящее время появился и находит все более широкое применение еще один международный стандарт кодировки -Unicode. Его особенность в том, что в нем использовано 16-битное кодирование, т.е. для представления каждого символа отводится 2 байта. Такая длина кода обеспечивает включения в первичный алфавит 65536 знаков. Это, в свою очередь, позволяет создать и использовать единую для всех распространенных алфавитов кодовую таблицу.
Содержание:
-
Готовлю школьников и студентов гарантированно на 100 баллов из 100 возможных!
-
Что такое равномерный код и в каких случаях его применяют?
-
Что такое неравномерный код и в каких случаях его применяют?
-
Равномерный код vs неравномерный код
-
Я хочу записаться к вам на индивидуальный урок по информатике и ИКТ
Готовлю школьников и студентов гарантированно на 100 баллов из 100 возможных!
Здравствуйте! Меня зовут Александр Георгиевич. Я являюсь профессиональным репетитором в области информационных технологий, математике, баз данных и программирования.
Если у вас возникли затруднения с обработкой равномерного или неравномерного кода, то срочно записывайтесь ко мне на первый пробный урок, на которых мы с вами очень детально разберем все ваши вопросы и прорешаем большое количество различных тематических упражнений.
Чтобы гарантированно набрать на официальном экзамене ОГЭ или ЕГЭ по информатике высоченный балл берите сотовый телефон, дозванивайтесь до меня и задавайте любые интересующие вопросы.
Несмотря на то, что вы являетесь чрезвычайно занятым человеком, я все-таки настаиваю на том, чтобы вы уделили $2-3$ минуты и ознакомились с отзывами клиентов, которые прошли подготовку под моим началом и добились ошеломительных результатов.
Также своим потенциальным клиентам я предлагаю на выбор $4$ различных территориальных формата, в которых могут проходить наши эффективные занятия:
Рекомендую использовать формат дистанционного обучения! Это выгодно, удобно и эффективно!
Что такое равномерный код и в каких случаях его применяют?
Допустим, вам требуется написать секретное письмо и отправить его своему другу. Вы – человек, проживающий на территории России, следовательно, использующий для написания слов буквы русского алфавита. И, вот, вы решаете закодировать ваше послание двоичным кодом, то есть вместо русских слов ваш друг получит набор цепочек, состоящий из нулей и единиц.
Но ваш соратник без особых проблем сможет провести дешифрацию вашего информационного сообщения, так как вы ему расскажете об алгоритме шифрации/дешифрации.
Чтобы провести кодирование вашего русскоязычного сообщения, необходимо воспользоваться равномерным кодом. В первую очередь нам необходимо вспомнить количество букв в русском алфавите – их $33$. Во вторую – необходимо воспользоваться формулой Хартли, чтобы определить количество бит, необходимых для кодирования одного символа.
Итак, давайте посчитаем, сколько требуется бит информации для кодирования одного символа из русского алфавита: $2^i >= 33$.
Поскольку $i$ – минимальное натуральное число, то $i = 6$. Делаем вывод, что для кодирования нашего сообщения нам требуется равномерный код длиной в $6$ бит. Приведу пример кодирования равномерным кодом первых и последних двух символов русскоязычного алфавита:
|
Символ |
‘А’ |
‘Б’ |
… |
‘Ю’ |
‘Я’ |
|
Равномерный код |
000000 |
000001 |
… |
011111 |
100000 |
|
Десятичное представление |
0 |
1 |
… |
31 |
32 |
Равномерный код – такой код, когда все символы какого-либо алфавита кодируются кодами одинаковой длины.
В примере выше, мы рассмотрели алфавит русского языка и закодировали абсолютно каждый его символ ровно $6$ битами. Кстати, для кодирования информации мы выбрали минимально возможное количество бит, так как при кодировании нужно стремиться к минимизации используемой памяти.
Что такое неравномерный код и в каких случаях его применяют?
Чтобы глубоко понять смысл неравномерного кодирования давайте представим, что вы работаете на продуктовом складе. Вы хотите оптимизировать свою работу и закодировать название каждого товара минимально возможным количеством бит.
На ум приходит вариант с равномерным кодом, то есть закодировать название каждого продукта информационным кодом одинаковой длины. Но в данном случае это не самый оптимальный вариант кодирования. Почему? Потому что один товар является наиболее популярным и востребованным, и вам, как кладовщику, приходится чаще с ним взаимодействовать.
Следует понять общий принцип неравномерного кода: суть его в том, чтобы кодировать наиболее часто используемые элементы как можно меньшим количеством бит, так как ими вы оперируете очень часто.
Неравномерный код – такой код, когда все элементы какого-либо множества кодируются кодом различной длины.
Давайте попробуем закодировать неравномерным кодом часть товаров, находящихся на вашем товарном складе. Предположим, что на вашем складе размещается около $3 000$ различных товаров, но наиболее ходовыми являются хлеб, соль, молоко и сахар.
Данные четыре товара покупают огромными партиями и вы уже устали вести записи в базе данных постоянно вбивая названиях этих продуктов. Давайте применим следующее кодирование:
|
Хлеб — 00 |
Соль — 01 |
Молоко — 10 |
Сахар — 11 |
Итого, нам потребовалось два бита информации, чтобы закодировать в бинарном виде наиболее ходовых четыре товара.
А как поступить с наименее популярными товарами, например, муку и перец также достаточно часто покупают. В этом случае данные товары можно запрограммировать так:
То есть мы выделяем на их кодирование уже по $3$ бита информации.
Вы должны уловить общий принцип: чем наименее популярный товар, тем большим количеством бит он будет закодирован.
И все бы хорошо, но есть одна существенная проблема, возникающая при создании неравномерного кода, – проблема с однозначной дешифрацией. Для полного понимания данной проблемы вам следует познакомиться с условием Фано.
Равномерный код vs неравномерный код
Чтобы хорошо понимать в каких ситуациях стоит применять то или иное кодирование, вам нужно очень хорошо разобраться с частотой использования элементов, которые вы планируете закодировать. Если частота применения приблизительно равна у всех элементов, то смело применяйте равномерный код, в других случаях – неравномерный код.
А сейчас я вам предлагаю ознакомиться с мультимедийным решением, в котором я показываю, как правильно оперировать равномерным и неравномерным кодом.
Я хочу записаться к вам на индивидуальный урок по информатике и ИКТ
Если у вас остались какие-либо вопросы по рассматриваемой теме, то записывайтесь ко мне на первый пробный урок. Я репетитор-практик, следовательно, на своих уроках я уделяю максимум внимания решению заданий. Из теории лишь записываются самые базовые сведения: определения, тезисы, формулировки теорем и аксиом.
Специально для своих потенциальных клиентов я разработал стабильную многопараметрическую систему, состоящую из 144 вариантов нашего будущего взаимовыгодного сотрудничества. Даже самый взыскательный клиент сумеет выбрать вариант, полностью покрывающий его запросы.
Не откладывайте свое решение в долгий ящик. Я все-таки достаточно востребованный и квалифицированный репетитор, поэтому звоните прямо сейчас – количество ученических мест ограниченно!
На этой странице вы узнаете
- Как закодировать сообщение “КУРЛЫК” правильно?
- Что такое равномерное кодирование?
- Так как кодировать сообщения максимально эффективно?
Понятие однозначного декодирования
Вы любите шпионов? А готовы почувствовать себя в их шкуре?
Нам нужно передать секретное сообщение на базу, а раз оно секретное, никто не должен понять, что мы передаем. Для этого надо представить наше сообщение в каком-то новом виде, который на первый взгляд будет бессмысленным, но мы будем знать, как его расшифровать.

Главное — чтобы расшифровать было возможно.
Мы уже знаем, что для компьютера информацию надо представить в двоичномкоде — подробнее об этом рассказано в статье «Основные понятия об информации». Но сам процесс кодирования информации — не такая простая вещь. Есть несколько факторов, которые нужно соблюсти, чтобы кодирование прошло хорошо.
Но чтобы научиться делать что-то правильно, сначала надо разобраться, как сделать неправильно. Давайте попробуем произвольным образом закодировать буквы К, У, Р, Л, Ы, чтобы составлять из них сообщения.
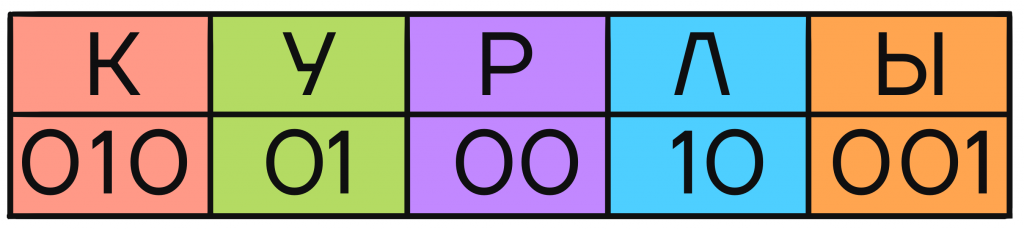
Каждой букве в табличке сопоставлено несколько символов, в нашем случае цифр. Эти символы — кодовое слово буквы, позволяющее отличить ее от других букв в закодированном сообщении.
С помощью кодовых слов каждой отдельной буквы закодируем сообщение КУРЛЫК, для этого на место каждой буквы будем подставлять соответствующее ей кодовое слово:

С проблемой мы столкнемся при попытке расшифровать сообщение. Чтобы это сделать, надо выделить в коде сообщения отдельные кодовые слова и подставить на их место соответствующие буквы. Но при расшифровке этого кода можно получить другой вариант:
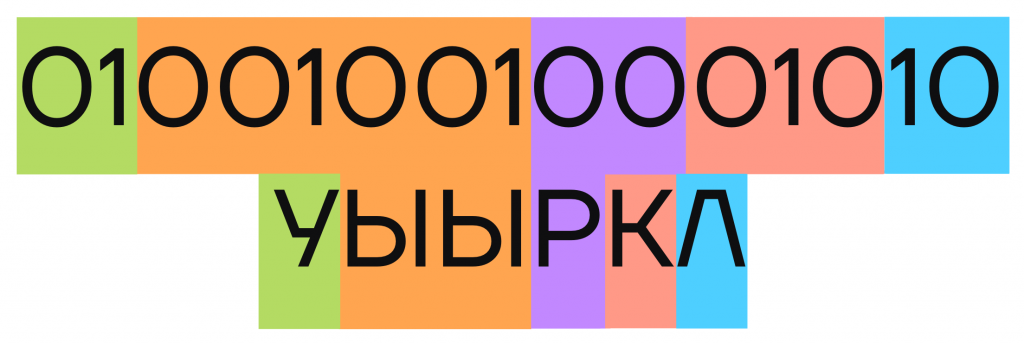
Чтобы кодирование считалось качественным и надежным, код должен удовлетворять условию однозначного декодирования — после кодирования сообщений у них должен быть единственный вариант расшифровки.
Равномерное кодирование
Но как можно соблюдать это условие? Или еще круче — как строить кодовые слова, которые заранее будут этому условию удовлетворять?
Это первый вариант подхода к однозначному декодированию.Он подразумевает кодирование отдельных элементов кодами, имеющими одинаковую длину.
И такой подход действительно спасает ситуацию. Если каждое кодовое слово будет иметь одинаковую длину, и при этом все они будут различны, выделять в зашифрованном сообщении отдельные кодовые слова не составит труда, как и сопоставлять их с соответствующими им буквами.
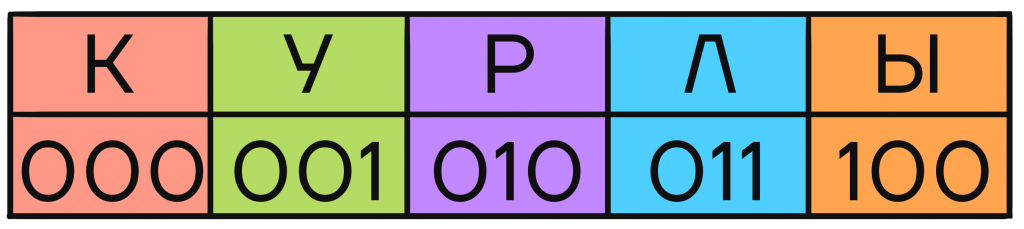
Кодируем сообщение КУРЛЫК:

И при попытке декодирования, поочередно выделяя кодовые слова одинаковой длины, мы не имеем никаких проблем с сопоставлением и получаем исходное сообщение без альтернативных вариантов.

Такой метод действительно прост и в освоении, и при составлении кодовых слов, и при расшифровке. Но есть один минус — он не всегда эффективен.
Выбирая длину одного кодового слова, мы можем заранее определить количество возможных кодов: так как на каждой позиции может быть либо 0, либо 1, количество возможных кодов N длины i будет равно
(N = 2^i).
Выбрав длину 3 для наших кодовых слов, мы имеем 8 различных кодов, хотя кодируем всего 5 букв.
В других ситуациях потери могут быть плачевнее: для кодирования, например, 33 букв русского алфавита длина кодового слова должна быть не меньше 6 (если выберем 5, получим максимум 25 = 32 кодового слова, но тогда 1 буква останется незакодированной).
Но имея 26 = 64 кодовых слова для 33-х букв алфавита, мы явно взяли кодов больше, чем нужно.
Почему это плохо? Рассмотрим следующую ситуацию.
Вася собирает вещи для переезда и ему надо упаковать какой-то набор вещей в коробку. Если в ней много свободного места — это плохо, потому что Вася может взять коробку поменьше и ему будет легче нести маленькую коробку. Также и здесь, если в нашей кодировке много неиспользованных кодов — это плохо, потому что можно оптимальнее перекодировать необходимый набор символов, и зашифрованные сообщения станут занимать меньше места на компьютере или быстрее передаваться по интернету.
Естественно, равномерное кодирование — все еще возможный вариант, при котором код будет однозначно декодируемым, но нет ли более рационального подхода?
Условие Фано и дерево вариантов
Хороший вариант — составление кодовых слов, которые удовлетворяют условию Фано.
Условие Фано гласит: «ни одно кодовое слово не должно быть началом другого кодового слова».
В составленных нами в самом начале статьи кодовых словах это условие нарушалось — код буквы К (010) начинался с кода буквы У (01), а код Ы (001) — с кода Р (00). Из-за этого мы не могли быть точно уверены, где закончилось кодовое слово, а где оно продолжается.
Очень просто строить код, который будет удовлетворять условию Фано, с помощью дерева вариантов — структуры, в нашем случае помогающей получить кодовые слова максимально просто и понятно. Принцип работы дерева состоит в том, что в его узлах будут находиться кодовые слова, а из узла могут выходить два ребра, соответствующие добавлению в конец кодового слова 0 и 1, таким образом заменяя одно кодовое слово на два новых, которые длиннее на один символ.
1. Начальный узел — пустой.
2. К любому узлу могут быть добавлены ребра, создающие два новых узла, в каждом из которых находится новое кодовое слово на 1 символ длиннее предыдущего (с добавленным в конец символом 0 и 1, соответственно).
3. Шаг 2 выполняется до тех пор, пока не будет получено необходимое количество конечных узлов (самых последних, из которых не выходит ни одного ребра).
Давайте попробуем таким образом получить ровно 5 кодовых слов, чтобы закодировать наши буквы К, У, Р, Л, Ы.
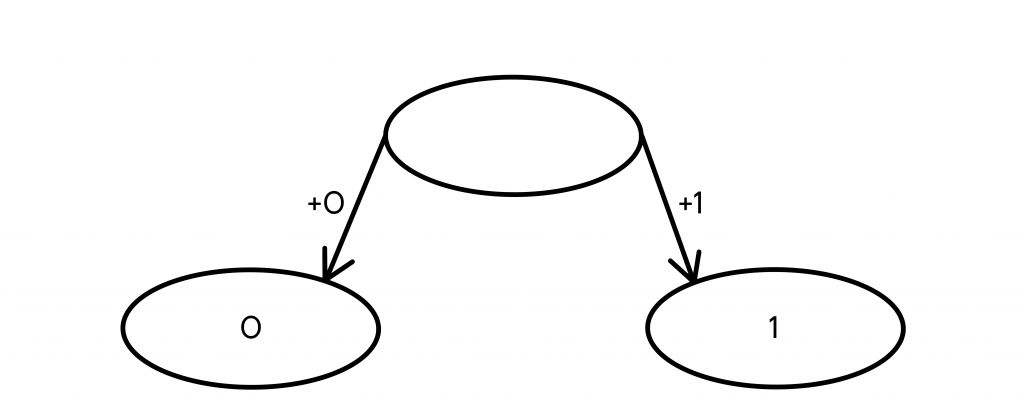
- Первые два кодовых слова, которые мы можем получить из ничего — 0 и 1.
Чтобы продолжить построение дерева, выбираем любой из конечных узлов и также добавляем ему 0 и 1 в конец.
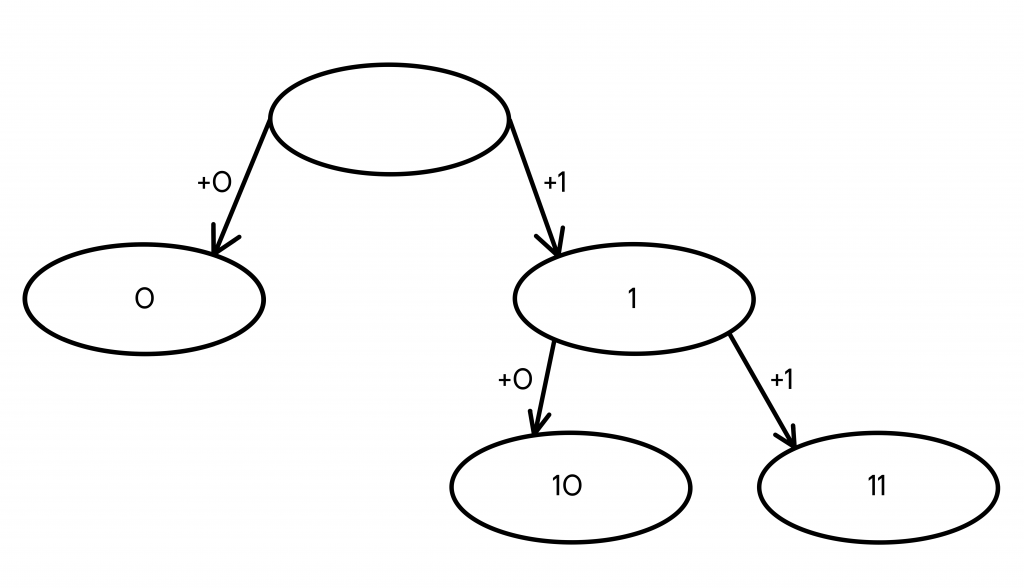
- Допустим, мы добавим 0 и 1 к кодовому слову 1, и вместо него теперь получим два новых — 10 и 11. Теперь кодовых слов у нас уже три — 0, 10 и 11.
Все еще мало, продолжаем построение дерева.
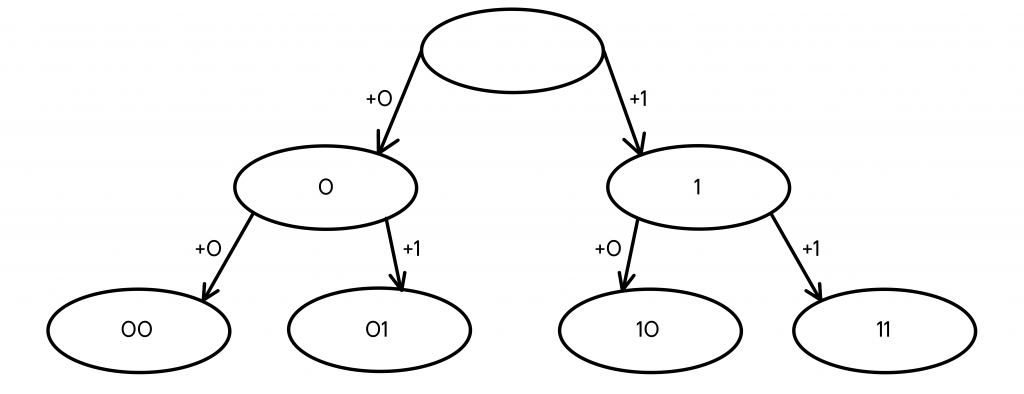
- Мы проделали ту же операцию с кодовым словом 0, заменив его на 2 новых — 00 и 01.
Кодовых слов стало 4, этого все еще мало, нужно продолжить построение дерева.
- Из конечных узлов можно выбрать любой для продолжения построения, например — 01, продолжив это кодовое слово, получаем два новых — 010 и 011.
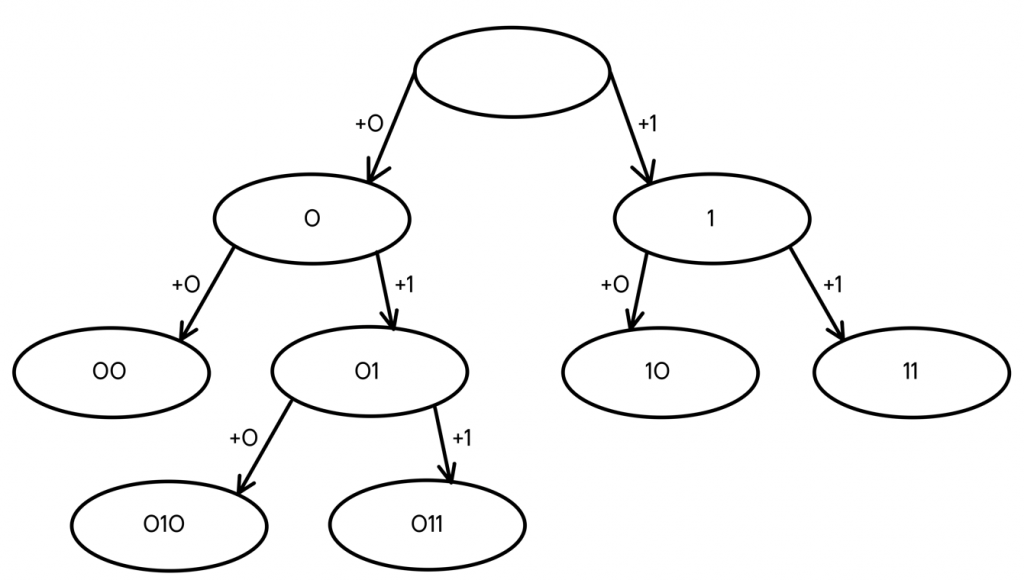
В итоге мы имеем 5 конечных узлов В них находятся кодовые слова, которые можно распределить любым удобным или необходимым способом между кодируемыми буквами. Например, так:
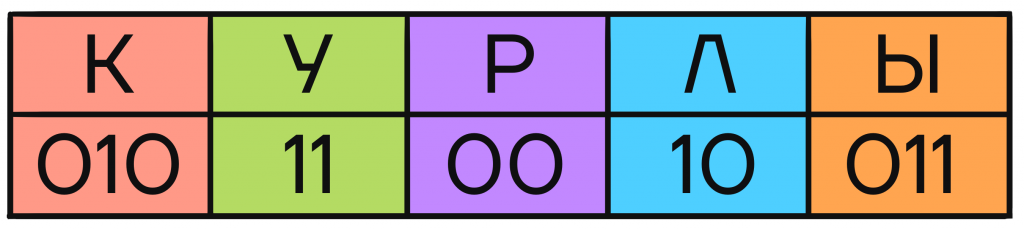
Такой код будет однозначно декодируемым, так как ни одно слово не заканчивается посередине другого, и мы всегда можем быть уверены, что одно кодовое слово закончилось и началось новое.
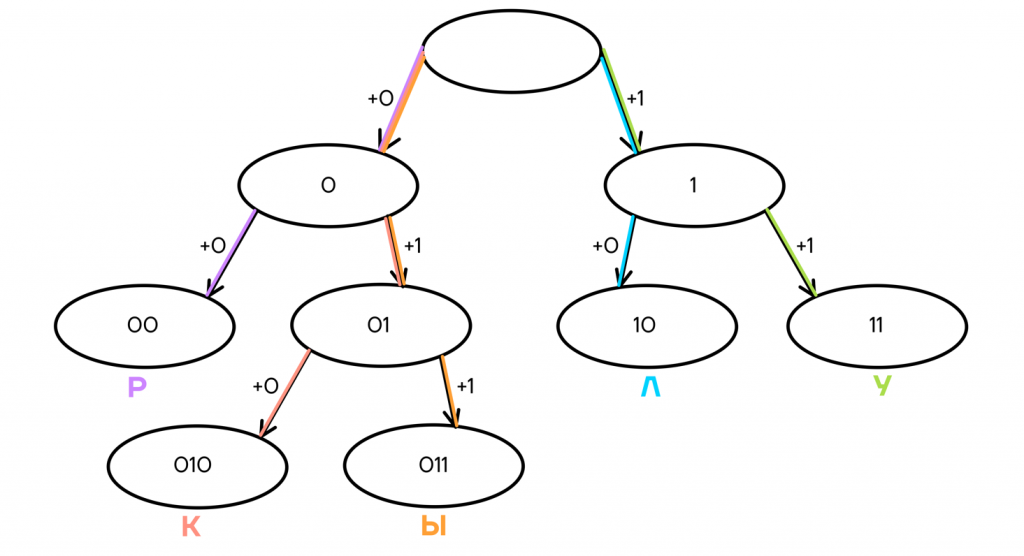
Так, код 010110010011010 мы можем однозначно декодировать, читая его слева направо:
Его формулировка немного отличается: «ни одно кодовое слово не должно быть окончанием другого». Такая формулировка уже допустит сосуществование кодовых слов 011 и 01, но не допустит 110 и 10, так как второе совпадает с окончанием первого.
Здесь построение дерева вариантов и чтение кодов происходит в точности до наоборот — при построении мы добавляем символы не в конец, а в начало предыдущего кодового слова и читаем код справа налево.
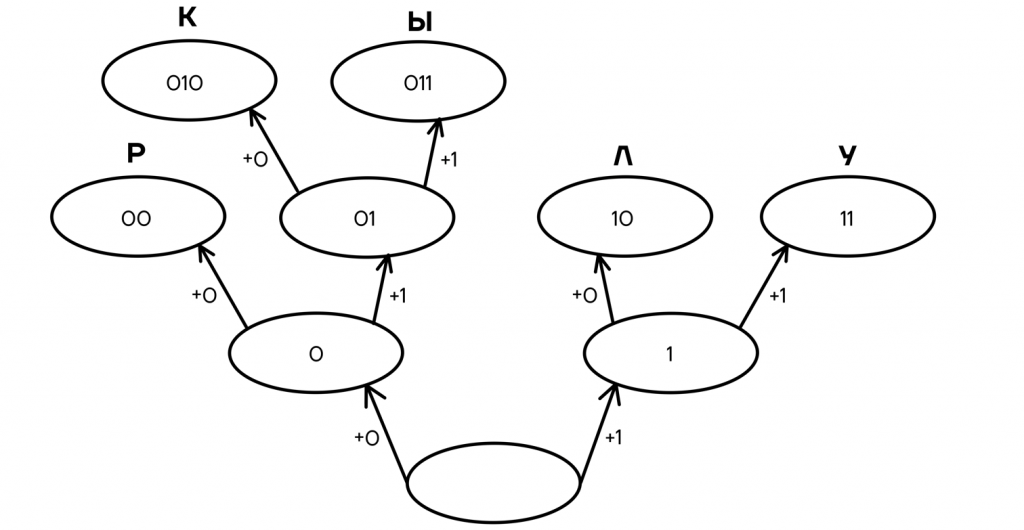
И код 010110001110010 будет читаться уже в другую сторону – из конца в начало:
Практика
В жизни чаще всего используются равномерные кодировки в силу многих причин, таких как:
- Большая устойчивость.
Представим, что мы передаем слово КУРЛЫК разными вариантами, но при передаче допускаем ошибку в четвертом бите (в четвертом символе нашего кода). Посмотрим, что получится в итоге.

Выводы:
- В первом случае из-за одного неправильного бита сломалась половина символов текста, и даже поменялось количество этих символов.
- Во втором случае текст отличается от первоначального только тем символом, на который влиял сломанный бит.
Таким образом, мы видим большую устойчивость равномерного кодирования.
2. Простота расширения.
Мы обсуждали, что проблема равномерного кодирования — в большом количестве «пустых мест». Но эти пустые места могут быть полезны. Например, захочет разработчик добавить в код несколько новых эмодзи. У него как раз есть незанятые коды для этих символов. Согласитесь, это удобнее, чем переписывать всю кодировку целиком.
Неравномерные же кодировки часто применялись еще до появления компьютеров. Например, одной из самых известных неравномерных кодировок являлась азбука Морзе, применявшаяся в работе телеграфов, передаче радиосигналов и других способах передачи информации.
Также применение неравномерной кодировки есть в 4 задаче ЕГЭ и во 2 задаче ОГЭ.
Разберем задачу №4 ЕГЭ:
По каналу связи передаются закодированные сообщения о состоянии системы, состоящие из пяти символов: A, B, C, D, E. При передаче сообщений используется двоичный код, при этом он допускает однозначное декодирование. Для символов A, B, C используются эти кодовые слова: 1, 010 и 001 (соответственно).
В ответе нужно указать наименьшее по длине кодовое слово для буквы D. Если таких кодов несколько, то в ответе укажите наименьший по значению.
Решение.
Шаг 1. Построим дерево вариантов кодовых слов и отметим на нем уже известные коды букв:
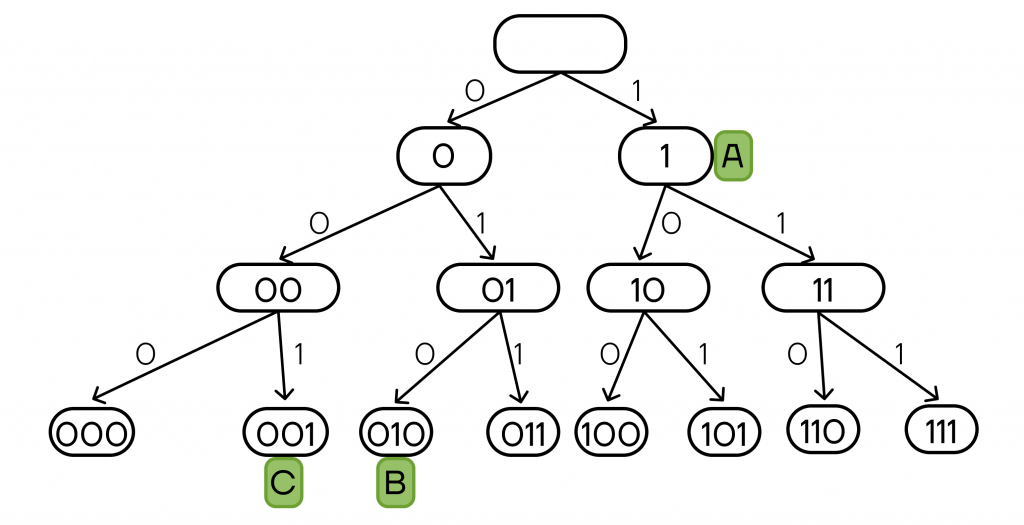
Шаг 2. Заметим, что раз для символа A кодовое слово 1, то в дальнейшем нам не подойдут любые коды, начинающиеся с 1, так как для них и символа A не будет выполняться условие однозначного декодирования.
Шаг 3. Начнем разбирать по возрастанию кодовые слова, начинающиеся с 0:
- 0 — не подойдет, будет началом для кодовых слов 001 и 010.
- 00 — не подойдет, будет началом слова 001.
- 01 — не подойдет, будет началом слова 010.
- 000 — подойдет.
- 001 — не подойдет, буква C.
- 010 — не подойдет, буква B.
- 011 — подойдет.
Шаг 4. Получаем два недостающих кодовых слова равной длины: 000 и 011. Значит, можем использовать их для букв Е и D, при этом сохранив однозначное декодирование. Для D нужно слово, меньшее по значению, тогда верным ответом будет 000.
Ответ: 000
В этой статье мы познакомились с условием Фано и научились правильно кодировать и декодировать сообщения. Но различные виды информации требуют собственных уникальных подходов. Приглашаем вас продолжить изучение темы в статьях «Кодирование изображения» и «Кодирование звука».
Фактчек
- Условие однозначного декодирования необходимо для того, чтобы у закодированного сообщения был ровно один вариант расшифровки — исходный.
- Однозначное декодирование может давать равномерное кодирование, при котором все кодовые слова имеют одинаковую длину, или кодовые слова, составленные по условию Фано, которое гласит: «ни одно кодовое слово не должно совпадать с началом другого кодового слова».
- Существует другая вариация этого условия — обратное условие Фано, оно гласит: «ни одно кодовое слово не должно совпадать с окончанием другого кодового слова».
- Для составления кодовых слов, удовлетворяющих условию Фано, используется дерево вариантов.
Проверь себя
Задание 1.
Для чего необходимо условие однозначного декодирования?
- Для более удобной шифровки сообщений.
- Для построения минимально возможных кодовых слов.
- Для сохранения возможности абсолютно точно получить исходное сообщение из закодированного.
- Для красоты.
Задание 2.
Выберите верные утверждения:
- При равномерном кодировании все кодовые слова имеют одну длину.
- При равномерном кодировании кодовые слова не могут начинаться на один и тот же символ.
- Для соблюдения условия Фано необходимо, чтобы ни одно кодовое слово не совпадало с окончанием другого кодового слова.
- Обратное условие Фано не гарантирует однозначное декодирование.
- Для составления кодовых слов, удовлетворяющих обратному условию Фано, используется дерево вариантов.
Задание 3.
Выберите наборы кодовых слов, которые удовлетворяют условию однозначного декодирования по любому из критериев, описанных в статье:
- 1, 11, 111, 1111, 11111, 0.
- 01, 001, 0001, 00001, 1
- 000, 111, 100, 001
- 10, 11, 00, 1001
- 10, 100, 1000, 10000
Задание 4.
Для передачи сообщений используются буквы А, Б, В, Г, Д. Известны некоторые кодовые слова: А = 01, Б = 111, В = 00, Г = 110. Какое кодовое слово может соответствовать кодовому слову для буквы Д, чтобы весь код удовлетворял условию Фано?
- 0
- 11
- 101
- 1100
Ответы: 1. — 3; 2. — 1, 5; 3. — 2, 3, 4, 5; 4. — 3.
На прошлом уроке мы
узнали:
· Для
удобства хранения и передачи информации её часто переводят из непрерывной формы
в дискретную. Такой процесс называется дискретизацией.
· В
процессе дискретизации информация записывается на одном из языков.
· Алфавитом
языка называются все существующие символы, которые
используются для представления информации на этом языке.
· Алфавит
характеризуется своей мощностью, это количество символов, которые в него
входят.
· Двоичный
алфавит состоит из двух символов. Запись информации с помощью
такого алфавита называется двоичным кодированием.
· Двоичный
код
– это код информации, получившийся в результате её двоичного кодирования.
· Любой
алфавит можно привести к двоичному.
Вопросы:
· Двоичное
кодирование звука.
· Двоичное
кодирование изображения.
· Равномерный
и неравномерный коды.
· Двоичное
кодирование текстовых сообщений методом Хаффмана.
Итак, на прошлом уроке мы
узнали, что любой алфавит можно представить в виде двоичного, для этого каждому
символу исходного алфавита присваивается его двоичный код. Записывая подряд
двоичные коды всех символов, мы можем кодировать текстовые сообщения. Ещё мы
узнали, что двоичный алфавит легко реализовать технически, с помощью наличия
или отсутствия электрического сигнала на некотором участке электрической цепи. Именно
поэтому любая информация на компьютере представлена в виде двоичного кода. Однако
мы знаем, что на компьютере может храниться любая информация, а не только
текстовая или числовая. Как же её представить в виде двоичного кода? Например
звук и изображение. Как мы знаем, они представляются в виде непрерывных
сигналов, разберёмся как же представить эти два вида информации в дискретной
форме.
Начнём с изображения.
Вполне логично, что любое изображение можно разделить на некоторые участки,
каждый из которых имеет свой цвет. Именно так происходит при представлении
изображений на компьютере. Изображение разбивается на маленькие фрагменты,
которые можно назвать точками. Каждое изображение имеет своё разрешение. Оно
состоит из двух цифр, которые разделяются крестиком или двоеточием. Число
слева, означает, на сколько точек делится изображение по горизонтали, а справа
– на сколько по вертикали. Таким образом изображение на компьютере
представляется в виде последовательности точек, каждая из которых имеет свой
цвет. То есть изображение на компьютере можно представить, последовательно
записав цвета всех точек, которые в него входят.
Но как же представить
цвет в виде двоичных кодов? Любой цвет на мониторе компьютера изображается
смешиванием в разных количествах трёх основных цветов: красного, зелёного и
синего. Такое представление цветов называется их RGB-моделью.
По первым буквам названий основных цветов на английском языке, то есть «Rad»,
«Green» и «Blue».
Так, как остальные цвета – это смеси трёх основных цветов в разных количествах,
их можно представить в виде трёх чисел, количеств основных цветов. Эти числа
можно заменить двоичными кодами одинаковой разрядности. Записав эти коды
последовательно, мы получим двоичный код цвета точки. Таким образом изображение
на компьютере представляется в виде списка двоичных кодов одинаковой
разрядности, каждый из которых обозначает цвет одной из точек изображения.
Немного иначе происходит
двоичное кодирование звука. Позже из курса физики вы узнаете, что любой звук
можно представить в виде непрерывной волны. Эту волну можно описать, зависимостью
её амплитуды, то есть громкости звука от времени. Такую зависимость легко
изобразить в виде графика. Чтобы представить звук в виде дискретных сигналов,
время, в течение которого продолжается звук, делится на равные небольшие
промежутки. И на каждом из промежутков заново определяется амплитуда волны, то
есть громкость звука.
Дискретизация
звука
То, есть звук можно
представить в виде списка чисел, каждое из которых означает амплитуду волны, в
течение небольшого промежутка времени. Эти числа можно представить в виде
двоичных кодов с одинаковым количеством разрядов. Таким образом звук на
компьютере представляется в виде списка двоичных кодов одинаковой разрядности,
каждый из которых обозначает амплитуду звуковой волны на некотором небольшом
промежутке времени.
Мы знаем, что с помощью
двоичного кодирования в виде последовательности единиц и нулей можно
представить любую информацию на естественном или формальном языке, в том числе
изображение и звук. То есть информацию из любой формы можно представить в виде
двоичного кода, что означает универсальность двоичного кодирования. Это и есть
его главное преимущество. Главный недостаток двоичного кодирования – это
большой размер двоичного кода. Так при кодировании текстового сообщения одному
символу текста может соответствовать несколько символов двоичного кода.
Давайте подумаем, как
можно уменьшить размер двоичного кода, и вообще любого кода. До этого все
двоичные коды, которые мы рассматривали, были равномерными. Равномерным
называется код, который состоит из равных по количеству разрядов кодовых
комбинаций. Так например при кодировании алфавита для каждой буквы мы
использовали двоичные коды с одинаковым количеством разрядов. Однако не все
символы алфавита в текстовом сообщении, встречаются одинаково часто. Поэтому,
для того, чтобы сократить длину двоичного кода мы можем присвоить разным
сигналам коды разной длины. Коды с меньшей разрядностью можно присвоить сигналам,
которые в сообщении встречаются чаще, а коды с большей разрядностью – сигналам,
которые встречаются в сообщении реже. Такой код называется неравномерным, то есть
он состоит из комбинаций различной длины.
Пример неравномерного
кода – азбука Морзе. В ней разным буквам алфавита, соответствует разное
количество сигналов, длинных и коротких. Например буква «А» обозначается всего
двумя сигналами: одним коротким и одним длинным. А твёрдый знак кодируется
пятью сигналами: двумя длинными, одним коротким и двумя длинными.
Рассмотрим один из
методов неравномерного кодирования текстовых сообщений. Он называется методом Хаффмана.
Посмотрим, как работает этот метод, закодировав с его помощью сообщение: «МАМА
МЫЛА РАМУ». Сначала выпишем все символы алфавита, который используется в
сообщении. В данном сообщении используются символы: «М», «А», пробел, «Ы», «Л»,
«Р» и «У». Затем нужно записать, как часто в сообщении встречается каждый из
символов. Буквы «М» и «А» повторяются по четыре раза. Пробел повторяется
дважды. Буквы «Ы», «Л», «Р» и «У» в сообщении встречаются по одному разу. Затем
символы сообщения записываются в порядке убывания частоты появления. У нас они
так и записаны.
Теперь строится дерево частоты
появления символов в сообщении. В начале берутся два символа, которые
встречаются в сообщении реже всех. У нас таких символа четыре, возьмём два
правых, буквы «Р» и «У», соединяем их линией, и складываем их частоту появления
в сообщении. 1 + 1 = 2.
Теперь повторим то же
действие. Реже всех у нас появлялись буквы «Ы» и «Л». Соединим их линиями
сложив частоту появления получим 2.
Теперь снова смотрим где
у нас самая маленькая частота появления. Таких частот у нас три. Пробел
появлялся дважды, двум равны и общие частоты появления символов «Ы» и «Л», и
символов «Р» и «У». Возьмём две правые частоты и объединим их. Их суммарная частота
равна 4.
Снова ищем минимальные
частоты появления. Возьмём две правые частоты и объединим их. Их сумма равна 6.
Теперь объединим две
левые частоты. Их сумма равна 8.
Объединим две оставшиеся
частоты. Их сумма равна 14. Именно четырнадцати равна длина кодируемого
сообщения.
Теперь двигаясь, сверху
вниз присвоим ветвям дерева значения 0 и 1. Ветви, с большей частотой будем
присваивать 1, а ветви с меньшей частотой – 0. Так левой ветви верхнего узла
присвоим 1, а правой – 0.
Затем рассмотрим левый
узел. Там две частоты равны. Поэтому левой ветви присвоим 0, а правой – 1.
Рассмотрим узел, частота
которого равна 6. Частота появления пробела меньше суммарной частоты правой
ветви. Поэтому левой ветви присвоим 0, а правой ветви – 1.
По такому же принципу
пронумеруем оставшиеся ветви дерева.
Теперь, двигаясь по
получившемуся дереву сверху вниз, мы можем записать двоичный код каждого
символа. Так у буквы «М» будет код 10, у буквы «А» – 11, у пробела – 00 и т. д…
Теперь нам остаётся лишь
заменить все символы в сообщении их двоичными кодами. В итоге двоичный код
нашего сообщения будет 101110110010010001011100011011100111. Всего в нём 36
разрядов.
У некоторых из вас может
возникнуть вопрос, а как же расшифровать такое сообщение, ведь в отличии от
равномерного кода мы не знаем точно сколько разрядов занимает каждый символ.
При неравномерном кодировании достаточно, чтобы код никакого из символов не
начинался с кода другого символа. Давайте попробуем расшифровать первые символы
нашего сообщения.
Итак, сообщение
начинается с единицы. С единицы у нас начинаются двоичные коды букв «М» и «А»,
посмотрев на следующий символ 0, мы можем точно определить, что первый символ –
это буква «М». По такому же принципу мы можем определить, что, следующий символ
буква «А» и до конца расшифровать слово «МАМА».
Следующая цифра – 0. С
нуля у нас начинаются коды пяти символов. После него идёт так же 0. С 00 у нас
начинается код пробела. Далее идёт буква «М». Следующая цифра – 0. С нуля у нас
начинаются коды 5 символов. Возьмём следующую цифру. С 01 начинаются коды
четырёх символов. Следующая цифра – 0. С 010 начинаются коды двух символов.
Следующий символ – снова 0. И мы можем однозначно определить, что это буква
«Ы». Так же расшифровывается и остальное сообщение.
Давайте посмотрим,
двоичный код из скольких разрядов получился бы при использовании равномерного
двоичного кодирования. Как мы помним сообщение записано с помощью алфавита
мощностью 7 символов. Определим, разрядность двоичного кода, необходимую для
кодирования одного символа такого алфавита. Как мы помним, для этого необходимо
определить, в какую степень возвести цифру 2, чтобы получить 7. Но цифру семь
мы так получить не можем, поэтому результат необходимо округлить в большую
сторону. Мы можем так получить 8, для этого двойку нужно возвести в 3 степень.
То есть для кодирования одного символа нам потребуется 3-разрядный двоичный
код. Определим, какой код потребуется для кодирования всего сообщения, для
этого нужно разрядность кода одного символа, то есть 3 умножить на длину всего
сообщения, то есть 14. 3 × 14 = 42. То есть при кодировании сообщения нам
потребовался бы 42-разрядный равномерный двоичный код. При использовании
неравномерного кода нам потребовалось всего 36 разрядов, то есть на 6 разрядов
меньше.
Сокращение длины
двоичного кода заметно даже при небольшой длине сообщения. Если длина сообщения
будет больше, например десятки тысяч символов, разница между длинами
равномерного и неравномерного кода тоже увеличится. Когда длина двоичного кода
составляет миллиарды разрядов – разница между равномерным и неравномерным кодом
просто огромна.
Важно запомнить:
· Универсальность
двоичного кодирования означает, что его можно применять для кодирования
информации на любом формальном или неформальном языке, а также изображений и
звука.
· Все
коды можно разделить на равномерные и неравномерные, где равномерный код
состоит из комбинаций равной длины, а неравномерный код состоит из
комбинаций разной длины.
· Использование
неравномерного кодирования позволяет сократить длину кода.

