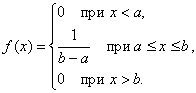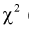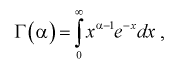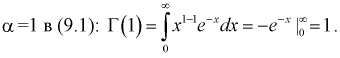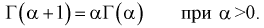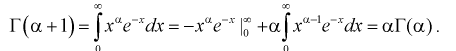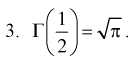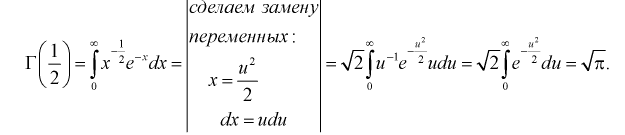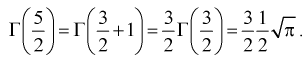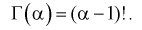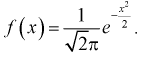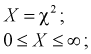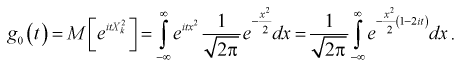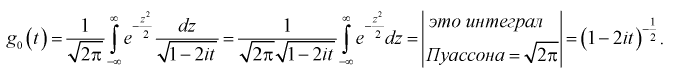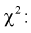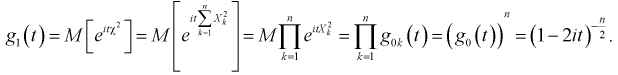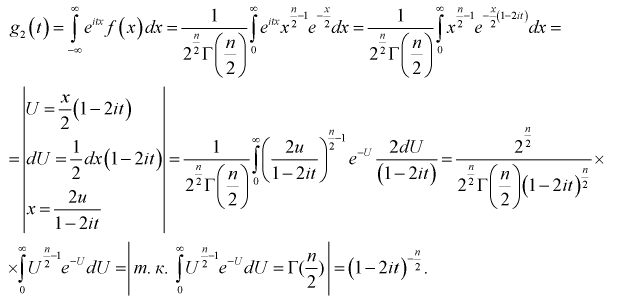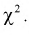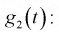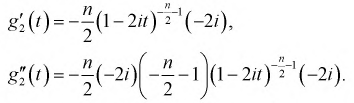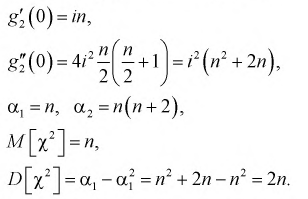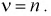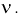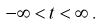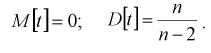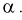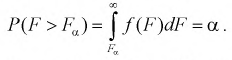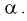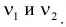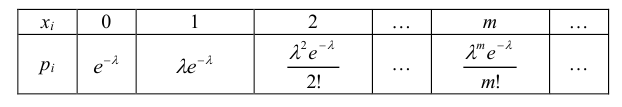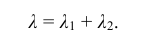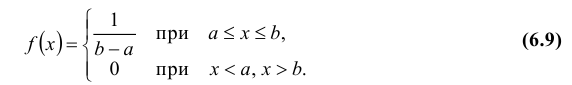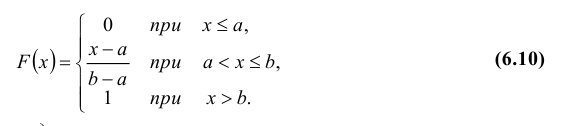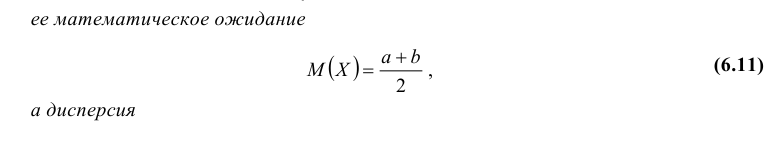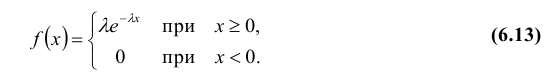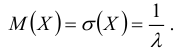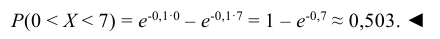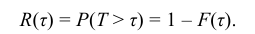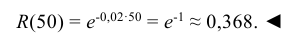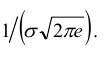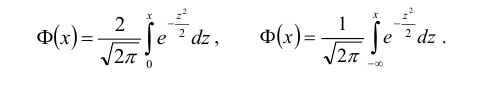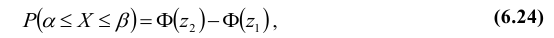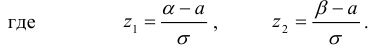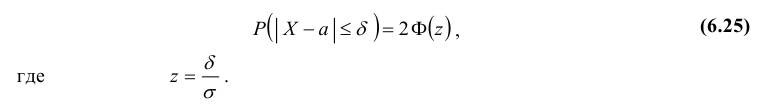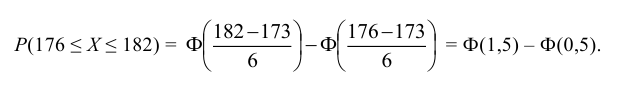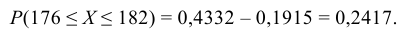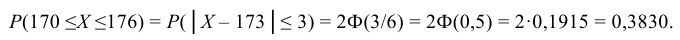19.
Равномерный закон распределения и его
числовые характеристики.
На практике встречаются
случайные величины, о которых заранее
известно, что они могут принять какое-либо
значение в строго определенных границах,
причем в этих границах все значения
случайной величины имеют одинаковую
вероятность (обладают одной и той же
плотностью вероятностей).
Например, при поломке
часов остановившаяся минутная стрелка
будет с одинаковой вероятностью
(плотностью вероятности) показывать
время, прошедшее от начала данного часа
до поломки часов. Это время является
случайной величиной, принимающей с
одинаковой плотностью вероятности
значения, которые не выходят за границы,
определенные продолжительностью одного
часа. К подобным случайным величинам
относится также и погрешность округления.
Про такие величины говорят, что они
распределены равномерно, т. е. имеют
равномерное распределение.
Определение.
Непрерывная случайная величина Х имеет
равномерное распределение на отрезке
[а, в], если на этом отрезке плотность
распределения вероятности случайной
величины постоянна, т. е. если
дифференциальная функция распределения
f(х) имеет следующий вид:
Иногда это распределение
называют законом равномерной плотности.
Про величину, которая имеет равномерное
распределение на некотором отрезке,
будем говорить, что она распределена
равномерно на этом отрезке.
Найдем значение
постоянной с. Так как площадь, ограниченная
кривой распределения и осью Ох, равна
1(исходя из св-в плотности вероятности
), то
откуда с=1/(b-a).
Таким образом,
непрерывная случайная величина X имеет
равномерный закон распределения, на
отрезке [a, b], если её плотность вероятности
Построим функцию
распределения F(x), для чего найдем
выражение F(x) на интервале [a, b]:
Теорема. Функция
распределения случайной величины X,
распределённой по равномерному закону,
есть
её математическое
ожидание
а её дисперсия
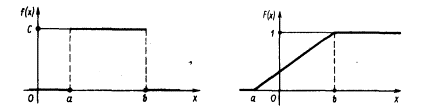
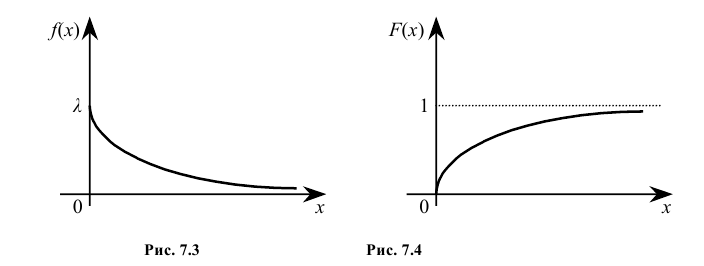
Графики функций f(x) и
F(x) имеют вид:
Равномерный закон
распределения используется при анализе
ошибок округления при проведении
числовых расчётов (например, ошибка
округления числа до целого распределена
равномерно на отрезке [-0,5; 0,5]), в ряде
задач массового обслуживания, при
статистическом моделировании наблюдений,
подчинённых заданному распределению.
Так, случайная величина X, распределённая
равномерно на отрезке [0; 1], называемая
«случайным числом от 0 до 1», служит
исходным материалом для получения
случайных величин с любым законом
распределения.
Найдем числовые
характеристики.
Используя формулу для
вычисления математического ожидания
НСВ, имеем:
Таким образом,
математическое ожидание случайной
величины, равномерно распределенной
на отрезке [a, b] совпадает с серединой
этого отрезка.
Найдем дисперсию
равномерно распределенной случайной
величины:
откуда сразу же следует,
что среднее квадратическое отклонение:
Найдем теперь вероятность
попадания значения случайной величины,
имеющей равномерное распределение, на
интервал (a,b), принадлежащий целиком
отрезку [a, b]:

Геометрически эта
вероятность представляет собой площадь
заштрихованного прямоугольника. Числа
а и b называются параметрами распределения
и однозначно определяют равномерное
распределение.
Пример1.
Автобусы некоторого маршрута идут
строго по расписанию. Интервал движения
5 минут. Найти вероятность того, что
пассажир, подошедший к остановке. Будет
ожидать очередной автобус менее 3 минут.
Решение:
СВ- время ожидания
автобуса имеет равномерное распределение.
Тогда искомая вероятность будет равна:
Пример2.
Ребро куба х измерено приближенно.
Причем
Рассматривая ребро
куба как случайную величину, распределенную
равномерно в интервале (a, b), найти
математическое ожидание и дисперсию
объема куба.
Решение:
Объем куба- случайная
величина, определяемая выражением У=
Х3. Тогда математическое ожидание равно:
Дисперсия:
Равномерное случайное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Равномерным называют распределение вероятностей непрерывной случайной величины
, если на интервале
, которому принадлежат все возможные
значения
, плотность сохраняет постоянное значение.
Функция распределения
равномерного закона:
Числовые характеристики равномерного распределения
Математическое ожидание равномерно распределенной случайной величины:
Дисперсия
равномерного случайного
распределения:
Среднее квадратическое отклонение случайной величины, распределенной равномерно:
Для равномерного распределения коэффициент асимметрии:
Коэффициент эксцесса
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Кроме равномерного, основные законы распределения непрерывных случайных величин:
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Экспоненциальный (показательный) закон распределения случайной величины
Примеры решения задач
Пример 1
Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность вероятности
равномерного распределения на интервале
:
Искомая вероятность:
Ответ:
.
Пример 2
Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).
Решение
Плотность
вероятности случайной величины, распределенной равномерно на интервале
В нашем
случае
Получаем:
Функцию
распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
Построим
графики:
График плотности распределения
График функции распределения
Математическое
ожидание величины, распределенной равномерно:
Дисперсия:
Среднее
квадратическое отклонение:
Пример 3
Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
равномерного распределения:
Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:
Ответ:
Пример 4
Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.
Решение
Дисперсия
равномерного распределения:
при
начале интервала
:
Искомый
интервал времени:
Ответ:
.
Задачи контрольных и самостоятельных работ
Задача 1
Случайные
величины X2, X3, X4 имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<Xi<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.
Задача 2
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, xmod, xmed, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.
Задача 3
Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].
Найти:
1) дифференциальную и интегральную
функцию распределения, а также построить их графики.
2) математическое ожидание и
дисперсию;
2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).
Задача 5
Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.
Задача 6
Равномерно распределенная случайная
величина
задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).
Задача 7
Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x0.2.
Задача 8
Случайная
величина
равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).
Задача 9
Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].
Задача 10
Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?
Задача 11
Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].
Задача 12
Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.
Задача 13
СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.
Задача 15
Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.
Задача 16
Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].
Задача 17
Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).
Задача 18
По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.
Задача 19
Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.
Задача 20
Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Непрерывная случайная величина Х имеет Равномерный закон распределения на отрезке , если ее плотность вероятности Р(Х) постоянна на этом отрезке и равна нулю вне его, т. е.
Функция распределения случайной величины Х, распределенной по равномерному закону, есть
Математическое ожидание дисперсия


Пример 8.14. Поезда метрополитена идут регулярно с интервалом 3 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше минуты. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х — времени ожидания поезда.
Решение. Случайная величина Х — время ожидания поезда на временном (в минутах) отрезке имеет равномерный закон распределения
. Поэтому вероятность того, что пассажиру придется ждать не более минуты, равна
От равной единице площади прямоугольника (рис. 8.11), т. е.
Мин,
мин.
 |
Рис. 8.11
Пример 8.15. Найти математическое ожидание и дисперсию произведения двух независимых случайных величин ξ и η с равномерными законами распределения: ξ в интервале , η — в интервале
.
Решение. Так как математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, то . Для нахождения дисперсии воспользуемся формулой
найдем по формуле

Аналогично рассчитаем

Следовательно,
.
Пример 8.16. Вычислить математическое ожидание и дисперсию определителя

Элементы которого — независимые случайные величины с
и
Решение. Вычислим математическое ожидание
Для нахождения дисперсии докажем, что если ξ и η — независимые случайные величины, то
Действительно,
Следовательно,
Замечание. Для определителя N-го порядка ;
Пример 8.17. Автоматический светофор работает в двух режимах: 1 мин. горит зеленый свет и 0,5 мин — красный и т. д. Водитель подъезжает к перекрестку в случайный момент времени. 1. Найти вероятность того, что он проедет перекресток без остановки. 2. Составить закон распределения и вычислить числовые характеристики времени ожидания у перекрестка.
Решение. 1. Момент проезда автомобиля T через перекресток распределен равномерно в интервале, равном периоду смены цветов светофора. Этот период равен 1 + 0,5 = 1,5 мин. Для того чтобы машина проехала через перекресток не останавливаясь, достаточно того, чтобы момент проезда пришелся на интервал времени . Тогда

2. Время ожидания является смешанной случайной величиной: с вероятностью
она равна нулю, а с вероятностью
принимает с равномерной плотностью вероятностей любые значения между 0 и 0,5 мин; тогда график функции распределения случайной величины
имеет вид, изображенный на рис. 8.12:
 |
Рис. 8.12
То есть при
;

;
при
.
Среднее время ожидания у перекрестка

Дисперсия времени ожидания

Мин.
| < Предыдущая | Следующая > |
|---|
ЛЕКЦИЯ 9
ТЕМА: ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
1.
Равномерный закон распределения.
2.
Нормальный закон распределения.
2.1.
Интегральная и дифференциальная функции
распределения. Вероятность попадания в
заданный интервал.
2.2.
Вычисление вероятности заданного
отклонения.
2.3.
Правило трех сигм.
3.
Показательный закон распределения.
3.1.
Интегральная и дифференциальная функции
распределения.
3.2.
Числовые характеристики.
3.3.
Функция надежности.

1.
Равномерный
закон распределения.
На
практике встречаются случайные величины, о
которых заранее известно, что они могут
принять какое-либо значение в строго
определенных границах, причем в этих
границах все значения случайной величины
имеют одинаковую вероятность (обладают
одной и той же плотностью вероятностей).
Например,
при поломке часов остановившаяся минутная
стрелка будет с одинаковой вероятностью (плотностью
вероятности) показывать время, прошедшее от
начала данного часа до поломки часов. Это
время является случайной величиной,
принимающей с одинаковой плотностью вероятности
значения, которые не выходят за границы,
определенные продолжительностью одного
часа. К подобным случайным величинам
относится также и погрешность округления.
Про такие величины говорят, что они
распределены равномерно, т. е. имеют
равномерное распределение.
Определение.
Непрерывная случайная величина Х имеет
равномерное распределение на отрезке [а,
в], если на этом
отрезке плотность распределения
вероятности случайной величины постоянна,
т. е. если дифференциальная функция
распределения f(х)
имеет следующий вид:
Иногда
это распределение называют законом
равномерной плотности. Про величину,
которая имеет равномерное распределение на
некотором отрезке, будем говорить, что она
распределена равномерно на этом отрезке.
Найдем
значение постоянной с. Так как площадь,
ограниченная кривой распределения и осью Ох,
равна 1, то
откуда
с=1/(b—a).
Теперь
функцию f(x)
можно представить в виде
Построим
функцию распределения F(x), для чего найдем выражение F(x)
на интервале [a, b]:
Графики
функций f(x)
и F(x)
имеют вид:
Найдем
числовые характеристики.
Используя
формулу для вычисления математического
ожидания НСВ, имеем:
Таким
образом, математическое ожидание случайной
величины, равномерно распределенной на
отрезке [a, b]
совпадает с серединой этого отрезка.
Найдем
дисперсию равномерно распределенной
случайной величины:
откуда
сразу же следует, что среднее
квадратическое отклонение:
Найдем
теперь вероятность попадания значения
случайной величины, имеющей равномерное
распределение, на интервал (a,b),
принадлежащий целиком
отрезку [a,
b]:
Геометрически
эта вероятность представляет
собой площадь
заштрихованного прямоугольника. Числа а
и b называются параметрами
распределения и однозначно
определяют равномерное распределение.
Пример1.
Автобусы некоторого маршрута идут строго
по расписанию. Интервал движения 5 минут.
Найти вероятность того, что пассажир,
подошедший к остановке. Будет ожидать
очередной автобус менее 3 минут.
Решение:
СВ-
время ожидания автобуса имеет равномерное
распределение. Тогда искомая вероятность
будет равна:
Пример2.
Ребро куба х измерено приближенно. Причем
Рассматривая
ребро куба как случайную величину,
распределенную равномерно в интервале (a,
b),
найти математическое ожидание и дисперсию
объема куба.
Решение:
Объем
куба- случайная величина, определяемая
выражением У= Х3. Тогда математическое
ожидание равно:
Дисперсия:
2.
Нормальный закон распределения.
2.1.Интегральная
и дифференциальная функции распределения.
Вероятность попадания в заданный интервал.
Одним
из наиболее часто встречающихся
распределений является нормальное
распределение. Оно играет большую роль в
теории вероятностей и занимает среди
других распределений особое положение.
Нормальный закон распределения является
предельным законом, к которому
приближаются другие законы распределения
при часто встречающихся аналогичных
условиях.
Если
предоставляется возможность рассматривать
некоторую случайную величину как сумму
достаточно большого числа других случайных
величин, то данная случайная величина
обычно подчиняется нормальному закону
распределения. Суммируемые случайные
величины могут подчиняться каким угодно
распределениям, но при этом должно
выполняться условие их независимости (или
слабой зависимости). При соблюдении
некоторых не очень жестких условий
указанная сумма случайных величин
подчиняется приближенно нормальному
закону распределения и тем точнее, чем
большее количество величин суммируется.
Ни
одна из суммируемых случайных величин не
должна резко отличаться от других, т. е.
каждая из них должна играть в общей сумме
примерно одинаковую роль и не иметь
исключительно большую по сравнению с
другими величинами дисперсию.
Для
примера рассмотрим изготовление некоторой
детали на станке-автомате. Размеры
изготовленных деталей несколько
отличаются от требуемых. Это отклонение
размеров от стандарта вызывается
различными причинами, которые более или
менее независимы друг от друга. К ним могут
относиться:
неравномерный
режим обработки детали; неоднородность
обрабатываемого материала; неточность
установки заготовки в станке; износ
режущего инструмента и деталей станков;
упругие
деформаций узлов станка; состояние
микроклимата в цехе; колебание напряжения в
электросети и т. д. Каждая из перечисленных
и подобных им причин влияет на отклонение
размера изготовляемой детали от стандарта.
Таким образом, общее отклонение размера,
фиксируемое измерительным прибором,
является суммой большего числа отклонений,
обусловленных различными причинами. Если
ни одна из этих причин не является
доминирующей, то суммарное отклонение
является случайной величиной, имеющей
нормальный закон распределения.
Так
как нормальному закону подчиняются только
непрерывные случайные величины, то это
распределение можно задать в виде
плотности распределения вероятности.
Определение:
Непрерывная случайная величина Х имеет
нормальное распределение (распределена по
нормальному закону), если плотность
распределения вероятности f(x) имеет вид
где
а
и s—некоторые
постоянные, называемые параметрами
нормального распределения.
Функция
распределения F(x) в
рассматриваемом случае принимает вид
Параметр
а— есть
математическое ожидание НСВХ, имеющей
нормальное распределение, s —
среднее квадратическое
отклонение, тогда дисперсия равна
Выясним геометрический смысл
параметров распределения а
и s.
Для этого исследуем
поведение функции f(x).
График функции f(x)
называется нормальной кривой.
Рассмотрим
свойства функции f(x):
1°.
Областью определения функции f(x)
является вся числовая ось.
2°.
Функция f{x)
может принимать только положительные
значения, т. е. f(x}>0.
3°.
Предел функции f(x) при
неограниченном возрастании |х| равен нулю,
т. е. ось ОХ является горизонтальной
асимптотой графика функции.
4°. Функция f{x)
имеет в точке х =
a максимум,
равный
5°.
График функции f(x)
симметричен относительно прямой х =
а.
6°.
Нормальная кривая в точках х = а
+s
имеет перегиб,
На
основании доказанных свойств построим
график плотности нормального
распределения f(x).
Использование
формул f(x)
и F(x)
для практических расчетов затруднительно.
Но решение задач по этим
формулам можно
упростить, если от нормального
распределения с произвольными параметрами а и s
перейти
к нормальному распределению с
параметрами а=0, s
= 1.
Функция
плотности нормального распределения f(x)
с параметрами а=0, s
=1 называется плотностью
стандартной нормальной
случайной величины и ее график имеет вид:
Функция
плотности и интегральная функция
стандартной нормальной СВ будут иметь вид:
Для
вычисления вероятности попадания СВ в
интервал (a,
b) воспользуемся
функцией Лапласа:
Перейдем
к стандартной нормальной случайной
величине
Тогда
Значения
функции Ф(u) необходимо взять из таблицы
приложений «Таблица значений функции Ф(х)»
.
Пример.
Случайная величина Х распределена по нормальному
закону. Математическое
ожидание и среднее квадратическое
отклонение этой величины соответственно
равны 30 и 10. Найти вероятность того, что Х
примет значение, принадлежащее интервалу
(10, 50).
Решение:
По
условию:a =10,
b=50, а=30,
s =10,
следовательно,
По
таблице находим Ф
(2) = 0,4772. Отсюда, искомая вероятность:
Р(10
< Х < 50) =2×0,4772=0,9544.
2.2.
Вычисление вероятности заданного
отклонения
Часто
требуется вычислить вероятность того, что
отклонение нормально распределенной
случайной величины Х
по абсолютной величине меньше заданного
положительного числа d,
т. е. требуется найти
вероятность осуществления неравенства |x
—а|<d.
Заменим
это неравенство равносильным ему двойным
неравенством
Тогда
получим:
Приняв
во внимание равенство:
(функция
Лапласа—нечетная), окончательно
имеем
Вероятность
заданного отклонения равна
На
рисунке наглядно показано, что если две
случайные величины нормально распределены
и а
= 0, то вероятность
принять значение, принадлежащее интервалу (-d,d),больше у
той величины, которая имеет меньшее
значение d.
Этот факт полностью
соответствует вероятностному смыслу
параметра s
.
Пример.
Случайная величина Х
распределена нормально. Математическое
ожидание и среднее квадратическое
отклонение Х соответственно равны 20 и 10. Найти
вероятность того, что отклонение по
абсолютной величине будет меньше трех.
Решение:
Воспользуемся
формулой
По
условию ,
тогда
2.3.
Правило трех сигм
Преобразуем
формулу
Введем
обозначение
Тогда
получим:
Если
t=3,
то
т.
е. вероятность того, что отклонение по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973.
Другими
словами, вероятность того, что абсолютная
величина отклонения превысит утроенное
среднее квадратическое отклонение, очень
мала, а именно равна 0,0027=1-0,9973.
Это означает, что лишь в 0,27% случаев так
может произойти. Такие события, исходя из
принципа невозможности маловероятных
событий можно считать практически
невозможными. В этом и состоит сущность
правила трех сигм:
Если случайная величина
распределена нормально, то абсолютная
величина ее отклонения от математического
ожидания не превосходит утроенного
среднего квадратического отклонения.
На
практике правило трех сигм применяют так:
если распределение изучаемой случайной
величины неизвестно, но условие, указанное
в приведенном правиле, выполняется, то есть
основание предполагать, что изучаемая
величина распределена нормально; в
противном случае она не распределена
нормально.
3.
Показательное
распределение.
3.1.
Интегральная и дифференциальная
функции распределения.
Определение:
Непрерывная случайная величина X, функция
плотности которой задается выражением
называется случайной
величиной, имеющей показательное, или
экспоненциальное, распределение.
Величина
срока службы различных устройств и времени
безотказной работы отдельных элементов
этих устройств при выполнении определенных
условий обычно подчиняется показательному
распределению. Другими словами, величина
промежутка времени между появлениями двух
последовательных редких событий
подчиняется зачастую показательному
распределению.
Как
видно из формулы , показательное
распределение определяется только одним
параметром m.
Найдем
функцию распределения показательного
закона, используя свойства
дифференциальной функции распределения:
Графики
дифференциальной и интегральной функций
показательного распределения имеют вид:
3.2.
Числовые характеристики.
Используя
формулы для вычисления математического
ожидания, дисперсии и среднего
квадратического отклонения нетрудно
убедится, что для показательного
распределения
.
Таким
образом, для показательного распределения
характерно, что среднее квадратическое
отклонение численно равно математическому
ожиданию.
Найдем
вероятность попадания СВ в интервал (a,b):
3.3.
Функция надежности.
Пусть
некоторое устройство начинает работать в
момент времени t0
= 0, а по истечении времени длительностью t происходит отказ. Обозначим
через Т НСВ — длительность времени
безотказной работы устройства. Если
устройство проработало безотказно время
меньшее t,
то, следовательно, за время длительностью t наступит отказ. Тогда
функция распределения F(t)=P(T<t)=1- e—mt определяет
вероятность отказа устройства за время t.
Найдем
вероятность противоположного события-
безотказной работы за время t:
.
Функция
R(t)
называется функцией надежности.
Выясним
смысл числовых характеристик и параметра
распределения.
Математическое
ожидание — это среднее время между двумя
ближайшими отказами устройства, а величина
обратная математическому ожиданию
(параметр распределения)- интенсивность
отказов, т.е. количество отказов в единицу
времени.
Пример.
Время безотказной работы устройства
распределено по закону
Найти
среднее время безотказной работы
устройства, вероятность того, что
устройство не откажет за среднее время
безотказной работы. Найти вероятность
отказа за время t= 100
часов.
Решение:
По
условию интенсивность отказов m
=0,02. Тогда
среднее время между двумя отказами, т.е.
математическое ожидание М(Х)=1/0,02=50часов.
Вероятность безотказной работы за этот
промежуток времени вычислим по функции
надежности:
По
функции F(t)
вычислим вероятность отказа за время t
=100
часов:
Контрольные
вопросы.
1.
Сформулировать равномерный закон
распределения. Записать дифференциальную и
интегральную функции.
2.
Записать формулы для вычисления
числовых характеристик равномерно
распределенной случайной величины.
3.
Сформулировать нормальный закон
распределения. Записать дифференциальную и
интегральную функции.
4.
Описать свойства дифференциальной
функции нормально распределенной
случайной величины. Пояснить
геометрический смысл параметров
нормального распределения.
5.
При каких значениях параметров функция
плотности нормального распределения
называется плотностью стандартной
нормальной случайной величины?
6.
Записать формулу для вычисления
вероятности отклонения нормально
распределенной СВ от математического
ожидания.
7.
Сформулировать правило трех сигм и
пояснить его суть.
8.
Сформулировать показательный закон
распределения. Записать дифференциальную и
интегральную функции.
9.
Каков смысл параметра показательного
распределения, если в качестве СВ
рассматривать время безотказной работы
устройства? Какими выражениями параметр
распределения связан с числовыми
характеристиками?
10.
Вероятность какого события определяет
функция надежности?
Содержание:
В статистике наиболее часто применяются такие распределения:
- Нормальное (Гауссовское) распределение.
- Распределение Пирсона, распределение
- Распределение Стьюдента (t — распределение).
- Распределение Фишера (F — распределение).
Нормальный закон распределения мы подробно рассмотрели при изучении раздела 6.5 теории вероятностей и здесь рассматриваться не будет.
Отметим, что в законы распределений математической статистики входит гамма-функция, поэтому необходимо познакомиться с этой функцией и рассмотреть ее свойства.
Гамма-функция и ее свойства
Гамма-функцией или интегралом Эйлера второго рода называется функция следующего вида:
где 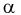
Свойства гамма-функции:
1. Г(1) = Г(2) = 1.
Доказательство:
Подставим
2.
Доказательство:
Вычислим интеграл в (9.1), используя интегрирование по частям:
Доказательство:
Значит, если значение 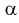
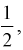
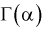
Для целых 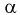
Например,
Г(3) = 2! = 2, Г(4) = 3! = 6, Г(5) = 4! = 24.
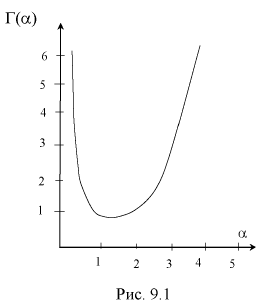
Отметим, что смысл гамма-функции — распространение понятия факториал на нецелые значения. На рис. 9.1 приведен график гамма-функции.
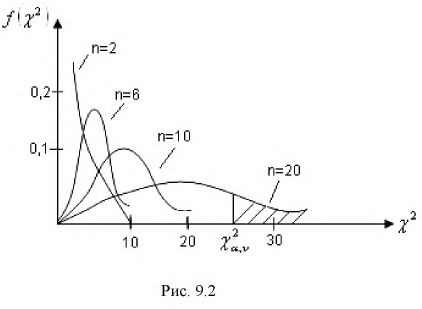
Распределение (хи-квадрат )
Распределение 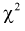
Случайная величина имеет закон распределения 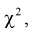
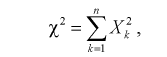
где 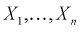
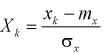
Распределение случайной величины, определенной по формуле (9.2), называется распределением Пирсона.
Покажем, что плотность распределения случайной величины 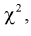
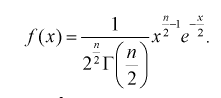
Здесь для краткости записи
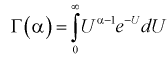
Для доказательства используем аппарат характеристических функций. Найдем характеристическую функцию случайной величины которая входит в формулу (9.2), учитывая, что 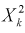
Используем подстановку 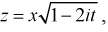
Согласно 5-му свойству характеристической функции (для суммы независимых случайных величин) найдем характеристическую функцию 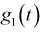
Найдем характеристическую функцию 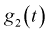
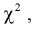
При сравнении правых частей характеристических функций 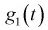
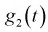
Найдем математическое ожидание и дисперсию случайной величины
Продифференцируем 2 раза
Значения производных при t = 0:
Таким образом, математическое ожидание 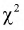
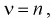
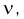
С ростом 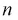
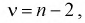
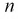
При 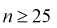
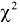
Квантилем 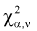
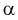
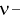
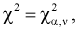
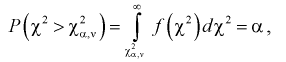
т. е. это то значение 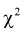
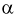
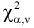
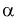
Распределение Стьюдента
Распределение Стьюдента 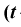
Случайная величина t имеет распределение Стьюдента, если она определяется так.
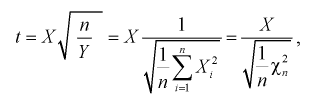
где X — нормированная нормальная случайная величина,
Y — величина 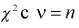
X и Y — независимые случайные величины.
Случайная величина t является функцией нормально распределенных нормированных случайных величин и называется безразмерной дробью Стьюдента. Плотность распределения случайной величины t определяется равенством
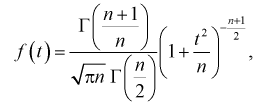
где
Числовые характеристики случайной величины t :
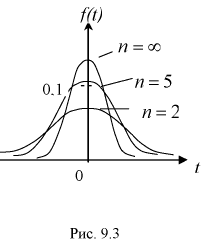
На рис. 9.3 приведены кривые распределения Стьюдента. Кривые на рис. 9.3 качественно напоминают кривые нормального закона распределения с математическим ожиданием, равным нулю, и при 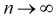
Квантили распределения Стьюдента 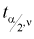
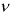
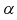
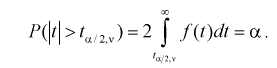
Рис. 9.4 иллюстрирует процесе определения квантилей, т. е. необходимо так выбрать 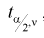
Распределение Фишера (F-распределение)
Случайная величина F имеет распределение Фишера, если она определяется так:
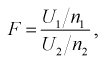
где 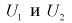
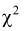
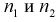
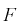
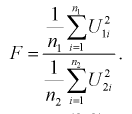
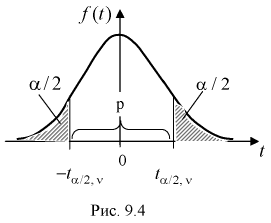
Безразмерная случайная величина F (9.8) имеет плотность распределения, определяемую следующей формулой:
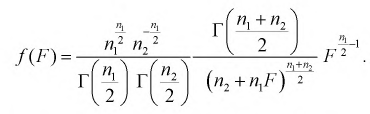
Распределение случайной величины F зависит от двух параметров 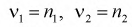
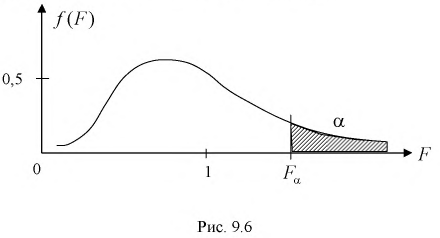
Квантили распределения Фишера 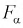
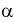
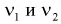
На рис. 9.6 показано, что надо так выбрать 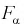
Как правило, квантили 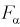
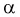
Биноминальный закон распределения
Определение: Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями 
Как видим, вероятности Р(Х = m) находятся по формуле Бернулли.
Следовательно, биноминальный закон распределения представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биноминального закона имеет вид:
Теорема. Математическое ожидание случайной величины, распределенной по биноминальному закону 
Следствие. Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью, равно 
Биноминальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Закон распределения Пуассона
Определение: Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m с вероятностями 
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.
При достаточно больших n (вообще при n → ∞) и малых значениях р (р → 0) при условии, что произведение np – постоянная величина (nр → λ = const), закон распределения Пуассона является хорошим приближением биноминального закона. Т.е. при n → ∞, р → 0, nр → λ = const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона часто называют законом редких явлений.
По закону Пуассона распределены, например, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание в единицу времени в системах массового обслуживания, и т.п.
Отметим еще, что если случайная величина представляет собой сумму двух независимых случайных величин, каждая из которых распределена по закону Пуассона, то она также распределена по закону Пуассона с параметром
Равномерный закон распределения
Определение: Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности f(x) постоянна на этом отрезке и равна нулю вне его, т.е.
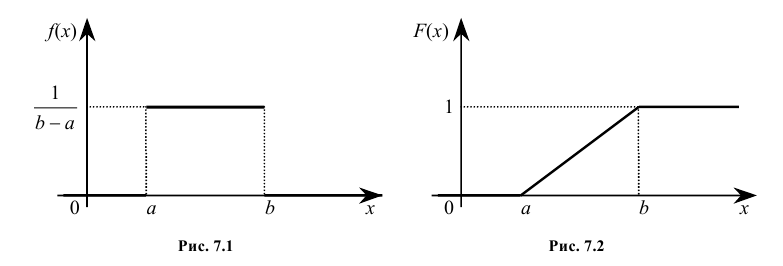
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.1 и рис. 7.2.
Теорема. Функция распределения случайной величины Х, распределенной по равномерному закону, есть
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач теории массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению, и т.д.
Показательный (экспоненциальный) закон распределения
Определение: Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности f(x) имеет вид:
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.3 и рис. 7.4.
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть 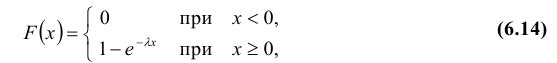

Отсюда следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е.
Вероятность попадания в интервал [a; b] непрерывной случайной величины Х, распределенной по показательному закону, находится как
Пример:
Установлено, что время ремонта железнодорожных вагонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт вагона потребуется менее 7 дней, если среднее время ремонта вагонов составляет 10 дней.
Решение:
По условию математическое ожидание М(Х) = 1/λ = 10, откуда параметр λ = 0,1. По формуле (6.17) находим вероятность попадания случайной величины Х в интервал [0, 7]:
Показательный закон распределения играет большую роль в теории массового обслуживания. Так например, интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока. Кроме того, показательное распределение широко применяется в теории надежности, одним из основных понятий которой является функция надежности.
Функция надежности
Будем называть элементом некоторое устройство. Пусть элемент начинает работать в момент времени 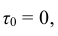
Таким образом, интегральная функция 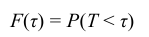
Функцией надежности R(τ), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью τ: 
Широкое использование показательного закона распределения обусловлено тем, что только он обладает следующим важным свойством: Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части 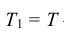
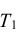
Пример:
Время безотказной работы устройства распределено по показательному закону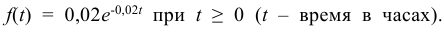
Решение:
По условию постоянная интенсивность отказов λ = 0,02. Используя формулу (6.18), получаем:
Нормальный закон распределения
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Определение: Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 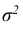
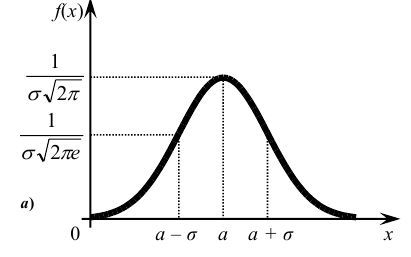
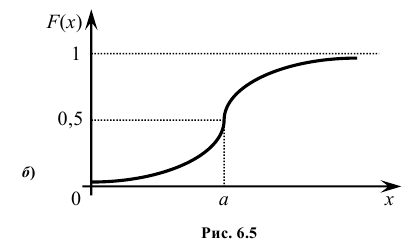
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 6.5 а), б) показана нормальная кривая с параметрами а и 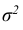
Обратим внимание на то, что нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 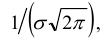
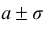
Можно заметить, что в выражении плотности нормального закона параметры распределения обозначены буквами а и 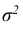
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру a этого распределения, т.е. 
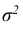
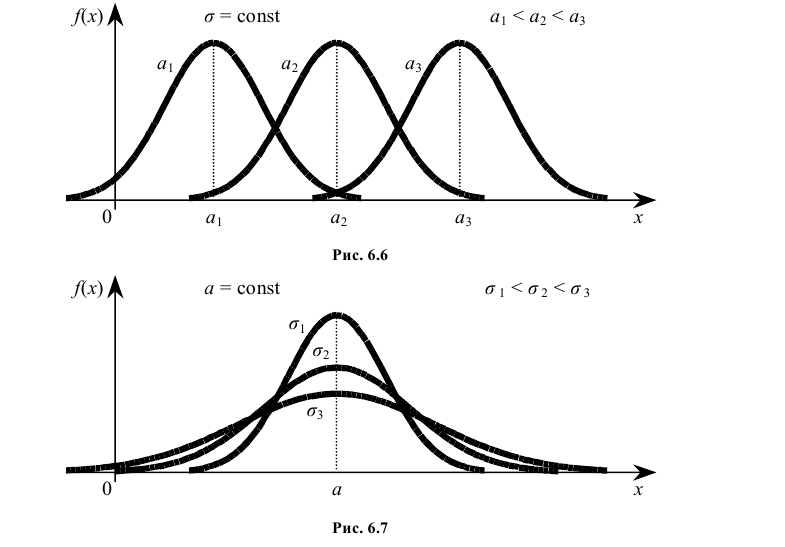
Выясним, как будет меняться нормальная кривая при изменении параметров а и σ. Если σ = const, и меняется параметр a (а1 < а2 < а3), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 6.6).
Если а = const и меняется параметр σ, то меняется ордината максимума кривой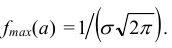
Таким образом, параметр a характеризует положение , а параметр σ – форму нормальной кривой.
Нормальный закон распределения случайной величины с параметрами a = 0 и σ = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции нормального распределения не выражается через элементарные функции. Однако его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения
Такую функцию называют функцией Лапласа, для нее составлены таблицы. Существует много разновидностей такой функции, например:
Мы будем использовать функцию:
Для такой функции табличные значения приведены в Приложении 2.
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле
Рассмотрим свойства случайной величины, распределенной по нормальному закону.
1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [α, β] равна
2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания a не превысит величину δ > 0 (по абсолютной величине), равна
Вычислим по этой формуле вероятности 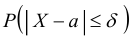
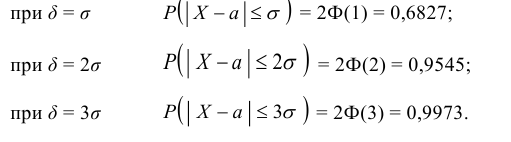
Пример:
Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а = 173 и 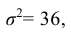
Решение:
1. Находим плотность вероятности 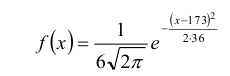
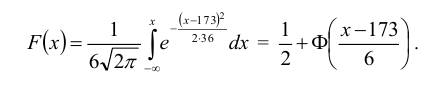
По таблице значений функции Лапласа (Приложение 2) находим:
Окончательно получаем
Долю костюмов 3-го роста (170 – 176 см) можно найти аналогично. Однако проще это сделать, если учесть, что данный интервал симметричен относительно математического ожидания а = 173, т.е. неравенство 170 ≤ Х ≤ 176 равносильно неравенству │Х – 173│≤ 3. Тогда
3. Сформулируем «правило трех сигм» для случайной величины Х: Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Ковариация в теории вероятности
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Нормальный закон распределения