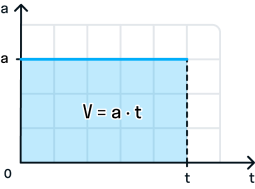
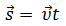Как найти равноускоренное движение по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

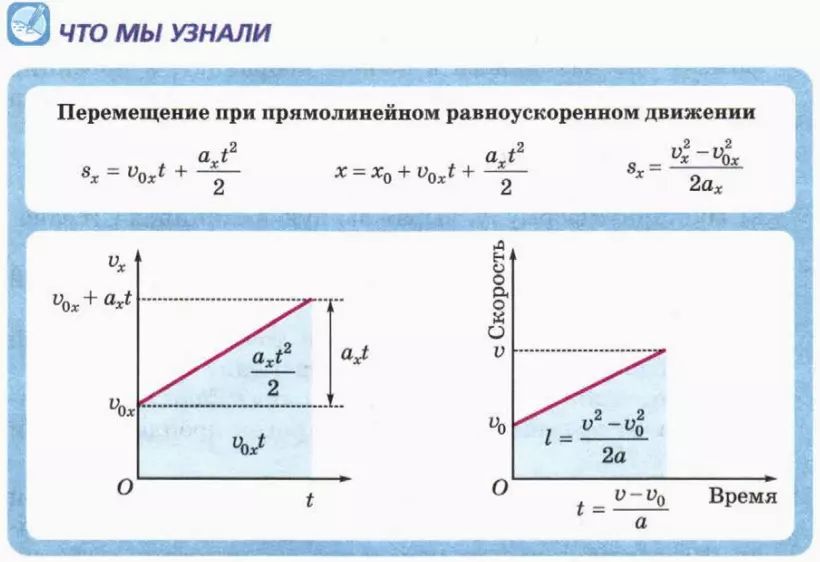
Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
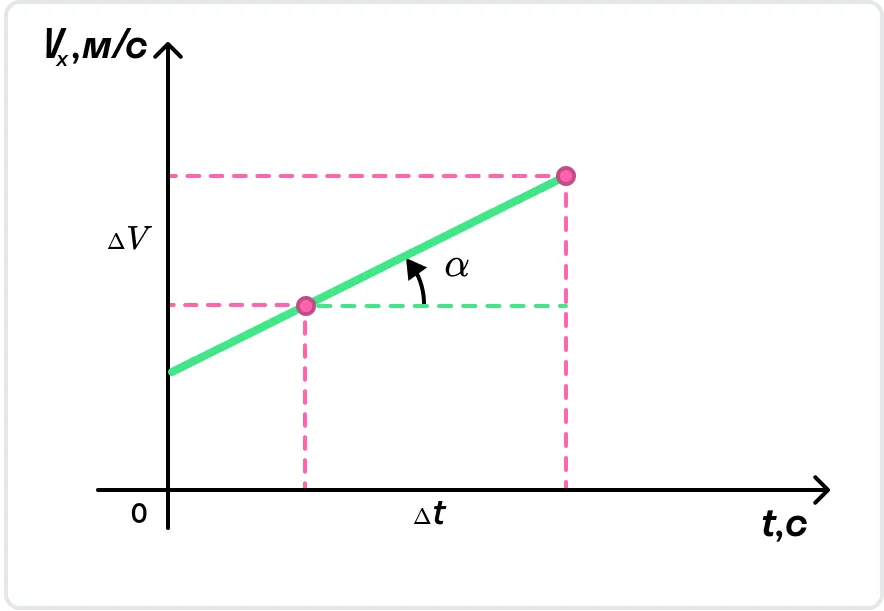
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

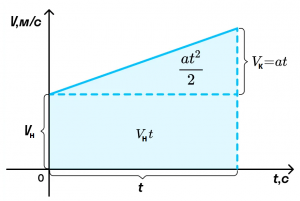
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

Равноускоренное движение.

Зависимость скорости от времени.
Закон движения.
Прямолинейное равноускоренное движение.
Свободное падение.
Горизонтальный бросок.
Бросок под углом к горизонту.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение — это движение с постоянным вектором ускорения vec a . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

$frac{displaystyle dvec{v}}{displaystyle dt}=vec{a}$ . (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор vec a ? Разумеется, функцию vec a t . Но не только: к ней можно добавить ещё произвольный постоянный вектор vec c (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы vec c ? В начальный момент времени t=0 скорость равна своему начальному значению: $vec v=vec v_{0}$ . Поэтому, полагая t=0 в формуле (2), получим:

$vec v_{0}=vec c$ .

Итак, константа vec c — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

$vec v=vec v_{0}+vec {a}t$ . (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

$v_{displaystyle x}=v{displaystyle 0x}+a_{displaystyle x}t$ , (4)

$v_{displaystyle y}=v{displaystyle 0y}+a_{displaystyle y}t$ . (5)

Формула для третьей компоненты скорости, $v_{displaystyle z}$ если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

$frac{displaystyle dvec{r}}{displaystyle dt}=vec{v}$

Подставляем сюда выражение для скорости, даваемое формулой (3):

$frac{displaystyle dvec{r}}{displaystyle dt}=vec v_{0}+vec {a}t$ (6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить $vec v_{0}$ , надо продифференцировать функцию $vec v_{0}t$ . Чтобы получить , нужно продифференцировать $vec {a} t^{2} /2$ . Не забудем добавить и произвольную константу vec c :

$vec r=vec c+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

Ясно, что vec c — это начальное значение $vec r_{0}$ радиус-вектора vec r в момент времени t=0 . В результате получаем искомый закон равноускоренного движения:

$vec r=vec r_{0}+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ . (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ . (8)

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ . (9)

$z=z_{0}+ v_{displaystyle 0z} t+frac{displaystyle a_{displaystyle z} t^{2}}{displaystyle 2}$ . (10)

Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что $vec r - vec r_{0}=vec s$ — перемещение тела. Тогда
получаем зависимость перемещения от времени:

$vec s= vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

$v_{displaystyle x}=v_{displaystyle 0x}+a_{displaystyle x}t$ ,

$x=x_{0}+ v_{0 displaystyle x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$s_{x}= v_{0x} t+frac{displaystyle a_{x} t^{2}}{displaystyle 2}$ ,

где $s_{x}= x-x_{0}$ — проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

$t=frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}$

и подставим в формулу для перемещения:

$s_{x}= v_{0x} frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}+frac{displaystyle a_{x}}{2} (frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}})^{2}$ .

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

$s_{x}=frac{displaystyle v_{displaystyle x}^{displaystyle 2}-displaystyle v_{displaystyle 0x}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}$ .

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения vec g , направленным вертикально вниз. Почти во всех задачах при расчётах полагают g=10 м/с $^{2}$ .

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи h=2 км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

$s_{y}=frac{displaystyle v_{displaystyle y}^{displaystyle 2}-displaystyle v_{displaystyle 0y}^{displaystyle 2}}{displaystyle 2a_{displaystyle y}}$ .

Имеем: $s_{y}=h, v_{y}=v$ — искомая скорость приземления, $v_{0y}=0, a_{y}=g$ . Получаем: $h^{2}=frac{v^{2}}{2g}$ , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью $v_{0}=30$ м/с. Найти его скорость через t=5 c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$v_{displaystyle y}=v_{displaystyle 0y}+a_{displaystyle y}t$ .

Здесь $v_{displaystyle 0y}=v_{0}, a_{y}=-g$ , так что $v_{displaystyle y}=v_{displaystyle 0}-gt$ . Вычисляем: $v_{displaystyle y}=30-10 cdot 5=-20$ м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте h=15 м, бросили вертикально вверх камень со скоростью $v_{0}=10$ м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

Имеем: $y=0, y_{0} = h, v_{0y}=v_{0}, a_{y}=-g,$ так что $0=h+v_{0}t-frac{displaystyle g t^{2}}{displaystyle 2}=15+10t-5t^{2}$ , или $t^{2}-2t-3=0$ . Решая квадратное уравнение, получим t=3 c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью $v_{0}$ с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат OXY так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$

В нашем случае $x_{0} = 0, v_{0x}=v_{0}, a_{x}=0, y_{0} = h, v_{0y}=0, a_{y}=-g$ . Получаем:

$x=v_{0}t, y=h-frac{displaystyle g t^{2}}{displaystyle 2}$ . (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

$y(T)=0Rightarrow h-frac{displaystyle gT^{displaystyle 2}}{displaystyle 2}=0Rightarrow T=sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Дальность полёта — это значение координаты в момент времени :

$L=x(T)=v_{0}T=v_{0} sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

$t=frac{displaystyle x}{displaystyle v_{displaystyle 0}}Rightarrow y=h-frac{displaystyle g}{displaystyle 2}(frac{displaystyle x}{displaystyle v_{displaystyle 0}})^{displaystyle 2}=displaystyle h-frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{displaystyle 0}}$ .

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью $v_{0}$ , направленной под углом alpha к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат OXY так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

В нашем случае $x_{0} =y_{0}=0, v_{0x}=v_{0}cos alpha, v_{0y}=v_{0}sin alpha , a_{x}=0, a_{y}=-g$ . Получаем:

$x=(v_{0}cos alpha )t, y=(v_{0}sin alpha)t- frac{displaystyle g t^{2}}{displaystyle 2}$ .

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

$T=frac{displaystyle 2v_{displaystyle 0}sinalpha }{displaystyle g}$ ,

$L=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin2alpha }{displaystyle g}$ ,

$y=x tgalpha -frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{0}cos^{displaystyle 2}alpha }$ .

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

$H=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin^{2} alpha }{displaystyle 2g}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Цели урока:

обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;

развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;

воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный (письменный) опрос, решение задач).

Связи:

межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;

внутрипредметные: равномерное и равноускоренное движение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

3. Объяснение нового материала.

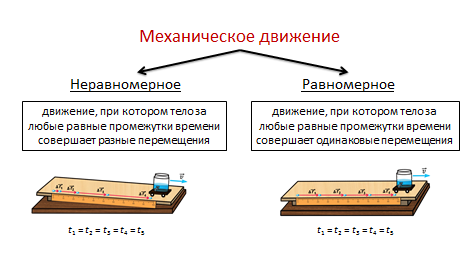
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.

Если движение равномерное, то:

1. Скорость тела не меняется с течением времени;

2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;

3. Уравнение перемещения имеет вид:

4. И — кинематическое уравнение равномерного движения.

Для равноускоренного:

1. Ускорение тела не изменяется с течением времени;

2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло

3. Уравнение скорости для равноускоренного движения имеет вид:

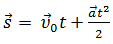
4. — уравнение перемещения для равноускоренного движения;

5. — кинематическое уравнение равноускоренного движения.

Для большей наглядности движение можно описывать с помощью графиков.

Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.

Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.

По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v₀ + at, т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.

При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.

Проекция перемещения — отрицательна.

Теперь рассмотрим зависимость пройденного пути от времени.

Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.

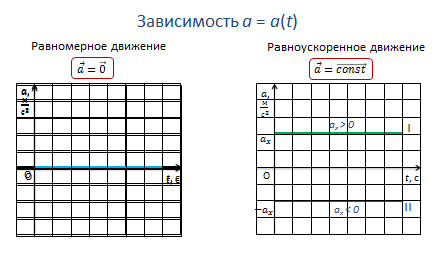
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.

Теперь перейдем к рассмотрению зависимости перемещения от времени.

Рассмотрим равномерное движение.

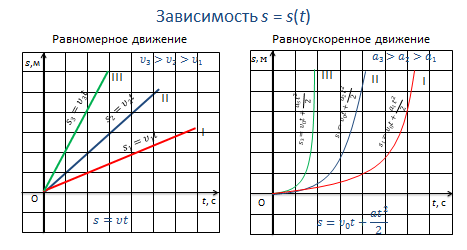
Т.к. при равномерном движении перемещение линейно зависит от времени (s_x = υ_xt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.

А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.

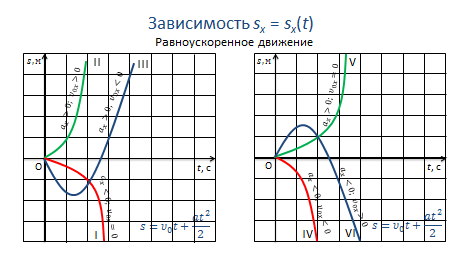
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.

Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.

Для 2-го тела ускорение и начальная скорость тела больше нуля.

Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.

У 4-го тела начальная скорость и ускорение меньше нуля.

Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.

И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.

И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.

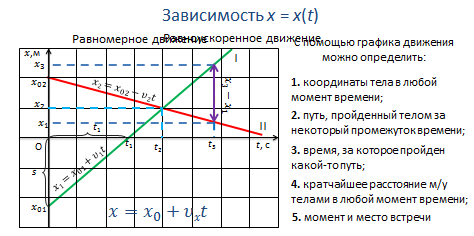
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).

Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).

С помощью графика движения можно определить:

1. координаты тела в любой момент времени;

2. путь, пройденный телом за некоторый промежуток времени;

3. время, за которое пройден какой-то путь;

4. кратчайшее расстояние м/у телами в любой момент времени;

5. момент и место встречи и т. д.

По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

4. Этап обобщения и закрепления нового материала

И так, сделаем главный вывод.

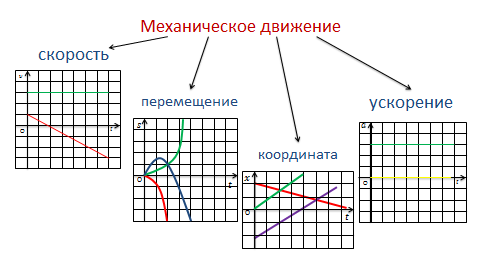
Механическое движение для большей наглядности можно описывать с помощью графиков:

1) Зависимости скорости от времени;

2) Зависимости ускорения от времени;

3) Зависимость координаты тела от времени;

4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

6. Домашнее задание.

Источник

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

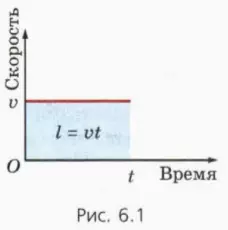
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

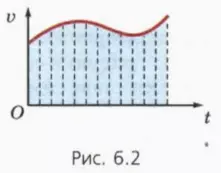
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

v = at. (1)

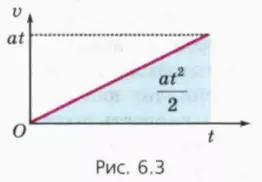
На рисунке 6.3 изображен график зависимости v(t).

? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

l = at²/2. (2)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

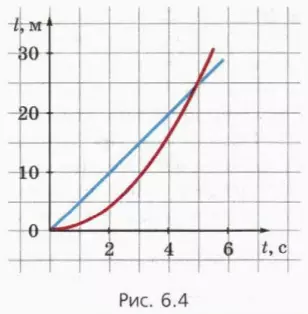
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

s_x = a_xt²/2. (3)

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x < 0. А путь отрицательным быть не может!

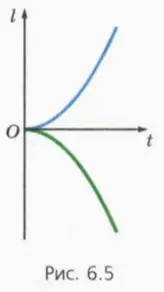
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

v_x = v_0x + a_xt, (4)

где v_0x – проекция начальной скорости на ось x.

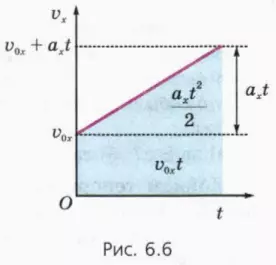
Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

s_x = v_0x + a_xt²/2. (5)

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

s_x = x – x₀,

где x₀ — начальная координата тела. Следовательно,

x = x₀ + s_x, (6)

Из формул (5), (6) получаем:

x = x₀ + v_0xt + a_xt²/2. (7)

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t².
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v₀, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

t = v/a. (8)

Подставим это выражение в формулу (2) для пути:

l = at²/2 = a/2(v/a)² = v²/2a. (9)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

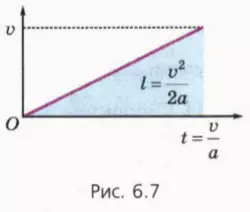
Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

Это соображение поможет вам легко справиться со следующим заданием.

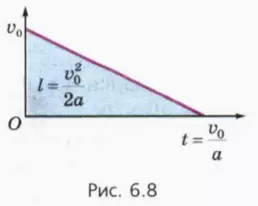
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v₀²/2a, где v₀ – начальная скорость тела, a – модуль ускорения.

В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v₀ и путь, пройденный при разгоне с места до скорости v₀ с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с². Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с². Сравните найденные вами значения тормозного пути с длиной классной комнаты.

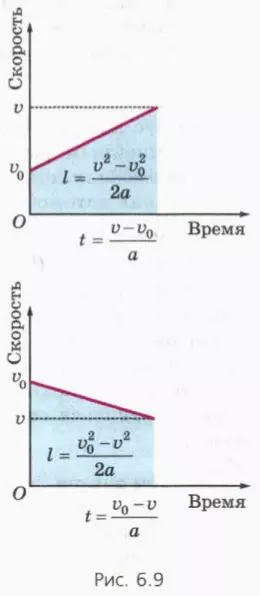
? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v² – v₀²)/2a, если скорость тела увеличивается;
б) l = (v₀² – v²)/2a, если скорость тела уменьшается.

? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

s_x = (v_x² – v_0x²)/2ax (10)

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

Лютый опыт

Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v₀ и a.
в) Решив эту систему уравнений, выразите v₀ и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v₀, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

Источник

Равноускоренное прямолинейное движение. Ускорение

Равноускоренное движение
Ускорение
Уравнение скорости и график скорости при равноускоренном прямолинейном движении
Определение пути и перемещения по графику скорости
Задачи

п.1. Равноускоренное движение

Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.

Движение, во время которого скорость тела за любые равные промежутки времени увеличивается на одну и ту же величину, называют равноускоренным.

Примеры равноускоренного движения:

скатывание велосипеда с горки, скатывание санок с горки;
старт и торможение автомобиля, автобуса, трамвая, поезда;
падение на землю камня, ракеты, метеорита.

Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.

п.2. Ускорение

Ускорение – это векторная величина, которая равна отношению изменения скорости тела к интервалу времени, за которое это изменение произошло: $$ overrightarrow{a}=frac{overrightarrow{v}-overrightarrow{v_0}} {t} $$ где (overrightarrow{v_0}) — начальная скорость тела, (overrightarrow{v}) — скорость тела в момент времени (t).

В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:

Единицей ускорения в системе СИ является метр на секунду в квадрате (1 м/с²) – ускорение равноускоренного прямолинейного движения, при котором тело за 1 с увеличивает скорость на 1 м/с.

При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).

Назовем проекцией вектора ускорения (overrightarrow{a}) на параллельную ему ось координат OX величину (a_x=pm|overrightarrow{a}|=pm a).
Знак проекции определяется следующим правилом:

если направление вектора (overrightarrow{a}) совпадает с направлением оси OX, то (a_x=agt 0)
если направление вектора (overrightarrow{a}) противоположно направлению оси OX, то (a_x=-alt 0)

При равноускоренном прямолинейном движении проекция ускорения равна: $$ a_x=frac{v_x-v_{0x}}{t} $$ где (v_{0x}) — проекция начальной скорости, (v_x) — проекция скорости в момент времени (t).

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_{0x}+a_x t $$ Сравним полученное уравнение с уравнением прямой (y(x)=kx+b ) (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента (k) играет проекция ускорения (a_x), а роль свободного члена (b) – начальная скорость (v_{0x}).

В осях (t) и (v) график (v_x(t)=v_{0x}+a_x t) является прямой.
Эта прямая:

возрастает, если (a_xgt 0)
убывает, если (a_xlt 0)
постоянна (параллельна оси (t)), если (a_x=0)

Пример построения графика скорости
1-й участок пути. Пусть автомобиль начал движение из состояния покоя с ускорением 4 м/с². Направим ось ОХ в направлении ускорения и получим уравнение скорости: $$ v_{0x}=0, a_x=4frac{text{м}}{c^2}, v_x(t)=0+4t=4t $$ Через 5 с скорость автомобиля станет равной (v_x(5)=4cdot 5=20) м/с.
2-й участок пути. Пусть автомобиль, набрав эту скорость, проехал с ней без ускорения в течение 10 с. На этом участке уравнение скорости: $$ a_{x}=0, v_x(t)=20frac{text{м}}{c}, 5 cleq tlt 15 c $$ Скорость не меняется, автомобиль движется прямолинейно равномерно.
3-й участок пути. Наконец, на последнем участке пути, автомобиль тормозил с ускорением 5 м/с² до полной остановки. Тогда уравнение скорости на этом участке: $$ v_{0x}=20frac{text{м}}{c}, a_x=5frac{text{м}}{c^2}, v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.

Опишем полностью движение на всех участках: $$ v_x(t)= begin{cases} 4t, 0leq tlt 5\ 20, 5leq tlt 15\ 20-5t, 15leq tleq 19 end{cases} $$ И построим график:

Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC — равномерному движению со скоростью 20 м/с, участок CD — торможению от 20 м/с до 0.

п.4. Определение пути и перемещения по графику скорости

В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.

Пусть график скорости при прямолинейном движении разбит на (n) участков, площади которых легко определить (треугольники, прямоугольники, трапеции). Тогда:
Весь пройденный путь равен сумме модулей площадей всех участков: $$ s=|s_1|+|s_2|+…+|s_n| $$ Величина перемещения по оси ОХ равна сумме площадей всех участков с учетом знака: $$ triangle x=s_1+s_2+…s_n $$ Конечная координата равна: (x_к=x_0+triangle x)

Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=frac12 AEcdot BE=frac12cdot 5cdot 20=50 (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EFcdot BE=10 cdot 20=200 (м) $$ 3) ΔCFD, его площадь равна $$ s_2=frac12 FDcdot GF=frac12cdot 4cdot20=40 (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290 (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ triangle x=s=290 (м) $$

п.5. Задачи

Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч. Найдите его ускорение, постройте график зависимости скорости от времени.

Дано:
(t=1 мин=60 с)
(v_0=28,8 км/ч=8 м/с)
(v=72 км/ч=20 м/с)
__________________
(a-?)
Как перевести км/ч в м/с – см. §7 данного справочника.

Направим ось ОХ по направлению движения автобуса. Автобус направления движения не меняет, и проекции ускорения и скорости все время положительны и по величине равны значениям величин: $$ a_x=a, v_x=v $$ Поэтому ускорение равно: $$ a=frac{v-v_0}{t} $$ Получаем: $$ a=frac{20-8}{60}=0,2 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=8+0,2t end{gather*} График:

Ответ: 0,2 м/с²

Задача 2. Поезд двигался прямолинейно равномерно со скоростью 18 км/ч, а в процессе торможения – равноускоренно и остановился через 10 с. Найдите модуль ускорения. Постройте график зависимости скорости от ускорения, найдите пройденный поездом путь за все время торможения.

Дано:
(v_0=18 км/ч=5 м/с)
(v=0)
(t=10 с)
__________________
(a, s-?)
Направим ось ОХ по направлению скорости (v_0). Тогда проекция ускорения: $$ a_x=frac{v-v_0}{t}, a_x=frac{0-5}{10}=-0,5 (м/с^2) $$ Проекция при торможении отрицательна.
Величина (модуль) ускорения: $$ a=|a_x|=0,5 м/c^2 $$ Зависимость скорости от времени: begin{gather*} v(t)=v_0+a_x t\ v(t)=5-0,5t end{gather*} График:

Пройденный путь равен площади треугольника ΔABC: $$ s=frac12 ACcdot BC=frac12cdot 5cdot 10=25 (м) $$ Ответ: 0,5 м/с²; 25 м

Задача 3*. С каким ускорением двигался автомобиль, если его скорость выросла с 36 км/ч до 72 км/ч на пути длиной 600 м? Постройте график зависимости скорости от времени, найдите время движения и путь с помощью графика, проверьте полученное значение пути.

Дано:
(v_0=36 км/ч=10 м/с)
(v=72 км/ч=20 м/с)
(s=600 м)
__________________
(a-?, t-?)
Ускорение равно: (a=frac{v-v_0}{t}). Откуда время равно: (t=frac{v-v_0}{a})
Средняя скорость на всем пути: (v_{cp}=frac{v_0+v}{2})
Весь путь: $$ s=v_{cp}t=frac{v_0+v}{2}cdotfrac{v-v_0}{a}=frac{v^2-v_0^2}{2a} $$ Значит, ускорение равно: $$ a=frac{v^2-v_0^2}{2s} $$ Подставляем: $$ a=frac{20^2-10^2}{2cdot 600}=0,25 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=10+0,25t end{gather*} График:

Скорость достигает значения (v=20 м/с) в момент времени (t=40 с).
Значит, время движения 40 с.

Путь по графику скорости равен площади четырехугольника ABCD. begin{gather*} S_{ABCD}=S_{ABE}+S_{AECD}=frac12 AEcdot EB+AEcdot AD=frac12cdot 40cdot 10+40cdot 10=200+400=600 (м)\ s=600 м end{gather*} Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с²; 40 c

Источник

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

Равноускоренное движение.

Зависимость скорости от времени.

Закон движения.

Прямолинейное равноускоренное движение.

Свободное падение.

Горизонтальный бросок.

Бросок под углом к горизонту.

1. Нахождение пути по графику зависимости скорости от времени

2. Путь и перемещение при прямолинейном равноускоренном движении

Начальная скорость тела равна нулю

Начальная скорость тела не равна нулю

3. Соотношение между путем и скоростью

Лютый опыт

Дополнительные вопросы и задания

Равноускоренное прямолинейное движение. Ускорение

п.1. Равноускоренное движение

п.2. Ускорение

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

п.4. Определение пути и перемещения по графику скорости

п.5. Задачи

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²