Равновеликие параллелограммы Евклида
На чер. 73 дано построение равновеликих параллелограммов, имеющееся у Евклида. Этим построением можно пользоваться для решения различных задач на превращение параллелограмма или прямоугольника в равновеликий ему, удовлетворяющий известным требованиям.
Например, легко решается, без сведения дела к измерению, задача: построить прямоугольник, равновеликий данному и имеющий данное основание (обычно, опираясь на знание того, что площадь прямоугольника равна произведению основания на высоту, задачу сводят к построению 4-го пропорционального отрезка).
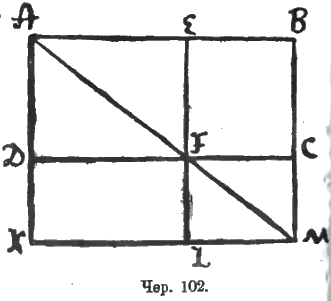
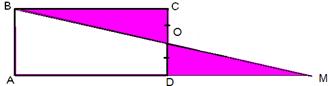
Решение этой задачи, без сведения к алгебре, таково: пусть ABCD (чер. 102) – данный прямоугольник; отложив отрезок AE, равный данному основанию искомого прямоугольника, и состроив EL || AD, а заем прямую AF, где F точка пересечения EL с DC, и построив MK || BA (точка M есть точка пересечения BC и AF), получим прямоугольник ABMK, для которого видим, что прямоугольник AELK имеет данное основание AE и равновелик данному прямоугольнику ABCD.
Это решение задачи было давно известно, хотя и не пользуется распространением. Под его влиянием может возникнуть мысль изыскать решение, построенное на той же идее, другой общеизвестной задачи: построить квадрат, равновеликий данному прямоугольнику.
Предварительно надо ознакомиться с так называемой «прямой Симсона».
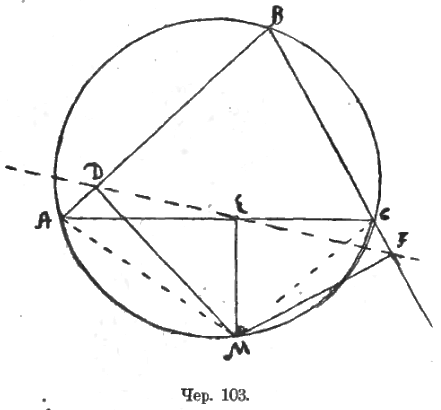
Если в круг вписан треугольник ABC (чер. 103) и если из какой-либо точки M окружности построены перпендикуляры MD, ME и MF на его стороны, то, как известно, основания этих перпендикуляров, точки D, E и F, лежат на одной прямой, называемой «прямая Симсона».
Вот выяснение этого.
Угол ADM – прямой; следов., точка D лежит на окружности, диаметром которой служит отрезок AM. Так как ∠AEM тоже прямой, то точка E лежит на той же окружности. Поэтому углы AMD и AED суть углы, вписанные в эту окружность и опирающиеся на одну и ту же дугу AD (она на чертеже не дана). Следов., ∠AED = AMD.
Так как ∠MEC = d и ∠MFC = d, то точка E и F лежат на окружности, диаметром которой служит отрезок MC, и углы CMF и CEF суть вписанные в эту окружность и опирающиеся на одну и ту же дугу CF (не нарисованную на чертеже). След., ∠CEF = ∠CMF.
Так как четырехугольник MABC вписан в круг, то ∠AMC + ∠B = 2d.
Так как углы при точках D и F в четырехугольнике MDBF прямые, то этот четыреугольник есть вписываемый и, следов., ∠DMF + ∠B = 2d.
Отсюда мы выводим, что ∠AMC = ∠DMF. Так как ∠AMC = ∠AMD + ∠DMC и ∠DMF = ∠DMC + ∠CMF, то отсюда имеем:
∠AMD + ∠DMC = ∠DMC + ∠CMF
или
∠AMD = ∠CMF.
Но мы получили, что ∠AED = ∠AMD и ∠CEF = ∠CMF. Следов., ∠AED = ∠CEF.
Так как AEC есть прямая линия, то равенство углов AED и CEF указывает на то, что DEF есть также прямая линия.
Известна и обратная теорема: если из какой-либо точки плоскости треугольника опущены перпендикуляры на его стороны и если их основания расположены на одной прямой, то указанная точка расположена на окружности, описанной около треугольника.
Выяснение этого немного отличается от предыдущего. Мы теперь не знаем, что четыреугольник ABCM есть вписываемый, но зато знаем, что DEF есть прямая и, следовательно, ∠AED = ∠CEF. Так как по-прежнему точки A и E лежат на окружности, диаметром которой служит отрезок DM, и точки E и F лежат на окружности, диаметром которой служит отрезок MC, то по-прежнему имеем: ∠AED = ∠AMD и ∠CEF = ∠CMF.
Отсюда заключаем, что ∠AMD = ∠CMF. Так как четыреугольник MDBF по-прежнему вписываемый (ибо углы при D и F прямые), то ∠DMF + ∠B = 2d или ∠DMC + ∠CMF + ∠B = 2d или ∠DMC + ∠AMD + ∠B = 2d или ∠AMC + ∠B = 2d, откуда и заключаем, что точка M лежит на круге, описанном около ∆ABC.
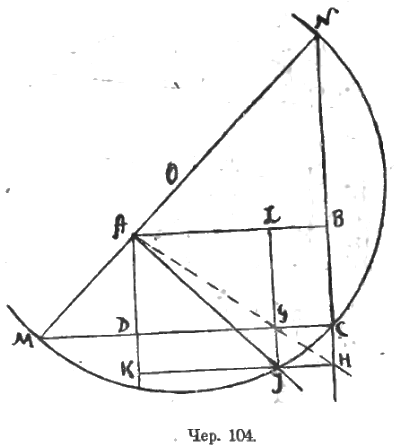
Пусть ABCD (чер. 104) есть данный прямоугольник и ALJK – искомый квадрат. Тогда вершина J этого квадрата должна лежать на биссекторе AJ прямого угла A данного прямоугольника. Далее искомая точка J должна занять на этом биссекторе такое положение чтобы точка A, G и Н лежали на одной прямой. Точки G и H суть основания перпендикуляров, опущенных из точки J на прямые DC и BC. Тогда возникает мысль применить сюда «прямую Симсона». Примем прямые DC и BC за 2 стороны треугольника, третьею же его стороною должна быть прямая, перпендикулярная к AJ. Эта прямая MN легко строится. Получим ∆MCN. Центр O этой окружности (ибо ∠MCN прямой) должен лежать в середине отрезка MN. Раз точка J определена, то построение квадрата KJLA не вызывает затруднений.
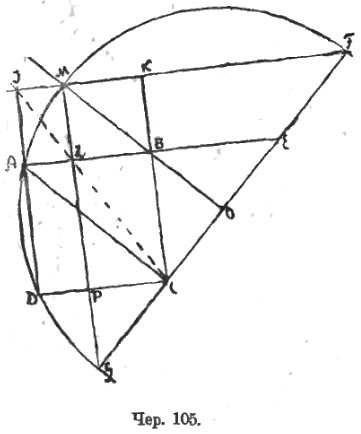
Та же идея может быть применена к задаче деления отрезка в крайнем и среднем отношении. Если дан отрезок AB, то задача сводится к разделению этого отрезка на такие две части AL и LB, чтобы квадрат, построенный на большей из них, на отрезке LB, был равновелик прямоугольнику, сторонами которого служат сам отрезок AB и другая часть его, именно AL.
Пусть (чер. 105) квадрат LMKB равновелик прямоугольнику ALPD, причем AD = AB. Продолжив стороны этого квадрата и прямоугольника, получим прямоугольник DJKC и квадрат DABC, причем точки C, L и J должны лежать на одной прямой, на диагонали прямоугольника DJKC. Построив диагональ AC, мы увидим, что точки J, L и C можно рассматривать, как основания перпендикуляров, построенных из точки A на стороны ∆GMF, причем сторона GF есть прямая , перпендикулярная к AC. Из этого следует, что ∠DCG = 45°, а, следовательно, ∠MGC = 45° и ∠MFG = 45°. Также ∠BCE = ∠BEC = 45° (точка E есть точка пересечения продолжения AB с прямою GF).
Точка A должна лежать, согласно обратной теореме о «прямой Симсона», на окружности, описанной около ∆GMF, а центр O этой окружности должен лежать на середине отрезка CE, откуда вытекает построение для определения точки M: 1) строим на AB квадрат ABCD и его диаг. AC, 2) строим через точку C прямую GF ⊥ AC, – тогда определится точка E, 3) делим отрезок CE пополам в точке O, 4) строим прямую через O и B, – эта прямая образует со сторонами BC и AB углы в 45° (ибо ∆CBE равнобедренный), 5) строим окружность, принимая точку O за центр и OA (или OD) за радиус, – пересечение этой окружности с прямою OB определит точку M. Раз точка M определена, то построив MLP ⊥ AB, соединив M с F и продолжив CB до пересечения в точке K с MF, получим квадрат LMKB (так как диагональ BM составляет со сторонами BL и BK углы по 45°), равновеликий прямоугольнику ALPD, что и дает решение задачи.
1 ВАРИАНТ
Фигуры, имеющие равную площадь, называются — равновеликими. Проверим это ниже.
формула площади параллелограмма выглядит следующим образом:
S=ah, где а-основание, h-высота.
Пусть 1 клетка равняется 1см, тогда:
б) a=1,5см, h=4см;
S=1,5*4=6(см²)
—————————————
в) а=3см, h=3см
S=3*3=9(см²)
—————————————
г) a=3см, h=2см
S=3*2=6(cм²)
—————————————
д) а=2см, h=3см
S=2*3=6(см²)
—————————————
ж) а=2см, h=4см
S=2*4=8(см²)
—————————————
и) а=6см, h=2см
S=6*2=12(см²)
Вывод: равновеликими параллелограммами будут б),г),д).
Ответ: б),г),д)
2 ВАРИАНТ
прямоугольник — это частный случай параллелограмма
формула площади прямоугольника:
S=ab, где а-сторона, b-сторона
——————————————————-
а) а=1см, b=8см
S=1*8=8(см²)
—————————————
б) a=1,5см, h=4см;
S=1,5*4=6(см²)
—————————————
в) а=3см, h=3см
S=3*3=9(см²)
—————————————
г) a=3см, h=2см
S=3*2=6(cм²)
—————————————
д) а=2см, h=3см
S=2*3=6(см²)
—————————————
е) а=2см, b=3см
S=2*3=6(см²)
—————————————
ж) а=2см, h=4см
S=2*4=8(см²)
—————————————
з) а=4см, b=2см
S=4*2=8(см²)
—————————————
и) а=6см, h=2см
S=6*2=12(см²)
Вывод: равновеликими параллелограммами будут б),г)д),е) и а),ж),з)
Ответ: б),г)д),е) и а),ж),з)
Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».
Ход урока
I. Повторение.
1) Устно по готовому чертежу вывести формулу площади параллелограмма.
2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?
(по готовому чертежу)
зависимость обратно пропорциональная.
3) Найти вторую высоту (по готовому чертежу)
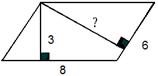
4) Найти площадь параллелограмма по готовому чертежу.
Решение:
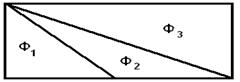
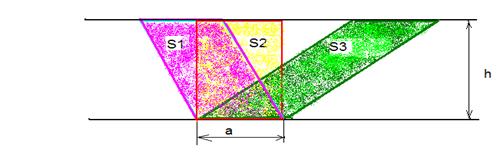
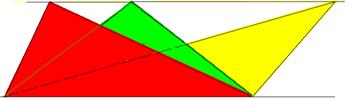
5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).
Определение: Фигуры, имеющие равные площади, называются равновеликими.
II. Решение задач.
1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.
Решение:
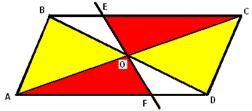
2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.
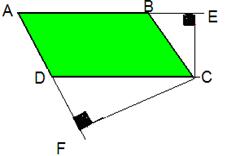
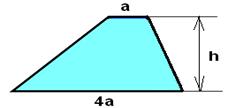
3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?
Решение: Можно. Все треугольники равновеликие.
4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.
Решение:
5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?
Решение: В точке пересечения диагоналей.
6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.
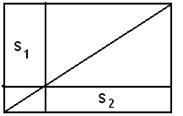
Решение:
III. Изучение темы «Площадь треугольника»
начать с задачи:
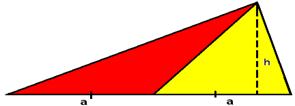
«Найти площадь треугольника, у которого основание a, а высота h».
Ребята, используя понятие равновеликих фигур, доказывают теорему.
Достроим треугольник до параллелограмма.
Площадь треугольника равна половине площади параллелограмма.
Задание: Начертите равновеликие треугольники.
Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).
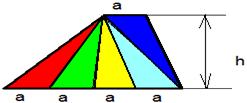
Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».
У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь
Вывод: Фигуры, имеющие равные площади, называются равновеликими.
Вопросы к классу:
- Равновелики ли равные фигуры?
- Сформулируйте обратное утверждение. Верно ли оно?
- Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
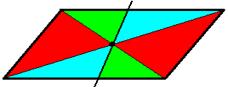
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)
IV. Шаг вперёд!
На доске написаны задания по выбору:
1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».
Решение:
2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».
Решение:
3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .
Решение:
Ответ:
3. Из олимпиадных задач:
«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.
Решение: провести диагональ BD.
Упражнение №475.
«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».
Использовать теорему Фалеса (разделить АC на 3 равные части).
V. Задача дня.
Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).
«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».
Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.
Дополнительные задачи (из олимпиадных задач):
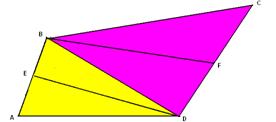
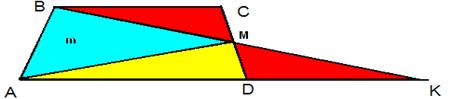
1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».
Решение:
Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S∆ABK = 2m, ∆BCM = ∆MDK, SABCD = S∆ABK = 2m.
Ответ: SABCD = 2m.
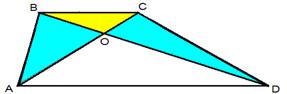
2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».
Решение:
S∆BCD = S∆ABC, т.к. у них общее основание BC и одинаковая высота.
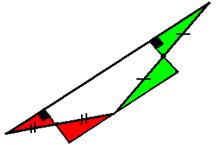
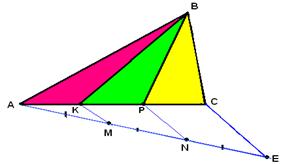
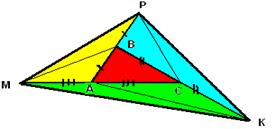
3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?
Решение:
В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,
Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.
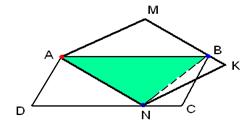
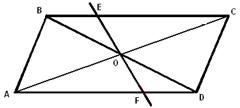
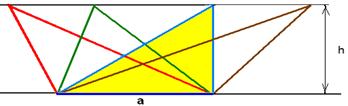
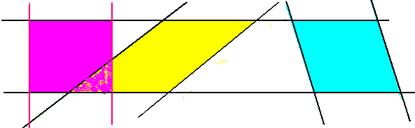
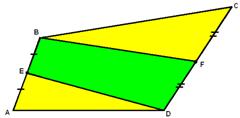
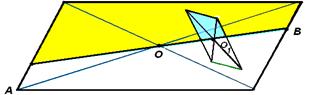
4) Сцепленные параллелограммы.
2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.
Решение:
и
, значит,
Список использованной литературы:
- Учебник «Геометрия 7-9» (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
- Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
- Подборка задач, накопленных за много лет работы.
Приложение.
mat:geom:area
Содержание
Площадь. Равновеликие фигуры
Равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами.

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.
Это следствие из теоремы Больяй — Гервина: равносоставленные фигуры являются равновеликими, а равновеликие многоугольники являются равносоставленными.
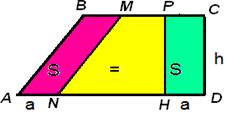
Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

Перекраивание трапеции в равносоставленный треугольник:

видео — Площадь трапеции. Сведение к площади треугольника
Подробнее
Равносоставленность
Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.
Вопросы
-
Квадраты с равными сторонами равновелики?
-
Равносторонние треугольники с равными сторонами равновелики?
-
Равносторонние треугольники равновелики?
Задачи
Задача A
Доказать, что всякая прямая, проходящая через точку пересечения диагоналей параллелограмма, делит его на 2 равновеликие части.

Доказательство.

Задача B — Про торт и бесстыдную птичку
Решается на основании задачи A.
У бабушки было два внука, которые должны были приехать на выходные погостить. Она, как любая добропорядочная бабушка, приготовила для них торт. И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые по площади части.
Бабушка имеет идеальный глазомер, она легко способна находить на глаз середины и пересечения любых отрезков. И у бабушки есть замечательный нож, которым она умеет лихо отрезать куски торта по любой намеченной прямой.

Решение.

Задание
Начертите равновеликие треугольники.
Решение.

Задача
Доказать, что медиана делит треугольник на два равновеликих треугольника.
Решение.
Следствие. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника.
Задача
Доказать, что медианы треугольника разбивают его на шесть равновеликих треугольников.
Решение.
Рассмотреть попарно эти шесть треугольников. У них одинаковые основания и одна и та же высота. Поэтому попарно треугольники имеют одинаковую площадь. В силу транзитивности все 6 треугольников равновелики.
Задача
Начертите треугольник ABC. Через вершину B проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади.
Решение.
Задача
Постройте полукруг, равновеликий данному кругу.
Постройте круг, равновеликий данному полукругу.
Задача
Доказать, что круг на рисунке разбит на 9 равновеликих частей

Решение
Задача
Найти площадь четвертой части

Решение

· Последние изменения: 2016/01/18 01:22 (внешнее изменение)
1
Равносоставленность Две фигуры называются равносоставленными, если они могут быть разрезаны на одинаковое число попарно равных фигур. Из свойств площади следует, что равносоставленные фигуры равновелики. Теорема. Любые два равновеликих многоугольника равносоставлены. Для многоугольников верно и обратное, а именно, имеет место следующая теорема.
2
Теорема 1 Две фигуры, равносоставленые с одной и той же фигурой, равносоставлены. Доказательство. Действительно, пусть фигуры Ф’ и Ф» равносоставлены с фигурой Ф. Рассмотрим линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф’ и, кроме того, линии, разбивающие фигуру Ф на части, из которых можно составить фигуру Ф». Те и другие линии разбивают фигуру Ф на более мелкие части, из которых можно составить как фигуру Ф’, так и Ф». Таким образом, фигуры Ф’ и Ф» равносоставлены.
3
Теорема 2 Любые два равновеликих параллелограмма равносоставлены. Доказательство. Рассмотрим сначала два параллелограмма, у которых есть равные стороны. По условию они равновелики, значит, имеют равные высоты, проведенные к равным сторонам. Проведем внутри каждого параллелограмма отрезки, параллельные сторонам другого параллелограмма. Тогда оба параллелограмма разобьются на одинаковое число попарно равных фигур, т.е. они равносоставлены.
4
Теорема 2 (продолжение) Пусть теперь равновеликие параллелограммы не имеют равных сторон. Построим третий параллелограмм, имеющий одну сторону и высоту, равные соответственно одной стороне и высоте первого параллелограмма. Поскольку при этом другую сторону третьего параллелограмма можно выбирать произвольно, сделаем ее равной одной из сторон второго параллелограмма. Тогда третий параллелограмм будет равновелик и с первым, и со вторым параллелограммами, и с каждым из них будет иметь по равной стороне. Следовательно, он равносоставлен и с первым, и со вторым. В силу теоремы 1 первый и второй параллелограммы равносоставлены.
5
Теорема 3 Любые два равновеликих треугольника равносоставлены. Доказательство. Каждый треугольник продолжением средней линии преобразуется в равновеликий ему параллелограмм. Поэтому два равновеликих треугольника преобразуются в два равновеликих параллелограмма. В силу теоремы 2 эти параллелограммы равносоставлены и, следовательно, равносоставлены исходные треугольники.
6
Теорема 4 Всякий многоугольник равносоставлен с некоторым треугольником. Доказательство. Рассмотрим многоугольник ABCDE…, и одну из его вершин, например C, перенесем параллельно диагонали BD на продолжение стороны DE. При этом исходный многоугольник преобразуется в равновеликий многоугольник с числом сторон на единицу меньшим. Имея в виду, что мы заменили один треугольник другим — равновеликим, а остальная часть многоугольника осталась неизменной, получим, что новый многоугольник будет равносоставлен с исходным. Продолжая этот процесс, мы превратим исходный многоугольник в равносоставленный с ним треугольник.
7
Теорема (основная) Любые два равновеликих многоугольника равносоставлены. Доказательство. Пусть М’ и М» — равновеликие многоугольники. Рассмотрим равносоставленные с ними треугольники Т’ и Т», соответственно. Эти треугольники равновелики, а следовательно, равносоставлены. Значит, равносоставлены и исходные многоугольники М’ и М».
8
Теорема Пифагора Теорема. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. На языке площадей теорему Пифагора можно переформулировать в следующем виде. Доказательство представлено на рисунке.
9
Упражнение 1 Параллелограмм разрежьте на две части, из которых можно сложить прямоугольник. Решение показано на рисунке.
10
Упражнение 2 Треугольник разрежьте на две части, из которых можно сложить параллелограмм. Решение показано на рисунке.
11
Упражнение 3 Треугольник разрежьте на три части, из которых можно составить прямоугольник. Решение показано на рисунке.
12
Упражнение 4 Трапецию разрежьте на две части, из которых можно сложить треугольник. Решение показано на рисунке.
13
Упражнение 5 Трапецию разрежьте на три части, из которых можно сложить прямоугольник. Решение показано на рисунке.
14
Упражнение 6 Параллелограмм (рисунок слева) разрежьте на несколько частей и сложите из них параллелограмм, зеркально симметричный данному (рисунок справа). Переворачивать части (использовать осевую симметрию) нельзя. Решение показано на рисунке.
15
Упражнение 7 Неравнобедренную трапецию (рисунок слева) разрежьте на несколько частей и сложите из них трапецию, зеркально симметричную данной (рисунок справа). Переворачивать части (использовать осевую симметрию) нельзя. Решение показано на рисунке.
16
Упражнение 8 Разносторонний треугольник (рисунок слева) разрежьте на несколько частей и сложите из них треугольник, зеркально симметричный данному (рисунок справа). Переворачивать части (использовать осевую симметрию) нельзя. Решение показано на рисунке.
17
Упражнение 9 Правильный шестиугольник разрежьте на две части, из которых можно составить параллелограмм. Решение показано на рисунке.
18
Упражнение 10 Используя разрезания, докажите, что площадь правильного восьмиугольника равна произведению его наибольшей и наименьшей диагоналей. Решение показано на рисунке.
19
Упражнение 11 Разрежьте квадрат на шесть квадратов. Решение показано на рисунке.
20
Упражнение 12 Разрежьте квадрат на семь квадратов. Решение показано на рисунке.
21
Упражнение 13 Разрежьте квадрат на восемь квадратов. Решение показано на рисунке.
22
Упражнение 14 Разрежьте трапецию на четыре равные трапеции. Решение показано на рисунке.
23
Упражнение 15 Разрежьте закрашенную фигуру на четыре равные части. Решение показано на рисунке.
24
Упражнение 16 Разрежьте прямоугольник на две равные части так, чтобы в каждой из них была звездочка. Решение показано на рисунке.
25
Упражнение 17 Многоугольник разрежьте на четыре равные части. Решение показано на рисунке.
26
Упражнение 18 Прямоугольник разрежьте на две части, из которых можно сложить квадрат. Решение показано на рисунке.
27
Упражнение 19 Восьмиугольник разрежьте на две части, из которых можно сложить квадрат. Решение показано на рисунке.
28
Упражнение 20 Шестиугольник, изображенный на рисунке, разрежьте на две части, из которых можно сложить квадрат. Решение показано на рисунке.
29
Упражнение 21 Фигуру, изображенную на рисунке, разрежьте на две части, из которых можно сложить квадрат. Решение показано на рисунке.
30
Упражнение 22 Греческий крест разрежьте на несколько частей и составьте из них квадрат. Решение показано на рисунке.
31
Упражнение 23 Греческий крест разрежьте по двум прямым и из полученных частей составьте квадрат. Решение показано на рисунке.
32
Упражнение 24 Решение показано на рисунке. Один из двух равных квадратов разрежьте на несколько частей и составьте из них и другого квадрата квадрат.
33
Упражнение 25 Один из двух неравных квадратов разрежьте на несколько частей и составьте из них и другого квадрата квадрат. Решение показано на рисунке.
34
Упражнение 26 Квадраты 6х6 и 8х8 разрежьте на части по линиям сетки (не разрезая квадратиков сетки) и составьте из них квадрат 10х10. Решение показано на рисунке.
35
Упражнение 27 Фигуру, изображенную на рисунке, разрежьте на семь частей, из которых можно сложить квадрат. Решение показано на рисунке.
36
Упражнение 28 Две фигуры, ограниченные дугами окружностей по 90 о каждая, разрежьте на части и составьте из них круг. Решение показано на рисунке.
37
Упражнение 29* Стороны АВ и CD параллелограмма ABCD площади 1 разбиты на n равных частей, AD и ВС — на m равных частей. Точки деления соединены так, как показано на рисунке, где n = 3, m = 4. Чему равны площади образовавшихся при этом маленьких параллелограммов? Ответ:.

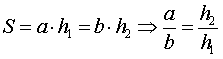


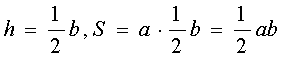
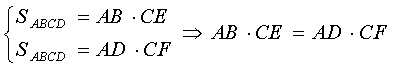
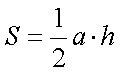



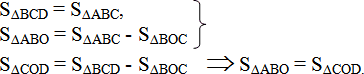
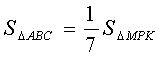
 и
и 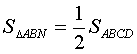 , значит,
, значит,