-
Равновесие по Нэшу в чистых стратегиях.
Набор
стратегий s=(s1,
… , sn)
образует равновесие по Нэшу если
для любого Pk,
(или ситуация s=(s1,
… , sn)
является равновесной по Нэшу)

где
s
альтернатива стратегииa-ого
игрока 

в результате выбора своих стратегий
всеми игроками кромеa-ого
Пример
. «Семейный спор».
Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
-
Равновесие по Нэшу в смешанных стратегиях.
Обозначим
набор смешанных стратегий s=(s1,
… , sn)
через σ=(
σ1,
… , σn).
Ситуация
(набор смешанных стратегий) σ=(σ1, … ,σn)
является равновесием по Нэшу в игре
{Σa}, {
если для любогоа=1, …,n
где
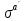
альтернатива стратегииa-ого
игрока


в результате выбора своих стратегий
всеми игроками кромеa-ого.
Однако
существуют дополнительные условия, при
которых ситуация в смешанных стратегиях
является равновесной по Нэшу.
Пусть
Sa+
– множество
чистых стратегий, которые игрок a
играет с положительной вероятностью в
ситуации σ=(
σ1,
… , σn).
Ситуация σ
является равновесной по Нэшу в смешанном
расширении
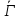
всехa=1,
2, …, n
-
Sa+
-
Sa+,
Sa+
Данные
условия можно описать следующим образом:
-
Каждый игрок при
данном распределении стратегий, которые
играют его противники, безразличен
между чистыми стратегиями, которые он
играет с положительной вероятностью;
Эти чистые
стратегии не хуже тех, которые он играет
с нулевой вероятностью
46. Аналитическое решение биматричных игр 2×2.
|
B1 |
B2 |
|
|
A1 |
a11 |
a12 |
|
А2 |
a21 |
a22 |
А=
Сначала
предположим, что матрица А имеет седловую
точку aij,
то есть элемент aij,
наименьший в i-той
строке и наибольший в j-том
столбце. Тогда игра имеет решение в
чистых стратегиях {Ai,
Bj,
V=aij},
где Ai
и Bj-
оптимальные стратегии соответственно
игроков A
и B,
а V=aij
– цена игры.
Рассмотрим
случай, когда матрица [2×2]-не
имеет седловой точки.
Тогда
по теореме, каждый из игроков A
и B
обладает единственной оптимальной
смешанной стратегией соответственно
PO=(p1O,p2O)
и QO=(q1O,q2O),
где
а
цена игры (в смешанных стратегиях) V
определяется формулой
Пояснение
(без строгого доказательства):
Рассмотрим
функцию выигрыша игрока A
более подробно:
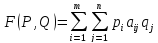

Примем
также следующие обозначения:




Пусть
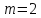

тогда функцию

Представим
в явном виде функцию

(независимой переменной)q.
Получим следующее выражение:

Если

т.е. если

график функции имеет положительный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать свои потери
(минимизировать функцию

выбирая свою второю чистую стратегию,
т.е. реализуя смешанную стратегию

В итоге исход игры определится результатом
Если

т.е. если
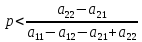
график функции имеет отрицательный
наклон. Это значит, что в ответ на действия
игрока A
игрок B
будем минимизировать функцию

выбирая свою первую чистую стратегию

В
итоге исход игры определится результатом

В итоге приходим к системе, решая которую,
получим формулы, представленные в
утверждении теоремы.
Соседние файлы в предмете Теория игр
- #
- #
Равновесие Нэша (сокращенно NGG или NGGW ) является центральным понятием в теории игр . В некооперативных играх он описывает комбинацию стратегий , при которой каждый игрок выбирает ровно одну стратегию, от которой для любого игрока нет смысла отклоняться от выбранной им стратегии как единственной. В равновесии по Нэшу каждый игрок соглашается со своей стратегией, даже ретроспективно, он ударил бы ее снова таким же образом. Таким образом, стратегии игроков являются взаимно лучшими ответами . Равновесие по Нэшу — это элементарное решение в теории игр. Определение и доказательство существования равновесия по Нэшу восходит к опубликованной в 1950 году диссертации математика Джона Форбса Нэша-младшего . Равновесие Нэша находит среди прочего. центральное значение в таких экономических областях, как микроэкономика , в распределении товаров и ценообразовании.
идея
Основная цель математической теории игр — охарактеризовать и определить рациональные решения для конфликтов, а также для ситуаций сотрудничества. Сложность состоит в том, что никто из лиц, принимающих решения («игроков»), не знает, какие планы преследуют другие игроки и как они будут принимать соответствующие решения. Поэтому для отдельного игрока неясно, как повлияет его конкретное решение в отношении плана действий («стратегии»). Но он может обдумать ситуацию с точки зрения других игроков, чтобы сформировать ожидание того, что они будут делать.
Равновесие по Нэшу основано на следующей идее: вы начинаете со всех возможных комбинаций, содержащих стратегию для каждого игрока. Такая комбинация стратегий называется равновесием по Нэшу, если можно предположить, что она имеет определенную стабильность из-за того, что ни у одного отдельного игрока нет стимула отклониться от своей стратегии. Формально это означает, что выплата игроку, который меняет свою индивидуальную стратегию, не может увеличиваться в результате этого изменения.
определение
Равновесие по Нэшу является пара стратегий (или стратегии кортеж а если есть более двух игроков), в которой он не стоит для любого игрока отклоняться от своей стратегии в одностороннем порядке (только). Стратегически, с точки зрения игрока, это означает: я делаю все, что в моих силах, с учетом того, что вы делаете; вы делаете все возможное, принимая во внимание то, что делаю я.
При изучении равновесий по Нэшу можно выделить три типа стратегий: доминирующие стратегии, чистые стратегии и смешанные стратегии. Следует отметить, что в некоторых играх равновесие по Нэшу отсутствует, если используются только чистые стратегии. С другой стороны, при использовании смешанных стратегий всегда существует одно или несколько равновесий, если предполагается конечное число чистых стратегий.
Доминирующие стратегии : то, что делает игрок, лучше всего для него, независимо от того, что делают другие. Такие доминирующие стратегии существуют редко, так как они в основном зависят от решений других, что лучше для игрока. Иногда — например, в дилемме заключенного — у каждого игрока есть доминирующая стратегия, которая затем составляет так называемое равновесие в доминирующих стратегиях.
Чистые стратегии : игрок принимает очень конкретное решение.
Смешанные стратегии : игрок принимает случайное решение между двумя или более возможными вариантами действий (чистые стратегии), но с определенными вероятностями для чистых стратегий.
Формальное определение для разных стратегий
Равновесие по Нэшу в чистых стратегиях
Это означает набор стратегий ( альтернативные курсы действий) в -й игроке и в декартово произведении этих множеств стратегий.
Под равновесием по Нэшу в чистых стратегиях понимается профиль стратегии, в котором стратегия каждого игрока является наилучшим ответом на выбранные стратегии других игроков. Если все остальные игроки придерживаются выбранных ими стратегий, равновесие по Нэшу в чистых стратегиях формально характеризуется тем, что для игроков нет ничего, что обещало бы игроку более высокую выплату:
-
.
Также сказано, что одностороннее отклонение не улучшает выплату игрока . Равновесие по Нэшу характеризуется тем фактом, что ни один игрок не может улучшить себя , изменив свою стратегию в одностороннем порядке. Если равновесие по Нэшу состоит только из доминирующих стратегий, его также называют строгим равновесием .
Равновесие по Нэшу в смешанных стратегиях
В некоторых случаях это может быть , что игроки не связаны какой — либо конкретной стратегии, а распределение вероятностей , с которой из составляется случайным образом . Если оно конечное или хотя бы счетное , распределение вероятностей может быть описано вектором с вероятностью того, что стратегия выбрана.

Смешанная стратегия является равновесием Нэша тогда и только тогда , когда ни один игрок не может достичь лучшего выплаты по отклоняясь в одиночку, то есть , если и только если
-
.
Равновесие по Нэшу в смешанных стратегиях характеризуется тем фактом, что любая стратегия, играемая как часть равновесия, имеет одинаковый ожидаемый выигрыш.
существование
С помощью теоремы Какутани о неподвижной точке можно показать, что по крайней мере одно равновесие по Нэшу должно существовать, если выполняются следующие условия:
- Функции выплат являются непрерывными и квазивогнуты в .
- Наборы стратегии являются выпукло и компактно .
Игры часто строятся таким образом, что они конечны, но конечные множества с более чем одним элементом не могут быть выпуклыми. Однако в этом случае количество смешанных стратегий через компактные и выпуклые и соответствующее расширение полилинейных. Хотя существование равновесия по Нэшу в чистых стратегиях не может быть гарантировано, по крайней мере одно равновесие по Нэшу существует в игре в смешанных стратегиях (если предполагается конечное число чистых стратегий).
Простой алгоритм определения равновесий по Нэшу
Если игра имеет стратегическую форму, все равновесия по Нэшу могут быть определены в чистых стратегиях, используя следующий алгоритм:
- Оптимизируйте решение игрока с помощью (произвольно) фиксированных стратегий всех других игроков: отметьте самые высокие выплаты, которые могут быть достигнуты для игроков при данных обстоятельствах (так называемые «лучшие ответы» на комбинацию стратегий других игроков). Повторите это для всех возможных комбинаций стратегий других игроков.
- Выполните 1. для всех игроков.
Тогда именно комбинации стратегий являются равновесиями по Нэшу, с выплатами, отмеченными для всех игроков. Если не отмечена комбинация стратегий для всех игроков, игра также не будет иметь равновесия по Нэшу в чистых стратегиях. — Этот подход подходит только для небольшого количества игроков и стратегий.
пример
Пусть следующая игра будет дана в нормальной форме :
| Левый | центр | верно | |
|---|---|---|---|
| выше | 4 , 2 | 1 , 1 | 2 , 0 |
| центр | 2, 3 | 1 , 1 | 1, 4 |
| ниже | 3, 0 | 0, 2 | 1, 3 |
|
Выплата биматричная для игрока 1 и игрока , 2 |
Тогда алгоритм работает следующим образом (выделено жирным шрифтом):
-
- данный игрок 2 играет правильно: для игрока 1 выше является оптимальным — метка 2 ( «выше , является лучшим ответом на право»)
- если игрок 2 играет посередине: оптимально верхняя и средняя — отметьте две единицы
- учитывая, что игроку осталось 2 ходов: выше оптимально — отметьте 4
-
- данный игрок 1 играет выше: для игрока 2 оптимально левое — отметьте 2
- учитывая, что игрок 1 играет посередине: оптимально справа — отметьте 4
- если игрок 1 проигрывает: оптимально правильно — отметьте 3
Таким образом, единственное равновесие по Нэшу — это пара стратегий (вверху, слева), которые приводят к выигрышу (4, 2).
Если нужно проверить, является ли набор смешанных стратегий равновесием по Нэшу, приведенный выше алгоритм работает только в ограниченной степени, поскольку необходимо проверить бесконечное количество смешанных стратегий. В качестве альтернативы, игра также может быть решена путем итеративного исключения строго доминируемых стратегий .
Алгоритм определения равновесий по Нэшу в смешанных стратегиях
При выявлении равновесий по Нэшу в смешанных стратегиях полезно определить те смешанные стратегии, которые делают оппонента безразличным между его альтернативными курсами действий. Как только такая стратегия найдена, все действия оппонента являются лучшими ответами. Если такие смешанные стратегии встречаются, то они являются взаимно лучшими ответами, нет причин для одностороннего отклонения, и смешанные стратегии образуют равновесие по Нэшу.
Для любых игр с нулевой суммой от двух человек с конечным набором стратегий ( матричная игра ) определение равновесий по Нэшу в смешанных стратегиях может быть представлено как линейная задача оптимизации, которую можно решить с помощью симплекс-алгоритма .
пример
Дана следующая биматрица :
| Опера | Футбольный | |
|---|---|---|
| Опера | 3, 2 | 2, 3 |
| Футбольный | 1, 3 | 4, 1 |
|
Матрица выплат для игрока 1 и игрока 2 |
Тогда алгоритм работает следующим образом:
Игрок 2 играет с вероятностью Opera и с отдаленной вероятностью футбола, поэтому для игрока 1 возникает следующая ожидаемая полезность ( ожидаемая полезность ):
Таким образом, игроку 1 безразлично, какая из его двух стратегий:

Для игрока 2 аналогично можно определить, что ему безразлично, играет ли игрок 1 с вероятностью оперу и футбол.
Поскольку все ответы оппонента на эти две стратегии являются наилучшими ответами, они также являются взаимно лучшими ответами. Таким образом, его можно определить как равновесие по Нэшу в смешанных стратегиях.
Особые случаи
Частным случаем теоремы Нэша о существовании равновесий является теорема Мин-Макса , действительная для игр двух лиц с нулевой суммой , которая была доказана Джоном фон Нейманом в 1928 году . В отличие от общего случая, каждая игра имеет уникальный вектор выплат , по которому вызывается значение игры.
Для игр с нулевой суммой для двух человек с точной информацией , включая такие настольные игры, как шахматы и мельница , всегда существует минимаксное равновесие в чистых стратегиях, которое может быть определено рекурсивно с помощью минимаксного алгоритма . Эта теорема была доказана еще в 1912 году Эрнстом Цермело .
Практические примеры
Рыночная экономика
Поиск стратегии, основанный на равновесии Нэша, может быть применен в равной степени к ценам и количеству . В рыночной экономике возможна ситуация, когда несколько поставщиков на рынке снизили цены на свои конкурирующие продукты до такой степени, что они едва могут работать экономически. Для отдельного поставщика не может быть возможна стратегия уклонения: если он снижает свою цену, чтобы увеличить свои продажи, он падает в рентабельность; если он ее увеличит, покупатели переключатся на конкурирующие товары, и его прибыль также уменьшится. Одним из выходов может быть внедрение инновационного продукта (почти) одновременно с конкурентом, чтобы оправдать более высокую цену. Такие сценарии более широко обсуждались в середине 1990-х годов под термином « сотрудничество» , и в качестве яркого примера приводился спор между авиакомпаниями США.
Дилемма заключенного
Другой пример — дилемма заключенного, проблема теории игр, в которой существует ровно одно равновесие по Нэшу.
| признается | не признается | |
|---|---|---|
| признается | -5, -5 | -1, -10 |
| не признается | -10, -1 | -2, -2 |
|
Матрица выплат для игрока 1 и игрока 2 |
Представьте себе следующую ситуацию: двое заключенных подозреваются в совместном совершении преступления. Максимальный срок наказания за преступление — 10 лет лишения свободы. Теперь обоим заключенным предлагают сделку, о которой оба проинформированы. Если один признается в одиночестве (ключевой свидетель) и, таким образом, также оговорит свою партнершу, он получает мягкий приговор в виде тюремного заключения сроком на 1 год — другой должен отбыть полные 10 лет. Если оба решат хранить молчание, останутся лишь косвенные улики, которых достаточно, чтобы заблокировать их обоих на 2 года. Но если оба признаются в этом деянии, каждого ожидает тюремное заключение сроком на 5 лет. Теперь заключенных допрашивают независимо друг от друга. Ни до, ни во время опроса у них двоих нет возможности поговорить друг с другом.
Верно, что для обоих заключенных оптимально, если они оба будут молчать. Однако такая комбинация стратегий нестабильна, потому что один заключенный может получить для себя преимущество, сделав признание. Комбинация стратегий, в которой оба заключенных признаются, стабильна в смысле равновесия по Нэшу: тогда никто не может получить преимущества посредством молчания, так что существует равновесие по Нэшу. Однако это равновесие по Нэшу дает худшие результаты для обоих заключенных, чем взаимное молчание, которое можно исправить только путем сотрудничества. Другими словами: равновесие по Нэшу в дилемме заключенного не является оптимальным по Парето , поскольку оба игрока могут улучшить его вместе.
Смотри тоже
- Различные связанные концепции можно найти в разделе « Баланс (теория игры)».
веб ссылки
- Теория игр и Нэш — Вывод и примеры (английский)
- Стратегия минимакс на практике: простая игра с блефом двух человек против компьютера.
Индивидуальные доказательства
- ^ Джон Форбс Нэш: Некооперативные игры. Диссертация, Принстонский университет, 1950 ( онлайн-версия ; PDF; 1,2 МБ).
В каждой из игр, рассмотренных в предыдущих разделах, было единственное равновесие Нэша в чистых стратегиях. Однако в целом в играх необязательно должно быть единственное равновесие Нэша. Мы проиллюстрируем этот результат посредством класса игр, имеющих много областей применения, который можно обозначить как координационные игры. У их участников есть общие интересы (хотя и не всегда полностью совпадающие), но поскольку игроки действуют независимо друг от друга (в силу характера некооперативных игр), координация действий, необходимых для достижения общего предпочтительного исхода, проблематична.
А. Встретятся ли Гарри и Салли? Чистая координация
Для того чтобы проиллюстрировать эту идею, давайте представим себе двух студентов-старшекурсников, встретившихся в университетской библиотеке[50]. Они понравились друг другу и хотели бы продолжить общение, но им нужно идти в разные аудитории на лекции. Гарри и Салли договариваются вместе выпить кофе после занятий, которые заканчиваются в 16:30. Во время лекций оба осознают, что из-за волнения забыли договориться о месте встречи. Существует два возможных варианта: Starbucks и Local Latte. К сожалению, эти кафе расположены на противоположных концах большого кампуса, поэтому оказаться в обоих примерно в одно и то же время невозможно. Кроме того, Гарри и Салли не обменялись телефонными номерами, из-за чего не могут отправить друг другу сообщения. Что же нужно сделать каждому из них?
На рис. 4.10 эта ситуация представлена в виде игры с матрицей выигрышей. У каждого игрока два варианта выбора: Starbucks и Local Latte. Выигрыш для каждого равен 1, если они встретятся, и 0, если нет. Анализ наилучших ответов позволяет быстро определить, что в игре два равновесия Нэша: одно — при котором Салли и Гарри выберут Starbucks, и второе — при котором они выберут Local Latte. Для обоих важно достичь одного из этих равновесий, причем какого — не играет роли, поскольку оба равновесия обеспечивают одинаковые выигрыши. Главное, чтобы они скоординированно выбрали одно и то же действие, неважно какое. Именно поэтому такую игру называют игрой с чистой координацией.
Рис. 4.10. Чистая координация
Но смогут ли Гарри и Салли успешно скоординировать свои действия? Или в конечном счете они окажутся в разных кафе и каждый будет думать, что другой его подвел? Увы, такой риск существует. Гарри может решить, что Салли отправится в Starbucks, потому что она что-то говорила о занятиях, которые проходят на той стороне кампуса, где расположен Starbucks. Но у Салли может быть противоположное убеждение относительно того, что сделает Гарри. При наличии множества равновесий Нэша игрокам при выборе одного из них необходим какой-то способ скоординировать свои убеждения или ожидания в отношении действий друг друга.
Эта ситуация аналогична тому, что произошло с героями истории «Какая шина?», рассказанной в главе 1, где мы обозначили метод координации термином «фокальная точка». В данном контексте одно из двух кафе может быть широко известно как место встречи студентов. Однако недостаточно, чтобы Гарри просто об этом знал. Он должен знать, что Салли знает, и что она знает, что он знает, и т. д. Иными словами, их ожидания должны сходиться в фокальной точке. В противном случае Гарри может сомневаться в том, куда пойдет Салли, поскольку он не знает, что она думает о том, куда пойдет он. Подобные сомнения могут возникнуть на третьем, или четвертом, или еще более высоком уровне размышлений о размышлениях[51].
Когда один из нас (Диксит) задал этот вопрос своим студентам, большинство первокурсников выбрали Starbucks, а старшекурсники — местное кафе в студенческом центре университетского городка. Такой расклад закономерен: первокурсники, которые прожили в кампусе совсем немного времени, фокусируют свои ожидания на всем известной национальной сети кафе, тогда как старшекурсники знают местное кафе, ставшее для них самым лучшим местом встречи, и считают, что их друзья придерживаются аналогичного мнения.
Если бы одно кафе было оформлено в оранжевых тонах, а другое — в багровых, то в Принстоне первое кафе служило бы в качестве фокальной точки, поскольку оранжевый — это цвет Принстонского университета, тогда как в Гарварде по той же причине фокальной точкой было бы кафе с багровым декором. Если один человек — студент Принстона, а другой — Гарварда, они могут вообще не встретиться: либо потому, что каждый из них считает свой цвет более приоритетным, либо по той причине, что каждый думает, что другой не проявит гибкость и не пойдет на компромисс. В более общем случае способность участников координационных игр найти фокальную точку зависит от наличия такой общеизвестной точки контакта, будь то историческая, культурная или языковая.
Б. Встретятся ли Гарри и Салли? И где? Игра в доверие
Теперь давайте немного изменим выигрыши в игре. Поведение студентов старших курсов позволяет предположить, что нашей паре может быть не совсем безразлично, какое именно кафе выбирать. В одном заведении может быть лучше кофе, в другом — атмосфера. Или они могут предпочесть менее популярное место встречи студентов, чтобы избежать возможного столкновения с бывшими парнями или девушками. Предположим, Гарри и Салли остановятся на Local Latte; следовательно, выигрыш каждого из них составит 2, если они встретятся в этом кафе, и 1, если они встретятся в Starbucks. Новая матрица выигрышей показана на рис. 4.11.
Рис. 4.11. Игра в доверие
Здесь снова присутствуют два равновесия Нэша. Однако в данной версии игры каждый предпочитает равновесие, при котором оба выбирают Local Latte. К сожалению, тот факт, что обоим участникам нравится такой исход игры, его не гарантирует. Прежде всего (как и всегда в нашем анализе) выигрыши должны быть элементом общего знания, оба игрока должны знать всю матрицу выигрышей, оба должны знать, что оба знают, и т. д. Знание игры во всех подробностях было бы возможным, если бы Гарри и Салли обсудили ситуацию и сошлись во мнениях по поводу преимуществ двух кафе, но просто забыли договориться о том, что встретятся в Local Latte. Но даже в этом случае Гарри мог бы подумать, что у Салли есть какая-то иная причина для выбора Starbucks, или он может подумать, что она подумает, что он подумает, и т. д. Без истинной сходимости ожиданий в отношении действий участники игры могут выбрать худшее равновесие или, что еще печальнее, вообще не скоординировать свои действия, и тогда каждый получит нулевой выигрыш.
Повторим еще раз: участники игры, представленной на рис. 4.11, могут получить предпочтительный равновесный исход, только если каждый из них достаточно убежден в том, что другой выберет надлежащее действие. По этой причине игры такого типа называются играми в доверие[52].
Во многих подобных реальных жизненных ситуациях обрести доверие довольно легко при наличии даже минимальной коммуникации между игроками. Их интересы полностью совпадают: если один скажет «Я пойду в Local Latte», у другого нет оснований сомневаться в истинности этого утверждения, поэтому он пойдет туда же, чтобы получить предпочтительный для обоих исход. Именно поэтому нам пришлось придумать историю с двумя студентами, которые посещают разные занятия и не имеют возможности общаться друг с другом. Если интересы игроков вступают в конфликт, правдивая коммуникация становится более проблематичной. Мы углубимся в эту проблему, когда будем рассматривать стратегическое манипулирование информацией в играх в главе 8.
В более многочисленных группах коммуникацию можно обеспечить посредством планирования встреч или размещения объявлений. Но эти способы эффективны только в случае, когда все знают, что остальные обращают на них внимание, поскольку для успешной координации действий необходимо, чтобы требуемый исход был фокальной точкой. Ожидания игроков должны сходиться в этой точке: все должны знать, что каждый знает, что … каждый делает этот выбор. Именно эту функцию выполняют многие общественные институты и договоренности. Собрания, во время которых присутствующие рассаживаются по кругу и смотрят в его центр, позволяют каждому видеть, что делают остальные. Рекламные объявления во время Суперкубка, особенно когда их показывают накануне матчей в качестве основной приманки, убеждают каждого зрителя, что многие тоже их смотрят. Это делает такие рекламные объявления особенно привлекательными для компаний, выпускающих продукты, которые становятся более желанными для каждого отдельного покупателя, если их покупают многие люди; к данной категории относится продукция компьютерной отрасли, телекоммуникаций и интернет-индустрии[53].
В. Встретятся ли Гарри и Салли? И где? Битва полов
Теперь давайте еще немного усложним игру с выбором кафе. Оба игрока хотят встретиться, но предпочитают разные кафе. Таким образом, Гарри может получить выигрыш 2, а Салли — 1, если они встретятся в Starbucks, и наоборот, если встреча состоится в Local Latte. Матрица выигрышей этой игры показана на рис. 4.12.
Рис. 4.12. Битва полов
Такая игра называется битвой полов. Название происходит от истории, которую специалисты по теории игр придумали для иллюстрации этой структуры выигрышей в сексистских 1950-х годах. В этой истории мужу и жене предстоял выбор между походом на боксерский матч и балет, причем (предположительно, по эволюционно-генетическим причинам) муж должен был выбрать бокс, а жена — балет. Это название прижилось, поэтому мы будем его использовать, хотя наш пример (в котором у любого из игроков вполне могла быть причина предпочесть любое из двух кафе, не имеющая отношения к полу) ясно дает понять, что такая игра необязательно должна иметь сексистский подтекст.
Как будут развиваться события в этой игре? В ней по-прежнему присутствуют два равновесия Нэша. Если Гарри убежден, что Салли выберет Starbucks, ему лучше сделать то же самое, и наоборот. По тем же причинам Local Latte также является равновесием Нэша. Для того чтобы достичь любого из этих равновесий и избежать исходов, при которых игроки отправятся в разные кафе, им необходима фокальная точка, или сходимость ожиданий, точно так же как в игре с чистыми стратегиями и игре в доверие. Однако в битве полов риск неудачи с координацией действий выше. Игроки с самого начала находятся в достаточно симметричных ситуациях, однако каждое из двух равновесий Нэша обеспечивает им асимметричные выигрыши, а их предпочтения в отношении двух возможных исходов вступают в противоречие: Гарри ратует за встречу в Starbucks, а Салли — в Local Latte. Они должны найти способ нарушить эту симметрию.
В стремлении достичь предпочтительного для себя равновесия каждый игрок может прибегнуть к жестким действиям и стратегии, ведущей к лучшему равновесию. В главе 9 мы рассмотрим в деталях такие инструменты ведения игры, как стратегические ходы, которые участники подобных игр могут предпринять для обеспечения предпочтительного исхода. Или каждый игрок попытается угодить другому, что может обусловить досадную ситуацию, когда Гарри отправится в Local Latte, чтобы порадовать Салли, но обнаружит, что она решила доставить удовольствие ему и пошла в Starbucks (очень похоже на то, как герои рассказа О’Генри «Дары волхвов» выбирали подарки друг другу на Рождество). В качестве альтернативы в случае повторяющейся игры успешная координация действий может стать предметом переговоров и поддерживаться как равновесие. Например, Гарри и Салли могут договориться встречаться то в одном, то в другом кафе. В главе 10 мы проанализируем такое неявное сотрудничество в повторяющихся играх в контексте дилеммы заключенных.
Г. Встретятся ли Джеймс и Дин? Игра в труса
Наш последний пример в этом разделе касается координационной игры несколько иного типа. В ней игроки стремятся предотвратить (или не выбирать) одни и те же действия. Кроме того, последствия неудачной попытки координации в подобных играх куда более разрушительны, чем в других играх.
Эта история взята из игры, в которую якобы играли американские подростки в 1950-х годах. Двое подростков садятся в полночь в свои автомобили на противоположных концах улицы какого-нибудь американского городка и мчатся навстречу друг другу. Тот, кто свернет в сторону, чтобы избежать столкновения, становится «трусом», а тот, кто продолжает ехать прямо, считается победителем. Если оба подростка придерживаются прямого курса, происходит столкновение, в котором оба автомобиля получают повреждения, а оба водителя — травмы[54].
Выигрыши «труса» зависят от того, насколько негативным для себя игрок считает «плохой» исход (в данном случае это травмы водителя и повреждения автомобиля) по сравнению с перспективой прослыть трусом. Если слова задевают меньше, чем хруст металла, то таблица разумных выигрышей в варианте игры в труса 1950-х годов выглядит так, как на рис. 4.13. Каждый игрок больше всего хочет стать победителем, а не трусом, и оба одинаково не хотят столкновения автомобилей. Между этими двумя крайностями для вас предпочтительна ситуация, чтобы ваш соперник оказался трусом в игре с вами (сохранить лицо), чем самому стать трусом.
Рис. 4.13. Игра в труса
У этой истории есть четыре важных свойства, которые определяют игру в труса. Во-первых, у каждого игрока есть одна «жесткая» и одна «слабая» стратегия. Во-вторых, в игре присутствуют два равновесия Нэша в чистых стратегиях (иными словами, исходы игры, при которых один из игроков становится трусом или придерживается слабой стратегии). В-третьих, каждый игрок выбирает именно то равновесие, при котором другой игрок предпочитает стать трусом или применяет слабую стратегию. В-четвертых, когда оба придерживаются жесткой стратегии, оба получают очень плохие выигрыши. В играх такого типа реальная игра сводится к проверке ее участниками способов достижения предпочтительного для себя равновесия.
Мы вернулись к ситуации, подобной рассмотренной при обсуждении игры «битва полов». Большинство происходящих в реальной жизни игр в труса предполагают еще более ожесточенные битвы, чем битва полов: преимущества от победы повышаются, так же как и цена поражения, поэтому все проблемы, связанные с конфликтом интересов и асимметрией между игроками, усугубляются. Каждый игрок стремится повлиять на исход такой игры. Может сложиться ситуация, когда один игрок попытается создать впечатление жесткости, которое видели бы все, чтобы запугать соперников[55]. Еще один вариант — найти какой-либо другой способ убедить соперника в том, что вы не сдадитесь, взяв на себя явное и непреложное обязательство ехать прямо. (В главе 9 мы поговорим о том, как делать ходы с обязательствами.) Кроме того, оба игрока могут захотеть предотвратить неблагоприятный исход (столкновение), если это вообще возможно.
Как и в битве полов, если игра повторяется, молчаливая координация — лучший путь к решению игры. Иначе говоря, если бы подростки играли в труса в полночь каждого воскресенья, при выборе равновесных стратегий они знали бы, что у игры есть и прошлое, и будущее. В подобной ситуации они могли бы выбрать такой логически правильный путь, как чередование равновесий, и по очереди бы становились победителями раз в две недели. (Однако если кто-то узнает об этой сделке, пострадает репутация обоих игроков.)
Существует еще один, последний, момент, касающийся координационных игр, о котором следует упомянуть. Концепция равновесия Нэша требует от каждого игрока наличия правильных убеждений в отношении выбора стратегии другим игроком. При поиске равновесий Нэша в чистых стратегиях эта концепция предписывает, чтобы каждый игрок был уверен в выборе другого игрока. Но наш анализ координационных игр показывает, что в размышлениях о выборе других игроков в таких играх присутствует элемент стратегической неопределенности. Как мы можем включить ее в анализ? В главе 7 мы вводим понятие смешанной стратегии, в которой фактический выбор делается случайным образом из доступных действий. Такой подход распространяет концепцию равновесия Нэша на ситуации, когда игроки могут быть не уверены в действиях друг друга.





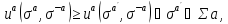
 Sa+
Sa+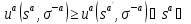 Sa+,
Sa+, Sa+
Sa+
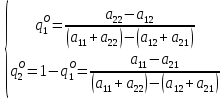
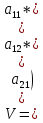






















![{ Displaystyle OperatorName {E} [U_ {1} (O)] = 3q + 2 (1-q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23e1754f40767b7e08388d497b84808cdf382b18)
![{ Displaystyle OperatorName {E} [U_ {1} (F)] = 1q + 4 (1-q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cb4a170f035089717a7afbff5b72e6fe7d359f2)


![[(2/3; 1/3), (1/2; 1/2)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/09d5dd8b8ae736f8ff6289e1cecce3d6f370cc28)

