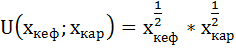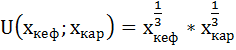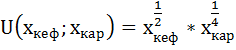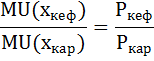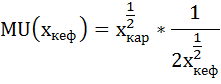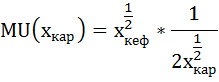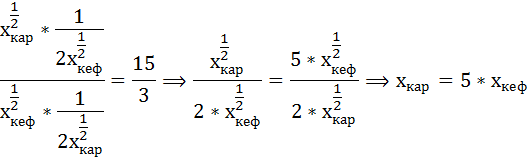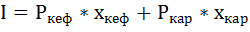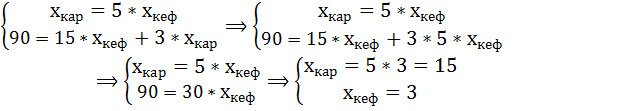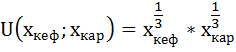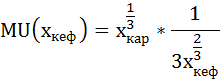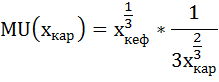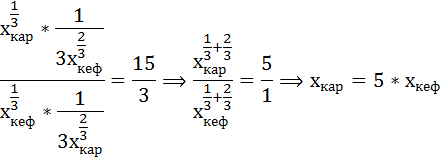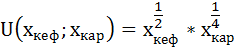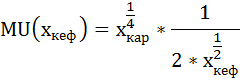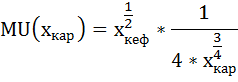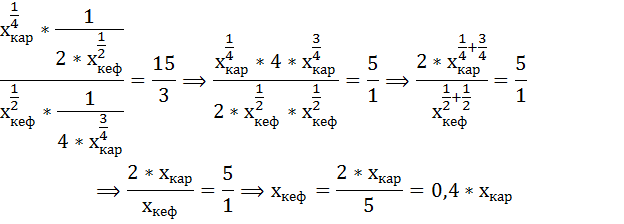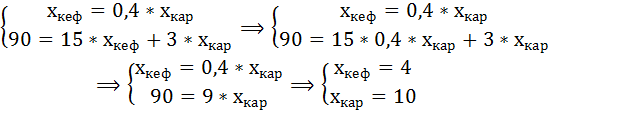Как найти равновесный набор для потребителя

Кривые безразличия отражают систему предпочтений индивида, но для анализа потребительского выбора необходимо учесть еще две важные переменные: доход потребителя и цены товаров. Кривые безразличия лишь показывают возможность замены для индивида одного блага другим без ущерба для его благополучия. Но они не определяют, какой именно набор товаров потребитель считает для себя наиболее выгодным. Для этого вводится понятие бюджетного ограничения. Оно показывает, какое количество благ (какие потребительские наборы) можно приобрести при данных ценах и доходе.

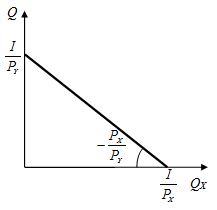
Рис. 2.18. Бюджетная линия

Предположим, что весь свой доход потребитель тратит на приобретение двух товаров X и Y. Тогда сумма его расходов на данные товары равна его доходу (бюджету), и уравнение бюджетного ограничения можно представить следующим образом:

,                                                  (2.14)

где I – доход потребителя; P_X – цена товара X; P_Y – цена товара Y; x – количество приобретенного блага X; y – количество купленного блага Y.

Бюджетная линия – это прямая, точки которой показывают различные комбинации двух товаров при равенстве расходов на их приобретение (рис. 2.18).

Бюджетная линия обладает следующими свойствами:

1) бюджетная линия характеризуется отрицательным наклоном, так как увеличение закупок одного товара возможно лишь путем сокращения расходов на другой товар;

2) точка пересечения бюджетной линии с осью абсцисс соответствует максимально возможному объему потребления продукта X. Точка пересечения бюджетной линии с осью ординат отвечает максимально возможному объему потребления продукта Y;

3) наклон бюджетной линии к осям координат определяется отношением цен продуктов. Он является величиной постоянной, поскольку потребитель не в состоянии повлиять на цены;

4) при увеличении дохода потребителя бюджетная линия сдвигается параллельно самой себе вправо (из положения AB в положение A₂B₂), а при уменьшении дохода – влево в положение A₁B₁ (рис. 2.19, а). При этом угол наклона бюджетной линии не меняется;

5) При изменении цены одного из благ меняется наклон бюджетной линии (при увеличении цены наклон становится круче, при уменьшении цены – более пологим):

а) увеличение цены товара X (P_Y = const) приведет к повороту бюджетной линии по часовой стрелке (влево) вокруг точки пересечения линии бюджетного ограничения с осью ординат (из положения AB в положение A₁B) и наоборот (см. рис. 2.19, б);

а) при увеличении цены товара Y (P_X = const) бюджетная линия повернется против часовой стрелке (влево) вокруг точки пересечения линии бюджетного ограничения с осью абсцисс (из положения AB в положение AB₁) и наоборот (см. рис; 2,19, в);

1) наборы, находящиеся слева от бюджетной линии, доступны для потребителя, а находящиеся справа – недоступны.

Рис. 2.19. Сдвиги бюджетной линии под влиянием изменения дохода и цен

Цель потребителя – сделать покупки таким образом, чтобы обеспечить себе максимум полезности в рамках своего бюджетного ограничения.

Равновесный (оптимальный) набор товаров – это набор на бюджетной линии, который обеспечивает потребителю максимальную полезность.

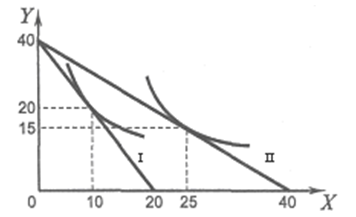
С формальной точки зрения решение проблемы равновесия состоит в поиске пары чисел (x;y), которая удовлетворяет бюджетному ограничению (см. формулу (2.14)) и максимизирует функцию полезности TU. Для этого необходимо совместить карту безразличия с бюджетной линией потребителя II (рис. 2.20). Это вполне правомерно, так как оси координат карты безразличия и линии бюджетного ограничения являются идентичными.

Рис. 2.20. Равновесное положение потребителя

Точка L на кривой безразличия U₃ характеризует такой набор товаров X и Y, который в данный момент (при заданном бюджете) является недоступным потребителю (хотя весьма желаемым).

Бюджетная линия II имеет три точки соприкосновения с кривыми безразличия. Рассмотрим их и определим точку равновесия.

В точках M и N, расположенных на кривой U₁, потребитель не достигнет состояния равновесия, так как, двигаясь от них влево вверх или вправо вниз соответственно, он может перейти на кривую безразличия, находящуюся выше (U₂) и характеризующую более высокий уровень совокупной полезности. Таким образом, оптимальным для потребителя будет товарный набор в точке K, которая является единственной точкой соприкосновения кривой безразличия U₂ и линии бюджетного ограничения II.

Следовательно, равновесие потребителя достигается в точке, в которой бюджетная линия касается наиболее высокой из всех доступных потребителю кривых безразличия. Стоит также отметить, что в точке равновесия K выполняется условие, названное нами ранее как правило максимизации полезности (2.11).

Примеры решения типовых задач

Задача 1

Функции совокупной полезности покупателя от потребления двух благ – хлеба (X) и мяса (Y) – заданы уравнениями:

;

,

где Q_X – количество хлеба, кг; Q_Y – количество мяса, кг.

Цена хлеба равна 2 ден. ед., а цена мяса – 5 ден. ед. Ежемесячный доход потребителя, расходуемый на эти два товара, составляет 39 ден. ед. Определите:

1) объем мяса и хлеба, приобретение которых позволит потребителю максимизировать совокупную полезность от потребления данных товаров;

2) величину максимальной общей полезности (TU_max).

Решение:

Согласно правилу максимизации полезности (2.11), наибольшую полезность обеспечивает такая структура покупок, при которой отношение предельной полезности блага (MU) к его цене (P) одинаково для всех благ. В нашем случае:

Определим функции предельной полезности для мяса и хлеба. Функция предельной полезности вычисляется как частная производная от функции общей полезности:

.

Тогда:

;

Подставив полученные выражения в уравнение максимизации полезности, получим:

или

Выбор потребителя ограничен его бюджетом. Уравнение бюджетного ограничения имеет вид:

.

Тогда:

Составим систему уравнений и найдем Q_X и Q_Y:

;

.

Отсюда

Q_X =7;                        Q_Y = 5.

Следовательно, потребляя в месяц 7 кг хлеба и 5 кг мяса, покупатель максимизирует совокупную полезность:

.

При этом он расходует весь доход:

Определим величину общей полезности для набора (7; 5):

.

Тогда:

Таким образом, потребителю необходимо приобрести 7 кг хлеба и 5 кг мяса, чтобы максимизировать совокупную полезность от потребления данных товаров, и величина максимальной общей полезности (TU_max) составит 125,5 ютилей.

Задача 2

Потребитель приобретает два товара: хлеб и молоко. Данные о количестве и полезности приобретаемых благ представлены в таблице 2.2. Цена хлеба 20 р./кг, цена молока

40р./кг. Доход потребителя составляет 220 р. Определите равновесный набор хлеба и молока, максимизирующий совокупную полезность потребителя. Изобразите ситуацию равновесия графически.

Таблица 2.2 Данные о количестве и полезности приобретаемых благ

Количество приобретаемых благ Q, кг	Общая полезность, ютили
хлеба (TUХ)	молока (TUМ)
1	15	12
2	25	23
3	33	33
4	40	40
5	45	46

Решение:

Для определения оптимального (равновесного) набора товаров необходимо воспользоваться правилом максимизации полезности (2.11), которое в данном случае будет иметь следующий вид:

где MU_Х и MU_М – предельные полезности хлеба и молока соответственно; P_Х и P_М – цены соответственно хлеба и молока.

Рассчитаем предельные полезности двух товаров, используя формулу (2.9):

Так как в данном случае объем товаров изменяется каждый раз на постоянную величину, то знаменатель в данной формуле можно принять равным единице и при расчетах не учитывать.

Затем рассчитаем величину предельной полезности, приходящуюся на один рубль  для хлеба и молока и сведем все полученные результаты в таблицу 2.3.

Необходимо найти такое соотношение двух товаров, которое бы удовлетворяло правилу максимизации полезности. Анализ данных таблицы 2.3 показывает, что потребление 5 кг хлеба и 3 кг молока принесет потребителю наибольшее удовлетворение, так как такая комбинация соответствует правилу ().

Таблица 2.3 Результаты расчётов

Количество приобретаемых благ (Q), кг	Хлеб	Молоко
TUХ, ютили	MUХ, ютили	ютили на рубль	TUМ, ютили	MUМ, ютили	ютили на рубль
1	15	15		12	12
2	25	25 – 15 = 10		23	23 – 12 = 11
3	33	33 – 25 = 8		33	33 – 23 = 10
4	40	40 – 33 = 7		40	40 – 33 = 7
5	45	45 – 40 = 5		46	46 – 40 = 6

Определим, доступен ли данный набор потребителю при имеющемся бюджете в 220 р.

Для этого используем уравнение бюджетного ограничения (2.14), подставив в него имеющиеся данные:

Данный набор доступен потребителю, при этом весь бюджет последнего будет израсходован. Таким образом, данный набор хлеба и молока полностью соответствует правилу максимизации полезности.

Для изображения ситуации равновесия потребителя графически необходимо на одном графике совместить бюджетную линию и кривую безразличия.

Для построения бюджетной линии достаточно определить координаты двух точек. Определим максимальное количество хлеба  и молока , которые может приобрести потребитель на свой бюджет:

Рис. 2.21. Равновесие потребителя

Расположим точки с координатами (11; 0) и (0; 5,5) на осях абсцисс и ординат соответственно и построим линию бюджетного ограничения (рис. 2.21). Также возьмем точку, принадлежащую данной линии с координатами (5; 3) и проведем через нее кривую безразличия (произвольной формы).

Задания для самоконтроля

1. Какое из следующих утверждений является неправильным?

а) Каждая точка на кривой безразличия означает определённую комбинацию двух товаров.

б) Каждая точка на бюджетной линии означает определённую комбинацию двух товаров.

в) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей.

г) Все точки на кривой безразличия означают одинаковый уровень денежного дохода.

2. Установите соответствие между приведенными терминами и определениями:

Термины	Определения
1. Предельная полезность	а) пропорция, в соответствии с которой одно благо может быть замещено другим без выигрыша или потери для удовлетворения потребителя
2. Карта кривых безразличия	б) приращение общей полезности при увеличении потребления блага на единицу
3. Предельная норма замещения	в) совокупность точек, представляющих различные сочетания двух благ, доступных потребителю при данных ценах и бюджете
4. Принцип убывающей предельной полезности	г) при заданных ценах и бюджете потребитель достигает максимума полезности тогда, когда отношение предельной полезности к цене одинаково для всех потребляемых благ
5. Линия бюджетного ограничения	д) метод описания предпочтений потребителя совокупностью его кривых безразличия
6. Принцип максимизации полезности	е) по мере увеличения потребления блага, предельная полезность каждой дополнительной единицы блага сокращается

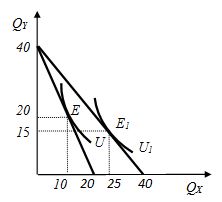
1. Еженедельный доход потребителя составляет 200 ден. ед. Используя бюджетные линии и соответствующие им кривые безразличия (рис. 2.22), определите цену товара Y, а также цены товара X до и после изменения.

Рис. 2.22. Бюджетные линии и соответствующие им кривые безразличия

2. Если потребитель выбирает комбинацию, представленную точкой, лежащей на плоскости, ограниченной бюджетной линией, то он:

а) максимизирует полезность;

б) желает купить больше товаров, чем позволяет его бюджет;

в) не полностью использует свой бюджет;

г) находится в положении потребительского равновесия.

3. Заданы равновесные объемы потребления продуктов X и Y при некоторых значениях дохода потребителя (табл. 2.4). Цены продуктов неизменны. Определите цены товаров и заполните пустые ячейки таблицы.

Таблица 2.4 Равновесные объемы потребления продуктов X и Y при некоторых значениях дохода потребителя

Доход потребителя I, ден. ед.	Количество, шт.
товара X	товара Y
40	4	14
35	5	10
34		8
	7	6
30	8

Задания повышенной сложности

1. Постройте кривые безразличия нетипичной формы и определите значение предельной нормы замещения в каждом случае. Приведите примеры товаров для различных форм кривых безразличия.

2. Изучите алгоритм построения кривых «цена – потребление» и «доход – потребление». На основе кривой «цена – потребление» постройте линию спроса для одного из товаров.

рекомендуемая литература

[4, с. 193 – 206]; [6, с. 120 – 157]; [7, с. 72 – 123]

Учебные материалы

Модель поведения потребителя предполагает, что покупатель стремится получить наивысший уровень полезности, т.е. максимизирует полезность при наличном бюджетном ограничении.

Для определения максимального уровня удовлетворения потребностей потребителя необходимо совместить бюджетную линию и карту кривых безразличия на одном графике. Мы практически совмещаем потребности потребителя и его возможности.

Максимизация достигается в точке, в которой бюджетная линия является касательной к кривой безразличия.

Эта точка является точкой потребительского равновесия.

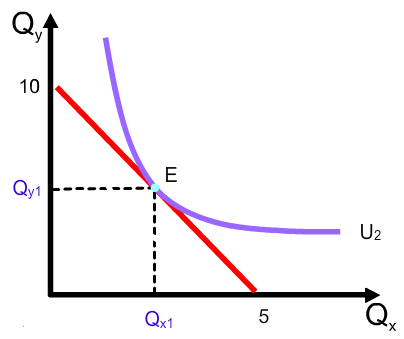
На рис. 6.9 мы используем модель, чтобы определить выбор потребителя относительно недельного потребления апельсинов и яблок в рамках своего бюджетного ограничения.

Максимальная полезность, достигаемая при данном бюджете, обеспечивается набором в точке Е с координатами Q_х1, Q_у1. Это и есть выбранный потребительский набор. Ни одна из других комбинаций не доставит потребителю большей полезности при данном доходе.

Равновесие потребителя соответствует такой комбинации покупаемых товаров, которые максимизируют полезность приданном бюджетном ограничении. Это есть равновесие в том смысле, что при известных предпосылках модели, как только потребитель получает такой набор, у него нет больше стимула менять его на другой.

Можно показать равновесие потребителя с помощью предельной полезности, исходя из предположения, что ее можно количественно измерить. Каждый потребитель стремится повысить свою общую полезность, а значит использовать и распределить доход так, чтобы предельная полезность от израсходованной денежной единицы на тот или иной товар была одинаковой.

Общее условие равновесия потребителя (принцип равной полезности) указывает, что потребитель в равновесии распределяет расходы на все товары таким образом, что их предельные полезности в расчете на доллар (рубль, франк и т.д.) должны быть равными.

Если МU_x – предельная полезность товара X, МU_y – предельная полезность товара Y, Р_x – цена товара X, Р_y – цена товара Y, то вышесказанное можно определить формулой:

Например, если предельная полезность товара Х (скажем корзина яблок) равна 100, а его цена 10 долл., предельная полезность товара Y (скажем корзина апельсинов) – 50, а его цена 5 долл., то предельная полезность на доллар будет в обоих случаях равна 10. Это уравнение показывает, что при этих условиях потребитель не может переместить ни цента на другой товар и повышать его полезность.

Данное уравнение можно преобразовать:

Это уравнение отражает установление равновесия, когда потребитель сделал все возможное, чтобы максимизировать свой выбор, свою полезность. Ведь когда он приходит на рынок, то сталкивается с огромным количеством цен, ему приходится регулировать свой выбор, отдавать предпочтение товарам таким образом, чтобы их предельная полезность на один доллар (на одну денежную единицу) были равны.

Например, как потратить 4 доллара в буфете, где потребителю предлагают лишь два товара: пирожное по цене 2 долл. за штуку и сок по цене 1 долл. за стакан (таблица 6.4).

Таблица 6.4 – Принцип максимизации полезности, усл.ед.

Равновесие потребителя

Равновесие потребителя (Consumer equilibrium) — точка, в которой потребитель максимизирует свою общую полезность или удовлетворение от расходования фиксированного дохода.

Равновесие потребителя может быть выражено следующим образом:

где MU — предельная полезность отдельных товаров;
P — их цена.

Если кривая безразличия показывает, что потребитель хотел бы купить, а бюджетная линия — что потребитель может купить, то в своем единстве они могут ответить на вопрос, как обеспечить максимальное удовлетворение от покупки при ограниченном бюджете. Кривые безразличия и бюджетная линия используются для графической интерпретации ситуации, когда потребитель максимизирует полезность, получаемую им от покупки двух разных благ при имеющемся бюджете.

Оптимальный набор потребительских благ должен отвечать двум требованиям:

• находиться на бюджетной линии;
• предоставить потребителю наиболее предпочтительное сочетание.

Данные условия и их реализация обеспечивают оптимальный выбор точки на бюджетной линии. Для этого необходимо наложить бюджетную линию на карту кривых безразличия, как это показано на графике.

В данном случае прямая mathrm — это бюджетная линия, а кривые <mathrm U>_1 , <mathrm U>_2 , <mathrm U>_3 , <mathrm U>_4 — это кривые безразличия. При имеющемся доходе потребитель, свободно перемещаясь по прямой mathrm , будет стремиться к точке mathrm M (бюджетная линия mathrm касается кривой безразличия <mathrm U>_2 ), где он получит наибольшую полезность. <mathrm U>_2 является наивысшей кривой которую может достичь потребитель при имеющемся доходе.

Уравнение равновесия потребителя и производителя

2. Величина спроса.

4. Эффект дохода.

5. Эффект замещения.

6. Принцип убывания маржинальной полезности.

7. Эффект Гиффена.

8. Детерминанты спроса.

9. Низшие товары.

10. Нормальные товары.

Групповая дискуссия по теме

Задача 1. Расчет параметров рыночного равновесия при отсутствии налогов на потребителей и производителей

Условие задачи

Спрос и предложение фирмы на рынке описываются уравнениями: Q d =200-5Р; Q s =50+Р. Определите параметры рыночного равновесия.

Решение

Рыночное равновесие достигается при равенстве объемов спроса Q d и предложения Q s :

Подставив в равенство функции спроса и предложения, получим:

200 — 5Р = 50 + Р
200 – 50 = Р + 5Р
Р = 25

Для того чтобы определить равновесный объем, необходимо в уравнение спроса или предложения подставить равновесную цену:

200 – 5 × 25 = 75 ед.

Таким образом, равновесная цена составляет 25 ден. ед., а равновесный объем – 75 ед.

Задача 2. Расчет параметров рыночного равновесия при введении налога на потребителей

Условие задачи

Кривая спроса описывается уравнением Q d =70-2Р, а кривая предложения — уравнением Q s =10+Р. Правительство ввело налог на потребителей в размере 9 долл. за единицу. Определите:

1. как изменятся равновесные цена и объем продукции;
2. каков доход государства от введения этого налога;
3. в какой степени пострадают от введения этого налога потребители и производители.

Решение

До введения налога рыночное равновесие достигалось при цене Р 0 и объеме Q 0 (на рисунке — в точке пересечения кривых спроса D и предложения S). Рассчитаем параметры равновесия:

70 — 2Р=10 + Р
3Р=60
Р=20 долл.
Q 0 =30 ед.

В результате введения налога произойдут следующие изменения:

Последствия введения налога

• Поскольку вводится налог на потребителей, то для них цена возрастет и составит P d . Количество товара, которое потребители приобретут по данной цене, составит Q 1 (на рисунке — точка пересечения кривой спроса D и цены P d ).
• Чистая цена, которую получат производители, составит P s . Количество товара, которое производится при данной цене P s , составит Q 1 (на рисунке — точка пересечения кривой предложения S и цены P s ).

Теперь по пунктам ответим на поставленные в задаче вопросы.

1. Как изменятся равновесные цена и объем продукции? Рыночное равновесие достигается тогда, когда объем продаж производителя равен объему покупок потребителя:

Равновесный объем продаж Q 1 после введения налога соответствует цене P d на кривой спроса и цене P s на кривой предложения. Разница между ценой покупки P d и ценой продажи P s составляет величину налога t:

Так как кривые спроса, предложения и размер налога заданы, параметры рыночного равновесия после введения налога можно найти из уравнений:

Q d = 70 — 2Р
Q s =10 + Р
Q d = Q s
P d — P s = 9

Подставив первые два уравнения в третье получим:

Введение налога на потребителей приведет к росту цены продажи. Она составит P d = P s + 9. Подставляем P d в уравнение и получим:

70 – 2(P s + 9) = 10 + P s
70 – 2 P s – 18 = 10 + P s
3 P s = 42
P s = 14
P d = 23

Подставив равновесную цену P s в уравнение предложения, получим равновесный объем Q 1 :

Q 1 = 10 + 14 = 24

Тот же результат можно получить, если подставить цену покупки P d в уравнение спроса:

Q 1 = 70 – 2 × 23 = 24

После введения налога на потребителей в размере 9 долл. за ед. равновесный объем на рынке составит 24 ед. при равновесной цене (P s ) 14 долл. за ед. Таким образом,введение налога на потребителей приведет к сокращению равновесного объема на 6 ед. (30 – 24) и равновесной цены на 6 долл. (20 – 14).

2. Каков доход государства от введения налога? За каждую единицу проданного товара государство получит 9 долл. Общая сумма налогов, полученных государством, составит:

Д г = Q 1 × t = 24 × 9 = 216 долл.

Графически общая сумма доходов государства представлена на рисунке суммарной площадью прямоугольников A и D.

3. В какой степени пострадают от введения этого налога потребители и производители? Для того чтобы определить, каким образом налоговое бремя распределяется между покупателями и производителями, необходимо определить размер их потерь в результате введения налога. Объем покупок потребителей в результате введения налога сократился с 30 ед. до 24 ед., а цена покупки возросла с 20 долл. до 23 долл. Общие потери потребителей (в результате роста цены и сокращения объема покупок) с введением налога графически представлены суммарной площадью фигур А и В. При налоге потребителям каждая единица товара обходится на 3 долл. дороже, чем без налога, т.е. они дополнительно тратят:

Q 1 × 3 = 24 × 3 = 72 долл.

Таким образом, оплачиваемая потребителями часть налоговых поступлений составит 72 долл. (на рисунке – площадь прямоугольника А) В результате введения налога цена продажи сократилась с 20 долл. до 14 долл. за ед. , а значит за каждую единицу товара производитель получит на 6 долл. меньше. Его потери в результате сокращения цены составят:

Q 1 × 6 = 24 × 6 = 144 долл.

Часть налоговых поступлений , оплачиваемая производителями, графически представлена на рисунке площадью прямоугольника D. Результаты расчета свидетельствуют о том, что при введении налога на потребителей производители оплачивают в 2 раза большую часть налоговых поступлений, чем сами потребители.

Задача 3. Расчет параметров рыночного равновесия при введении налога на производителей

Условие задачи

Предположим, что кривая спроса описывается уравнением Q d =400- Р, а кривая предложения — уравнением Q s = 100 + 2Р. Правительство ввело налог на производителей в размере 15 долл. за единицу продукции.

1. как изменятся равновесные цена и объем продукции;
2. каков доход государства от введения этого налога;
3. в какой степени пострадают от введения этого налога потребители.

Решение

1. Задача решается аналогично предыдущей (см. Задача 2), с той лишь разницей, что налогом облагаются не потребители, а производители. Определяем параметры рыночного равновесия до введения налога:

400 — P d = 100 + 2(P d – 15)
3P d = 330
P d = 110 ден. ед.
P s = 110-15 = 95 ден. ед.
Q 1 = 400 – 110 = 290 ед.

Параметры рыночного равновесия после введения налога определяем с помощью уравнений:

Q d = 400 — Р
Q s =100+ 2Р
Q d = Q s
P d — P s = 15

Введение налога на производителей приведет к тому, что получаемая ими чистая цена уменьшится. Введение налога на производителей не отразится на цене покупки P d , а цена продажи будет равна P s = P d – 15. Сделав все необходимые подстановки, получаем:

400 — P d = 100 + 2(P d – 15)
3 P d = 330
P d = 110 долл.
P s = 110 – 15 = 95 долл.
Q 1 = 400 – 110 = 290 ед.

После введения налога на производителей равновесный объем составил 290 ед., а равновесная цена – 110 долл. Таким образом, равновесный объем сократился на 10 ед., а равновесная цена возросла на 10 долл.

2. За каждую единицу проданного товара государство получит 15 долл. Общая сумма налогов, полученных государством, составит:

Д г = Q 1 × t = 290 × 15 = 4350 долл.

3. При налоге на производителей каждая единица товара обходится потребителям на 10 долл. дороже (до налога цена покупки составляла 100 долл., при налоге -110 долл.). Часть налоговых поступлений, оплачиваемая потребителями, составит:

Q 1 × 10 = 290 × 10 = 2900 долл.

До введения налога цена продажи составляла 100 долл., а после введения налога – 95 долл., т.е. при налоге производители за каждую проданную единицу товара получают на 5 долл. меньше. Часть налоговых поступлений, оплачиваемая производителями, составит:

Q 1 × 5 = 290 × 5 = 1450 долл.

Таким образом, при введении налога на производителей покупатели оплачивают в 2 раза большую часть налоговых поступлений, чем производители.

Подведение итогов дискуссии

Проверка рабочей тетради

Проверка выполнения тренировочных тестов

Тестовые задания

1. Закон спроса гласит, что при прочих равных условиях:

а) если цена на товар растет, предложение этого товара увеличивается;

б) если цена на товар растет, предложение этого товара снижается

в) если цена на товар падает, предложение этого товара увеличивается;

г) если цена на товар падает, предложение этого товара сокращается.

2. Для товара, относящегося к категории нормальных, понижение дохода ведет к:

а) смещению кривой спроса на этот товар вверх;

б) смещению кривой спроса на этот товар влево;

в) смещению кривой спроса на этот товар вправо;

г) смещению кривой спроса на этот товар вниз.

3. Если товар X является субститутом (взаимозаменяющим) для товара

У, то повышение цены на товар X приведет к:

а) понижению спроса на товар У;

б) понижению спроса на товар X;

в) увеличению спроса на товар X;

г) увеличению спроса на товар У.

4. Для издательства, выпускающего учебники, повышение цены на

бумагу приведет к тому, что кривая предложения:

а) переместится так, что возникнет потребительский выигрыш;

б) сместится влево — вверх;

в) сместится вправо — вниз;

г) станет параллельной оси цен.

5. Максимальная цена, которая может быть установлена на рынке по закону, — это:

а) ценовой потолок;

б) полная экономическая цена;

в) выигрыш производителя;

6. Если куриные окорочка — это товар низшей категории, то как

повлияет экономический бум в стране на их цену и продажу:

а) цена увеличится, объем продаж упадет;

б) цена увеличится, объем продаж возрастет:

в) цена снизится, объем продаж упадет;

г) цена снизится, объем продаж возрастет;

7. Что из перечисленного ниже не является фактором, приводящим к смещению спроса:

а) цены субститутов.

б) потребительский доход.

в) затраты на рекламу.

г) цены взаимодополняющих товаров.

д) цена самого товара.

8. Закон предложения, если цены растут, а прочие условия неизменны, проявляется в:

а) росте предложения;

б) снижении предложения;

в) росте объема предложения;

г) падении объема предложения.

9. Рынок товаров и услуг находится в равновесном состоянии, если:

а) спрос равен предложению;

б) цена равна издержкам плюс прибыль;

в) уровень технологии меняется постепенно:

г) объем предложения равен объему спроса.

10. Если спрос возрастает, а предложение снижается, то:

а) равновесная цена повышается, а равновесное количество сокращается;

б) и равновесная цена, и равновесное количество повышаются;

в) и равновесная цена, и равновесное количество сокращаются;

г) равновесная цена сокращается, а равновесное количество повышается.

Примеры решений задач: функция полезности

В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.

Функция полезности: задачи с решениями

Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y — количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X — 400 р., товара Y — 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.

Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.

Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб.
Функции общей полезности разных благ: $F(TU(x))=3sqrt{Qx}$, $F(TU(y))=5sqrt{Qy}$, $F(TU(z))=5sqrt{Qz}$.

Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%

Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.

Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.

Задача 5. Общая полезность благ $alpha$ и $beta$ для некоего потребителя описывается уравнениями $U_alpha = q_alpha(15 — 0,5q_alpha)$, $U_beta = q_beta(30 — q_beta)$. Допустим, потребитель располагает бюджетом для покупки $alpha$ и $beta$ в размере 120 руб., цены на $alpha$ и $beta$ равны соответственно 5 и 10 руб. Определить количество $alpha$ и $beta$, максимизирующее полезность потребителя.

Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ — количество X в шт. MU товара Y: $21 – 2y$, где $y$ — количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?

Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.

Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.

Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?

Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^{1/7}x_2^{1/6}$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.

Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^{1/7}(x_2-40)^{1/6}$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^{1/3}x_2^{1/4}$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.

Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=sqrt{xy}$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.

Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.

Может быть интересно:

Общая полезность

Общая полезность — удовлетворение, которое получают от потребления определенного набора товара или услуги.

Предельная полезность — это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу.

Mu = (Tu₁ — Tu₀)/(Q₁ — Q₀)

Производная по количеству Q

Mu = dTu/dQ
Как найти производную.

Например, TU = x*y. Mu_x = d(x*y)/dx = y; Mu_y = d(x*y)/dy = x

Например, TU = 10x² + 2x + 2. Mu_x = d(10x² + 2x + 2)/dx = 20x + 2

Функция полезности — функция, показывающая убывание полезности блага с ростом его количества:

Tu = f(Q_i)

Условия равновесия потребителя

Условия равновесия потребителя можно выразить формулой:Mu_x / Mu_y = P_x / P_yгде P_x и P_y — цены на товары X и Y.

Точка касания кривой безразличия с бюджетной линией означает равновесие потребителя.

Пример задачи на нахождение оптимального набора покупок

Пример задачи на нахождение оптимального набора товаров при заданной функции полезности

Кривая безразличия

Кривая безразличия — это множество точек на кривой, которые показывают различные комбинации двух экономических благ, имеющих одинаковую полезность для потребителя.

Предельная норма замещения (marginal rate of substitution — MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную единицу:

MRS_xy = ΔY / ΔXΔY = Y₁ — Y₀ΔX = X₁ — X₀илиMRS_xy = Mu_x / Mu_y

Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.

Бюджетная линия

Бюджетная линия представляет собой прямую линию с отрицательным наклоном, графически отображающую множество наборов из двух товаров, требующих одинаковых затрат на их потребление. Она показывает, какие потребительские наборы можно приобрести за данную сумму денег.I = P_xX + P_yYгде I — доход потребителя;
P_x — цена блага Х;
P_y — цена блага Y;
X,Y — составляют соответственно купленные количества благ.

Пример. Функция полезности U(xy)=xy. Доход потребителя равен 80 ден. ед. Цены товаров x и y соответственно равны P_x=2 руб. и P_y=4 руб. Найдите равновесный набор.

Решение: Из условия равновесия потребителя: Mu_x / Mu_y = P_x / P_y получаем: Mu_x = d(x*y)/dx = y; Mu_y = d(x*y)/dy = x

Тогда: y / x = 2 / 4 = ¹/₂ или y = ¹/₂x

Для наших данных уравнение бюджетной линии запишем как: 80 = 2x + 4y = 2x + 4*1/2x = 4x

Откуда: x = 20 ед., y = ¹/₂*20 = 10 ед.

Ответ: потребитель приобретет 20 ед. товара x и 10 ед. товара y.

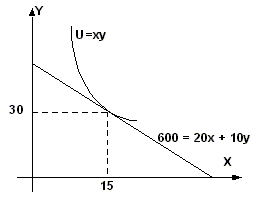
Пример решения определения оптимума потребителя

Потребитель тратит 600 рублей в месяц на приобретение двух товаров. Цена товара Х — 20 рублей, а товара Y — 10 рублей. Задана функция полезности потребителя U = ХY. Составить уравнение бюджетной линии. Найти предельную норму замещения. Определить оптимум потребителя. Представить графически. Если цена товара Х уменьшится на 5 руб., на сколько единиц изменится объем спроса данного товара всего?|Уравнение бюджетной линии:I = P_xX + P_yY 600 = 20X + 10Y

Предельная полезность товаров:

Mu_x = dU/dx = d(xy)/dx = yMu_y = dU/dy = d(xy)/dy = x

Оптимум потребителя достигается при равенстве:

Mu_x / Mu_y = P_x / P_yMu_x / Mu_y = 20 / 10 = 2

Предельная норма замещения

MRS_xy = Mu_x / Mu_y = 2

Выразим y через x.

Mu_x / Mu_y = y / x = 2y = 2x

Подставим в уравнение бюджетной линии:

600 = 20x + 10*2x = 20x + 20xоткуда X = 15; Y = 2x = 30

Точка касания кривой безразличия с бюджетной линией означает оптимальный набор товаров потребителя.

Проверка: 20 х 15 + 10 х 30 = 300 + 300 = 600.

При уменьшении цены товара X на 5 руб.
P_x = 20 — 5 = 15
Найдем новый оптимум потребителя.

600 = 15X + 10Y = 15X + 20X = 35Xоткуда x = 17.14; y = 2x = 34.29
Спрос на товар Х увеличился на 2.14 (17.14 — 15)

Проверка: 15 х 17.14 + 10 х 34.29 = 257.1 + 342.9 = 600.

Пример нахождения цен товаров при оптимальном выборе покупателя

Утилитарное решение и решение, оптимальное по Нэшу

Определить утилитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны u₁ = х₁ + 3, u₂= 3х₂ — 2 при х₁ + x₂ = 3 . Проверить независимость от масштаба для указанных ПКБ, если функция полезности первого агента была уменьшена в три раза.

Решение. Определим эгалитарное решение, для этого должно выполняться условие u₁ = u₂ или x₁ + 3 = 3x₂ — 2. Учитывая, что x₂ = 3- x₁, получаем x₂ = 2, тогда x₁ = 1. Вектор полезностей (4,4).

Утилитарное решение находим, максимизируя сумму полезностей агентов: x₁ + 3 + 3x₂ — 2 → max, подставив x₁ вместо x₂, получаем 4x₂ + 1 → max. Рассматриваемая функция возрастает от x₁ и достигает своего максимума при x₁ = 3, тогда x₂ = 0. Здесь вектор полезностей (1,1).

Независимость от масштаба

Определим эгалитарное решение, для этого должно выполняться условие u₁ = u₂ или x₁/3 + 1 = 3x₂ — 2. Учитывая, что x₂ = 3- x₁, получаем 10/3 x₁ — 6 = 0, тогда x₁ = 9/5, то x₂ = 6/5. Вектор полезностей (8/5,8/5).

Множество допустимых распределений пары продуктов на неотрицательные количества определяется так:x₁,x₂ 0, x₁ + x₁ = a, x₂ = b.

Максимизируя ФКП Нэша, мы выбираем эффективное распределение. Оптимальное распределение определяется как решение задачи:

Минимум достигается x₁ = 2,17; x₂ = 0,83.

Видим, что соблюдается условия:
а) ,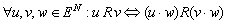
б)

Потребитель свой располагаемый доход в размере 90 руб. тратит на приобретение кефира и картофеля.

Стоимость продуктов питания:

Р_кеф = 15 руб. за 1 л.

Р_кар= 3 руб. за 1 кг.

Предпочтения потребителя описываются следующей функцией полезности:

Насколько изменится оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:

1)

2)

Решение:

Оптимальный набор потребителя должен удовлетворять условию второго закона Госсена:

Найдём предельную полезность кефира и картофеля как частные производные от общей полезности:

На основе формулы

получим уравнение бюджетного ограничения: 90 = 15*х_кеф + 3*х_кар

Составим и решим систему уравнений:

Оптимальный набор потребителя состоит из 15 кг картофеля и 3 литров кефира.

Найдём оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:

Предельную полезность кефира и картофеля найдём как частные производные от общей полезности:

Подставим эти выражения в условие второго закона Госсена:

Данное равенство ничем не отличается от предыдущего случая, следовательно, оптимальный набор потребителя не изменится.

Найдём теперь оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:

Предельная полезность при этом будет равна:

Тогда

Уравнение бюджетного ограничения не изменилось и равно: 90 = 15*х_кеф + 3*х_кар

Составим и решим систему уравнений:

Оптимальный набор потребителя теперь состоит из 10 кг картофеля и 4 литров кефира.

Таким образом, объём потребления картофеля снизится на 5 кг, а потребление кефира возрастёт на 1 литр.