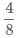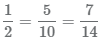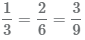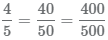Действия с дробями регулируются основным свойством дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Равные дроби по сути являются записью одного и того же числа.
Сравним, 2/5 = 0,4 и 4/10 = 0,4.
Числа, которые мы можем записать в виде дробей, называются рациональными числами, множество которых обозначается латинской буквой Q. Вспомним, что любое целое число мы можем записать в виде дроби: 4 = 4/1, следовательно, любое целое число рационально. Иными словами, множество целых чисел Z – это подмножество Q, или Z принадлежит Q.
Итак, умножим дробь на 5: 1/5 ∙ 5 = 1 ∙ 5/5 ∙ 5 = 5/25.
Разделим дробь на 3: 33/21 : 3 = 33 : 3/21 : 3 = 11/7 = 14/7.
Умножение числителя и знаменателя дроби на одно и то же число называется приведение дроби к знаменателю.
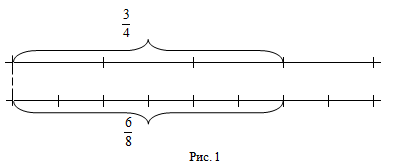
Например: если дробь 3/4 мы умножим на 2 и получим 6/8, то мы скажем, что мы привели дробь 3/4 к знаменателю 8, причем число 2 называется дополнительным множителем.
Приведем дробь 4/5 к знаменателю 30.
1. Найдем дополнительный множитель: 30 : 5 = 6. Итак, наш дополнительный множитель 6.
2. Умножим числитель и знаменатель дроби на 6: 4 ∙ 6/5 ∙ 6 = 24/30.
Итак, наша дробь 24/30.
Основываясь на главном свойстве дроби, мы приходим к понятию «сокращение дроби». Сокращением дроби называется деление числителя и знаменателя дроби на их общий делитель (отличный от единицы).
Рассмотрим дробь 15/20. Число 5 для чисел 15 и 20 является общим делителем. Значит, и числитель, и знаменатель дроби можно разделить на общий делитель дроби 5. Получим: 15 : 5/20 : 5 = 3/4.
Наибольшим общим делителем называется наибольшее число, на которое можно сократить дробь. Например, дробь 30/45 можно сократить на 3 и 5, но наибольшим числом, на которое можно сократить нашу дробь, является число 15: 30 : 15 / 45 : 15 = 2/3.
Бывает так, что числитель и знаменатель дроби не имеют общих делителей, кроме единицы; такую дробь мы называем несократимой, а числа, которые не имеют общих делителей, кроме единицы, называют взаимно простыми.
Приведение дробей к общему знаменателю позволяет сравнивать дроби с разными знаменателями. Иными словами, чтобы сравнить дроби с разными знаменателями, необходимо:
1. привести дроби к общему знаменателю;
2. сравнить числители получившихся дробей.
Рассмотрим пример 3/5 ??? 4/7.
1. Приведем дроби к общему знаменателю 35. Для этого домножим первую дробь на 7 (и числитель, и знаменатель), а вторую (и числитель, и знаменатель) на 5. Получим: 21/35 ??? 20/35.
2. Сравним числители получившихся дробей: 21 больше 20, следовательно, 3/5 > 4/7.
Рассмотрим пример: 6/9 ??? 8/12.
Общим знаменателем наших дробей будет число 9 ∙ 12. Но, чтобы облегчить решение примера, нужно заметить, что наши дроби можно сократить (6/9 на 3, 8/12 на 4): 2/3 ??? 2/3, т.е. 2/3 = 2/3, следовательно, 6/9 = 8/12. Как видим, в таком случае нам понадобилось гораздо меньше времени на установление равенства дробей.
Закрепим материал и докажем неравенство: 123/800 > 1/8.
1. Приведем дроби к общему знаменателю 800. Домножим вторую дробь на 100 и получим 100/800.
2. Итак, наши дроби для сравнения 123/800 и 100/800.
3. Т.к. 123/800 > 100/800, то и 123/800 > 1/8. Следовательно, неравенство верно, что нам и требовалось доказать.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Математика
5 класс
Урок № 48
Равенство дробей
Перечень рассматриваемых вопросов:
– обыкновенная дробь;
– числитель, знаменатель обыкновенной дроби;
– сократимая, несократимая дробь;
– равные дроби;
– основное свойство дроби.
Тезаурус
Дробь в математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя.
Несократимая дробь – это дробь, в которой числитель и знаменатель являются взаимно простыми числами (имеют только один общий делитель – 1).
Сократимая дробь – это дробь, у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
«Все, что без этого было темно, сомнительно и неверно, математика сделала ясным, верным и очевидным», – сказал Михаил Васильевич Ломоносов.
Эти слова как нельзя кстати походят к теме нашего занятия, на котором мы будем устанавливать между, казалось бы, разными дробями равенство, хоть и не вполне очевидное с первого взгляда.
Итак, выясним, какие дроби можно назвать равными.
Для начала нарисуем отрезок. Далее разделим его на две части. Затем каждую из половинок разделим ещё на две части.
Получается, что весь отрезок поделён на четыре части. Если теперь сложить две части из четырёх, то получится ровно половина отрезка, которая в виде обыкновенной дроби будет записана как одна вторая.
Получается, что одна вторая это тоже самое, что и две четвёртых, т. е. это равные дроби.
Возьмём торт и разделим его на 10 частей.
Половина торта – это 5 частей. В виде обыкновенной дроби получается, что частям торта. Отсюда получается так называемое основное свойство дроби, которое заключается в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
С помощью этого свойства всегда получаются равные дроби. Например,
Аналогично, представим семь в виде дроби:
Если возьмём число один, представим его в виде дроби, то получим:
Получается, что две равные дроби являются различными записями одного и того же числа.
Это свойство можно применить и в обратном порядке, в этом случае говорят, что дробь можно сократить. Если числитель и знаменатель дроби имеют общий множитель, то дробь можно сократить на этот множитель, т. е. разделить на него числитель и знаменатель.
В этом случае тоже получается равная дробь. Такие дроби называются сократимыми.
Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице. Например,
Или возьмём дробь :
Рассмотрим ещё один пример, возьмём дробь :
Стоит отметить, что общий множитель числителя и знаменателя можно найти как их НОД. Например,
Стоит отметить, что сокращать дроби можно постепенно, эти действия всё равно приведут к нужному результату.
Но дроби не всегда можно сократить.
Если числитель и знаменатель дроби являются взаимно простыми числами (имеют только один общий делитель – 1), то такая дробь называется несократимой.
Например, ; – несократимые дроби.
Стоит отметить, что для любой дроби существует единственная равная ей несократимая дробь. Например, дробь равна несократимой дроби , а дробь равна несократимой дроби .
Отметим ещё одно свойство: если числитель дроби делится на знаменатель, то дробь равна частному от деления числителя на знаменатель. Например, возьмём дробь . Мы знаем, что 45 делится на девять, значит, .
Решим задание, связанное с сокращением дробей.
Укажите все общие делители, НОД числителя и знаменателя дроби и сократите дробь.
Решение: начнём с того, что определим общие делители числителя и знаменателя дроби, разложив их на множители:
Общие делители у 66 и 90 – это числа 1, 2, 3, 6.
НОД (66; 90) = 6
Сократим дробь. Так как НОД (66; 90) = 6, то разделим числитель и знаменатель на 6 и получим:
Ответ: общие делители – это числа 1, 2, 3, 6.
НОД (66; 90) = 6, .
Тренировочные задания
№ 1. Сократите дробь .
Решение: для решения этой задачи достаточно определить НОД (15; 20) = 3, это и есть число, на которое будем делить и числитель, и знаменатель, поэтому .
Ответ: .
№ 2. На полке лежат 20 книг. Взяли 4 книги. Какой дробью можно выразить взятую часть книг?
Варианты ответа: ; ; .
Решение: для решения этой задачи сначала найдём дробь, равную взятой части. Это будет дробь . Далее посмотрим на варианты ответов – такой дроби нет, следовательно, нужно сократить полученную дробь. Числитель и знаменатель делятся на 4, поэтому получаем .
Ответ: .
Равенство дробей.
Данная тема достаточно важна на основных свойствах дробей основана вся дальнейшая математика и алгебра. Рассмотренные свойства дробей, не смотря на свою важность очень просты.
Чтобы понять основные свойства дробей рассмотрим окружность.

На следующей окружности видно, что закрашена одна часть из двух возможных. Запишем получившеюся дробь (frac{1}{2})
Если внимательно приглядимся, то увидим, что в первом случае, что во втором случае у нас закрашено половина круга, поэтому полученные дроби равны (frac{4}{8} = frac{1}{2}), то есть это одно и тоже число.
Как же это доказать математически? Очень просто, вспомним таблицу умножения и распишем первую дробь на множители.
(frac{4}{8} = frac{1 cdot color{red} {4}}{2 cdot color{red} {4}} = frac{1}{2} cdot color{red} {frac{4}{4}} =frac{1}{2} cdot color{red}{1} = frac{1}{2})
Что мы сделали? Расписали числитель и знаменатель на множители (frac{1 cdot color{red} {4}}{2 cdot color{red} {4}}), а потом разделили дроби (frac{1}{2} cdot color{red} {frac{4}{4}}). Четыре поделить на четыре это 1, а единица умноженное на любое число это и есть само число. То что мы проделали в приведенном примере называется сокращением дробей.
Посмотрим еще один пример и сократим дробь.
(frac{6}{10} = frac{3 cdot color{red} {2}}{5 cdot color{red} {2}} = frac{3}{5} cdot color{red} {frac{2}{2}} =frac{3}{5} cdot color{red}{1} = frac{3}{5})
Мы опять расписали числитель и знаменатель на множители и одинаковый числа в числители и знаменатели сократили. То есть два деленное на два дало единицу, а единица умноженная на любое число дает тоже самое число.
Основное свойство дроби.
Отсюда следует основное свойство дроби:
Если и числитель, и знаменатель дроби умножить на одно и тоже число (кроме нуля), то величина дроби не изменится.
(bf frac{a}{b} = frac{a cdot n}{b cdot n})
Также можно дроби числитель и знаменатель делить на одно и тоже число одновременно.
Рассмотрим пример:
(frac{6}{8} = frac{6 div color{red} {2}}{8 div color{red} {2}} = frac{3}{4})
Если и числитель, и знаменатель дроби делить на одно и тоже число (кроме нуля), то величина дроби не изменится.
(bf frac{a}{b} = frac{a div n}{b div n})
Дроби у которых есть и в числители, и в знаменатели общие простые делители называются сократимыми дробями.
Пример сократимой дроби: (frac{2}{4}, frac{6}{10}, frac{9}{15}, frac{10}{5}, …)
Так же есть и несократимые дроби.
Несократимая дробь – это дробь у которые нет в числители и знаменатели общих простых делителей.
Пример несократимой дроби: (frac{1}{2}, frac{3}{5}, frac{5}{7}, frac{13}{5}, …)
Любое число можно представить в виде дроби, потому что любое число делиться на единицу, например:
(7 = frac{7}{1})
Вопросы к теме:
Как вы думаете любую можно дробь сократить или нет?
Ответ: нет, бывают сократимые дроби и несократимые дроби.
Проверьте справедливо ли равенство: (frac{7}{11} = frac{14}{22})?
Ответ: распишем дробь (frac{14}{22} = frac{7 cdot 2}{11 cdot 2} = frac{7}{11}), да справедливо.
Пример №1:
а) Найдите дробь со знаменателем 15, равную дроби (frac{2}{3}).
б) Найдите дробь с числителем 8, равную дроби (frac{1}{5}).
Решение:
а) Нам нужно чтобы в знаменателе стояло число 15. Сейчас в знаменателе число 3. На какое число нужно умножить цифру 3, чтобы получить 15? Вспомним таблицу умножения 3⋅5. Нам надо воспользоваться основным свойством дробей и умножить и числитель, и знаменатель дроби (frac{2}{3}) на 5.
(frac{2}{3} = frac{2 cdot 5}{3 cdot 5} = frac{10}{15})
б) Нам нужно чтобы в числителе стояло число 8. Сейчас в числители стоит число 1. На какое число нужно умножить цифру 1, чтобы получить 8? Конечно, 1⋅8. Нам надо воспользоваться основным свойством дробей и умножить и числитель, и знаменатель дроби (frac{1}{5}) на 8. Получим:
(frac{1}{5} = frac{1 cdot 8}{5 cdot 8} = frac{8}{40})
Пример №2:
Найдите несократимую дробь, равную дроби: а)(frac{16}{36}), б) (frac{10}{25}).
Решение:
а) (frac{16}{36} = frac{4 cdot 4}{9 cdot 4} = frac{4}{9})
б) (frac{10}{25} = frac{2 cdot 5}{5 cdot 5} = frac{2}{5})
Пример №3:
Запишите число в виде дроби: а) 13 б)123
Решение:
а) (13 = frac{13} {1})
б) (123 = frac{123} {1})
Содержание:
- Равные дроби
- Принципы сравнения дробей
- Сравнение дробей с разными знаменателями
Равные дроби
Пример
Задание. Найти при каком значении $x$ и $y$ дроби $frac{x}{3}$ и $frac{4}{y}$ будут равны.
Решение. Заданные дроби равны, то есть $frac{x}{3}=frac{4}{y}$ , если равны их числители и знаменатели
соответственно. А тогда имеют место следующие равенства:
$x=4$ $3=y$ или $x=4$ $y=3$
Ответ. $x=4, y=3$
Две дроби считаются равным, если величины, выражаемые этими числами при одной и той же единице измерения, равны между собой.
Например. Дроби $frac{3}{4}$ и
$frac{6}{8}$ равны, так как две длины, из которых одна составляет $frac{3}{4}$ м, а вторая — $frac{6}{8}$ м, равны (рис 1).
Принципы сравнения дробей
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Например. $frac{7}{18}>frac{5}{18}$ , так как $7>5$
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Например. $frac{7}{3}>frac{7}{6}$, так как $3<6$ .
Любая правильная дробь меньше 1.
Например. $frac{4}{5} < 1$
Неправильная дробь, числитель которой равен знаменателю, равна 1.
Например. $frac{3}{3}=1, frac{7}{7}=1$
Неправильная дробь, у которой числитель больше знаменателя, больше 1.
Например. $frac{7}{6}>1$
Любая правильная дробь меньше произвольной неправильной дроби.
Например. $frac{4}{5}<frac{5}{4}$
В общем случае дроби по величине сравниваются следующим образом. Умножают числитель первой дроби на
знаменатель второй, а знаменатель первой на числитель второй. И сравнивают полученные произведения. Если первое
из этих произведений больше/равно/меньше второго, то соответственно и первая дробь больше/равно/меньше второй.
Например. $frac{5}{6}>frac{7}{9}$ , так как $5 cdot 9>6 cdot 7 Leftrightarrow 45>42$
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю. Для этого
приводят либо к общему знаменателю, либо числитель и знаменатель первой дроби домножают на знаменатель второй и наоборот,
числитель и знаменатель второй дроби на знаменатель первой. И далее дроби сравнивать как дроби с одинаковым знаменателем
(описано выше).

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сравнить дроби
$frac{3}{4}$ и $frac{5}{7}$
Решение. Приведем дроби к общему знаменателю, для этого
числитель и знаменатель
первой дроби домножим на 7 (знаменатель второй дроби); а числитель и знаменатель второй дроби — на 4, будем иметь:
$frac{3 cdot 7}{4 cdot 7}$ и $frac{5 cdot 4}{7 cdot 4}$
$frac{21}{28}$ и $frac{20}{28}$
Первая дробь больше: $frac{21}{28}>frac{20}{28} Leftrightarrow frac{3}{4}>frac{5}{7}$ , так как ее числитель $21 > 20$
Ответ. $frac{3}{4}>frac{5}{7}$
Читать следующую тему: основное свойство дроби.
Доли введение
Доли
Круг состоит из 4 разноцветных равных частей. Учащиеся разрезали круг на 4 равные части. Эти равные части называются долями.
Каждому досталась «одна четвертая доля круга», или, короче, «одна четвертая круга». Записывают 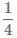
Разноцветный круг
1
1/4
1/4
1/4
1/4
Долю 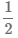
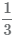
долю 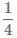
Половина, треть, четверть
1/2
1/3
1/4
Дроби
Обыкновенные дроби
Записи вида 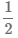
В дроби 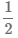
На примере круга: знаменатель — общее количество долей на которые разделили, числитель — количество долей полученных вами.
Пример: Красным цветом отмечена половина отрезка. Можно сказать что красным выделена 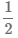
Вы должна запомнить расположение и названия числителя и знаменателя.
Равенство дробей
Равные дроби
Дроби могут различаться по записи, но при этом быть равными. Имеются 3 равных половинки круга, первая половина закрашена красным цветом,
вторая половина разделена на 2 части и закрашена, 3 половина разделена на 3 части.
Каждую из этих половинок круга можно представить в виде дроби 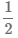
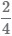
которые равны между собой 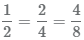
Равные дроби, состоящие из разного количества долей.
1/2
2/4
4/8
Примеры равных дробей:
Сложение дробей
Сложение дробей
Вы можете легко складывать дроби с одинаковыми знаменателями, для этого достаточно сложить их числители, а знаменатель останется тем же.
Ниже представлены примеры сложения частей 2 кругов.
Смотрите также
Другие страницы