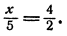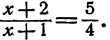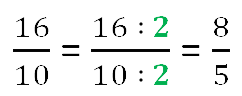Просмотров 1.4к. Опубликовано 30.09.2022
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Отношения
Мы знаем это, чтобы ответить на вопрос, насколько часто одно число больше (или меньше) другого, или насколько одно число является дробью другого. найти частное данных чисел.
Частное двух чисел не равный нулю, называется отношением чисел , или отношением числа .
Где — члены отношения число перед термином отношенияследующий срок отношения.
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
количество
1,15 : 0,36 — отношение от числа 1,15 до числа 0,36.
Отношение двух чисел Показывает, как часто одно число больше другого или как сильно одно число зависит от другого. Это отношение чисел указывает, сколько раз число или сколько частей числа .
Помните, что деление можно заменить дробью, поэтому, отношение чисел можно записать двумя способами: и
Основное свойство отношения:
Отношение не меняется, когда его члены умножаются или делятся на одно и то же число, которое не равно нулю.
Запишем отношение от 3 до 10 и найти его значение:
То есть отношение двух чисел Он может быть выражен в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, какой процент число составляет от другого числа.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и добавить знак процента к результату.
Пример:
В каком проценте число 5 равно числу 10?
5 10 2 1 — 100 % = 1 2 — 100 % = 100 2 % = 50 % .
Ответ: 50% равно 5 умножить на 10.
Если значение двух величин выражено в одних и тех же единицах, то. их отношение называют также отношением. Если две величины выражены в разных единицах, то отношения эти величины должны быть сначала переведены в одну и ту же единицу измерения.
Например:
Дан прямоугольник длиной 12 см и шириной 1 м. Найти отношение длины сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 12 : 100 = 100.
Отношение ширины прямоугольника к его длине равно 100 : 12 =
Дробь взаимно обратная, поэтому и отношения 12 к 100 и 100 к 12 называются взаимно обратными.
На практике отношение Обратные дроби используются, например, при составлении чертежей и географических карт. В этом случае земельные участки рисуются на бумаге в уменьшенном виде, а на карте или картографии изображаются отношение, указывает, как часто длина отрезка на чертеже меньше длины соответствующего отрезка на местности.
Соотношение между длиной отрезка на карте и длиной соответствующего отрезка на местности называется масштабом карты (чертежа).
Предположим, что карта имеет масштаб
Давайте выясним, какова длина отрезка в 5 см на карте на земле.
Для решения обозначим длину отрезка на земле (в сантиметрах). Затем отношение длина отрезка на карте к длине отрезка на местности составляет: 5 :, данная отношение равна масштабу карты, что дает уравнение:
5 :
Решите это уравнение:
10 000;
50 000 см = 500 м = 0,5 км.
Ответ: Отрезок в 5 см на карте равен 0,5 км на местности.
Давайте выясним, какая длина на карте соответствует отрезку 9,5 км на карте.
Для решения обозначьте длину участка на карте (в километрах). Затем отношение длина отрезка на карте с длиной отрезка на местности: : 9,5, данная отношение равна масштабу карты, что дает уравнение:
Решите это уравнение:
0,00095 км = 0,95 м = 95 см.
Ответ: Отрезок 9,5 км на карте равен 95 см на карте.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Отношение чисел
Отношение чисел — это коэффициент от деления одного числа на другое.
Отношение чисел A и b можно записать двумя способами: со знаком деления или через косую черту (как дробь):
Эти признаки следующие: отношение a к b или отношение числа a к числу b.
Числа a и b, составляющие отношение a : b становятся терминами отношения. Делителем является предыдущий член отношения, а делитель — предпоследний член. отношения. Таким образом, a — предыдущий член, b — следующий.
Соотношение используется для сравнения двух чисел. Так, отношение a : b показывает, во сколько раз a больше b (если делитель больше делимого) или сколько процентов от числа b составляет a (если делитель меньше делимого).
Отношение 35 к 7 показывает, что число 35 в пять раз больше числа 7.
2)
Отношение 12 к 15 показывает, что число 12 в 0,8 раза больше числа 15.
Из основного свойства квоты следует, что. отношения :
Отношение не меняется, когда его члены умножаются или делятся на одно и то же ненулевое число.
На этом уроке мы узнаем, что такое 9,5 см линии на карте в 95 см линии. отношения. Мы также поймем, что такое отношение двух чисел. И, наконец, мы научимся определять пропорцию одного числа к другому.
Помните.
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Давайте на примере покажем, в чем суть концепции. отношение двух чисел.
В городе Липецке проходят соревнования по велоспорту. В прошлом году было 15 участников, в этом году — 75. На сколько больше участников в этом году, чем в прошлом?
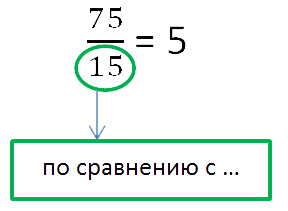
Прежде чем решить проблему, давайте остановимся на самых важных фактах. Запишите отношение количество участников в этом году с количеством участников в прошлом году.
Помните.
При записи отношения двух чисел Напишите в знаменателе дроби (сверху вниз) число, с которым она сравнивается. За этим числом обычно следует дополнение «по сравнению с…». или префикс «по…».
Помните.
Если вы умножите или разделите оба термина отношения на одно и то же число, которое не равно нулю, вы получите отношение, равное данному.
Если вы внимательно изучите приведенное выше правило, то обнаружите, что написанное выше правило — это не что иное, как основное свойство дробей, с помощью которого мы можем легко их сокращать.
Основное свойство коэффициента заключается в том, что он остается неизменным при умножении или делении делителя и делимого на одно и то же число.
Задания для самостоятельной работы
На пост президента претендовали два кандидата. Явка составила 120 человек. Распределение голосов соответствует соотношению 3:5. Необходимо определить количество голосов, полученных победителем.
Соотношение между количеством хвойных и лиственных деревьев в лесу можно представить как 1:4. Необходимо рассчитать долю лиственных деревьев.
На площади 24 га выращиваются сельскохозяйственные культуры. Зерновые и овощи распределяются в соответствии с с отношением 5:3. Необходимо рассчитать площадь возделывания овощных культур в гектарах.
Основное свойство отношения: Путем умножения или деления членов отношения на одно и то же число, отличное от нуля, данный отношение останется неизменным.
Отношения в задачах
Теперь давайте узнаем, как отношения в задачах.
Давайте сразу перейдем к примерам, чтобы увидеть, какой может быть формулировка отношения.
Проблема 1
Протяженность дороги составляет 25 километров. Он освещен на протяжении 15 километров.
(α) Найдите, какая часть дороги освещена.
(b) Во сколько раз вся проезжая часть длиннее освещенной части?
Решение:
В начале урока мы обнаружили отношение меньшего числа в большее, определяя тем самым, какая часть первого числа содержится во втором.
Это первый вопрос.
Для нахождения отношения Отношение длины освещенного участка к длине всей дороги делится на единицу:
Значит, длина освещенного участка составляет (mathbf>) по всей длине дороги.
Второй вопрос: «Во сколько раз больше?». — соответствует отношению от большего числа к меньшему.
Чтобы найти это отношения это разделить длину всей дороги на длину освещенной части дороги:
Это отвечает на вопрос второго пункта.
Важно также всегда следить за тем, чтобы количество было одинаковым.
Так, если что-то дано нам в тоннах и килограммах, и мы хотим найти отношения Чтобы узнать эти количества, мы должны либо перевести тонны в килограммы, либо наоборот.
Проблема 2
Масса груза составляет 2 тонны. Известно, что часть груза — это одежда, масса которой составляет 350 кг.
Определите, сколько процентов от массы груза составляет масса одежды.
Решение:
Давайте сначала переведем тонны в килограммы. Оказывается, что масса груза составляет 2000 кг.
Теперь давайте найдем неизвестное. отношение:
Теперь попробуйте решить задачу самостоятельно и воспользуйтесь подсказками, если у вас возникнут трудности.
Вы можете пройти тест и получить результат после того, как войдете в систему или зарегистрируетесь.
Интересная информация
Сегодня вы научитесь математическим фокусам!
Их идея заключается в том, что можно запутать людей с помощью математических преобразований, которые дают нам то, что нам нужно.
Уловка 1.
Попросите зрителя придумать число и никому его не называть.
Теперь попросите их умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть число в уме.
Теперь вы можете с уверенностью сказать, что зритель получил число 4.
Это происходит потому, что при преобразовании исходное число удаляется из арифметической цепочки, оставляя только четверку.
Попробуйте доказать это с помощью формул, вычитая исходное число X
Уловка 2
В этой игре вы можете угадать день рождения человека.
Попросите зрителя умножить количество дней рождения на 2. Затем попросите его прибавить к результату 5 и умножить целое число на 50. Затем попросите зрителя добавить номер месяца, в котором он родился (1 января, 2 февраля и т.д.).
Чтобы узнать день рождения человека по полученному числу, вычтите 250 из числа, указанного зрителем — вы получите трех- или четырехзначное число, где первые одна или две цифры обозначают день рождения, а последние две цифры — месяц.
Определение пропорции:
Связь между четырьмя алгебраическими выражениями А, В, С и D, имеющая вид
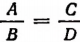
называется пропорцией.
(Равенство 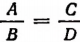
Примеры пропорции:
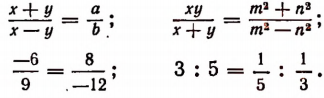
В пропорции 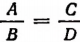
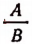
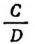
Главное свойство пропорции
Умножив левую и правую части пропорции
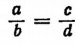
на произведение bd, получим ad = be, т. е. во всякой пропорции произведение крайних членов равно произведению средних.
Составление пропорции по данному равенству двух произведений
Пусть pq = ху. Разделив левую и правую части этого равенства на qx, получим
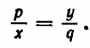
Этот результат можно сформулировать следующим образом.
Если произведение двух чисел равно произведению двух других, то из этих четырех чисел можно составить пропорцию, беря множители одного произведения за крайние, а множители другого произведения за средние члены пропорции. (При этом дополнительно требуется, чтобы оба последующих члена пропорции не оказались равными нулю.)
Перестановка членов пропорции
Пусть ad = be и числа а, b, с, d — все отличны от нуля. Разделив левую и правую части равенства ad = bc первый раз на bd, второй на ab, третий на ас и четвертый на cd, получим соответственно четыре пропорции:
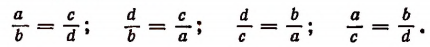
Поменяв местами отношения в этих равенствах, получим еще четыре пропорции:
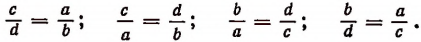
Этот результат показывает, что в пропорции можно менять местами средние и крайние члены и ставить оба крайних члена на места средних, а оба средних на места крайних.
Производные пропорции
1. Прибавив к левой и правой частям пропорции 
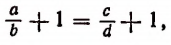
или
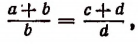
т. е. во всякой пропорции сумма членов первого отношения так относится к своему последующему, как сумма членов второго отношения — к своему последующему.
2. Вычтя из левой и правой частей пропорции 
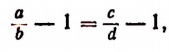
или
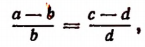
т. е. во всякой пропорции разность членов первого отношения так относится к своему последующему, как разность членов второго отношения — к своему последующему.
3. Разделив левую часть равенства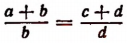
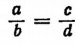
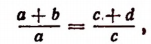
т. е. во всякой пропорции сумма членов первого отношения так относится к своему предыдущему, как сумма членов второго отношения — к своему предыдущему.
4. Разделив левую часть равенства 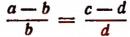

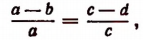
т. е. во всякой пропорции разность членов первого отношения так относится к своему предыдущему, как разность членов второго отношения —к своему предыдущему.
5. Разделив левую часть равенства 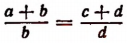
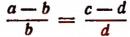
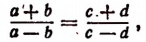
т. е. во всякой пропорции сумма членов первого отношения так относится к их разности, как сумма членов второго отношения — к их разности.
Из пропорции 

Например, умножив обе части пропорции 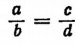
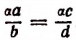
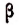
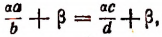
или
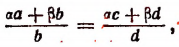
т. е. получим новую производную пропорцию.
Определение неизвестного члена пропорции
Пусть в пропорции 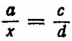
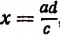
Примеры:
1. Найти неизвестное число х из пропорции 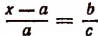
Составим производную пропорцию по правилу: сумма членов первого отношения так относится к своему последующему члену, как сумма членов второго отношения к своему последующему:
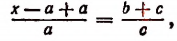
т. е.
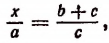
откуда
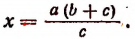
2. Найти неизвестное х из пропорции 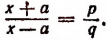
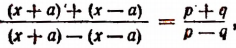
или
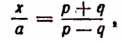
отсюда
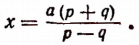
Ряд равных отношений
Иногда бывает удобно вместо различных букв употреблять для обозначения чисел одну и ту же букву, снабженную дополнительными значками — индексами. Например 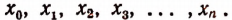
Основное свойство ряда равных отношений
Пусть имеется ряд равных отношений:
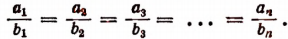
Обозначим общее значение всех этих отношений буквой k. Тогда
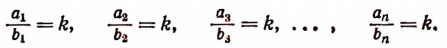
Отсюда
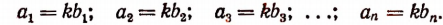
Складывая левые и правые части этих равенств, получим:
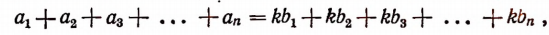
или
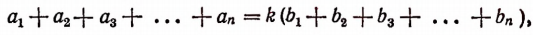
или
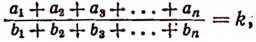
т.е.
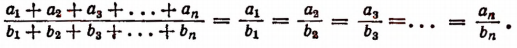
Итак, доказано следующее:
если несколько отношений равны друг другу, то отношение суммы их предыдущих членов к сумме последующих равно каждому из этих отношений.
Пример:
Пусть длины 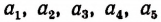
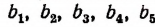
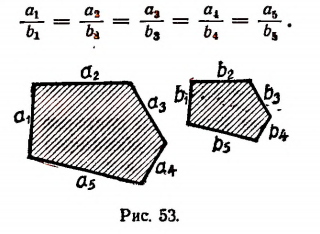
По свойству ряда равных отношений получим:
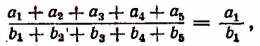
или
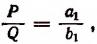
где Р и Q периметры многоугольников.
Прямая пропорциональность
Сначала рассмотрим несколько примеров.
Пример:
Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.
Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения 
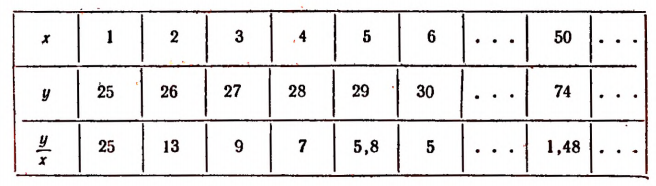
В этом примере отношение 
Пример:
Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.
Составим таблицу, подобную предыдущей.
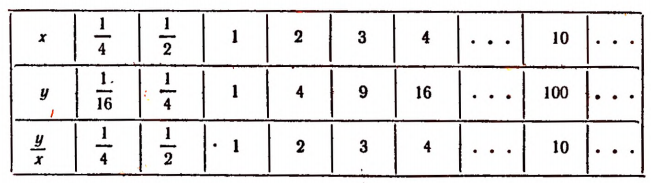
Отношение 
Пример:
Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.
Опять составим таблицу значений х, у и 

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение 
Определение:
Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение 
Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.
Возраст отца и возраст сына не пропорциональны.
Также не пропорциональны сторона квадрата и его площадь.
Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение 
Обозначая это постоянное число буквой k, получим:
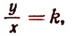
или
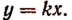
Следовательно, если величины у и х пропорциональны и отношение 
Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).
Теперь докажем обратное положение. Пусть
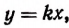
где k — постоянное число.
Отсюда следует, что при х = 0 и у = 0 и что 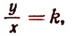
Из того что 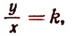
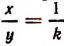
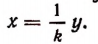
Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число 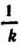
Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.
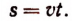
Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).
Сделаем еще два замечания.
Замечание:
Если имеется два ряда чисел:

и

и если
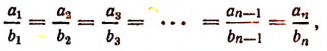
то числа одного из этих рядов называются пропорциональными числам другого ряда.
Замечание:
Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.
В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.
В заключение решим две простые задачи на пропорциональные величины.
Задача:
На карте в масштабе 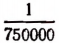
Решение:
Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:
С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)
Решение:
Обозначив искомое изменение (в мм) буквой х, получим:
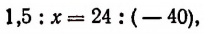
откуда
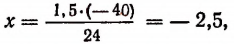
т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.
Обратная пропорциональность
Сначала приведем примеры.
1. Рассмотрим изменяющийся прямоугольный параллелепипед с квадратным основанием, имеющий неизменный объем, равный 3600 куб. см (рис. 54).
Пусть буква х обозначает в сантиметрах изменяющуюся сторону основания, а буква у — изменяющуюся высоту параллелепипеда.
Рассматривая таблицу:
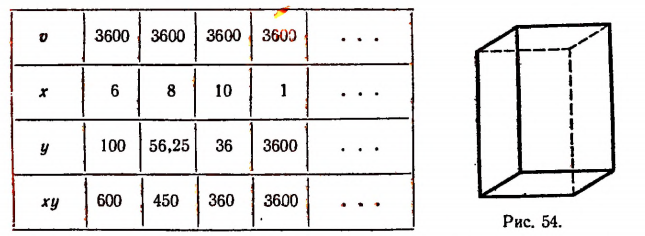
легко видеть, что произведение ху не остается неизменным при постоянстве объема.
2. Рассмотрим изменяющийся прямоугольник, имеющий неизменную площадь, равную 100 кв. см.
Пусть буква х обозначает одно изменяющееся измерение (например, длину прямоугольника), а буква у — другое изменяющееся измерение (ширину). Пусть х и у выражены в сантиметрах.
Так как произведение измерений прямоугольника равно его площади, то величины х и у при всех своих возможных изменениях будут давать в своем произведении число 100, т. е. произведение изменяющихся величин х и у будет оставаться неизменным.
Существенное отличие второго примера от первого заключается в том, что в нем произведение ху остается неизменным, в то время как в первом оно изменяется.
Определение:
Две величины х и у называются обратно пропорциональными, если при всех их возможных изменениях произведение ху остается равным одному и тому же числу.
Обозначая это число буквой k, получим
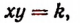
или
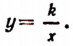
Следовательно, если величины х и у обратно пропорциональны, то величина у выражается через величину х по формуле следующего вида:
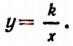
Число k называется коэффициентом обратной пропорциональности.
Длина прямоугольника и ширина прямоугольника при заранее заданной площади прямоугольника являются величинами обратно пропорциональными. Коэффициентом обратной пропорциональности служит как раз эта площадь.
Сторона основания прямоугольного параллелепипеда с квадратным основанием и высота параллелепипеда при заранее заданном объеме не являются величинами обратно пропорциональными.
Задача:
Зал освещается m лампами по а свечей каждая. Сколькими лампами в b свечей можно получить ту же освещенность зала?
Число ламп и число свечей каждой лампы при данной освещенности зала являются величинами обратно пропорциональными. Поэтому, обозначая число ламп в b свечей буквой x, получим

откуда
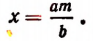
Пропорциональное деление
Задача:
Число А разделить на n слагаемых прямо пропорционально числам
Обозначим искомые слагаемые буквами 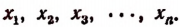
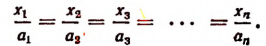
Пользуясь свойством ряда равных отношений, получим
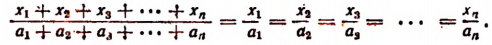
Но
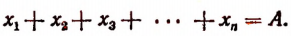
Поэтому
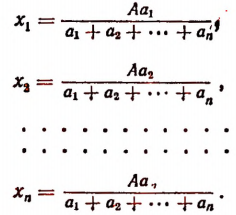
Задача:
Число А разделить на n слагаемых обратно пропорционально числам
Обозначим искомые слагаемые буквами 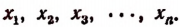
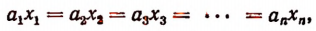
или
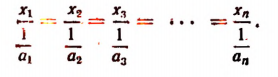
По свойству ряда равных отношений получим
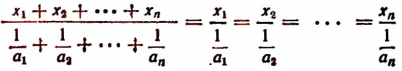
Но

Поэтому
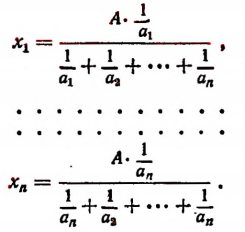
Пропорции и пропорциональная зависимость
- Отношением числа а к числу b называется частное
, а называется предыдущим, b — последующим членом отношения.
- Пропорцией называется равенство, каждая часть которого является отношением двух чисел. В пропорции
члены а и d называются крайними, а b и с средними.
При изложении свойств пропорции будем считать, что ни один из членов пропорции не равен нулю.
Пример:
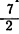
Пример:
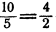
Главное свойство пропорции
Теорема:
Во всякой пропорции произведение крайних
членов равно произведению средних.
Доказательство:
Дана пропорция

Умножим обе части равенства (1) на bd, получим
Теорема доказана.
Теорема:
Если произведение двух чисел
равно произведению двух других чисел, то из этих четырех чисел можно составить пропорцию^ крайними членами которой являются сомножители одного из двух произведений, а средними—сомножители другого.
При этом предполагается, что ни один из сомножителей не равен нулю.
Доказательство:
Пусть
a, b, с, d все отличны от нуля. Разделим обе части равенства на bd, получим
Теорема доказана.
Пример:
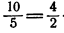
Пример:
8 • 9 = 3 • 24 — равенство двух произведений.
Разделим обе части этого равенства на 9 • 24, получим пропорцию
Определение неизвестного члена пропорции
Теорема:
Средний член пропорции равен произведению крайних, деленному на другой средний. Крайний член пропорции равен произведению средних, деленному на другой крайний.
Пусть

Покажем, что

На основании теоремы 1 имеем

Разделим обе части равенства (4) на с, получим равенство (2). Разделим обе части равенства (4) на d, получим равенство (3). Теорема доказана.
Пример:
Найти х, если
Решение:
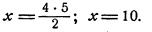
Пример:
Найти х, если 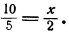
Решение:
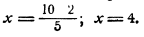
Перестановка членов пропорции
Теорема:
Во всякой пропорции можно переставить
средние члени, переставить крайние члени, переставить и средние члени и крайние, средние поставить на место крайних, а крайние на место средних.
Иными словами, если

то

(переставлены средние члены),

(в (1) переставлены крайние члены),

(в (1) переставлены и средние и крайние члены),

(средние поставлены на место крайних, крайние — на место средних).
Доказательство:
В пропорций (1)

Разделим обе части равенства (6) на cd, получим равенство (2). Точно так же, разделив обе части равенства (6) на аb, а затем на ас, получим равенства (3) и (4). Равенство (5) получается из равенства (4) посредством перестановки отношений. Теорема доказана.
Следствие:
Переставим отношения в равенствах (I), (2), (3), получим еще три пропорции
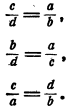
Таким образом, всякую пропорцию посредством перестановки ее членов можно представить в восьми различных видах.
Производные пропорции
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к последующему члену этого отношения, как сумма членов второго отношения относится к своему последующему.
2) Во всякой пропорции разность членов первого отношения так относится к последующему члену этого отношения, как разность членов второго отношения относится к своему последующему.
Иными словами, если

то

Доказательство:
Прибавим к каждой части равенства (1)
по 1, получим равенство (2). Вычтем из каждой части равенства (1) по 1, получим равенство (3). Теорема доказана.
Теорема:
1) Во всякой пропорции сумма членов первого отношения так относится к предыдущему члену этого отношения, как сумма членов второго отношения относится к своему предыдущему.
2) Во всякой пропорции разность членов первого отношения так относится к предыдущему члену этого отношения, как разность членов второго отношения относится к своему предыдущему.
Иными словами, если
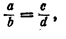
то

Доказательство:
Разделим равенство (2) почленно на
равенство (1), т. е., левую часть равенства (2) разделим на левую часть равенства (1), а правую часть равенства (2) на правую часть равенства (1). Получим равенство (4). Разделив равенство (3) почленно на равенство (1), получим равенство 5). Теорема доказана.
Теорема:
Во всякой пропорции сумма членов первого
отношения так относится к их разности, как сумма членов второго отношения относится к их разности, если только эти разности отличны от нуля.
Иными словами, если
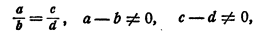
то

Доказательство:
Разделив почленно равенство (4) на
равенство (5), получим равенство (6).
Ряд равных отношений
Теорема:
Если даны несколько равных отношений* то
сумма всех предыдущих членов отношений относится к сумме всех последующих как любой из предыдущих к своему последующему.
Доказательство:
Пусть имеется несколько равных отношений
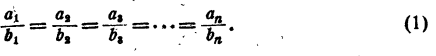
Обозначим результат деления 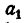
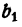
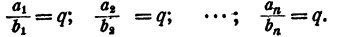
Отсюда
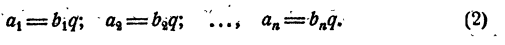
Сложив почленно все равенства (2), имеем
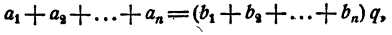
откуда
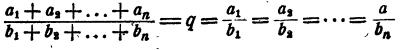
Теорема доказана.
Задача:
Дано, что
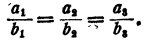
Доказать, что при любых 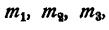
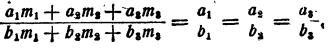
Решение:
Умножим каждый, член первого отношения на 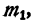
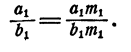
Точно так же
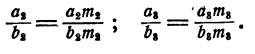
Значит,
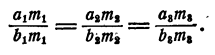
На основании теоремы 8 имеем
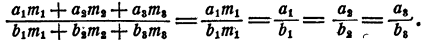
Задача:
Решить уравнение
Решение:
Пользуясь теоремой 7 § 5, имеем
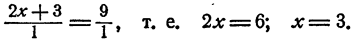
Пропорциональная зависимость
Мы много раз составляли уравнения, выражающие зависимость между величинами, и могли наблюдать, что. зависимости эти бывают весьма разнообразны.
При решении многих задач мы встречаемся с двумя величинами, зависимость между которыми такова, что при изменении этих величин их отношение остается неизменным. Такие величины называются прямо пропорциональными, а зависимость между ними — пропорциональной зависимостью.
Для примера приведем несколько задач, в которых мы встретимся с величинами, находящимися в пропорциональной зависимости.
Задача:
Скорость течения реки 3 км в час. Плот за t часов прошел вниз по реке S км. Составить уравнение, выражающее зависимость между S и t.
Ответ. S = 3t.
Задача:
С каждого гектара собрано 30 ц ржи и, таким образом, с k га собрано А ц. Составить уравнение, выражающее зависимость между А и k.
Ответ. А = 30k
Задача:
Основание прямоугольника 2 см, высота h см, площадь Q 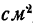
Ответ. Q = 2h.
Задача:
1 м материи стоит 20 руб. За m м этой материи
уплатили N pyб. Составить уравнение, выражающее зависимость между N и m.
Ответ. N=20m.
Мы рассмотрели четыре задачи, которые по своему содержанию относятся к различным областям практической деятельности. Нетрудно убедиться, что в каждой из этих задач мы действительно имеем дело с прямо пропорциональными величинами.
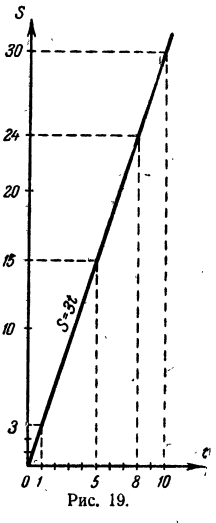
Так, в первой задаче отношение расстояния (в kм), пройденного плотом, к времени (в часах), в течение которого плот находился в пути, всегда одно и то же и равно 3. Поэтому расстояние, которое проходит плот вниз по реке, пропорционально времени, в течение которого плот находится в пути, при условии, что скорость течения реки повсюду одна и та же.
Точно так же во второй задаче количество ржи, собранной с нескольких гектаров, пропорционально количеству ржи, собранной с одного гектара, при условии, что с каждого гектара собрано по одному и тому же количеству ржи и т. д.
Заметим, что уравнения, к которым мы пришли в рассмотренных задачах, имеют один и тот же вид. В этих уравнениях одна, из величин равна произведению некоторого числового множителя на другую величину. Этот множитель называется коэффициентом пропорциональности. В первой задаче коэффициент
пропорциональности равен 3, во второй задаче он равен 30, в третьей задаче он равен 2, в четвертой задаче он равен 20.
Таким образом, пропорциональная зависимость между величинами всегда выражается уравнением y = kx, где k — коэффициент пропорциональности. Известно, что зависимость между двумя величинами может быть наглядно представлена таблицей, а затем и графиком.
Для примера представим таблицей зависимость, выражаемую уравнением S = 3/ (первая задача):
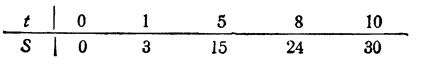
Построим график зависимости S = 3t (рис. 19). Обратим внимание на следующие обстоятельства:
- Отношение чисел, находящихся в одном столбце таблицы, повсюду одно и то же и равно коэффициенту пропорциональности:
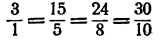
и т. д. (для первого столбца это отношение не имеет смысла; так как на нуль делить нельзя).
2, График представляет собой луч, выходящий из начала координат (при t= 0, S = 0). (Доказательство этого утверждения здесь провести нельзя, так как для этого требуются некоторые сведения из геометрии.)
То же самое можно наблюдать и при графическом представлении любой другой пропорциональной зависимости между двумя величинами.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
Слайд 1
Тема урока:
Отношение двух чисел.

Слайд 2
ВСПОМНИМ ТЕОРИЮ.
1. Когда говорят, что натуральное число а

делится нацело на натуральное число b?
2. Как называются компоненты
при делении?
3. Как найти неизвестное делимое? А делитель?
4.
На какие числа делится нацело любое число?
5. Можно ли делить на нуль? А если разделить нуль на любое число?
Слайд 3
ОПРЕДЕЛЕНИЕ
Частное двух не равных нулю чисел a и

b называют еще отношением чисел a и b.
Запись:
или
.
Читают: «Отношение числа a к числу b».
Числа a и b называют членами отношения.
Слайд 4
3)

.
2) ;
1)
;
Запись:
или .
Читают: «Отношение числа a к числу b».
Пример 1. Используя слово «отношение», прочитайте запись:
Слайд 5
Пример 2. Найдите отношение:
=
=
=

Слайд 6
Вспомним основное свойство частного.
Делимое и

делитель можно умножить или разделить нацело на одно и
то же натуральное число – частное от этого не изменится.
Слайд 8
Из основного свойства частного следует свойство отношения.

Отношение не изменится, если его члены умножить или
разделить на одно и то же число, не равное нулю.
Слайд 10
Частное двух величин называется отношением этих величин.
Сами

величины называют членами отношения.
Слайд 12
Отношение величин одного наименования (длин, скоростей, стоимостей и

т.д., выраженных одинаковыми единицами измерения) есть число.
Такие величины
называют однородными.
Пример 3. Найдите отношение величин:
Отношение однородных величин показывает во
сколько раз одна величина больше другой.
Слайд 13
Можно ли математически описать сложные и

разнообразные системы отношений?
В математике
отношение двух чисел —
это
частное от деления
одного из них на другое
Слайд 14
Задача №1: Укажите выражения, которые являются отношениями.

Слайд 15
Математические отношения
В математике рассматривают отношение только для положительных

чисел.
Отношение записывают при помощи знака деления или дробной черты
Например
17:2
или 17
2
Слайд 16
Задача:
укажите равные отношения
1) 2:5

2) 7: 16
3)14 : 35
4)21:48 5)20:50
Слайд 17
Задача:
укажите равные отношения
1) 2:5

2) 7: 16
3)14 : 35
4)21:48 5)20:50
1 →3, 2→4, 1 →5, 3 →5
Слайд 18
Угадайте,
как в математике называют равенство двух отношений?

В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Эта информация доступна зарегистрированным пользователям
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как (mathbf{a div b}) или же через дробную черту: (mathbf{frac{a}{b}})
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
- может получиться натуральное число
- обыкновенная дробь
- смешанное число
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
(mathbf{256div8=32})
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
- если отношение получилось больше 1, значит, первое число больше второго
- если меньше 1, то второе число больше первого
- если отношение оказалось равно 1, значит, числа равны
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
(mathbf{15div12=frac{15}{12}=frac{5cdot3}{4cdot3}=frac{5}{4}=1frac{1}{4}})
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в (mathbf{1frac{1}{4}}) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
(mathbf{16div24=frac{16}{24}=frac{8cdot2}{8cdot3}=frac{2}{3}})
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в (mathbf{frac{2}{3}}) раза.
Мы можем сформулировать вывод и так: 16 составляет (mathbf{frac{2}{3}}) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
(mathbf{14div28=frac{14}{28}=frac{14cdot1}{14cdot2}=frac{1}{2}})
И посчитаем отношение 28 к 14
(mathbf{28div14=2})
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно (mathbf{frac{2}{5}}), найдем отношение b к a
Для этого надо найти обратное число к (mathbf{frac{2}{5}})
(mathbf{1divfrac{2}{5}=frac{5}{2}=2frac{1}{2}})
Значит, отношение b к a равняется (mathbf{2frac{1}{2}})
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно (mathbf{frac{1}{3}})
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно (mathbf{frac{1}{3}})
Эта информация доступна зарегистрированным пользователям
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него (mathbf{frac{3}{8}})
Перемножив, мы получим:
(mathbf{4cdotfrac{3}{8}=frac{4cdot3}{8}=frac{4cdot3}{4cdot2}=frac{3}{2}=1frac{1}{2}})
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
(mathbf{1frac{1}{2}div4=frac{3}{2}div4=frac{3}{2cdot4}=frac{3}{8}})
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна (mathbf{2frac{1}{2}})
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
(mathbf{2frac{1}{2}div10=frac{2cdot2+1}{2}div10=frac{5}{2}div10=frac{5}{2cdot10}=frac{1}{2cdot2}=frac{1}{4}})
Ответ: дробь, взяв которую от 10 получили (mathbf{2frac{1}{2}}), равняется (mathbf{frac{1}{4}})
Пример 2
Отношение первого числа ко второму равно (mathbf{1frac{1}{5}}), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к (mathbf{1frac{1}{5}})
(mathbf{1div1frac{1}{5}=1divfrac{6}{5}=1cdotfrac{5}{6}=frac{5}{6}})
Теперь можно найти второе число, домножим первое на эту дробь:
(mathbf{6cdotfrac{5}{6}=frac{6cdot5}{6}=5})
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
(mathbf{6div5=frac{6}{5}=1frac{1}{5}})
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно (mathbf{1frac{1}{2}})
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
(mathbf{1div1frac{1}{2}=1divfrac{3}{2}=frac{2}{3}})
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
(mathbf{8divfrac{2}{3}=8cdotfrac{3}{2}=frac{8cdot3}{2}=4cdot3=12})
Ответ: число a равняется 12
Эта информация доступна зарегистрированным пользователям
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
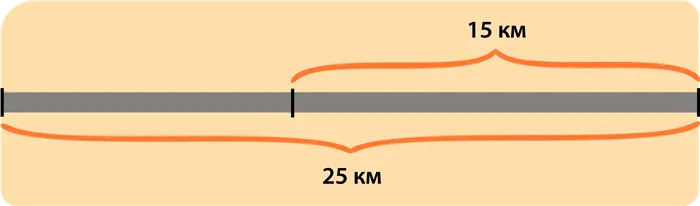
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Эта информация доступна зарегистрированным пользователям
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
(mathbf{15div25=frac{15}{25}=frac{3cdot5}{5cdot5}=frac{3}{5}})
Значит, длина освещенного участка составляет (mathbf{frac{3}{5}}) от длины всей улицы.
Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
(mathbf{25div15=frac{25}{15}=frac{5cdot5}{3cdot5}=frac{5}{3}=1frac{2}{3}})
Что отвечает на вопрос второго пункта.
Ответ: a) (mathbf{frac{3}{5}}), б) (mathbf{1frac{2}{3}})
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
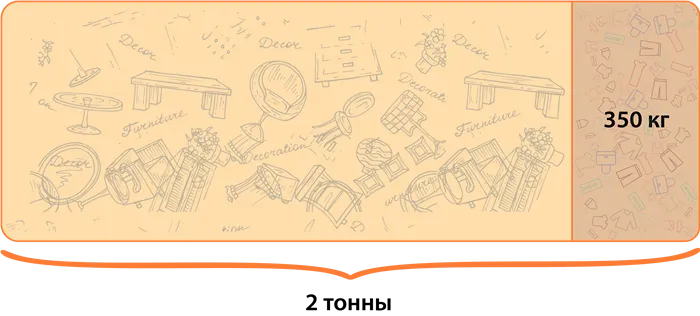
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Эта информация доступна зарегистрированным пользователям
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
(mathbf{frac{350}{2000}=frac{35}{200}=frac{7cdot5}{5cdot40}=frac{7}{40}})
Ответ: (mathbf{frac{7}{40}}).
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.

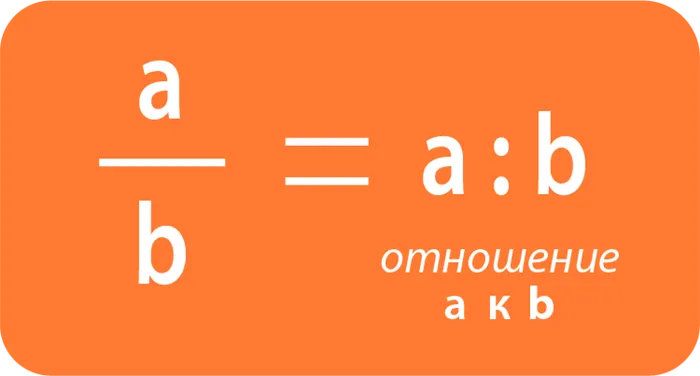


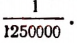
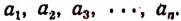
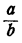 , а называется предыдущим, b — последующим членом отношения.
, а называется предыдущим, b — последующим членом отношения.