Как найти равные углы 5 класс - Исправление недочетов и поиск решений вместе с Examum.ru

Ответы к учебнику для 5 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Вопросы к параграфу

1. Какой угол называют развёрнутым? Развёрнутый угол — это угол, лучи которого образуют прямую и их начала совпадают.

2. В каких единицах измеряют углы? Углы измеряют в градусах (например ∠45° — это угол величиной 45 градусов).

3. Какова градусная мера развёрнутого угла? 180°

4. Что означает измерить угол? Измерить угол — это значит посчитать сколько единичных углов в нём помещаются.

5. Как называется прибор, который используют для измерения углов? Транспортир.

6. Расскажите, как пользоваться транспортиром. Для того, чтобы измерить угол транспортиром надо:

приложить линейку транспортира к одной из сторон угла;
совместить центр транспортира с вершиной угла;
определить, какой из штрихов шкалы транспортира пересекает вторая сторона угла;
определить градусную величину, которой соответствует пересекаемый штрих шкалы транспортира.

Важно:

Одна из сторон транспортира должна точно лежать на линейке прибора.
Центр транспортира должен точно совпадать с вершиной угла.
Если вторая сторона угла не доходит до шкалы транспортира, то надо мысленно продолжить луч до пересечения с прибором, либо начертить продолжение луча до нужной длины.

7. Какие градусные меры имеют равные углы? Равные углы имеют равные градусные меры.

8. Какой из двух неравных углов считают большим? Большим считается угол, градусная мера которого больше.

9. Каким свойством обладает величина угла? Если между сторонами угла АОС провести луч ОВ, то градусная мера угла АОС равна сумме градусных мер углов АОВ и ВОС:

∠АОС = ∠АОВ +∠ВОС, если луч ОВ лежит между сторонами угла АОС.

10. Какой угол называют острым? Острым углом называют угол, градусная мера которого меньше 90°.

11. Какой угол называют прямым? Прямым углом называют угол, градусная мера которого равна 90°.

12. Какой угол называют тупым? Тупым углом называют угол, градусная мера которого больше 90°, но меньше 180°.

13. На какие углы делит развёрнутый угол его биссектриса? Биссектриса делит угол на два прямых угла, то есть градусная мера каждого из этих углов равна 90°.

14. В каких случаях говорят, что от данного луча отложен данный угол? Говорят, что от данного луча отложен данный угол в том случае, если дан определённый луч, например ОА, и от него построен заданный угол, например ∠АОС = 63°, причём вершиной угла является вершина заданного луча.

Решаем устно

1. Назовите два числа, одно из которых:

на 27 больше другого — 1 и 28 — число 28 на 27 больше числа 1.
на 15 меньше другого — 2 и 17 — число 2 на 15 меньше числа 17.
в 7 раз меньше другого — 3 и 21 — число 3 в 7 раз меньше исла 21.
в 3 раза больше другого — 4 и 12 — число 12 в 3 раза больше 4.

2. Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?

10 ч 8 мин — 10 мин = 9 ч 58 мин

Ответ: сейчас 9 ч 58 мин.

3. Часы отстают на 7 мин и сейчас показывают время 16 ч 55 мин. Который час на самом деле?

16 ч 55 мин + 7 мин = 17 ч 2 мин.

Ответ: сейчас 17 ч. 2 мин.

4. Какие из следующих уравнений не имеют корней:

2х = х. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
0х = 0. Это равенство будет верным при любом значении х, значит у этого уравнение бесконечное множество корней.
3 — х = 3. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
0х = 6. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
х • х = х. Это равенство будет верным только при х = 0 и х = 1, значит у этого уравнения 2 корня: 0 и 1.
х + 6 = х + 7. Это равенство не будет верным ни при каких значениях х, значит это уравнение не имеет корней.
8х = 0. Это равенство будет верным только при х = 0, значит у этого уравнения есть единственный корень — 0.
3 — х = 2. Это равенство будет верным только при х = 1, значит у этого уравнения есть единственный корень — 1.
1 • х = 5. Это равенство будет верным только при х = 5, значит у этого уравнения есть единственный корень — 5.

Ответ: не имеют корней уравнения под номером 4 и 6.

5. Для озеленения улицы длиной 3 км на одной из её сторон посадили деревья на расстоянии 20 м друг от друга. Первое дерево было посажено в начале улицы, а последнее — в её конце. Сколько деревьев было посажено? Чему равно расстояние между первым и пятым деревьями?

3 км = 3 000 м.

1) 3 000 : 20 + 1 = 151 (дерево) — было посажено.

2) 20 • (5 — 1) = 20 • 4 = 80 (метров) — расстояние между 1-м и 5-м деревом.

Ответ: Было посажено 151 дерево. Между первым и пятым деревом 80 метров.

Упражнения

296. Начертите:

острый угол EFC
прямой угол ORT
тупой угол D
развёрнутый угол КАР

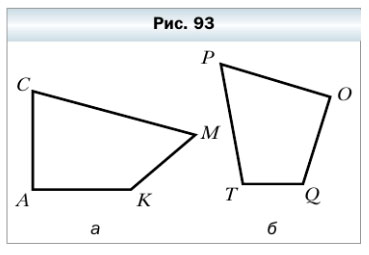
297. Найдите на рисунке 93 острые, тупые и прямые углы.

Острые углы: ∠C, ∠M, ∠P
Тупые углы: ∠K, ∠Q, ∠T
Прямые углы: ∠A, ∠O

298. Какие из данных углов острые, тупые, прямые, развёрнутые: ∠А = 96°, ∠B = 84°, ∠S= 180°, ∠D=90°, ∠R = 162°, ∠E= 60°, ∠Q = 100°, ∠M= 72°?

Острые углы: ∠B = 84°, ∠E= 60°, ∠M= 72°
Тупые углы: ∠А = 96°, ∠R = 162°, ∠Q = 100°
Прямые углы: ∠D=90°
Развёрнутые углы: ∠S= 180°

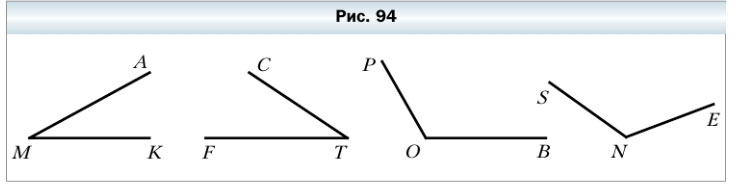
299. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 94. Определите вид каждого угла.

∠AMK = 28º — острый угол
∠CTF = 33º — острый угол
∠POB = 120º — тупой угол
∠SNE = 125º — тупой угол

300. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 95. Определите вид каждого угла.

∠PRT = 133º — тупой угол
∠EFM = 40º — острый угол
∠BCQ = 110º — тупой угол
∠AKS = 67º — острый угол

301. Начертите угол, градусная мера которого равна: 1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°; 65°. Определите вид каждого угла.

∠A = 38º — острый угол
∠B = 124º — тупой угол
∠C = 92º — тупой угол
∠D = 90º — прямой угол
∠E = 87º — острый угол
∠F = 54º — острый угол
∠K = 170º — тупой угол
∠R = 65º — острый угол

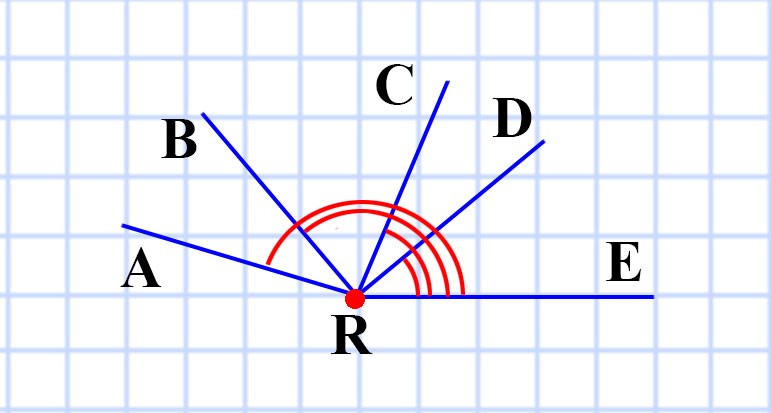
302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Определите вид каждого из построенных углов.

Луч RE

∠ERD = 40º — острый угол
∠ERB = 130º — тупой угол
∠ERC = 68º — острый угол
∠ERA = 164º — тупой угол

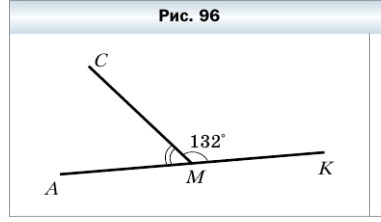
303. На рисунке 96 ∠CMK = 132°, а угол АМК — развёрнутый. Вычислите величину угла АМС.

∠АМК = 180° — развёрнутый

∠АМС = ∠АМК — ∠CMK = 180° — 132° = 48°

Ответ: ∠АМС = 48°.

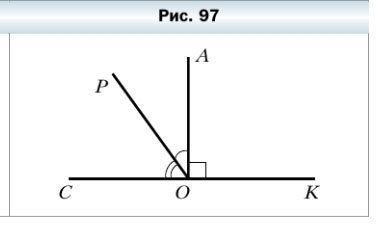
304. На рисунке 97 угол АОК — прямой, ∠POC — 54°, а угол СОК — развёрнутый. Вычислите величину угла АОР.

∠AOK = 90° — прямой

∠COК = 180° — развёрнутый

∠АOP = ∠COK — ∠POC — ∠AOK = 180° — 54° — 90° = 36°

Ответ: ∠АOP = 36°

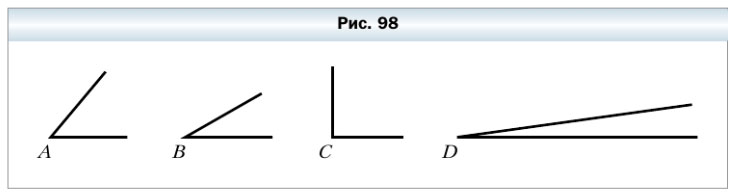
305. Какой из углов, изображённых на рисунке 98, наибольший? Наименьший?

∠D — наименьший угол
∠C — наибольший угол

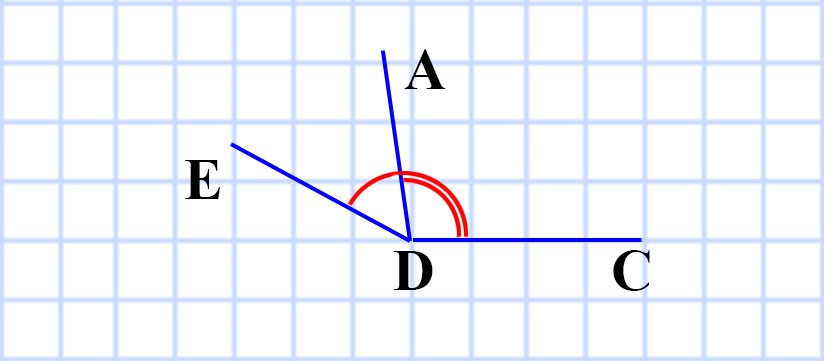
306. Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.

∠CDE = 152°

∠CDA = 98°

∠ADE = ∠CDE — ∠CDA = 152° — 34° = 54°

Ответ: ∠ADE = 54°.

307. Начертите угол ABC, равный 106°. Лучом BD разделите этот угол на два угла так, чтобы ∠ABD = 34°. Вычислите величину угла DBC.

∠ABC = 106°

∠ABD = 34°

∠DBC = ∠ABC — ∠ABD = 106° — 34° = 72°

Ответ: ∠DBC = 54°.

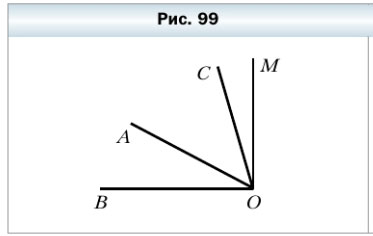
308. Из вершины прямого угла ВОМ (рис. 99) проведены два луча ОА и ОС так, что ∠BOC = 74°, ∠AOM = 62°. Вычислите величину угла АОС.

∠ВОМ = 90° — прямой

∠BOC = 74°

∠AOM = 62°

∠MOC = ∠BOM — ∠BOC = 90° — 74° = 16°

∠AOC = ∠AOM — ∠MOC = 62° — 16° = 46°

Ответ: ∠AOC = 46°.

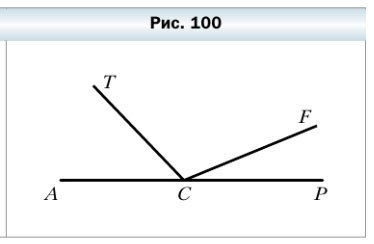
309. Из вершины развёрнутого угла АСР (рис. 100) проведены два луча СТ и CF так, что ∠ACF = 158°, ∠TCP = 134°. Вычислите величину угла TCF.

∠ACP = 180° -развёрнутый

∠ACF = 158°

∠TCP = 134°

∠PCF = ∠ACP — ∠ACF = 180° — 158° = 22°

∠TCF = ∠TCP — ∠PCF = 134° — 22° = 112°

Ответ: ∠TCF = 112°.

310. Верно ли утверждение:

1) угол, который меньше тупого, — острый. Неверно, так как меньше тупого не только острые углы, но и прямой угол.

2) угол, который меньше развёрнутого, — тупой. Неверно, так как меньше развёрнутого угла все тупые углы, все острые углы и прямой угол.

3) половина тупого угла — острый угол. Верно, так как половина даже самого большого тупого угла будет меньше 90º.

4) сумма градусных мер двух острых углов больше 90°. Неверно, так как сумма двух острых углов может быть и меньше 90°.

5) угол, который больше прямого, — тупой. Неверно, так как больше прямого могут быть как тупые углы, так и развёрнутый угол.

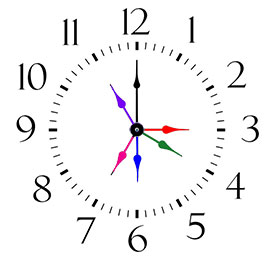
311. Найдите градусную меру утла между стрелками часов, если они показывают:

3 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 3 часа (красная стрелка) — прямой угол. Градусная мера этого угла — 90º.
6 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 6 часов (синяя стрелка) — развёрнутый угол. Градусная мера этого угла — 180º.
4 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 4 часа (зелёная стрелка) — 4/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 4 = 30 • 4 = 120º.
11 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 11 часов (фиолетовая стрелка) — 1/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 1 = 30 • 1 = 30º.
7 ч — это угол между минутной стрелкой, указывающей на 12 часов (чёрная стрелка) и часовой стрелкой, указывающей на 7 часов (розовая стрелка) — 5/6 от развёрнутого угла. Градусная мера этого угла — 180 : 6 • 5 = 30 • 5 = 150º.

Ответ: 1) 90º, 2) 180º, 3) 120º, 4) 30º, 5) 150º.

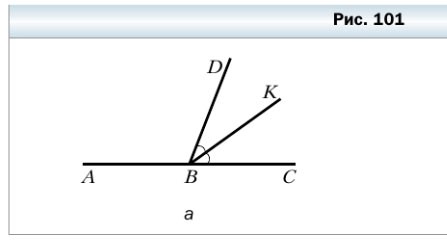
312. Луч BK является биссектрисой угла CBD, ∠ABK = 146° (рис. 101, a). Вычислите градусную меру угла CBD.

∠ABC = 180º — развёрнутый

∠ABK = 146º

∠KBC = ∠ABC — ∠ABK = 180º — 146º = 34º

так как луч BK — это биссектриса ∠CBD, значит луч BK делит тот угол пополам. Мы заем, что ∠KBC = 34º. Значит:

∠CBD = ∠KBC • 2 = 34º • 2 = 68º

Ответ: ∠CBD = 68º.

313. Луч ОА является биссектрисой угла СОМ, ∠СОМ = 54° (рис. 101, б). Вычислите градусную меру угла ВОА.

∠COM = 54º

так как луч OA — это биссектриса ∠COM, значит луч OA делит тот угол пополам. Мы заем, что ∠COM = 54º. Значит:

∠COA = ∠COM : 2 = 54º : 2 = 27º

∠BOC = 180º — развёрнутый

∠BOA = ∠BOC — ∠COA = 180º — 27º = 153º

Ответ: ∠BOA = 153º.

314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развёрнутые углы, образовавшиеся при этом.

Каждая прямая образует по 2 развёрнутых угла. Значит образовались следующие развёрнутые углы: AOD, BOE, COF, DOA, EOB, FOC.

315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 31°?

Каждая прямая образует по 2 развёрнутых угла. Например, прямая MH образует развёрнутые углы MOH и HOM. Каждый из этих углов равен 180º. Значит сумма углов между соседними лучами на рисунке равна 180º • 2 = 360º.

Всего образовалось 12 углов, расположенных между соседними лучами. 360º : 12 = 30º. Значит как минимум один (а на самом деле два) угла будут иметь градусную меру менее 31º.

Ответ: верно.

Упражнения для повторениях

316. Заполните цепочку вычислений:

4 см • 300 = 1 200 см
1 200 см = 120 дм; 120 дм — 12 дм = 108 дм
108 дм : 9 = 12 дм
12 дм = 1 м 2 дм; 1 м 2 дм + 3 м = 4 м 2 дм

8 мин • 15 = 120 мин
120 мин = 2 ч; 2 ч + 2 ч = 4 ч
4 ч = 240 мин; 240 мин : 6 = 40 мин
40 мин — 54 сек = 39 мин 6 сек

317. Верно ли неравенство (а + 253) • 7 < (9 864 — а) : 4 при а = 124?

Ответ: при а = 124 неравенство неверно, так как 2 639 > 2 435.

318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?

Так как в одной банке помещается столько же молока, сколько и в 4 стаканах, то в банке и стакане будет содержаться столько же молока сколько в 5 стаканах (4 + 1 = 5).

1 кг 200 г = 1 200 г

1 200 : 5 = 240 (г) — молока помещается в стакан.

Ответ: 240 г.

319. Длина границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7 694 км, а с Китаем и Казахстаном — 11 808 км.

1) 15 293 — 11 808 = 3 485 (км) — граница России с Монголией.

2) 7 694 — 3 485 = 4 209 (км) — граница России с Китаем.

3) 11 808 — 4 209 = 7 599 (км) — граница России с Казахстаном.

Ответ: граница России с Китаем — 4 209 км, с Монголией — 3 485 км, с Казахстаном — 7 599 км.

Задача от мудрой совы

320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберётся до вершины столба, высота которого равна 20 м?

Каждые сутки улитка способна подняться по столбу на 1 м:

1) 3 метра днём — 2 метра ночью = 1 метр за сутки

Но в последний день она как обычно поднимется на 3 метра, а спускаться уже не будет. Значит, за все дни, кроме последнего, улитка поднимется на 17 м:

2) 20 — 3 = 17 (метров) — преодолеет улитка за все дни, кроме последнего.

То есть ей потребуется 17 дней для преодоления 17 метров и ещё 1 день для преодоления последних 3 метров:

3) 17 : 1 + 1 = 17 + 1 = 18 (дней) — нужно улитке для того, чтобы подняться на столб.

Ответ: улитка доберётся до вершины на 18-й день.

Ответы к учебнику для 5 класса. А. Г. Мерзляк

Переход на главную страницу сайта

Источник

В прошлом уроке мы познакомились с понятием угла, теперь настало время узнать, какие виды углов существуют.

Равные углы

Возьмём лист бумаги и изобразим на нём угол DEF. Теперь сложим листок так, чтобы лучи ED и EF совпали, и по полученному сгибу проведём луч EG.

Рисунок 1

Так как совпадают стороны угла DEF, то совпадают ∠DEG и ∠FEG.

Если два угла совпадают при наложении, то они называются равными.

Равенство углов записывается так: ∠DEG=∠FEG.

Для обозначения равенства углов на рисунке проводят равное количество дужек.

Рисунок 2

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Тогда на рисунке 2 луч BD – биссектриса угла ABC.

Неравные углы

Изобразим угол КON и проведём произвольный луч ОР. По рисунку 3 видно, что при наложении углы КОP и NОР не совпадут.

Рисунок 3

Если два угла не совпадают при наложении, то они не равны друг другу и называются неравными.

Неравенство углов записывается так: ∠ КОP≠∠NОР

Для обозначения неравенства углов на рисунке изображают разное количество дужек.

Рисунок 4

Развёрнутый угол

Рассмотрим рисунок 5. Лучи ML и MN дополняют друг друга до прямой, поэтому называются дополнительными лучами.

Рисунок 5

Два дополнительных друг другу луча образуют развёрнутый угол.

Стороны такого угла вместе составляют прямую линию, на которой лежит вершина развёрнутого угла.

Развёрнутый угол — это угол, стороны которого образуют прямую.

Прямой угол

Возьмём лист бумаги и дважды сложим его пополам. Развернув лист, можно увидеть линии сгиба, которые образовывают 4 равных угла.

Рисунок 6

Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми и на рисунках обозначаются знаком «∟».

Прямой угол – это половина развёрнутого угла.

Для построения прямого угла используют чертёжный треугольник.

Рисунок 7

Острые и тупые углы

Острый угол – угол, который меньше прямого угла.

Тупой угол – угол, который больше прямого, но меньше развёрнутого угла.

На рисунке 8 изображён острый угол ABC и тупой угол DEF.

Рисунок 8

Источник

Как доказать, что углы треугольников равны

Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5) Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

5 Comments

На вопрос вы так и не ответили. «Как доказать, что углы равны?» а не «В каких случаях углы равны?». Как-то так; информация не полная, а так все отлично.

Равенство углов следует из равенства треугольников. Значит, в большинстве задач, чтобы доказать, что углы равны, нужно доказать равенство треугольников.
Еще можно доказать, что два угла являются углами при основании равнобедренного треугольника, соответственными или внутренними накрест лежащими углами при параллельных прямых и т.д. — об этом сказано выше.

А если в «моём» случае не подходит?

Значит, искать «свой», подходящий вариант.

Спасибо, очень много вариантов! Я уж думала никогда не найду ответ, а тут белая куча ответов! Спасибо!

Признаки равенства треугольников

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

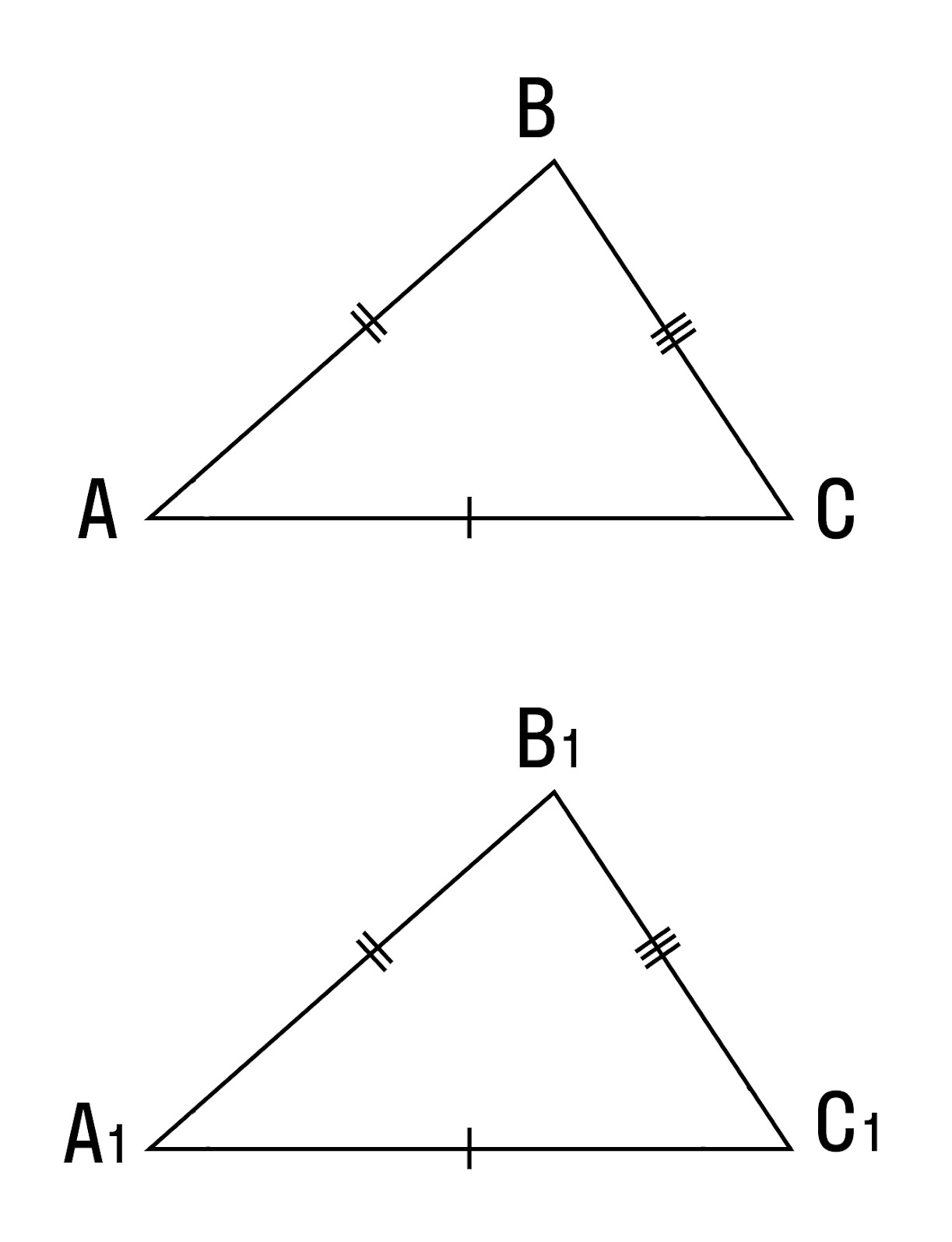
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Как установить и доказать, что треугольники равны

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

∠ α = ∠ β исходя из построения фигур.
Дано в условии задания.
При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
Всегда сходны вертикальные ∠ α и ∠ β
Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
Биссектриса делит ∠ α на два равнозначных.
Смежный с ∠90° — угол, равный исходному.
Смежные равным углам равны.
Высота образует два смежных ∠90° .
В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , => треугольники равны.
III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

Первый — о двух соответственно равных углах двух рассматриваемых треугольных фигур.
Второй — об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
Третий — указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

источники:

http://skysmart.ru/articles/mathematic/priznaki-ravenstva-treugolnika

Как установить и доказать, что треугольники равны

Источник

Скачать материал

Сейчас обучается 247 человек из 63 регионов

Сейчас обучается 49 человек из 26 регионов

Сейчас обучается 142 человека из 49 регионов

Описание презентации по отдельным слайдам:

1 слайд

Угол.Измерение углов.

Выполнила учитель математики:
Плужникова И. Ю.
г. Тамбов
2 слайд

Единица измерения времени
2. Единица измерения массы
3. Сотая часть числа
4. Инструмент для измерения длины отрезков
М
И
Н
У
Т
А
Г
Р
А
М
М
П
Р
О
Ц
Е
Н
Т
Л
И
Н
Е
Й
К
А
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0 1 2 3 4 5 6 7 8 9 10 11 12
Грамм
4 слайд

Как образовалась эта фигура?
5 слайд

Углом называют фигуру,
образованную двумя лучами, выходящими из одной точки.
О
А
В
АОВ
Сторона угла
Вершина угла
6 слайд

Знак для обозначения угла ввел в 18 веке французский математик Пьер Эригон
Эригон применял для обозначения прямого угла знак
7 слайд

Запиши с помощью знака «  » изображенные углы, укажи их стороны и вершины.
М
О
К
А
В
С
Если ты выполнил задание правильно,
то у тебя записано:
КОМ:
ОК и ОМ-стороны КОМ
О — вершина КОМ
ВАС:
АВ и АС-стороны ВАС
А – вершина ВАС
8 слайд

Рассмотри внимательно рисунок.
На нем изображены точки, которые принадлежат
 АВС и не принадлежат  АВС .
Так, точки Р, Е, Д, К принадлежат  АВС,
точки М, О не принадлежат  АВС , причём
точки Р, К лежат на сторонах  АВС.

А
В
С
Р
К
Е
Д
М
О
9 слайд

Рассмотри внимательно рисунок и назови точки,
которые принадлежат  РОД и не принадлежат
 РОД .
Если ты выполнил задание верно, то у тебя
названы точки:
Точки Т, А, В, С, К принадлежат  РОД .
Точки М, Н не принадлежат  РОД .
Р
О
Д
Т
С
В
А
Н
К
М
10 слайд

А
В
Z
С
М
K
L
Как сравнить углы?
P
12 слайд

Равные углы при наложении
совпадают
Если один угол наложить на другой и они совпадут, то эти углы равны
или
14 слайд

ОСТРЫЙ
ТУПОЙ
ПРЯМОЙ
РАЗВЕРНУТЫЙ
15 слайд

О
А
В
Два дополнительных друг другу луча образуют развернутый угол
18 слайд

Рассмотри внимательно рисунок.
Запиши углы в порядке возрастания их величин.
Если выполнил задание правильно, то у тебя записано:
АВД, РОС, МКЕ
К
М
Е
Р
О
С
В
А
Д
19 слайд

12
3
9
6
1
2
11
10
5
4
7
8
Определите вид углов, которые образуют стрелки часов.
ПРОВЕРКА
О — ОСТРЫЙ
П — ПРЯМОЙ
Т-ТУПОЙ
Р-РАЗВЕРНУТЫЙ
20 слайд

Транспортир
центр, шкала, цена деления

Транспортир (от лат. transporto «переношу») — инструмент для построения и измерения углов.
21 слайд

Что такое транспортир?
0
0
Центр полуокружности
Начало отсчёта по внутренней полуокружности
Начало отсчёта по внешней полуокружности
У
Я
Я
Н
В
Е
Н
Ш
Я
Я
П
Л
О
К
У
Ж
Р
О
С
О
У
Н
Т
Ь
Н
В
Н
Т
У
Р
Н
О
Л
К
О
У
Р
П
Е
Ж
Н
С
Т
Ь
О
22 слайд

1 градус – одна стовосьмидесятая часть развернутого угла.
Градус – это единица измерения углов.

0°
90°
180°
Что такое градус?
23 слайд

Первые транспортиры возникли много тысяч лет тому назад. Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько частей, сколько дней в году. Но они думали. Что в году не 365 или 366 дней, а 360. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень полезным, на нем можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Градусная мера сохранилась и до наших дней. Картинку с древним календарем легко сделать, имея транспортир.
24 слайд

Виды транспортиров
25 слайд

Алгоритм измерения углов с помощью транспортира?

1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть величина этого угла.
Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.
26 слайд

Измерение углов
40о
острый угол
27 слайд

Измерение углов
122о
тупой угол
28 слайд

Физкультурная пауза

Покажите руками угол 90°, 180°.
Покажите руками острый угол, тупой угол.
Покажите рукой, где вокруг нас есть прямые углы.
Повернитесь на 180°. А теперь на 90°.
29 слайд

Определите градусные меры углов.
 NOB = ___
 BOA = ___
 BOC = ___
 BOK = ___
 BOP = ____
 BOD = ____
 NOD = ___
 DOP = ___
30 слайд

Проверь себя.
 NOB = 180°
 BOA = 45°
 BOC = 70°
 BOK = 90°
 BOP = 135°
 BOD = 160°
 NOD = 20°
 DOP = 25°
31 слайд

Алгоритм построения угла:

1) Начертить луч.
2) Совместить центр транспортира с началом луча
так, чтобы луч проходил через начало отсчета
на шкале транспортира.
3) Найти на нужном ряду необходимое значение
угла и поставить на бумаге точку.
4) Соединить начало луча с отмеченной точкой.
5) Проверить вид угла, который нужно построить.
Искомый угол построен.
32 слайд

Построение углов
60о
●
33 слайд

Построение углов
136о
●
34 слайд

Построение углов
90о
35 слайд

Задание №1.
Леша и Ваня измеряли один и тот же угол, но получили разные ответы. Определи по рисунку, кто из них прав.

Лёша
Ваня
36 слайд

ЗАДАНИЕ №2.
Найдите на рисунке острые, прямые и тупые углы.
Е
В
С
D
К
А
Прямые:

Острые:

Тупые:
37 слайд

Работа в парах
Задание:
Постройте острый угол. Измерьте его. Поменяйтесь с соседом по парте тетрадями. Проверьте работу друг друга.
Сделайте то же задание, построив тупой угол.
Постройте угол в 78о. Запишите вид построенного угла. Попросите соседа по парте проверить ваше построение.
Сделайте то же задание, построив углы в 145о и 90о.
38 слайд

Домашнее задание:
№ 424, 425,
№ 432, 1096(а,б) на стр. 246

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 267 119 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

21.11.2015
1044
0

21.11.2015
720
0

21.11.2015
931
12

Рейтинг:
5 из 5

21.11.2015
2659
7

Рейтинг:
4 из 5

21.11.2015
10659
294

21.11.2015
919
0

21.11.2015
1138
3

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»