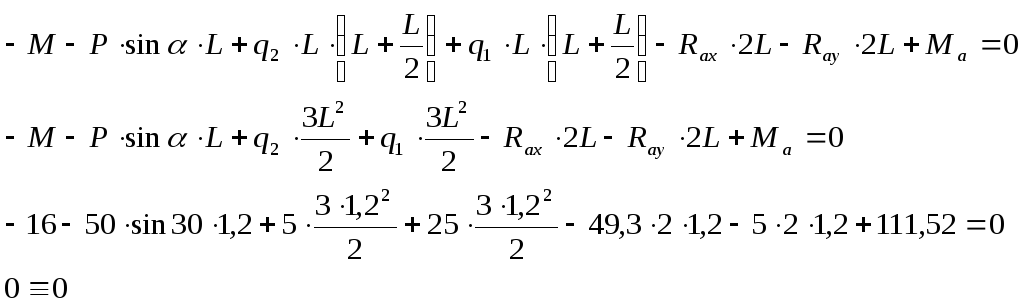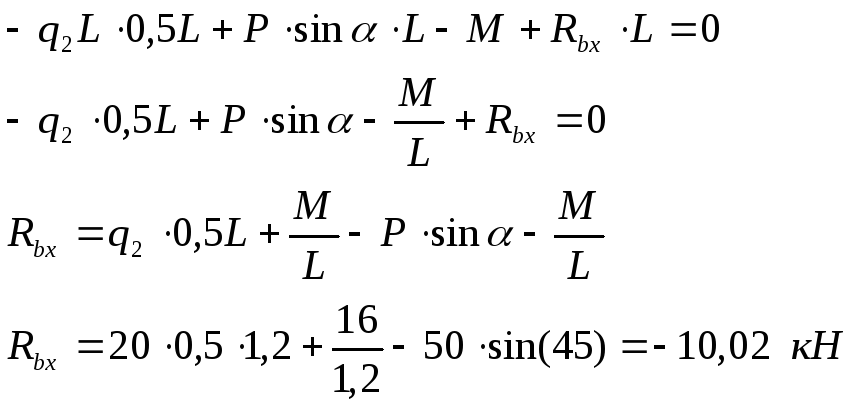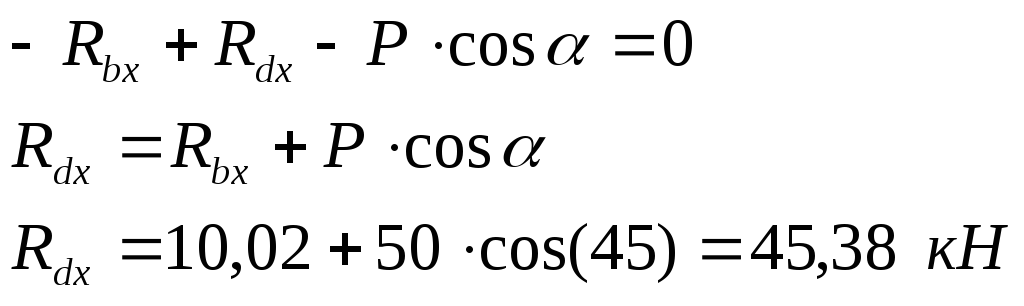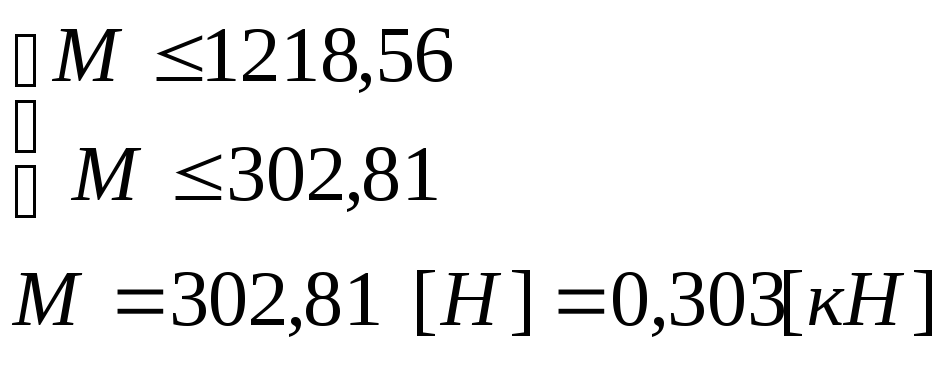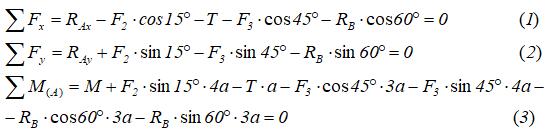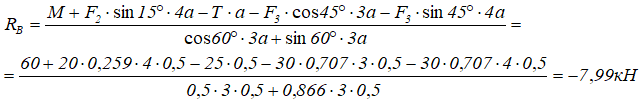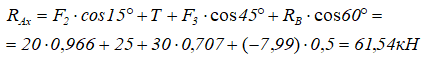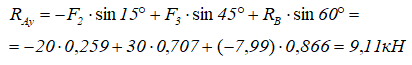Как найти rax ray техмеханика

Российский
химико-технологический университет
имени

Д.
И. Менделеева

Кафедра
прикладной механики

Расчётно-графическая

работа
№2

Тема:
«Кручение. Определение реакции опор»

Работу
выполнил: Chipits,
гр. П-11

Работу
проверил доцент Соколов-Бородкин Евгений
Сергеевич

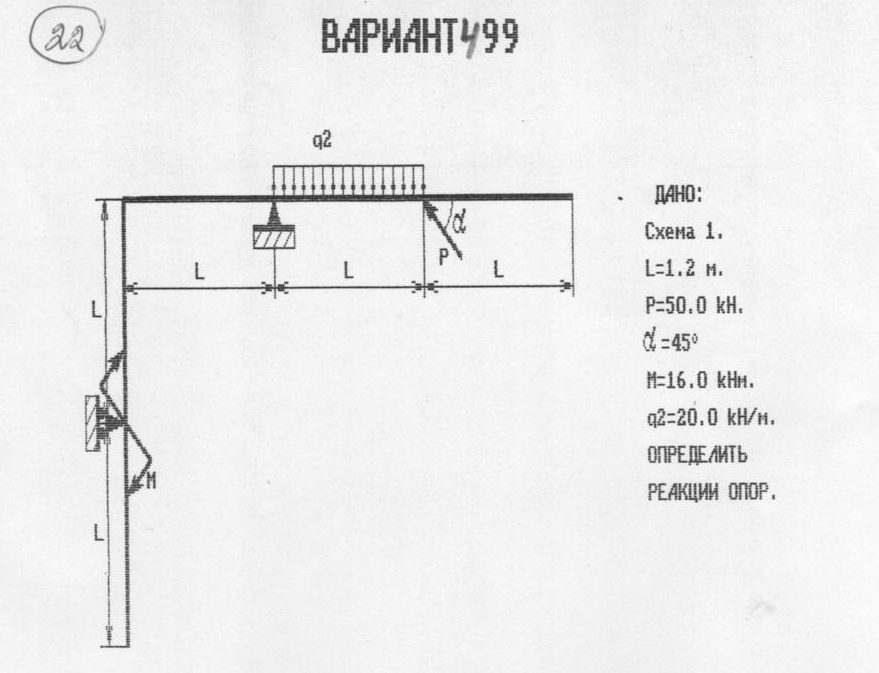
Дано:

L
= 1,2 м

P
= 50 кН

α=30⁰

M=16
кН

q1=25
кН/м

q2=5
кН/м

Определить:

R_ax,R_ay,M_a

Решение:

1)Из
условия

найдем R_ax:

Значит,
искомая сила R_ax
направлена в другую сторону.

2)
Из условия

найдем R_ay:

Значит,
искомая сила R_ay
направлена в другую сторону.

3)
Из условия

найдем
M_a:

4)
Проверка: найдем
,
которая должна быть равна нулю:

Верно.

Дано:

L
= 1,2 м

P
= 50 кН

α=30⁰

M=16
кН

q1=25
кН/м

q2=5
кН/м

Определить:

R_bx,
R_dx
R_dy.

Решение:

1)
Запишем условие
:

Это
уравнение содержит две неизвестные
величины, поэтому его решить не можем.

2)Запишем
условие
:

Значит,
искомая сила R_dy
направлена в другую сторону.

3)
Из условия

найдем
R_bx:

Значит,
искомая сила R_bx
направлена в другую сторону.

4)Запишем
условие (1) с учетом направления сил:

4)
Проверка: найдем
,
которая должна быть равна нулю:

Верно.

Дано:

D
= 60 мм =
0,06
м

L
= 0,8 м

G
=0,36∙10⁵
МПа = 0,36∙10¹¹
Па

[τ]
=50 МПа = 50∙10⁶
Па

[θ]
=1,5∙10^-2
рад

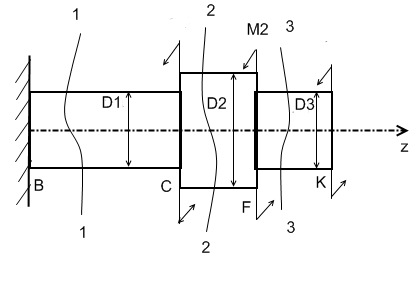
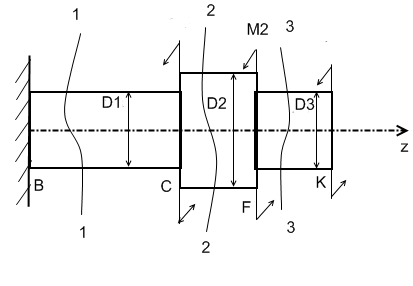
Построить
эпюры:

M_z,
τ_z,
φ.

Найти
М и значения M_z,
τ_z,
φ

в
узловых точках

Решение:

Используя
метод сечений, найдем моменты сил на
участках. Так же найдем касательные
напряжения на этих участках по формуле:

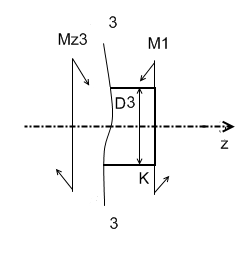
Участок
3-3,KF:

Участок
2-2,FC:

Участок
1-1,CB:

Найдем
относительные углы закручивания по
формуле:

Найдем
углы закручивания по формуле:

Найдем
искомый параметр из условия
прочности:

Найдем
искомый параметр из условия
жесткости:

Решая
систему, составленную из (1) и (2) получаем
значение момента, удовлетворяющее обоим
условиям:

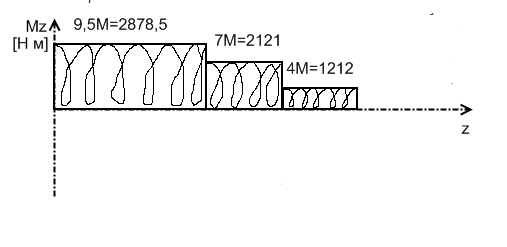
Найдем
численные данные:

Построим
эпюры:

13

Теорема Вариньона гласит: момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

В некоторых случаях при определении момента силы возникают трудности в расчете плеча силы.

Теорема Вариньона значительно упрощает решение этого вопроса.

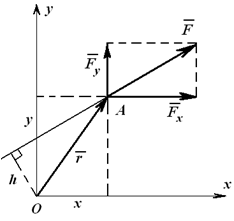
Рисунок 1.17

Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил F_x и F_y (на которые можно разложить силу F) относительно той же точки O (рисунок 1.17). То есть

M_O(F)= -Fh = -F_x y + F_y x, (1.8)

где F_x , F_y , x и y – проекции на оси координат силы F и радиуса-вектора r.

Применение теоремы Вариньона

Рассмотрим способ использования теоремы Вариньона на примере выполнения РГР 1 — равновесие тела под действием произвольной плоской системы сил.

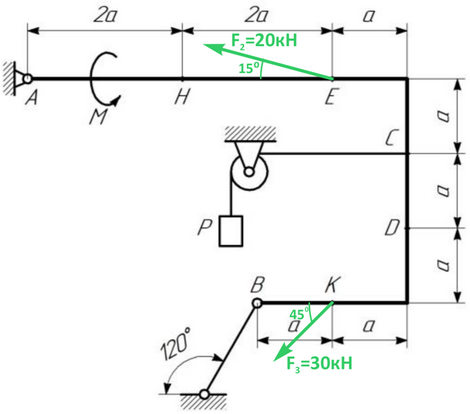
Задача

Жесткая рама закреплена в точке А шарнирно, а в точке В прикреплена к невесомому стержню с шарнирами на концах или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р=25кН.

На раму действует пара сил с моментом М=60кН∙м и две силы F₂ и F₃, величины которых, направления и точки приложения показаны на расчетной схеме.

Требуется определить реакции связей в точках А и В, вызываемые действующими нагрузками. При окончательных расчетах принять а=0,5 м.

При решении данной задачи следует учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми.

Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух неизвестных реакций связей. При вычислении момента силы F часто удобно разложить ее на составляющие F’ и F», для которых плечи сил легко определяются, и воспользоваться теоремой Вариньона, тогда М₀F = М₀F’+ М₀F».

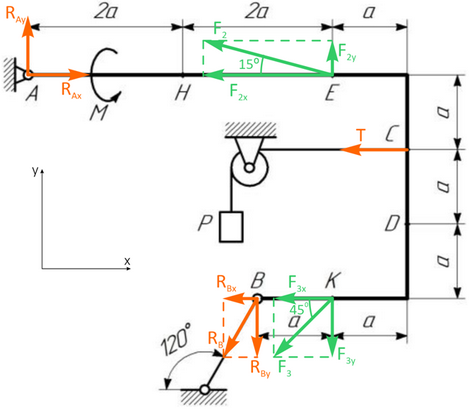
Решение

Рассмотрим равновесие жесткой рамы. Проведем координатные оси x-y и изобразим действующие на раму силы: силу F₂ в точке E, силу F₃ в точке K, натяжение троса Т (по модулю Т=Р) и реакции связей R_Ax и R_Ay в точке А (неподвижной шарнирной опоре), R_B в точке В.

Для полученной плоской системы сил составляем три уравнения равновесия. При вычислении моментов сил F₂, F₃ и реакции R_B воспользуемся теоремой Вариньона, т.е. раскладываем силы на составляющие (проекции сил на оси координат).

Получаем следующие уравнения статики:

Из уравнения (3) получаем:

Знак «минус» показывает, что реакция R_B направлена в противоположную сторону.

Из уравнения (1) находим R_Ax:

Из уравнения (2) определяем R_Ay:

Полная реакция шарнирно-неподвижной опоры определяется по формуле:

Ответ: R_A=62,21кН, R_B=7,99кН

Примеры решения задач >
Момент силы относительно оси >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

государственное
автономное профессиональное образовательное учреждение

Челябинской области
«Политехнический колледж»

ГАПОУ ЧО ПК

Методическая разработка

практического занятия

ОП 07 Техническая механика

Для специальности «22.02.06 Сварочное производство»

 Тема 1.1 Основы
статики

Урок 15-16 «Определение опорных реакций
балок»

Разработал: преподаватель

Смородина Н. В.

Практическое
занятие

Тема: «Определение опорных реакций
балок»

Цель занятия: закрепить
теоретические знания и умения определять реакции в опорах балочных
систем

Краткие теоретические сведения

Очень часто в машинах и
конструкциях встречаются тела удлиненной формы, называемые балками (или
балочными системами). Балки в основном предназначены для восприятия поперечных
нагрузок. Балки имеют специальные опорные устройства для сопряжения их с
другими элементами и передачи на них усилий.

По способу приложения нагрузки делятся на:

·    сосредоточенные – если  реально
передача нагрузки происходит на пренебрежимо малой площадке (в точке);

·    распределенные – если  нагрузка  распределена
по значительной площадке или ли­нии (давление воды на плотину, давление снега
на крышу и т.п.).

В задачах статики для абсолютно твердых тел
распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).

Рис. 1

q — интенсивность на­грузки; I — длина стержня; G = ql — равнодей­ствующая распределенной нагрузки.

Жесткая заделка (защемление) (рис. 2)

Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы Rax и и парой с моментом Mr. Для определения этих неизвестных удобно использовать систему уравнений в виде Каждое уравнение имеет одну неиз­вестную величину и решается без подста­новок.

Для контроля правильности решений используют дополни­тельное уравнение моментов
относительно любой точки на балке, например

Шарнирно-подвижная опора (рис. 3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности. Шарнирно-неподвижная опора (рис. 4) Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

Балка на двух шарнирных опорах (рис. 5)

Не
известны три силы, две из них — вертикальные, следовательно, удобнее для
определения неизвестных использовать систему уравнений во второй форме:

Составляются
уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы,
проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная
сила.

Для контроля правильности решения используется дополни­тельное
уравнение

Упражнения при подготовке к
самостоятельной работе

1.
Привести систему сил к точке В, определить главный вектор и главный
момент системы сил (рис. 6). АВ = 2м; ВС = 1,5м; CD = 1м. F₁ = 18кН; F₂ = 10кН; F₃ = 30кН; т = 36кН-м.

Рис. 6

2. Система сил находится в равновесии. Определить величину момента пары
т (рис. 7).

F₁ = F₁’ = 10
кН; F₂ = F₂’ = 20кН.

Рис. 7

3.   
Нанести реакции в опорах
балок 1 и 2 (рис. 8).

Рис.  8

4.    Определить величину реакции в опоре А. Приложена распре­деленная
нагрузка интенсивностью q = 5кН/м (рис. 9).

Рис. 9

5. Записать систему уравнений равновесия для
определения ре­акций в опоре защемленной балки.

6.   
Записать систему уравнений
равновесия для определения ре­акций в опорах двухопорной балки, закрепленной на
двух шарнирах.

Примеры решения задач

Пример№1. Одноопорная (защемленная)
балка нагружена со­средоточенными силами и парой сил (рис. 10). Определить
реакции заделки.

Рис. 10

Решение

1.                 
В заделке
может возникнуть реакция, представляемая двум: составляющими (R_Ay, R_Ax), и реактивный момент М_A. Наносим на схему балки возможные
направления реакций.

Замечание. Если направления выбраны
неверно, при расчетах получим отрицательные значения реакций. В этом случае
реакции на схеме следует направить в противоположную сторону, не повторяя
расчета.

В силу малой высоты считают, что все точки балки
находятся на одной прямой; все три неизвестные реакции приложены в одной точке.
Для решения удобно использовать систему уравнений равновесия в первой форме.
Каждое уравнение будет содержать одну неизвестную.

2.                 
Используем
систему уравнений:

Знаки полученных реакций (+), следовательно,
направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем
уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

Решение выполнено верно.

Пример №2. Двухопорная балка с шарнирными опорами А и В
нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т
(рис. 11). Определить реакции опор.

Рис. 11

Решение

1.                 
Левая
опора (точка А) — подвижный шарнир, здесь реакция направлена
перпендикулярно опорной поверхности.

Правая опора (точка В) — неподвижный шарнир, здесь
наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем
с продольной осью балки.

2.                 
Поскольку
на схеме возникнут две неизвестные вертикальные реакции, использовать первую
форму уравнений равновесия нецеле­сообразно.

3.                 
Заменяем
распределенную нагрузку сосредоточенной:

G = ql; G = 2*6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета,
далее за­дача решается с сосредоточенными силами (рис. 2б).

4.                 
Наносим
возможные реакции в опорах (направление произвольное).

5.                 
Для
решения выбираем уравнение равновесия в виде

6. Составляем уравнения моментов
относительно точек крепления:

Реакция отрицательная, следовательно, R_Аy нужно направить н противоположную
сторону.

7.       
Используя
уравнение проекций, получим:

R_Bx — горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее
направление будет противоположно выбранному.

8.           
Проверка
правильности решения. Для этого используем чет­вертое уравнение равновесия

Подставим полученные значения реакций. Если условие
выполнено, решение верно:

-5,1 — 12 + 34,6 – 25 -0,7 =
0.

Решение выполнено верно.

Порядок выполнения работы:

1.        
Заменить распределенную нагрузку ее равнодействующей и указать
точку ее приложения (если действует на балку).

2.        
Освободить балку от связей, заменив их реакциями.

3.        
Выбрать систему уравнений равновесия.

4.        
Решить уравнения равновесия.

5.        
Выполнить проверку решения.

Задания для самостоятельной
работы:

Задание №1:  Определить величины реакций в опоре защемлен­ной
балки. Провести проверку правильности решения.

Задание №2: Определить величины реакций в
шарнирных опорах балки. Провести проверку правильности решения.

Контрольные вопросы

1. Какую из форм уравнений равновесия
целесообразно использовать при определении реакций в заделке?

2. Какую форму системы уравнений равновесия
целесообразно использовать при определении реакций в опорах двухопорной балки и
почему?

3. Сколько уравнений равновесия необходимо
составить при параллельных внешних силах?

4. Как определить равнодействующую силу
равномерно распределённой нагрузки?

5. Назовите формулу для определения момента силы
относительно точки.

6. Сформулируйте правила знаков для определения
моментов сил.

7. Как проверить правильность определения реакций
опор балочных систем?

8. В каком случае момент силы равен 0?