Пусть
задано непустое множество X.
Множество всех подмножеств этого
основного множества, включая его само
и пустое множество, называется булеаном
данного множества и обозначается Р(X)
или 2х.
Если X
содержит n
элементов, то булеан содержит 2п
элементов, которыми есть подмножества
множества А,
собственные и несобственные.
Говорят,
что элементы Х1,
Х2,…Хп
булеана 2х
образуют разбиение
множества X,
если
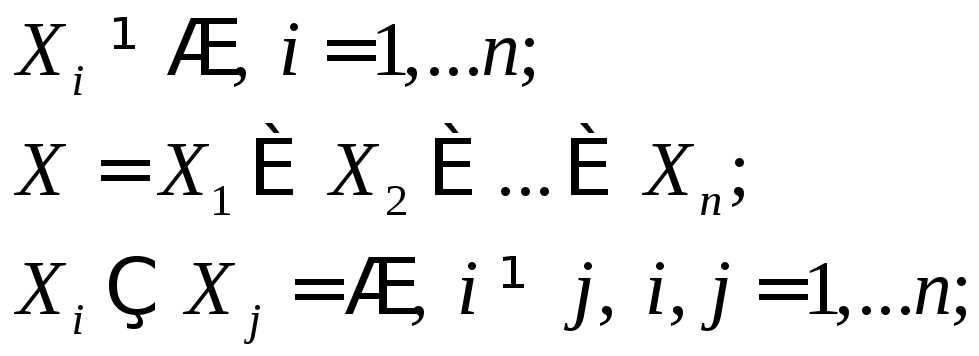
В
этом случае множества Х1,
Х2,…Хп
называются блоками
разбиения
множества X.
Правило
суммы (лежащее
в основе многих комбинаторных вычислений
и оценок). Пусть X
– конечное множество,
,X-
его мощность (число его элементов). Тогда
имеет место условие:
X
Х1
+Х2+…+Хп,
(4.2.2)
причём
равенство
достигается, когда Х1,
Х2,…Хп
образуют разбиение множества
X,
т.е. удовлетворяют (4.2.1).
Задача
4.2.1. Найти
булеаны множеств А={1,
2}; B={a,
b,
c};
C={1,
2, 3, 4}.
Решение.
Р(А)
= {{1}, {2}, {1, 2}, {}};
P(B)
= {{a},
{b},
{c},
{a,
b},
{a,
c},
{b,
c},
{a,
b,
c},
{}};
P(С)
= {{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3,
4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}, {}}.
Задача
4.2.2.
Найти разбиение множеств А={1,
2}; B={a,
b,
c};
C={1,
2, 3, 4}.
Решение.
Множество
А:
Х1
= {1}, X2
= {2}; A
= X1X2.
Это единственный
способ разбиения множества А.
Множество
В:
первый способ: Х1
= {a},
X2
= {b};
X3
= {c};
второй
способ: Х1
= {a,
b},
X2
= {c};
третий
способ:
Х1
= {a},
X2
= {b,
c}.
Множество
С:
первый способ: Х1
= {1}, X2
= {2}; X3
= {3}; Х4
= {4};
второй
способ: Х1
= {1}, X2
= {2, 3}; X3
= {4};
третий
способ: Х1
= {1, 2}, X2
= {2}; X3
= {3, 4};
четвёртый
способ: Х1
= {1, 2}, X2
= {3, 4};
пятый
способ: Х1
= {1, 2, 3}, X2
= {4}; и т.д.
Задачи для
самостоятельного решения.
1.
Найти булеаны следующих множества: А
={1},
B
={3, 5}, C
={7, 8, 10}, D
={m,
n,
p,
q}.
Найти разбиение множеств A,
B,
C,
D.
4.3. Декартово произведение множеств. Понятие упорядоченного множества
Пусть
X
и Y
– некоторые
непустые множества, где xX,
yY.
Рассмотрим
двухэлементное
множество,
состоящее
из пар x
и
y.
Пара
(или двойка) {x,
y}
называется неупорядоченной.
Здесь порядок записи элементов не важен,
поэтому {x,
y}
= {y,
x}.
Пара (x,
y)
называется упорядоченной.
Здесь порядок записи существенен,
поэтому (x,
y)
(y,
x).
Множество,
для которого имеет значение порядок
записи его элементов, называется
упорядоченным.
В противном случае – неупорядоченным.
Декартовым
(или прямым)
произведением
множеств X
и
Y
называется
множество всех упорядоченных пар, где
первый элемент принадлежит множеству
X,
а второй – Y.
XY
= {(x,
y)
xX,
yY}
Аналогично
определяется декартово произведение
любого конечного числа n
множеств:
X1
X2
…
Xn
= {(x1,
x2,
…, xn)
x1X1,
x2X2,…,
xnXn}
Упорядоченные
элементы этого произведения (x1,
x2,
…, xn)
называются векторами, последовательностями,
кортежами или просто «энками».
Если
декартово произведение выполняется на
одном и том же множестве, то его называют
декартовой
степенью
этого множества.
X1
X2
…
Xn
= Xп
Правило
произведения (лежащее
в основе многих комбинаторных вычислений
и оценок). Для конечных множеств Х1,
Х2,…Хп
:
|
X1
X2
…
Xn
| = | X1|
| X2|
… |
Xn|
Декартово
произведение обладает следующими
свойствами:
-
некоммутативность:
АВ
ВА,
если А
В; -
неассоциативность:
(АВ)С
А(ВС); -
дистрибутивность
относительно операций :
(АВ)С
= (АС)(ВС),
(АВ)С
= (АС)(ВС),
(А
В)С
= (АС)
(ВС),
(АВ)С
= (АС)(ВС),
(А
В)С
= (АС)
(ВС).
Для
случая двух множеств декартово
произведение можно иллюстрировать с
помощью диаграммы Венна. Пусть А
= {a1,
a2,…,
an};
B
= {b1,
b2,…,
bm}.
Рис.
4.5
Рассмотрим
прямое произведение множества R
действительных
чисел самое на себя. Множество RR
или R2
состоит из
всех упорядоченных пар вещественных
чисел (х,
у).
Их можно трактовать как координаты
точек плоскости XOY,
то есть декартовой плоскости. Часто в
дискретной математике множество
вещественных чисел обозначают D
(вместо R).
Смысл этого обозначения станет понятным
из дальнейшего изложения.
Задача
4.3.1. Найти
декартово произведение АВ
и ВА
на множествах А={1,
2} и B={a,
b,
c}.
Решение.
АВ
= {1, 2}
{a,
b,
c}
= {(1, a),
(1, b),
(1, c),
(2, a),
(2, b),
(2, c)};
BA
= {a,
b,
c}
{1, 2} = {(a,
1), (a,
2), (b,
1), (b,
2), (c,
1), (c,
2)}.
Задача
4.3.2. Найти
декартовы степени А2,
А3,
В2,
А={1,
2} и B={a,
b,
c}.
Решение.
А2
= АА
= {1, 2}{1,
2} = {(1,1), (1,2), (2,1), (2,2)};
A3
= AAA
= A2
A
= {1, 2}{1,
2}{1,
2} = {(1,1), (1,2), (2,1), (2,2)}{1,
2}= = {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2),
(2,2,1), (2,2,2)};
B2
= BB
= {a,
b,
c}{a,
b,
c}
=
=
{(a,a),
(a,b),
(a,c),
(b,a),
(b,b),
(b,c),
(c,a),
(c,b),
(c,c)}.
Задача
4.3.3. Найти
геометрическую интерпретацию множеств:
-
[1,
4]
[2,3]; -
[1,
2]2; -
[1,
2]3.
Решение.
-
Пусть
А ={x1
x
4},
B = {у2
у
3}.
Отложим на оси ОХ множество А, а множество
В – на оси OY.
Совершенно ясно, что множества А и В
содержат бесконечное множество
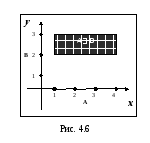
элементов. Их произведение АВ={(x,y)xA,
yB}
есть множество точек прямоугольника
с вершинами в точках (1,2), (1,3), (4,2) и (4,3).
-
Множество
[1,2]2 =
[1,2]
[1,2] – это множество точек квадрата с
вершинами в точках (1,1), (1,2), (2,1), (2,2). -
Множество
[1, 2]3
– это множество точек куба с вершинами
в точках (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1),
(2,1,2), (2,2,1), (2,2,2).
Задача
4.3.4.
Проверить справедливость равенства
С(ВА)=(СВ)(С(АВ))
для
множеств А={a,
d},
B={b,
d},
C={c}
.
Решение.
Найдём
множество в левой части равенства:
ВА
= {b, d}{a, d} = {b}; C(BA)
= {c}{b}
= {(c, b)};
Аналогично находим
множество в правой части равенства:
СВ
= {c}{b,
d} = {(c, b), (c, d)}; AB
= {a, d}
{b, d} = {d};
C(AB
) = {c}{d}
= {(c, d)}; (СВ)(С(АВ))
=
=
{(c, b), (c, d)}
{(c, d)}
= {(c,
b)};
В
левой и правой части равенства имеем
одно и то же множество. Следовательно,
для данных множеств равенство справедливо.
Задача
4.3.5.
Доказать, что (АВ)С
= (АС)(ВС).
Решение.
Воспользуемся определением равенства
множеств. Ясно, что мы имеем дело с
множествами, состоящими из упорядоченных
пар. Пусть элемент (х,
у)(АВ)С,
откуда имеем, что х(АВ),
уС.
Значит хА
или хВ,
а тогда (х,
у)АС
или (х,
у)ВС.
Мы показали, что всякий элемент,
принадлежащий множеству слева, принадлежит
также и множеству справа, то есть (АВ)С
(АС)(ВС).
Пусть
теперь (х,
у)
(АС)(ВС).
Отсюда вытекает, что (х,
у)(АС)
или что (х,
у)(ВС).
В первом случае хА,
уС,
во втором – хВ,
уС.
Следовательно, хАВ,
а (х,
у)(АВ)С.
Итак, (АС)(ВС)
(АВ)С.
Что и доказывает наше равенство.
Задачи для
самостоятельного решения.
1.
Найти
декартово произведение АВ
и ВА
на множествах
-
А={2,
4} и B={3,
5, 7}; -
A={k,
m}
и
B={m,
n,
l}.
2.
Найти
декартовы степени А2,
А3,
если А={a,
b,
c}.
3.
Проверить справедливость равенства
С(AB)=(СA)(С(BA))
для множеств А={1,
2}, B={2,
3}, C={1,
3} .
4.
Доказать, что
-
если
ВА
и СА,
то (ВС)(АА);
b)
A(BC)
= (AB)(AC).
From Wikipedia, the free encyclopedia
A set of stamps partitioned into bundles: No stamp is in two bundles, no bundle is empty, and every stamp is in a bundle.
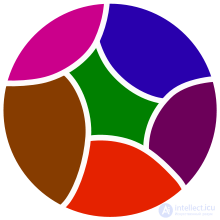
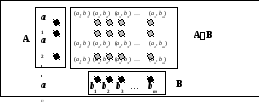
The 52 partitions of a set with 5 elements. A colored region indicates a subset of X that forms a member of the enclosing partition. Uncolored dots indicate single-element subsets. The first shown partition contains five single-element subsets; the last partition contains one subset having five elements.
The traditional Japanese symbols for the 54 chapters of the Tale of Genji are based on the 52 ways of partitioning five elements (the two red symbols represent the same partition, and the green symbol is added for reaching 54).[1]
In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset.
Every equivalence relation on a set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory.
Definition and notation[edit]
A partition of a set X is a set of non-empty subsets of X such that every element x in X is in exactly one of these subsets[2] (i.e., X is a disjoint union of the subsets).
Equivalently, a family of sets P is a partition of X if and only if all of the following conditions hold:[3]
The sets in P are called the blocks, parts, or cells, of the partition.[4] If 
![[a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
![[a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
Every partition, P, may be identified with an equivalence relation on X, namely the relation 


![{displaystyle ain [b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8abb5047c33633d5a0697408f3df2aead151e4ea)
![{displaystyle bin [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd1c441d4221216c8947ac50d43331042f72672b)



The rank of P is |X| − |P|, if X is finite.
Examples[edit]
- The empty set
has exactly one partition, namely
. (Note: this is the partition, not a member of the partition.)
- For any non-empty set X, P = { X } is a partition of X, called the trivial partition.
- Particularly, every singleton set {x} has exactly one partition, namely { {x} }.
- For any non-empty proper subset A of a set U, the set A together with its complement form a partition of U, namely, { A, U ∖ A }.
- The set {1, 2, 3} has these five partitions (one partition per item):
- { {1}, {2}, {3} }, sometimes written 1 | 2 | 3.
- { {1, 2}, {3} }, or 1 2 | 3.
- { {1, 3}, {2} }, or 1 3 | 2.
- { {1}, {2, 3} }, or 1 | 2 3.
- { {1, 2, 3} }, or 123 (in contexts where there will be no confusion with the number).
- The following are not partitions of {1, 2, 3}:
- { {}, {1, 3}, {2} } is not a partition (of any set) because one of its elements is the empty set.
- { {1, 2}, {2, 3} } is not a partition (of any set) because the element 2 is contained in more than one block.
- { {1}, {2} } is not a partition of {1, 2, 3} because none of its blocks contains 3; however, it is a partition of {1, 2}.
Partitions and equivalence relations[edit]
For any equivalence relation on a set X, the set of its equivalence classes is a partition of X. Conversely, from any partition P of X, we can define an equivalence relation on X by setting x ~ y precisely when x and y are in the same part in P. Thus the notions of equivalence relation and partition are essentially equivalent.[5]
The axiom of choice guarantees for any partition of a set X the existence of a subset of X containing exactly one element from each part of the partition. This implies that given an equivalence relation on a set one can select a canonical representative element from every equivalence class.
Refinement of partitions[edit]
Partitions of a 4-element set ordered by refinement
A partition α of a set X is a refinement of a partition ρ of X—and we say that α is finer than ρ and that ρ is coarser than α—if every element of α is a subset of some element of ρ. Informally, this means that α is a further fragmentation of ρ. In that case, it is written that α ≤ ρ.
This «finer-than» relation on the set of partitions of X is a partial order (so the notation «≤» is appropriate). Each set of elements has a least upper bound (their «join») and a greatest lower bound (their «meet»), so that it forms a lattice, and more specifically (for partitions of a finite set) it is a geometric lattice.[6] The partition lattice of a 4-element set has 15 elements and is depicted in the Hasse diagram on the left.
The meet and join of partitions α and ρ are defined as follows. The meet 



Based on the equivalence between geometric lattices and matroids, this lattice of partitions of a finite set corresponds to a matroid in which the base set of the matroid consists of the atoms of the lattice, namely, the partitions with 
Another example illustrates refinement of partitions from the perspective of equivalence relations. If D is the set of cards in a standard 52-card deck, the same-color-as relation on D – which can be denoted ~C – has two equivalence classes: the sets {red cards} and {black cards}. The 2-part partition corresponding to ~C has a refinement that yields the same-suit-as relation ~S, which has the four equivalence classes {spades}, {diamonds}, {hearts}, and {clubs}.
Noncrossing partitions[edit]
A partition of the set N = {1, 2, …, n} with corresponding equivalence relation ~ is noncrossing if it has the following property: If four elements a, b, c and d of N having a < b < c < d satisfy a ~ c and b ~ d, then a ~ b ~ c ~ d. The name comes from the following equivalent definition: Imagine the elements 1, 2, …, n of N drawn as the n vertices of a regular n-gon (in counterclockwise order). A partition can then be visualized by drawing each block as a polygon (whose vertices are the elements of the block). The partition is then noncrossing if and only if these polygons do not intersect.
The lattice of noncrossing partitions of a finite set forms a subset of the lattice of all partitions, but not a sublattice, since the join operations of the two lattices do not agree.
The noncrossing partition lattice has recently taken on importance because of its role in free probability theory.
Counting partitions[edit]
The total number of partitions of an n-element set is the Bell number Bn. The first several Bell numbers are B0 = 1,
B1 = 1, B2 = 2, B3 = 5, B4 = 15, B5 = 52, and B6 = 203 (sequence A000110 in the OEIS). Bell numbers satisfy the recursion
and have the exponential generating function
The Bell numbers may also be computed using the Bell triangle
in which the first value in each row is copied from the end of the previous row, and subsequent values are computed by adding two numbers, the number to the left and the number to the above left of the position. The Bell numbers are repeated along both sides of this triangle. The numbers within the triangle count partitions in which a given element is the largest singleton.
The number of partitions of an n-element set into exactly k (non-empty) parts is the Stirling number of the second kind S(n, k).
The number of noncrossing partitions of an n-element set is the Catalan number
See also[edit]
- Exact cover
- Block design
- Cluster analysis
- List of partition topics
- Lamination (topology)
- MECE principle
- Partial equivalence relation
- Partition algebra
- Partition refinement
- Point-finite collection
- Rhyme schemes by set partition
- Weak ordering (ordered set partition)
Notes[edit]
- ^ Knuth, Donald E. (2013), «Two thousand years of combinatorics», in Wilson, Robin; Watkins, John J. (eds.), Combinatorics: Ancient and Modern, Oxford University Press, pp. 7–37
- ^ Halmos, Paul (1960). Naive Set Theory R. Springer. p. 28. ISBN 9780387900926.
- ^ Lucas, John F. (1990). Introduction to Abstract Mathematics. Rowman & Littlefield. p. 187. ISBN 9780912675732.
- ^ Brualdi 2004, pp. 44–45.
- ^ Schechter 1997, p. 54.
- ^ Birkhoff, Garrett (1995), Lattice Theory, Colloquium Publications, vol. 25 (3rd ed.), American Mathematical Society, p. 95, ISBN 9780821810255.
References[edit]
- Brualdi, Richard A. (2004). Introductory Combinatorics (4th ed.). Pearson Prentice Hall. ISBN 0-13-100119-1.
- Schechter, Eric (1997). Handbook of Analysis and Its Foundations. Academic Press. ISBN 0-12-622760-8.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 августа 2013;
проверки требуют 4 правки.
Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
Определение[править | править вики-текст]
Пусть 



для любых
, таких что
;
.
При этом множества 

Разбиения конечных множеств[править | править вики-текст]
Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес в комбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.
Например, число Стирлинга второго рода 



Примеры[править | править вики-текст]
См. также[править | править вики-текст]
- Замощение
Привет, сегодня поговорим про разбиение множества, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
разбиение множества, множества множеств, разбиение на классы множеств , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
разбиение множества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
Определение
Пусть 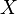
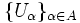
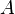
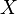
для любых
, таких что
;
.
При этом множества 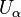
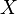
Традиционные японские символы для 54 глав « Повести о Гэндзи» основаны на 52 способах разделения пяти элементов (два красных символа представляют одно и то же разделение, а зеленый символ добавляется при достижении 54).
Рисунок 1 — пример разбиения множества.
Разбиения конечных множеств
Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес вкомбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.
Например, число Стирлинга второго рода 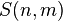
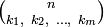
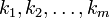
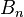
Примеры разбиения множеств
- Пустой набор
имеет ровно один раздел, а именно
. (Примечание: это раздел, а не член раздела.)
- Для любого непустого множества X , Р = { Х } есть разбиение X , называется тривиальное разбиение .
- В частности, каждый одноэлементный набор { x } имеет ровно один раздел, а именно {{ x }}.
- Для любого непустого собственного подмножества A множества U множество A вместе со своим дополнением образуют разбиение U , а именно { A , U ∖ A }.
- Набор {1, 2, 3} имеет эти пять разделов (по одному разделу на элемент):
- {{1}, {2}, {3}}, иногда пишется 1 | 2 | 3.
- {{1, 2}, {3}} или 1 2 | 3.
- {{1, 3}, {2}} или 1 3 | 2.
- {{1}, {2, 3}} или 1 | 2 3.
- {{1, 2, 3}} или 123 (в случаях, когда не будет путаницы с числом).
- Следующие элементы не являются разделами {1, 2, 3}:
- {{}, {1, 3}, {2}} не является разделом (любого набора), потому что один из его элементов является пустым набором .
- {{1, 2}, {2, 3}} не является разделом (любого набора), потому что элемент 2 содержится более чем в одном блоке.
- {{1}, {2}} не является разделом {1, 2, 3}, потому что ни один из его блоков не содержит 3; однако это раздел {1, 2}.
Примеры
множества множеств .
Мы можем рассматривать множества, состоящие из самых различных элементов . Об этом говорит сайт https://intellect.icu . В частности, можем рассматривать множества множеств, т. е. множества, элементы которых сами суть множества. Таково, например, множество всех пар весел, имеющихся на данной лодочной станции. Множеством множеств является также множество всех спортивных команд города Н. (каждая спортивная команда есть множество составляющих ее спортсменов).
Множество всех профессиональных союзов, а также множество всех воинских частей (дивизий, полков, батальонов, рот, взводов и т. д.) данной армии являются множествами множеств. Эти примеры показывают, что множества, являющиеся элементами данного множества множеств, могут в одних случаях пересекаться, в других случаях, наоборот, не иметь общих элементов.
Так, например, множество всех партий страны есть множество попарно не пересекающихся множеств, так как гражданин не может быть одновременно членом двух политическирх партий. С другой стороны, множество всех воинских частей какой-либо армии есть пример множества множеств, некоторые элементы которого являются подмножествами других элементов: так, каждый взвод есть подмножество некоторого полка, полк есть подмножество дивизии и т. д.
Множество спортивных команд данного города состоит, вообще говоря, из пересекающихся множеств, так как одно и то же лицо может входить в несколько спортивных команд (например, в команду пловцов и в команду волейболистов или лыжников).
Замечание. Для облегчения речи иногда вместо выражения «множество множеств» употребляются как совершенно равнозначащие выражения «система множеств» или «совокупность множеств».
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
Считают, что множество Х разбито на классы Х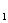
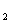
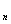
1) подмножества Х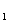
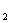
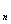
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
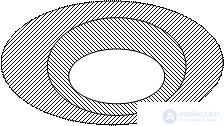
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается
на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
примеры Разбиение на классы.
Очень важный класс систем множеств получаем, если рассматриваем всевозможные разбиения какого-нибудь множества на попарно не пересекающиеся множества. Дано множество X, представленное в виде суммы попарно не пересекающихся подмножеств; множества, слагаемые нашей суммы, и являются элементами данного разбиения множества X.
Пример 1. М есть множество всех учащихся в средних школах Москвы. Множество М можно разбить на попарно не пересекающиеся подмножества, например, следующими двумя способами:
1) мы объединяем в одно слагаемое всех учащихся одной и той же школы (т. е. разбиваем множество всех учащихся по школам);
2) мы объединяем в одно слагаемое всех учащихся одного и того же класса (хотя бы и разных школ).
Пример 2. Пусть X есть множество всех точек плоскости; возьмем на этой плоскости какую-нибудь прямую g и разобьем всю плоскость на прямые, параллельные прямой g. Множества точек каждой такой прямой и являются теми подмножествами, на которые мы разбиваем множество X.
Если данное множество X разбито на попарно не пересекающиеся подмножества, дающие в сумме множество М, то для краткости говорят просто о разбиении множества М на классы.
Задача разбиения множества чисел
Задача разбиения множества чисел — это задача определения, можно ли данное мультимножество S положительных целых чисел разбить на два подмножества S1 и S2, таких, что сумма чисел из S1 равна сумме чисел из S2. Хотя задача разбиения чисел является NP-полной, существует решение псевдополиномиального времени методом динамического программирования и существуют эвристические алгоритмы решения для многих конкрентных задач либо оптимально, либо приближенно. По этой причине задачу называют «простейшей NP-трудной задачей» .
Существует оптимизационная версия задачи разбиения, в которой требуется разбить мультимножество S на два подмножества S1 и S2, таких, что разность между суммой элементов S1 и суммой элементов S2 минимальна. Оптимизационная версия является NP-трудной задачей, но на практике может быть решена эффективно .
Примеры разбиения множества чисел
Если дано множество S={3,1,1,2,2,1}, допустимым решением задачи разбиения являются два множества S1={1,1,1,2} и S2={2,3}. Оба множества имеют сумму 5, и они являются разбиением множества S. Заметим, что это решение не уникально. S1={3,1,1} и S2={2,2,1} является другим решением.
Не любое мультимножество положительных целых чисел имеет разбиение на две части с равными суммами. Пример такого множества — S={2,5}.
Подсчет разбиений
Общее количество разбиений n -элементного набора — это Белловское число B n . Первые несколько чисел Белла: B 0 = 1, B 1 = 1, B 2 = 2, B 3 = 5, B 4 = 15, B 5 = 52 и B 6 = 203 (последовательность A000110 в OEIS ). Числа Белла удовлетворяют рекурсии
и имеют экспоненциальную производящую функцию
Количество разбиений n -элементного набора ровно на k (непустых) частей — это число Стирлинга второго рода S ( n , k ).Числа Белла также могут быть вычислены с использованием треугольника Белла, в котором первое значение в каждой строке копируется из конца предыдущей строки, а последующие значения вычисляются путем добавления двух чисел, числа слева и числа к указанному выше. слева от позиции. Числа Белла повторяются по обеим сторонам этого треугольника. Числа внутри треугольника подсчитывают разделы, в которых данный элемент является наибольшим синглтоном .
Количество непересекающихся разделов набора n -элементов — это каталонское число.
Вау! Вы еще не читали? Ну это зря!
- Замощение
- Разбиение числа
- Точное покрытие
- Блочная конструкция
- Кластерный анализ
- Слабый порядок (разделение упорядоченного набора)
- Отношение частичной эквивалентности
- Уточнение раздела
- Список тем разделов
- Ламинирование ( топология )
- Схемы рифм по множеству разделов
Я хотел бы услышать твое мнение про разбиение множества Надеюсь, что теперь ты понял что такое разбиение множества, множества множеств, разбиение на классы множеств
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
Определение
Пусть 



для любых
, таких что
;
.


Разбиения конечных множеств
Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес в комбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.
Например, числа Стирлинга второго рода 








Примеры












 для любых
для любых  , таких что
, таких что  ;
; .
.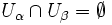 для любых
для любых 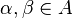 , таких что
, таких что 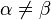 ;
; .
.