МОУ «Пожарская основная
общеобразовательная школа»
РЕФЕРАТ
Метод разбиения в геометрии
Исполнитель:
Руководитель: Ловчикова Г.А. учитель математики
20__ год
ПЛАН
1. Введение……………………………………………………стр.3
2. Равносоставленность
фигур ………………………………стр.4
3. Теорема Больяи —
Гервина ……………………………….стр.9
4. Метод дополнения
………………………………………..стр.12
5. Игры на
разрезание и складывания………………………стр.13
6. Заключение
………………………………………………..стр.17
7. Литература…………………………………………………стр.18
1. Введение
Имеется много различных задач на разрезание и складывание
плоских и пространственных фигур. Считается, что такие задачи относятся к числу
развлекательных и не очень серьезных. До некоторой степени это действительно
так. Однако эта тематика не очень далека от серьезной математической
задачи — задачи о равновеликих и равносоставленных фигурах, которая
исходит от античных геометров и в которой имеется ряд интересных вопросов, не
решенных до сих пор, хотя теория равносоставленности за последние годы
обогатилась рядом новых результатов.
Метод разбиения фигуры на части является одним из приемов
при вычислении площадей многоугольников.
2. Равносоставленность фигур
Геометрическая фигура, составленная из отрезков так, что смежные
отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек,
называется многоугольником.
Два многоугольника называются равносоставленными, если один
из них можно разбить (разрезать) на некоторые другие многоугольники, из которых
затем можно составить второй многоугольник. (Рис. 1)
 |
|||
 |
Рис.1
По свойству равносоставленности: равносоставленные многоугольники
имеют одинаковую площадь (равновелики). Свойство равносоставленности позволяет
иногда получить формулы для вычисления площадей или сравнить площади фигур (как
говорят, методом разбиения или разложения). Примером является сравнение
площадей параллелограмма и прямоугольника: проводится высота H, которая является стороной
прямоугольника той же площади. (Рис. 2).

Рис. 2
Еще один пример треугольник равносоставлен с параллелограммом, имеющим то
же основание и вдвое меньшую высоту; из этого легко выводится формула площади
треугольника. Этот способ вычисления площадей многоугольников был известен еще
Евклиду, который жил более 2000 лет назад и описал его в знаменитых «Началах» (III век до н.э.).

Рис.3
Этот пример иллюстрирует метод разбиения, состоящий в том, что для
вычисления площади многоугольника пытаются разбить его на конечное число частей
таким образом, чтобы из этих частей можно было составить более простой
многоугольник, площадь которого нам уже известна.
При помощи разрезания и складывания американский ученый Генри Перигаль
получил любопытное доказательство теоремы Пифагора. Его способ состоит в том,
что квадраты со сторонами a и b (катеты треугольника, с–гипотенуза)
прикладываются друг другу, как на рисунке 4, затем полученная фигура
разбивается на три части, и из них составляется квадрат со стороной, равной
гипотенузе c.
Рис. 4
Другими словами, он показал, что из частей двух квадратов можно
сконструировать один большой квадрат. Тем самым, два квадрата равносоставлены с
одним квадратом.
Интересным примером задачи на разрезание является шестиконечная
звезда и правильный треугольник. Как видно по рисунку разрезав определенным
образом шестиконечную звезду можно составить равносторонний треугольник, значит
эти фигуры равносоставлены. (Рис. 5)
Рис. 5
Можно доказать, что равносоставленными являются прямоугольник и
равновеликий ему квадрат (два многоугольника называются равновеликими, если они
имеют одинаковую площадь)
Пусть стороны прямоугольника равны a и b, a b.
Рассмотрим три случая.

как прямоугольник равен квадрату. (Рис.6)
Рис.6
Случай 2. b<a≤4b. Обозначим через c сторону квадрата AEFH, равновеликого прямоугольнику ABCD, и расположим квадрат и
прямоугольник так, как показано на рисунке 7;

Рис.7
Из подобия треугольников MDH и EDA
замечаем, что
MH · AD = AE · HD, тем самым,
В рассматриваемом случае 4b ≥ a, и поэтому
.
Следовательно, 2b ≥ c, и поэтому c—b ≤ b. Другими словами, данный случай отвечает взаимному
расположению квадрата и прямоугольника, когда точка M принадлежит отрезку HL.
Заметим, что EB
= c – b = MH, следовательно, прямоугольные
треугольники MHD и EBK равны.
Также равны и прямоугольные треугольники EFM и KCD,
так как FM= c–(c–b)=CD.
Таким образом, и прямоугольник, и квадрат состоят из одних и тех же трех
частей – фигуры ABKMH, треугольников MHD и EFM и треугольников KCD и EFM .То есть прямоугольник и
равновеликий ему квадрат равносоставлены.
Случай 3. a>4b. В этом случае построим
новый прямоугольник, основание которого a’ в два раза меньше, а высота b’ в два раза больше. Если для него
выполняется a’≤4b’, то это случай 2. Если нет, то будем
повторять эту операцию до тех пор, пока это неравенство не будет выполняться.
Итак, нами
установлено, что равновеликие прямоугольник и квадрат равносоставлены.
Вопрос о том, какое наименьшее число разрезов достаточно, чтобы
сконструировать из одной фигуры другую, остается открытым и по сегодняшний
день. Пример, что прямоугольник со стороной 9 и 16 можно разрезать на два
многоугольника и сложить квадрат, показан на рисунке 8.

Рис. 8
Утверждение о том, что 2 любых многоугольника равновелики тогда и
только тогда, когда они равносоставлены. Теорему Больяи –
Гервина, которую доказали независимо друг от друга венгерский математик и поэт
Фаркаша Больяй (1832), друг К.Ф. Гаусса, и (годом позже) простой любитель
математики Пауль Гервин, который был лейтенантом пехотного полка прусской
армии. Доказательство Фаркаша Больяи (он отец Яноша Больяи, одного из
создателей неевклидовой геометрии) было довольно громоздким, а доказательство
П. Гервина – элегантным и простым, оно и по сей день излагается в
математической литературе, поэтому эту теорему называют теоремой Больяи –
Гервина.

Два любых
многоугольника равновелики тогда и только тогда, когда они равносоставлены.
(Два многоугольника называются равновеликими если они имеют одинаковую
площадь.)
Фаркаша
Больяи
Доказательство
То, что если два многоугольника равносоставлены, то они имеют одинаковые
площади, не требуют доказательства.
Пусть P и Q два данных равновеликих
многоугольника. Идея доказательства состоит в следующем. Рассмотрим сначала
многоугольник P и покажем, что его можно разрезать
на части, из которых можно составить как P, так и Q.

последовательно внутренние диагонали в многоугольниках, разрежем P на треугольники T1, T2 ,…, Tn (на рис. 9 показаны примеры нужных
разбиений как для P, так и для Q), все вершины, которых являются
вершинами многоугольника P.
Сделаем это так. Проведем какую – либо внутреннюю диагональ в многоугольнике P. Она разобьет многоугольник P на два новых простых
многоугольника. Если они не треугольники, то в каждом из них снова проведем по
одной внутренней диагонали и т. д. Ясно, что описанная процедура приведет к
нужному разбиению на треугольники.
Однако нужно иметь в виду, что такая триангуляция (разбиение на
треугольники), конечно, не единственна. Можно, например, выбирать на каждом
шаге различные диагонали. Более того, возможны разбиения на
треугольники, не все вершины которых являются вершинами многоугольника и т. д.
Рис. 10
По доказанному выше, каждый из треугольников T1, T2, …, Tn можно разрезать на части и получить
из них некоторые прямоугольники R1, R2, …, Rn: они, тем самым, равносоставлены с T1, T2,…,Tn соответственно (рис.10). Каждый из
этих прямоугольников равносоставлен, как мы видели выше, с некоторым квадратом
(рис.11).
 |
Рис. 11
Квадрат S, равный по площади сумме
площадей всех этих квадратов, равносоставлен с объединением квадратов S1, S2, …, Sn (рис.12). Это является следствием
доказанного выше утверждения о двух квадратах. Применяя этот
способ
объединения двух квадратов (n-1) раз,
мы и получим «маленькие» части, из которых можно сложить один «большой»
квадрат.
Рис.12
Таким образом, многоугольник P равносоставлен с равновеликим ему квадратом S.
Аналогично действуя с многоугольником Q, мы получаем, что он равносоставлен
равновеликому ему квадрату. Объединяя эти два разбиения квадратов в один,
заключаем, что равновеликие многоугольники P и Q равносоставлены.
Теорема Бойяи – Гервина полностью доказана.
Эту теорему можно пояснить так: если имеется пряник в форме
многоугольника и многоугольная коробка совершенно другой формы, но той же
площади, то можно так разрезать пряник на конечное число кусков, что удастся
вложить в эту коробку.
Вариант этой задачи был предложен на одной из московских математических
олимпиад в следующей шуточной форме.
Чудак-кондитер испек торт (а у торта, в отличие от пряника, верхняя
сторона покрыта кремом) в форме разностороннего треугольника. Сделали и коробку
к торту, но по недосмотру склеили ее неверно, так что торт и коробка оказались
симметричными друг другу. Нужно (по возможности экономно) разрезать торт на
части, которые удалось бы уложить в эту коробку. Разумеется, части торта нельзя
укладывать кремом вниз. (Решение: на каждой стороне треугольника
построим серединные перпендикуляры, точку пересечения которых соединим с
вершинами треугольника. Получится три равнобедренных треугольника, которые
можно уложить в коробку.)
4. Метод дополнения
При решение задач помимо рассмотренного нами метода разложения часто
используется и метод дополнения. Он состоит в том, чтобы одновременно дополнить
эти фигуры равными частями так, чтобы в результате получилась одна и та же
фигура (а не пытаться найти разложение фигуры на части и потом из этих частей
собрать другую фигуру, как это было в методе разложения). Примером применения
(рис.13) является стандартное доказательство равновеликости прямоугольника и
параллелограмма, имеющих одинаковые основания и высоту. Они дополняются равными
треугольниками, и в результате получаются равные трапеции. Следовательно,
прямоугольник и параллелограмм равновелики.

Рис. 13
С помощью этого метода можно получить одно из древних доказательств
теоремы Пифагора. Построим квадраты на катетах и гипотенузе. Дополним одними и
теми же треугольниками квадрат со стороной, равной длине гипотенузы, и два
квадрата, построенных на катетах, как показано на рисунке 14. В результате
получатся два равных квадрата.
 |
Рис. 14
5. Игры на разрезание и
складывание
Об авторстве первого решения задачи на разрезание говорить в принципе
невозможно, т.к. первым человеком, который столкнулся с такой задачей был
кто-то из первобытного общества. Это было при создании первых образцов
одежды — нужно было разрезать шкуру животного. В общем, авторство
постановки и решения таких задач затерялось где-то в глубинах истории.
На основе равносоставленности существуют различные логические игры
«Пентамино», «Стомахион» («приводящая в ярость»), «Танграм» и другие.

50-х годах ХХ века американским математиком С. Голомбом и очень быстро увлекла
не только школьников и студентов, но и профессоров математики. Она заключается
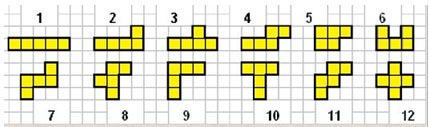
в складывании различных фигур из заданного набора пентамино. Набор пентамино
содержит двенадцать фигурок, каждая из которых составлена из пяти одинаковых
квадратов, причем квадраты «соседствуют» друг с другом только сторонами.
(Рис.15)
Рис.15
Игра «Стомахион» была известна еще до нашей эры. Создателем ее считали
Архимеда. В 1890 году швейцарский историк Генри Зютер обнаружил в
книгохранилищах Берлина и Кембриджа арабскую рукопись «Книга Архимеда о
разбиении фигуры стомахиона на четырнадцать частей, находящихся в рациональных
отношениях». Позже датский историк математики Гейберг подтвердил, что
создателем игры является Архимед. Для создания игры требуется взять
прямоугольник, одна сторона которого в два раза больше ругой, и выполнить в нем
построения, как на рисунке 16. Разрезав прямоугольник по сплошным линиям,
требуется составить фигурки курицы, мельницы и петуха. (Рис.17)
Суть игры «Танграм» заключается в конструировании на плоскости
разнообразных предметных силуэтов. Все фигуры имеют равную площадь, т. к.
собираются из одинаковых элементов (танов) получаемых при разрезании квадрата
(рис.18) определенным образом. Отсюда следует что:
1. В каждую собираемую фигуру должны войти непременно все семь элементов.
2. При составлении фигуры элементы не должны налегать друг на друга, т.
е. располагать только в одной плоскости.

один к другом.
Существует целый ряд версий и
гипотез возникновения игры танграм. Наиболее распространенной и известной
является та, что игра танграм насчитывает около 4000 лет. Такую дату можно
прочитать у Кордемского Б.А. или Котова А.Я., а так же у различных иностранных
авторов. Мнение о танграме, как о самой древней головоломке является весьма
распространенным. Однако, это всеобщее заблуждение. Миф об этом создал С.Лойд.
Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому
его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он
расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы
начинаются с символических изображений хаоса и принципа «инь и ян». Затем
следуют простейшие формы жизни, по мере продвижения по древу эволюции
появляются фигуры рыб, птиц, животных и человека. По пути в различных местах
попадаются изображения того, что создано человеком: орудию труда, мебель,
одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция,
философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного
профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по
преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить.
Встречаются у Лойда и ссылки на «известные» китайские пословицы типа «Только
глупец взялся бы написать восьмую книгу Тана».
В Китае название Танграм неизвестно, а игра имеет название Ши-Чао-Тю
(семь хитроумных фигур). В Оксфордском словаре английского
языка — название Танграм появляется с ссылкой на авторитетного Генри
Э.Дьюдени, его версию принял составитель словаря Д.Мюррей. Он обнаружил, что
слово танграм впервые встречается в словаре Вебстера издания 1864
г. По мнению в Мюррея, само слово танграм было придумано в середине прошлого
столетия неким американцем, образовавшим неологизм из слова Тан, что означает
на кантонском диалекте китайский, и распространенного суффикса — грам (как в
словах анаграмма или криптограмма). Иная теория происхождения слова танграм
была выдвинута Питером Ван Ноутом в предисловии к новому изданию книги Ллойда: китайские
семьи, живущие на лодках, называются танка, тан по-китайски
означает — падшая женщина. Американские моряки, покупавшие
головоломку у девушек — танка, могли назвать ее
танграмом — головоломкой доступных девушек. В книге «Китайский
философский и математический танграм» (1817
г.) слово танграм — трактуется, как старинное английское
слово — обозначающие игрушка головоломка.
Игрой внешне близкой танграму являются пазлы. В начале пазлы
являлись большим набором фигур неправильной формы из которых необходимо было
сложить картинку — задание. Несмотря на эту
схожесть — танграм, задача противоположная, так как семь базовых
элементов позволяет значительное множество фигур, а в случае пазла мы ограничены
только одним решением.
Сравнительный анализ танграма с другими аналогичными играми
был сделан Р.Ридом в книге «Танграмы: 330 головоломок». Для игры танграм
основным требованием к человеку является логическое мышление и геометрическая
интуиция, а для игры пазл — все-таки всего лишь усидчивость и терпение.
6. Заключение
Теорема Больяи –
Гервина является, по мнению математиков одной из красивейших математических
жемчужин. Существует ряд интересных задач, основанных на понятиях
равносоставленности:
1)
Сложите
квадрат из трех данных квадратов разной площади.
2)
Разрежьте
правильный треугольник на пять частей, из которых можно сложить прямоугольник,
параллелограмм и квадрат.
Как правило, задачи на
разрезание не имеют универсального метода решение, поэтому есть возможность в полной
мере проявить интуицию и способность к творческому мышлению. Они занимательны и
доступны людям любого возраста
Однако, вопрос о том, какое
наименьшее число разрезав достаточно, чтобы сконструировать из одной фигуры
другую, остается открытым и на сегодняшний день, а, значит, есть возможность
сделать новое открытие.
7. Литература
1. Атанасян Л.С. Геометрия 7-9 класс// М.: «Просвещение», 2006.
2. Болтянский В.Г. Равновеликие и равносоставленные фигуры.// М.-Л.:
Гостехиздат, 1956.
3. Вавилов В., Красников П. Разрезание и складывание многоугольников. //
Математика. №3, 2006. С. 9-13.
4. Корнеева А. Равновеликие и равносоставленные многоугольники. //
Математика. №14, 2007. С. 35-36.
5. Линдгрен Г. Занимательные задачи на разрезание. // М.: «Мир», 1977.
6. Надеждина В. Танграм 1000+1 фигура. // Минск: «Харвест», 2007.
7. Савин А.П. Энциклопедический словарь юного математика. // М.:
«Педагогика», 1989.
8. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. // М.: КПЦ «МАРТА»,
1992.
Сообщения без ответов | Активные темы | Избранное
|
|
алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
|
24/10/05 |
У меня есть невыпуклая фигура. Ее нужно разбить на фигуры, которые являются выпуклыми. Какие существуют алгоритмы для решения данной задачи? Всем заранее спасибо! ссылка на изображение, где указан пример разбиения http://content.foto.mail.ru/mail/zurix/2/i-24.jpg
|
|
|
|
|
worm2 |
|
||
01/08/06 |
Фигура, как я полагаю — это многоугольник? (а то, если ограничивающие отрезки непрямые, то может получиться, что на конечное число частей нельзя разбить).
|
||
|
|
|||
|
Zai |
|
||
11/04/07 |
worm2 писал(а): затем пытаться объединять смежные треугольники Насколько я понимаю треугольник является выпуклой фигурой и триангуляции вполне достаточно.
|
||
|
|
|||
|
Brukvalub |
|
||
01/03/06 |
Zai писал(а): Наиболее простой алгоритм триангуляции — поиск минимального угла в внешней однополостной петле . Это как? Все слова по отдельности знаю, но вот вместе — просто не укладываются в голове, и всё тут….
|
||
|
|
|||
|
antoshka1303 |
|
|
24/10/05 |
а как быть если нужно построить миниамальное число триангуляций?
|
|
|
|
|
Zai |
|
||
11/04/07 |
Brukvalub писал(а): Zai писал(а): Наиболее простой алгоритм триангуляции — поиск минимального угла в внешней однополостной петле . Это как? Все слова по отдельности знаю, но вот вместе — просто не укладываются в голове, и всё тут…. Пусть контур буквы «З» разбит на отрезки (назовем его петлей, угловые точки — вершины). Вычислим все углы между отрезками. Вычисление углов следующее. Если линия соединяющая две соседние вершины к данной лежит внутри разбиваемой области — угол меньше 180 градусов. Если нет — больше 180 градусов. Для вырожденного треугольника 180 градусов. Находим вершину с минимальным уголом. Образуем из двух отрезков, примыкающих к вершине треугольник. Исключаем из петли два отрезка прилежащих к данной вершине. Взамен вставляем один, соединяющий две соседние вершины. Проводим повторный поиск минимального угла и исключение. Буду очень признателен Вам, если еще что-то нужно уточнить. Данный алгоритм я использовал для конечно-элементных сеток лет десять назад, до повсеместного в настоящее время использования коммерческих генераторов сеток.
|
||
|
|
|||
|
Brukvalub |
|
||
01/03/06 |
Zai писал(а): Буду очень признателен Вам, если еще что-то нужно уточнить. Спасибо, теперь мне стало понятно.
|
||
|
|
|||
|
Massaraksh |
Re:
|
|
18/09/14 |
Zai писал(а): Вычисление углов следующее. Если линия соединяющая две соседние вершины к данной лежит внутри разбиваемой области — угол меньше 180 градусов. Если нет — больше 180 градусов. Для вырожденного треугольника 180 градусов. Находим вершину с минимальным уголом. Образуем из двух отрезков, примыкающих к вершине треугольник. Исключаем из петли два отрезка прилежащих к данной вершине. Взамен вставляем один, соединяющий две соседние вершины. Проводим повторный поиск минимального угла и исключение. Буду очень признателен Вам, если еще что-то нужно уточнить. Данный алгоритм я использовал для конечно-элементных сеток лет десять назад, до повсеместного в настоящее время использования коммерческих генераторов сеток. Каким образом с помощью этого алгоритма можно разбить, скажем, четырёхугольник с координатами (0;10) (2;-1) (0;-0.5) (-2;-1) ?
|
|
|
|
|
ewert |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
||
11/05/08 |
Находим вершину с минимальным уголом. Образуем из двух отрезков, примыкающих к вершине треугольник. Исключаем из петли два отрезка прилежащих к данной вершине. Взамен вставляем один, соединяющий две соседние вершины. И если повезёт, то запросто получаем самопересечение.
|
||
|
|
|||
|
Skeptic |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
|
01/12/11 |
На рисунке ТС изображён ключ с отверстием, т.е. ключ содержит кольцо. Как кольцо разбить на выпуклые части?
|
|
|
|
|
slavav |
Re:
|
||
26/05/14 |
Наиболее простой алгоритм триангуляции — поиск минимального угла в внешней однополостной петле. Устранение узла с меньшим углом дает новую петлю. Перед устранением узла необходимо проверить, что новая сторона не пересекается со старыми. Ваш алгоритм близок к otectotomy (алгоритм отрезания ушей). — 10.07.2015, 17:17 — На рисунке ТС изображён ключ с отверстием, т.е. ключ содержит кольцо. Как кольцо разбить на выпуклые части? Если это честное кольцо, то конечным разбиением ничего добиться нельзя. Если это полигональное кольцо, то в каждой его вершине будет диагональ разбиения.
|
||
|
|
|||
|
ewert |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
||
11/05/08 |
(алгоритм отрезания ушей) А почему, кстати, его обзывают
|
||
|
|
|||
|
slavav |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
||
26/05/14 |
(алгоритм отрезания ушей) А почему, кстати, его обзывают Это правда, если без опитимизации.
|
||
|
|
|||
|
ewert |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
||
11/05/08 |
(Оффтоп) и никому не интересно потому что сама сложность в Всего предыдущего я, естественно, не понял, т.к. лень врубаться. А вот тут скромно позволю себе понять так: не нужна нафик потому, что нафик не нужна триангуляция именно в этом смысле. К разбиению на треугольнички в смысле, скажем, МКЭ это ведь имеет отношение как минимум косвенное.
|
||
|
|
|||
|
slavav |
Re: алгоритм разбиение невыпуклой фигуры на выпуклые фигуры
|
||
26/05/14 |
(Оффтоп) и никому не интересно потому что сама сложность в Всего предыдущего я, естественно, не понял, т.к. лень врубаться. А вот тут скромно позволю себе понять так: не нужна нафик потому, что нафик не нужна триангуляция именно в этом смысле. К разбиению на треугольнички в смысле, скажем, МКЭ это ведь имеет отношение как минимум косвенное. Триангуляция в этом смысле важна и нужна. Например, для задачи Art Gallery. Не интересен медленный алгоритм. Практически полезные алгоритмы работают за
|
||
|
|
|||
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Разрезание на две равные части, часть первая
Время на прочтение
4 мин
Количество просмотров 53K
Задачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество отдельных проблем, но по сути нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.
Введение
Для начала освежим школьный курс геометрии и вспомним, что такое равные фигуры. Яндекс услужливо подсказывает:
Две фигуры на плоскости называются равными, если существует движение, взаимно однозначно переводящее одну фигуру в другую.
Теперь расспросим Википедию про движения. Она расскажет нам, во-первых, что движение — это преобразование плоскости, которое сохраняет расстояния между точками. Во-вторых, там даже приведена классификация движений на плоскости. Все они относятся к одному из следующих трёх типов:
- Параллельный перенос
- Поворот
- Скользящая симметрия (сюда я удобства ради и пользы для включаю зеркальная симметрию, как вырожденный случай, где параллельный перенос производится на нулевой вектор)
Введём некоторые обозначения. Разрезаемую фигуру мы будем называть фигурой A, а две гипотетеческих равных фигуры, на которые мы будто бы можем её разрезать, обзовём B и C соответственно. Часть плоскости, не занятую фигурой A, мы назовём областью D. В тех случаях, когда в качестве разрезаемой фигуры рассматривается конкретный многоугольник с картинки, мы будем называть его A0.
Так вот, если фигуру A можно разрезать на две равных части B и C, то существует движение, переводящее B в C. Это движение может быть либо параллельным переносом, либо поворотом, либо скользящей симметрией (начиная с этого момента, я больше не оговариваю, что зеркальная симметрия также считается скользящей). На этом нехитром и, я бы даже сказал, очевидном, базисе и будет строиться наше решение. В этой части мы рассмотрим самый простой случай — параллельный перенос. Поворот и скользящая симметрия попадут во вторую и третью часть соответственно.
Случай 1: параллельный перенос
Параллельный перенос задаётся единственным параметром — вектором, на который происходит сдвиг. Введём ещё несколько терминов. Прямую, параллельную вектору сдвига и содержащую хотя бы одну точку фигуры A, будем называть секущей. Пересечение секущей прямой и фигуры A будем называть сечением. Секущую, относительно которой фигура A (за вычетом сечения) целиком лежит в одной полуплоскости, будем называть границей.
Лемма 1. Сечение границей должно содержать более одной точки.
Доказательство: очевидно. Ну или более развёрнуто: докажем от противного. Если эта точка принадлежит фигуре B, то её образ (т.е. точка, в которую она перейдёт при параллельном переносе) принадлежит фигуре C => образ принадлежит фигуре A => образ принадлежит сечению. Противоречие. Если эта точка принадлежит фигуре C, то её прообраз (точка, которая при параллельном переносе перейдёт в неё) принадлежит фигуре B, и далее аналогично. Получается, в сечении должно быть хотя бы две точки.
Руководствуясь этой нехитрой леммой, нетрудно понять, что искомый параллельный перенос может происходить лишь вдоль вертикальной оси (в текущей ориентации картинки) Если бы он был в любом другом направлении, хотя бы одно из граничных сечений состояло бы из единственной точки. Это можно понять, мысленно повращав вектор сдвига и посмотрев, что при этом происходит с границами. Чтобы исключить случай вертикального параллельного переноса, нам понадобится более хитрый инструмент.
Лемма 2. Прообраз точки, находящейся на границе фигуры C, находится либо на границе фигур B и C, либо на границе фигуры B и области D.
Доказательство: неочевидно, но сейчас мы это исправим. Напомню, граничной точкой фигуры называется такая точка, что сколь угодно близко от неё найдутся как точки, принадлежащие фигуре, так и точки, не принадлежащие ей. Соответственно, вблизи граничной точки (назовём её O’) фигуры C найдутся как точки фигуры C, так и другие точки, принадлежащие либо фигуре B, либо области D. Прообразами точек фигуры C могут быть только точки фигуры B. Следовательно, сколь угодно близко к прообразу точки O’ (будет логично назвать его точкой O) найдутся точки фигуры B. Прообразами точек фигуры B могут быть любые точки, не принадлежащие B (то есть либо точки фигуры С, либо точки области D). Аналогично для точек области D. Следовательно, сколь угодно близко к точке O найдутся либо точки фигуры C (и тогда точка O будет на границе B и C), либо точки области D (и тогда прообраз на границе B и D). Если вы сумеете продраться через все эти буквы, то согласитесь, что лемма доказана.
Теорема 1. Если сечение фигуры A представляет собой отрезок, то его длина кратна длине вектора сдвига.
Доказательство: рассмотрим «дальний» конец этого отрезка (т.е. тот конец, прообраз которого также принадлежит отрезку). Этот конец, очевидно, принадлежит фигуре C и является её граничной точкой. Следовательно, его прообраз (кстати говоря, также лежащий на отрезке и отстоящий от образа на длину вектора сдвига) будет либо на границе B и C, либо на границе B и D. Если он на границе B и C, то возьмём также и его прообраз. Будем повторять эту операцию, пока очередной прообраз не перестанет быть на границе C и не окажется на границе D — а это произойдёт как раз на другом конце сечения. В результате мы получим цепочку прообразов, которые разбивают сечение на некоторое количество маленьких отрезочков, длина каждого из которых равняется длине вектора сдвига. Следовательно, длина сечения кратна длине вектора сдвига, ч.т.д.
Следствие из теоремы 1. Любые два сечения, являющиеся отрезками, должны быть соизмеримы.
Используя это следствие, нетрудно показать, что вертикальный параллельный перенос тоже отпадает.
Действительно, сечение раз имеет длину три клетки, а сечение два — три минус корень из двух пополам. Очевидно, эти величины несоизмеримы.
Вывод
Если фигуру A0 и можно разрезать на две равные фигуры B и C, то B не переводится в C параллельным переносом. Продолжение следует.
Введение
«Решение задач – практическое искусство, подобное
плаванию, катанию на лыжах или игре на фортепиано;
научиться ему можно, только подражая хорошим
образцам и постоянно практикуясь.»
Д.Пойя
Увлекаясь математикой, мы часто размышляем над какой-либо особенно понравившейся нам задачей. Источниками самых интересных задач служат различные олимпиады – школьные, городские, районные, областные, дистанционные, международные. Когда мы готовимся к олимпиадам, мы рассматриваем великое множество заданий различных видов и уровня сложности. Для себя мы обычно выделяем группу задач, подход к решению которых нам кажется интересным и наиболее оригинальным. Для нас это задачи на разрезание. Именно такие задачи развивают логику, что является неотъемлемой частью учебного процесса. Изучение логики способствует пониманию красоты и изящества рассуждений, умению рассуждать, творческому развитию личности, эстетическому воспитанию человека. Каждый культурный человек должен быть знаком с логическими задачами, головоломками, играми, известными уже несколько столетий или даже тысячелетий во многих странах мира [1]. У нас возникали вопросы:
- в чём заключается особенность логических задач?
- существуют ли специальные методы и приёмы решения задач на разрезание?
А также нам нравится «играть» с такими задачами. Особенно нам нравится создавать новые фигуры из разрезанных частей. Это могут быть как фигуры геометрические, так и различные фигуры, напоминающие нам какого-то животного, предмет или что-то особенное. Составлять что-то новое из разрезанных частей исходной геометрической фигуры довольно интересно, весело и развивает наше мышление. А вот задачи на разрезание, требующие составить какую-то новую геометрическую существующую фигуру, сложнее, но еще сложнее сравнить площади таких фигур. Так как в этом случае нужно методом долгих вычислений узнавать площадь и исходной фигуры и новой построенной фигуры. Что далеко не всегда получается или возникает вопрос «Почему?».
Оказывается, что задачами на разрезания занимались ещё в древности многие великие учёные и многие задачи дошли до наших дней. Нам кажется, что задачи на разрезание формируют самое первое геометрическое представление школьников.
В своем исследовании мы будем решать задачи на разрезание, используя именно первоначальную фигуру квадрат, а уже из частей квадрата составлять другие фигуры. Это будут как фигуры геометрические для сравнения площадей, так и игровые моменты составления фигур.
Актуальность работы:
- Задачи на разрезание получают стандартные методы решения, переходя из разряда творческих в разряд технических задач, то есть требуют применения известных методов для своего решения.
- Задачи на разрезание помогают не только раньше формировать геометрические представления у школьников на разнообразном материале, но и развивают логическое, нестандартное мышление школьников. При решении таких задач возникает ощущение красоты, закона и порядка в природе.
Объект исследования: задачи на разрезание.
Предмет исследования: многообразие задач на разрезание, методы и приёмы их решения.
Методы исследования: моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, поиск и анализ информации.
Цель исследования: расширить знания о многообразии задач на разрезание.
Чтобы достичь нашей цели мы должны решить ряд необходимых задач.
Задачи:
- изучить необходимую литературу, интернет-ресурсы;
- научиться разрезать геометрические фигуры на части, необходимые для составления той или иной другой геометрической фигуры;
- научится использовать в решении задач на разрезание свойства и признаки геометрических фигур;
- научиться доказывать, что площади фигур равны, разрезая их на определенные части и доказывая, что эти фигуры равносоставленные;
- научиться доказывать, что площади фигур не всегда могут быть равны, даже если состоят из равных фигур;
- исследование чисел Фибоначчи;
- провести геометрическое исследование, конструирование в решении задач различных типов.
- отобрать материал для исследования, выбрать главную, интересную, понятную информацию;
- найти различные методы и приёмы решения задач на разрезание;
- классифицировать исследуемые задачи;
- создать электронную презентацию работы.
Гипотеза: во всем многообразии задач на разрезание отсутствуют, как известно, общие правила и методы их решения. У школьников это вызывает затруднения при их решении. Предположим, что при более внимательном исследовании задач на разрезание, мы убедимся в их необходимости, оригинальности и полезности.
При решении задач на разрезание нам не нужно будет изучать основы планиметрии, а будут нужны именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем с начальной школы.
Историческая справка
Поиском решения задач на разрезание ученые начали еще с древнейших времен. Возникли они из потребностей практиков-землемеров и строителей архитектурных сооружений древнего мира. Первые попытки к решению были разработаны в Древней Греции и Китае. Так, в древнем Китае зародилась головоломка «Танграм», а в Греции – головоломка «Пентамино», где используется метод комбинаторной геометрии. Но обобщить подход к решению задач на разрезание смог только арабский математик и астроном Абул Вефа, который жил в X веке. Он разработал множество приемов решения геометрических задач, которые связанны с разложением фигур на части. И только в конце XX века ученые вновь занялись изучением, а также поиском новых путей решения задач на разрезание фигур на наименьшее число частей и последующее составление из них новых фигур. Известные специалисты в этой области – Генри Эрнест Дьюдени и Гарри Ландгрен. В своей книге «Занимательные задачи на разрезание» Ландгрен приводит пример, как составить новую фигуру, при этом разрезав начальную на наименьшее число частей, а также дает возможность разработать свой подход к решению задач и найти новые способы их решения.
В 1832 году на основе полученных знаний о разрезании фигур, была разработана теорема Бояи-Гервина, в основу которой вошло положение о том, что любые два равновеликих многоугольника равносоставлены. Эта теорема позволила сократить и упростить ход решений и доказательств в задачах различного рода.
Задачи на разрезание вызывают постоянный интерес. Однако до сих пор остается не до конца исследованным вопрос о системе задач на разрезания и методах решения этих задач.[2]
Геометрические задачи в нашем исследовании будут связаны с одной самой простой на первой взгляд фигурой – квадратом. Главная заслуга квадрата – это использование его, как единицы площади удобной при вычислениях. Действительно, квадратами очень удобно замащивать плоские участки, а скажем, кругами такого не сделаешь без дыр и наложений.[3] Очень часто математики вместо слов «нахождение площади» говорят «квадрирование».
Наше исследование задач на разрезание квадратов мы начали с древнекитайской игры «Танграм». Танграм — это головоломка, которая представляет квадрат, который разрезали на 7 частей определенным образом. Из этих частей можно собрать животных, птиц, предметы или геометрические фигуры. Игра появилась в Китае, и по одной из легенд это просто было забавой для сына императора. Забавляясь такой игрой, учителя мальчика стремились воспитать его так, чтобы он постиг начала математики, смотрел на мир глазами художника и понимал бы то, что все сложные вещи состоят из простых частей, постигал бы все это как истинный философ. Первоначально три мудреца (математик, художник и философ) игру назвали «Ши-Чао-Тю», что означает «составленный из семи частей». Может это имеет связь и с 7 чудесами света? Впервые об этой игре стало известно более 4000 лет назад. Сохранились некоторые экземпляры игры 1802 года из слоновой кости в Америке. А первые изображения некоторых фигур появились в Китае в 1813 году в китайской книге.
Вторая часть нашего исследования состояла в разрешении задач на разрезание в сравнении площадей исходной фигуры и новой, составленной из частей прежней фигуры. Исследование подобных задач связано с последовательностью чисел Фибоначчи. Фибоначчи — это известный и выдающийся математик Европы позднего Средневековья. Он известен и как Леонардо из Пизы или Леонардо Пизанский.
Фибоначчи внес огромнейший вклад в основы математической науки, смог объединить множество разрозненных математических знаний Восточных культур и привел их к единой числовой системе, которая прослеживается во всех аспектах человеческой жизни. Фибоначчи связал основы своей теории со многими науками и искусствами, смог показать то, как правильно воспринять красоту числового мира. Фибоначчи – это тот, кто смог вывести математическую науку на новый уровень ее развития.
Задачи на разрезание представляют для многих некоторую головоломку, а для многих это развивает логическое мышление.
Глава 1
Игра «Танграм»
Игра «Танграм» — древнекитайская головоломка. Эта игра появилась около 4 тыс. лет назад и известна до сих пор и очень увлекательна. В переводе с китайского это переводиться как «умственная головоломка из семи частей». Обычно в такой игре используют клетчатую обычную бумагу, рисуют на ней квадрат и разбивают на семь частей, согласно правилам игры. Но пользуясь линейкой, никто не запрещает построить такой же квадрат на цветной бумаге и сделать соответствующие разбиения на семь частей. Впервые такую игру мы провели в ноябре 2018 года на неделе математике. Мы построили на листе в клетку квадрат, разбили его на семь соответствующих частей, и должны были составить из семи деталей любого животного насколько хватит нашего воображения. Варианты были различные: заяц, черепаха, белка, собака, кошка, кенгуру и многое другое.
Первое, что нас особенно заинтересовало в исследовании это то, можно ли из семи частей данного квадрата составить прямоугольник. Нельзя сказать, что было слишком просто, но животных составлять куда легче. Так как геометрические фигуры при составлении тела животного можно располагать так, как подсказывает твоя фантазия. А вот прямоугольник нужно уметь правильно составить, подобрать детали так, чтобы образовалоись четыре прямых угла и внутри все пространство прямоугольника должно быть заполненоь фигкрами. Получился прямоугольник следующего вида (рисунок). Пральнее всего начать использовать в это работе квадрат и тот, который больше. Квадрат удобно тспользовать потому, что у него уже есть прямые угла. А альше дело техники и всё зависит от дальнейшего расположения фигур.
Вторым нашим вопросом было равны ли площади первоначального квадрата и фигуры новой, составленной из разрезанных частей квадрата. Однозначно на этот вопрос ответить сложно. Но пользуясь следующей теоремой:
Если фигура состоит из двух (или более частей) частей, то ее площадь равна сумме площадей этих частей.
Сначала мы убедились в этом на обыкновенных квадратах. Поэтому мы взяли в рассмотрение квадрат из 16 клеток 4х4. Далее разделим квадрат на две части следующим образом (рисунок). Из двух частей составим прямоугольник как показано на рисунке (рис. + слайд)
Пусть 1 клетка имеет площадь 1 см2, тогда мы сможем найти площадь и всего квадрата, так как его длина и ширина по 4 см, или иначе можно посчитать все клетки квадрата:
S = 16 (см2).
Теперь найдем площадь построенного нами прямоугольника из двух частей квадрата. Имеем два способа нахождения площади.
1 способ. Сложить площади всех частей, из которых состоит прямоугольник:
S = 8 + 8 = 16 (см2).
2 способ. Посчитать, сколько клеток приходится на длину, сколько на ширину и вычислить привычным для нас способом.
S = 2*8 = 16 (см2)
Можно проверить наши вычисления и третьим способом:
3 способ. Посчитать все клетки, из которых состоит прямоугольник, а их как раз 16. Значит площадь равна 16 см2. Что и требовалось доказать. А, следовательно, наш пример подтверждает теорему.
Парадокс с площадью
Перейдем к следующей геометрической задаче. Очень часто её называют «геометрический парадокс». Рассмотрим квадрат со стороной 8 см. Разрежем данный квадрат на две части так же, как и в предыдущей задаче.
Исходя из рассуждений, задачи площади квадрата и прямоугольника равны:
S = 8 * 8 = 64 (см2) – площадь квадрата.
S = 16 * 4 = 64 (см2) – площадь прямоугольника.
Теперь снова рассмотрим исходный квадрат, но разрежем его на четыре части как показано на рисунке. Сложим из полученных четырех частей прямоугольник. Прямоугольник, сложенный из частей квадрата, имеет размеры 5 на 13 (рисунок). А теперь сравним площади полученных фигур. Так как эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны, что следует по теореме о том, что если фигура состоит из двух (или более частей) частей, то ее площадь равна сумме площадей этих частей. Сравним фигуры и их площади.
Так как эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны, что следует по теореме.
Sквадрата = 8 ∙ 8 = 64 (см2)
Sпрямоугольника = 13 ∙ 5 = 65 (см2)
В этом и заключается «парадокс» задачи. Кажется, что задача неразрешима. Возникает один вопрос: «Откуда появился лишний квадратный сантиметр в площади прямоугольника?» Трудно представить, что внезапно появилась так сказать «лишняя единица площади».
Первым в нашем исследованием в этой задаче стало то, что мы стали искать площади всех частей прямоугольника. Так как прямоугольник мы составили из двух прямоугольных треугольников и двух прямоугольных трапеций. При этом треугольники равны между собой, а трапеции являются так же равными.
Найдем площадь треугольника. А так как треугольник прямоугольный, то площадь прямоугольного треугольника равна половине произведения катета на гипотенузу:
Найдём площадь трапеции. Так как трапеция прямоугольная, то сторона, содержащая прямой угол с одним из оснований является высотой, а значит площадь трапеции равна половине произведения высоты на сумму основании трапеции:
Найдём площадь всей фигуры, составленной из четырех частей квадрата:
S = 2 Sтреуг. + 2 Sтрап.=24 + 40 = 64 (см2).
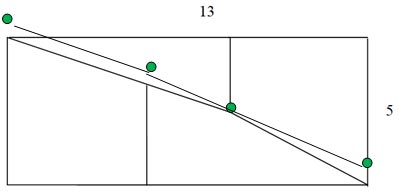
Но наш результат снова не сходится с площадью прямоугольника. При вычисления мы снова теряем 1 см2. Рассмотрим внимательно наш прямоугольник. После тщательных измерений с помощью линейки мы пришли к выводу, что точки, выделенные на рисунке зелёным цветом, не лежат на одной прямой. А это значит, что нам кажется, что эти точки лежат на диагонали прямоугольника. На самом же деле это вершины параллелограмма со сторонами см и 3 см. Площадь найденного параллелограмма как раз равна 1 см2.
Рассмотрим еще одно решение нахождения площади прямоугольника. Итак, квадрат разрезан на две трапеции и два прямоугольных треугольника.
Рассмотрим прямоугольный большой треугольник 1 и найдем значение тангенса его угла:
Теперь рассмотрим маленький треугольник 2 на рисунке 10 и найдем значение тангенса угла:
Значение тангенсов углов не совпадают. Это означает, что гипотенуза маленького синего прямоугольного треугольника и боковая сторона первой трапеции (внизу) не лежит на одной прямой, а являются звеньями ломаной. Аналогично доказывается, что гипотенуза маленького треугольника и боковая сторона второй трапеции (трапеция расположена вверху) не лежит на одной прямой. Следовательно, площадь прямоугольника равна сумме площадей фигуры, составленной из частей квадрата и черной так называемой «щели», которую сложно заметить при составлении частей квадрата.
Но на этом наше исследование не закончилось. Нас заинтересовал вопрос, почему именно квадрат с такими измерения, разбитый на 4 части, и прямоугольник с такими измерениями дают такой результат. Мы стали искать закономерность именно среди измерений квадрата и прямоугольника. Как известно сторона квадрата 8 см, а стороны прямоугольника равны соответственно 5 см и 13 см. Расставим эти числа в порядке возрастания для наглядности:
5, 8, 13.
А эти числа, как известно, являются членами ряда Фибоначчи. То есть длины сторон четырех частей, составляющих фигуры это некая последовательность. А расположенные части, на которые был разрезан квадрат, в виде прямоугольника показывают нам одно из свойств ряда Фибоначчи. Рассмотрим это свойство.
Согласно формулировке данного свойства следует, что если возвести в квадрат любой член ряда Фибоначчи, то получим произведение двух соседних членов ряда и плюс либо минус единица:
- 52 = (3 ∙
+ 1
- 82 = (5 ∙ 13) – 1
- 132 = (8 ∙ 21) + 1
Вернемся к нашим измерениям. Сторона квадрата равна 8 см, а площадь равна 64 см2. Восьмерка в ряду Фибоначчи расположена как раз между числами 5 и 13. А число 5 стало шириной прямоугольник и 13 стало его длиной соответственно. Отсюда получаем произведением чисел 5 и 13 равно 65, что дает прирост площади на одну единицу.
В ходе нашего исследования нам так же нужно было познакомимся с последовательностью чисел Фибоначчи. Узнать, по какому правилу составлена данная последовательность. А так же нам нужно выяснить, существуют ли еще квадраты с такими измерениями, которые впоследствии разбиения либо добавляют единицу к площади или же ее отнимают.
Числа Фибоначчи — элементы числовой последовательности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …
В рассматриваемой последовательности первые два числа равны либо 1 и 1, либо 0 и 1. Согласно правилу составления данного ряда, каждое последующее число равно сумме двух предыдущих чисел.
Попробуем, используя числа Фибоначчи построить квадрат, стороной которого будет являться любое число из последовательности Фибоначчи.
Возьмем число 21.Пусть 21 – это сторона квадрата. Так как число 21 расположено между числами 13 и 34, то эти числа должны является сторонами прямоугольника. Проверим это, используя выводы нашей рассмотренной задачи:
S = 212=441 (см2) – площадь квадрата
S = 13 * 34 =442 (см2) – площадь прямоугольника.
Снова получили прирост на 1 см2 к площади прямоугольника.
Так мы, решив задачу и рассмотрев произвольную новую задачу, мы пришли к выводу, что длины сторон в таких фигурах являются членами последовательности чисел Фибоначчи.
Существует великое множество таких квадратом и прямоугольников, длины сторон которых связаны числами последовательности Фибоначчи. Каждые три рядом стоящие числа последовательности дают нам пару квадрат – прямоугольник с разницей в площади ровно на 1 см2.
Решая подобные задачи, мы не только развиваем логику, но и стараемся применить все свои знания на практике.
Занимательные задачи
Представим вашему вниманию несколько задач разного уровня сложности, в которых не нужно применять никакие другие геометрические и алгебраические познания. Первую задачу рассмотрим несложную. Попробуем на практическом опыте убедиться в том, что ты уже умеем складывать новые фигуры из частей квадратов. Вторая задача будет представлять собой игру Пентамино – игра из 12 готовых деталей, каждая деталь определенной формы.
Задача 1. Перед вами два квадрата, один из которых уже разделен на четыре одинаковых треугольника. Как при помощи этих треугольников и маленького квадрата сложить один большой квадрат? Ничего больше разрезать не требуется.

Задача 2. Сложите из двенадцати фигур Пентамино прямоугольник 6 × 10, причем так, чтобы каждый элемент касался какой-нибудь стороны этого прямоугольника.
Вообще данная задача напоминает нам детскую игру тетрис. Увлекательно и полезно для детей начиная с 5-летнего возраста, что развивает логику и мышление.
Детали для игры – задачи должны быть подготовлены заранее. Удобнее всего это делать на клетчатой бумаге.
Заметим, что каждая часть содержит в себе пять одинаковых квадратиков. А теперь применяя логическое мышление, решаем задачу. Строить прямоугольник начнем с прямого угла.
Заключение
Те, кто любит головоломки и увлекается решением различных задач на разрезание, прежде всего, развивает логику своего мышления. Различные универсальные методы решения таких задач способствуют развитию геометрического мышления, даже с малого возраста, и каждый, кто берётся за решение таких задач, может в полной мере проявить свою интуицию, смекалку и развить в полном объеме способность к творческому мышлению. Так как в таких задачах не требуется глубокое знание геометрии, то учащиеся иногда могут даже превзойти профессионалов – математиков, своих учителей в поиске новых открытий.
Так же, задачи на разрезание не являются несерьёзными или бесполезными. Такие задачи наоборот не так уж и далеки от серьёзных математических задач. Из задач на разрезание родилась теорема Бояи — Гервина о том, что любые два равновеликих многоугольника равносоставлены (обратное очевидно). Так же мы применили последовательность чисел Фибоначчи. Ученик сам способен в таких задач показать себя, найти свое решение, индивидуальное, а не стандартное.
Рассмотренные нами задания имеют различный уровень трудности – от простых задач до олимпиадных. Самые простые задачи лучше начать решать на клетчатой бумаге. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.
Список используемой литературы и интернет-ресурсы
- М.А. Екимова, Г.П. Кукин «Задачи на разрезание» — М.: МЦНМО, 2002.— 120 с.: ил. Серия: «Секреты преподавания математики».
- Интернет – ресурс: https://scienceforum.ru/2018/article/2018000620
- https://infourok.ru/geometricheskie-zadachi-na-razrezanie-805621.html
- https://ru.wikipedia.org/wiki/Числа_Фибоначчи
- http://www.mathedu.ru/lib/books/lindgren_zanimatelnye_zadachi_na_razrezanie_1977/#7 — Линдгрен Г. Занимательные задачи на разрезание. — 1977
- http://gimn1567.ru/dost/fibonach/geometr.htm
- http://lovingmama.ru/article/1110-igra-tangram-istoriya-kitayskoy-golovolomki-pravila-shemy-polza-dlya-detskogo-razvitiya
- https://ucthat-v-skole.ru/podgotovka-k-shkole/356-tanq
- https://svikk.biz/chisla-fibonachchi/
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Искать решение задач на разрезание ученые начали еще с древнейших времен. Возникли они из потребностей практиков-землемеров и строителей архитектурных сооружений древнего мира. Первые попытки к решению были разработаны древними греками, китайцами. Так, в древнем Китае зародилась головоломка «Танграм», а в Греции – «Пентамино», где используется метод комбинаторной геометрии. Но систематизировать подход к решению задач на разрезание смог арабский математик, астроном Абул Вефа, который жил в X веке. Он разработал приемы решения геометрических задач, связанных с разложением фигур. В конце XX века ученые вновь занялись изучением, а также поиском новых путей решения задач на разрезание фигур на наименьшее число частей и последующее составление из них новой фигуры. Известные специалисты в этой области – Генри Эрнест Дьюдени и Гарри Ландгрен. Например, в своей книге «Занимательные задачи на разрезание» Ландгрен приводит пример, как составить новую фигуру, при этом разрезав начальную на наименьшее число частей, а также дает возможность разработать свой подход к решению задач и найти новые способы их решения.
В 1832 году на основе полученных знаний о разрезании фигур, была разработана теорема Бояи-Гервина, в основу которой вошло положение о том, что любые два равновеликих многоугольника равносоставлены. Эта теорема позволила сократить и упростить ход решений и доказательств в различного рода задачах.
Возможности для решения практических проблем и математическое «изящество» задач на разрезание вызывает постоянный интерес к этой теме. Однако остается не до конца исследованным вопрос о системе задач на разрезания и методах решения этих задач. Обозначенная проблема определила актуальность нашего исследования по теме «Задачи на разрезание».
Объект исследования: многоугольники.
Предмет исследования: задачи на разрезание многоугольников.
Цель исследования: систематизировать теоретический материал по теме «Задачи на разрезание» и исследовать возможности его применения к решению задач.
Задачи исследования:
систематизировать основные определения и теоремы по данной теме;
рассмотреть примеры задач, применив изложенный материал.
Результаты исследования были представлены на конференциях:
1) IV внутривузовская студенческая научно-практическая конференция «Молодежь в мире науки» (ноябрь 2016 год, г. Сургут). По итогам выступления опубликована статья (Иманова К. Задачи на разрезание / Молодежь в мире науки : материалы IV внутривузов. студенч. науч.-практ. конф., 25 нояб. 2016 г. / Бюджет. учреждение высш. образования ХМАО – Югры «Сургут. гос. пед. ун-т», фак. соц.-культур. коммуникаций ; [редкол.: С.С. Богдан (отв. ред.) и др.]. – Сургут : РИО СурГПУ, 2017. – С. 61-63).
2) XXI студенческая научно-практическая конференция «Студенчество в научном поиске» (апрель 2017 год, г. Сургут), по итогам которой доклад занял первое место в секции.
Работа состоит из введения, двух частей и заключения. Список используемой литературы включает 25 наименований.
Теоретическая часть
Определение 1.Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону.
Свойство 1.У выпуклого многоугольника все углы меньше 180̊
Свойство 2.Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его диагональ), содержится в этом многоугольнике.
Свойство 3.Сумма углов выпуклого n-угольника равна 180̊ ∙ ( n − 2)
Определение 2. Определить площадь многоугольника – значит поставить в соответствие каждому плоскому многоугольнику величину («площадь»), обладающую следующими свойствами:
Два равных многоугольника имеют одну и ту же площадь.
Многоугольник, составленный из нескольких многоугольников, имеет площадь, равную сумме их площадей.
За единицу площади принимается площадь квадрата со стороной, равной единице длины.
Площадь многоугольника F будем обозначать S(F).
Аксиомы площади:
1) Равные фигуры имеют равные площади.
2) Площадь некоторого квадрата, сторона которого является единицей длины, равна единице.
3) Если фигура F разбита на две части B и C то S (F) = S (B) + S (C)
Определение 3. Фигуры, имеющие одну и ту же площадь, называются равновеликими.
Приведем формулы для вычисления площадей некоторых многоугольников.
Площадь квадрата равна квадрату его стороны: .
Площадь прямоугольника равна произведению его сторон. А именно, если – прямоугольник со сторонами a и b, то его площадь: .
Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты: .
Площадь трапеции равна произведению полу суммы оснований и высоты, т. е, если а и b – основания трапеции, – высота и – площадь трапеции, то .
Площадь параллелограмма равна произведению его стороны и проведенной к ней высоты: .
Пусть дан многоугольник F. Соединим точки Н и К, принадлежащие контуру его простой ломаной, все точки которой, исключая ее концы, лежат внутри этого многоугольника. В результате мы получим два многоугольника F1 и F2) имеющих общей частью указанную ломаную (рис. 1).
Рис. 1
Множество точек, принадлежащих многоугольнику F, представляет соединение множеств точек многоугольников F1 и F2. Поэтому мы скажем, что многоугольник F разложен на многоугольники F1 и F2, и условно запишем это так: F~F1+F2.
В свою очередь каждый из многоугольников F1 и F2 можно разложить на два новых многоугольника и так далее. Таким путем мы можем получить некоторые многоугольники Q1, Q2, …, Qk, соединение множеств точек которых даст нам множество точек прямоугольника F. Ясно при этом, что любые два многоугольника Qi и Qj или не имеют общих точек, или общие точки этих многоугольников принадлежат их контурам. Будем говорить в этом случае, что многоугольник F разложен на многоугольники Q1, Q2, …, Qk и условно писать: Q~Q1+Q2+…+Qk[7].
Определение 4. Будем говорить, что многоугольник F представляет соединение многоугольников Q1, Q2, …, Qk. Два многоугольника F1 и F2 называются равносоставленными, если каждый из них можно разложить на одно и то же конечное число многоугольников так, что каждому многоугольнику одного разложения соответствует равный ему многоугольник другого разложения, и обратно. Из определения следует, что равносоставленные многоугольники обладают свойством симметрии.
Прямоугольник равносоставлен параллелограмму, зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты.
Треугольник равносоставлен параллелограмму, который имеет то же основание, и его высота в два раза меньше. Из этого свойства можно вывести формулу площади треугольника. В изучении равносоставленных фигур ключевую роль играет теорема Бояи-Гервина.
Теорема Бояи—Гервина. Два многоугольника, имеющих равные площади, равносоставлены.
Доказательство теоремы распадается на ряд лемм.
Лемма 1. Две многоугольные фигуры P и Q, равносоставленные с третьей фигурой R, равносоставлены.
Доказательство. Так как P~R,то найдутся такие разбиения фигур P и R на многоугольные фигуры P1,…,Pkи R1,…,Rk, что P1=R1,…,Pk=Rk. Аналогично, так как Q~R, то найдутся такие разбиения фигур Q и R на многоугольные фигуры Q1,…,Qnи R′1,…,R′n что Q1 = R′1,…,Qn=R′n.
Каждое разбиение многоугольной фигуры осуществляется некоторой сетью отрезков. На фигуре R «нарисованы» две сети: от разбиения R1,..,Rkи от разбиения R′1,…,R′n. Объединение этих двух сетей даст новую сеть из отрезков, которая разобьет фигуру R на более мелкие многоугольные фигуры. Эти многоугольные фигуры Rijполучаются в пересечении фигуры Ri с фигурой R′j. Каждая из фигур R1,…,Rk разбита на эти фигуры .R1
R1=R11+R12+…+R1n,
R2=R21+R22+…+R2n,
…………………….
Rk=Rk1+Rk2+…+Rkn
Так как P1=R1,то фигуруP1 можно разбить также, как иR1: P1=P11+…+P1n. Аналогичные разбиения получаем и для остальных фигурP2,…,Pk: P2=P21+P22+…+P2n,Pk=Pk1+…+Pkn. При этом для любых индексов iи j фигуры Pij и Rij равны.
Но и фигуры Q1,…,Qn, равные фигурам R′1,…,R′n , так же можно разбить на фигуры Qij , равные фигурам Rij:
Q1=Q11+Q21+…+Qk1,
…………………….
Qn=Q1n+Q2n+…+Qkn.
Так как Qij=Rij и Pij=Rij , то Qij=Pij . Следовательно, P~Q, что и требовалось доказать.
Лемма 2.Равновеликие параллелограммы P и Q,имеющие равную сторону, равносоставлены.
Доказательство. Расположим параллелограммы P и Q так, что их равные стороны АВ совпадают, а сами параллелограммы лежат с одной стороны от прямой АВ. Так как параллелограммы P и Q равновелики, то их высоты на сторону AB равны. Поэтому их стороны CD и KL, противоположные стороне AB, лежат на одной прямой, параллельной прямой АВ (рис. 2).
Рис. 2
Возможны два случая:
Случай 1. Боковые стороны параллелограммов P и Q не пересекаются. Пусть точка K лежит на стороне СD. Тогда параллелограмм P составлен из трапеции ABCK и треугольника ADK, а параллелограмм Q составлен из той же трапеции ABCK и треугольника BCL. Так как ∆ADK=∆BCL, то P~Q.
Случай 2. Боковые стороны параллелограммов P и Q пересекаются. Например, стороны AK и BC пересекаются в точке O. В параллелограммах P и Q разместим одинаковое число треугольников T, равных треугольнику AOB.
Если эти треугольники не заполняют полностью параллелограммы P и Q , то в P и Q, кроме треугольников T, останутся еще два параллелограмма A′B′CD и A′′B′′LK, соответствующие случаю 1. A′B′CD ~ A′′B′′LK, поэтому P~Q, что и требовалось доказать.
Лемма 3. Два равновеликих прямоугольника равносоставленные.
Доказательство. Пусть прямоугольник P со сторонами и прямоугольник Q со сторонами равновелики. Тогда . Можно считать, что и , а также что . Так как , то . Построим параллелограмм R со сторонами и c и высотой а на сторону (рис. 3). Поскольку S(P)=S(Q) и параллелограммы P и R имеют по стороне, равной , то P~R (по лемме 2).
Рис. 3
Далее, S(Q)=S(P)=S(R) и параллелограммы Q и R имеют по стороне, равной c. Поэтому Q~R (по лемме 2). А тогда P~Q по лемме 1, что и требовалось доказать.
Лемма 4.Каждый треугольник равносоставлен с прямоугольником, одной из сторон которого можно выбрать любой заданный отрезок.
Доказательство. В треугольнике ABC проведем высоту AD на большую сторону и среднюю линию KL || BC. Построим прямоугольник P, одной стороной которого является BC, а другая сторона лежит на прямой KL. Очевидно, что P~∆ABC. По лемме 3 прямоугольник Р равносоставлен с Q вытекает, что ∆ABC~Q, что и требовалось доказать.
Теорема 1. Равновеликие многоугольные фигуры, равносоставлены.
Доказательство. Пусть многоугольные фигуры P и Q равновелики. Они составлены из некоторых треугольников. Пусть фигура Р составлена из треугольников Т1,…,Тk. Фиксируем некоторый отрезок АВ и построим на нем прямоугольник АВВ1А1=Р1, равновеликий треугольнику Т1 (т.е. ). По лемме 4 P1~T1. Затем на А1В1 строим прямоугольник Р2=А1В1В2А2, равновеликий треугольнику Т2 (рис. 4). По лемме 4 Р2~Т2. Продолжая эти построения, построим прямоугольник Р′=ААkBkB=P1+P2+…+Pk. Так как S(T)=S(P1),…,S(Tk)=S(Pk),то S(P)=S(P′). Поскольку P=T1+…+Tk, P ′=P1+…+Pk, то P~P′ (T1~P1,…,Tk~Pk).
Рис. 4
Проведем теперь аналогичное построение для фигуры Q , строя на АВ прямоугольник, равновеликий фигуре Q. Так как S(Q)=S(P′), то в итоге построим тот же самый прямоугольник P′. Но тогда по лемме 1 P~Q. Теорема доказана.
Равносоставленность позволяет находить множество решений задач и доказательств теорем. Благодаря свойствам равносоставленных фигур стало возможным применение задач на разрезание. А они, в свою очередь, позволяют сократить и упростить ход решений и доказательств, особенно, если речь идет о площадях [7].
Решение задач на разрезание предполагает владение специальными приемами, с помощью которых проводятся дополнительные линии, разбивающие фигуры на части.
Так, Г. Лингрен в своей книге: «Занимательные задачи на разрезание» предлагает выделить некоторые виды разрезания, опишем далее три базовых разрезания.
Разрезание типа S– преобразование одного параллелограмма в другой.
Сначала мы проводим разрез AB, равный по длине стороне второго параллелограмма. Затем, прикладываем часть С к противоположной стороне DE (рис. 5).
Рис. 5
В некоторых случаях полученные углы могут не совпадать с углами требуемого параллелограмма. Поэтому, мы проводим второй разрез DF (равный другой стороне искомого параллелограмма) и прикладываем часть G к противоположной верхней стороне (рис. 6).
Рис. 6
Разрезание типа P-сдвиг.
Сначала мы проводим разрез NO и сдвигаем часть Р вверх вправо вдоль линии разреза, до тех пор, пока точка О не попадет на продолжение правой стороны параллелограмма. Затем мы проводим разрез, вдоль пунктирной линии и вставляем полученный треугольник в выемку, расположенную ниже О. В итоге получили новый параллелограмм, стороны которого отличны от прежнего, но углы равны (рис. 7).
Рис. 7
Ступенчатое разрезание.
При использовании такого разрезания, прямоугольник размерностью 9×4 можно преобразовать в квадрат, при этом, число частей окажется равным не трем, а двум (рис. 8).
Рис. 8
Если часть X передвинуть на одну ступеньку вверх, поместив ее над частью Y, то сразу получим квадрат [14].
Таким образом, мы исследовали понятие многоугольника. Дали его определение, вывели свойства. Изучили определение площади многоугольника и требования, которым она должна соответствовать. Привели формулы площадей многоугольников (квадрата, прямоугольника, треугольника, параллелограмма и трапеции). Увидели связь между равносоставленностью и равновеликостью многоугольников, используя теорему Бояи-Гервина. С помощью разрезания можно разбить один многоугольник на множество, используя разрезы типа S-сдвиг, P-сдвиг, ступенчатое разрезание.
Практическая часть
Для решения задач на разрезание необходимо знать: основы планиметрии, теорию геометрии, геометрические фигуры (их признаки и свойства).
Исследуя материал, выделим следующие виды задач на разрезание:
танграм;
пентамино;
задачи на клетчатой бумаге;
разбиение плоскости;
задачи на площади фигур (равносоставленность);
превращение фигур;
задачи на разрезание в пространстве;
другие задачи на разрезание.
1. Танграм – головоломка, которая состоит из семи плоских геометрических фигур, полученных делением квадрата на семь частей. Существуют разновидности танграмов. Цель задачи – получение новых фигур (рис. 9).
Рис. 9
Задача 1.Сколько различных частей танграма потребуется, чтобы из них можно было составить прямоугольник.
Решение. Прямоугольник можно составить из следующих частей: из двух маленьких треугольников параллелограмма (рис. 10, а), из двух маленьких треугольников и квадрата (рис. 10, б), из пяти частей танграма (рис. 10, в).
Рис. 10
2. Пентамино состоит из плоских фигур, каждая из которых содержит пять одинаковых квадратов.
Задача 2. Сложить из всех фигурок, без перекрытий и зазоров, прямоугольник.
Решение. Каждая из 12 фигур состоит из пяти квадратов. Получается, что прямоугольник должен быть площадью 60 единичных квадратов. Это значит, что возможны прямоугольники 6×10, 5×12, 4×15 и 3×20
Для случая 6×10 эту задачу впервые решил в 1965 году Джон Флетчер. Существует 2339 различных укладок пентамино в прямоугольник 6×10.
Для прямоугольника 5×12 существует 1010 решений, для 4×15 –368 решений, а для 3×20 – всего 2 решения. В частности, существует 16 способов сложить два прямоугольника 5×6, из которых можно составить как прямоугольник 6×10, так и 5×12 (рис. 11).
Рис. 11
3. Задачи на клетчатой бумаге
Основываются на разрезании фигур:
а) на заданное число равных частей;
б) на заданное число равных и подобных ей фигур ;
в) определённым количеством прямых на максимально возможное число частей, не обязательно равных.
Задача 3. Квадрат включает в себя 16 клеток. Разбейте квадрат на две равные части таким образом, чтобы линия разреза шла по сторонам клеток [11].
Решение. Ломаная линия, которая делит квадрат на две равные части, симметрична относительно центра квадрата, это позволяет рисовать ломаную с двух концов. Например, если начало ломаной в точке A, то конец ее будет в точке B (рис. 12).
Рис. 12
Задача 4.Разрежьте фигуру на четыре равные по форме части (рис. 13).
Рис. 13
Решение. Маленькие фигуры будут состоять из трех клеток, Их всего два вида: «уголок» и прямоугольник 1×3 (рис. 14).
Рис. 14
Разбиение на плоскости. Включают в себя следующие задачи:
Сплошные разбиения прямоугольников на плитки прямоугольной формы. Разбиение прямоугольника называется сплошным (сплошным паркетом), если в нём нет «линий разрыва», т. е. любая линия, проходящая от стороны до стороны, пересекает, хотя бы одну плитку.
Задачи на составление паркетов.
Задаче о наиболее удобной укладке фигур в прямоугольнике или квадрате.
Задача 5. Покройте плоскость одинаковыми фигурами, изображенными на рисунке 15.
Рис. 15
Решение. Первый способ: «Паркет с линиями разрыва».
Сначала из двух фигур складываем прямоугольник, а ими затем покрываем всю плоскость (рис. 16).
Рис. 16
Второй способ: «Сплошной паркет».
Укладываем части плотно друг к другу, как показано на рисунке 17. Далее покрываем ими всю плоскость.
Рис. 17
Задача 6.Выложить плитками 2×1 пол в комнате размером 5×6.
Решение. Если пол в прямоугольной комнате p×q выложен плитками 2×1, то p ∙ q четно. И обратно: если p ∙ q четно, то пол можно выложить плитками 2×1.
Задача 7.Есть четыре квадрата со сторонами 1, восемь – со стороной 2, двенадцать – со стороной 3. Можно ли из них сложить один квадрат?
Решение. Должен получиться квадрат 12×12. По его периметру уложится двенадцать квадратов 3×3. Останется квадрат 6×6, по его периметру уложим восемь квадратов 2×2, и останется квадрат 2×2 – как раз четыре квадрата 1×1.
Задача 8.Можно ли прямоугольник 35×23 клетки разрезать без остатка на прямоугольники размером 5×7?
Решение. Это не возможно, потому что число 23 нельзя представить в виде суммы пятерок и семерок.
5. Задачи на площади фигур. Цель – доказать равносоставленность фигур, путем их разрезания.
Задача 9.Преобразовать один параллелограмм в другой, равновеликий ему параллелограмм [17].
Решение. Сначала проведем разрез AB, который будет равен длине стороне второго параллелограмма, далее мы прикладываем часть С к противоположной стороне DE.
У получившегося путем преобразований параллелограмма сторона AB и высота, опущенная на AB, имеют уже нужную нам длину, но углы могут еще не совпадать с углами требуемого параллелограмма. Поэтому мы проводим второй разрез DF (равный другой стороне искомого параллелограмма) и прикладываем часть G к противоположной, верхней стороне. При этом, у полученного параллелограмма ни одна из сторон и ни один из углов не совпадут со сторонами и углами исходного параллелограмма (рис. 18).
Рис. 18
Задача 10. Известно, что для некоторого выпуклого шестиугольника AB1CA1BC1 выполнены равенства
AB1=B1C, CA1=A1B, BC1=C1A,
∠ A+∠B+∠C=∠A1+∠B1+∠C1.
Докажите, что площадь треугольника A1B1C1 составляет половину площади всего шестиугольника.
Решение. Сумма всех углов шестиугольника равна 720̊, так, что ∠A+∠B+∠C=∠A1+∠B1+∠C1=360̊, получается, что из треугольников B1CA1,A1BC1 и C1AB1 можно сложить треугольник. Его стороны будут равны A1B1, B1C1,A1C1, то есть треугольник A1B1C1 распадается на треугольники, соответственно равные B1CA1, A1BC1, и C1AB1, ч.т.д.
6.Задачи на разрезание в пространстве.
Задача 11.Какое минимальное число плоских разрезов нужно сделать, чтобы разделить куб на 64 маленьких кубика? После каждого разреза разрешается перекладывать части куба как угодно.
Решение. После каждого разреза число частей может возрасти не больше, чем в два раза. После первого разреза куб распался на 2 части, затем после второго – на 4, затем эти четыре части складываем в столбик и разрезаем их плоским разрезом, получается 8 частей, затем 16, затем 32, и, наконец, 64.
Ответ: 6 разрезов.
Другие задачи на разрезание
Задача о разрезанном треугольнике – известная оптическая иллюзия. Два прямоугольных треугольника составлены из одинаковых частей 13×15, но в одном из них есть дыра размером 1×1.
Задача 12.Треугольник составлен из четырех частей. После того, как переставили части, визуально сохранив изначальные пропорции, внутри треугольника появился квадрат, который не занят ни одной частью (рис. 19).
Рис. 19
Решение. Синий и красный треугольники имеют неравные углы, что визуально незаметно из-за слишком малой разницы. Поэтому на первом рисунке создаётся излом внутрь, а на втором – наружу. Это можно проверить вычислениями.
Площадь каждого треугольника 13×5 не равна площади частей, из которых они составлены.
«Гипотенуза» на самом деле является ломаной линией. Действительно, общая площадь четырёх частей (жёлтой, красной, синей и зелёной) равна кв. ед., а площадь треугольника 13×5 равна 32,5 кв. ед. Отношение длин катетов синего треугольника 5:2, а красного – 8:3, поэтому эти треугольники не являются подобными, а значит, имеют разные углы. Гипотенузы в обоих треугольниках 13×5 на самом деле являются ломаными линиями. Если наложить треугольники 13×5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь.
Задача 13. На листе бумаги нарисовали произвольный многоугольник. Можно ли так сложить лист бумаги, чтобы вырезать многоугольник одним прямолинейным разрезом?
Решение. Рассмотрим простейший случай – произвольный треугольник. Проведём биссектрисы и из точки их пересечения опустим перпендикуляры на стороны треугольника (рис. 20).
Рис. 20
По этим лучам и будем сгибать лист бумаги. Все границы треугольника – стороны – оказались лежащими на одной прямой. Сделаем вдоль неё прямолинейный разрез. Развернём отрезанный уголок – это наш изначальный треугольник (рис. 21).
Рис. 21
Если развернуть оставшуюся часть листа, то видно, что ничего лишнего не вырезано — дырка тоже имеет вид изначального треугольника (рис. 22).
Рис. 22
Задача 14. Сложить лист бумаги так, чтобы можно было вырезать многоугольник одним прямолинейным разрезом?
Решение. Нарисуем пятиконечную звезду. Это невыпуклый многоугольник с 10 вершинами. Однако в этом случае задача облегчается симметричностью звезды.
Проведём лучи, исходящие из центра и проходящие через вершины. По этим лучам сложим лист бумаги (рис. 23).
Рис. 23
Отрежем уголок. После разворачивания получим вырезанную звезду и дырку в виде звезды [25].
Таким образом, в практической части исследования рассмотрены 8 видов задач на разрезание.
Заключение
Исследуя теоретический вопрос о системе задач на разрезания многоугольников, а также методы решения этих задач, мы поставили цель – систематизировать данный материал и найти возможность его применения.
За основу было взято понятие «многоугольник», мы дали определение данного понятия, рассмотрели его свойства, выяснили, что такое площадь многоугольника. Далее мы ввели понятия равновеликости и равносоставленности, рассмотрели площади некоторых многоугольников, привели доказательство теоремы Бояи-Гервина. Затем мы привели примеры некоторых типов разрезаний.
В практической части работы мы выделили некоторые виды задач на разрезание и рассмотрели их решение.
В совокупности мы пришли к выводу, что данные задачи составляют основу для решения многих практических задач, а приемы их решения используются в доказательстве серьезных математических утверждений. Они имеют различный уровень трудности, тем самым помогая развивать комбинаторные навыки, формировать геометрические представления о разнообразном материале, проявлять свою смекалку, интуицию, способность творчески мыслить.
Список использованных источников
Александров, А.Д. Геометрия [Текст]: Учеб. Пособие для 8 кл. с углубл. Изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2008. – 240 с.
Атанасян, Л.С. Геометрия, 7–9 [Текст]: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – М.: Просвещение, 2008. – 384 с.
Балк, М.Б. Математика после уроков [Текст] / М.Б Балк, Г.Д. Балк. – М.: Просвещение, 1971 – 360 с.
Барр, С. Т. Россыпи головоломок [Текст] / С. Т. Барр. – М.: Мир, 1987. – 207 с.
Болтянский, В.Г. Равновеликие и равносоставленные фигуры [Текст] / В.Г. Болтянский. – М.: 1956. – 241 с.
Бугаенко, В.О. Математический кружок. 9 класс. Методическая разработка вечернего отделения МММФ [Текст] / В.О. Бугаренко. – М.: Изд–во механико–математического факультета МГУ и центра прикладных исследований, 2011. – 72 с.
Вернер, А.Л. Геометрия. Ч.1 [Текст]: учеб. пособие для физико-мат. фак. пед. ин-тов / А.Л. Вернер, Б.Е. Кантор, С.А. Франгулов. – СПб.: Спец.лит., 1997. – 351 с.
Гарднер, М. Есть идея! [Текст] / М. Гарднер. – М.: Мир, 1982. – 367 с.
Григорьева, Г.И. Подготовка школьников к олимпиадам по математике: 5 – 6 классы [Текст]: Метод. Пособие / Г.И. Григорьева. – М.: Глобус, 2009. – 287 с.
Дьюдени, Г.Э. 250 головоломок [Текст] / Сост. и ред. амер. изд. М. Гарднер. Пер. с анг. Ю.Н. Сударева. – М.: Мир, 1975. – 426 с.
Екимова, М.А. Задачи на разрезание [Текст] / М.А. Екимова, Г.П. Кукин. – М.: МЦНМО, 2014. – 120 с.
Кордемский, Б.А. Удивительный квадрат [Текст] / Б. А. Кордемский. – М.: Книга по Требованию, 2012. – 158 с.
Жарковская, Н.М. Геометрия клетчатой бумаги. Формула Пика [Текст] / Н.М. Жаровская, Е.А. Рисс // Математика, 2009, № 17, с. 24–25.
Лингрен, Г. Занимательные задачи на разрезание [Текст]. Пер. с анг. Ю.Н. Сударева. Под ред. и с послесл. И.М. Яглома. – М.: Мир, 1977. – 341 с.
Погорелов, А.В. Геометрия. 7 – 9 кл [Текст] / А.В. Погорелов. – М.: Просвещение, 2004. – 132 с.
Прасолов, В.В. Задачи по планиметрии. – 2-е изд. – Часть II [Текст] / В.В. Прасолов. – М.: Наука, 2007. –87 с.
Савин, А.П. Задачи на разрезание [Текст] / А.П. Савин // Квант. — 1987. – № 7.
Савин, А.П. Задачи на разрезание [Текст] / А.П. Савин // Квант. – 1987. – № 8
Смирнова, И.М. Геометрия. 7 – 9 классы [Текст]: учеб. Для общеобразоват. Учреждений –2-е изд., испр / И.М. Смирнова, В.А. Смирнов. – М: Мнемозина, 2007. – 376 с.
Смирнова, И.М. Геометрия на клетчатой бумаге [Текст] / И.М. Смирнова, В.А. Смирнов. – М.: Чистые пруды, 2009. – 241 с.
Чулков, П.В Математика: Школьные олимпиады [Текст] / П.В. Чулков. – М: Энас, 2004. – 88 с
Шарыгин И.Ф. Геометрия. 7-9 кл [Текст] / И.Ф. Шарыгин. – М.: Дрофа, 2015. – 464 с
Шарыгин И.Ф. Математика. Наглядная геометрия 5–6 классы. 2-е изд [Текст] / И.Ф. Шарыгин, Л.Н. Ерганжиева. – М: 2015. – 192 с.
Шашкин, Ю.А. Паркеты [Текст] / Ю.А. Шашкин // Миф. – 1998. – № 3. – С. 99.
Фонд «Математические этюды»: [Электронный ресурс]. М., 2002–2017. – Режим доступа: http://www.etudes.ru, свободный. (Дата обращения: 17. 03. 2017).






 ? Гарантировано ведь вроде лишь
? Гарантировано ведь вроде лишь  — ведь на каждом шаге бог весть, через сколько подшагов очередное ухо встретится.
— ведь на каждом шаге бог весть, через сколько подшагов очередное ухо встретится. ). Флажки с валидностью собираются в кольцо. При удалении валидной вершины, надо удалить из кольца три значения и вставить два. Эти два надо вычислить. На это уйдёт
). Флажки с валидностью собираются в кольцо. При удалении валидной вершины, надо удалить из кольца три значения и вставить два. Эти два надо вычислить. На это уйдёт  . В совокупности, на модификацию кольца тоже уйдёт
. В совокупности, на модификацию кольца тоже уйдёт  . Теоретически триангулировать можно за линейное время.
. Теоретически триангулировать можно за линейное время.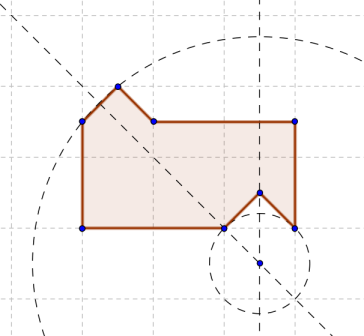
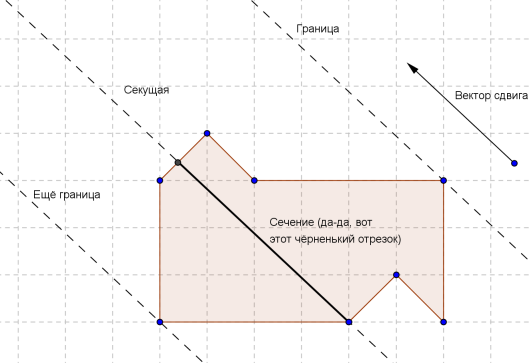

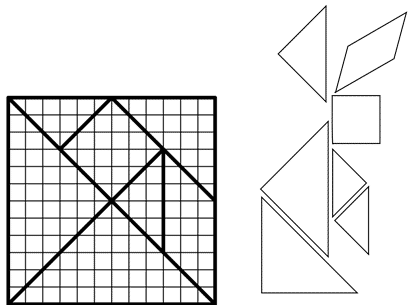
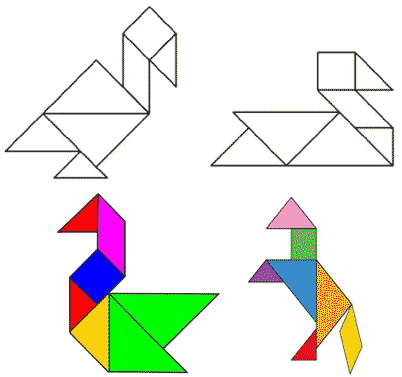
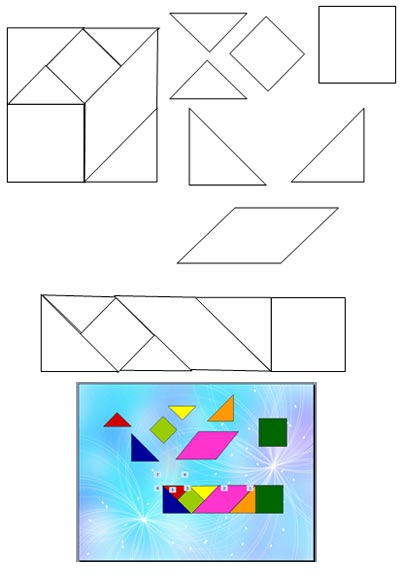
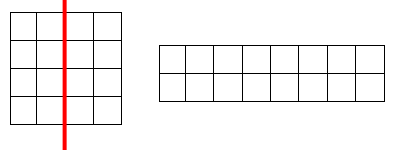
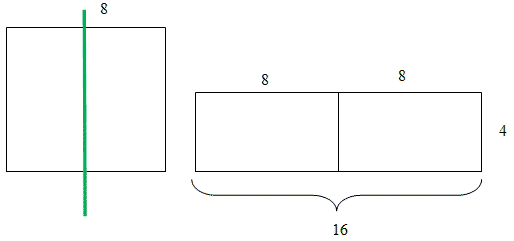
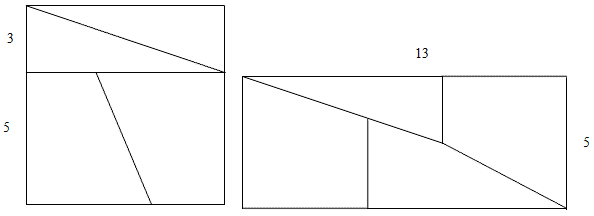
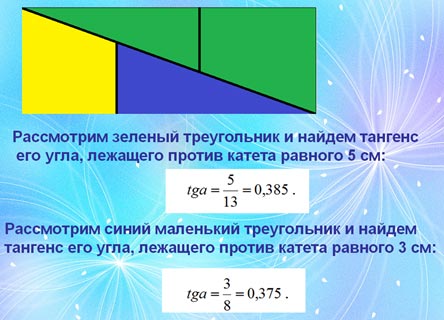
 + 1
+ 1