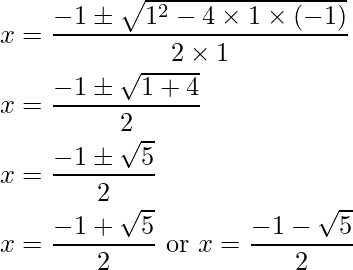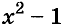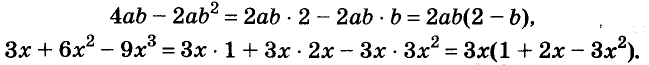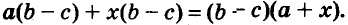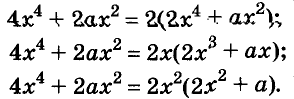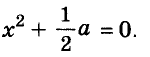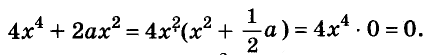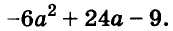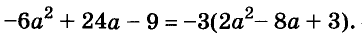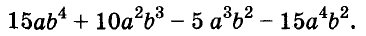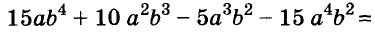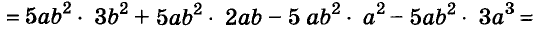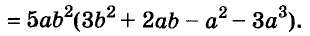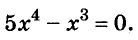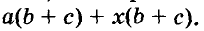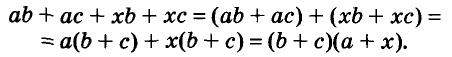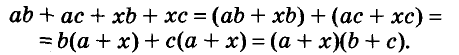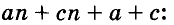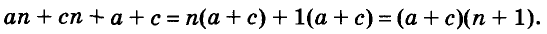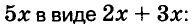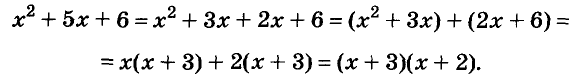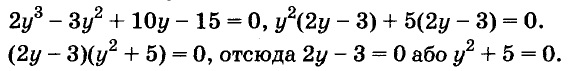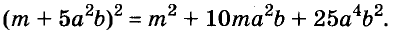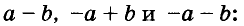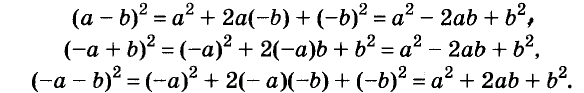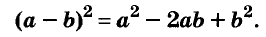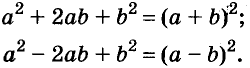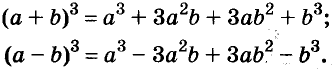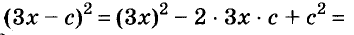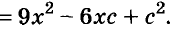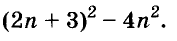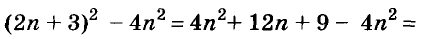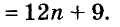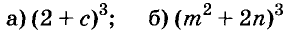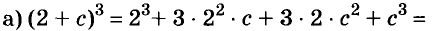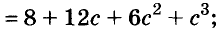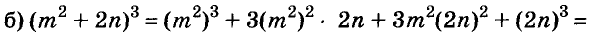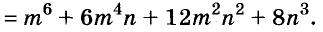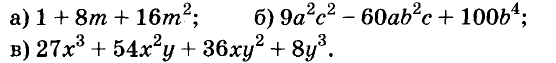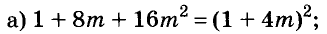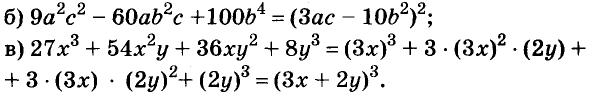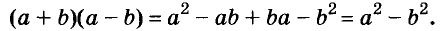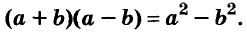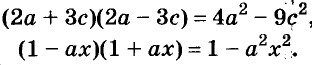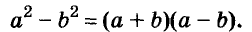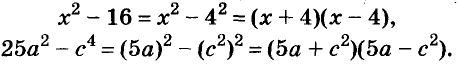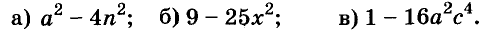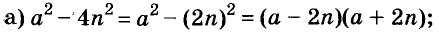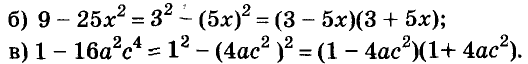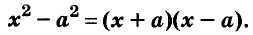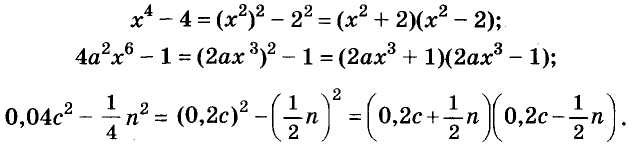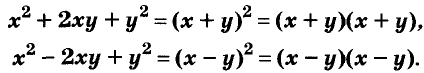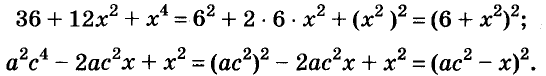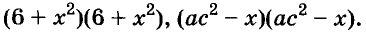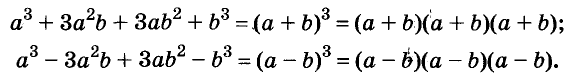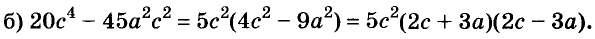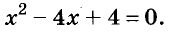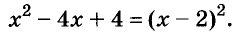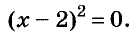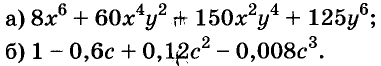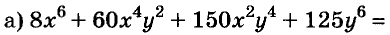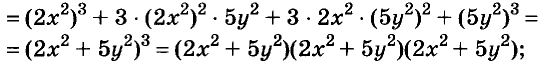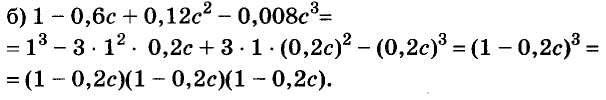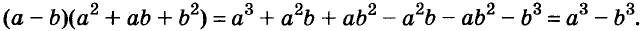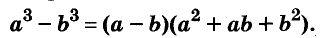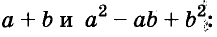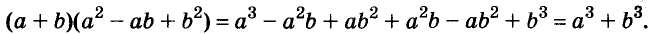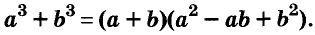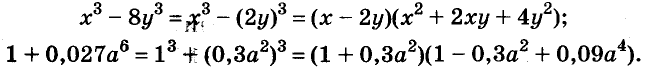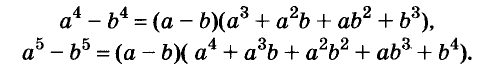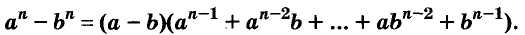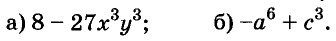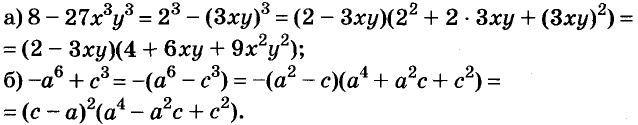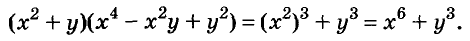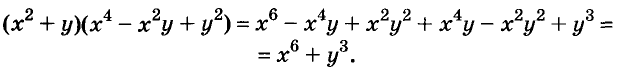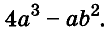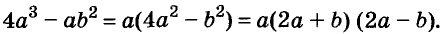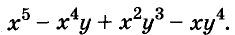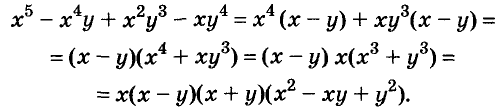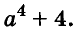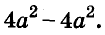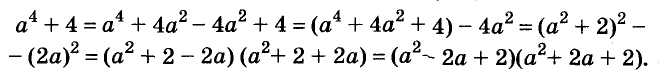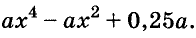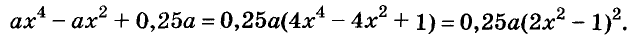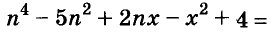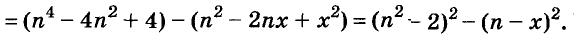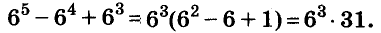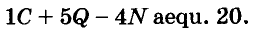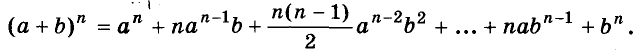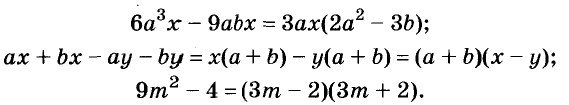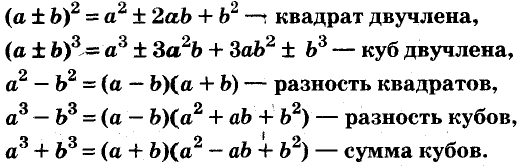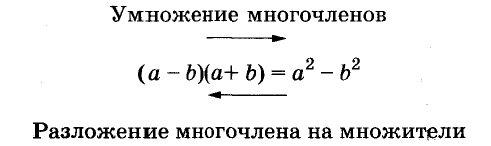Как найти разложение полиномов

A basic algebraic concept called factoring polynomials involves breaking down a polynomial equation into simpler parts. Factoring can be used to solve equations, simplify complicated expressions, and locate the roots or zeros of polynomial functions. 

In several fields of mathematics, including engineering, physics, and computer science, the ability to factor is a crucial skill. Finding the common factors, or roots, of the equation and breaking them down into a set of simpler expressions are the general steps involved in factoring a polynomial. 

What is Factoring of Polynomials?

The process by which we find the constituent factors of a higher-degree polynomial is called factoring polynomials.

For example, by multiplying x+2 and x -1 we get x²+x-2, where x + 2 and x -1 are the factors of the expression x²+x-2.

Thus, finding these factors from a given expression is called Factoring of Polynomial.

By the fundamental theorem of algebra, we know that any polynomial of degree n has n roots, either real or complex. Thus, it also has n factors as well. as every unique root gives a unique factor to the provided expression. 

Steps for Factoring a Polynomial 

For factorizing any polynomial, we need to follow three steps as follows:

• Firstly, factor out the common factor of all the terms of the given polynomial.
• Secondly, choose the best technique for factoring polynomials.
• And last, write all the factors as the product, as it gives the provided polynomial.

Techniques for Factoring Polynomials

Common Factors 

The first method is the common factors method, in which if there is a common factor for each term in the polynomial, we factor that common term out and write the remaining polynomial.

The first approach is known as the “common factors method,” in which the common factors of each term are factored out in the polynomial.

Example: What are the factors of 3x² + 6x +12?

Solution:

Let f(x) = 3x² + 6x +12

As 3 is present in each term as expression can be rewritten as

f(x) =3x²+3×2x-3×4

⇒ f(x) = 3(x²+2x+4)

Thus, factors of the 3x² + 6x +12 are 3 and x² + 2x +4.

Grouping Method 

This method factors polynomials by grouping terms with two or more terms together and finding the greatest common factor for each grouping. Once the common factors for each grouping were found, each group had the same factor.

Example: Factorize the expression ax²+7abx+ax+7ab as a and b are some real numbers.

Solution:

Let f(x) = ax²+7abx+ax+7ab

Grouping two elements at a time,

⇒ f(x) = (ax²+ax)+(7abx+7ab)

⇒ f(x) = ax(x+1)+7ab(x+1)

⇒ f(x) = (ax+7ab)(x+1)

Thus, ax+7ab and x + 1 are the required factors.

Splitting the Middle Term 

Using this technique; the quadratic polynomials with a leading coefficient of 1, are factorized. This method is highly useful since higher-degree polynomials are frequently converted to quadratic polynomials using the factor theorem.

Step 1: f(x) = x²+(a+b)x+ab 

Step 2: f(x)= x²+ax+bx+ab 

Step 3: f(x)=  x(x+a)+b(x+a) 

Step 4: f(x)= (x+a)(x+b)

So all quadratic polynomial of form x²+(a+b)x+ab, can be factorize using Splitting the Middle Term method,

Example: Factorize x²+5x+6.

Solution:

Let f(x) = x²+5x+6

f(x)= x² + (2+3)x+2×3 

⇒ f(x)= x²+2x+3x+2×3 

⇒ f(x)= x(x+2)+3(x+2) 

⇒ f(x)= (x+2)(x+3)  

Thus, x+2 and x+3 are the factors of the expression x²+5x+6.  

Algebraic Identities 

There are numerous Algebraic Identities that can be used to factorize different kinds and forms of polynomials. The following are some of the most commonly used identities:

• a²+b²+2ab = (a+b)2 = (a+b)(a+b)
• a²+b²-2ab = (a-b)² = (a-b)(a-b)
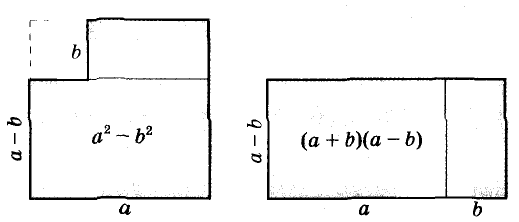
• a² – b² = (a + b)(a – b)
• a²+b²+c²+2ab+2bc+2ca = (a+b+c)² = (a+b+c)(a+b+c)
• a³ – b³ = (a – b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² – ab + b²)
• a⁴ – b⁴ = (a² + b²)(a + b)(a – b)

Example: Factorize 16x⁴ – 9

Solution:

Let f(x) = 16x⁴ – 81

⇒ f(x) =  (2x)⁴ – (3)⁴

⇒ f(x) =  [(2x)²+3²](2x+3)(2x-3)

⇒ f(x) =  (4x²+9)(2x+3)(2x-3)

Thus, 4x²+9, 2x+3 and 2x-3 are the factors of expression 16x⁴ – 9.

Long Division Method

Long Division is a method for dividing polynomials similar to numbers, where a higher-degree polynomial can be divided by the lower-degree polynomial to find the quotient and remainder. Using long division and the factor and remainder theorem together, we can factorize any polynomial with an integer coefficient easily.

For example, Long division of  x³-5x²+9x-5 by x -1 is shown in the following illustration.

Factor Theorem

Factor Theorem states that for any polynomial f(x) = 0,  x – a is the factor of f(x) if and only if x = a is the zero of the polynomial.

Example: Use the Factor Theorem to determine whether x – 3 is a factor of f(x) = x³ – 6x² + 11x – 6.

Solution:

By Factor Theorem we know, x – 3 is a factor of f(x) when f(3) = 0. 

f(3) = 3³ – 6(3)² + 11(3) – 6 

⇒ f(3)= 27 – 54 + 33 – 6 = 0

Since f(3) = 0, thus x – 3 is a factor of f(x).

Reminder Theorem

Remainder Theorem states that if x-a is the factor of a polynomial f(x)=0 then f(a) is the reminder of the polynomial when divided by x-a.

Example : Find the remainder when f(x) = 2x³ + 3x² – 5x + 2 is divided by (x – 2).

Solution: 

To find the remainder, we need to evaluate f(x) at x = 2, since the divisor is (x – 2). 

Therefore, the remainder is:

f(2) = 2(2)³+ 3(2)² – 5(2) + 2 

f(2) = 16 + 12 – 10 + 2 = 20

Therefore, the remainder when f(x) is divided by (x – 2) is 20.

With the help of both the above-mentioned theorems and the long division method, most of the polynomials can be factorized. One of the examples is as follows

Example: f(x) = x³-6x²+3x+10

Solution:

Step 1: Consider all the divisors of the constant part of the polynomial and out of those divisors one should satisfy the given polynomial.

Constant part in the polynomial is 10 whose divisors are ±1, ±2, ±5.

Now, f(1) = 1 – 6 +3 +10 = 8 ≠ 0, So x – 1 is not a factor of f(x).

f(-1) = -1 – 6 -3 +10 = 0, thus x+1 is factor of f(x).

Step 2: Divide the polynomial f(x) with the newly found factor i.e., divide f(x) using long division by x+1.

So, f(x) = (x+1)(x²-7x+10)

Step 3: Factorize the remaining part using Splitting the Middle Term,

f(x) = (x+1)(x²-7x+10)

⇒ f(x) = (x+1)(x²-2x-5x+10)

⇒ f(x) = (x+1)[x(x-2)-5(x-2)]

⇒ f(x) = (x+1)(x-2)(x-5)

Thus, x+1, x-2 and x-5 are the factors of the polynomial f(x) = x³-6x²+3x+10

Sridharacharya Formula 

For any quadratic equation ax²+bx+c =0, its two roots can be calculated using Sridharacharya Formula

and using factor theorem,  and  are the factors of the quadratic polynomial x²+(b/a)x+(c/a) 

Related Resources

• Types of Polynomials
• Linear Equations in One Variable
• Quadratic Equations

Solved Examples of Factoring Polynomial

Example 1: Factorize 7x² – 21x.

Solution:

Let f(x) = 7x² – 21x

As 7 and x is common in each term of the given polynomial

f(x) = 7x(x -3)

Hence, 7x and x – 3 are the factors of the given polynomial.

Example 2: What are the factors of y²-8y+7?

Solution:

Let g(y) = y²-8y+7

⇒ g(y) = y²-8y+7

⇒ g(y) = y²-7y-y+7

⇒ g(y) = y(y-7)-(y-7)

⇒ g(y) = (y-7)(y-1)

Thus, y-7 and y-1 are the factors of y²-8y+7.

Example 3: Factorize x²+x-1.

Solution:

Comparing x²+x-1 with the general quadratic expression ax²+bx+c, we get

a=1, b=1 and c=-1 

Using Sridharacharya Formula, 

Thus, using factor theorem  and   are the factors of the given polynomial.

Example 4: Factorize x³-5x²+9x-5.

Solution:

Let f(x) = x³-5x²+9x-5

As constant part is 5, and it’s divisors are  ±1, ±5.

f(1) = 1 – 5 +9 -5 = 0

Thus, x-1 is factor of f(x).

Now, dividing f(x) using long division by x-1

Thus, f(x) = (x-1)(x²-4x+5)

As x²-4x+5 can’t be factored further,

So, x-1 and x²-4x+5 are the required factors of x³-5x²+9x-5.

FAQs on Factoring Polynomial

Question 1: What is factoring a polynomial?

Answer:

Factoring a polynomial is the process of expressing a higher-degree polynomial as the product of lower-degree polynomials. For example, the polynomial f(x) = 7x² – 21x can be factorized as 7x(x-3), where 7, x, and x-3 are the factors of the given polynomial.

Question 2: What are the methods for factoring polynomials?

Answer: 

There are a lot of methods for factoring polynomials, including factoring by grouping, factoring using the Sridharacharya Formula, factoring quadratic polynomials using the splitting the middle term method, using algebraic identities to factorize different polynomials, etc.

Question 3: What is the difference between a factor and a root of a polynomial?

Answer: 

Factor is the lower-degree polynomial that can evenly divide the given polynomial and leave no remainder.

On the other hand, the root, or zero, of a polynomial is the real number for which the value of the polynomial becomes zero.

For example, for the polynomial f(x) = x²+ 2x+1 = (x + 1)², (x + 1) is the factor of the polynomial, and x = -1 is the root of the polynomial.

Question 4: How can you check if a factor is correct?

Answer: 

If the factors of the given polynomial are correct, then the product of all the factors is the polynomial itself. In other words, by multiplying all the factors of a polynomial together, we end up with the polynomial itself.

Question 5: How to Factorize Polynomials in 3 Degree?

Answer:

Follow the following steps to factorize a three-degree polynomial.

Step 1: For polynomial f(x) find its factor x – a such that f(a) = 0 by the hit and trial method.

Step 2: Using the long division method divide f(x) by x – a to get a two-degree polynomial.

Step 3: Factorize the two-degree polynomial obtained by the methods as discussed in the article.

Now, the three-degree polynomial f(x) is factorized.

План урока:

Вынесение общего множителя за скобки

Способ группировки

Применение разложение многочленов на множители

Вынесение общего множителя за скобки

В предыдущем уроке мы изучили умножение многочлена на одночлен. Например, произведение монома a и полинома b + c находится так:

a(b + c) = ab + bc

Однако в ряде случае удобнее выполнить обратную операцию, которую можно назвать вынесением общего множителя за скобки:

ab + bc = a(b + c)

Например, пусть нам надо вычислить значение полинома ab + bc при значениях переменных a = 15,6, b = 7,2, c = 2,8. Если подставить их напрямую в выражение, то получим

ab + bc = 15.6 * 7.2 + 15.6 * 2.8

что, скорее всего, не получится посчитать в уме. Если же вынести a за скобки, то получим иную запись:

ab + bc = a(b + c) = 15.6 * (7.2 + 2.8) = 15.6 * 10 = 156

В данном случае мы представили полином ab + bc как произведение двух множителей: a и b + с. Данное действие называют разложением многочлена на множители.

При этом каждый из множителей, на которые разложили многочлен, в свою очередь может быть многочленом или одночленом.

Рассмотрим полином 14ab – 63b². Каждый из входящих в него одночленов можно представить как произведение:

14ab = 7b * 2a

63b² = 7b * 9b

Видно, что у обоих многочленов есть общий множитель 7b. Значит, его можно вынести за скобки:

14ab — 63b² = 7b*2a — 7b*9b = 7b(2a-9b)

Проверить правильность вынесения множителя за скобки можно с помощью обратной операции – раскрытия скобки:

7b(2a — 9b) = 7b*2a — 7b*9b = 14ab — 63b²

Важно понимать, что часто полином можно разложить несколькими способами, например:

5abc + 6bcd = b(5ac + 6cd) = c(5ab + 6bd) = bc(5a + 6d)

Обычно стремятся вынести, грубо говоря, «наибольший» одночлен. То есть раскладывают полином так, чтобы из оставшегося полинома больше нечего нельзя было вынести. Так, при разложении

5abc + 6bcd = b(5ac + 6cd)

в скобках осталась сумма одночленов, у которых есть общий множитель с. Если же вынести и его, то общих множителей в скобках не останется:

b(5ac + 6cd) = bc(5a + 6d)

Разберем детальнее, как находить общие множители у одночленов. Пусть надо разложить сумму

8a³b⁴ + 12a²b⁵v + 16a⁴b³c¹⁰

Она состоит из трех слагаемых. Сначала посмотрим на числовые коэффициенты перед ними. Это 8, 12 и 16. В 3 уроке 6 класса рассматривалась тема НОД и алгоритм его нахождения.Это наибольший общий делитель.Почти всегда его можно подобрать устно. Числовым коэффициентом общего множителя как раз будет НОД числовых коэффициентов слагаемых полинома. В данном случае это число 4.

Далее рассмотрим буквенную часть. В ней должны быть переменные, которые есть во ВСЕХ слагаемых. В данном случае это a и b, а переменная c общей не является, так как не входит в первое слагаемое.

Далее смотрим на степени у этих переменных. В общем множителе у букв должны быть минимальные степени, которые встречаются в слагаемых. Так, у переменной a в многочлене степени 3, 2, и 4 (минимум 2), поэтому в общем множителе будет стоять a². У переменной b минимальная степень равна 3, поэтому в общем множителе будет стоять b³:

8a³b⁴ + 12a²b⁵v + 16a⁴b³c¹⁰ = 4a²b³(2ab + 3b²c + 4a²c¹⁰)

В результате у оставшихся слагаемых 2ab, 3b²c, 4a²c¹⁰ нет ни одной общей буквенной переменной, а у их коэффициентов 2, 3 и 4 нет общих делителей.

Выносить за скобки можно не только одночлены, но и многочлены. Например:

x(a-5) + 2y(a-5) = (a-5)(x+2y)

Еще один пример. Необходимо разложить выражение

5t(8y — 3x) + 2s(3x — 8y)

Решение. Напомним, что знак минус меняет знаки в скобках на противоположные, поэтому

-(8y — 3x) = -8y + 3x = 3x — 8y

Значит, можно заменить (3x – 8y) на – (8y – 3x):

5t(8y — 3x) + 2s(3x — 8y) = 5t(8y — 3x) + 2*(-1)s(8y — 3x) = (8y — 3x)(5t — 2s)

Ответ: (8y – 3x)(5t – 2s).

Запомним, что вычитаемое и уменьшаемое можно поменять местами, если изменить знак перед скобками:

(a — b) = — (b — a)

Верно и обратное: минус, уже стоящий перед скобками, можно убрать, если одновременно переставить местами вычитаемое и уменьшаемое:

Этот прием часто используется при решении заданий.

Способ группировки

Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение

ab — 5a + bc — 5c

Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:

ab — 5a + bc — 5c = (ab — 5a) + (bc — 5c) = a(b — 5) + c(b — 5)

Теперь можно вынести выражение b – 5:

a(b — 5) + c(b — 5) = (b — 5)(a + c)

Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.

Пример. Разложим полином 6xy + ab– 2bx– 3ay.

Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:

6xy + ab — 2bx — 3ay = 6xy — 2bx + ab — 3ay = (6xy — 2bx) + (ab — 3ay) = 2x(3y — b) + a(b — 3y)

Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:

(b — 3y) = — (3y — b)

Используем эту замену:

2x(3y — b) + a(b — 3y) = 2x(3y — b) — a(3y — b) = (3y — b)(2x — a)

В результате получили тождество:

6xy + ab — 2bx — 3ay = (3y – b)(2x – a)

Ответ: (3y – b)(2x – a)

Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме

x² — 3xy + xz + 2x — 6y + 2z

можно сгруппировать первые три и последние 3 одночлена:

x² — 3xy + xz + 2x — 6y + 2z = (x² — 3xy + xz) + (2x — 6y + 2z) = x(x — 3y + z) + 2(x — 3y + z) = (x + 2)(x — 3y + z)

Теперь рассмотрим задание повышенной сложности

Пример. Разложите квадратный трехчлен x²– 8x +15.

Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:

-8x = -3x — 5x

Тогда исходный трехчлен можно представить следующим образом:

x² — 8x + 15 = x² — 3x — 5x + 15

Сгруппируем слагаемые:

x² — 3x — 5x + 15 = (x² — 3x) + (- 5x + 15) = x(x — 3) — 5(x — 3) = (x — 5)(x — 3)

Ответ: (x– 5)(х – 3).

Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:

(x + a)(x + b) = x² + xa + xb + ab = x² + (a + b)x + ab

Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x²– 8x +15, надо подобрать подходящие коэффициенты при переменных:

С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда

(x — 3)(x — 5) = x² * 8x + 15

в чем можно убедиться, раскрыв скобки.

Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:

x² * 8x + 15 = (2x — 6)(0.5x — 2.5)

Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:

(2x — 6)(0.5x — 2.5) = (x — 3) * 2 * (0.5x — 2.5) = (x — 3)(x — 5)

В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,

x² — x + 1

невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.

Применение разложение многочленов на множители

Разложение полинома на множители может упростить выполнение некоторых операций. Пусть необходимо выполнить вычисление значения выражения

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹ 

Вынесем число 2, при этом степень каждого слагаемого уменьшится на единицу:

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹ = 2(1 + 2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ )

Обозначим сумму

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸

за х. Тогда записанное выше равенство можно переписать:

x + 2⁹ = 2(1 + x)

Получили уравнение, решим его (см. урок уравнения):

x + 2⁹ = 2(1 + x)

x + 2⁹ = 2 + 2x

2x — x = 2⁹ — 2

x = 512 — 2 = 510

Теперь выразим искомую нами сумму через х:

2 + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ + 2⁸ + 2⁹ = x + 2⁹ = 510 + 512 = 1022

При решении этой задачи мы возводили число 2 только в 9-ую степень, а все остальные операции возведения в степень удалось исключить из вычислений за счет разложения многочлена на множители. Аналогично можно составить формулу вычисления и для других подобных сумм.

Теперь вычислим значение выражения

38.4² — 61.6 * 29.5 + 61.6 * 38.4 — 29.5 * 38.4

Посчитать это напрямую достаточно сложно. Однако можно применить метод группировки:

38.4² — 61.6 * 29.5 + 61.6 * 38.4 — 29.5 * 38.4 = 38.4² — 29.5 * 38.4 + 61.6 * 38.4 — 61.6 * 29.5 = 38.4(38.4 — 29.5) + 61.6(38.4 — 29.5) = (38.4 + 61.6)(38.4 — 29.5) = 8.9*100 = 890

Далее посмотрим, как можно использовать разложение полинома для доказательства делимости чисел. Пусть требуется доказать, что выражение

81⁴ — 9⁷ + 3¹²

делится на 73. Заметим, что числа 9 и 81 являются степенями тройки:

9 = 3²

81 = 9² = (3²)² = 3⁴

Зная это, произведем замену в исходном выражении:

81⁴ — 9⁷ + 3¹² = (3⁴)⁴ — (3²)⁷ + 3¹² = 3¹⁶ — 3¹⁴ + 3¹²

Вынесем 3¹²:

3¹⁶ — 3¹⁴ + 3¹² = 3¹²(3⁴ — 3² + 1) = 3¹² * (81 — 9 + 1) = 3¹² * 73

Произведение 3¹²•73 делится на 73 (так как на него делится один из множителей), поэтому и выражение 81⁴ – 9⁷ + 3¹² делится на это число.

Вынесение множителей может использоваться для доказательства тождеств. Например, докажем верность равенства

(a² + 3a)² + 2(a² + 3a) = a(a + 1)(a + 2)(a + 3)

Для решения тождества преобразуем левую часть равенства, вынеся общий множитель:

(a² + 3a)² + 2(a² + 3a) = (a² + 3a)(a² + 3a) + 2(a² + 3a) = (a² + 3a)(a² + 3a + 2)

Далее произведем замену 3a = 2a + a:

(a² + 3a)(a² + 3a + 2) = (a² + 3a)(a² + 2a + a + 2) = (a² + 3a)((a² + 2a) + (a + 2) = (a² + 3a)(a(a + 2) + (a + 2)) = (a² + 3a)(a + 1)(a + 2) = a(a + 3)(a + z)(a + 2) = a(a + 1)(a + 2)(a + 3)

Ещё один пример. Докажем, при любых значениях переменных x и у выражение

(x — y)(x + y) — 2x(x — y)

не является положительным числом.

Решение. Вынесем общий множитель х – у:

(x — y)(x + y) — 2x(x — y) = (x — y)(x + y — 2x) = (x — y)(y — x)

Обратим внимание, что мы получили произведение двух похожих двучленов, отличающихся лишь порядком букв x и y. Если бы мы поменяли местами в одной из скобок переменные, то получили бы произведение двух одинаковых выражений, то есть квадрат. Но для того, чтобы поменять местами x и y, нужно перед скобкой поставить знак минус:

(x — y) = -(y — x)

Тогда можно записать:

(x — y)(y — x) = -(y — x)(y — x) = -(y — x)²

Как известно, квадрат любого числа больше или равен нулю. Это относится и к выражению (у – х)². Если же перед выражением стоит минус, то оно должно быть меньше или равным нулю, то есть не является положительным числом.

Разложение полинома помогает решать некоторые уравнения. При этом используется следующее утверждение:

Если в одной части уравнения стоит ноль, а в другой произведение множителей, то каждый из них следует приравнять нулю.

Пример. Решите уравнение (s – 1)(s + 1) = 0.

Решение. В левой части записано произведение мономов s – 1 и s + 1, а в правой – ноль. Следовательно, нулю должно равняться или s – 1, или s + 1:

(s — 1)(s + 1) = 0

s — 1 = 0 или s + 1 = 0

s = 1 или s = -1

Каждое из двух полученных значений переменной s является корнем уравнения, то есть оно имеет два корня.

Ответ: –1; 1.

Пример. Решите уравнение 5w² – 15w = 0.

Решение. Вынесем 5w:

5w² – 15w = 0

5w(w — 3) = 0

Снова в левой части записано произведение, а в правой ноль. Продолжим решение:

5w = 0 или (w — 3) = 0

w = 0 или w = 3

Ответ: 0; 3.

Пример. Найдите корни уравнения k³– 8k² + 3k– 24 = 0.

Решение. Сгруппируем слагаемые:

k³– 8k² + 3k– 24 = 0

(k³– 8k²) + (3k– 24) = 0

k²(k — + 3(k — = 0

(k³ + 3)(k — = 0

k² + 3 = 0 или k — 8 = 0

k² = -3 или k = 8

Заметим, что уравнение k² = – 3 решения не имеет, так как любое число в квадрате не меньше нуля. Поэтому единственным корнем исходного уравнения является k = 8.

Ответ: 8.

Пример. Найдите корни уравнения

(2u — 5)(u + 3) = 7u + 21

Решение: Перенесем все слагаемые в левую часть, а после сгруппируем слагаемые:

(2u — 5)(u + 3) = 7u + 21

(2u — 5)(u + 3) — 7u — 21 = 0

(2u — 5)(u + 3) — 7(u + 3) = 0

(2u — 5 — 7)(u + 3) = 0

(2u — 12)(u + 3) = 0

2u — 12 = 0 или u + 3 = 0

u = 6 или u = -3

Ответ: – 3; 6.

Пример. Решите уравнение

(t² — 5t)² = 30t — 6t²

Решение:

(t² — 5t)² = 30t — 6t²

(t² — 5t)² — (30t — 6t²) = 0

(t² — 5t)(t² — 5t) + 6(t² — 5t) = 0

(t² — 5t)(t² — 5t + 6) = 0

t² — 5t = 0 или t² — 5t + 6 = 0

Далее решим по отдельности эти уравнения:

t² — 5t = 0

t(t — 5) = 0

t = 0 или t — 5 = 0

t = 0 или t = 5

Теперь займемся вторым уравнением. Перед нами снова квадратный трехчлен. Чтобы разложить его на множители методом группировки, нужно представить его в виде суммы 4 слагаемых. Если произвести замену – 5t = – 2t – 3t, то дальше удастся сгруппировать слагаемые:

t² — 5t + 6 = 0

t² — 2t — 3t + 6 = 0

t(t — 2) — 3(t — 2) = 0

(t — 3)(t — 2) = 0

T — 3 = 0 или t — 2 = 0

t = 3 или t = 2

В результате получили, что у исходного уравнения есть 4 корня.

Ответ: 0, 2, 3, 5

Основные определения (разбираемся со «сложными» словами)

Одночлены

Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)

Например:

• ( 4)
• ( x)
• ( 4x)
• ( 4{{x}^{2}})
• ( 4{{x}^{2}}y)

Все это – одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов.

Многочлены

Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:

• ( 4{{x}^{2}}+9x)
• ( 2{{x}^{3}}-16{{x}^{2}}+4x)
• ( 8xcdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}})

Множители

Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».

Возьмем, например, число ( 12), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей. 

Так ( 12) мы можем получить, умножив ( 2) на ( 6).

А ( 6), в свою очередь, можно представить как произведение ( 2) и ( 3).

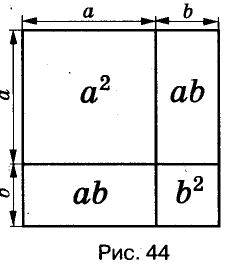
Чтоб было более наглядно, обратимся к картинке:

На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя. 

То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).

Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, ( 12=2cdot 6), а ( 6=2cdot 3)? 

Вот и я говорю, что элементарно!

Иными словами, ( 2cdot 2cdot 3=12). 

Тут ( 2), еще раз ( 2) и ( 3) – это и есть множители, на которые мы раскладываем.

Зачем нужно раскладывать многочлен на множители?

Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь. 

Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.

А теперь «официальное» определение.

Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.

Для чего нужно знать все пять способов?

Потому что нет универсального способа, подходящего для всех многочленов.

Давай посмотрим на каждый из них…

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки

( displaystyle ac+bc=c(a+b))

2. Формулы сокращенного умножения

( begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})

3. Метод группировки

Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:

4. Выделение полного квадрата

Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения

( {{x}^{4}}-4{{x}^{2}}-1=underbrace{{{x}^{4}}-2cdot 2cdot {{x}^{2}}+4}_{text{ }{{left( {{x}^{2}}-2 right)}^{2}}}-4-1={{left( {{x}^{2}}-2 right)}^{2}}-5=left( {{x}^{2}}-2+sqrt{5} right)left( {{x}^{2}}-2-sqrt{5} right))

5. Разложение квадратного трехчлена на множители

Квадратный трехчлен – многочлен вида

( a{{x}^{2}}+bx+c=0)

Теорема. Если квадратное уравнение ( a{{x}^{2}}+bx+c=0) имеет корни ( {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде:

( a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).

Подробнее о каждом из 5-ти способов разложения на множители

1. Вынесение общего множителя за скобки

Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).

Закон гласит:

Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.

Иначе говоря, ( aleft( btext{ }+text{ }c right)text{ }=text{ }abtext{ }+text{ }ac).

Так же можно проделать и обратную операцию, ( abtext{ }+text{ }actext{ }=text{ }aleft( btext{ }+text{ }c right)).

Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.

Подобную операцию можно проделывать как с переменными, такими как ( x) и ( y), например, так и с числами: ( 6text{ }+text{ }8text{ }=text{ }2left( 3text{ }+text{ }4 right)).

Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа ( 12), ведь все знают, что числа ( 6), (  и ( 12) делятся на ( 2).

А как быть, если вам досталось выражение посложнее:

( 3xy+123y)?

Как узнать на что, например, делится число ( 123).

Нееет! С калькулятором-то любой сможет, а без него слабо? 

А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.

Что ж, вернемся к выражению ( 3xy+123y), может вынести за скобку ( y) да и хватит с него? 

Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!

И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на ( 2) разделить не удастся.

Можно воспользоваться признаком делимости на ( 3), сумма цифр ( 1), ( 2) и ( 3), из которых состоит число ( 123), равна ( 6), а ( 6) делится на ( 3), значит и ( 123) делится на ( 3).

Зная это, можно смело делить в столбик, в результате деления ( 123) на ( 3) получаем ( 41) (признаки делимости пригодились!). 

Таким образом, число ( 3) мы можем вынести за скобку, так же, как y и в результате имеем:

( 3xytext{ }+text{ }123ytext{ }=text{ }3ycdot left( xtext{ }+text{ }41 right)).

Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением! 

Также общий множитель можно выносить и в степенных выражениях. 

Вот тут, например, ( 2{{x}^{3}}-16{{x}^{2}}+4x), видишь общий множитель?

У всех членов этого выражения есть иксы – выносим, все делятся на ( 2) – снова выносим, смотрим что получилось: ( 2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)).

3. Метод группировки

А вот тебе еще примерчик:

( displaystyle  {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}})­­

Ну и что с ним делать будешь? Вроде бы и на ( displaystyle  3) что-то делится и на ( displaystyle  5), а что-то на ( displaystyle  x) и на ( displaystyle  y)

Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?

Тут надо смекалку проявить, а имя этой смекалке – группировка!

Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.

Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.

Не очень понятно все это? Объясню на примере:

В многочлене ( displaystyle  {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}})­­ ставим член – ( displaystyle  3xy) после члена – ( displaystyle  5x2y) получаем:

( displaystyle  ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))

А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.

Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.

Из обеих скобок выносим за скобки общие множители членов, из первой скобки ( displaystyle  {{x}^{2}}), а из второй ( displaystyle  3y), получаем:

После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…

НО! Этот многочлен имеет общий множитель. Это ( displaystyle  (x-5y))

( displaystyle  (x-5y))за скобку и получаем финальное произведение ( displaystyle  ({{x}^{2}}-3y)(x-5y))

Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.

Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения ( displaystyle  (x-5y)), которые опять же мы и вынесли за скобку.

И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.

Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: ( displaystyle  {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)).

Согласись, уже не такой громоздкий, как был?

4. Выделение полного квадрата

Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.

В каком случае приходится это делать, узнаешь из примера:

Многочлен ( displaystyle  {{x}^{2}}-4x+2) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать.

Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.

Для полной формулы квадрата разности здесь нужно ( displaystyle  4) вместо ( displaystyle  2).

Представим третий член ( displaystyle  2) как разность ( displaystyle  4-2), получим: ( displaystyle  {{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2) 

К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: ( displaystyle  {{left( x-2 right)}^{2}}-2), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив ( displaystyle  2), как ( displaystyle  sqrt{2}), получим: ( displaystyle  (x-2-sqrt{2})(x-2+sqrt{2})).

Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.

Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.

Примеры:

• ( displaystyle  25{{m}^{2}}-49{{n}^{2}};)
• ( displaystyle  {{b}^{2}}-{{(a+1)}^{2}};)
• ( displaystyle  {{(x-y)}^{2}}-{{(x+y+1)}^{2}};)
• ( displaystyle  {{x}^{2}}+2{x}-3)
• ( displaystyle  {{x}^{2}}+6x+5;)

Решения:

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

• вынесении общего множителя за скобки;
• способе группировки;
• формулах сокращённого умножения;
• применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 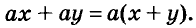Это означает, что данный многочлен ах + ау разложен на два множителя:

Другие примеры:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 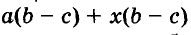общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 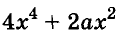при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

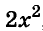
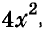
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

Пример:

Разложите на множители многочлен

Решение:

Пример:

Докажите, что число делится на 20.

Доказательство:

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

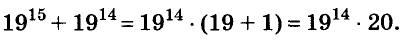
Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

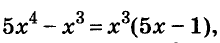
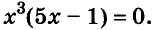
Значит, 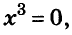отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

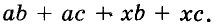
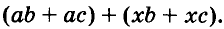
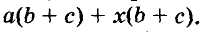
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 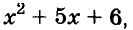• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Ответ. у = 1,5.

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 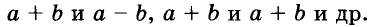Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

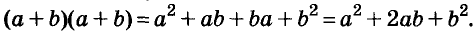
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Запомните формулу

Формулы квадрата двучлена используют и в «обратном направлении»:

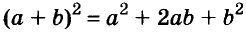
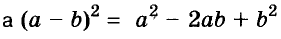
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

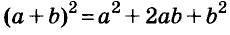
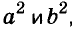
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

• Заказать решение задач по высшей математике

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 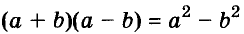можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

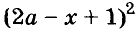
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

.

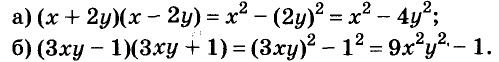
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 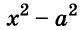можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 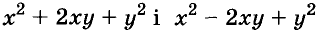раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 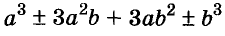можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 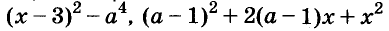— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Ответ. х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов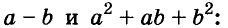

Следовательно, при любых значениях а и b

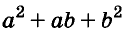
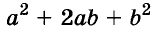
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Следовательно,

Трёхчлен 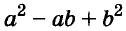называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

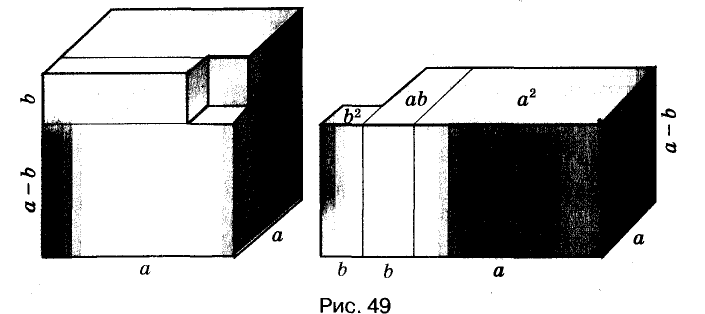
Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

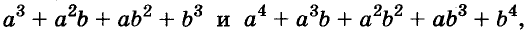
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •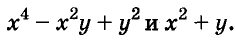

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

1. Вынести общий множитель (если он есть) за скобки.
2. Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
3. Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
4. Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 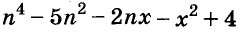в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 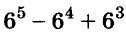делится на 31.

Доказательство:

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

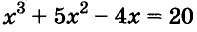
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 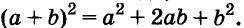Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

• вынесение общего множителя за скобки;
• способ группировки;
• использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

Метод неопределённых коэффициентов

26 июля 2022

Метод неопределённых коэффициентов — это «полуолимпиадный» приём, с помощью которого вы сможете раскладывать на множители многочлены, которые не раскладываются, и решать уравнения, которые не решаются.:)

В двух словах этот метод звучит так:

В любой непонятной ситуации вводим новую переменную. А затем думаем, что с этой переменной делать.

Сегодня мы детально изучим метод неопределённых коэффициентов. Мы разберём столько разных задач, что не понять этот приём будет просто невозможно. И да: речь пойдёт не только о многочленах.:)

Содержание

1. Основная идея
2. Разложение многочлена на множители
3. Решение уравнений
4. Деление многочлена на многочлен
5. Выделение точного квадрата
6. Избавление от иррациональности
7. Зачем всё это нужно

1. Основная идея

Чтобы понять основную идею метода неопределённых коэффициентов, рассмотрим простую наводящую задачу. Допустим, у нас есть квадратный трёхчлен, разложенный на множители:

[Pleft( x right)=left( x-3 right)left( x+2 right)]

Если раскрыть скобки и привести подобные слагаемые, то получится тот же многочлен, записанный в стандартном виде:

[Pleft( x right)={{x}^{2}}-x-6]

Зная разложение на множители, легко получить стандартный вид многочлена. А вот обратный переход — от стандартного вида к множителям — является вычислительно сложной операцией, но всё ещё возможной: считаем дискриминант, находим корни, вспоминаем теорему Виета и т.д.

Немного усложним задачу. Рассмотрим разложение на множители многочлена четвёртой степени (почему именно четвёртой — см. урок. «Разложение на множители»):

[Pleft( x right)=left( {{x}^{2}}-3x+1 right)left( {{x}^{2}}+x+4 right)]

Раскроем скобки и приведём подобные. Вновь получим многочлен в стандартном виде:

[Pleft( x right)={{x}^{4}}-2{{x}^{3}}+2{{x}^{2}}-11x+4]

Но как выполнить обратную операцию? Как по стандартному виду многочлена определить, на какие множители его можно разложить? Тут на помощь и приходит метод неопределённых коэффициентов.

Проблема разложения на множители

Рассмотрим задачу в общем виде. Допустим, нам нужно разложить на множители многочлен четвёртой степени:

[Pleft( x right)= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]

Из курса алгебры мы знаем, что произвольный многочлен не всегда раскладывается на линейные двучлены вида $x-color{red}{a}$. Однако он совершенно точно раскладывается на квадратные трёхчлены вида $color{red}{a}{{x}^{2}}+color{red}{b}x+color{red}{c}$:

[Pleft( x right)=left(color{blue}{a}{{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+color{blue}{e}x+color{blue}{f} right)]

Записав такое разложение, мы уже наполовину выполнили задачу. Но нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ и $color{blue}{d}$, $color{blue}{e}$, $color{blue}{f}$. Отсюда, кстати, и название приёма — «метод неопределённых коэффициентов». И чтобы найти эти самые неопределённые коэффициенты, воспользуемся следующей теоремой.

Теорема о нулевом многочлене

Теорема (критерий многочлена, тождественно равного нулю). Многочлен

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]

тождественно равен нулю (т.е. при любом значении переменной $x$) тогда и только тогда, когда все его коэффициенты равны нулю:

[color{blue}{{a}_{n}}= color{blue}{{a}_{n-1}}= ldots = color{blue}{{a}_{1}}= color{blue}{{a}_{0}}= color{red}{0}]

Доказательство я вынесу на отдельную страницу (см. урок «Корни многочлена»). Потому что у этой теоремы много применений, но нас сейчас интересует не сама теорема, а лишь одно-единственное следствие из неё:

Следствие (критерий равенства двух многочленов). Пусть даны два многочлена:

[begin{align}Aleft( x right) &= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}\ Bleft( x right) &= color{blue}{{b}_{n}}{{x}^{n}}+ color{blue}{{b}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{b}_{1}}x+ color{blue}{{b}_{0}}\ end{align}]

Эти два многочлена тождественно равны друг другу (т.е. $Aleft( x right)=Bleft( x right)$ при любом $x$) тогда и только тогда, когда равны их коэффициенты при соответствующих степенях:

[color{blue}{{a}_{n}}= color{blue}{{b}_{n}}; color{blue}{{a}_{n-1}}= color{blue}{{b}_{n-1}}; ldots ; color{blue}{{a}_{1}}= color{blue}{{b}_{1}}; color{blue}{{a}_{0}}= color{blue}{{b}_{0}}]

Вот тут всё становится на свои места!

Основной алгоритм

Пусть даны два представления одного и того же многочлена. Например, в стандартном виде и разложение на множители:

[begin{align} Pleft( x right) &= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right) end{align}]

Тогда для нахождения неизвестных коэффициентов в любом из этих разложений необходимо выполнить три шага:

1. Раскрыть все скобки и привести подобные, чтобы получить две записи в стандартном виде;
2. Приравнять соответствующие коэффициенты, составить систему уравнений;
3. Решить эту систему и правильно интерпретировать ответ.

Вот и вся суть метода. Первые два пункта очевидны. Проблемы возникают лишь на третьем шаге, поскольку зачастую системы уравнений получаются нелинейными. И мы детально разберём, как решать подобные системы.

Но для начала — парочка простых задач.:)

Задача 1.1. Основная идея

Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:

[begin{align}Pleft( x right) &=2{{x}^{4}}+3{{x}^{3}}-5x-2\ Qleft( x right) &=left( ax+3 right)left( {{x}^{3}}-b right)-3x+c\ end{align}]

Решение. Согласно Теореме 1, многочлены $Pleft( x right)$ и $Qleft( x right)$ равны, когда в точности равны их коэффициенты. Поэтому раскроем скобки в многочлене $Qleft( x right)$ и найдём эти коэффициенты:

[begin{align}Qleft( x right) &=a{{x}^{4}}+3{{x}^{3}}-abx-3b-3x+c= \ &=color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right) end{align}]

Для удобства коэффициенты выделены синим цветом. Сравним их с коэффициентами многочлена $Pleft( x right)$:

[begin{align}& color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right)= \ = & color{red}{2}{{x}^{4}}+ color{red}{3}{{x}^{3}}+left( color{red}{-5} right)x+left( color{red}{-2} right) \ end{align}]

Чтобы многочлены были равны, должны выполняться равенства

[color{blue}{a}= color{red}{2};quad color{blue}{-ab-3}= color{red}{-5};quad color{blue}{c-3b}= color{red}{-2}]

Получили систему уравнения, которая легко решается:

[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]

Ответ: $a=2$, $b=1$, $c=1$.

Задача 1.2. Альтернативный подход

Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:

[begin{align}Pleft( x right) &=3{{x}^{4}}+7{{x}^{3}}+3{{x}^{2}}+x+2\ Qleft( x right) &=left( x+1 right)left( a{{x}^{3}}+b{{x}^{2}}-x+c right)\ end{align}]

Решение. Решим эту задачу двумя способами: «чистым» методом неопределённых коэффициентов и с привлечением схемы Горнера.

Способ 1. «Чистый» метод неопределённых коэффициентов. Раскрываем скобки в многочлене $Qleft( x right)$:

[begin{align}Qleft( x right) &=a{{x}^{4}}+b{{x}^{3}}-{{x}^{2}}+cx+a{{x}^{3}}+b{{x}^{2}}-x+c= \ &= color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c} end{align}]

Приравниваем многочлены $Qleft( x right)$ и $Pleft( x right)$:

[begin{align}& color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c}= \= & color{red}{3}{{x}^{4}}+ color{red}{7}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{1}x+ color{red}{2} \ end{align}]

Получим набор из пяти уравнений:

[begin{array}{rrr}color{blue}{a}= color{red}{3}; & color{blue}{b-1}= color{red}{3}; & color{blue}{c}= color{red}{2}.\ color{blue}{a+b}= color{red}{7}; & color{blue}{c-1}= color{red}{1}; & {}\ end{array}]

Решаем систему из этих уравнений и получаем ответ:

[color{blue}{a}=color{red}{3}; color{blue}{b}=color{red}{4}; color{blue}{c}=color{red}{2}]

Способ 2. Привлечение схемы Горнера. Поскольку многочлен $Qleft( x right)$ разложен на множители, сделаем то же самое и с многочленом $Pleft( x right)$ — выделим из него множитель-двучлен $x+1$. Для этого заполним таблицу для $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{3} & color{blue}{7} & color{blue}{3} & color{blue}{1} & color{blue}{2}\ hline color{red}{-1} & 3 & 4 & -1 & 2 & color{green}{0}\ end{array}]

Получили остаток $r=color{green}{0}$, и многочлен $Pleft( x right)$ можно переписать так:

[Pleft( x right)=left( x+1 right)left( 3{{x}^{3}}+4{{x}^{2}}-1x+2 right)]

Приравняем многочлены $Pleft( x right)$ и $Qleft( x right)$:

[begin{align}&left( x+1 right)left( color{red}{3}{{x}^{3}}+ color{red}{4}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{2} right)= \ = &left( x+1 right)left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+left( color{blue}{-1} right)x+ color{blue}{c} right) \ end{align}]

И сразу получаем ответ:

[color{blue}{a} =color{red}{3}; color{blue}{b} =color{red}{4}; color{blue}{c} =color{red}{2}]

Ответ: $a=3$, $b=4$, $c=2$.

Если вам непонятно, как работает схема Горнера и при чём тут разложение на множители, см. урок «Схема Горнера» — это ещё один универсальный алгоритм. Который, как и метод неопределённых коэффициентов, будет полезен во многих нестандартных задачах.

2. Разложение многочлена на множители

Переходим к серьёзным задачам. Всё, что мы решали выше, сводилось к простым линейным уравнениям, которые решались обычной подстановкой.

Теперь мы разберём многочлены четвёртой степени — те самые, с которых начинали рассуждения. И заодно научимся решать нелинейные системы методом целочисленного перебора.

Задача 2.1. Самая стандартная

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+2{{x}^{3}}+2{{x}^{2}}+10x+25]

Этот многочлен вообще не имеет действительных корней, в чём легко убедиться, выделив точные квадраты:

[begin{align}Pleft( x right) &=left( {{x}^{4}}+2{{x}^{3}}+{{x}^{2}} right)+left( {{x}^{2}}+10x+25 right)= \ &={{x}^{2}}{{left( x+1 right)}^{2}}+{{left( x+5 right)}^{2}} end{align}]

Полученная сумма равна нулю только если $x=-5$ и одновременно $x=0$ или $x=-1$. Что, очевидно, невозможно. Следовательно, линейных множителей в разложении не будет.

Зато квадратные множители точно будут, поэтому используем метод неопределённых коэффициентов. Предположим, что многочлен раскладывается на произведение двух квадратных трёхчленов:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Раскрываем скобки и приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ & +left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем коэффициенты полученного многочлена с коэффициентами исходного:

[Pleft( x right)={{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{2}{{x}^{2}}+ color{red}{10}x+ color{red}{25}]

Выписываем равенства:

[begin{array}{rr}color{blue}{b+d}= color{red}{2}; & color{blue}{be+dc}= color{red}{10};\ color{blue}{bd+c+e}= color{red}{2}; & color{blue}{ce}= color{red}{25}.\ end{array}]

Получили систему из четырёх нелинейных уравнений. Универсального алгоритма для решения таких систем не существует. Однако здесь хорошо работает метод целочисленного перебора.

Рассмотрим последнее уравнение:

[ color{blue}{c} cdot color{blue}{e}= color{red}{25}]

Какие числа нужно перемножить, чтобы в произведении получилось 25? Вот несколько вариантов:

[begin{align}color{blue}{c} cdotcolor{blue}{e} &= color{red}{1} cdotcolor{red}{25}= color{red}{5} cdotcolor{red}{5} = \ & =left( color{red}{-1} right)cdot left( color{red}{-25} right)= \ & =left( color{red}{-5} right)cdot left( color{red}{-5} right) end{align}]

Рассмотрим вариант, когда $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$. Именно он будет правильным ответом, в чём мы сейчас убедимся.

Подставим $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$ в оставшиеся три уравнения. Получим систему

[left{ begin{align}b+d &=2 \ bd+5+5 &=2 \ 5b+5d &=10 \ end{align} right.]

Последнее уравнение является следствием первого, поэтому система равносильна двум уравнениям:

[left{ begin{align}b+d &=2 \ bd &=-8 \ end{align} right.]

Эта система имеет два решения, которые легко находятся методом подбора: $color{blue}{b} = color{red}{4}$ и $color{blue}{d}= color{red}{-2}$, либо наоборот $color{blue}{b}= color{red}{-2}$ и $color{blue}{d}= color{red}{4}$. Получаем два варианта разложения:

[begin{align}{{P}_{1}}left( x right) &=left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right)left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right) \ {{P}_{2}}left( x right) &=left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right)left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right) \ end{align}]

Но ведь на самом деле это одно и то же разложение — просто множители поменялись местами. Поэтому мы вправе выбрать любой вариант.

Запишем окончательный ответ:

[Pleft( x right)=left( {{x}^{2}}+4x+5 right)left( {{x}^{2}}-2x+5 right)]

Важное замечание. После приведения подобных и сравнения коэффициентов мы получили систему из нескольких нелинейных уравнений, которые затем начали решать методом целочисленного перебора.

Такие уравнения будут преследовать нас постоянно — это основная трудность метода неопределённых коэффициентов.

Чтобы в процессе перебора не упустить из виду какой-нибудь вариант, целесообразно составлять таблицу всех возможных вариантов. Например, для равенства $color{blue}{c}cdot color{blue}{e}= color{red}{25}$ таблица выглядит так:

[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{-1} & color{red}{5} & color{red}{-5}\ hline color{blue}{e} & color{red}{25} & color{red}{-25} & color{red}{5} & color{red}{-5}\ end{array}]

Обратите внимание: в таблице нет варианта $color{blue}{c}= color{red}{25}$, $color{blue}{e}= color{red}{1}$ и $color{blue}{c}= color{red}{-25}$, $color{blue}{e}= color{red}{-1}$, потому что они получаются из первых двух вариантов перестановкой множителей в итоговом разложении.

Тем не менее, в некоторых примерах придётся рассматривать все возможные варианты. Один из таких примеров мы рассмотрим чуть позже, а пока давайте потренируемся на более адекватных задачах.:)

Задача 2.2. Снова стандартная

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+5{{x}^{3}}+5{{x}^{2}}-4x-2]

Решение. Запишем искомое разложение:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Нужно найти четыре числа: $color{blue}{b}$, $color{blue}{c}$, $color{blue}{d}$, $color{blue}{e}$. Собственно, это и есть «неопределённые коэффициенты». Раскрываем скобки и приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем коэффициенты этого многочлена с коэффициентами исходного:

[Pleft( x right)={{x}^{4}}+ color{red}{5}{{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-4} right)x+left( color{red}{-2} right)]

Получаем четыре уравнения, которые должны выполняться одновременно:

[begin{array}{rr}color{blue}{b+d}= color{red}{5}; & color{blue}{be+dc}= color{red}{-4};\ color{blue}{bd+c+e}= color{red}{5}; & color{blue}{ce}= color{red}{-2}.\ end{array}]

Произведение коэффициентов $color{blue}{c}cdot color{blue}{e}= color{red}{-2}$ — отрицательное число. Положим для определённости, что $color{blue}{c} gt 0$ и $color{blue}{e} lt 0$. Выпишем все возможные варианты:

[begin{array}{r|r|r}color{blue}{c} & color{red}{1} & color{red}{2}\ hline color{blue}{e} & color{red}{-2} & color{red}{-1}\ end{array}]

Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$ и $color{blue}{e}=color{red}{-2}$. Получим систему

[left{ begin{align}b+d &=5 \ bd+1-2 &=5 \ -2b+d &=-4 end{align} right.]

Вычтем почленно из последнего уравнения первое и получим

[begin{align}-3b &=-9 \ color{blue}{b} &= color{red}{3}end{align}]

Подставляем $color{blue}{b}= color{red}{3}$ в первое уравнение и получаем $color{blue}{d}= color{red}{2}$. Найденные значения $color{blue}{b}$ и $color{blue}{d}$ удовлетворяют всем трём равенствам. Следовательно, мы нашли решение системы:

[color{blue}{b}= color{red}{3}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{2}; color{blue}{e}= color{red}{-2}]

Откуда получаем искомое разложение на множители:

[Pleft( x right)=left( {{x}^{2}}+3x+1 right)left( {{x}^{2}}+2x-2 right)]

Важное замечание. К сожалению, в процессе целочисленного перебора далеко не всегда верный вариант будет попадаться сразу, на первом же шаге. Когда я собирал материалы для этого урока, иногда верным оказывался лишь четвёртый вариант из четырёх возможных.:)

Поэтому не переживайте, когда видите несовместную систему. Это нормально и даже неизбежно.

И вообще давайте посмотрим, как это выглядит на практике. Например, рассмотрим второй вариант в только что решённой задаче: $color{blue}{c}=color{red}{2}$ и $color{blue}{e}=color{red}{-1}$. Это приведёт нас к системе уравнений:

[left{ begin{align}b+d &=5 \ bd+2-1 &=5 \ -b+2d &=-4 end{align} right.]

Складываем первое уравнение с последним — и тут же получаем проблему:

[begin{align}3d &=1 \ color{blue}{d} &= color{red}{{1}/{3};} \ end{align}]

Получили дробный коэффициент $color{blue}{d}$, откуда следует, что коэффициент $color{blue}{b}$ тоже дробный:

[color{blue}{b}=5- color{blue}{d}=color{red}{{14}/{3};}]

Но тогда не выполняется второе равенство. Следовательно, система несовместна.

Задача 2.3. Упрощённые выкладки

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+{{x}^{3}}+3{{x}^{2}}+32x-10]

В этот раз распишу всё кратко — только основные выкладки. Разложим многочлен $Pleft( x right)$ на два квадратных трёхчлена:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Раскрываем скобки, приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем с исходным многочленом:

[Pleft( x right)={{x}^{4}}+ color{red}{1}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{32}x+left( color{red}{-10} right)]

Получаем четыре уравнения:

[begin{array}{rr}color{blue}{b+d}= color{red}{1}; & color{blue}{be+dc}= color{red}{32};\ color{blue}{bd+c+e}= color{red}{3}; & color{blue}{ce}= color{red}{-10}.\ end{array}]

Поскольку $color{blue}{ce}= color{red}{-10} lt 0$, положим $color{blue}{c} gt 0$, $color{blue}{e} lt 0$. Возможные варианты:

[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{5} & color{red}{10} \ hline color{blue}{e} & color{red}{-10} & color{red}{-5} & color{red}{-2} & color{red}{-1} \ end{array}]

Первые три варианта дают несовместные системы с дробными коэффициентами $color{blue}{b}$ и $color{blue}{d}$ (проверьте это!). Рассмотрим последний вариант: $color{blue}{c}= color{red}{10}$, $color{blue}{e}= color{red}{-1}$. Получим систему

[left{ begin{align}b+d &=1 \ bd+10-1 &=3 \ -b+10d &=32 end{align} right.]

Решение системы: $color{blue}{b}= color{red}{-2}$, $color{blue}{d}= color{red}{3}$. Окончательное разложение на множители:

[Pleft( x right)=left( {{x}^{2}}-2x+10 right)left( {{x}^{2}}+3x-1 right)]

3. Решение уравнений методом неопределённых коэффициентов

Одно из важнейших приложений метода неопределённых коэффициентов — это решение уравнений высших степеней. В самом деле, зачем мы раскладываем многочлен $Pleft( x right)$ на множители? Обычно по одной из двух причин:

1. Решить уравнение $Pleft( x right)=0$. Ведь произведение равно нулю, когда хотя бы один из множителей равен нулю;
2. Сократить рациональную дробь вида ${Pleft( x right)}/{Qleft( x right)};$. В этом случае многочлен $Qleft( x right)$ также придётся разложить на множители.

Про рациональные дроби мы поговорим в отдельном уроке (см. урок «Разложение на простейшие»). А вот уравнения мы разберём сейчас.

Допустим, нужно решить уравнение вида

[color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}=0]

В левой части равенства стоит стандартный многочлен. И если коэффициенты многочлена целые, то мы уже знаем как минимум два способа решения таких уравнений:

• Теорема Безу для отыскания рациональных корней-кандидатов;
• Схема Горнера для быстрой проверки этих кандидатов.

И эта связка отлично работает, когда многочлен имеет рациональные корни вида $x={color{blue}{p}}/{color{red}{q}};$. Вот буквально: мы найдём все такие корни и решим уравнение.

А если корни иррациональны? Безу и Горнер тут бесполезны. Зато полезным оказывается разложение на множители, когда вместо большого и страшного многочлена $Pleft( x right)$ в левой части уравнения появится произведение двух многочленов меньшей степени:

[Hleft( x right)cdot Qleft( x right)=0]

А дальше всё стандартно: произведение равно нулю, когда $Hleft( x right)=0$ или $Qleft( x right)=0$. И вот мы свели исходную задачу к двум уравнениям меньших степеней, которые наверняка легко решаются.:)

Задача 3.1. «Нерешаемое» уравнение

Задача. Решите уравнение методом неопределённых коэффициентов

[{{x}^{4}}+2{{x}^{3}}+3{{x}^{2}}+2x-3=0]

Это приведённое целочисленное уравнение, но его нельзя решить по теореме Безу и схеме Горнера. Ведь целые корни этого уравнения являются делителями свободного члена $color{blue}{{a}_{0}}=-3$. Таких делителей ровно четыре:

[x=pm 1; pm 3]

И все они дают ненулевой остаток в схеме Горнера:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{2} & color{blue}{3} & color{blue}{2} & color{blue}{-3}\ hlinecolor{red}{1} & 1 & 3 & 6 & 8 & color{red}{5}\ hlinecolor{red}{-1} & 1 & 1 & 2 & 0 & color{red}{-3}\ hlinecolor{red}{3} & 1 & 5 & 18 & 56 & color{red}{165}\ hlinecolor{red}{-3} & 1 & -1 & 6 & -16 & color{red}{45}\ end{array}]

Остаётся только метод неопределённых коэффициентов. Разложим уравнение на произведение двух квадратных трёхчленов:

[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]

Раскроем скобки и приведём подобные в правой части равенства:

[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]

Вспоминаем коэффициенты многочлена в исходном уравнении:

[{{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{2}x+left( color{red}{-3} right)=0]

Получаем уже привычный набор из четырёх уравнений:

[begin{array}{rr} color{blue}{b+d}=color{red}{2}; & color{blue}{be+dc}=color{red}{2};\ color{blue}{bd+c+e}=color{red}{3}; & color{blue}{ce}=color{red}{-3}.\ end{array}]

Рассмотрим последнее уравнение: $color{blue}{ce}=color{red}{-3}$. Произведение отрицательно, значит, множители разных знаков. Без ограничения общности положим $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Составим таблицу вариантов:

[begin{array}{r|r|r} color{blue}{c} & color{red}{1} & color{red}{3}\ hlinecolor{blue}{e} & color{red}{-3} & color{red}{-1}\ end{array}]

Итого два варианта. Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$, $color{blue}{e}=color{red}{-3}$. Получим систему

[left{ begin{align}b+d &=2\ bd+1-3 &=3\ -3b+d &=2 end{align} right.]

Вычитая из первого уравнения последнее, получаем $color{blue}{b}=color{red}{0}$, $color{blue}{d}=color{red}{2}$, что противоречит второму уравнению. Система несовместна.

Второй вариант: $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-1}$. Система уравнений:

[left{ begin{align}b+d &=2 \ bd+3-1 &=3 \ -b+3d &=2 end{align} right.]

Складывая первое и последнее уравнение, получаем $color{blue}{b}=color{red}{1}$, $color{blue}{d}=color{red}{1}$. При подстановке во второе уравнение получаем верное числовое равенство. Следовательно, мы нашли решение:

[color{blue}{b}=color{red}{1}; color{blue}{c}=color{red}{3}; color{blue}{d}=color{red}{1}; color{blue}{e}=color{red}{-1}]

Переписываем уравнение:

[left( {{x}^{2}}+x+3 right)left( {{x}^{2}}+x-1 right)=0]

Многочлен в первой скобке не имеет действительных корней, во второй — имеет:

[{{x}^{2}}+x-1=0]

Дискриминант положителен:

[D={{1}^{2}}-4cdot 1cdot left( -1 right)=1+4=5]

Корней будет два:

[x=frac{-1pm sqrt{5}}{2}]

Неудивительно, что эти корни не были обнаружены по теореме Безу. Ведь они являются иррациональными.:)

Ответ: $x=frac{-1pm sqrt{5}}{2}$.

Задача 3.2. «Нерешаемое» уравнение — 2

Задача. Решите уравнение методом неопределённых коэффициентов:

[{{x}^{4}}-4{{x}^{3}}+5{{x}^{2}}-2x-6=0]

Это задание похоже на предыдущее, поэтому распишем всё кратко. Ожидаемое разложение на множители:

[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]

Найдём такое разложение методом неопределённых коэффициентов. Раскрываем скобки, приводим подобные:

[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]

Сравниваем с коэффициентами исходного многочлена:

[{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-2} right)x+left( color{red}{-6} right)=0]

Выписываем четыре уравнения:

[begin{array}{rr} color{blue}{b+d}=color{red}{-4}; & color{blue}{be+dc}=color{red}{-2};\ color{blue}{bd+c+e}=color{red}{5}; & color{blue}{ce}=color{red}{-6}.\ end{array}]

Поскольку $color{blue}{ce}=color{red}{-6}$, полагаем $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Возможные варианты

[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{3} & color{red}{6}\ hlinecolor{blue}{e} & color{red}{-6} & color{red}{-3} & color{red}{-2} & color{red}{-1}\ end{array}]

Перебирая варианты, обнаруживаем, что правильная комбинация — это $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-2}$:

[left{ begin{align} b+d &=-4 \ bd+3-2 &=5 \ -2b+3d &=-2 end{align} right.]

Дважды прибавим к последнему уравнению первое — получим

[begin{align} 5d&=-10 \ color{blue}{d} &= color{red}{-2} \ color{blue}{b} &= color{red}{-2} end{align}]

Следовательно, исходное уравнение примет вид

[left( {{x}^{2}}-2x+3 right)left( {{x}^{2}}-2x-2 right)=0]

Многочлен в первой скобке корней не имеет (в этом легко убедиться, посчитав дискриминант). Рассмотрим вторую скобку:

[{{x}^{2}}-2x-2=0]

Дискриминант положительный:

[D={{left( -2 right)}^{2}}-4cdot1cdot left( -2 right)=4+8=12]

Уравнение имеет два корня:

[x=frac{2pm sqrt{12}}{2}=frac{2pm 2sqrt{3}}{2}=1pm sqrt{3}]

Ответ: $x=1pm sqrt{3}$.

Задача 3.3. Более сложное уравнение

Задача. Решите уравнение методом неопределённых коэффициентов:

[2{{x}^{4}}-4{{x}^{3}}+{{x}^{2}}-6x-3=0]

Это уравнение принципиально отличается от предыдущих тем, что старший коэффициент $color{blue}{{a}_{4}}=2$. Многочлен не является приведённым, поэтому разложение на множители, вообще говоря, выглядит так:

[left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]

Итого шесть неизвестных коэффициентов. Для сравнения: раньше их было всего четыре.

Однако задачу можно существенно упростить, если сделать два допущения:

1. Оба старших коэффициента — $color{blue}{a}$ и $color{blue}{d}$ — являются целыми и положительными.
2. Положим для определённости, что $color{blue}{a} gt color{blue}{d}$.

В этом и состоит ключевая идея метода неопределённых коэффициентов: мы вводим дополнительные ограничения, которые в итоге почти наверняка выполняются. Да, есть небольшой риск «промахнуться» в своих допущениях, но это компенсируется многократным упрощением дальнейших выкладок.

В нашем случае из двух допущений немедленно следует, что $color{blue}{a}=color{red}{2}$, $color{blue}{b}=color{red}{1}$, и уравнение примет вид

[left( color{red}{2}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]

Осталось всего четыре неизвестных коэффициента. Раскроем скобки и приведём подобные:

[begin{align}color{red}{2}{{x}^{4}}+left( color{blue}{b+2e} right){{x}^{3}} &+left( color{blue}{be+c+2f} right){{x}^{2}}+ \ &+left( color{blue}{bf+ce} right)x+ color{blue}{cf}=0 \ end{align}]

Сравним с коэффициентами исходного уравнения:

[color{red}{2}{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+color{red}{1}{{x}^{2}}+left( color{red}{-6} right)x+left( color{red}{-3} right)=0]

Получим четыре уравнения, но из-за коэффициента $color{blue}{a}=color{red}{2}$ они отличаются от привычных:

[begin{array}{rr} color{blue}{b+2e}= color{red}{-4}; & color{blue}{bf+ce}= color{red}{-6};\ color{blue}{be+c+2f}= color{red}{1}; & color{blue}{cf}= color{red}{-3}.\ end{array}]

Многочлены в первой и второй скобке не являются взаимозаменяемыми (поскольку у них разные коэффициенты при ${{x}^{2}}$), поэтому необходимо рассмотреть все возможные комбинации, дающие $color{blue}{cf}= color{red}{-3}$:

[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{3} & color{red}{-1} & color{red}{-3}\ hlinecolor{blue}{f} & color{red}{-3} & color{red}{-1} & color{red}{3} & color{red}{1}\ end{array}]

Рассмотрим каждую комбинацию. В первом случае быстро обнаружится, что система несовместна. А вот второй случай, когда $color{blue}{c}= color{red}{3}$ и $color{blue}{f}= color{red}{-1}$, представляет интерес:

[left{ begin{align}b+2e &=-4 \ be+3-2 &=1 \ -b+3e &=-6 end{align} right.]

Складываем первое уравнение с последним — получаем

[begin{align}5e &=-10 \ color{blue}{e} &= color{red}{-2} \ color{blue}{b} &= color{red}{0} end{align}]

Итак, система совместна. Получили разложение на множители:

[left( 2{{x}^{2}}+3 right)left( {{x}^{2}}-2x-1 right)=0]

Многочлен в первых скобках принимает только положительные значения, поэтому не имеет корней:

[2{{x}^{2}}+3ge 0+3 gt 0]

Рассмотрим вторые скобки:

[{{x}^{2}}-2x-1=0]

Это квадратное уравнение. Дискриминант положительный:

[D={{2}^{2}}-4cdot 1cdot left( -1 right)=4+4=8]

Следовательно, уравнение имеет два различных корня:

[x=frac{2pm sqrt{8}}{2}=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]

Это и есть корни исходного уравнения четвёртой степени.

Ответ: $x=1pm sqrt{2}$.

4. Деление многочлена на многочлен

Ещё одна задача, где работает метод неопределённых коэффициентов — это деление одного многочлена на другой с остатком. Напомню, что разделить многочлен $Pleft( x right)$ на двучлен $Tleft( x right)$ с остатком — это значит представить его в виде

[Pleft( x right)=Qleft( x right)cdot Tleft( x right)+Rleft( x right)]

При этом степень остатка $Rleft( x right)$ должна быть меньше степени делителя $Tleft( x right)$. Кроме того,

[deg Qleft( x right)+deg Tleft( x right)=deg Pleft( x right)]

При соблюдении таких ограничений многочлены $Qleft( x right)$ и $Rleft( x right)$ всегда определяются однозначно. Их коэффициенты мы как раз и будем находить.

Задача 4.1. Деление на двучлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)={{x}^{3}}-5{{x}^{2}}+15x-6]

на двучлен $Tleft( x right)=x-3$.

Итак, мы хотим представить многочлен $Pleft( x right)$ в виде

[Pleft( x right)=Qleft( x right)cdot left( x-3 right)+Rleft( x right)]

где $Qleft( x right)$ — неполное частное. Точнее, $Qleft( x right)$ — квадратный трёхчлен, потому что

[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)= \ &=3-1=2end{align}]

Кроме того, степень делителя $deg Tleft( x right)=1$, поэтому степень остатка $deg Rleft( x right)=0$, т.е. $Rleft( x right)$ — это просто число. С учётом этих фактов многочлен $Pleft( x right)$ примет вид

[Pleft( x right)=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x-3 right)+ color{blue}{d}]

Раскроем скобки, приведём подобные слагаемые:

[Pleft( x right)= color{blue}{a}{{x}^{3}}+left( color{blue}{b-3a} right){{x}^{2}}+left( color{blue}{c-3b} right)x+left( color{blue}{d-3c} right)]

С другой стороны, изначально тот же многочлен $Pleft( x right)$ имел вид

[Pleft( x right)= color{red}{1}{{x}^{3}}+left( color{red}{-5} right){{x}^{2}}+ color{red}{15}x+left( color{red}{-6} right)]

Приравниваем коэффициенты и получаем четыре равенства:

[begin{array}{rr} color{blue}{a}= color{red}{1}; & color{blue}{c-3b}= color{red}{15};\ color{blue}{b-3a}= color{red}{-5}; & color{blue}{d-3c}= color{red}{-6}.\ end{array}]

Это система из четырёх уравнений с четырьмя неизвестными, которая легко решается:

[color{blue}{a}= color{red}{1}; color{blue}{b}= color{red}{-2}; color{blue}{c}= color{red}{9}; color{blue}{d}= color{red}{21}]

Подставим найденные числа в $Qleft( x right)$ и $Rleft( x right)$:

[begin{align} & Qleft( x right)={{x}^{2}}-2x+9 \ & Rleft( x right)=21 \end{align}]

Ответ: $Qleft( x right)={{x}^{2}}-2x+9$, $Rleft( x right)=21$.

Поскольку мы делим $Pleft( x right)$ на двучлен $x-color{red}{3}$, составим таблицу для $x=color{red}{3}$:

[begin{array}{r|r|r|r|r} {} & color{blue}{1} & color{blue}{-5} & color{blue}{15} & color{blue}{-6}\ hlinecolor{red}{3} & 1 & -2 & 9 & color{green}{21}\ end{array}]

Перепишем многочлен $Pleft( x right)$ согласно этой таблице и сравним с записью для метода неопределённых коэффициентов:

[begin{align}Pleft( x right) &=left( color{red}{1}{{x}^{2}}- color{red}{2}x+ color{red}{9} right)left( x-color{red}{3} right)+ color{green}{21}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x- color{red}{3} right)+ color{blue}{d} end{align}]

Получили те же числа, что и при решении «напролом».

Впрочем, такие рассуждения актуальны лишь при делении на двучлен вида $x-color{red}{a}$. В следующем задании они нам уже не помогут.:)

Задача 4.2. Многочлен с параметром

Задача. При каких значениях параметров $a$ и $b$ многочлен

[Pleft( x right)={{x}^{3}}+a{{x}^{2}}-x+b]

делится без остатка на многочлен

[Tleft( x right)={{x}^{2}}+2x+5]

Решение. Если многочлен $Pleft( x right)$ делится без остатка на многочлен $Tleft( x right)$, то его можно представить в виде

[Pleft( x right)=Qleft( x right)cdot Tleft( x right)]

Здесь многочлен $Qleft( x right)$ — это частное, и его степень равна

[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=3-2=1]

Итак, $Qleft( x right)$ — линейный двучлен вида $color{blue}{c}x+color{blue}{d}$ (коэффициенты $color{blue}{a}$ и $color{blue}{b}$ уже заняты в условии задачи). Выражение для $Pleft( x right)$ можно переписать так:

[Pleft( x right)=left( color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x+5 right)]

Найдём коэффициенты $color{blue}{c}$ и $color{blue}{d}$. Раскрываем скобки (стандартная процедура для метода неопределённых коэффициентов) и приводим подобные:

[Pleft( x right)= color{blue}{c}{{x}^{3}}+left( color{blue}{2c+d} right){{x}^{2}}+left( color{blue}{5c+2d} right)x+ color{blue}{5d}]

Сравниваем с коэффициентами исходного многочлена:

[Pleft( x right)= color{red}{1}{{x}^{3}}+ color{red}{a}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{b}]

Приравниваем соответствующие «красные» и «синие» коэффициенты и получаем четыре равенства:

[begin{array}{rr}color{blue}{c}= color{red}{1}; & color{blue}{5c+2}d= color{red}{-1};\color{blue}{2c+d}= color{red}{a}; & color{blue}{5d}= color{red}{b}.\end{array}]

Итак, у нас четыре линейных уравнения и четыре переменных. Эта система имеет только одно решение:

[ color{blue}{a}= color{red}{-1}; color{blue}{b}= color{red}{-15}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{-3}]

Впрочем, нас интересуют лишь переменные $color{blue}{a}$ и $color{blue}{b}$.

Ответ: $a=-1$, $b=-15$.

Задача 4.3. Квадратный трёхчлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)=2{{x}^{2}}+3x-3]

на двучлен $Tleft( x right)=2x-1$.

Решение. Частное $Qleft( x right)$ имеет степень

[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=2-1=1]

Следовательно, $Qleft( x right)$ — линейный двучлен вида $color{blue}{a}x+ color{blue}{b}$, а остаток $Rleft( x right)$ — просто число $color{blue}{c}$. С учётом этого перепишем многочлен $Pleft( x right)$:

[begin{align}Pleft( x right) &=left( ax+b right)left( 2x-1 right)+c= \ &=2a{{x}^{2}}-ax+2bx-b+c= \ &= color{blue}{2a}{{x}^{2}}+left( color{blue}{2b-a} right)x+left( color{blue}{c-b} right) end{align}]

Сравним с исходным видом этого же многочлена:

[Pleft( x right)= color{red}{2}{{x}^{2}}+color{red}{3}x+left( color{red}{-3} right)]

Приравниваем соответствующие коэффициенты — получаем три уравнения:

[color{blue}{2a}=color{red}{2};quadcolor{blue}{2b-a}=color{red}{3};quadcolor{blue}{c-b}=color{red}{-3}]

Эта система легко решается:

[color{blue}{a}=color{red}{1}; color{blue}{b}=color{red}{2}; color{blue}{c}=color{red}{-1}]

Следовательно, неполное частное $Qleft( x right)=x+2$ и остаток $Rleft( x right)=-1$.

Ответ: $Qleft( x right)=x+2$, $Rleft( x right)=-1$.

Задача 4.4. Сложный многочлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)={{x}^{5}}-1]

на квадратный трёхчлен $Tleft( x right)={{x}^{2}}+2x-1$.

Решение. На самом деле это несложная задача, но вычислений будет много. Запишем результат деления с остатком:

[Pleft( x right)=Qleft( x right)cdot left( {{x}^{2}}+2x-1 right)+Rleft( x right)]

Сразу найдём степени неполного частного и остатка:

[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)=5-2=3 \ deg Rleft( x right) & lt deg Tleft( x right)=2Rightarrow deg Rleft( x right)=1 \ end{align}]

Переходим к методу неопределённых коэффициентов. Сначала запишем общий вид многочленов $Qleft( x right)$ и $Rleft( x right)$:

[begin{align}Qleft( x right) &= color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} \ Rleft( x right) &= color{blue}{k}x+ color{blue}{l} \ end{align}]

Пусть вас не пугает большое количество переменных. Это нормально для многочленов высших степеней. Подставим наши выражения в формулу для $Pleft( x right)$:

[begin{align}Pleft( x right) &=left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x-1 right)+ \ &+ color{blue}{k}x+ color{blue}{l} \ end{align}]

Раскрываем скобки. Для удобства запишем одночлены одинаковой степени в одном и том же столбце:

[begin{array}{rrrrrr} color{blue}{a}{{x}^{5}} & + color{blue}{2a}{{x}^{4}} & — color{blue}{a}{{x}^{3}} & {} & {} & {}\ {} & + color{blue}{b}{{x}^{4}} & + color{blue}{2b}{{x}^{3}} & — color{blue}{b}{{x}^{2}} & {} & {}\ {} & {} & + color{blue}{c}{{x}^{3}} & + color{blue}{2c}{{x}^{2}} & — color{blue}{c}x & {}\ {} & {} & {} & + color{blue}{d}{{x}^{2}} & + color{blue}{2d}x & — color{blue}{d}\ {} & {} & {} & {} & + color{blue}{k}x & + color{blue}{l}\ end{array}]

Приводим подобные слагаемые:

[begin{align}Pleft( x right) &=color{blue}{a}{{x}^{5}}+left( color{blue}{2a+b} right){{x}^{4}}+left( color{blue}{-a+2b+c} right){{x}^{3}}+ \ &+left( color{blue}{-b+2c+d} right){{x}^{2}}+left( color{blue}{-c+2d+k} right)x+left( color{blue}{-d+l} right) \ end{align}]

Сравниваем эту запись с исходным многочленом:

[Pleft( x right)= color{red}{1}cdot {{x}^{5}}+ color{red}{0}cdot {{x}^{4}}+ color{red}{0}cdot {{x}^{3}}+ color{red}{0}cdot {{x}^{2}}+ color{red}{0}cdot x+left( color{red}{-1} right)]

Получаем шесть уравнений, которые последовательно решаются:

[begin{array}{ll}color{blue}{a}= color{red}{1} & color{blue}{d}=b-2c= color{red}{-12}\ color{blue}{b}=-2a= color{red}{-2} & color{blue}{k}=c-2d= color{red}{29}\ color{blue}{c}=a-2b= color{red}{5} & color{blue}{l}=d-1= color{red}{-13}\ end{array}]

Подставим найденные коэффициенты в выражения для $Qleft( x right)$ и $Rleft( x right)$:

[begin{align}Qleft( x right) &={{x}^{3}}-2{{x}^{2}}+5x-12 \ Rleft( x right) &=29x-13 \ end{align}]

Мы нашли неполное частное и остаток от деления. Это и есть окончательный ответ.

Ответ: $Qleft( x right)={{x}^{3}}-2{{x}^{2}}+5x-12$, $Rleft( x right)=29x-13$.

5. Выделение точного квадрата

Ещё одно приложение метода неопределённых коэффициентов — это «сворачивание» многочленов по формулам сокращённого умножения:

[begin{align}{{left( apm b right)}^{2}} &={{a}^{2}}pm 2ab+{{b}^{2}} \ {{left( apm b right)}^{3}} &={{a}^{3}}pm 3{{a}^{2}}b+3a{{b}^{2}}pm {{b}^{3}} \ end{align}]

Здесь всё как в разложении на множители: раскрывать скобки и привести подобные легко, а вот обратный переход — по коэффициентам «угадать» формулу сокращённого умножения — операция весьма нетривиальная.

Такие «нетривиальные операции» регулярно встречаются в задачах с параметрами и при работе с корнями. Параметрам посвящён отдельный урок, а вот корни мы рассмотрим прямо сейчас.

Задача 5.1. Избавление от корня

Задача. Упростите выражение

[sqrt{7+4sqrt{3}}]

Решение. Единственное, что здесь можно упростить — это избавиться от внешнего большого корня. Для этого нужно представить подкоренное выражение в виде точного квадрата:

[7+4sqrt{3}={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}}]

Почему именно такая конструкция возводится в квадрат? Всё просто: в исходной сумме мы видим одно слагаемое с корнем и одно слагаемое без него. Для получения такой суммы исходные слагаемые тоже должны быть разными: одно с корнем, а другое — без него.

В этом случае числа $color{blue}{a}$ и $color{blue}{b}$ будут либо рациональными, либо вообще целыми. И в этом вся суть метода неопределённых коэффициентов, потому что найти такие числа не составит особого труда — достаточно раскрыть скобки по формуле квадрата суммы:

[begin{align}{{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}} &={color{blue}{a}^{2}}+2color{blue}{ab}sqrt{3}+{{left( color{blue}{b}sqrt{3} right)}^{2}}= \ &=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3} end{align}]

Сравниваем полученное разложение с исходным выражением:

[color{red}{7}+color{red}{4}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3}]

Чтобы эти выражения были гарантированно равны друг другу, достаточно потребовать, чтобы слагаемые без корня совпадали. Как и слагаемые с корнем:

[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=7 \ 2color{blue}{ab} &=4 end{align} right.]

Это нелинейная система с двумя переменными, которая легко решается методом подбора:

[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{2}^{2}}+3cdot {color{red}{1}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{2}cdotcolor{red}{1} end{align} right.]

Научиться раскладывать целые числа на «правильные» слагаемые и множители — вопрос небольшой практики. Просто попробуйте — и вы поймёте, насколько это быстро и легко.

Нам остаётся лишь записать решение:

[color{blue}{a}=color{red}{2}; color{blue}{b}=color{red}{1}]

Затем подставить найденные числа в исходное выражение:

[begin{align}sqrt{7+4sqrt{3}} &=sqrt{{{left( 2+sqrt{3} right)}^{2}}}= \ &=left| 2+sqrt{3} right|= \ &=2+sqrt{3} end{align}]

Ответ: $2+sqrt{3}$.

Важное замечание. Помните, что корень не просто «сжигает» квадрат вокруг выражения — на их месте появляется модуль:

[sqrt{{{a}^{2}}}=left| a right|]

Потому что арифметический квадратный корень — это по определению всегда неотрицательное число:

[begin{align}sqrt{{{5}^{2}}} &=left| 5 right|=5 \ sqrt{{{left( -8 right)}^{2}}} &=left| -8 right|=8 end{align}]

Когда под модулем стоит иррациональное выражение, его знак следует проверять отдельно. Иначе даже при правильном ответе его можно счесть недостаточно обоснованным.

Если вы забыли, как проверять знаки таких выражений, вернитесь к уроку «Знаки иррациональных выражений». В двух словах: для такой проверки используются либо цепочки неравенств, либо цепочки равносильных преобразований.

В следующем задании мы отработаем оба способа.

Задача 5.2. Предварительные преобразования

Задача. Упростите выражение

[sqrt{37-5sqrt{48}}]

Под корнем мы видим ещё один корень: $sqrt{48}$ — это большое число, с ним сложно работать. Поэтому прежде чем искать точный квадрат, немного упростим выражение:

[begin{align}sqrt{37-5sqrt{48}} &=sqrt{37-5sqrt{color{red}{16}cdot 3}}= \ &=sqrt{37-5cdot color{red}{4}cdot sqrt{3}}= \ &=sqrt{37-20sqrt{3}} end{align}]

Теперь представляем подкоренное выражение в виде точного квадрата

[37-20sqrt{3}={{left( color{blue}{a}- color{blue}{b}sqrt{3} right)}^{2}}]

Обратите внимание: перед нами квадрат разности. Потому что в исходном подкоренном выражении элементы не складывались, а именно вычитались. Этот факт ещё даст о себе знать, когда будем выяснять знак подмодульного выражения.

Ну а пока всё просто. Сравниваем старую запись и новую:

[color{red}{37}-color{red}{20}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)-2color{blue}{ab}sqrt{3}]

Получаем систему уравнений:

[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=37 \ 2color{blue}{ab} &=20 end{align} right.]

Второе уравнение перепишем в виде $color{blue}{ab}=10$, а затем разложим правые части равенств на «правильные» слагаемые и множители:

[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{5}^{2}}+3cdot {color{red}{2}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{5}cdotcolor{red}{2} end{align} right.]

Получили красивое решение:

[color{blue}{a}=color{red}{5}; color{blue}{b}=color{red}{2}]

Возвращаемся к исходному выражению и извлекаем корень:

[sqrt{37-20sqrt{3}}=sqrt{{{left( 5-2sqrt{3} right)}^{2}}}=left| 5-2sqrt{3} right|]

Чтобы раскрыть модуль, нужно выяснить знак иррационального числа $5-2sqrt{3}$. Для этого можно заметить, что $sqrt{3} lt 2$, поэтому

[5-2sqrt{3} gt 5-2cdot 2=1 gt 0]

Это и есть цепочка неравенств. Также можно напрямую сравнить число $5-2sqrt{3}$ с нулём:

[begin{align}5-2sqrt{3} &vee 0 \ 5 &vee 2sqrt{3} \ 25 &vee 12 end{align}]

Очевидно, что $25 gt 12$, поэтому мы ещё раз убеждаемся, что исходное число положительное, и модуль раскрывается со знаком «плюс»:

[left| 5-2sqrt{3} right|=5-2sqrt{3}]

Ответ: $5-2sqrt{3}$.

Но всё это были довольно простые примеры с квадратным корнем. Как насчёт корней $n$-й степени?

Задача 5.3. Проблема с корнем

Задача. Упростите выражение

[sqrt[3]{sqrt{10}-3}cdot sqrt[6]{19+6sqrt{10}}]

Решение. Для начала вспомним свойства корней $n$-й кратности. Их можно умножать:

[sqrt[n]{a}cdot sqrt[n]{b}=sqrt[n]{acdot b}]

А также извлекать корень из корня:

[sqrt[k]{sqrt[m]{a}}=sqrt[mcdot k]{a}]

В частности, второй корень из задачи можно переписать так:

[sqrt[6]{19+6sqrt{10}}=sqrt[3]{sqrt{19+6sqrt{10}}}]

Чтобы избавиться от внутреннего квадратного корня, представим подкоренное выражение в виде точного квадрата. Но поскольку $sqrt{10}=sqrt{5}cdot sqrt{2}$, возможны два варианта:

[begin{align}19+6sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}} \ 19+6sqrt{10} &={{left( color{blue}{a}sqrt{2}+ color{blue}{b}sqrt{5} right)}^{2}} \ end{align}]

Однако в исходном выражении (т.е. прямо в условии задачи) есть ещё один $sqrt{10}$, который пока никак не преобразуется и никуда не денется, поэтому целесообразно рассмотреть лишь первый вариант:

[begin{align} color{red}{19}+ color{red}{6}sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}}= \ &=ldots =left( {color{blue}{a}^{2}}+10{color{blue}{b}^{2}} right)+ 2color{blue}{ab}sqrt{10} end{align}]

Получаем стандартную систему:

[left{ begin{align}{color{blue}{a}^{2}}+10{color{blue}{b}^{2}} &=19 \ 2 color{blue}{ab} &=6 end{align} right.]

Второе уравнение равносильно $color{blue}{ab}=3$, и всю систему можно переписать так:

[left{ begin{align}{color{blue}{a}^{2}}+10cdot {color{blue}{b}^{2}} &={color{red}{3}^{2}}+10cdot {color{red}{1}^{2}} \ color{blue}{a} cdotcolor{blue}{b} &= color{red}{3}cdotcolor{red}{1} end{align} right.]

Очевидно, что $color{blue}{a}=color{red}{3}$, $color{blue}{b}=color{red}{1}$, поэтому

[begin{align}sqrt{19+6sqrt{10}} &=sqrt{{{left( 3+sqrt{10} right)}^{2}}}= \ &=left| 3+sqrt{10} right|= \ &=3+sqrt{10} end{align}]

Возвращаемся к исходному заданию:

[sqrt[3]{sqrt{10}-3}cdot sqrt[3]{3+sqrt{10}}=sqrt[3]{{{left( sqrt{10} right)}^{2}}-{{3}^{2}}}=1]

Ответ: 1.

Наконец, рассмотрим задание, где требуется выделить куб суммы и куб разности. Как вы понимаете, это задание совершенно другого уровня сложности.:)

Задача 5.4. Куб суммы и куб разности

Задача. Упростите выражение

[sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}]

Чтобы «красиво» извлечь корень третьей степени, нужно представить подкоренное выражение в виде точного куба. Начнём с суммы:

[begin{align}color{red}{10}+ color{red}{6}sqrt{3} &={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{3}}= \ &={color{blue}{a}^{3}}+3{color{blue}{a}^{2}} color{blue}{b}sqrt{3}+3color{blue}{a}{color{blue}{b}^{2}}cdot 3+{color{blue}{b}^{3}}cdot 3sqrt{3}= \ &=left( {color{blue}{a}^{3}}+9color{blue}{a}{color{blue}{b}^{2}} right)+left( 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} right)sqrt{3} end{align}]

Получаем систему с двумя неизвестными:

[left{ begin{align}{color{blue}{a}^{2}}+9color{blue}{a}{color{blue}{b}^{2}} &=10 \ 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} &=6 end{align} right.]

Методом подбора находим решение: $color{blue}{a}=color{red}{1}$, $color{blue}{b}=color{red}{1}$. Несмотря на грозный внешний вид, такие системы часто легко решаются простым перебором с проверкой:

[{{left( 1+1cdot sqrt{3} right)}^{3}}=1+3sqrt{3}+9+3sqrt{3}=10+6sqrt{3}]

Возвращаемся к исходному выражению:

[begin{align}& sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}= \ = &sqrt[3]{left( 1+sqrt{3} right)}+sqrt[3]{left( 1-sqrt{3} right)}= \ = & 1+sqrt{3}+1-sqrt{3}=2 \ end{align}]

Ответ: 2.

6. Избавление от иррациональности в знаменателе

Последний приём, который мы рассмотрим в этом уроке — избавление от иррациональностей в знаменателе с помощью неопределённых коэффициентов.

Из курса алгебры мы помним, как избавлять от простых иррациональностей. Например, домножение на квадратный корень:

[frac{1}{sqrt{2}}=frac{1cdotcolor{red}{sqrt{2}}}{sqrt{2}cdotcolor{red}{sqrt{2}}}=frac{sqrt{2}}{2}]

Или домножение на сопряжённое:

[frac{1}{sqrt{3}-1}=frac{1cdot left( color{red}{sqrt{3}+1} right)}{left( sqrt{3}-1 right)cdot left( color{red}{sqrt{3}+1} right)}=frac{sqrt{3}+1}{2}]

Но всё это касается лишь самых простых корней — квадратных. Уже в случае с кубическими корнями такой фокус не пройдёт. Тут-то на помощь к нам и приходят коэффициенты-переменные.

Задача 6.1. Корень третьей степени

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{10}{1+sqrt[3]{9}}]

Поскольку это иррациональное число, то никакие преобразования не избавят нас от корней полностью.

Заметим, что $sqrt[3]{9}=sqrt[3]{3}cdot sqrt[3]{3}$. Попробуем возвести число $sqrt[3]{3}$ в разные степени:

[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{3} right)}^{n}} & sqrt[3]{3} & sqrt[3]{9} & 3 & 3sqrt[3]{3} & 3sqrt[3]{9} & 9\ end{array}]

Итак, все степени числа $sqrt[3]{3}$ можно разделить на три типа:

1. Целые числа $color{blue}{a}in mathbb{Z}$;
2. Иррациональные выражения вида $color{blue}{b}sqrt[3]{3}$ где $color{blue}{b}in mathbb{Z}$;
3. Выражения вида $color{blue}{c}sqrt[3]{9}$, где $color{blue}{c}in mathbb{Z}$.

Логично предположить (и это можно доказать), что результат деления на $1+sqrt[3]{9}$ можно представить в виде комбинации слагаемых этих трёх типов:

[frac{10}{1+sqrt[3]{9}}=color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]

Однако нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$ и $color{blue}{c}$. Найти их — в этом и состоит суть задачи.:)

И тут к делу подключается метод неопределённых коэффициентов. Преобразуем уравнение так, чтобы найти эти коэффициенты. Для начала умножим обе части на $1+sqrt[3]{9}$:

[10=left( 1+sqrt[3]{9} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)]

Раскрываем скобки:

[color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}+ color{blue}{a}sqrt[3]{9}+ 3color{blue}{b}+ 3color{blue}{c}sqrt[3]{3}=10]

Группируем слагаемые относительно одинаковых корней:

[begin{align}& left( color{blue}{a}+ 3color{blue}{b} right)+left( color{blue}{b}+ 3color{blue}{c} right)sqrt[3]{3}+left( color{blue}{a} + color{blue}{c} right)sqrt[3]{9}= \ = &color{red}{10}+ color{red}{0}cdot sqrt[3]{3}+ color{red}{0}cdot sqrt[3]{9} \ end{align}]

Выше мы предположили, что все коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ — целые (в крайнем случае рациональные). Следовательно, множители при корнях $sqrt[3]{3}$ и $sqrt[3]{9}$ должны быть равны нулю (иначе число слева будет иррациональным):

[begin{align}color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align}]

С учётом этих двух условий само уравнение примет вид

[color{blue}{a}+ 3color{blue}{b}= color{red}{10}]

Получили систему из трёх уравнений с тремя неизвестными:

[left{ begin{align}color{blue}{a}+ 3color{blue}{b} &= color{red}{10} \ color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align} right.]

Все уравнения линейные, система решается элементарно. Решением будут числа $color{blue}{a}= color{red}{1}$, $color{blue}{b}= color{red}{3}$, $color{blue}{c}= color{red}{-1}$, поэтому исходное выражение можно переписать так:

[frac{10}{1+sqrt[3]{9}}= color{red}{1}+ color{red}{3}cdot sqrt[3]{3}- color{red}{1}cdot sqrt[3]{9}]

Ответ: $1+3sqrt[3]{3}-sqrt[3]{9}$.

Важное замечание. Чтобы избавиться от иррациональности конкретно в этой задаче, достаточно было домножить числитель и знаменатель дроби на недостающую часть куба суммы:

[begin{align} frac{10}{1+sqrt[3]{9}} &=frac{10cdot left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}{left( 1+sqrt[3]{9} right)left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}= \ &=ldots =1+3sqrt[3]{3}-sqrt[3]{9} end{align}]

Однако такой подход не работает, когда в знаменателе стоит конструкция вида $color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}$. А метод неопределённых коэффициентов работает всегда.:)

Попробуем решить ещё одну задачу такого же типа.

Задача 6.2. То же самое, но чуть сложнее

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{46}{2-3sqrt[3]{2}}]

Решение. Найдём несколько степеней числа $sqrt[3]{2}$:

[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{2} right)}^{n}} & sqrt[3]{2} & sqrt[3]{4} & 2 & 2sqrt[3]{2} & 2sqrt[3]{4} & 4\ end{array}]

На будущее: для корня $n$-й степени достаточно рассмотреть первые $n$ степеней. В нашем случае достаточно было выписать $sqrt[3]{2}$, $sqrt[3]{4}$ и $sqrt[3]{8}=2$ — новых иррациональных чисел мы уже не получим.

Итак, решаем задачу методом неопределённых коэффициентов. Попробуем подобрать целые (или рациональные) числа $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ такие, что

[frac{46}{2-3sqrt[3]{2}}= color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4}]

Умножаем обе части уравнения на $2-3sqrt[3]{2}$:

[left( 2-3sqrt[3]{2} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4} right)=46]

Раскрываем скобки, приводим подобные:

[begin{align}2color{blue}{a}+ 2color{blue}{b}sqrt[3]{2}+ 2color{blue}{c}sqrt[3]{4} -3color{blue}{a}sqrt[3]{2} -3color{blue}{b}sqrt[3]{4} -6color{blue}{c} &= color{red}{46} \ left( 2color{blue}{a}- 6color{blue}{c} right)+left( 2color{blue}{b}- 3color{blue}{a} right)sqrt[3]{2}+left( 2color{blue}{c}- 3color{blue}{b} right)sqrt[3]{4} &= color{red}{46}end{align}]

Это равенство верно при соблюдении трёх условий:

[left{ begin{align}2color{blue}{a}- 6color{blue}{c} &= color{red}{46} \ 2color{blue}{b}- 3color{blue}{a} &=color{red}{0} \ 2color{blue}{c}- 3color{blue}{b} &=color{red}{0} \ end{align} right.]

Это система из трёх линейных уравнений с тремя неизвестными. Её решение:

[color{blue}{a}= color{red}{-4}; color{blue}{b}= color{red}{-6}; color{blue}{c}= color{red}{-9}]

Следовательно, исходное выражение можно переписать так:

[frac{46}{2-3sqrt[3]{2}}= color{red}{-4-6}cdot sqrt[3]{2} color{red}{-9}cdot sqrt[3]{4}]

Ответ: $-4-6sqrt[3]{2}-9sqrt[3]{4}$.

Важное замечание. Здесь тоже можно «составить» куб суммы в знаменателе:

[begin{align}frac{46}{2-3sqrt[3]{2}} &=frac{46cdot left( color{red}{{{2}^{2}}+2cdot 3sqrt[3]{2}+9sqrt[3]{4}} right)}{{{2}^{3}}-{{left( 3sqrt[3]{2} right)}^{3}}} \ &= ldots =-4-6sqrt[3]{2}-9sqrt[3]{4} end{align}]

Почему не использовать этот приём всегда? Потому что в следующей задаче он уже не сработает. Там помогут только неопределённые коэффициенты и решение системы уравнений.

Задача 6.3. Когда кубы уже не помогают

Это задание чуть сложнее, потому что здесь не помогут формулы сокращённого умножения. Да и сами вычисления будут чуть сложнее, чем в предыдущих задачах.

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}]

Мы уже встречались с числами $sqrt[3]{3}$ и $sqrt[3]{9}$, поэтому знаем, что исходное выражение можно представить в виде

[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}= color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]

Преобразуем выражение, избавившись от дроби:

[left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)cdot left( 1+sqrt[3]{3}-sqrt[3]{9} right)= color{red}{2}]

Раскроем скобки, приведём подобные:

[begin{align}left( color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} right) &+left( color{blue}{a}+ color{blue}{b} -3color{blue}{c} right)sqrt[3]{3}+ \ &+left( -color{blue}{a}+ color{blue}{b}+ color{blue}{c} right)sqrt[3]{9}= color{red}{2} \ end{align}]

Это равенство возможно при соблюдении трёх условий:

[left{ begin{align}color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} &= color{red}{2} \ color{blue}{a}+ color{blue}{b}- 3color{blue}{c} &= color{red}{0} \ -color{blue}{a}+ color{blue}{b}+ color{blue}{c} &= color{red}{0} end{align} right.]

Три линейных уравнения, три переменных. Всё решается легко:

[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]

Следовательно, исходное выражение перепишется так:

[frac{2}{1+ sqrt[3]{3}- sqrt[3]{9}}= color{red}{2}+ color{red}{1}cdot sqrt[3]{3}+ color{red}{1}cdot sqrt[3]{9}]

Ответ: $2+sqrt[3]{3}+sqrt[3]{9}$.

Как видите, никакие кубы суммы здесь уже не помогут.:)

7. Зачем всё это нужно

В этом уроке мы рассмотрели пять типов задач, которые можно решить методом неопределённых коэффициентов. У внимательного читателя наверняка возник вопрос: зачем вообще нужен этот метод, когда многие из этих задач можно решить проще и быстрее с помощью отдельных специальных приёмов?

В самом деле:

• Большинство многочленов отлично раскладываются на множители с помощью теоремы Безу и схемы Горнера — об этом мы говорили в отдельном уроке. Но только при условии, что среди корней есть рациональные.
• То же самое можно сказать и про решение уравнений.
• Делить многочлены друг на друга с остатком вообще лучше столбиком. Это самый быстрый и самый надёжный способ — при условии, что среди коэффициентов нет параметров.
• Точные квадраты зачастую можно подобрать, если немного подумать. Как и дополнительные множители для избавления от иррациональности. Если только это не «тяжёлый» случай, где формулы сокращённого умножения не работают.

Так зачем же нужен метод неопределённых коэффициентов? Всё дело в тех самых оговорках: «при условии», «только если не тяжёлый случай» и т.д.

Основная сила этого метода — в его универсальности. Да, считать придётся чуть больше, чем при использовании более специализированных приёмов. И да: целочисленный перебор не всегда приводит нас к успеху.

Но перед нами прежде всего универсальный алгоритм. Который точно работает — всегда, везде, без всяких оговорок. И если задача не решается методом неопределённых коэффициентов, то «специализированные» приёмы тем более не помогут.

Более того: область применения этого метода намного шире. Например, мы не рассмотрели разложение рациональных дробей в простейшие, а это очень важный приём, например, в интегрировании — и ему тоже нет альтернативы.

Поэтому берите на вооружение всё, что вы сегодня узнали, практикуйтесь — и да прибудут с вами решённые задачи, олимпиады и университетские зачёты и экзамены.:)

Смотрите также:

1. Бином Ньютона
2. Схема Горнера
3. Сравнение дробей
4. Четырехугольная пирамида в задаче C2
5. Задача B5: площадь кольца
6. Сечения и двугранные углы