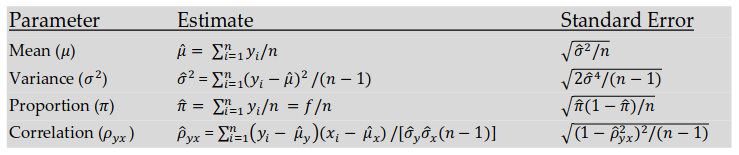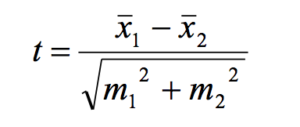Как найти размер критерия - Исправление недочетов и поиск решений вместе с Examum.ru

Как определить размер выборки?

Время на прочтение
4 мин

Количество просмотров 56K

Статистика знает все. И Ильф и Е. Петров, «12 Стульев»

Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.

Теоретический минимум

Не будет лишним освежить память, эти термины нам пригодятся далее.

Популяция – Множество всех объектов, среди которых проводится исследования.
Выборка – Подмножество, часть объектов из всей популяции, которая непосредственно участвует в исследовании.
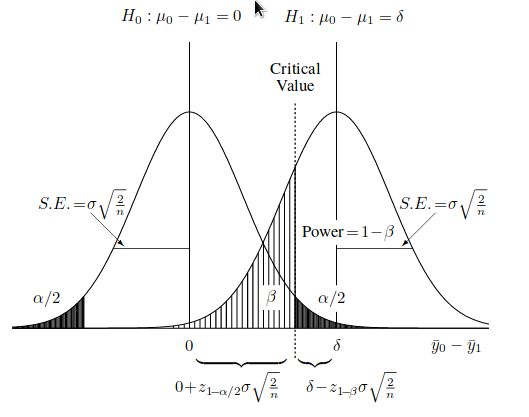
Ошибка первого рода — (α) Вероятность отвергнуть нулевую гипотезу, в то время как она верна.
Ошибка второго рода — (β) Вероятность не отвергнуть нулевую гипотезу, в то время как она ложна.
1 — β — Статистическая мощность критерия.
μ₀ и μ₁ — Средние значения при нулевой и альтернативной гипотезе.

Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.

Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.

Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).

$hat{mu} pm t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

df — Степень свободы = n — 1, от английского «degrees of freedom».
$t_{{alpha/2};df}$ — Двусторонняя критическая величина, t-критерий Стьюдента.

Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.

H₀: μ = h
H₁: μ > h
H₂: μ < h

С доверительным интервалом 100(1-α) для μ можно сделать выбор в пользу H₁ и H₂ :

Если нижний предел доверительного интервала 100(1-α) < h, то тогда отвергаем H₀ в пользу H₂.
Если верхний предел доверительного интервала 100(1-α) > h, то тогда отвергаем H₀ в пользу H₁.
Если доверительного интервала 100(1-α) включает в себя h, то тогда мы не может отвергнуть H₀ и такой результат считается неопределенным.

Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.

Где $t = (hat{mu} - h)/sqrtfrac{hatsigma^2}{n}$ .

Доверительный интервал, погрешность и размер выборки

Возьмем самое первое уравнение и выразим оттуда ширину доверительного интервала (Ур. 2).

$w = 2t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

В некоторых случаях мы можем заменить t-статистику Стьюдента на z стандартного нормального распределения. Еще одним упрощением заменим половину от w на погрешность измерения E. Тогда наше уравнения примет вид (Ур. 3).

$E = z_{alpha/2}sqrt{frac{hatsigma^2}{n}}$

Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).

$n = left[frac{z_{alpha/2}*sigma}{E}right]^2$

Практика — считаем с R

Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.

H₀: μ = 1
H₁: μ > 1

Насекомые	0	1	2	3	4	5	6
Ловушки	10	9	5	5	1	2	1

> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883

Обратите внимание, что среднее и стандартное отклонение практически равны, что естественно для распределения Пуассона. Доверительный интервал 95% для t-статистики Стьюдента и df=32.

> qt(.975, 32)
[1] 2.036933

и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.

> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568

В итоге, следует отбраковать H₀ и принять H₁ так как с вероятностью 95%, μ > 1.

В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.

> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144

Поправка на ветер

На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).

$n = 4tildesigma^2 (z_{alpha/2}/w)^2 + z^2_{alpha/2}/2$

Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (~). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — , и вместо нее мы используем запланированное — . Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.

А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как $z_{alpha/2} < t_{{alpha/2};df}$ , необходима поправка Гюнтера.

Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.

Использованные материалы

Sample sizes
Hypothesis testing

Источник

Г Л А В А VII

КРИТЕРИИ СОГЛАСИЯ

Критериями согласия обычно называют критерии, предназначенные для проверки простой гипотезы H1 = {F = F1} при сложной альтернативе, состоящей в том, что H1 неверна. Мы рассмотрим более широкий класс основных гипотез, включающий в том числе и сложные гипотезы, а критериями согласия будем называть любые критерии, устроенные по одному и тому же принципу. А именно, пусть задана некоторая случайная величина, измеряющая отклонение эмпирического распределения от теоретического, распределение которой существенно разнится в зависимости от того, верна или нет основная гипотеза. Критерии согласия принимают или отвергают основную гипотезу исходя из величины этой функции отклонения.

§ 1. Общий вид критериев согласия

Мы опишем конструкцию критерия для случая простой основной гипотезы, а в дальнейшем будем её корректировать по мере изменения задачи.

~ F

Пусть X = (X1, . . . , Xn) — выборка из распределения . Проверяется основная гипотеза H1 = {F = F1} при альтернативе H2 = {F 6= F1}.

ρ ~

О п р е д е л е н и е 21. Предположим, что нашлась функция (X) со следующими свойствами:

(K1) если гипотеза H1 верна, т. е. если Xi F1, то распределение ве-

~
личины ρ(X) либо целиком известно, либо при больших n сближается с
известным распределением G;
(K2) если гипотеза H1 неверна, т. е. если Xi	имеют какое-то распределе-
~	p
ние F2 6= F1, то \|ρ(X)\| −→ ∞ при n → ∞ для любого такого F2.
Для случайной величины η G определим постоянную C из равенства
ε = P(\|η \| > C). Построим критерий	если	\|ρ(X~ )\|			(12)
	δ(X~ ) = (H2,		C.
	H1,	если	~		< C,
	ρ(X)
			\|	\| >

Этот критерий называется критерием согласия.

Критерий согласия «работает» по принципу: если для данной выборки функция отклонения велика по абсолютному значению, то это свидетель-

52 ГЛАВА VII. КРИТЕРИИ СОГЛАСИЯ

ствует в пользу альтернативы, и наоборот. При этом степень «великости» определяется исходя из того, как функция отклонения должна себя вести, если бы основная гипотеза была верна. Действительно, если H1 верна, стати-

~	G. Следовательно, она должна себя
стика ρ(X) имеет почти распределение

вести подобно типичной случайной величине η из этого распределения. Но для случайной величины η попадание в область {|η | > C} маловероятно: вероятность этого события равна малому числу ε. Поэтому попадание вели-

ρ ~

чины (X) в эту область заставляет подозревать, что гипотеза H1 неверна.

|ρ ~ |

Тем более, что больших значений величины (X) следует ожидать именно при альтернативе H2.

Убедимся в том, что этот критерий имеет (асимптотический) размер ε

и является состоятельным.
Условие (K1) отвечает за размер критерия:
		~	→ P (\|η \| > C ) = ε.
α1(δ) = PH1 \|ρ(X)\| > C
Расшифруем условие	(K2), отвечающее за состоятельность критерия.
	p
По определению, запись ξn −→ ∞ означает, что для любого C > 0
	P(ξn < C) → 0	при n → ∞.

Согласно этому определению, для любого распределения F2 из числа альтернатив вероятность ошибки второго рода стремится к нулю:

		~	→ 0,
α2(δ, F2) = PF2 \|ρ(X)\| < C
что доказывает состоятельность	критерия.

З а м е ч а н и е 10. Если в (K1) известно точное, а не приближённое рас-

~	ε.
пределение ρ(X), то критерий (12) будет иметь точный размер

Проверяя гипотезу, мы задали ε, затем по точному или предельному рас-

ρ ~

пределению (X) вычислили «барьер» C, с которым сравнили значение

|ρ ~ |

(X) . На практике часто поступают иначе. Пусть по данной числовой выборке ~x вычислено число ρ = ρ ~x . Число

ε = P(|η | > |ρ |)

называют реально достигнутым уровнем значимости критерия. По величине ε можно судить о том, следует принять или отвергнуть основную гипотезу. Именно это число является результатом проверки гипотезы в любом статистическом пакете программ. Критерий (12) можно с её помощью записать так: H1 отвергается при ε 6 ε.

Каков же смысл величины ε ? Вероятность
PH1 (\|ρ(X~ )\| > \|ρ \|)	(13)

§ 2. Проверка простых гипотез о параметрах

равна или приближённо равна ε . Вероятность (13) имеет следующий смысл: это вероятность, взяв выборку из распределения F1, получить по ней боль-

|ρ ~ |

шее отклонение (X) эмпирического от истинного рапсределения, чем получено по проверяемой выборке. Больш´ие значения вероятности (13) или ε свидетельствуют в пользу основной гипотезы. Напротив, малые значения вероятности (13) или ε свидетельствуют в пользу альтернативы.

Если, например, вероятность (13) равна 0,2, следует ожидать, что в среднем 20 % «контрольных» выборок, удовлетворяющих основной гипотезе

|ρ ~ |

(каждая пятая), будут обладать б´ольшим отклонением (X) по сравнению с тестируемой выборкой, в принадлежности которой распределению F1 мы не уверены. Можно отсюда сделать вывод, что тестируемая выборка ведёт себя не хуже, чем 20 % «правильных» выборок.

Но попадание в область вероятности 0,2 не является редким или «почти невозможным» событием. В статистике редкими обычно считают события с вероятностями ε = 0,01 или ε = 0,05 (это зависит от последствий ошибочного решения). Поэтому при ε = 0,2 > 0,05 основную гипотезу можно принять.

§ 2. Проверка простых гипотез о параметрах

Проверка гипотезы о среднем нормального распределения с известной дисперсией. Имеется выборка из нормального распределения Na, σ2 с известной дисперсией σ2. Проверяется гипотеза H1 = {a = a0} против альтернативы H2 = {a 6= a0}. Построим критерий точного размера ε с помощью функции

	√
ρ(X~ ) =			X − a0	.
n
					σ
Очевидно свойство (K1): если H1							~
верна, то ρ(X) N0, 1.
По ε выберем C = τ1−ε/2 — квантиль стандартного нормального распре-
деления. Критерий выглядит как все критерии согласия:	(14)
δ(X~ ) = (H2,	если	\|ρ(X~ )\|		C.
H1,	если	~		< C,
ρ(X)
					\|	\| >

У п р а ж н е н и е. Доказать, что критерий 14 имеет точный размер ε и

является состоятельным.

Можно переписать этот критерий по-другому:

δ(X~ ) =

− σ n

H1,

если

Cσ

; a0 +

Cσ

√

a0 + C .

если

либо X

− √n

√n

54	ГЛАВА VII. КРИТЕРИИ СОГЛАСИЯ

Вид критической области в критерии согласия зависит от вида альтернативной гипотезы. Так, для «двусторонней» альтернативы H2 = {a 6= a0} критическая область имеет вид |ρ| > C, т. е. эта область есть объединение двух интервалов:

		Cσ	Cσ
X 6 a0 −	либо X > a0 +
√		√
n	n

Если же альтернатива будет односторонней, например, H2 = {a < a0}, то

Cσ

и критическую область следует брать одностороннюю: X 6 a0 − √n . При

этом постоянную C следует выбирать так, чтобы при верной основной гипотезе вероятность попасть в критическую область равнялась ε. В данном случае C = τ1−ε, а не τ1−ε/2. Действительно: вероятность ε должна теперь соответствовать не двум «хвостам» нормального стандартного распределения, а одному.

Проверка гипотезы о среднем нормального распределения с неизвестной дисперсией. Проверяется та же гипотеза, что и в предыдущем разделе, но

в случае, когда дисперсия σ2

неизвестна. Критерий, который мы построим,

называют одновыборочным критерием Стьюдента.

Введём функцию отклонения

√

ρ ~

X − a0

, где S0 = n

(X) =

n √

−

(Xi − X) .

По п. 4 полезного следствия леммы Фишера (c. 44) выполнено свойство (K1): если a = a0, то ρ имеет распределение Стьюдента Tn−1.

Критерий строится в точности как в формуле (14), но в качестве C следует брать квантиль распределения Стьюдента, а не стандартного нормального распределения (почему?).

Критерии, основанные на доверительных интервалах. Имеется выборка из семейства распределений Fθ, где θ — неизвестный числовой параметр. Проверяется гипотеза H1 = {θ = θ0} против альтернативы H2 = {θ 6= θ0}.

Пусть имеется точный доверительный интервал (θ−, θ+) для параметра θ уровня доверия 1 − ε. Его можно использовать для проверки гипотезы H1.

Критерий	(H2,	если	θ0	(θ−, θ+)
δ(X~ ) =
	H1,	если	θ0	(θ−, θ+),
				6

имеет точный размер ε :

α1(δ) = PH1 (δ = H2) = PH1 (θ0 6 (θ−, θ+)) = 1 − PH1 (θ− < θ0 < θ+) = ε.

§ 2. Проверка простых гипотез о параметрах

Критерий для проверки гипотезы о вероятности успеха или доле признака.

Пусть дана выборка из распределения Бернулли с неизвестной вероятностью успеха p. Проверяется гипотеза H1 = {p = p0} против альтернативы H2 = = {p 6= p0}.

Используем ЦПТ для построения критерия. Пусть основная гипотеза верна. Тогда Xi Bp0 и по теореме Муавра — Лапласа распределение случайной величины

nX − np0

np0(1 − p0)

с ростом n приближается к стандартномуp

нормальному. Поэтому эту функ-

цию можно взять в качестве функции ρ(X).

Построим критерий:

если

(1 − p0)

δ(X~ ) =

H1,

np0

< C,

− np0

H2,

иначе,

где

выбирается как

квантиль уровня 1

−

ε/2 стандартного нормального

распределения, т. е. Φ(C) − Φ(−C) = ε.

Этот критерий имеет асимптотический размер ε и является состоятельным.

П р и м е р 28. Монету подбросили 1 000 раз для проверки симметричности. При этом герб выпал 483 раза. Можно ли считать монету симметричной?

Сформулируем математическую задачу: по выборке из распределения Бернулли, в которой 483 единицы и 1 000-483 нуля, проверяется основная гипотеза H1 = {p = 0,5} против альтернативы H2 = {p 6= 0,5}.

Мы можем либо воспользоваться критерием с каким-нибудь стандартным размером ε (например, 0,05 ), либо вычислить статистику критерия и реально достигнутый уровень значимости, по величине которого решить, принимать или отвергать основную гипотезу.

Пусть ε = 0,05 . По таблице функции распределения стандартного нормального закона вычислим C = 1, 96 — квантиль уровня 0,975 = 1 − ε/2 .

Найдём статистику критерия. Величина nX = X1 + . . . + Xn	равна числу
единиц в выборке (числу гербов), поэтому
ρ	~	483 − 1 000 · 0,5	= −1,075.
	(X) =	√
	1 000		0,5		0,5
				·		·
~							можно при-
Поскольку \|ρ(X)\| = 1,075 меньше, чем C = 1,96 , гипотезу H1

нять. Таким образом, критерий с (асимптотическим) размером 0,05 сделал вывод о том, что выборочные данные не противоречат проверяемой гипотезе.

56 ГЛАВА VII. КРИТЕРИИ СОГЛАСИЯ

Вычислим реально достигнутый уровень значимости критерия:

ε = P(|ξ| > 1,075) = 2Φ(−1,075) = 2 · 0,141 = 0,282,

где ξ имеет стандартное нормальное распределение.

Значение ε = 0,282 говорит о следующем: есть почти 30% шансов за то, что число гербов при бросании симметричной монеты будет больше отличаться от 500, чем полученное нами число гербов 483. Мы получили хорошее согласие с проверяемой гипотезой: есть целых тридцать процентов шансов получить худшее согласие даже для симметричной монеты. Любой критерий с вероятностью ошибки первого рода ε < 0,282 будет принимать основную гипотезу.

§ 3. Критерии для проверки гипотезы о распределении

Следующие два критерия используют для проверки гипотез о принадлежности выборки конкретному, целиком известному, распределению. Чаще всего таким распределением оказывается равномерное распределение. Например, оба этих критерии позволяют проверить равномерность результата генерации случайного числа на отрезке [0, 1] . Критерий хи-квадрат Пирсона годится также для проверки гипотез о дискретном равномерном распределении. Например, о равномерности распределения дней рождения по дням недели, о симметричности монетки и т. п.

Критерий Колмогорова. Имеется выборка X = (X1, . . . , Xn) из распределения F. Проверяется простая гипотеза H1 = {F = F1} против сложной альтернативы H2 = {F 6= F1}. В том случае, когда распределение F1 имеет непрерывную функцию распределения F1, можно пользоваться критерием Колмогорова. Критерий основан на следующей теореме.

Т е о р е м а 12 (К о л м о г о р о в а). Пусть дана выборка объёма n из рас-

пределения с непрерывной функцией распределения

F1, а

Fn —

эмпириче-

ская функция распределения. Тогда при любом y > 0

· y R

−

)

→

при

→ ∞

√n

sup

(y)

< y

K(y)

где K(y) есть функция распределения Колмогорова

K(y) =

∞

(−1)je−2j2y2 .

j=−∞

Значения этой функции (рис. 9) находят из соответствующих таблиц.
Положим	ρ	~	√			F1(y)	.

	(X) =	n sup F (y)	−
				y \| n	\|

§ 3. Критерии для проверки гипотезы о распределении

0,5

Рис. 9. График функции K(y)

По заданному ε с помощью таблицы значений функции K(y) можно найти C такое, что ε = K(y). Тогда критерий Колмогорова выглядит так:

H1,	если	~
ρ(X) < C,
δ(X~ ) = (H2,	если	ρ(X~ ) > C.

Этот критерий имеет асимптотический размер ε и является состоятельным.

Критерий χ2 Пирсона. Критерий χ2 основывается на группированных данных. Область значений предполагаемого распределения F1 делят на некоторое число интервалов. После чего строят функцию отклонения ρ по разностям теоретических вероятностей попадания в интервалы группировки и эмпирических частот.

Дана выборка объёма n из распределения F. Проверяется простая гипотеза H1 = {F = F1} при альтернативе H2 = {F 6= F1}.

Пусть A1, . . . , Ak — интервалы группировки в области значений случайной величины с предполагаемым распределением F1. Пусть для каждого j = 1, . . . , k величина νj равна числу элементов выборки, попавших в ин-

тервал Aj :

νj = {число Xi Aj} = I(Xi Aj), i=1

Пусть число pj > 0 равно теоретической вероятности попадания в интервал Aj случайной величины с распределением F1. Здесь p1 + . . . + pk = 1. Как правило, длины интервалов выбирают так, чтобы p1 = . . . = pk = 1/k. Пусть

ρ ~	k	− npj)2
	(νj
(X) =	Xj		.	(15)

	=1		npj

З а м е ч а н и е 11. Поскольку мы строим критерий, опираясь только на частоту попадания элементов выборки в интервалы группировки, мы долж-

δ ~

(X) =

ρ ~

(X) < C,

ρ ~

(X) > C.

58 ГЛАВА VII. КРИТЕРИИ СОГЛАСИЯ

ны заранее понимать, что критерий не сможет отличить два распределения, у которых одинаковы вероятности попасть во все интервалы группировки.

Верна теорема.

Т е о р е м а 13 (П и р с о н а). Если верна гипотеза H1, то при фикси-

рованном k и при n → ∞	~
распределение величины ρ(X) приближается

к распределению Hk−1, где Hk−1 есть χ2-распределение с k−1 степенью свободы.

Осталось построить критерий согласия по определению 21. Пусть случайная величина η имеет распределение Hk−1. По таблице распределения Hk−1 найдём C, равное квантили уровня 1 − ε этого распределения: ε = P(η > C). Критерий χ2 устроен обычным образом:

(

H1, если

H2, если

Число интервалов k выбирают так, чтобы значения np1 = . . . = npk были не менее 5—6. Если выборка уже сгруппирована, то группы, в которые попало менее пяти элементов выборки, объединяют с соседними, уменьшая тем самым число интервалов группировки.

П р и м е р 29. Для проверки равномерности распределения дней рождения по месяцам года взят список дней рождений 683 студентов ИВТ СибГУТИ по данным на сентябрь 2007 г. Получено следующее распределение дней рождения: январь — 60, февраль — 62, март — 60, апрель — 63, май — 69, июнь — 59, июль — 62, август — 54, сентябрь — 41, октябрь — 45, ноябрь — 48 и декабрь — 60.

Итак, есть 12 интервалов группировки. Проверяемая гипотеза состоит в том, что вероятность элементу выборки попасть в каждый из них одна и та же и равна 1/12 (можно было взять разные вероятности, пропорциональные числу дней каждого месяца).

Вычислим статистику критерия:

ρ(X~ ) =	(60 − 683/12)2	+	(62 − 683/12)2	+ . . . +	(60 − 683/12)2	= 13,193.
683/12	683/12	683/12

Возьмём ε = 0,05 и найдём по таблице критических точек распределения

χ211 величину C такую, что P(χ211 > C) = 0,05 . Получим C = 19,68 . Величина ρ оказалась меньше C , поэтому критерий принимает основную гипотезу.

Реально достигнутый уровень значимости ε = P(χ211 > 13,193) равен 0,281 (для его вычисления следует воспользоваться более подробными таблицами или любым подходящим пакетом программ). Он показывает, что достигнуто достаточно хорошее согласие с проверяемой гипотезой.

§ 4. Критерии для проверки параметрических гипотез

Очень часто требуется проверить, например, нормальность распределения выборки безо всякого знания о параметрах распределения. Предыдущие два критерия не годятся, поскольку проверяемая гипотеза является сложной. Следующий критерий является вариантом критерия Пирсона.

Критерий χ2 для проверки параметрической гипотезы. Критерий χ2 часто применяют для проверки гипотезы о принадлежности распределения выборки некоторому параметрическому семейству.

Пусть дана выборка из неизвестного распределения F. Проверяется гипотеза о том, что это распределение принадлежит некоторому семейству распределений Fθ, где θ — неизвестный векторный параметр (размерности d).

Разобьём всю числовую ось на k > d + 1 интервалов группировки A1, . . . Ak и вычислим νj — число элементов выборки, попавших в интервал Aj. Но теперь вероятность pj = PH1 (X1 Aj) = pj(θ) зависит от неизвестного параметра θ. Функция отклонения (15) также зависит от неизвестного параметра θ, и использовать её в критерии Пирсона нельзя:

ρ ~ θ	k	− npj(θ))2
(νj
(X; ) =	Xj		.	(16)

	=1		npj(θ)

Пусть θ — такое значение параметра θ, при котором функция ρ(X~ ; θ)	при-

нимает наименьшее значение. Подставив вместо истинных вероятностей pj их оценки pj (θ ), получим функцию отклонения

ρ ~ θ	k	− npj(θ ))2
	(νj
(X; ) =	Xj		.	(17)

	=1		npj(θ )

Т е о р е м а 14 (Р. Ф и ш е р). Пусть верна гипотеза H1. Если число d есть размерность вектора параметров θ и выполнены некоторые условия гладкости функций pj(θ), то при фиксированном k и при n → ∞ распреде-

ρ ~ θ

ление величины (X; ) сближается с распределением Hk−1−d, где Hk−1−d есть χ2-распределение с k − 1 − d степенями свободы.

Построим критерий χ2. Пусть случайная величина η имеет распределение Hk−1−d. По заданному ε найдём C такое, что ε = P(η > C).

Критерий согласия χ2 устроен обычным образом:

H1,	если	ρ(X~ ; θ ) < C,
δ(X~ ) = (H2,	если	ρ(X~ ; θ ) > C.

60	ГЛАВА VII. КРИТЕРИИ СОГЛАСИЯ
З а м е ч а н и е 12.	~
Вычисление точки минимума функции ρ(X; θ) в об-

щем случае возможно лишь численно. Поэтому часто вместо оценки θ используют оценку максимального правдоподобия, построенную по выборке X1, . . . , Xn. Однако при такой замене предельное распределение величи-

~	и зависит от θ.
ны ρ(X; θ) уже не равно Hk−1−d

Данный вариант критерия Пирсона годится для проверки любой параметрической гипотезы. Но для проверки нормальности распределения выборки можно использовать специальные критерии.

Критерий Андерсона — Дарлинга. Пусть X = (X1, . . . , Xn) — выборка из неизвестного распределения и X(1), . . . , X(n) — соответствующий вариационный ряд (выборка, упорядоченная по возрастанию).

Проверяется гипотеза H1 о том, что распределение выборки принадлежит классу нормальных распределений (с неизвестными параметрами).

Вычислим выборочное среднее X , выборочную дисперсию S2 и преобразуем элементы вариационного ряда:


	X(i) − X
Yi =		.

	S

Построим статистику критерия Андерсона — Дарлинга так:

A2 = −n − n1 Xh(2i − 1) ln Φ(Yi) + (2n − 2i + 1) ln (1 − Φ(Yi))i.

i=1

Обычно вводят поправочный коэффициент, необходимый для небольших объёмов выборки:

A 2 = A2 1 +	0n	+	n2	.
	,75		2, 25

Предельное распределение статистики Андерсона — Дарлинга при верной основной гипотезе имеет весьма сложный вид. Приведём значения квантилей этого распределения для нескольких часто используемых уровней:

h0,9 = 0,631; h0,95 = 0,752; h0,975 = 0,873; h0,99 = 1, 035.

Критерий Андерсона — Дарлинга принимает гипотезу о нормальности распределения выборки, если A 2 < h1−ε , и отвергает в противном случае. Вероятность ошибки первого рода этого критерия с ростом n стремится к ε .

Заметим, что критерий Андерсона — Дарлинга годится не только для проверки нормальности: используя в статистике критерия вместо Φ другие непрерывные функции распределения, можно проверять принадлежность выборки соответствующему распределению. Однако предельное распределение статистики критерия зависит от теоретического распределения, поэтому для проверки других гипотез следует использовать другие квантили.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

17 авг. 2022 г.
читать 2 мин

Один из частых вопросов, который часто задают студенты:

Требуется ли минимальный размер выборки для проведения t-критерия?

Краткий ответ:

Нет. Для выполнения t-критерия не требуется минимального размера выборки.

Фактически, первый когда-либо выполненный t-тест использовал только размер выборки четыре .

Однако, если предположения t-критерия не выполняются, результаты могут быть ненадежными.

Кроме того, если размер выборки слишком мал, мощность теста может быть слишком низкой для обнаружения значимых различий в данных.

Давайте рассмотрим каждую из этих потенциальных проблем более подробно.

Понимание предположений t-тестов

Одновыборочный t-критерий используется для проверки того, равно ли среднее значение совокупности некоторому значению.

Этот тест делает следующие предположения:

Независимость : наблюдения в выборке должны быть независимыми.
Случайная выборка : наблюдения должны собираться с использованием метода случайной выборки, чтобы максимизировать шансы того, что выборка репрезентативна для интересующей совокупности.
Нормальность : Наблюдения должны быть примерно нормально распределены.

Двухвыборочный t-критерий используется для проверки того, существует ли значительная разница между двумя средними значениями генеральной совокупности.

Этот тест делает следующие предположения:

Независимость : наблюдения в каждой выборке должны быть независимыми.
Случайная выборка : наблюдения в каждой выборке должны быть собраны с использованием метода случайной выборки.
Нормальность : Каждый образец должен быть примерно нормально распределен.
Равная дисперсия : каждая выборка должна иметь примерно одинаковую дисперсию.

При выполнении каждого типа t-теста, если одно или несколько из этих предположений не выполняются, результаты теста могут стать ненадежными.

В этом случае лучше использовать непараметрический альтернативный тест, который не делает таких предположений.

Непараметрической альтернативой одновыборочному t-критерию является знаковый ранговый критерий Уилкоксона .

Непараметрической альтернативой двухвыборочному t-критерию является U-критерий Манна-Уитни .

Понимание силы t-тестов

Статистическая мощность относится к вероятности того, что тест обнаружит некоторый эффект, когда он действительно есть.

Можно показать, что чем меньше размер используемой выборки, тем ниже статистическая мощность данного теста. Вот почему исследователям обычно нужны выборки большего размера, чтобы они имели большую мощность и, следовательно, большую вероятность обнаружения истинных различий.

Например, предположим, что истинный размер эффекта между двумя популяциями равен 0,5 — «средний» размер эффекта. Мы можем использовать следующий R-код для вычисления мощности двухвыборочного t-критерия с использованием различных размеров выборки:

#sample size n=10
power. t.test (n=10, delta=.5, sd=1, sig.level=.05, type='two.sample')$power

[1] 0.1838375

#sample size n=30
power. t.test (n=30, delta=.5, sd=1, sig.level=.05, type='two.sample')$power

[1] 0.477841

#sample size n=50
power. t.test (n=50, delta=.5, sd=1, sig.level=.05, type='two.sample')$power

[1] 0.6968888

Вот как интерпретировать результаты:

Когда каждый размер выборки равен n = 10, мощность равна 0,184 .
Когда каждый размер выборки равен n = 30, мощность равна 0,478 .
Когда каждый размер выборки равен n = 50, мощность равна 0,697 .

Мы видим, что мощность теста увеличивается с увеличением размера выборки.

Таким образом, нам не нужен минимальный размер выборки для выполнения t-критерия, но небольшие размеры выборки приводят к меньшей статистической мощности и, следовательно, к снижению способности обнаруживать истинное различие в данных.

Вывод

Вот краткое изложение того, что мы узнали:

Для проведения t-критерия не требуется минимального размера выборки.
Если предположения t-критерия не выполняются, мы должны использовать непараметрическую альтернативу.
Если размер выборки слишком мал, мощность t-теста будет низкой, и способность теста обнаруживать истинные различия в данных будет низкой.

Дополнительные ресурсы

Следующие руководства предлагают дополнительную информацию о t-тестах.

Введение в одновыборочный t-критерий
Введение в двухвыборочный t-критерий
Введение в t-критерий парных выборок
Четыре предположения, сделанные в t-тесте

Источник

Термины курса «Математическая статистика»

Здесь собраны все (или почти все) термины, без знания содержания которых понимание курса практически невозможно

Обзор по алфавиту
Обзор по категориям

Обзор глоссария по алфавиту

Специальные | А | Б | В | Г | Д | Е | Ё | Ж | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я | Все

Равномерное распределение

Это распределение абсолютно непрерывного типа с плотностью, постоянной на основном множестве и равной 0 вне него. Конкретное значение плотности определяется с привлечением основного свойства плотности распределения — определенный интегорал от нее должен равняться единице.

Чаще всего имеется в виду равномерное распределение на отрезке, скажем, [a, b]. Тогда плотность распределения на этом отрезке равна 1/(b-a) и 0 вне него.

Размер критерия

Альтернативный термин для вероятности ошибки первого рода. Он же иногда называется уровнем критерия.

Рандомизация

Буквально «добавление случайности».

Первоначально поняти возникло для описания ситуации, возникающей при работе критериев согласия. Как поступать, если мера различия двух картин — реальной и идеальной — оказалась точно равной соответствующему критическому значению? С целью повышения мощности такого критерия оказалось целесообразным в этой ситуации поставить дополнительный случайный эксперимент с двумя исходами и принять решение в зависимости от его результата («подбросить монетку»).

Описание того, как именно должен быть устроен этот эксперимент в дополнение к основному критерию согласия и иназывают рандомизацией критерия, а сам полученный таким образом критерий рандомизированным. Понятно, что любой критерий может рассматриваться как рандомизированый с дополнительным случайным экспериментом, который всегда заканчивается успехом.

Рандомизированные критерии тесно связаны с так называемыми нечеткими множествами. Действительно, критическое множество здесь нечеткое — принадлежность ему элементов границы имеет место только с определенно вероятностью.

В дальнейшем понятие рандомизации очень расширилось. Подобные приемы позволяяют генерировать недостающие выборочные данные с высокой степенью достоверности (метод бутстрэп), группировать выборки с высокой степенью повторяемости элементов или даже приближенно вычислять интегралы (метод Монте-Карло) и многое другое.

Рао-Крамера неравенство

Неравенство, которое в достаточно широких и естественных условиях регулярности параметрического семейства указывает нижнюю границу дисперсии для возможных оценок неизвестного параметра для этого семейства и определяет необходимые и достаточные условия того, чтобы для оценки эта нижняя граница достигалась.

Поскольку в обычных, регулярных задачах при фиксированном смещении оценки ее дисперсия служит мерой качества оценки, то это неравенство тесно связано с понятием эффективной в классе оценки. С физической точки зрения соответствует принципу неопределенности Гейзенберга в квантовой механике.

За точной формулировкой отсылаем читателя к учебнику, а вот само неравенство имеет вид

где f_Θ — обобщенная плотность распределения. I(θ) называется информацией Фишера.

Равенство в неравенстве достигается только для случая экспоненциальных относительно θ^* семейств распределений.

Распределение

Это довольно общий термин, в зависимости от контекста может интерпретироваться совсем по-разному. К тому же, это скорее термин курса теории вероятностей.

Тем не менее, в математической статистике он употребляется в контекстах «распределение случайной величины» или «Такое-то распределение». Приведем здесь разъяснения обоих контекстов.

1. Под распределением случайной величины понимают функцию множества, значение которой равно вероятности попадания специфицированной случайной величины в это множество.

Таким образом, распределение на фиксированном множестве может быть суммой вероятностей всех точек данного множества, которые являются значениями случайной величины (в дискретном случае) или интегралом от плотности распределения случайной величины по этому множеству в случае абсолютно непрерывном.

2. На вопрос «Что такое … распределение?» следует отвечать «это распределение дискретного типа» и выписывать ряд распределения (см. Биномиальное распределение, Пуассоновское распределение» или «это распределение абсолютно непрерывного типа» и выписывать плотность распределения (см. Равномерное распределение, Нормальное распределение).

Регулярности условия

Для того, чтобы изучать эффективные оценки в классах оценок с фиксированным смещением, а также некоторых других специальных вопросов, оказывается удобным ввести некие формальные условия регулярности, обозначаемые в нашем курсе (R), которые для большинства реально встречающихся параметрических семейств распределений оказываются выполненными, но для корректного использования все же должны проверяться.

Вот эти условия: каждое из распределений параметрического семейства обладает плотностью относительно некоторой меры µ, причем квадратный корень из этой плотности дифференцируем как функция θ. Кроме этого так называемая информация Фишера

при каждом значении своего аргумента определена, строго положительна и непрерывна как функция θ.

Напомним, что под условие существования плотности относительно какой-либо меры подпадают, в частности, все абсолютно непрерывные и все дискретные распределения. В последнем случае имеется в виду считающая мера. В этом случае

представляет собой вероятности отдельных значений наблюдаемой величины ξ.

Роль и место математической статистики

Математическая статистика играет подчиненную роль в исследованиях. Всегда следует отдавать предпочтение мнению опытного практика — хотя нет правил без исключений. Обычно статистические методы используют лишь для придания наукообразности и как бы строгости выводов, сделанных эмпирически — и чаще всего это удается! Классическим примером является ложный вывод о наличии связи между тем, носит ли человек шляпу-котелок и его шансами заболеть туберкулезом, сделанный английскими статистиками на рубеже 19 и 20 веков. Математическую сторону вопроса здесь изучать бесполезно, а философия, увы, вне нашей компетенции.

Источник

Т-критерий Стьюдента (t-тест) простым языком

Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.

При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:

Этапы статистического вывода (statistic inference)

Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.

Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.

Видео-версия статьи

Пример использования т-критерия Стьюдента

А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.

Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.

Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.

Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅₁₉₁₄ и в 2014 году x̅₂₀₁₄. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅₁₉₁₄≠x̅₂₀₁₄). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅₁₉₁₄=x̅₂₀₁₄), то есть о том, что все эти находки случайны, и я, по сути, не прав.

Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:

Условия применения статистического критерия т-теста (критерия Стьюдента)

— данные распределялись по закону нормального распределения;

— данные были количественными;

— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).

В итоге Мы определились с тем, что это будет t-критерий Стьюдента.

Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:

Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.

Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (m^r).

Давайте остановимся на том, что же значат эти значения:

— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;

— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;

— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки (m_r=).

Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.

Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.

Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.

Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.

Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.

На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!

Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:

Источник