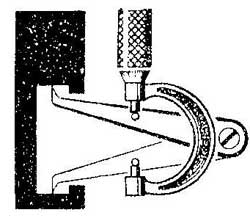
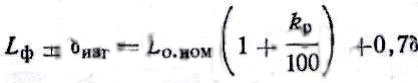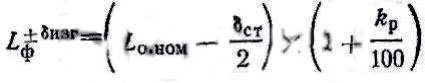Для определения размеров полости внутри детали достаточно иметь под руками микрометр или штангенциркуль и кронциркуль с приклепанными к его ножкам металлическими шпеньками цилиндрической формы.
Введите ножки кронциркули в полость, разведите их до предела так, чтобы концы ножек касались стенок полости, и зафиксируйте с помощью микрометра или штангенциркуля положение шпеньков относительно друг друга. Затем выньте кронциркуль, снова установите шпеньки в зафиксированное положение и измерьте расстояние между концами ножек.
Рекомендуемые сообщения
Решение задач по фото за 30 минут! Мы онлайн – кликай!
-
- Поделиться
Подскажите, пожалуйста, как найти объем полости частицы? Заранее благодарю
Ссылка на комментарий
—>
-
- Поделиться
2 часа назад, 35coco24 сказал:
как найти объем полости частицы?
….обьем частиц (атомов 🙈) найти — не представляется возможным ! — потому что ! радиус атома водорода (примерно) 25 пикометров… это где то 25 умножить на 10 — 12 степени метра ! А количество молекул (из двух атомов) в 22.413 литров 6.02214082 на 10 в 23 степени… Если вычислить обьем полости с размерами 25 на 10 в минус 12 степени метра и умножить на 12.044 на 10 в 23 степени — то выходит охрененный обьем в 1000 Миллиардов кубических метров !!! Видать где то кого то охрененно сжимает в 100 миллиардов раз !!
Ссылка на комментарий
-
- Поделиться
2 часа назад, _agrixolus_ сказал:
….обьем частиц (атомов 🙈) найти — не представляется возможным ! — потому что ! радиус атома водорода (примерно) 25 пикометров… это где то 25 умножить на 10 — 12 степени метра ! А количество молекул (из двух атомов) в 22.413 литров 6.02214082 на 10 в 23 степени… Если вычислить обьем полости с размерами 25 на 10 в минус 12 степени метра и умножить на 12.044 на 10 в 23 степени — то выходит охрененный обьем в 1000 Миллиардов кубических метров !!! Видать где то кого то охрененно сжимает в 100 миллиардов раз !!

ВЫ перепутали линейные размеры и объем. радиус атома и объем атома — это ПРО РАЗНОЕ
Ссылка на комментарий
-
- Поделиться
16 часов назад, Arkadiy сказал:
радиус атома и объем атома — это ПРО РАЗНОЕ
ну понятно что не стыковка — радиус один — обьем другой….
Ссылка на комментарий
-
- Поделиться
19.10.2021 в 06:48, 35coco24 сказал:
как найти объем полости частицы?
так это чистая геометрия. отними от радиуса толщину корки.
Ссылка на комментарий
Для публикации сообщений создайте учётную запись или авторизуйтесь
Вы должны быть пользователем, чтобы оставить комментарий
Войти
Уже есть аккаунт? Войти в систему.
Войти
Расчет исполнительных размеров полости пресс-формы. Точность размеров отливки.
Точность
размеров отливки
— одно из важнейших условий хорошего
качества литья. Перед тем как определить
размеры деталей оформляющих частей
пресс-формы, составляют так называемый
условный литейный чертеж отливки, на
котором проставляют размеры с учетом
усадки и литейных уклонов, а также классы
точности, с которой должна быть выполнена
полость пресс-формы.
Порядок
назначения исполнительных размеров
пресс-формы следующий. Сначала по чертежу
детали, предназначенной для изготовления
методом литья под давлением, выполняют
чертеж отливки. На чертеже отливки
указывают все технологические требования,
необходимые для проектирования
пресс-форм.
Разъем
пресс-формы
рекомендуется выполнять в одной
плоскости, так как это значительно
облегчает ее изготовление. Криволинейный
разъем пресс-формы применяют лишь в тех
случаях, когда это необходимо из-за
конфигурации отливки. Разъем пресс-формы
должен быть выполнен с таким расчетом,
чтобы при раскрытии пресс-формы отливка
вместе с литниками оставалась в подвижной
части пресс-формы.
Припуск
на механическую обработку
предусматривают на те размеры отливки,
на которые требуется допуск. Припуск
на обработку в зависимости от размеров
обрабатываемой площади колеблется в
пределах от 0,4 до 1 мм на сторону и должен
быть не меньше допуска, назначаемого
на размер отливки.
Место
подвода литника
выбирают в зависимости от конфигурации
и расположения отливки в пресс-форме с
учетом наилучшего заполнения полости
пресс-формы расплавом.
Места
выталкивания отливок
из пресс-формы и конфигурацию выталкивателей
выбирают в соответствии с отливкой. Как
правило, выталкиватели устанавливают
в наиболее глубоких местах, а также
вблизи неподвижных стержней. Кроме
того, предусматривают возможность
коробления отливки при выталкивании.
На обрабатываемых плоскостях отливки
отпечатки выталкивателей должны быть
выступающими, а на необрабатываемых —
выступающими или углубленными до 0,5 мм
по согласованию с конструктором изделия.
Литейные
уклоны
назначают на поверхностях отливок,
расположенных перпендикулярно плоскости
разъема, для облегчения съема отливок
со стержней и удаления из полости
пресс-формы. Особенно важны литейные
уклоны на внутренних поверхностях
отливки, образуемых стержнями.
Если
литейный уклон необходимо выполнить в
пределах допуска на размер изделия, он
не должен превышать одной трети допуска,
т. е. должен удовлетворять условию n<=
δ/3,
где
n — двусторонний литейный уклон
(конусность); δ — допуск на соответствующий
номинальный размер изделия.
Литейные
уклоны в отверстиях под болты и резьбу
выполняют в пределах допуска на размер
отверстия.
Литейные
радиусы
назначают для предотвращения возникновения
в отливках усадочных трещин, для
сопряжения поверхностей. Литейные
радиусы повышают стойкость оформляющих
деталей пресс-формы. Их принимают не
менее 0,5 мм.
Исполнительные
размеры пресс-формы можно разделить на
две основные группы: размеры,
не охватываемые отливкой в пресс-форме,
и размеры,
охватываемые отливкой.
При
расчете исполнительных размеров усадка,
т. е. уменьшение объема сплава при
переходе из жидкого состояния в твердое,
учитывается коэффициентом литейной
усадки, который выбирают по табл. 9.
Исполнительные
размеры оформляющих деталей пресс-формы
(полостей, вкладышей, вставок, стержней
и т. д.) подсчитывают с учетом усадки
сплава, допусков на размеры отливки и
допусков на неточность изготовления
пресс-формы по формулам, приведенным в
табл.
10.
Таб.10
Исполнительные размеры полостей
пресс-формы
|
Оформляющие |
Наименование |
Эскиз |
Расчетные |
|
Вкладышей |
Наружный |
|
|
|
Lф |
Размер |
|
|
|
Вкладышей |
Размер |
|
|
|
Оформляющие |
Наименование |
Эскиз |
Расчетные |
|
Стержня |
Внутренний |
|
|
|
Стержня |
Размер |
|
|
|
Стержня |
Размер |
|
|
|
Оформляющие |
Наименование |
Эскиз |
Расчетные |
|
Вкладышей, |
Размер |
|
|
|
Размер |
|
|
Примечание:
L
ф
— номинальный исполнительный размер
оформляющей полости пресс-формы, мм;
L
о.ном—
номинальный размер отливки по чертежу,
мм;
L
о
— действительный размер отливки, мм;
k
р
— коэффициент усадки заливаемого сплава,
%;
δ
— допуск на соответствующий номинальный
размер элемента отливки, мм;
δ
1
— дополнительный допуск на размеры
отливок, связанный с разъемом пресс-формы,
мм;
δ
ст—
дополнительный допуск на размеры
отливок, связанный с подвижными стержнями,
мм;
δ
изг—
допуски на исполнительный размер
оформляющей полости пресс-формы, мм.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Задача №1. Есть ли в теле полость?
Имеются ли в стальном шаре массой 250 г полости, или этот шар сплошной, если его объем составляет 0,0005 м3?
Начнем с записи краткого условия задачи. В нем говорится, что шар стальной, поэтому в справочных таблицах мы находим плотность стали (она равна 7800 кг/м3) и записываем ее в краткое условие наряду с данными из текста задачи.
Чтобы узнать, имеются ли в шаре полости (пустоты), необходимо вычислить плотность шара, разделив его массу на объем. Мы получим так называемую среднюю плотность, то есть отношение массы шара к его объему, независимо от того, заполнен ли шар веществом целиком, или в нем имеется пустое пространство.
Если плотность шара совпадает с плотностью стали, значит, шар целиком состоит из этого материала. Если же в шаре имеются полости, то его плотность будет меньше плотности стали. Итак, для ответа на вопрос задачи необходимо сравнить плотности шара и стали, что мы и записываем внизу краткого условия.
Прежде чем переходить к решению, необходимо проверить, все ли величины заданы в системе СИ, и при необходимости выполнить перевод величин в эту систему. Так, в нашей задаче необходимо массу шара перевести в килограммы. Масса 250 г составляет 0,25 кг.
Рис. 1. Краткое условие задачи № 1.
Далее записываем расчетную формулу и проводим проверку размерности результата.
Подставляем данные из условия в расчетную формулу
Сравнив полученную плотность с табличным значением плотности стали (7800 кг/м3), получаем, что в шаре имеются полости. Зафиксируем полученный результат в ответе. Задача решена.
Рис. 2. Полное решение задачи № 1
2. Задача №2. Вычисление массы тела
Определить массу свинцового тела объемом 0,35 м3.
Перед записью краткого условия из справочных таблиц определим плотность свинца. Она составляет 11 300 кг/м3. Так как все величины в условии заданы в системе СИ, можно сразу перейти к решению задачи.
Поскольку в условии задачи фигурирует плотность, то вначале записываем знакомую формулу для плотности, а затем по правилам алгебраических преобразований выражаем из этой формулы массу тела.
Затем проводим проверку размерности.
Обратите внимание, что кубические метры в числителе и в знаменателе сокращаются, и остаются только единицы измерения массы, килограммы.
Подставим числовые данные
Остается записать ответ. Полное решение задачи № 2 выглядит так.
Рис. 3. Полное решение задачи № 2
3. Заключение
Мы рассмотрели только небольшую часть задач на расчет параметров тела по плотности материала, из которого оно изготовлено. Для того, чтобы научиться решать более сложные задачи, необходимо регулярно самостоятельно выполнять домашние задания.
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Абдикаримов Ф.Б.
1
Наврузов К.Н.
1
Хужатов Н.Д.
1
1 Ургенчский государственный университет им. Ал-Хорезми
В статье рассматривается определение объема полости левого желудочка сердца по данным эхокардиографии, имеющие большое значения в кардиологии. Здесь основное, внимания исследователей сосредоточено на левом желудочке сердца, как имеющим наиболее правильную форму и наиболее хорошо доступному визуализацию. В статье определяются площадь и длина полости в парастернальной позиции ультразвукового датчика по короткой оси, чуть ниже уровня митральных клапанов. Далее ультразвуковой датчик устанавливается в апикальном с четырехкамерным доступом. Изображение фиксируется, исследуемая полость по длинному осью равномерно разбивается n отрезок. Его средней точке, проводится параллельная линия, перпендикулярно межжелудочковой перегородке. Каждому короткому осью соответствуют определенные площади полости левого желудочка, которые также перпендикулярные межжелудочковой перегородке. Определяя величины этих площадей и умножая их на длину отрезки и суммируя, их, найдены объем левого желудочка сердца. Показано ее преимущества перед другим способом, что данный способ точные и надежные.
Эхокардиография
ультразвуковое
митральное
апикальное
парастернальное
неинвазивное
1. Толыжников В.А. , Семенова Е.Н. Основные принципы расчета объемных показателей сердца // Кардиология, 1987. т. 27. 6, С. 119-123.
2. Алпатов А.В. Способ определения объема полостей желудочков сердца: А. с. № 2194450 , 2002.
3. Teichholz L.E., Kreulen T., Herman M.V., Gorlin R. Problems in echocardiographic volume determinations: echocardiographic-angiographic correlations in presence or absence of asynergy // Amer. J. Cardiology. – 1976. – Vol. 3. – P. 7.
4. Мухарлямов Н.М.,Беленков Ю.Н. Ультразвуковая диагностика в кардиологии – М.: Медицина, 1981, 157 с.
5. Клиническая ультразвуковая диагностика / Под ред. Мухарлямова. – М., 1987. – Т.1. – 185 с.
Параметры кровообращения рассчитываются, с использованием значения объема желудочков и его необъективное значение может в целом повлиять на окончательный диагноз. Поэтому более точному измерению объема полости левого желудочка имеет важные значение при лечении и прогнозирование сердечно-сосудистых заболеваний. Разнообразие способов расчета объемов желудочковых камер вызвано сложностью их пространственной конфигурации. Это обусловливает необходимость представления полостей пространственной фигурой правильной геометрической формы. Такая модель позволяет рассчитать объемные показатели полости, имея лишь несколько ее линейных размеров. В основном, внимания исследователей сосредоточено на левом желудочке сердца, как имеющим наиболее правильную форму и наиболее хорошо доступному визуализацию. Самым распространенным способом расчета объема левого желудочка является расчет по формуле Тейчхольца (Teichholz) [1, 2, 3, 4, 5]:
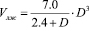
где D – переднезадний размер желудочка.
Существует способ расчета [2], основанный на эллипсоидной модели
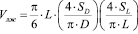
а также на основе представления левого желудочка в виде эллипсоида вращения
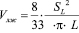
где SD, SL – площадь левого желудочка по длинной и короткой осям соответственно; D, L – размер полости левого желудочка по длинной и короткой осям соответственно. В зависимости от имеющейся патологии [3] для описания формы левого желудочка, также применяются гиперболоид, полусфера, усеченная сфера и другие фигуры вращения. Основными недостатками, перечисленными в [3, 5] и [2], являются, неадекватность отражения конфигурации нормального и патологического состояния сердца человека, несопоставимость результатов расчета объема одной полости разными методами и, как следствие, отсутствие единых критериев патологии. Наиболее близким к предлагаемому методу определения объемов полости левого желудочка, можно считать метод сечений; – разделение объема на n подобных объемов, проделанные в работе. Они основаны на анатомической особенности строения желудочковых камер. Заключающаяся в том, что форма внутреннего и внешнего контуров желудочков по короткой оси, несмотря на сложный характер, сохраняется на разрезе подобных фигур вдоль длинной оси сердца (перпендикулярно межжелудочковой перегородке) – правило подобия [2]. Наличие этой особенности подтверждает статистический анализ данных, полученных в результате патологоанатомических исследований серийных срезов сердца человека. Используя эту особенность, можно рассчитать объем желудочков сердца, имея лишь два сечения: по короткой и длинной осям, в терминах эхокардиографии – парастернально по короткой оси и апикальном с четырехкамерным доступом. Сущность способа состоит в следующем. Определяются площадь и длина полости в парастернальной позиции ультразвукового датчика по короткой оси на уровне конца митрального клапана. Далее ультразвуковой датчик устанавливается в апикальном с четырехкамерным доступом, изображение фиксируется. Исследуемая полость равномерно разбивается n параллельными линиями перпендикулярно межжелудочковой перегородке, с помощью штатных средств эхокардиографа, определяются размер желудочка по длинной оси и длина каждого отрезка, заключенного между точками пересечения внутреннего контура полости указанными линиями (рис. 1).
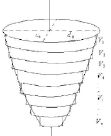
Рис. 1. Равномерное разбиение длинной оси на n отрезков, содержащих n криволинейного цилиндрического объема
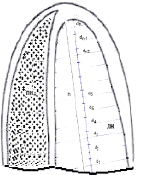
Рис. 2. Апикальная четырехкамерная позиция (предсердия не показаны)
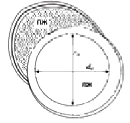
Рис. 3. Парастернальная позиция по короткой оси на уровне конца створк митрального клапана
В работе [2], имеется некоторые недостатки, так например;
- при вычислении объема учитывается подобные длины коротких осей, в разбиение длинной оси на n отрезок, а не площадь.
- предложенной формулы для определения объема полостей желудочков сердца не обосновано с математической точки зрения. Поэтому точность формулы оказывается невысокой.
Предлагаемый нами, здесь способ определения объема отличается от предыдущих исследование с тем, что здесь устранены все вышеперечисленные недостатки при сохранении точности расчетов. Сущность метода заключается в том, что сначала определяются площадь и длина полости в парастернальной позиции ультразвукового датчика по короткой оси, чуть ниже уровня митральных клапанов. Далее ультразвуковой датчик устанавливается в апикальном с четырехкамерным доступом. Изображение фиксируется, исследуемая полость по длинному осью равномерно разбивается n отрезок (рис. 2). Его средней точке, проводится параллельная линия, перпендикулярно межжелудочковой перегородке. Каждому короткому осью соответствуют определенные площади полости левого желудочка, которые также перпендикулярные межжелудочковой перегородке (рис. 3). Подобные площадь определяются с помощи формулы
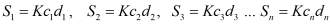
где K – коэффициент пропорциональности; 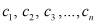
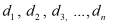
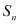
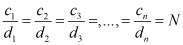
Отсюда легко находим
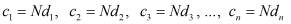
Учитывая (6) в (4), определим
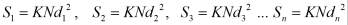
Умножая каждый площадь, на длину отрезки и суммируя, их, найдем объем левого желудочки по формуле
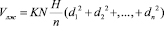
KN – коэффициент определяется из любой выбранной площади подобной плоской фигуры (рис. 2), поэтому его найдем с помощью формулы
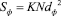
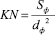
Подставляя (9) в (8), окончательно находим формулы для вычисления объема полости левого желудочка сердца
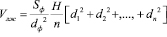
где dn – размер по короткой оси, проведенный средней точки n-ого отрезка перпендикулярно межжелудочковой перегородке; H – размер желудочка по длинной оси; dф – фиксирований размер полости в парастернальном доступе по короткой оси; Sф – фиксирований площадь полости в парастернальном доступе по короткой оси.
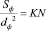
Для шара 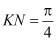
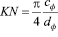
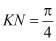
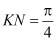
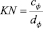
Предложенная формула в работе [2] для вычисления объема полости левого желудочка, верны только при условии, когда 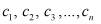
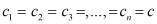
Умножая каждый площадь приведенные в формулы (4) , на длину отрезки и суммируя, их, при условии (11), найдем объем левого желудочки по формуле
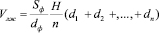
Однако (11) подобных плоских геометрических фигур не выполняется. Так как условия (11) доказывает также равенство других осей 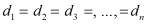
- резкое уменьшение времени анализа данных эхокардиографического обследования;
- установление более точного измерения объема полости левого желудочка и надежно ставить диагноз для пациента.
- тестирование имеющейся известной геометрической фигуры (шар, конус, эллипсоид и др.) предложенной формулы, несколько раз точнее, чем в [2] Предложенный нами способ позволяет достичь следующего положительного эффекта:
- резкое уменьшение времени анализа данных эхокардиографического обследования;
- установление более точного измерения объема полости левого желудочка и надежно ставить диагноз для пациента.
- в тестирование имеющейся известной геометрической фигуры (шар, конус, эллипсоид и др.) предложенной формулы, пять раза точнее, чем предложенной формулы [2].
- предложенной формулы строго математически обоснованы, и каждый ее член имеет физический смысл.
Библиографическая ссылка
Абдикаримов Ф.Б., Наврузов К.Н., Хужатов Н.Д. НОВЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОБЪЕМА ПОЛОСТИ ЛЕВОГО ЖЕЛУДОЧКА СЕРДЦА ПО ДАННЫМ ЭХОКАРДИОГРАМИИ // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8-1.
– С. 40-43;
URL: https://applied-research.ru/ru/article/view?id=5634 (дата обращения: 28.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)