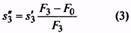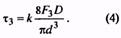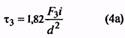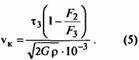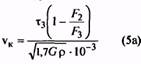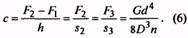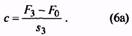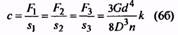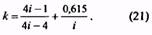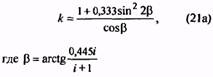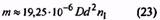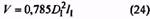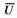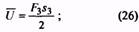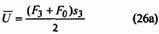Как найти размер пружины

10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.

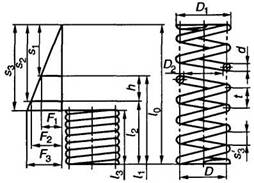
Пружина сжатия

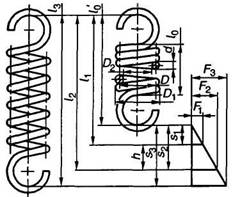
Пружина растяжения

Продолжение табл. 10

Продолжение табл. 10

Методика определения разме­ров пружин по ГОСТ 13765-86.

1. Исходными величинами для определения размеров пружин являются силы F₁ и F₂, ра­бочий ход h, наибольшая скорость перемеще­ния подвижного конца пружины при нагружении или при разгрузке v_mах, выносливость N_F и наружный диаметр пружины D₁ (пред­варительный).

Если задана только одна сила F₂, то вместо рабочего хода h для подсчета берут величину рабочей деформации s₂, соответствующую заданной силе.

2. По величине заданной выносливости N_F предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.

3. По заданной силе F₂ и крайним значени­ям инерционного зазора δ вычисляют по фор­муле (2) значение силы F₃.

4. По значению F₃, пользуясь табл. 2, пред­варительно определяют разряд пружины.

5. По табл. 11-17 находят строку, в кото­рой наружный диаметр витка пружины наибо­лее близок к предварительно заданному значе­нию D₁. В этой же строке находят соответствующие значения силы F₃ и диаметра прово­локи d.

6. Для пружин из закаливаемых марок ста­лей максимальное касательное напряжение τ₃ находят по табл. 2, для пружин из холоднотя­нутой и термообработанной τ₃ вычисляют с

учетом значений временного сопротивления R_m. Для холоднотянутой проволоки R_m опре­деляют из ГОСТ 9389-75, для термообрабо­танной — из ГОСТ 1071-81.

7. По полученным значениям F₃ и τ₃, aтакже по заданному значению F₂ по формулам (5) и (5а) вычисляют критическую скорость v_K и отношение v_max/v_K, подтверждающее или

отрицающее принадлежность пружины к предварительно установленному классу.

При несоблюдении условий v_max/v_K<1 пружины I и II классов относят к последую­щему классу или повторяют расчеты, изменив исходные условия. Если невозможно измене­ние исходных условий, работоспособность обеспечивается комплектом запасных пружин.

8. По окончательно установленному классу и разряду в соответствующей таблице на па­раметры витков пружин, помимо ранее най­денных величин F₃, D₁, и d, находят величины c₁ и s₃, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).

Основные
понятия

Пружина
растяжения — это спирально-цилиндрическая
пружина, витки которой прилегают друг
к другу. Пружина подвергается действию
противоположно направленных усилий,
приложенных вдоль ее оси.

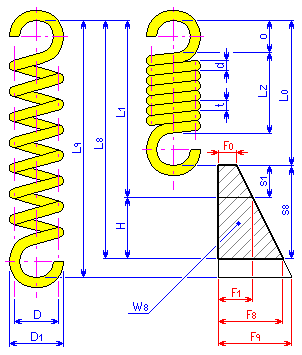
Размеры

d	диаметр проволоки [мм, д]
D	средний диаметр пружины [мм, д]
D1	наружный диаметр пружины [мм, д]
D2	внутренний диаметр пружины [мм, д]
H	рабочая деформация [мм, д]
t	шаг активных витков в ненагруженном состоянии [мм, д]
o	высота ушка [мм, д]
sx	деформация пружины [мм, д]
Lx	длина пружины [мм, д]
Fx	рабочая сила, действующая на пружину [Н, фунт]
W8	энергия деформации [Дж, фут фунт]
x	индекс, обозначающий состояние пружины

Навивка

1. Вправо
   (стандарт)

2. Влево
   (должна отображаться соответствующая
   надпись)

Состояния

1. Свободное:
   пружина не нагружена (индекс 0)

2. Предварительная
   нагрузка: пружина с минимальной рабочей
   нагрузкой (индекс 1)

3. Полная
   нагрузка: пружина с максимальной рабочей
   нагрузкой (индекс

4. Предел:
   пружина вдавлена до касания витков
   (индекс 9).

Зацепы
пружин растяжения

Высота
зацепа пружины растяжения

Где:

L0	длина пружины в свободном состоянии [мм]
LZ	длина части пружины с витками [мм]

Часто
используемые зацепы пружин растяжения

Тип зацепа и информация о размерах	Изображение
Половина витка, o = 0,55…0,8 D2
Обычно d ≤ 6,3 мм, D >= 3,15 мм, i >= 9
Полный виток, o = 0,8…1,1 D2
Используется без ограничений
Полный виток сбоку, o  D2
Когда нагрузка не обязательно должна прикладываться по оси
Полный виток внутри, o = 1,05…1,2 D2
Обычно d  ≥ 10 мм, i >= 7
Поднятый зацеп, o = 1,2 D2 … 30 d
Обычно для d = от 0,5мм до 4 мм, o ≤ 100 мм
Два полных витка, o D
Используется без ограничений
Два полных витка сбоку, o  D2
Когда нагрузка не обязательно должна прикладываться по оси

Расчет
пружин в метрических единицах

Общие
формулы расчета

Коэффициент
использования материала

Наружный
диаметр пружины

D₁ =
D + d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Внутренний
диаметр пружины

D₂ =
D — d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Рабочая
деформация

H
= L₈1_=
s8₁[мм]

Где:

	L8	длина полностью нагруженной пружины [мм]
	L1	длина предварительно нагруженной пружины [мм]
	s8	деформация полностью нагруженной пружины [мм]
	s1	деформация предварительно нагруженной пружины [мм]

Высота
зацепа пружины

Где:

	L0	длина пружины в свободном состоянии [мм]
	LZ	длина части пружины с витками [мм]

Индекс
пружины

c
= D/d [-]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Поправочный
коэффициент Валя

Где:

	c	индекс пружины [-]
	LZ	длина части пружины с витками [мм]

Начальное
растяжение

Где:

	d	диаметр проволоки [мм]
	0	напряжение в свободном состоянии [Мпа]
	D	средний диаметр пружины [мм]
	Kw	поправочный коэффициент Валя [-]

Общая
сила, действующая в пружине

Где:

	d	диаметр проволоки [мм]
	G	напряжение при кручении – это усилие на единицу площади материала пружины при изгибе [фн/кв. материала пружины в общем случае [МПа]
	D	средний диаметр пружины [мм]
	Kw	поправочный коэффициент Валя [-]
	G	модуль упругости материала пружины [МПа]

Жесткость
пружины

Где:

	d	диаметр проволоки [мм]
	G	модуль упругости материала пружины [МПа]
	D	средний диаметр пружины [мм]
	n	количество активных витков [-]
	F8	рабочее усилие в полностью нагруженной пружине [МПа]
	F1	рабочее усилие в минимально нагруженной пружине [МПа]
	H	рабочая деформация [мм]

Расчет
конструкции пружины

При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L₀ для
заданной нагрузки, материала и сборочных
размеров.

Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для данного напряжения ₀ согласно
формуле, расчет пружины повторяется с
использованием скорректированного
значения напряжения в свободном состоянии
из рекомендуемого диапазона.

Пружине
без начального растяжения соответствует
средний рекомендуемый шаг витков t =
0,35 D [мм].

Если
рассчитанная пружина не соответствует
ни одному значению диаметра проволоки
для выбранного шага, расчет пружины
повторяется с использованием
скорректированного значения шага из
рекомендуемого диапазона 0,3 D ≤ t ≤ 0,4
D [мм].

Конструкция
пружины определяется с учетом условия
прочности ₈≤ u_s_A и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:
L₀≤ D
и L₀≤ 31,5
д и 4 ≤ D/d ≤16 и n  2.

Задание
нагрузки, материала и сборочных размеров
пружины

Вначале
выполняется проверка входных величин
для расчета.

Затем
вычисляется длина пружины в свободном
состоянии.

После
расчета выбирается диаметр проволоки,
количество витков и диаметры пружины
– так, чтобы высота зацепа соответствовала
выбранному типу зацепа. Кроме того,
должны выполняться упомянутые выше
прочностные и геометрические условия.
Конструкция пружины должна удовлетворять
по диаметрам всем заданным начальным
условиям. При отсутствии таких
дополнительных условий предельный
диаметр пружины устанавливается по
геометрическим условиям для
минимально/максимально допустимого
диаметра проволоки.

Отбираются
все диаметры проволоки (от меньшего к
большему), которые проходят по прочностным
и геометрическим условиям. Проверяются
высота зацепа и количество витков. Если
все условия выполнены, расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.

Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Комбинация
диаметра проволоки, количества витков
и диаметра пружины должна давать в итоге
такую высоту зацепа, которая удовлетворяет
его типу. Вначале в качестве типа зацепа
берется полный виток, затем, если он не
годится–полный виток внутри и т.д.

Задание
нагрузки, материала и диаметра пружины

Вначале
выполняется проверка входных величин
для расчета.

После
проверки выбирается диаметр проволоки,
количество витков, длина пружины в
свободном состоянии и сборочные размеры
пружины – так, чтобы высота зацепа
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия. Если сборочный
размер L₁ или
L₈ взят
из спецификации или значение рабочей
деформации пружины ограничено, конструкция
пружины должна соответствовать этому
условию. В остальных случаях предельные
значения сборочных размеров пружины и
ее длины в свободном состоянии определяются
геометрическими условиями для заданного
диаметра пружины и минимального/максимального
допустимого диаметра проволоки.

Формула
для проектирования пружины по заданному
диаметру проволоки.

где
значение ₈ =
0,85 _A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.

Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.

Вычисленное
значение высоты зацепа должно находиться
в пределах d ≤ o ≤ 30 d. Для
высоты, вычисленной таким способом,
выбирается соответствующий тип зацепа.
Комбинация диаметра проволоки, количества
витков, длины пружины в свободном
состоянии и сборочных размеров пружины
должна давать в итоге такую высоту
зацепа, которая удовлетворяет его типу.
Вначале в качестве типа зацепа берется
полный виток, затем, если он не
годится–полный виток внутри и т.д.

Задание
максимального рабочего усилия, материала,
сборочных размеров и диаметра пружины

Вначале
выполняется проверка входных величин
для расчета.

Затем
подбирается диаметр проволоки, количество
витков, длина свободной пружины и
минимальное рабочее усилие F₁ таким
образом, чтобы высота зацепа пружины
соответствовала выбранному типу зацепа.
Кроме того, должны выполняться прочностные
и геометрические условия.

Формула
для проектирования пружины по заданному
диаметру проволоки.

где
значение ₈ =
0,9 _A используется
в качестве величины напряжения материала
пружины при кручении в полностью
нагруженном состоянии.

Если
для данного диаметра проволоки не
удается подобрать подходящую комбинацию
размеров пружины, расчетная процедура
оценивает другие диаметры проволоки.
Они проверяются, начиная от меньшего к
большему, до тех пор пока не будет
достигнуто такое количество витков,
при котором высота зацепа удовлетворяет
всем условиям. Расчет конструкции
завершается, и текущие значения параметров
принимаются в качестве его результатов,
независимо от того, как прошел бы расчет
при других подходящих диаметрах
проволоки. Таким образом, полученная
пружина имеет минимально возможный
диаметр проволоки и минимально возможное
количество витков.

Проверочный
расчет пружины

Расчет
соответствующих значений сборочных
размеров и рабочего отклонения для
указанной нагрузки, материала и размеров
пружины.

Сначала
проверяются расчетные входные значения.
Затем на основании приведенных ниже
формул вычисляются сборочные размеры.

Длина
предварительно нагруженной пружины

Длина
полностью нагруженной пружины

Где:

	L0	длина пружины в свободном состоянии [мм]
	F1	рабочая сила в минимально нагруженной пружине [мм]
	D	средний диаметр пружины [мм]
	n	количество активных витков [-]
	G	модуль упругости материала пружины [МПа]
	d	диаметр проволоки [мм]
	F8	рабочее усилие в полностью нагруженной пружине [МПа]

Рабочая
деформация

H
= L₁8_[мм]

Расчет
рабочих сил

Расчет
соответствующих сил, действующих в
пружинах в рабочем состоянии для
указанного материала, сборочных размеров
и размеров пружины. Сначала проверяются
и рассчитываются входные данные, а затем
выполняется расчет рабочих сил с помощью
следующих формул.

Минимальное
рабочее усилие

Максимальное
рабочее усилие

Расчет
выходных параметров пружины

Эта
часть является общей для всех типов
расчета пружины. Расчет производится
в следующем порядке.

Коэффициент
высоты зацепа

Жесткость
пружины

Длина
части с витками

Пружина без начального растяжения
	Lz = t n + d [мм]
Пружина с начальным растяжением
	Lz = 1,03 (n + 1) d [мм]

Деформация
предварительно нагруженной пружины

s₁ =
L₁ —
L₀ [мм]

Полная
деформация пружины

s₈ =
L₈ —
L₀ [мм]

Напряжение
при кручении материала пружины в
состоянии предварительной нагрузки

Напряжение
материала пружины при кручении при
полном нагружении

Предельное
усилие в пружине

Деформация
в предельном состоянии

Где:

	k	жесткость пружины [Н/мм]
	F9	рабочее усилие в пружине, нагруженной до предела [Н]
	F0	начальное растяжение пружины [Н]

Предельная
длина пружины

L₉ =
L₀ +
s₉ [мм]

Энергия
деформации пружины

Длина
развернутой проволоки

l = 3.2 D n + l0 [мм]
	Где длина развернутого зацепа l0:
		для половины витка
			l0 =  D + 4 o — 2 D — 2 d [мм]
		для полного витка
			l0 = 2 ( D — 2 d) [мм]
		для полного витка сбоку
			l0 = 2 ( D — 2 d) [мм]
		для полного витка внутри
			l0 = 2 ( D — d) [мм]
		для поднятого зацепа
			l0 =  D + 2 o — D + 3 d [мм]
		для двух полных витков
			l0 = 4  D [мм]
		для двух полных витков сбоку
			l0 = 4  D [мм]
		для неуказанного типа зацепа
			l0 = 0 [мм]

Масса
пружины

Собственная
частота колебаний пружины

Проверка
нагрузки пружины


₈≤ u_s
_A

Обзор
используемых переменных:

d	диаметр проволоки [мм]
k	жесткость пружины [Н/мм]
D	средний диаметр пружины [мм]
D1	наружный диаметр пружины [мм]
D2	внутренний диаметр пружины [мм]
F	обобщенное усилие, приходящееся на пружину [Н]
G	модуль упругости материала пружины при сдвиге [МПа]
H	рабочая деформация [мм]
c	индекс пружины [-]
Kw	поправочный коэффициент Валя [-]
l	длина развернутой проволоки [мм]
L	обобщенная длина пружины [мм]
LZ	длина части пружины с витками [мм]
m	масса пружины [N]
n	количество активных витков [-]
o	высота зацепа пружины [мм]
t	шаг активных витков в ненагруженном состоянии [мм]
s	обобщенная деформация (растяжение) пружины [мм]
us	коэффициент использования материала
	плотность материала пружины [Н/мм3]
	напряжение при кручении – это усилие на единицу площади материала пружины при изгибе [фн/кв. материала пружины в общем случае [МПа]
 A	допустимое напряжение материала пружины при кручении [МПа]

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Калькулятор пружин

Добавить в избранное

Калькулятор пружин — позволяет произвести онлайн расчёт и определить силовые и геометрические характеристики изделия. Функционал позволяет сохранить чертеж пружины на Ваш компьютер, распечатать или отправить его нам на Email. При проектировании ответственных и силовых пружин — сообщайте о необходимости проверки важных для Вас параметров специалистами нашего тех. отдела.

Расчёт пружин онлайн

---

Расчёт пружин сжатия и растяжения происходит онлайн и основывается на сложных формулах, данные меняются в момент изменения Вами геометрических параметров или количества изделий.
Калькулятор позволяет посчитать вес одной пружины и всей партии изделий, сохранить чертёж, напечатать или отправить на наш Email в виде заявки.

Не целые значения необходимо разделять точкой «.»
При проектировании изделия повышенной точности и ответственности — необходима проверка чертежа нашими технологами.
Все расчётные данные несут исключительно информационный характер.

Перейти к калькулятору пружин растяжения.

Калькулятор пружин сжатия

Добавить в избранное

Калькулятор пружин — позволяет произвести онлайн расчёт и определить силовые и геометрические характеристики изделия. Функционал позволяет сохранить чертеж пружины на Ваш компьютер или распечатать. При проектировании ответственных и силовых пружин — сообщайте о необходимости проверки важных для Вас параметров специалистами нашего тех. отдела.

Расчёт пружин онлайн

---

Расчёт пружин сжатия и растяжения происходит онлайн и основывается на сложных формулах, данные меняются в момент изменения Вами геометрических параметров или количества изделий.
Калькулятор позволяет посчитать вес одной пружины и всей партии изделий, сохранить чертёж или напечатать.

Не целые значения необходимо разделять точкой «.»
При проектировании изделия повышенной точности и ответственности — необходима проверка чертежа нашими технологами.
Все расчётные данные несут исключительно информационный характер.