В данной публикации мы рассмотрим, что такое тупой угол, а также разберем примеры задач, в которых он участвует.
- Определение тупого угла
- Примеры задач
Определение тупого угла
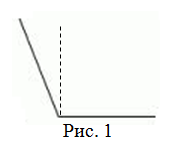
Угол является тупым, если его градусная мера находится между 90 и 180 градусами.
∠α – тупой, если 90° < α < 180°.
То есть тупой угол больше прямого (90°), но меньше развернутого (180°).
Примеры задач
Задание 1
Дан треугольник, у которого известны два угла – 34° и 27°. Найдем третий и определим, является ли он тупым.
Решение:
Примем неизвестную величину за “α“. Как мы знаем, сумма углов треугольника равняется 180 градусам, значит:
α = 180° – 34° – 27° = 119°.
Следовательно, угол α – тупой.
Задание 2
Дан ромб, площадь (S) которого составляет 12,5 см2, а длина (a) стороны – 5 см. Найдем его углы и определим, являются ли они тупыми.
Решение:
Синус угла ромба (α) можно найти следующим образом (выведено из формулы расчета площади фигуры):
Следовательно, α = 30° (arcsin 0,5), является острым.
Как мы знаем, сумма соседних углов ромба составляет 180 градусов, значит второй угол β равен 150° (180° – 30°), и он является тупым.
Тупоугольный треугольник: длина сторон, сумма углов. Описанный тупоугольный треугольник
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является тупым углом.
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения площади треугольника математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о .
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, биссектрисы делят угол пополам, а противоположную сторону – на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2 : 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр – это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
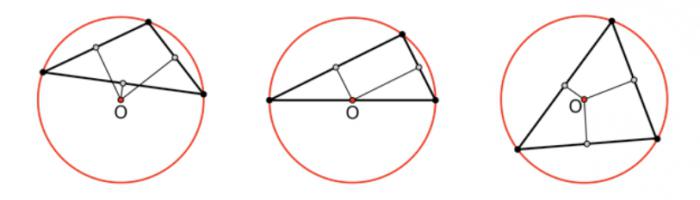
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном – за его пределами.
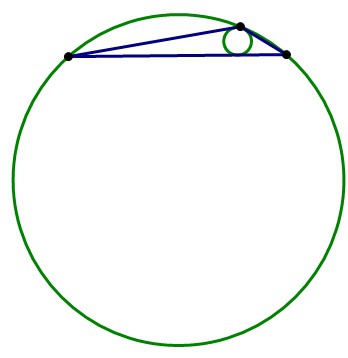
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R – это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о .
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
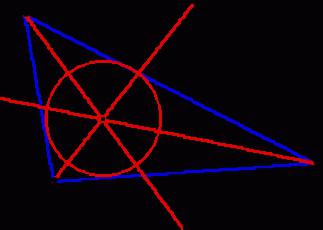
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется квадратному корню из частного (p-c) х (p-v) х (p-b) : p. При этом p – это полупериметр треугольника, c, v, b – его стороны.
Остроугольный, прямоугольный и тупоугольный треугольники.
Виды треугольников
Остроугольный треугольник — это треугольник,
в котором все углы острые.
Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.
Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.
Как определить вид треугольника
Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.
Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.
В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.
В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.
Градусные меры острого, тупого, прямого углов в треугольниках
Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:
- Острый угол в любом из треугольников не больше 90 градусов.
- Прямой угол в любом из треугольников равен 90 градусам.
- Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.
Тупоугольный треугольник
Что такое тупоугольный треугольник
Тупоугольный треугольник — геометрическая фигура на плоскости, которая представляет собой треугольник, один из углов которого является тупым, то есть больше 90º.
Такой треугольник не может быть прямоугольным и равносторонним, но может быть равнобедренным.
Сумма углов треугольника равна 180º. Именно поэтому только один из них может быть больше 90º, два других всегда острые. Это единственная особенность данной фигуры. Подход к решению задач с такой фигурой не отличается от решения задач с треугольниками других типов.
Элементы тупоугольного треугольника
Помимо сторон и углов, тупоугольный треугольник имеет следующие элементы:
- Внешний угол — тот, который смежен с внутренним, всего их шесть, по два на один внутренний. Внешний угол тупого всегда будет острым, острого — тупым.
- Медиана — отрезок, который соединяет вершину треугольника с противолежащей стороной и делит ее пополам. Все медианы пересекаются друг с другом в одной точке (центроиде). Эта точка делит медианы в соотношении 2:1, считая от вершины.
- Высота — перпендикуляр, который проведен из высоты треугольника на противоположную сторону. В тупоугольном треугольнике может лежать за пределами фигуры.
- Биссектриса — прямая, делящая угол пополам. Делит противоположную сторону на отрезки, которые пропорциональны прилежащим сторонам фигуры. Точка, которая является пересечением биссектрис, также является центром вписанной окружности.
Формулы площади тупоугольного треугольника
Для нахождения площади, периметра и других показателей тупоугольного треугольника используются те же формулы, что и для вычисления любого произвольного треугольника.
Площадь данной фигуры можно найти при помощи следующих формул:
S = ½ * x * h , где х — сторона;
S = √ p * ( p — x ) * ( p — y ) * ( p — z ) ,
p — полупериметр, p = ( x + y + z ) / 2
S = x * y * z / 4 * R , R — радиус описанной окружности;
S = p * r , p — полупериметр, r — радиус вписанной окружности.
Пример решения задачи
Найти площадь тупоугольного треугольника, у которого стороны равны x=9, y=5, z=6.
Для решения задачи стоит использовать формулу площади с полупериметром.
p = ( x + y + z ) / 2 , p = ( 9 + 5 + 6 ) / 2 = 20 / 2 = 10 .
S = √ p * ( p — x ) * ( p — y ) * ( p — z ) , S = √ 10 * ( 10 — 9 ) * ( 10 — 5 ) * ( 10 — 6 ) = √ 10 * 1 * 5 * 4 = √ 200 = 10 √ 2
http://colibrus.ru/ostrougolnyy-pryamougolnyy-i-tupougolnyy-treugolniki/
http://wika.tutoronline.ru/geometriya/class/7/tupougolnyj-treugolnik
Содержание:
- Определение тупого угла
- Примеры решения задач с тупыми углами
Определение тупого угла
Определение
Угол называется тупым, если его
градусная мера лежит в пределах от
$90^{circ}$ до
$180^{circ}$ (рис. 1).
$angle alpha$ — тупой, если
$90^{circ} lt angle alpha < 180^{circ}$.
То есть тупой угол больше
прямого и меньше, чем
развернутый.
Примеры решения задач с тупыми углами
Пример
Задание. Найти тупой угол параллелограмма
$ABCD$, если известно, что его
острый угол равен
$30^{circ}$.
Решение. Известно, что сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$. Тогда искомый тупой угол равен
$$angle alpha=180^{circ}-30^{circ}=150^{circ}$$
Ответ. $angle alpha=150^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два угла треугольника равны
$30^{circ}$ и
$40^{circ}$. Найти третий угол треугольника, определить
тупым или острым он является.
Решение. Пусть $alpha$ — искомый угол.
Согласно теореме про сумму углов треугольника имеем, что
$$angle alpha+30^{circ}+40^{circ}=180^{circ}$$
Отсюда получаем
$$angle alpha=110^{circ}$$
Так как $90^{circ} < angle alpha=110^{circ} < 180^{circ}$, то он является тупым.
Ответ. $angle alpha=110^{circ}$
Читать дальше: что такое плоский угол.
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
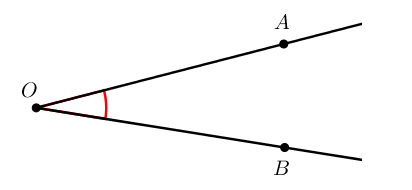
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
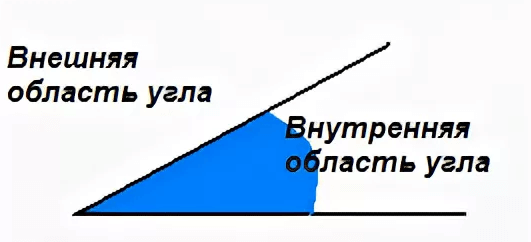
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
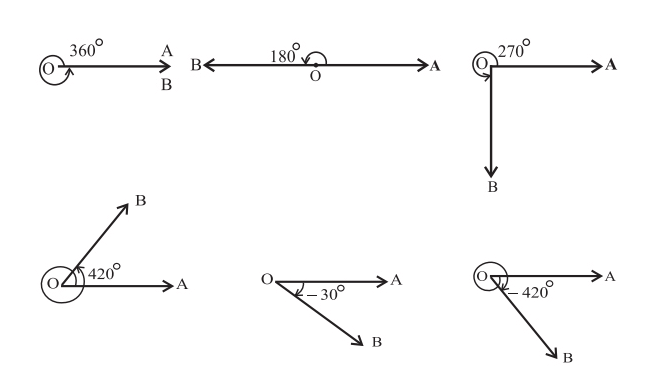
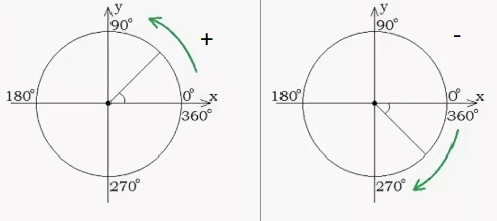
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
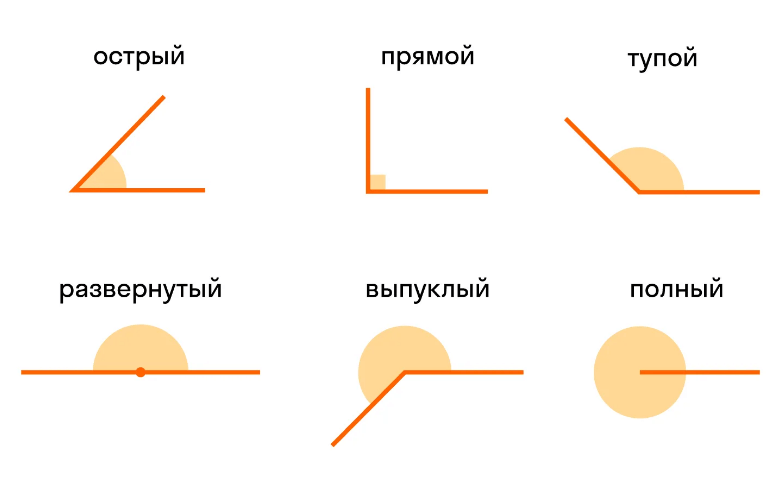
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
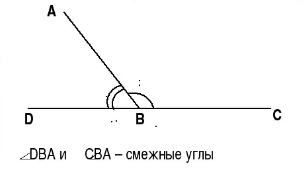
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
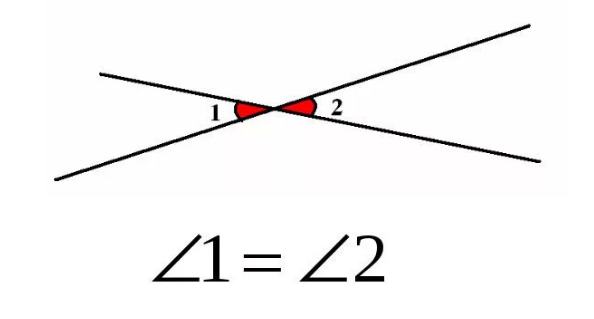
Пример:
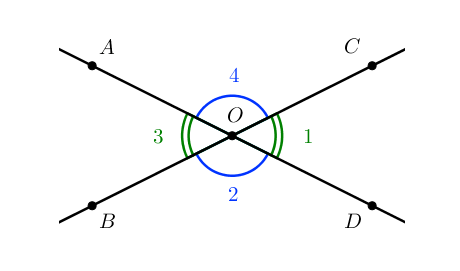
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
[angle C O D=angle A O B]
[angle B O D=angle A O C]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
[angle C O D+angle D O B=180^{circ}]
[angle D O B+angle B O A=180^{circ}]
[angle B O A+angle A O C=180^{circ}]
[angle A O C+angle C O D=180^{circ}]
| Смежные углы | Вертикальные углы |
| Два угла с общей стороной и вершиной называются смежными. | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
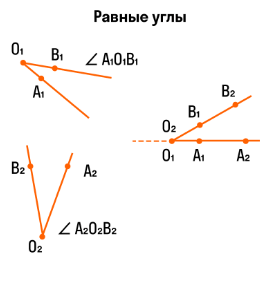
[angle A_{1} O_{1} B_{1}] и [angle A_{2} O_{2} B_{2}] полностью совмещаются при наложении следовательно: [angle A_{1} O_{1} B_{1}=angle A_{2} O_{2} B_{2}]
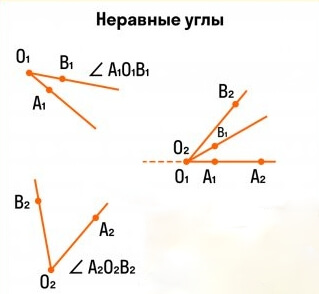
[angle A_{1} O_{1} B_{1}] и [ angle A_{2} O_{2} B_{2}] не совмещаются при наложении: [angle A_{1} O_{1} B_{1} neq angle A_{2} O_{2} B_{2}]
Причем: [angle A_{1} O_{1} B_{1}<angle A_{2} O_{2} B_{2}]
При этом развернутые углы всегда являются равными.
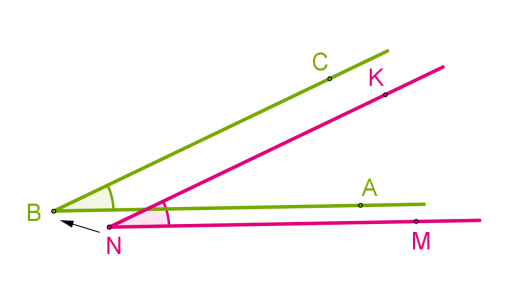
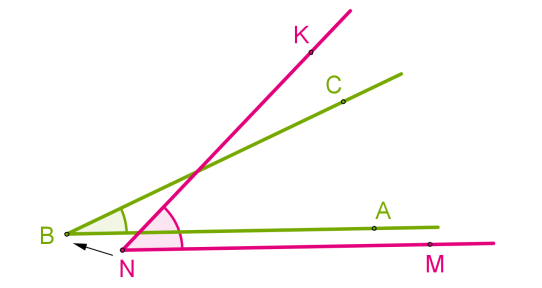
Совмещение углов [angle A B C] и [angle M N K] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет [left(frac{1}{360}right)] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
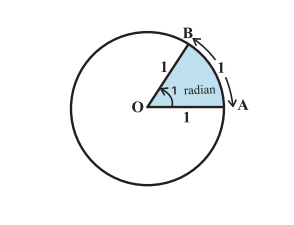
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
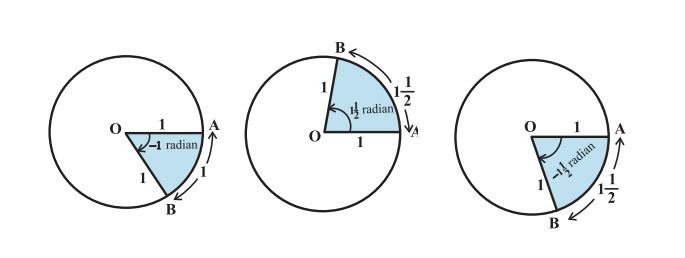
Вот еще несколько примеров углов: -1 радиан, радиан, [1 frac{1}{2}] радиан, [-1 frac{1}{2}] радиан.
Длина окружности = [2 pi r ldots] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна [2 pi]. Следовательно, один полный оборот начальной стороны образует в центре угол [2 pi] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = [frac{l}{r}] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
[theta=frac{l}{r}]
[l=r theta]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- [2 pi] радиан — в радианах
Следовательно, [2 pi] радиан = 360° ⇒ [pi] радиан = 180°. Теперь подставим приблизительное значение [pi] как [frac{22}{7}] в уравнении выше и получить, 1 радиан [frac{180^{circ}}{pi}=57^{circ} 16^{prime}]. Кроме того, [1^{0}=frac{pi}{180^{circ}}] радиан = 0,01746 радиан примерно. Ниже таблица, изображающая соотношение между градусами и радианами некоторых распространенных углов:
| Градусы | [30^{circ}] | [45^{circ}] | [60^{circ}] | [90^{circ}] | [180^{circ}] | [270^{circ}] | [360^{circ}] |
| Радианы | [frac{pi}{6}] | [frac{pi}{4}] | [frac{pi}{3}] | [frac{pi}{2}] | [pi] | [frac{3pi}{2}] | [2pi] |
Пример
Преобразуйте 40° 20′ в радианы.
Решение: мы знаем, что 1° = 60′, следовательно, 20′ = [frac{1^{0}}{3}].
Следовательно,
[40^{circ} 20^{prime}=40 frac{1}{3}=frac{121}{3}];
Кроме того, мы знаем, что
радианная мера = [frac{pi}{180^{0}} x] градусную меру
Следовательно, радианная мера [40^{circ} 20^{prime}=frac{pi}{180} times frac{121}{3}=frac{121 pi}{540}] радиан.
Нет времени решать самому?
Наши эксперты помогут!
Как измерить угол
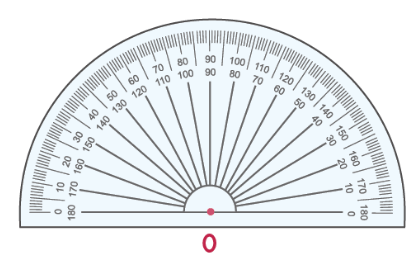
Для измерения углов используется транспортир:
Попробуем измерить угол [angle A O B]
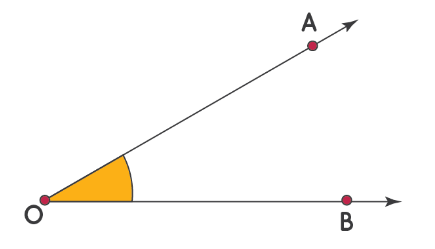
Шаги для измерения угла [angle mathrm{AOB}].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
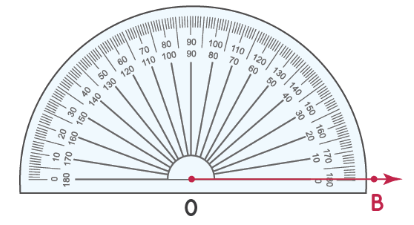
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
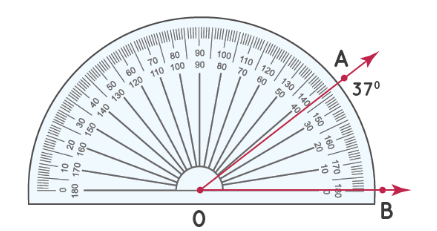
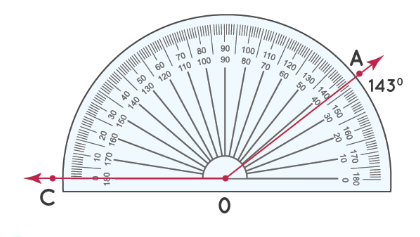
Далее попробуем измерить этот ∠AOC:
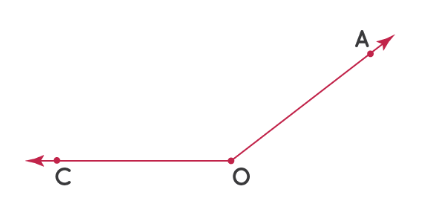
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
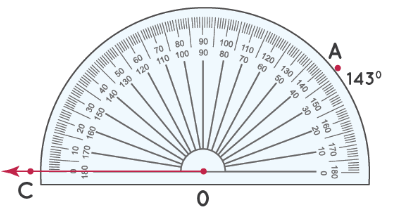
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
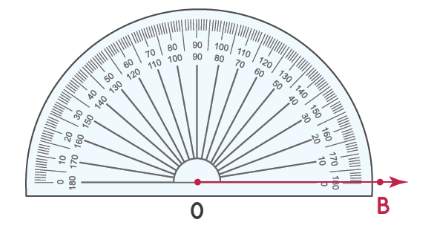
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
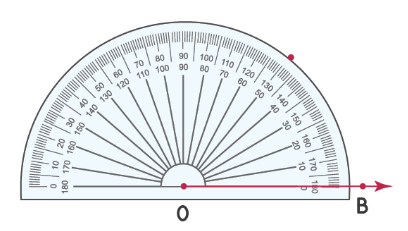
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.

Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
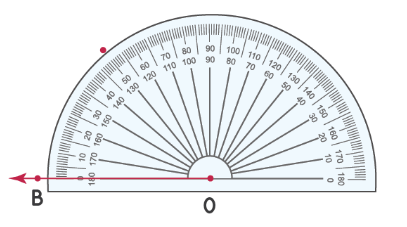
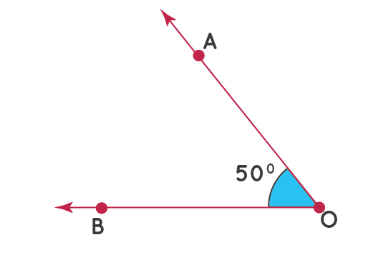
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
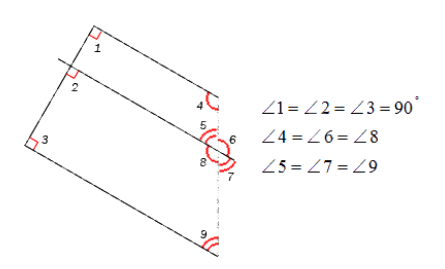
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
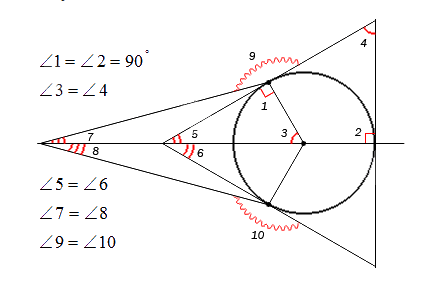
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
Тупоугольный треугольник

4.6
Средняя оценка: 4.6
Всего получено оценок: 146.
4.6
Средняя оценка: 4.6
Всего получено оценок: 146.
Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.
Опыт работы учителем математики — более 33 лет.
Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном, это обычный треугольник и подход к решению таких фигур ничем не отличается.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Пример решения задачи
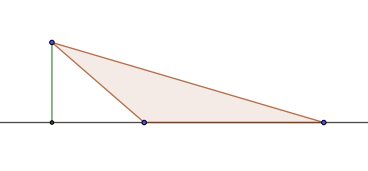
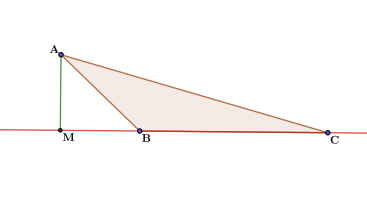
В тупоугольном треугольнике АВС известно, что косинус тупого угла равен $-2/sqrt{13}$. Сторона АС находится напротив тупого угла, $АВ=sqrt{13}$, ВС=2. Необходимо найти внешнюю высоту треугольника АМ.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно – как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
$$sin(ABC)=sqrt{1-cos^2(ABC)}=sqrt{13-4 over13}=sqrt{9 over13}={3oversqrt{13}}$$
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
$$S={1over2}*AM*BC$$
$$S={1over2}*AB*BC sin(ABC)$$
$${1over2}*AM*BC={1over2}*AB*BC*sin(ABC)$$
$$AM*ВС=AB*BC*sin(ABC)$$
$$AM=AB*sin(ABC)$$
$$AM=sqrt{13}*{3 over sqrt{13}}=3$$
- Второй способ – это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем, через значение косинуса найти значение синуса того же угла. А синус – это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза – это сторона АВ прямоугольного треугольника.
$$cos(ABM)=cos(180-ABC)=-cos(ABC)$$
$$cos(ABM)=-cos(ABC)={2over sqrt{13}}$$
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
$$Sin(ABM)=sqrt{1-cos(ABM)^2}=sqrt{13-4over13}=sqrt{9over13}={3oversqrt{13}}$$
$$Sin(ABM)=AM/AB$$
$$AM=AB*sin(ABM)=sqrt{13}*{3oversqrt{13}}=3$$
- Третий метод – это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$АС=sqrt{AB^2+BC^2-2AB*BC*cos(ABC)}=$$
$$sqrt {sqrt{13}^2+2^2-2*sqrt{13}*{-2oversqrt{13}}}=$$
$$sqrt{13+4+8}=sqrt{25}=5$$ – по теореме косинусов.
$${АСover{sin(ABC)}}={ABover{sin(ACB)}}$$ – по теореме синусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
$$ Sin(ABC)=sqrt{1-cos^2(ABC)}=sqrt{13-{4over{4}}}=sqrt{9over{13}}={3oversqrt{13}}$$
Выразим искомый синус угла АСВ.
$$Sin(ACB)=AB*{sin(ABC)over{AC}}$$
$$Sin(ACB)=(sqrt{13}*{{3oversqrt{13}}over{5}})={3over5}$$
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
$$Sin(ACB)={AMover AC}$$
$$AM=sin(ACB)*AC$$
$$AM={3over5}*{5}=3$$
Ответы всех трех способов совпали, а, значит, задача решена верно.
Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а также выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Азамат Дильдабаев
5/5
-
Арина Алисултанова
5/5
-
Иван Дарьин
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 146.
А какая ваша оценка?