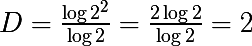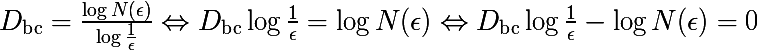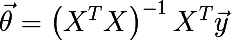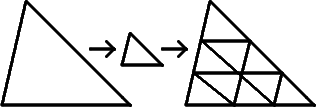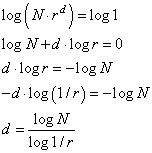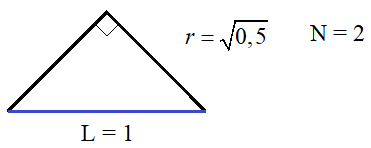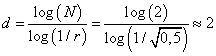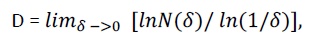Размерность
Как обычно для того что бы понять смысл алгоритма, необходимо немного окунуться в теорию. Википедия сообщает нам, что размерность в физике (и скорее всего большинство людей именно так воспринимают смысл размерности) — это количество независимых параметров, необходимых для описания состояния объекта, или количество степеней свободы физической системы. Но в математике все обстоит немного по-другому, тут у нас есть ряд определений размерности, которые часто зависят от рабочего пространства. В рамках общей топологии дается несколько определений размерности, и из них нам интересны будут размерность Хаусдорфа, размерность Минковского и фрактальная размерность.
Для начала вспомним формальный смысл тех размерностей, которые для нас интуитивно понятны, в векторном пространстве которое нас окружает. Под базисом векторного пространства мы понимаем максимальное множество линейно не зависимых векторов. Количество этих векторов мы называем размерностью векторного пространства, или его рангом. И любой элемент векторного пространства можно представить в виде линейной комбинации базисных векторов.
Размерность Хаусдорфа
Размерность Хаусдорфа обобщает понятие размерности действительного векторного пространства, и является естественным способом определения размерности подмножества в метрическом пространстве. Например размерность Хаусдорфа n-мерного (размерность в смысле векторного пространства) унитарного пространства (особый случай векторного пространства) будет тоже равна n. Хорошее математическое описание размерности Хаусдорфа дано в русской википедии, нам же важно понять смысл этой размерности интуитивно. Представим полное покрытие множества X шарами радиуса не более чем r, обозначим количество этих шаров за N( r ).
Значение N( r ) будет расти при уменьшении r (для полного покрытия будет требоваться все больше шаров). Размерностью Хаусдорфа хорошего множества X будет являться такое уникальное число d, что N( r ) будет расти как 1/rd при стремлении r к нулю. Под хорошим множеством понимаются гладкие множества без особенностей, какими например обладают фракталы. Примерами хороших множеств могут быть любые идеализированные геометрические объекты такие как куб, сфера и так далее.
Фрактальная размерность
Опишем один простой способ задания фрактальной размерности, хотя например размерность Минковского так же является одой из фрактальных размерностей, и она как раз тесно связана с размерностью Хаусдорфа, но об этом позже. Вот он простой способ задания фрактальной размерности:
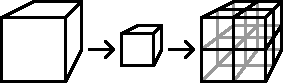
- Возьмем некоторую D-мерную геометрическую структуру и будем делить итеративно ее стороны на M равных частей (на следующей итерации, будем делить каждую полученную на предыдущей итерации часть так же на M частей)
- Каждый уровень будет состоять из MD частей предыдущего уровня
- Обозначим следующим образом количество полученных частей N = MD
Выполним следующее преобразование для вычисления формулы для значения фрактальной размерности D:
Рассмотрим простые примеры, которые я почерпнул из очень крутого курса по комплексным системам. Возьмем отрезок (одномерное ограниченное множество), разделим его на две равные части, таким же образом будем поступать с каждой полученной частью. Таким образом мы будем создавать полное покрытие множества.
Т.е. M = 2 и N = 2, т.к. из каждой части производится два новых куска отрезка, вычислим D:
Если разделять отрезок не на 2 части, а на 3, то D все равно будет равна 1, т.к. M = 3 и N = 3. Эта размерность совпадает с размерностью Хаусдорфа для хорошего множества.
Давайте рассмотрим аналогичную процедуру для квадрата.
Получаем M = 2 и N = 4, т.к. разделяя стороны на 2 равные части, мы получаем 4 новых, вычислим фрактальную размерность
И опять полученная размерность совпала с размерностью Хаусдорфа. Такой же результат можно получить если делить стороны на 3 равные части и т.д.
Бенуа Мандельброт при исследовании реальных объектов сделал очевидное замечание:
clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line
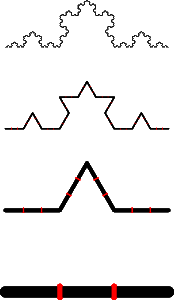
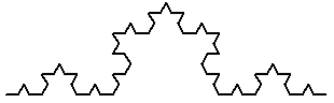
В реальном мире мы редко имеем дело с идеализированными объектами, что же будет если мы рассмотрим не совсем хороший геометрический объект, например кривую Коха (не путать с палочкой), вспомним алгоритм генерации такого множества. На каждой новой итерации, каждый кусок кривой, который является прямым отрезком, делится на три равные части, затем средний кусок убирается, а на его место становится конструкция напоминающая перевернутую букву V, каждое ребро которой равно убранной части отрезка (а так же равно и оставшимся).
Другими словами M = 3, т.к. отрезок делится на три равные части, а N = 4, т.к. каждая часть превращается в 4 части равных 1/4 от оригинала. Тогда фрактальная размерность такого множества при бесконечном итерировании будет равна следующему значению:
В качестве другого примера давайте глянем на треугольник Серпинского
На каждой итерации одна сторона делится на 2 части, т.е. M = 2, а в результате получается 3 части, т.е. N = 3, тогда
Возникает конечно вопрос, вот мы получили цифры некоторые, ну размерность стала дробной, и что? Есть ли в этом какой-то смысл, или это просто математические штучки. Строгой формулировки с описанием смысла дробности размерности нет, но можно ее интерпретировать следующим образом, на некотором интуитивном уровне. Фрактальная размерность чувствительна
ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо (источник)
В курсе по анализу комплексных систем упоминается следующая трактовка: дробная размерность — это своего рода плотность самоподобия.
Но говоря о реальных объектах читатель сразу же скажет, но ведь и кривая Коха и треугольник Серпинского далеки от реальности, что же делать тогда? Как я упомянул выше, приведенное определение фрактальной размерности является простым, и одним из нескольких. Давайте перейдем к более сложному определению фрактальной размерности. А пока взгляните, например, на капусту брокколи Романеско, вот такая вот реальность.
Размерность Минковского
Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:
- где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.
Если предел не существует, то рассматривают верхний и нижний пределы и говорят соответственно о верхней и нижней размерности Минковского. Верхняя и нижняя размерности Минковского тесно связанны с размерностью Хаусдорфа, интуитивно это легко уловить по способу задания размерности. Обычно упомянутые три размерности совпадают, и только в очень специфичных случаях имеет смысл их различать, но это не наши случаи.
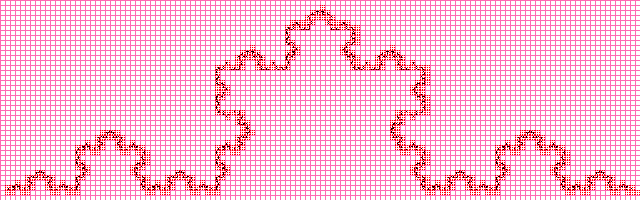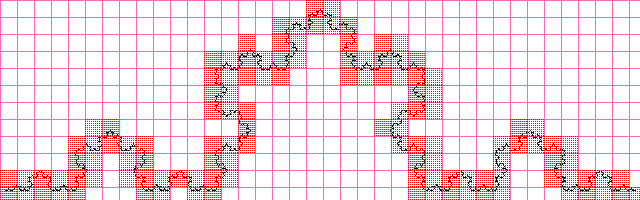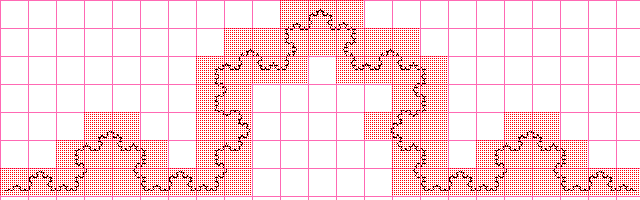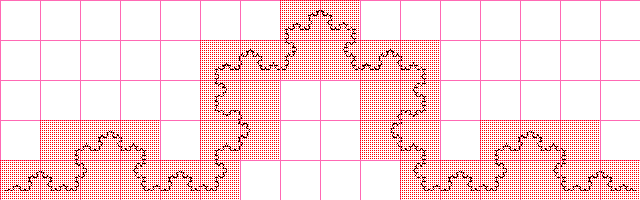
Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.
Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. Эта фраза может быть не сразу понятна, но думаю все прояснит алгоритм, используемый для вычисления приближенного значения размерности Минковского.
Box-counting алгоритм
Алгоритм выводится следующим образом, обозначим за Dbc приближенное значение размерности Минковского. Запишем определение этой размерности, убрав предел, его мы будем имитировать в итерациях, в которых будет изменяться размер ячеек.
Если зафиксировать размеры ячеек ε и рассматривать Dbc как неизвестное, то легко заметить, что приведенное выражение является формулой линии. Мы можем запустить цикл по различным размерам ячеек ε и записывать результат. Давайте нанесем эти результаты на график и построим линию регрессии для полученного множества данных, это значение и будет являться аппроксимацией фрактальной размерности Минковского.
Вот кстати список объектов с их фрактальными размерностями.
Надеюсь у меня получилось передать связь между естественной размерностью, и тем каким образом и зачем люди пришли к другим определениям размерности. Давайте перейдем к коду, а затем к примерам.
Box-counting алгоритм, C# код
Для вычисления размерности Минковского нам необходимы будут две процедуры, начнем с линейной регрессии. Вообще решить задачу линейной регрессии можно различными способами, чаще всего для этого используется метод градиентного спуска и метод наименьших квадратов (Normal equations). Первый хорошо работает на больших и широких данных, второй слабоват на широких данных из-за необходимости вычислять обратную матрицу, ширина которой равна ширине массива данных. В нашем случае ширина всего 2, так что это наш случай. В векторизованном виде решение линейной регрессии записывается следующим образом:
Обратную матрицу будем искать по следующей формуле:
Normal equations
public static double[] NormalEquations2d(double[] y, double[] x)
{
//x^t * x
double[,] xtx = new double[2, 2];
for (int i = 0; i < x.Length; i++)
{
xtx[0, 1] += x[i];
xtx[0, 0] += x[i] * x[i];
}
xtx[1, 0] = xtx[0, 1];
xtx[1, 1] = x.Length;
//inverse
double[,] xtxInv = new double[2, 2];
double d = 1/(xtx[0, 0]*xtx[1, 1] - xtx[1, 0]*xtx[0, 1]);
xtxInv[0, 0] = xtx[1, 1]*d;
xtxInv[0, 1] = -xtx[0, 1]*d;
xtxInv[1, 0] = -xtx[1, 0]*d;
xtxInv[1, 1] = xtx[0, 0]*d;
//times x^t
double[,] xtxInvxt = new double[2, x.Length];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < x.Length; j++)
{
xtxInvxt[i, j] = xtxInv[i, 0]*x[j] + xtxInv[i, 1];
}
}
//times y
double[] theta = new double[2];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < x.Length; j++)
{
theta[i] += xtxInvxt[i, j]*y[j];
}
}
return theta;
}
В нулевом элементе выходного вектора содержится угловой коэффициент (это и будет искомая размерность Минковского), а в следующем элементе — смещение. И собственно ключевая функция, которая возвращает датасет, по которому необходимо вычислить угловой коэффициент
Box-counting
/// <summary>
/// Box-counting algorithm
/// </summary>
/// <param name="bw">black-white bitmap</param>
/// <param name="startSize">initial size of square of grid</param>
/// <param name="finishSize">final size of square of grid</param>
/// <param name="step">step of changing of the grid</param>
/// <returns>baList.Add(Math.Log(1d/b), Math.Log(a)), where b is swuare length size, a is the number of intersection of image with grid squares</returns>
public static IDictionary<double, double> BowCountingDimension(BwBitmap bw, int startSize, int finishSize, int step = 1,
string dataPath = "")
{
//length size - number of boxes
IDictionary<double, double> baList = new Dictionary<double, double>();
for (int b = startSize; b <= finishSize; b += step)
{
int hCount = bw.Height/b;
int wCount = bw.Width/b;
bool[,] filledBoxes =
new bool[wCount + (bw.Width > wCount*b ? 1 : 0), hCount + (bw.Height > hCount*b ? 1 : 0)];
for (int x = 0; x < bw.Width; x++)
{
for (int y = 0; y < bw.Height; y++)
{
if (bw.GetBwPixel(x, y))
{
int xBox = x/b;
int yBox = y/b;
filledBoxes[xBox, yBox] = true;
}
}
}
int a = 0;
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
if (filledBoxes[i, j])
{
a++;
}
}
}
baList.Add(Math.Log(1d/b), Math.Log(a));
if (dataPath.Length > 0)
{
if (dataPath[dataPath.Length - 1] != '\')
{
dataPath += '\';
}
if (Directory.Exists(dataPath))
{
XBitmap bmp = new XBitmap(bw);
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
bmp.DrawLine(i * b, 0, i * b, bmp.Height, Color.HotPink);
}
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
bmp.DrawLine(0, j * b, bmp.Width, j * b, Color.HotPink);
}
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
if (filledBoxes[i, j])
{
bmp.FillRectangle(i * b, j * b, i * b + b, j * b + b, Color.Red, 2);
}
}
}
bmp.ConvertToNativeBitmap().Save(dataPath + b + ".bmp");
}
}
Logger.Instance.Log("BoxCounting: b is " + b + " of " + finishSize);
}
if (dataPath.Length > 0)
{
using (StreamWriter sw = new StreamWriter(dataPath + "ba.csv"))
{
sw.WriteLine("NumberOfBoxes,LengthOfSideInv");
foreach (double bInv in baList.Keys)
{
sw.WriteLine(baList[bInv] + "," + bInv);
}
sw.Close();
}
}
return baList;
}
Остается только связать две процедуры:
IDictionary<double, double> baList = BowCountingDimension(bwContour, 5, 100, 1, dir + "boxing\");
double[] y = new double[baList.Count];
double[] x = new double[baList.Count];
int c = 0;
foreach (double key in baList.Keys)
{
y[c] = baList[key];
x[c] = key;
c++;
}
double[] theta = NormalEquations2d(y, x);
Примеры
Буква
Рассмотрим простое изображение без особенностей, т.е. с гладкими краями. В компьютерном зрении часто анализируется не изображение целиком, а его контур.
Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.
Кривая Коха
Значение получилось почти такое же как и при вычислении фрактальной размерности аналитически, очевидно, что при увеличении разрешения изображения, аппроксимированное значение будет приближаться к вычисленному аналитически.
JanSetler
Карта России
Возьмем что нибудь более изрезанное, например карту нашей страны.
Получается что попа Дженифеер немного интереснее контура России, ну что ж поделать.
Фрактал
А будет ли значительно отличаться значение размерности для фрактала? Давайте проверим. Рассмотрим одно из множеств Жюлиа, точнее его границу. Гифку пришлось порезать, т.к. программка не справлялась с высоким разрешением, а масштабирование затирало сетку.
Как видите фрактал интереснее даже чем попа Дженифер.
Ссылки
Всю инфу вы найдете по ссылкам выше, в конце же я повторюсь только насчет двух курсов, второй кстати начался только пару дней назад, так что всем советую.
- Introduction to Complexity
- Introduction to Dynamical Systems and Chaos
Как то я в послал письмо одминам хабра с просьбой создать хаб по машинному обучению, получил такой вот ответ «Если наберется постов 15-20, которые просто обязаны быть в этом хабе — подумаем». Вообще таких постов уже давно больше, чем 15-20, у меня их только минимум штук 10. Я понимаю, что одминистрация больше занята хабами с политотой, но может попробуем обратить их внимание на действительно важные хабы.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Нужен ли отдельный хаб по машинному обучению?
Проголосовали 875 пользователей.
Воздержались 204 пользователя.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Нужен ли отдельный хаб по компьютерному зрению?
Проголосовали 908 пользователей.
Воздержались 202 пользователя.
☰ Оглавление
- Первая страница
- Онлайн инструменты ▽
- Редактор иконок favicon.ico онлайн
- Игра «Жизнь» онлайн
- Онлайн навигатор по множеству (фракталу) Мандельброта
- Онлайн конвертер PNG в favicon.ico
- Интерактивная схема солнечной системы
- Пересчёт дат в Юлианские дни
- Объяснение и онлайн-демо, как работает HTML5 canvas transform
- Онлайн генератор периодических фонов
- Онлайн конвертер цветов из HSV в RGB
- Онлайн URL-перекодировщик
- Онлайн генератор QR-кодов
- Покрутить 4D-гиперкуб
- Получение географических координат точки на карте
- «Сапёр» на бесконечном поле онлайн
- Черепаший язык онлайн
- Калькулятор индекса массы тела
- Для самых маленьких ▽
- Рисовалка для детей до трёх лет
- «Робот» для детей с трёх-четырёх лет
- «Морской бой» для самых маленьких
- Простой чат
- Инструменты ▽
- Docker ▽
- Docker устанавливаем и разбираемся
- Пример использования Docker для изучения Ruby on Rails
- Пример использования Docker для запуска MySQL
- Почему docker требует root-прав
- JavaScript ▽
- Букмарклеты для JavaSctipt/HTML-разработчика
- Использование «use strict» в JavaScript
- Небольшая памятка по JavaScript
- Простой минификатор/оптимизатор JavaScript
- Мои плагины для хрома
- Python ▽
- Сводная таблица методов основных типов данных Python 2 и 3
- Инструменты для Python-разработчика
- Удобная командная строка Python
- Утечки памяти в Python: метод
__del__и сборка мусора - Работа с нитями в Python
- Файловая система ▽
- FS: перемещение, переименование, архивирование
- Монтирование sshfs с помощью systemd
- Shell ▽
- Работа с историей команд bash
- Консоль/bash. настройка
- Отправка e-mail с картинками чистым shell скриптом
- Конвертирование аудио
- Конвертирование видео
- Управляем тактовой частотой процессора
- Совместный доступ к mercurial по SSH
- Передача файлов по сети
- Безопасное хранение и передача данных
- Нотификатор
- Xorg. Настройка
- Xorg. Настройка нестандартной клавиатуры
- Synergy: Много мониторов с одной клавиатурой и мышкой
- Ssh. Настройка
- Ssh. Настройка туннелирования через NAT и firewall
- Pidgin для хакеров
- Печать
- USB-Flash. монтирование
- Доступ к данным по MTP
- Настройка aspell
- Iptables. Port knocking
- Sudo, sudoers, visudo
- Swap в файле в Linux
- Добрый kill (gdb)
- Изменить размер tmp (tmpfs)
- Установка Arch Linux на USB-Flash
- Эмуляция в QEMU
- GRUB2 вручную
- Системные утилиты
- Настройка редактора vi
- Краткое руководство по vi
- HTML-валидатор
- VDS/VPS
- Начальная настройка
- Сборка nginx
- Настройка nginx
- Сборка uWSGI (Django+CGI)
- Настройка uWSGI
- Управление сетью в Ubuntu с помощью netctl (Arch Linux)
- Настройка WiFi точки доступа под Linux
- Docker ▽
- CS: Искусственный интеллект ▽
- Метрики в машинном обучении: precision, recall и не только
- Оценка точности классификатора
- Нейронные сети на простейших примерах
- Что такое нейрон (очень коротко)
- Пример задачи и демонстрация, как нейрон её решает
- Пример обучения нейрона
- Что осталось за сценой в задаче для одного нейрона
- Деревья принятия решений
- Байесовское машинное обучение
- Примеры кода numpy, scipy, matplotlib
- Метод наименьших квадратов
- Построение системы рекомендаций, на основе текстов
- Диффузионные реакции (реакции с диффузией)
- CS: Разное ▽
- RSA-шифрование на пальцах
- SQRT-декомпозиция
- О пользе рекурсии
- Дискретная бисекция
- Top-K из N (куча)
- Быстрое возведение в степень и подсчёт чисел Фибоначчи
- Алгебра логики
- Небольшая памятка по C++
- Проблема останова
- Примеры простейших серверов на Python
- Простейший форкающийся сервер
- Простейший prefork-сервер
- Простейший многонитевой сервер
- Многонитевой сервер с простым взаимодействием между нитями
- Асинхронный сервер
- Кумулятивное вычисление статистических характеристик
- Пять задач, которые хорошо бы уметь решать за час
- Теория относительности ▽
- Об этих заметках
- Пространство-время как геометрия
- Физическая интерпретация
- Универсальность скорости света
- Эквивалентность инерциальных систем отсчёта
- Относительность пространственных и временных интервалов
- Движение быстрее света
- Парадокс близнецов
- Заключение
- Теория вероятностей ▽
- Как нас обманывает интуиция
- Парадокс Монти Холла
- Парадокс двух конвертов
- Квантовая механика ▽
- Принцип неопределённости на классических примерах
- Фракталы ▽
- Фрактальная размерность
- Фрактальные деревья
- Применение фракталов
- Комплексная размерность
- Гиперкуб
- Обучение и преподавание ▽
- О репетиторстве
- Типичные ошибки на экзаменах
- Лёгкая подготовка к экзаменам
- Как отвечать на экзамене
- Как я худел
- Личное ▽
- Обо мне (как бы резюме)
- Благодарности
- Мои ошибки
- Немного фотографий
- Копирование этих материалов
Фрактальная размерность
О фракталах говорят много. В Паутине созданы сотни сайтов,
посвящённых фракталам. Но большая часть информации сводится к тому,
что фракталы это красиво. Загадочность фракталов объясняют их
дробной размерностью, но мало кто понимает, что же такое дробная
размерность.
Где-то в 1996 меня заинтересовало, что же такое дробная размерность
и каков её смысл. Каково же было моё удивление, когда я узнал, что
это не такая уж сложная вещь, и понять её может любой школьник.
Я постараюсь изложить здесь популярно, что же такое дробная размерность.
Чтобы компенсировать острый дефицит информации по этой теме.
Измерение тел
Сперва небольшое введение, чтобы привести наши бытовые
представления об измерении тел в некоторый порядок.
Не стремясь к математической точности формулировок, давайте разберёмся,
что же такое размер, мера и размерность.
Размер
Размер объекта можно померить линейкой.
В большинстве случаев размер получается малоинформативен.
Какая «гора» больше?
Если сравнивать высоты, то больше красная, если ширины —
зелёная.
Сравнение размеров может быть информативным если
предметы подобны друг другу:
Теперь какие бы размеры мы ни сравнили: ширину, высоту, сторону,
периметр, радиус вписанной окружности или любые другие, всегда получится,
что зелёная гора больше.
Далее мы будем говорить о подобных объектах, поэтому размер
нам пригодится.
Мера
Мера тоже служит для измерения объектов, но она измеряется не
линейкой. О том, как именно она измеряется мы ещё поговорим,
а пока отметим её главное свойство — мера аддитивна.
Выражаясь на бытовом языке, при слиянии двух объектов, мера
суммы объектов равна сумме мер исходных объектов.
Для одномерных объектов мера пропорциональна размеру.
Если вы возьмёте отрезки длиной 1см и 3см, «сложите» их вместе,
то «суммарный» отрезок будет иметь длину 4см (1+3=4см).
Для не одномерных тел, мера вычисляется по некоторым правилам,
которые подбираются так, чтобы мера сохраняла аддитивность.
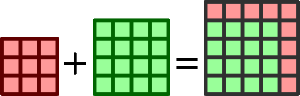
Например, если вы возьмёте квадраты со сторонами 3см и 4см и
«сложите» их (сольёте их вместе), то сложатся площади (9+16=25см²),
то есть сторона (размер) результата будет 5см.
И слагаемые, и сумма являются квадратами.
Они подобны друг другу и мы можем сравнивать их размеры.
Оказывается, что размер суммы не равен сумме размеров слагаемых
(5≄4+3).
Как же связаны мера и размер?
Размерность
Как раз размерность и позволяет связать меру и размер.
Давайте обозначим размерность — D, меру — M, размер — L.
Тогда формула, связывающая эти три величины будет имеют вид:
M = LD
Для привычных нам мер эта формула приобретает всем знакомые обличия.
Для двухмерных тел (D=2) мерой (M) является площадь (S),
для трёхмерных тел (D=3) — объём (V):
S = L2, V = L3
Внимательный читатель спросит, по какому праву мы написали знак равенства?
Ну хорошо, площадь квадрата равна квадрату его стороны, а площадь круга?
Работает ли эта формула для любых объектов?
И да и нет. Вы можете заменить равенства на пропорциональности и ввести
коэффициенты, а можете считать, что мы вводим размеры тел именно так,
чтобы формула работала. Например для круга мы будем называть размером длину дуги
равной корень из «пи» радиан. А почему нет?
В любом случае, наличие или отсутствие коэффициентов не
изменит суть дальнейших рассуждений. Для простоты, я не буду вводить
коэффициенты; если хотите, вы можете их добавить самостоятельно,
повторить все рассуждения и убедиться, что они (рассуждения) не утратили
своей справедливости.
Итого
Из всего сказанного нам следует сделать один вывод, что
если фигуру уменьшить в N раз (отмасштабировать), то
она будет укладываться в исходной ND раз.
Действительно, если уменьшить отрезок (D=1) в 5 раз, то он
поместится в исходном ровно пять раз (51=5);
Если треугольник (D=2) уменьшить в 3 раза, то он уложится в исходном
9 раз (32=9).
Если куб (D=3) уменьшить в 2 раза, то он
уложится в исходном 8 раз (23=8).
Верно и обратное: если при уменьшении размера фигуры в N
раз, оказалось, что она укладывается в исходной n раз
(то есть мера её уменьшилась в n раз), то размерность
можно вычислить по формуле:
D = ln(n)/ln(N)
Не очень строго и опуская многие важные детали, мы всё же получили
формулу для размерности.
Дробная размерность
Простейший пример
Про дробную размерность обычно рассказывают на примерах
различных ломаных. Я не буду изобретать велосипед и обращусь
к звезде Коха.
Процедура её построения показана на рисунке (снизу вверх):
В начале берётся отрезок, делится на три равные части и
средняя часть заменяется на два отрезка, равных изъятому.
Получается ломаная из четырёх равных отрезков.
На втором шаге действия повторятся с каждым из четырёх отрезков
и получается ломаная из 16 отрезков.
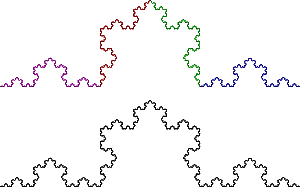
Эти построения повторяются бесконечное число раз и в конце концов
у нас получается ломаная, состоящая из бесконечного числа отрезков.
Сколько бы мы её не масштабировали, мы всё равно будем получать
одно и тоже.
Это и есть звезда Коха.
Строго говоря, полученное множество точек уже нельзя
называть ломаной. По определению, ломаная должна состоять из
конечного числа отрезков. Но я буду использовать слово
«ломаная» в «нестрогом» смысле для краткости.
Давайте теперь воспользуемся нашим приёмом, чтобы определить её размерность.
Из построения и рисунка видно, что звезду можно разбить на
четыре равные части, при этом размер (скажем, длина исходного
отрезка) каждой части будет равен трети размера исходной фигуры.
То есть будучи уменьшена в три раза, она уложится в себе четыре раза:
По аналогии с нашими предыдущими рассуждениями получаем, что
размерность равна
D = ln(4)/ln(3) ≈ 1.26185950714291487419
То есть это уже не просто отрезок или ломаная (длина звезды Коха бесконечна),
но и не плоская фигура, полностью покрывающая некоторую площадь.
Если мы слегка модифицируем алгоритм построения и будем извлекать
не 1/3 отрезка, а 1/9, то ломаная получится более плотной:
Какова же её размерность? Теперь фигура уложится сама в себе
четыре раза после уменьшения в 9/4 раза, то есть размерность можно
вычислить по той же формуле:
D = ln(4)/ln(9/4) ≈ 1.70951129135145477696
Как видите, «плотность» покрытия сразу отразилась на размерности.
Чуть сложнее
Давайте теперь получим более общую формулу для вычисления размерности.
Для этого снова рассмотрим пример:
Итерации снова начинаются с одного отрезка.
На каждом шаге итерации количество отрезков удваивается.
Каждый порождает два новых: один в 0.88 раз меньше (или, вернее больше)
родителя, второй — в 0.41 раз. В пределе получается следующее
множество:
Давайте вернёмся к первому шагу итераций, на котором мы
получили два отрезка, и посмотрим, какая часть фрактала
образована из каждого из них:
Если принять, что размер полного фрактала 1, то размер
зелёной части (полученной из большего отрезка) будет 0.88,
а размер красной (полученной из меньшего) — 0.41.
Та формула, которой мы располагаем, уже не годится, так как мы
имеем не один, а два коэффициента масштабирования. Но мы можем воспользоваться
нашими знаниями о свойства меры, размера и размерности. Мера, как мы
помним, аддитивна, то есть мера полного фрактала, равна сумме мер
его частей:
M0 = M1 + M2
И сам фрактал, и его части имеют одинаковую размерность (D) и мы можем
выразить меры, через размеры:
L0D = L1D + L2D
А размеры мы знаем. То есть для размерности нашего фрактала мы можем написать уравнение:
1D = 0.88D + 0.41D
или просто
1 = 0.88D + 0.41D
Решить это уравнение аналитически невозможно, но «приблизительный» ответ
можно «подобрать». В нашем случае
D ≈ 1.7835828288192
Можете проверить на калькуляторе.
1 ≈ 0.881.78358 + 0.411.78358
Таким образом, если фрактал образован из N подобных элементов, с коэффициентами
подобия k1, k2 … kN, то его
размерность можно найти из уравнения:
1 = k1D + k2D + … + kND
По этой формуле уже можно рассчитать размерность многих итерационных систем.
Обратите внимание, что, если все коэффициенты равны,
то наша формула превращается в
уже известную простую формулу:
1 = kD + kD + … + kD = N * kD
1/N = kD
D = ln(1/N)/ln(k)
или
D = ln(N)/ln(1/k)
Последнее выражение есть наша первая простая формула
для вычисления размерности простейших самоподобных фракталов.
В заключение
В этом рассказе (именно рассказе) о размерности даже не
упомянуты многие важные аспекты. Он ни сколько не претендует
на полноту, точность или строгость. Но, надеюсь, что
он будет понятен любому старшекласснику и развеет многие
непонимания и мистификации. Про одну из таких распространённых
мистификаций вы можете прочитать в
моей следующей заметке.
- СИФ, множества Жюлиа и Мандельброта
- Как вычисляется фрактальная размерность по Хаусдорфу
- Системы итерированных функций СИФ
- Рандомизированная система итерированных функций
- Примеры фракталов, сгенерированных СИФ
- Как построить множества Жюлиа
- Рисуем множество Мандельброта
- Главная
- Фракталы
- СИФ, множества Жюлиа и Мандельброта
Как вычисляется фрактальная размерность по Хаусдорфу
На предыдущих
занятиях мы с вами последовательно рассматривали разные вариации L-системы по
принципу «от простого к сложному». Я решил не прерывать это повествование и
довести его до логического конца. Теперь же можно вернуться к одному важному
вопросу, который остался в стороне – о вычислении размерности фрактальных
кривых.
Как я говорил во
введении, фракталы принадлежат дробной размерности. Например, кривая Коха имеет
размерность, равную, примерно, 1,2618. Но как она была вычислена? Именно это мы
и разберем на этом занятии.
Первый
математический аппарат для расчета дробных размерностей предложил немецкий
ученый Феликс Хаусдорф в 1919 году.
Феликс Хаусдорф
(1868-1942 гг.)
Чтобы получить
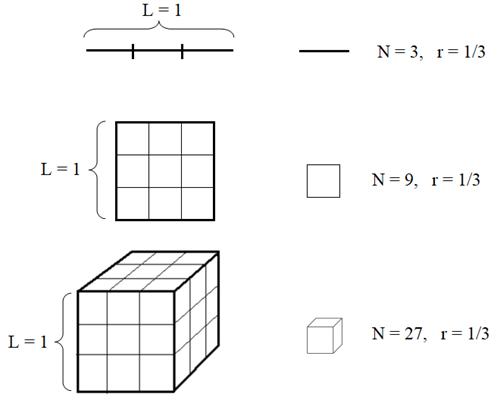
формулу расчета размерности фигуры, можно рассуждать следующим образом. Если
взять линейный отрезок и разделить его на N = 3 равные
части, то длина каждого фрагмента будет в три раза меньше исходной длины. Пусть
начальная длина, условно равна 1, тогда длины фрагментов будут равны r = 1/3.
Очевидно, что общая длина отрезка, равна:
Проделаем ту же
операцию с квадратом. Каждую из его сторон длиной в одну единицу также разделим
на три равные части. То есть, линейные размеры маленьких квадратов будут равны r = 1/3. И таких
квадратов всего N = 9. В этом случае площадь большого квадрата будет
равна:
Как вы уже
догадались, если взять куб и каждую из его сторон также разбить на три равных
отрезка, то получим N = 27 кубиков со сторонами r = 1/3. Тогда
объем куба можно выразить формулой:
То есть,
смотрите, размерность фигуры проявляется как степень коэффициента подобия r. И в общем
случае можно записать:
Чтобы из этой
формулы выразить степень d, прологарифмируем левую и правую части
этого уравнения, получим:
Логарифм можно
взять по любому основанию, обычно это 2, 10 или e – натуральный
логарифм. Величину d называют фрактальной размерностью или размерностью
подобия.
Вот это
выражение и есть формула Хаусдорфа для вычисления размерностей произвольных
кривых, которые могут быть разбиты на одинаковые фрагменты. Фрактальные кривые,
как раз обладают таким свойством – они составлены их однотипных кривых меньшей
размерности поэтому принцип расчета размерности, предложенный Хаусдорфом,
хорошо для них подходит.
Давайте
воспользуемся этой формулой, вычислим размерность кривой Коха и проверим,
действительно ли она равна 1,2816.
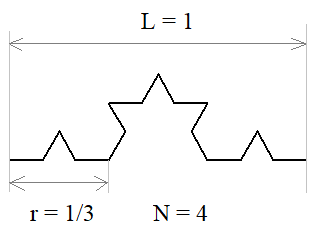
Смотрите, длина
уменьшенных сегментов равна r = 1/3 от общей длины L = 1. Всего
таких сегментов N = 4. Подставляем величины в формулу фрактальной
размерности, имеем:
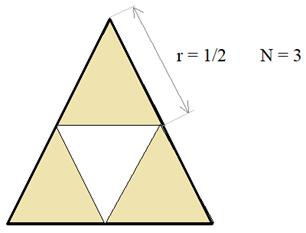
Давайте
проделаем тот же ход для вычисления размерности фрактала «ковер Серпинского».
Здесь
коэффициент подобия r = 1/2. Всего уменьшенных треугольников N = 3. Получаем
размерность этого фрактала, равной:
Ну и последний
пример – размерность фрактала «дракон Хартера-Хейтуэя».
На каждой
итерации прямые заменяются на прямоугольные уголки. Если длину прямой принять
за единицу (L = 1), то длины
сторон прямоугольного уголка будут равны .
Всего таких сторон N = 2. Получаем размерность этого фрактала:
То есть, при
числе итераций стремящихся к бесконечности, дракон покроет собой все двумерное
пространство. На самом деле – это один из примеров кривой Пеано, которая будучи
одномерной, способна обходить все точки на плоскости. И метрика Хаусдорфа это
подтверждает.
Видео по теме
- Следующая
Теги: математика для data science, фрактальная размерность, метод ричардсона, расчёт размерности, показатель хаусдорфа, формула каплана-йорке, аттрактор, фракталы
Значимую роль в разработке подхода к анализу нелинейных динамических систем сыграла теория подобия. Теория подобия выдвигает понятия аттрактора для описания подобных объектов. Для понимания понятия аттрактора приведу наглядный пример. По колеистой дороге двигается автомобиль. Аттрактором для такого объекта, как автомобиль, будет колея, по которой он двигается. Если на автомобиль оказывается какая-то сила, стремящаяся вытолкнуть с колеи, то после того, как сила прекратит свое воздействие, автомобиль снова вернется на прежнюю колею, потому что его колеса будут сами стремиться ехать по данной колее.
Теперь обратимся к критериям, описывающим геометрические свойства аттракторов. Необходимо отметить важность размерности, которая тесно связана с динамикой системы. Размерность играет основную роль в определении диапазона возможной динамической характеристики, например, размерность аттрактора дает числовую оценку числа активных степеней свободы рассматриваемой системы.
Геометрические объекты с размерностями, которые не являются целыми числами, выполняют фундаментальную роль в динамике хаотических систем. Такие объекты называются фракталами. Объект с нецелой размерностью обладает фрактальной размерностью.
Фрактальная размерность даёт новые возможности для изучения нелинейной динамики. Нелинейные системы обладают чувствительностью к начальным условиям в том смысле, что траектории, вначале близкие в пространстве состояний, могут под воздействием внешних и внутренних сил смешаться к различным аттракторам. В некоторых случаях эти аттракторы соответствуют неподвижным точкам или предельным циклам, в других — такие аттракторы могут быть хаотическими.
Как известно, аттрактор характеризуется своим бассейном притяжений, и для многих нелинейных систем границы бассейнов притяжения представляют собой сложные геометрические объекты, которые лучше определяются фрактальной размерностью. Эти границы в сильной степени обладают сильной «колеистостью», что приводит к чувствительности от начальных условий: небольшое изменение в начальных условиях может сдвинуть траекторию непредсказуемым образом от одного бассейна притяжения к другому.
В современных экономических рядах эмпирически отмечается тот факт, что фрактальная размерность меняется по ходу ряда. Изменение фрактальной размерности приводит к тому, что поведение значений ряда усложняется ещё в большей степени. Подобное усложнение также демонстрирует некомпетентность традиционных методов анализа и прогнозирования.
Б. Мандельброт даёт следующее определение фракталам: «фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». Существуют различные способы расчёта размерности. Практически все из них включают в себя подсчет объёма или площади фрактальной формы и того, как она изменяется в масштабах в том случае, если этот объём или форма увеличиваются.
Методы расчёта фрактальной размерности сводятся или к подсчету степени изрезанности ряда с помощью окружностей определённого радиуса (метод Ричардсона), или к определению числа ячеек в пространстве, занимаемом фрактальной кривой (емкостная размерность), или посредством так называемой корреляционной суммы (корреляционная размерность), или к расчёту показателя Херста H.
В настоящее время фрактальный анализ, как один из инструментов, предлагаемый теорией хаоса, применяется успешно во многих областях. Основной характеристикой самоподобных структур является фрактальная размерность D. Данная характеристика была предложена Хаусдорфом в 1919 году. Позднее Мандельброт доработал некоторые идеи Хаусдорфа.
N(δ) – минимальное число шаров радиуса δ, которые покроют это множество. Часто на практике при попытке вычислить показатель D возникают проблемы, связанные с тем, что временной ряд всегда имеет минимальный масштаб для δ. Показатель D получил название показатель Хаусдорфа (размерность Хаусдорфа). Однако для надежного вычисления требуется большой объем данных для проведения расчета. Иначе результаты могут получиться нерепрезентативными.
Если известно достаточное количество показателей Ляпунова, то можно оценить ляпуновскую размерность аттрактора по формуле Каплана-Йорке:
Материал является отрывком из научной работы «Теория нелинейной динамики».
Хотите знать больше? Добро пожаловать на мой Телеграм-канал!
Понятие размерности и ее расчет
В
своей повседневной жизни мы постоянно
встречаемся с размерностями. Мы
прикидываем длину дороги, узнаем площадь
квартиры и т.д. Это понятие вполне
интуитивно ясно и, казалось бы, не требует
разъяснения. Линия имеет размерность
1. Это означает, что, выбрав точку отсчета,
мы можем любую точку на этой линии
определить с помощью 1 числа –
положительного или отрицательного.
Причем это касается всех линий –
окружность, квадрат, парабола и т.д.
Размерность
2 означает, что любую точку мы можем
однозначно определить двумя числами.
Не надо думать, что двумерный – значит
плоский. Поверхность сферы тоже двумерна
(ее можно определить с помощью двух
значений – углов наподобие ширины и
долготы).
Если
смотреть с математической точки зрения,
то размерность определяется следующим
образом: для одномерных объектов –
увеличение в два раза их линейного
размера приводит к увеличению размеров
(в данном случае длинны) в два раза (2^1).
Для
двумерных объектов увеличение в два
раза линейных размеров приводит к
увеличению размера (например, площадь
прямоугольника) в четыре раза (2^2).
Для
3–х мерных объектов увеличение линейных
размеров в два раза приводи к увеличению
объема в восемь раз (2^3) и так далее.
Таким
образом, размерность D можно рассчитать
исходя из зависимости увеличения
«размера» объекта S от увеличения
линейных размеров L. D=log(S)/log(L). Для линии
D=log(2)/log(2)=1. Для плоскости D=log(4)/log(2)=2. Для
объема D=log(8)/log(2)=3.
Рассчитаем
размерность для кривой Пеано. Исходная
линия, состоящая из трех отрезков длинны
Х, заменяется на 9 отрезков втрое меньшей
длинны. Таким образом, при увеличении
минимального отрезка в 3 раза длина всей
линии увеличивается в 9 раз и
D=log(9)/log(3)=2 – двумерный объект.
Когда
размерность фигуры получаемой из
каких–то простейших объектов (отрезков)
больше размерности этих объектов – мы
имеем дело с фракталом.
Геометрические фракталы
Именно
с них и начиналась история фракталов.
Этот тип фракталов получается путем
простых геометрических построений.
Обычно при построении этих фракталов
поступают так: берется «затравка» –
аксиома – набор отрезков, на основании
которых будет строиться фрактал. Далее
к этой «затравке» применяют набор
правил, который преобразует ее в
какую–либо геометрическую фигуру.
Далее к каждой части этой фигуры применяют
опять тот же набор правил. С каждым шагом
фигура будет становиться все сложнее
и сложнее, и если мы проведем бесконечное
количество преобразований – получим
геометрический
фрактал.
Рассмотренная
ранее кривая
Пеано
является геометрическим фракталом. На
рис. ниже приведены другие примеры
геометрических фракталов (слева направо
Снежинка Коха, Лист, Треугольник
Серпинского).
Рис.
Снежинка Коха

Лист

Треугольник Серпинского
Из
этих геометрических фракталов очень
интересным и довольно знаменитым
является – снежинка
Коха.
Строится она на основе равностороннего
треугольника. Каждая линия которого
заменяется на 4 линии каждая длинной в
1/3 исходной. Таким образом, с каждой
итерацией длинна кривой увеличивается
на треть. И если мы сделаем бесконечное
число итераций – получим фрактал –
снежинку Коха бесконечной длинны.
Получается, что наша бесконечная кривая
покрывает ограниченную площадь.
Размерность
снежинки Коха (при увеличении снежинки
в 3 раза ее длина возрастает в 4 раза)
D=log(4)/log(3)=1.2619…
Для
построения геометрических фракталов
хорошо приспособлены так называемые
L–Systems.
Суть этих систем состоит в том, что
имеется определенных набор символов
системы, каждый из которых обозначает
определенное действие и набор правил
преобразования символов.