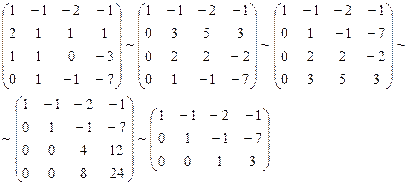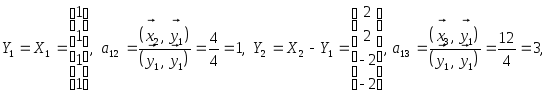Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Линейные оболочки и подпространства
Определение. Подпространством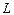 
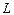
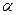
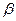
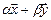
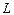
линейного пространства 
называется множество векторов из такое, что для любых двух векторов
и 
из и любых двух вещественных чисел 
и 
линейная комбинация 
также принадлежит .
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 
называется множество всех линейных комбинаций векторов . Обозначается 
.
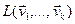
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 
и 
называется множество всех векторов 
, представимых в виде 
, где 
, 
. Обозначается 
.
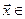
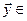
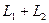
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством
+ 
= + .
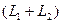
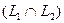
Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами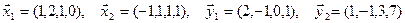 
.
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 
, порождённого векторами 
, равенство нулю линейной комбинации 
, эквивалентное системе уравнений 
, достигается лишь при условии 
. Следовательно, векторы линейно
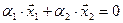
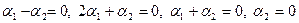
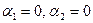
независимы и размерность подпространства равна 2: 
. Для подпространства , порождённого векторами 
, проводя аналогичный анализ, получим 
.
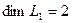
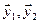
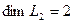
Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор 
подпространства является линейной комбинацией базисных векторов : 
. Аналогично для подпространства имеем 
, тогда условие принадлежности пересечению есть 
или 
.
Это условие представляет собой систему уравнений относительно коэффициентов 
. Составим матрицу системы и упростим её с помощью элементарных преобразований: 
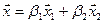
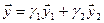
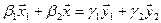
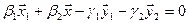
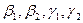
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим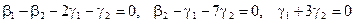 
,
откуда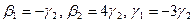 
.
Полагая свободное неизвестное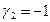 
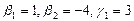
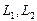
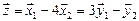
, для остальных имеем
. Итак, пересечение подпространств 
имеет один базисный вектор
.
Размерность пересечения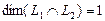 
. Следовательно, в соответствии с равенством
размерность суммы подпространств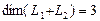 
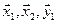
. В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором 
. В линейной независимости векторов 
убедиться нетрудно.
Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами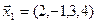 
, 
, 
, 
, 
.
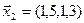
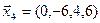
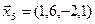
3.40. Найти размерность и какой-либо базис линейной оболочки векторов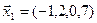 
, 
, 
, 
, 
.
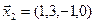
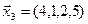
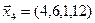
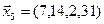
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
последовательностей в пространстве сходящихся последовательностей;
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 
функций в пространстве функций, непрерывных на отрезке 
.
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
;
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве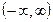 
функций в пространстве функций, ограниченных на том же множестве.
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а)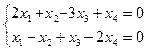 
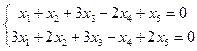
; б) 
;
в)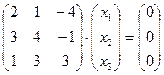 
.
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению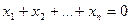 
;
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами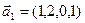 
, 
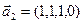
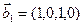
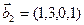
и 
, 
. Является ли эта сумма прямой суммой?
3.46. Найти размерность суммы и пересечения линейных оболочек векторов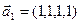 
, 
, 
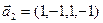
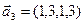
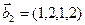
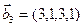
и 
, 
, 
. Является ли их cумма прямой?
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
и 
, если
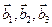
а)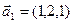 
, 
, 
, 
, 
, 
;
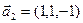
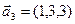
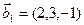
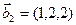
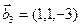
б)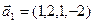 
, 
, 
, 
, 
, 
.
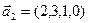
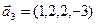
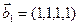
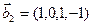
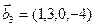
3.48. Найти базис суммы и пересечения линейных оболочек 
и 
, если
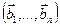
а) 
, 
, 
, 
;
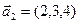
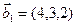
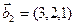
б)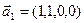 
, 
, 
, , 
, 
.
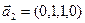
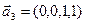
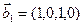
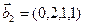
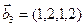
Является ли прямой сумма этих подпространств?
http://lektsii.org/10-6017.html
Определение
1.
Линейной
оболочкой
заданной
конечной совокупности
элементов векторного пространства
n
над полем К называется множество всех
линейных комбинаций этих элементов с
коэффициентами из поля К. При этом сама
совокупность
называется порождающей
системой
данной линейной оболочки, а сама линейная
оболочка обозначается символом
.
Линейные оболочки
обладают следующими свойствами:
.
Линейная оболочка элементов векторного
пространства
n
является подпространством М векторного
пространства
n.
Данный
результат следует из определения
линейной оболочки: сумма
двух векторов из линейной оболочки
будет принадлежать линейной оболочки
(одна из линейных комбинаций), произведение
вектора из линейной оболочки также
будет принадлежать линейной оболочки.
.
Линейная оболочка может совпадать со
всем пространством Rn
(если образующая
система является базисом
в пространстве Rn
)
.
Линейная оболочка
является наименьшим подпространством,
содержащим элементы
.
Все остальные подпространства могут
только содержать вектора порождающей
системы или их возможные комбинации.
.
Если какой-нибудь элемент из порождающей
системы элементов
есть линейная комбинация остальных
элементов этой системы, то его можно
удалить из порождающей системы, не
изменив при этом линейной оболочки.
.
Если координатная матрица системы
образующих
имеет ранг р, где
,
то любая линейно независимая система
,
является базисом линейной оболочки
,
а сама линейная оболочка будет
подпространством размерности р,
.
Примеры.
-
Если
a,
b,
с – геометрические векторы, лежащие
на одной прямой. В этом случае линейная
оболочка L(а,b,c)=
L(a).Здесь
линейная оболочка является одномерным
пространством, которое состоит из всех
вектор, лежащих на прямой, причем вектор
а
–является базисом. -
Пусть
a,
b,
с – геометрические векторы, причем a,
b
не коллинеарны, с = а + b.
В этом случае линейная оболочка L(а,b,c)=
L(a,b).Здесь
линейная оболочка является двумерным
пространством, состоящем из всех
векторов, компланарных с векторами a
и b.
Вектора а,b
составляют базис в L(a,b).
Любой вектор из L
представляется в виде линейной комбинации
векторов а
и b.
Вообще,
в конечномерном пространстве R
всякое подпространство L
является линейной
оболочкой некоторой системы векторов.
Рассмотри
следующую задачу.
В евклидовом пространстве En
задана линейная оболочка
,
где k
n.
Требуется:
1)Найти
размерность и базис линейной оболочки
;
2)Выделить в линейной оболочке
ортогональный базис и
достроить
его до
ортонормированного базиса евклидова
пространства
En.
Если
схема решения первой задачи нам знакома,
то решение второй задачи строится на
следующем теоретическом результате.
Теорема
(Грама
– Шмидта)
Пусть
— система линейно независимых векторов
в евклидовом пространстве, где k
n,
являющихся образующей системой линейной
оболочки
.
Система векторов
,
описываемая формулами
,
,
,
. . .
где
коэффициенты
,
,
образует
ортогональный
базис
линейной оболочки
.
Доказательство.
Для
доказательства теоремы достаточно
доказать следующее утверждение: вектор
ортогонален вектору
.
Действительно,
умножая скалярно вектор
на вектор
,
получим
=
=0
Следствие.
Результат теоремы дает
алгоритм последовательной ортогонализации
системы линейно независимых элементов
( так
называемый
метод Грама — Шмидта).
Пример
-
В
евклидовом пространстве E4
линейная оболочка
задана образующей системой векторов
с координатами
.
Требуется:
а)
найти размерность и базис линейной
оболочки
б)
указать в линейной оболочке
ортонормированный базис
и
достроить его до ортонормированного
базиса евклидова
пространства
E4.
Решение.
Рассмотрим координатную матрицу
.
Так как
,
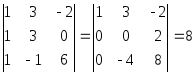
то
,
элементы
линейно независимы в E4
и образуют базис данной линейной
оболочки, являющейся подпространством
в E4.
Для
построения ортонормированного базиса
в E4
применим метод
ортогонализации
Грама-Шмидта. Получим
,
,
.
Записывая векторы
столбцами их координат, последовательно
найдем
.
Легко
проверить, что полученные элементы
попарно ортогональны. Найдем ортогональный
им вектор
.
Пусть
,
то неизвестные координаты
вектора Y4
найдутся из условий
,
,
.
Так
как
,
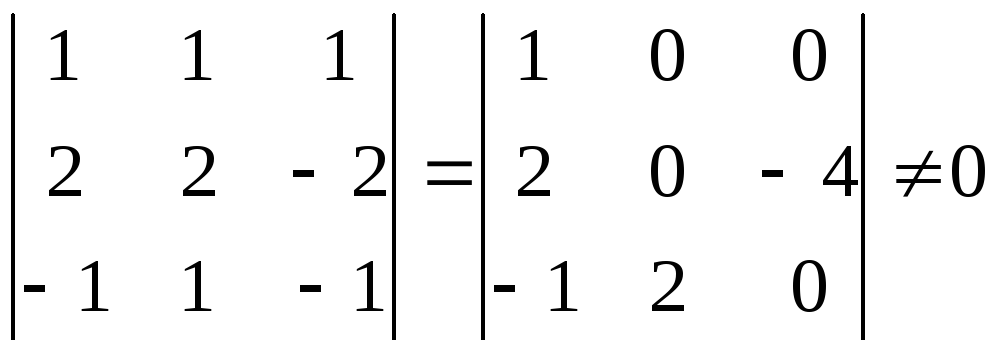
в последней системе неизвестные
можно взять в качестве базисных
неизвестных.
Если
для свободной (небазисной) неизвестной
,
то
.
Нормировав
найденные векторы
,
построим ортонормированный базис в E4:
.
Задача
решена.
В
завершении параграфа введем важное
определение.
Пусть
— — базис в En
и векторы
представлены в этом базисе своими
разложениями
.
Тогда
скалярное произведение этих векторов
имеет вид
или в матричной форме
,
где
— столбцы координат векторов
в базисе
а симметричная матрица
составлена из скалярных произведений
базисных векторов:
.
В
общем случае в качестве элементов
матрицы А рассматривают скалярные
произведения произвольной системы
векторов а1,
а2,…,
аn
Определение
3.
Определитель
матрицы А
скалярных произведений заданной системы
векторов
называют определителем
Грама.
Теорема
Произвольная
система
векторов,
заданных в ортонормированном
базисе,
будет линейно
независимой,
если ее определитель
Грама отличен от нуля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти базис и размерность линейной оболочки векторов
Пример1)
Найти базис и размерность линейной оболочки векторов a1=(1, 2, 3, 4), a2=( -1, 3, 2, 1),
a3=(- 1, 8, 7, 6), a4=(1, 4, -2, 5).
По определению базис максимальный набор линейно независимых векторов.
А) проверим, что вектора < a1, a2,a3, a4>–линейно независимы?
*a1+ 
*a2+ 
*a3+ 
*a4=0
= 
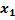
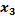
С помощью элементарных преобразований приводим матрицу к треугольному виду:
Выписываем решение….. Получаем, что вектора линейно зависимы значит вектора < a1, a2,a3, a4>не базис.
В) Из набор вектора < a1, a2,a3, a4>уберем один вектор, например a3.Проверим, что вектора < a1, a2, a4>образуют базис.
Дата добавления: 2015-09-07 ; просмотров: 2766 . Нарушение авторских прав
Сайт о разделе высшей математики — линейной алгебре
п.5. Вычисление ранга матрицы и нахождение базиса линейной оболочки ее системы строк (столбцов).
Для вычисления ранга матрицы часто применяют метод Гаусса приведения матрицы к ступенчатому виду. Метод Гаусса основан на элементарных преобразованиях строк матрицы, которые, как мы уже знаем, не изменяют ранга системы строк, а значит не изменяют и ранга матрицы.
Таким образом, ранг данной матрицы равен рангу получившейся после преобразований ступенчатой матрицы. В свою очередь, ранг ступенчатой матрицы легко вычисляется, так как легко увидеть ее максимальный ненулевой минор и его порядок.
Пример. Вычислить ранг матрицы 
и найти базис и размерность линейной оболочки натянутой на ее столбцы.
1-й шаг: умножим первую строку на 2 и прибавим ко второй строке:
;
2-й шаг: прибавим к третьей строке первую, умноженную на (–3):
;
3-й шаг: прибавим ко второй строке 3-ю, умноженную на (–1):
;
4-й шаг: умножаем вторую строку на (–3) и прибавляем к третьей строке:
.
Ранг последней матрицы равен 3, так как в первых трех столбцах стоит ненулевой минор 3-го порядка
, а миноров 4-го порядка не существует.
Приведенные преобразования не изменяют величину определителя, построенного на первых трех столбцах матрицы А, поэтому он отличен от нуля и, следовательно, его столбцы линейно независимые и образуют максимальную линейно независимую подсистему системы столбцов матрицы А. Отсюда можно сделать вывод, что первые три столбца матрицы А образуют базис линейной оболочки натянутой на столбцы матрицы А, т.е. 
и 
.
Ответ: 
, 
– базис линейной оболочки 
, .
Определение. Любой ненулевой минор матрицы А максимального порядка называют базисным минором матрицы А.
Из этого определения следует, что порядок базисного минора матрицы А равен рангу матрицы А.
Замечание. Максимальную линейно независимую подсистему системы строк матрицы, которая образует базис линейной оболочки системы строк матрицы, мы будем, для краткости, называть базисными строками матрицы. И то же самое для столбцов.
Из приведенного примера можно сделать вывод, что если, вычисляя ранг матрицы, мы не переставляем строки и столбцы матрицы, то найдя базисный минор матрицы и определив номера строк и столбцов на которых он построен, мы, тем самым, находим номера базисных строк и столбцов исходной матрицы.
Так в примере, базисный минор матрицы А построен на первых трех строках и первых трех столбцах, следовательно именно они и образуют базисы системы строк и столбцов матрицы А.
Определения размерности и базиса
Линейное пространство [math]V[/math] называется n-мерным , если в нем существует система из [math]n[/math] линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число [math]n[/math] называется размерностью (числом измерений) линейного пространства [math]V[/math] и обозначается [math]operatornameV[/math] . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве [math]V[/math] найдется система, состоящая из [math]n[/math] линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: [math]operatornameV=infty[/math] ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность [math]n[/math] линейно независимых векторов ( базисных векторов ).
Теорема 8.1 о разложении вектора по базису. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис n-мерного линейного пространства [math]V[/math] , то любой вектор [math]mathbfin V[/math] может быть представлен в виде линейной комбинации базисных векторов:
и притом единственным образом, т.е. коэффициенты [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства [math]V[/math] равна [math]n[/math] . Система векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] линейно независима (это базис). После присоединения к базису любого вектора [math]mathbf[/math] , получаем линейно зависимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_n, mathbf[/math] (так как это система состоит из [math](n+1)[/math] векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
Следствие 1. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис пространства [math]V[/math] , то [math]V=operatorname (mathbf_1,mathbf_2, ldots,mathbf_n)[/math] , т.е. линейное пространство является линейной оболочкой базисных векторов.
В самом деле, для доказательства равенства [math]V=operatorname (mathbf_1,mathbf_2, ldots, mathbf_n)[/math] двух множеств достаточно показать, что включения [math]Vsubset operatorname(mathbf_1,mathbf_2, ldots,mathbf_n)[/math] и [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)subset V[/math] выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)subset V[/math] . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. [math]Vsubset operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)[/math] . Отсюда следует равенство рассматриваемых множеств.
Следствие 2. Если [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — линейно независимая система векторов линейного пространства [math]V[/math] и любой вектор [math]mathbfin V[/math] может быть представлен в виде линейной комбинации (8.4): [math]mathbf=v_1mathbf_1+ v_2mathbf_2+ldots+v_nmathbf_n[/math] , то пространство [math]V[/math] имеет размерность [math]n[/math] , а система [math]mathbf_1,mathbf_2, ldots,mathbf_n[/math] является его базисом.
В самом деле, в пространстве [math]V[/math] имеется система [math]n[/math] линейно независимых векторов, а любая система [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] из большего количества векторов n)»>[math](k>n)[/math] линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] . Значит, [math]operatorname V=n[/math] и [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис [math]V[/math] .
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему [math]k[/math] векторов n-мерного линейного пространства [math](1leqslant k можно дополнить до базиса пространства.
В самом деле, пусть [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] — линейно независимая система векторов n-мерного пространства [math]V
(1leqslant k . Рассмотрим линейную оболочку этих векторов: [math]L_k=operatorname(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] . Любой вектор [math]mathbfin L_k[/math] образует с векторами [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно зависимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_k,mathbf[/math] , так как вектор [math]mathbf[/math] линейно выражается через остальные. Поскольку в n-мерном пространстве существует [math]n[/math] линейно независимых векторов, то [math]L_k
e V[/math] и существует вектор [math]mathbf_in V[/math] , который не принадлежит [math]L_k[/math] . Дополняя этим вектором линейно независимую систему [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , получаем систему векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k,mathbf_[/math] , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что [math]mathbf_in operatorname(mathbf_1, mathbf_2, ldots,mathbf_k)=L_k[/math] , а это противоречит условию [math]mathbf_
otin L_k[/math] . Итак, система векторов [math]mathbf_1,mathbf_2,ldots, mathbf_k, mathbf_[/math] линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: [math]L_=operatorname (mathbf_1, mathbf_2,ldots, mathbf_k, mathbf_)[/math] . Если [math]L_=V[/math] , то [math]mathbf_1,mathbf_2, ldots,mathbf_k, mathbf_[/math] — базис и теорема доказана. Если [math]L_
e V[/math] , то дополняем систему [math]mathbf_1,mathbf_2, ldots,mathbf_k,mathbf_[/math] вектором [math]mathbf_
otin L_[/math] и т.д. Процесс дополнения обязательно закончится, так как пространство [math]V[/math] конечномерное. В результате получим равенство [math]V=L_n=operatorname (mathbf_1,ldots,mathbf_k,ldots,mathbf_n)[/math] , из которого следует, что [math]mathbf_1,ldots,mathbf_k,ldots,mathbf_n[/math] — базис пространства [math]V[/math] . Теорема доказана.
1. Базис линейного пространства определяется неоднозначно. Например, если [math]mathbf_1,mathbf_2, ldots, mathbf_n[/math] — базис пространства [math]V[/math] , то система векторов [math]lambda mathbf_1,lambda mathbf_2,ldots,lambda mathbf_n[/math] при любом [math]lambda
e0[/math] также является базисом [math]V[/math] . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
4. Если множество [math]mathbb[/math] является линейной оболочкой [math]operatorname(mathbf_1,mathbf_2,ldots,mathbf_k)[/math] , то векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] называют образующими множества [math]mathbb[/math] . Следствие 1 теоремы 8.1 в силу равенства [math]V=operatorname (mathbf_1,mathbf_2,ldots,mathbf_n)[/math] позволяет говорить, что базис — это минимальная система образующих линейного пространства [math]V[/math] , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора [math]mathbf_1, mathbf_2,ldots,mathbf_n[/math] ) без нарушения равенства [math]V=operatorname( mathbf_1,mathbf_2,ldots,mathbf_n)[/math] .
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] . Количество базисных векторов определяет размерность пространства . Разумеется, что эти определения эквивалентны приведенным выше.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
1. Нулевое линейное пространство [math]<mathbf>[/math] не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: [math]dim<mathbf>=0[/math] . Это пространство не имеет базиса.
2. Пространства [math]V_1,,V_2,,V_3[/math] имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства [math]V_1[/math] , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства [math]V_1[/math] коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, [math]dim=1[/math] , а базисом пространства [math]V_1[/math] является любой ненулевой вектор. Аналогично доказывается, что [math]dim=2[/math] и [math]dim=3[/math] . Базисом пространства [math]V_2[/math] служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства [math]V_3[/math] являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в [math]V_1[/math] является единичный вектор [math]vec[/math] на прямой. Стандартным базисом в [math]V_2[/math] считается базис [math]vec,,vec[/math] , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве [math]V_3[/math] считается базис [math]vec,,vec,,vec[/math] , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.
3. Пространство [math]mathbb^n[/math] содержит не более, чем [math]n[/math] , линейно независимых векторов. В самом деле, возьмем [math]k[/math] столбцов из [math]mathbb^n[/math] и составим из них матрицу размеров [math]n imes k[/math] . Если n»>[math]k>n[/math] , то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, [math]dim<mathbb^n>leqslant n[/math] . В пространстве [math]mathbb^n[/math] не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы
линейно независимы. Следовательно, [math]dim<mathbb^n>=n[/math] . Пространство [math]mathbb^n[/math] называется n-мерным вещественным арифметическим пространством . Указанный набор векторов считается стандартным базисом пространства [math]mathbb^n[/math] . Аналогично доказывается, что [math]dim<mathbb^n>=n[/math] , поэтому пространство [math]mathbb^n[/math] называют n-мерным комплексным арифметическим пространством .
4. Напомним, что любое решение однородной системы [math]Ax=o[/math] можно представить в виде [math]x=C_1varphi_1+C_2varphi_2+ldots+C_varphi_[/math] , где [math]r=operatornameA[/math] , a [math]varphi_1,varphi_2,ldots,varphi_[/math] — фундаментальная система решений. Следовательно, [math]=operatorname (varphi_1,varphi_2,ldots,varphi_)[/math] , т.е. базисом пространства [math][/math] решений однородной системы служит ее фундаментальная система решений, а размерность пространства [math]dim=n-r[/math] , где [math]n[/math] — количество неизвестных, а [math]r[/math] — ранг матрицы системы.
5. В пространстве [math]M_<2 imes3>[/math] матриц размеров [math]2 imes3[/math] можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
равна нулевой матрице только в тривиальном случае [math]alpha_1=alpha_2= ldots= alpha_6=0[/math] . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из [math]M_<2 imes3>[/math] линейным образом выражается через выбранные 6 матриц, т.е. [math]M_<2 imes>= operatorname (mathbf_1,mathbf_2,ldots,mathbf_6)[/math] . Следовательно, [math]dim>=2cdot3=6[/math] , а матрицы [math]mathbf_1, mathbf_2,ldots,mathbf_6[/math] являются базисом (стандартным) этого пространства. Аналогично доказывается, что [math]dim>=mcdot n[/math] .
6. Для любого натурального [math]n[/math] в пространстве [math]P(mathbb)[/math] многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены [math]mathbf_1=1,[/math] [math]mathbf_2=z,[/math] [math]mathbf_3=z^2,,ldots,[/math] [math]mathbf_n=z^[/math] линейно независимы, так как их линейная комбинация
равна нулевому многочлену [math](o(z)equiv0)[/math] только в тривиальном случае [math]a_1=a_2=ldots=a_n=0[/math] . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство [math]P(mathbb)[/math] бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства [math]P(mathbb)[/math] многочленов с действительными коэффициентами. Пространство [math]P_n(mathbb)[/math] многочленов степени не выше, чем [math]n[/math] , конечномерное. Действительно, векторы [math]mathbf_1=1,[/math] [math]mathbf_2=x,[/math] [math]mathbf_3=x^2,,ldots,[/math] [math]mathbf_=x^n[/math] образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из [math]P_n(mathbb)[/math] можно представить в виде линейной комбинации этих векторов:
7. Пространство [math]C(mathbb)[/math] непрерывных функций является бесконечно мерным. Действительно, для любого натурального [math]n[/math] многочлены [math]1,x,x^2,ldots, x^[/math] , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).
В пространстве [math]T_<omega>(mathbb)[/math] тригонометрических двучленов (частоты [math]omega
e0[/math] ) с действительными коэффициентами базис образуют одночлены [math]mathbf_1(t)=sinomega t,
mathbf_2(t)=cosomega t[/math] . Они линейно независимы, так как тождественное равенство [math]asinomega t+bcosomega tequiv0[/math] возможно только в тривиальном случае [math](a=b=0)[/math] . Любая функция вида [math]f(t)=asinomega t+bcosomega t[/math] линейно выражается через базисные: [math]f(t)=a,mathbf_1(t)+b,mathbf_2(t)[/math] .
8. Пространство [math]mathbb^X[/math] действительных функций, определенных на множестве [math]X[/math] , в зависимости от области определения [math]X[/math] может быть конечномерным или бесконечномерным. Если [math]X[/math] — конечное множество, то пространство [math]mathbb^X[/math] конечномерное (например, [math]X=<1,2,ldots,n>[/math] ). Если [math]X[/math] — бесконечное множество, то пространство [math]mathbb^X[/math] бесконечномерное (например, пространство [math]mathbb^N[/math] последовательностей).
9. В пространстве [math]mathbb^<+>[/math] любое положительное число [math]mathbf_1[/math] , не равное единице, может служить базисом. Возьмем, например, число [math]mathbf_1=2[/math] . Любое положительное число [math]r[/math] можно выразить через [math]mathbf_1[/math] , т.е. представить в виде [math]alphacdot mathbf_1colon[/math] [math]r=2^<log_2r>=log_2rast2=alpha_1ast mathbf_1[/math] , где [math]alpha_1=log_2r[/math] . Следовательно, размерность этого пространства равна 1, а число [math]mathbf_1=2[/math] является базисом.
10. Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис вещественного линейного пространства [math]V[/math] . Определим на [math]V[/math] линейные скалярные функции [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] , положив:
При этом, в силу линейности функции [math]mathcal_i[/math] , для произвольного вектора [math]mathbf=v_1 mathbf_1+v_2 mathbf_2+ldots+v_n mathbf_n[/math] получаем [math]mathcal(mathbf)=sum_^v_j mathcal(mathbf_j)=v_i[/math] .
Итак, определены [math]n[/math] элементов (ковекторов) [math]mathcal_1, mathcal_2, ldots, mathcal_n[/math] сопряженного пространства [math]V^<ast>[/math] . Докажем, что [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] — базис [math]V^<ast>[/math] .
Во-первых, покажем, что система [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов [math](alpha_1 mathcal_1+ldots+alpha_nmathcal_n)(mathbf)=[/math] и приравняем ее нулевой функции
forall mathbfin V)colon
forall mathbfin V.[/math]
Подставляя в это равенство [math]mathbf=mathbf_i,
i=1,ldots,n[/math] , получаем [math]alpha_1=alpha_2cdot= alpha_n=0[/math] . Следовательно, система элементов [math]mathcal_1,mathcal_2,ldots,mathcal_n[/math] пространства [math]V^<ast>[/math] линейно независима, так как равенство [math]alpha_1mathcal_1+ldots+ alpha_nmathcal_n =mathbf[/math] возможно только в тривиальном случае.
Во-вторых, докажем, что любую линейную функцию [math]fin V^<ast>[/math] можно представить в виде линейной комбинации ковекторов [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] . Действительно, для любого вектора [math]mathbf=v_1 mathbf_1+v_2 mathbf_2+ldots+v_n mathbf_n[/math] в силу линейности функции [math]f[/math] получаем:
т.е. функция [math]f[/math] представлена в виде линейной комбинации [math]f=eta_1 mathcal_1+ldots+eta_nmathcal_n[/math] функций [math]mathcal_1,mathcal_2,ldots, mathcal_n[/math] (числа [math]eta_i=f(mathbf_i)[/math] — коэффициенты линейной комбинации). Следовательно, система ковекторов [math]mathcal_1, mathcal_2,ldots, mathcal_n[/math] является базисом сопряженного пространства [math]V^<ast>[/math] и [math]dim>=dim[/math] (для конечномерного пространства [math]V[/math] ).