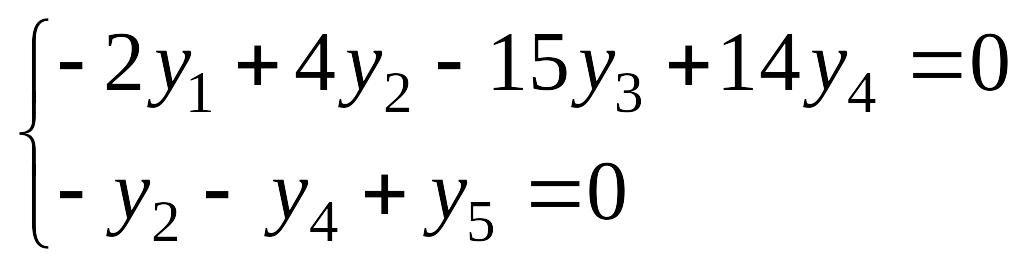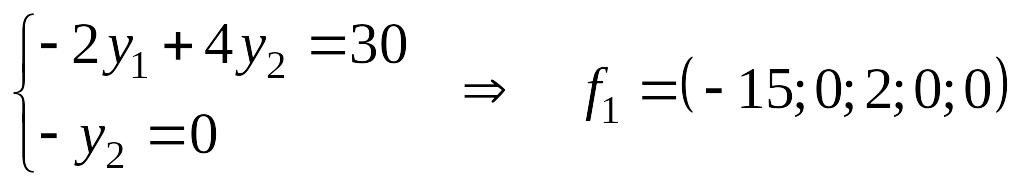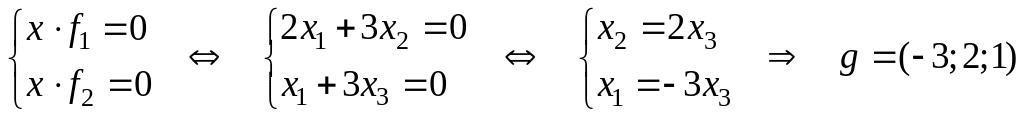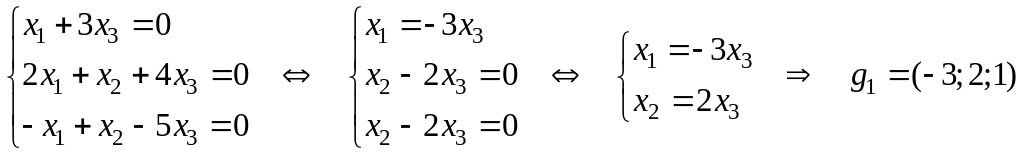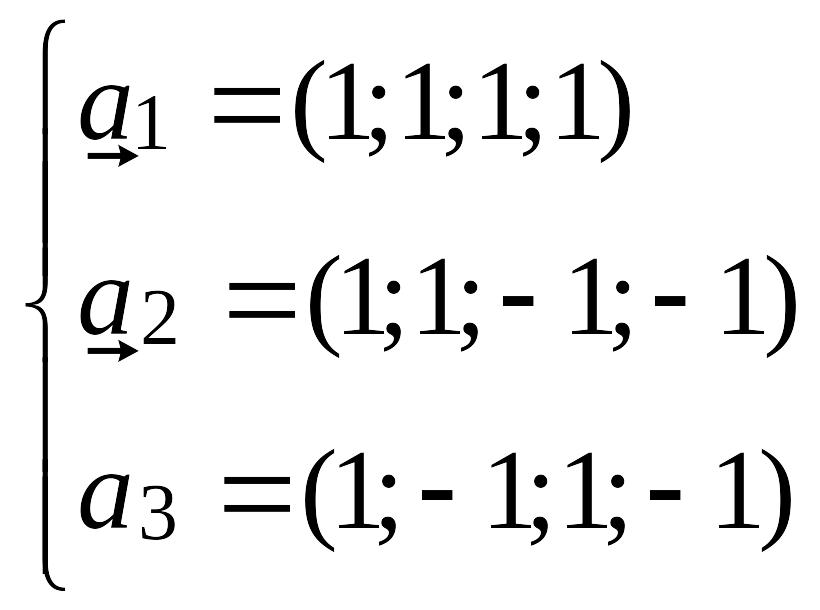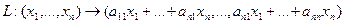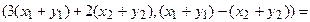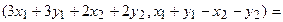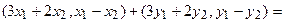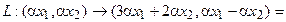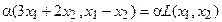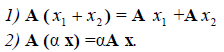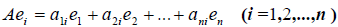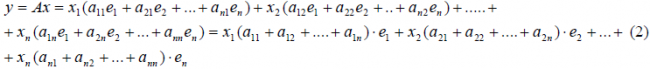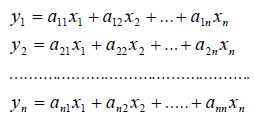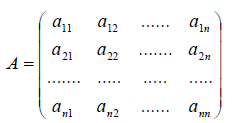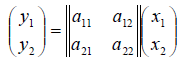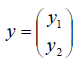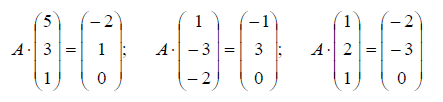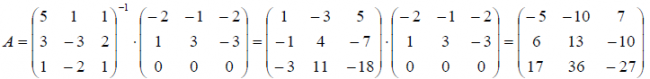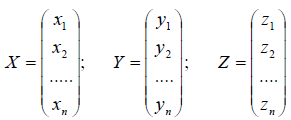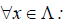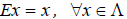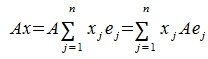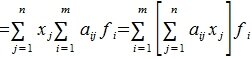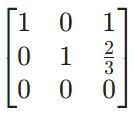Как найти размерность образа матрицы - Исправление недочетов и поиск решений вместе с Examum.ru

Ядро и образ линейного отображения

Ядром линейного отображения mathcal{A}colon Vto W называется множество таких векторов mathbf{v}in V , что $mathcal{A}(mathbf{v})= mathbf{o}_W$ , т.е. множество векторов из {V} , которые отображаются в нулевой вектор пространства {W} . Ядро отображения mathcal{A}colon Vto W обозначается:

$ker mathcal{A}= Bigl{mathbf{v}colon, mathbf{v}in V,~ mathcal{A}(mathbf{v})=mathbf{o}_WBigr}.$

Образом линейного отображения mathcal{A}colon Vto W называется множество образов mathcal{A}(mathbf{v}) всех векторов из {V} . Образ отображения обозначается operatorname{im}mathcal{A} или mathcal{A}(V)colon

operatorname{im}mathcal{A}= mathcal{A}(V)= Bigl{mathbf{w}colon, mathbf{w}=mathcal{A}(v),~ forall mathbf{v}in VBigr}.

Заметим, что символ operatorname{im}mathcal{A} следует отличать от operatorname{Im}z — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения mathcal{O}colon Vto W является все пространство {V} , а образом служит один нулевой вектор, т.е. $ker mathcal{O}=V,~ operatorname{im}mathcal{O}={mathbf{o}_W}.$

2. Рассмотрим отображение $mathsf{a!e}colon Vto mathbb{R}^n$ , которое ставит в соответствие каждому вектору mathbf{v} n-мерного линейного пространства {V} его координатный столбец $v=begin{pmatrix}v_1&cdots&v_n end{pmatrix}^T$ относительно заданного базиса $mathbf{e}_1,ldots,mathbf{e}_n$ . Ядром этого отображения является нулевой вектор $mathbf{o}_V$ пространства {V} , поскольку только этот вектор имеет нулевой координатный столбец $mathsf{a!e}(mathbf{o}_V)=oin mathbb{R}^n$ . Образ преобразования совпадает со всем пространством $mathbb{R}^n$ , так как это преобразование сюръективно (любой столбец из $mathbb{R}^n$ является координатным столбцом некоторого вектора пространства {V} ).

3. Рассмотрим отображение $operatorname{pr}_{mathbf{e}}colon mathbb{E}to mathbb{R}$ , которое каждому вектору mathbf{v} n-мерного евклидова пространства ставит в соответствие алгебраическое значение $operatorname{pr}_{mathbf{e}}(mathbf{v})= langle mathbf{e},mathbf{v}rangle$ его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение ${mathbf{e}}^{perp}$ — множество векторов, ортогональных . Образом является все множество действительных чисел mathbb{R} .

4. Рассмотрим отображение $mathcal{D}colon P_n(mathbb{R})to P_{n-1}(mathbb{R})$ , которое каждому многочлену степени не выше {n} ставит в соответствие его производную. Ядром этого отображения является множество $P_0(mathbb{R})$ многочленов нулевой степени, а образом — все пространство $P_{n-1}(mathbb{R})$ .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения mathcal{A}colon Vto W является подпространством: ${mathbf{o}_V}triangleleft ker mathcal{A} triangleleft V$ .

В соответствии с определением требуется доказать, что множество ker mathcal{A} является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

$mathcal{A}(mathbf{o}_V)= mathcal{A}(0cdotmathbf{v})= 0cdot mathcal{A}(mathbf{v})= mathbf{v}_W,$

т.е. нулевой вектор $mathbf{o}_V$ отображается в нулевой вектор $mathbf{o}_W$ . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: $mathbf{o}_Vin ker mathcal{A}$ . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

$begin{gathered} left.{begin{matrix} mathbf{v}_1in ker mathcal{A}~ Rightarrow~ mathcal{A} (mathbf{v}_1)= mathbf{o}_W\ mathbf{v}_2in ker mathcal{A}Rightarrow mathcal{A} (mathbf{v}_2)= mathbf{o}_W end{matrix}}right} Rightarrow~ mathcal{A}(mathbf{v}_1+mathbf{v}_2)= mathcal{A} (mathbf{v}_1)+ mathcal{A}(mathbf{v}_2)= mathbf{o}_W~ Rightarrow~ mathbf{v}_1+ mathbf{v}_2in ker mathcal{A},;\[5pt] mathbf{v}in ker mathcal{A}~ Rightarrow~ mathcal{A}(mathbf{v})=mathbf{o}_W~ Rightarrow~ mathcal{A}(lambdacdot mathbf{v})= lambdacdotmathcal{A}(mathbf{v})= lambda cdot mathbf{o}_W= mathbf{o}_W~ Rightarrow~ lambdacdot mathbf{v}in ker mathcal{A},. end{gathered}$

Следовательно, множество ker mathcal{A} является линейным подпространством пространства {V} .

2. Образ любого линейного отображения mathcal{A}colon Vto W является подпространством: operatorname{im}mathcal{A}triangleleft W .

В самом деле, докажем, например, замкнутость множества operatorname{im} mathcal{A} по отношению к операции умножения вектора на число. Если mathbf{w}in operatorname{im}mathcal{A} , то существует вектор mathbf{v}in V такой, что mathbf{w}=mathcal{A} (mathbf{v}) . Тогда mathcal{A}(lambdacdot mathbf{v})= lambdacdot mathcal{A}(mathbf{v})= lambdacdot mathbf{w} , то есть lambdacdot mathbf{w}in operatorname{im}mathcal{A} .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: d=dim ker mathcal{A} , а рангом линейного отображения — размерность его образа: operatorname{rg}mathcal{A}=r=dim operatorname{im}mathcal{A} .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если $mathbf{e}_1,ldots,mathbf{e}_n$ любой базис пространства {V} , то $operatorname{im}mathcal{A}= operatorname{Lin}[ mathcal{A} (mathbf{e}_1),ldots,mathcal{A}(mathbf{e}_n)]$ . Поэтому максимальное число линейно независимых векторов системы $mathcal{A} (mathbf{e}_1),ldots,mathcal{A} (mathbf{e}_n)$ (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы {A} отображения, т.е. рангу матрицы: dim operatorname{im} mathcal{A}= operatorname{rg}A= operatorname{rg}mathcal{A} .

4. Линейное отображение mathcal{A}colon Vto W инъективно тогда и только тогда, когда $ker mathcal{A}={mathbf{o}_V}$ , другими словами, когда дефект отображения равен нулю: d=dim ker mathcal{A}=0 .

Действительно, образом нулевого вектора $mathbf{o}_v$ служит нулевой вектор $mathbf{o}_W$ . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор $mathbf{o}_v$ , иначе два разных вектора имели бы один и тот же образ $mathbf{o}_W$ . Обратно, при условии $ker mathcal{A}= {mathbf{o}_V}$ разные векторы $mathbf{v}_1ne mathbf{v}_2$ не могут иметь одинаковые образы $mathcal{A}(mathbf{v}_1)= mathcal{A}(mathbf{v}_2)$ , так как в этом случае из равенств $mathcal{A}(mathbf{v}_1)- mathcal{A}(mathbf{v}_2)= mathcal{A} (mathbf{v}_1-mathbf{v}_2)= mathbf{}_W$ , следует, что ненулевой вектор $(mathbf{v}_1-mathbf{v}_2)in ker mathcal{A}$ (приходим к противоречию).

5. Линейное отображение mathcal{A}colon Vto W сюръективно тогда и только тогда, когда operatorname{im}mathcal{A}=W , другими словами, когда ранг отображения равен размерности пространства образов: r=dim operatorname{im}mathcal{A}= dim{W} .

6. Линейное отображение mathcal{A}colon Vto W биективно (значит, обратимо) тогда и только тогда, когда $ker mathcal{A}={mathbf{o}_V}$ и operatorname{im}mathcal{A}=W одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения mathcal{A}colon Vto W равна размерности пространства прообразов:

dim ker mathcal{A}+ dim operatorname{im}mathcal{A}= dim{V},.

(9.3)

Действительно, пусть d=dim ker mathcal{A},~ dim{V}=n . Выберем в подпространстве kermathcal{A} triangleleft V базис $mathbf{e}_1,ldots, mathbf{e}_d$ и дополним его векторами $mathbf{e}_{d+1},ldots,mathbf{e}_n$ до базиса $mathbf{e}_1,ldots,mathbf{e}_n$ всего пространства {V} . Покажем, что векторы $mathcal{A}(mathbf{e}_{d+1}),ldots,mathcal{A}(mathbf{e}_n)$ образуют базис подпространства operatorname{im}mathcal{A}triangleleft W .

Во-первых, $operatorname{im}mathcal{A}= operatorname{Lin}[mathcal{A} (mathbf{e}_{d+1}), ldots,mathcal{A}(mathbf{e}_n)]$ , так как образ любого вектора $mathbf{v}= v_1 mathbf{e}_1+ldots+v_d mathbf{e}_d+v_{d+1}mathbf{e}_{d+1}+ldots+ v_n mathbf{e}_n$ линейно выражается через векторы $mathcal{A}(mathbf{e}_{d+1}),ldots, mathcal{A}(mathbf{e}_n):$

$mathcal{A}(mathbf{v})= mathcal{A} Biggl( sum_{i=1}^{n} v_i mathbf{e}_iBiggr)= sum_{i=1}^{n}v_imathcal{A}(mathbf{e}_i)= sum_{i=1}^{d}v_i underbrace{mathcal{A} (mathbf{e}_i)}_{mathbf{o}_W}+ sum_{i=d+1}^{n} v_imathcal{A} (mathbf{e}_i)= sum_{i=d+1}^{n} v_imathcal{A}(mathbf{e}_i).$

Во-вторых, образующие $mathcal{A}(mathbf{e}_{d+1}), ldots, mathcal{A} (mathbf{e}_n)$ линейно независимы. Если их линейная комбинация равна нулевому вектору:

$mathbf{o}_W= sumlimits_{i=d+1}^{n} lambda_i mathcal{A} (mathbf{e}_i)= mathcal{A}!left(sum_{i=d+1}^{n}lambda_i mathbf{e}_iright)!,$

то вектор $textstyle{sumlimits_{i=d+1}^{n}lambda_i mathbf{e}_i}$ принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению $(ker mathcal{A})^{+}$ . Учитывая, что $ker mathcal{A}cap (ker mathcal{A})^{+}={mathbf{o}_V}$ , заключаем: $textstyle{sumlimits_{i=d+1}^{n}lambda_i mathbf{e}_i}=mathbf{o}_V$ . Получили разложение нулевого вектора по линейно независимой системе $mathbf{e}_{d+1},ldots, mathbf{e}_n$ векторов, значит, все коэффициенты lambda_i=0 . Поэтому равенство $textstyle{sumlimits_{i=d+1}^{n}lambda_i mathcal{A}(mathbf{e}_i)= mathbf{o}_W}$ справедливо только для тривиальной линейной комбинации, т.е. система векторов $mathcal{A}(mathbf{e}_{d+1}),ldots, mathcal{A} (mathbf{e}_n)$ линейно независимая.

Таким образом, векторы $mathcal{A}(mathbf{e}_{d+1}),ldots, mathcal{A} (mathbf{e}_n)$ образуют базис подпространства $operatorname{im}mathcal{A}= operatorname{Lin} mathcal{A}(mathbf{e}_{d+1}),ldots, mathcal{A} (mathbf{e}_n)$ , а его размерность определяется количеством базисных векторов, т.е. dimoperatorname{im} mathcal{A}=n-d , что равносильно (9.3).

Следствие. Линейное отображение mathcal{A}colon Vto W биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования mathcal{A}colon Vto W (см. свойство 6) его матрица (размеров mtimes n ) должна удовлетворять условиям (см. свойства 3,4,5):

operatorname{rg}A= operatorname{rg}mathcal{A}= dim operatorname{im}mathcal{A}= dim{W}=m,quad d=dim ker mathcal{A}=0.

Тогда по теореме 9.1 заключаем, что m=n-d=n , т.е. матрица — квадратная n-го порядка и невырожденная (operatorname{rg}A=n) , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Решение. Очевидно,
что данное линейное преобразование
действует

,
т.к. умножение матриц

определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность

(т.к. в матрице A
5 строк).

Совокупность N
векторов x
таких, что Ax=0,
называется ядром
преобразования A.

Совокупность M
векторов вида Ax,
когда x
пробегает все R
(в нашем случае

)
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).

1) Находим ядро.
Пусть

— вектор столбец. Решаем систему уравнений

Решаем систему
методом Гаусса

Переменные

— базисные, а

— небазисная.

Находим все
фундаментальные решения. В нашем случае
оно одно: положив

,
получаем

— который и будет образовывать базис
ядра (т.к. все вектора вида

отображаются в 0). Размерность базиса
равна 1.

2) Находим образ.
Пусть

— вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

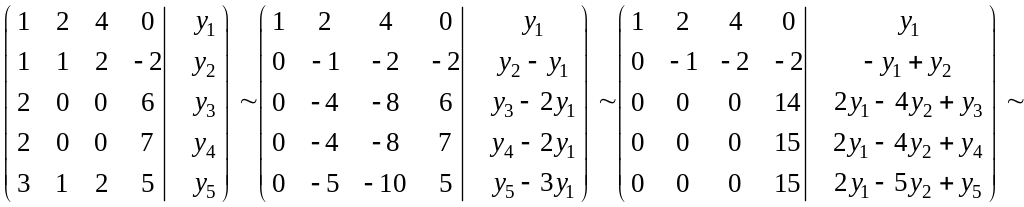
Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

Находим фундаментальные
решения (базис образа). Т.к. определитель
из коэффициентов при

:

,
то

— базисные, а

— небазисные.

1-е фундаментальное
решение. Положим

,
находим решение системы

— первое базисное
решение.

2-е фундаментальное
решение. Положим

,
находим решение системы

— второе базисное
решение.

3-е фундаментальное
решение. Положим

,
находим решение системы

— второе базисное
решение.

Итак, размерность
образа равна 3, базис – вектора

.

(Видно, что
размерность образа + размерность ядра
= размерности пространства R⁴).

7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .

Решение.

— ядро,

— образ. Преобразование

.

1) Находим ядро.
Решаем систему уравнений

Следовательно,
одно базисное решение

— базис ядра. Размерность

.

2) Находим образ.

Пусть

— вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

Отсюда,

—
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

— базис образа. Размерность

.

3) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

— фундаментальное
решение системы или базис

.

4) Найдем базис
линейной оболочки векторов

,

.
Т.к.

,
то заключаем, что

— базис в

,
и следовательно, размерность

.

5) Находим пространство
решений системы уравнений

— фундаментальное
решение системы или базис M.

6) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

Отсюда,

—
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

— базис

.
Размерность

.

7) Найдем базис
линейной оболочки векторов

Очевидно, что

,
а

— базис в

,
и следовательно, размерность

.

8. Пусть U
— подпространство
линейного пространства R⁴,
являющееся линейной оболочкой. векторов

,
V
— подпространство
линейного пространства R⁴являющееся
линейной оболочкой векторов

.
Найдите: базис U
+ V
и
базис

.

Решение.

1) Находим базис в
U.

rang=3
, сл-но,

— базис U.

1) Находим базис в
V.

rang=3
, сл-но,

— базис V.

3) Находим базис в
U
+ V.

Находим линейно
независимые вектора в объединении

.

,
а вектора

— базис U
+ V
, а размерность
dim(U
+ V)=4.

4) Найдем общие
вектора в U
и
V
.

Нам известно, что
в конечномерном пространстве
подпространства могут быть заданы
системами линейных уравнений. Тогда их
пересечение задаётся системой уравнений,
полученной объединением систем, задающих
подпространства.

Система уравнений
задающая U:

Для того, чтобы
вектор

принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Система уравнений
задающая V:

Для того, чтобы
вектор

Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Решаем общую
систему:

Отсюда фундаментальные
решения (которые получаются при

и при

),
а следовательно базис

есть:

.

9. Подпространство
L₁
в R⁴
порождено векторами (1;-4;6;7) и (0;1;-3;1), а
подпространство L₂
— векторами
(0;1;-4;5) и (1;-4;7;-11). Постройте базисы следующих
подпространств: пересечения

и ортогонального дополнения к сумме

.

Решение.

1) Находим базис в
L₁.
Т.к. матрица, составленная из координат
векторов

,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка

),
то заключаем, что вектора

=(1;-4;6;7)
и

=(0;1;-3;1)
линейно независимые и образуют базис
в L₁.

2) Аналогично,
заключаем, что вектора

=(0;1;-4;5)
и

=(1;-4;7;-11)
линейно независимые и образуют базис
в L₂.

3) Находим базис
L₁+
L₂.

Рассматриваем
объединенную систему векторов

=(1;-4;6;7),

=(0;1;-3;1),

=(0;1;-4;5),

=(1;-4;7;-11)

и находим среди
них линейно независимые. Находим ранг
матрицы, столбцами которой являются
координаты

:

Ранг = 4, следовательно,
все вектора

— линейно независимые и образуют базис
в L₁+
L₂.

4)
Находим базис ортогонального дополнения

Каждый вектор из

ортогонален любому вектору из L₁+
L₂.
Следовательно, скалярные произведения

на вектора базиса из L₁+
L₂
равны 0. Получаем однородную систему

Т.к. определитель
системы не равен 0 (показано выше, что
ранг=4), то система имеет единственное
тривиальное решение

.

Следовательно,

состоит
только из одного вектора

.

(Это и так было
видно, т.к. линейная оболочка

,
ибо 4 линейно независимых вектора

образуют базис в

,
а

).

5) Находим систему
уравнений описывающую L₁.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Находим систему
уравнений описывающую L₂.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Решаем общую
систему:

Т.к. определитель
матрицы коэффициентов

,
то система имеет единственное решение

.
Следовательно,

состоит из
одного вектора (0;0;0;0).

(Это и так было
видно, т.к. вектора

— линейно независимые,
линейные оболочки

не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов

не может дать вектора

,
а следовательно и их линейные комбинации).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

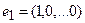
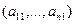
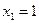
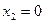
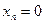
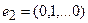
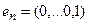
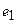
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

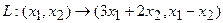
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

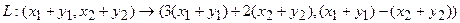
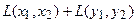
Теперь каждую координату получившегося вектора можем преобразовать:

Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

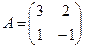
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .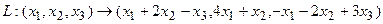

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

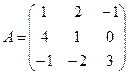
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

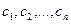
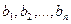
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

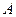
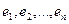
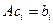
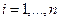
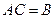
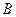
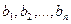
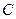
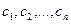
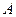
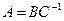
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

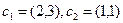
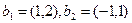
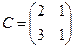
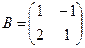
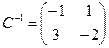
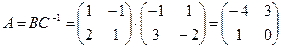
Здесь , , , и получаем:

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .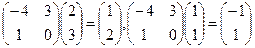

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

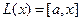
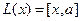
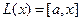
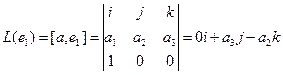
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

Аналогично, ,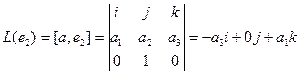

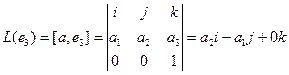
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .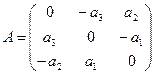

Аналогично можно построить матрицу линейного оператора :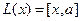

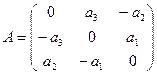
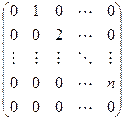
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .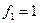

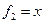
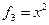
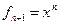
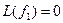
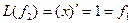
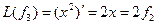
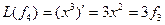
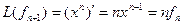
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 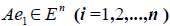, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 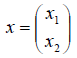с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .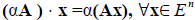

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 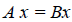. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 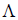он ставит в соответствие тот же самый элемент, то есть

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

8. Образ линейного оператора

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

источники:

http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya

http://matworld.ru/linear-algebra/linear-operator.php

Источник

Как найти размерность матрицы

Матрица записывается в виде прямоугольной таблицы, состоящей из некоторого количества строк и столбцов, на пересечении которых располагаются элементы матрицы. Основное математическое применение матриц – решение систем линейных уравнений.

Число столбцов и строк задают размерность матрицы. К примеру, таблица размерностью 5×6 имеет 5 строк и 6 столбцов. В общем случае, размерность матрицы записывается в виде m×n, где число m указывает на количество строк, n – столбцов.

Размерность матрицы важно учитывать при совершении алгебраических операций. Например, складывать можно матрицы только одного и того же размера. Операция сложения матриц с разной размерностью не определена.

Если массив имеет размерность m×n, его можно умножить на массив n×l. Число столбцов первой матрицы должно равняться числу строк второй, иначе операция умножения не будет определена.

Размерность матрицы указывает на число уравнений в системе и количество переменных. Число строк совпадает с количеством уравнений, а за каждым столбцом закреплена своя переменная. Решение системы линейных уравнений «записано» в действиях над матрицами. Благодаря матричной системе записи становится возможным решать системы высоких порядков.

Если число строк равно числу столбцов, матрица называется квадратной. В ней можно выделить главную и побочную диагонали. Главная идет от левого верхнего угла к правому нижнему, побочная – от правого верхнего к левому нижнему.

Массивы размерностью m×1 или 1×n являются векторами. Также в виде вектора можно представить любую строку и любой столбец произвольной таблицы. Для таких матриц определены все операции над векторами.

Поменяв в матрице A строки и столбцы местами, можно получить транспонированную матрицу A(Т). Таким образом, при транспонировании размерность m×n перейдет в n×m.

В программировании для прямоугольной таблицы задается два индекса, один из которых пробегает длину всей строки, другой – длину всего столбца. При этом цикл для одного индекса помещен внутрь цикла для другого, за счет чего обеспечивается последовательное прохождение всей размерности матрицы.

Источник

Все курсы > Линейная алгебра > Занятие 6 (часть 1)

Сегодня мы еще раз рассмотрим полученные ранее знания о векторных пространствах, линейных преобразованиях, системе линейных уравнений и определителе матрицы в контексте новых понятий ранга и четырех фундаментальных подпространств матрицы, а именно пространства столбцов, пространства строк, ядра и коядра матрицы.

Продолжим работать в том же ноутбуке⧉

Ранг матрицы

При нулевом определителе в трехмерном пространстве матрица может «схлопнуть» пространство до плоскости, линии или точки (во всех трех случаях определитель равен нулю).

Ранее мы сказали, что для того чтобы в системе уравнений, например, трехмерная матрица $A$ при нулевом определителе все же имела решение, вектор $mathbf b$, на который матрица $A$ переводит вектор $mathbf x$, должен лежать на плоскости или линии, в которые «схлопывается» трехмерное пространство.

Размерность пространства после трансформации принято описывать рангом матрицы (rank).

Если преобразование трехмерной матрицы «сворачивает» размерность до линии, то ранг такого преобразования равен единице, до плоскости — двум и т.д. В случае матрицы $2 times 2$ самый высокий ранг матрицы — два. Это значит, что при преобразовании размерность сохранилась (и соответственно определитель не равен нулю).

Пространство столбцов

Пространством столбцов (column space, а также образом, image) называют множество всех возможных линейных комбинаций вектор-столбцов.

С точки зрения линейных преобразований, пространством столбцов называют векторы, которые определяют пространство после трансформации.

В случае линейно зависимых векторов таких векторов будет меньше, чем в исходной матрице. Приведем пример линейно зависимых векторов и рассчитаем ранг матрицы.

M = np.array([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

np.linalg.matrix_rank(M)

Приведем матрицу к упрощенному ступенчатому виду (reduced row-echelon form) с помощью Питона. Для этого воспользуемся методом .rref() библиотеки sympy.

from sympy import *

M = Matrix([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

M_rref = M.rref()

M_rref[0]

Как мы видим, с одной стороны, пространство сократилось до двух измерений (поэтому ранг матрицы равен двум), с другой, двумерное пространство можно описать первыми двумя столбцами (их еще называют разрещающими, ведущими или базисными, pivot columns), где все элементы кроме одного равны нулю.

Разрешающие столбцы и образуют пространство столбцов. Найдем пространство столбцов с помощью Питона.

# вторым элементом метод .rref() выводит

# индексы разрешающих столбцов (pivot columns),

# используем их для нахождения пространства столбцов

M.col(M.rref()[1])

# то же самое можно найти с помощью

# метода .columnspace()

M_columnspace = M.columnspace()

M_columnspace[0]

Откуда такое название? Столбцы матрицы говорят куда «приземлятся» координаты базисных векторов. В этом смысле, оболочка вектор-столбцов то же самое, что и пространство столбцов.

В матрице $2 times 2$ первый столбец показывает, где окажется вектор $mathbf i$, второй — вектор $mathbf j$. И оболочка этих столбцов определит пространство столбцов. Если, например, в матрице $2 times 2$ столбцы линейно независимы и преобразование не приводит к снижению размерности, то пространство столбцов задается этими двумя векторами.

Замечу, что столбцы, не являющиеся разрешающими, называются свободными (free).

Ядро матрицы

Если преобразование уменьшает размерность (например, преобразовывает плоскость в линию), то несколько векторов оказываются в начале координат (становятся нулевыми векторами). Видео ниже прекрасно иллюстрирует эту трансформацию.

Множество таких «исчезающих» векторов называется ядром матрицы или ее нуль-пространством (null space, kernel).

Видео про обратные матрицы, ранг и ядро⧉.

Система уравнений

$Ax = b$

Рассмотрим пространство столбцов и ядро с точки зрения системы линейных уравнений. В первую очередь представим пространство столбцов, как решение системы $ A mathbf x = mathbf b $, т.е. линейную комбинацию вектор-столбцов $A$, умноженных на компоненты $mathbf x$.

$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf b \ vdots end{bmatrix} $$

Всегда ли $A mathbf x = mathbf b$ будет иметь решение? Нет. Возьмем некоторую матрицу $A$ и соответствующие ей векторы $mathbf x$ и $mathbf b$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} b_1 \ b_2 \ b_3 \ b_4 end{bmatrix} $$

В такой системе будет много векторов $mathbf b$, которые не будут являться линейной комбинацией трех столбцов матрицы A.

В каком случае такое решение все-таки будет существовать? Если $mathbf b$ будет являться линейной комбинацией векторов $A$, т.е. будет находиться в пространстве столбцов $A$, $mathbf b in col(A) $.

Например, если $mathbf b$ будет равен одному из столбцов $A$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

Тогда решением может быть

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} $$

Что интересно, все возможные решения $mathbf x$ именно такой системы $A mathbf x = mathbf b$, где $mathbf b in col(A) $ сами по себе не образуют векторное пространство (хотя бы потому что нулевой вектор не включен в эти решения).

Дополнительно замечу, что так как в матрице $A$ только два линейно независимых вектора (третий вектор является суммой первых двух), то в данном случае мы имеем двумерное подпространство $R^4$.

$Ax = 0$

В системе линейных уравнений $A mathbf x = mathbf b$, если $mathbf b$ — нулевой вектор, т.е. $A mathbf x = mathbf 0$, то ядро дает все возможные решения этой системы (все возможные $mathbf x$). Можно также сказать, что ядро $mathbf x $ представляет собой комбинацию вектор-столбцов $A$, обращающихся в ноль.

В примере выше обратите внимание, что $col(A) in R^4$, в то время как $null(A) in R^3$. Решением же этой системы при нулевом векторе $mathbf b$, $A mathbf x = mathbf 0$ будет

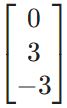
$$ null(A) = k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

где $k in mathbb{R} $. Другими словами, $null(A)$ представляет собой линию в $R^3$.

Убедимся, что для матрицы $M$ выше мы правильно нашли ядро (а также решение $M mathbf x = 0$).

M = np.array([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

Null = np.array([—1, —2/3, 1])

M @ Null

Общее и частное решение

Приведем общее решение (complete solution) следующей системы, состоящее из частного решения (particular solution) системы $A mathbf x = mathbf b$ и ядра, то есть решения $A mathbf x = mathbf 0$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} + k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

Независимость векторов, базис и размерность

В свете новых знаний еще раз рассмотрим линейную независимость векторов и базис векторного пространства. Возьмем некоторую матрицу $A$.

Независимые вектор-столбцы

Можно сказать, что вектор-столбцы, образующие матрицу $A$ независимы, если ядро матрицы состоит только из нулевого вектора, $null(A) = { mathbf 0 }$ (решением $A mathbf x = mathbf 0$ будет только нулевой вектор $mathbf x$). Одновременно все столбцы такой матрицы являются разрешающими, и матрица имеет полный ранг, равный количеству столбцов $n$, $rank(A) = n$.

Если матрица $А$ квадратная и ее столбцы линейно независимы, то можно сказать, что

Вектор-столбцы матрицы образуют базис $R^n$
Такая матрица будет обратима (!)

Приведем примеры обратимых матриц, столбцы которых формируют базис.

$$ begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix}, begin{bmatrix} 1 & 2 & 3 \ 1 & 2 & 1 \ 2 & 5 & 8 end{bmatrix} $$

A = np.array([[1, 2, 3],

[1, 2, 1],

[2, 5, 8]])

np.linalg.matrix_rank(A)

array([[ 5.5, -0.5, -2. ],

[-3. , 1. , 1. ],

[ 0.5, -0.5, 0. ]])

Зависимые вектор-столбцы

Если же столбцы зависимы, то ядро матрицы содержит также ненулевые векторы и решением $A mathbf x = mathbf 0$ будет или будут некоторые ненулевые векторы $mathbf x$. Столбцы матрицы будут как разрешающими, так и свободными. Ранг матрицы будет равен количеству разрещающих столбцов.

Базис пространства будет определяться именно линейно независимыми векторами, входящими в пространство столбцов. Размерностью (dimension) векторного пространства будет как раз количество векторов базиса.

Например, возьмем следующую матрицу $A$.

$$ A = begin{bmatrix} 1 & 2 & 3 & 1 \ 1 & 1 & 2 & 1 \ 1 & 2 & 3 & 1 end{bmatrix} $$

В данном случае у матрицы два линейно независимых столбца. В частности, это

$$ col(A) = left{ begin{bmatrix} 1 \ 1 \ 1 end{bmatrix}, begin{bmatrix} 2 \ 1 \ 2 end{bmatrix} right} $$

Как следствие,

$$ dim(col(A)) = rank(A) = dim(basis) = text{# of pivots} = 2 $$

Одновременно, нулевое пространство задано векторами

$$ null(A) = left{ begin{bmatrix} -1 \ -1 \ 1 \ 0 end{bmatrix}, begin{bmatrix} -1 \ 0 \ 0 \ 1 end{bmatrix} right} $$

Как следствие,

$$ dim(null(A)) = text{# of free columns} = 2 $$

Код на Питоне для нахождения пространства столбцов и ядра приведен в ноутбуке к занятию⧉.

В качестве дополнения, замечу, что размерность векторного пространства характеризуется следом (trace) единичной матрицы этого пространства или суммой элементов главной диагонали. Например, размерность $R^3$ можно охарактеризовать через

$$ dim(col(A)) = tr left( begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix} right) = 3 $$

Пространство строк и коядро

Пространством строк (row space) называют множество всех возможных линейных комбинаций вектор-строк.

Если матрицу транспонировать, то можно сказать, что

$$ row(A) = col(A^T) $$

Коядром или левым нуль-пространством (left null-space, cokernel) матрицы $A$ будет ядро матрицы $A^T$.

$$ leftnull(A) = null(A^T) $$

Продемонстрируем, почему это пространством называется именно левым нуль-пространством. По определению ядра, как решения $A mathbf x = mathbf 0$, можно сказать, что коядро будет решением $A^T mathbf y = mathbf 0$.

$$ A^T mathbf y = mathbf 0 $$

$$ mathbf y^T(A^T)^T = mathbf 0^T $$

$$ mathbf y^T A = mathbf 0^T $$

Схематично это можно представить следующим образом.

Можно также сказать, что коядро $ mathbf y $ в системе $ A^T mathbf y = mathbf 0 $ дает все возможные комбинации столбцов $A^T$, обращающиеся в нулевой вектор (что то же самое, что линейные комбинации строк $mathbf x^T A = 0$). Приведем пример. Найдем коядро матрицы $A$.

A = Matrix([[1, 2, 3, 1],

[1, 1, 2, 1],

[1, 2, 3, 1]])

A.T.nullspace()[0]

Другими словами, нам нужно взять $-1R_1 + 0R_2 + 1R_3$, чтобы получить нулевой вектор. Проверим полученный результат.

A = np.array([[1, 2, 3, 1],

[1, 1, 2, 1],

[1, 2, 3, 1]])

Leftnull = np.array([—1, 0, 1])

Leftnull.T @ A

Фундаментальные подпространства матрицы

Обобщим изложенную выше информацию. Возьмем матрицу $A$ размерностью $m times n$. Тогда

$ null(A) in R^n$ (так как должно быть решением $A mathbf x = mathbf 0$)
$ col(A) in R^m $ (количество строк $A$)
$ row(A) = col(A^T) in R^n $ (количество столбцов $A$)
$ leftnull(A) = null(A^T) in R^m $ (так как должно быть решением $A^T mathbf y = mathbf 0$)

Тогда схематично эти подпространства можно представить следующим образом.

Несколько пояснений и дополнений:

$r$ означает ранг (rank) матрицы
$r+(n-r) = n$, т.е. столбцы матрицы $A$
$r+(m-r) = m$, т.е. строки матрицы $A$ или столбцы $A^T$

Про пересечение подпространств. Может ли вектор $mathbf v = begin{bmatrix} 1 \ 2 end{bmatrix}$ быть одновременно в нуль-пространстве и являться частью пространства строк A (или в целом строкой в A)? Нет.

$$ begin{bmatrix} 1 & 2 \ dots & dots end{bmatrix} begin{bmatrix} 1 \ 2 end{bmatrix} not= begin{bmatrix} 0 \ 0 end{bmatrix} $$

Пересечением пространства строк и нуль-пространства будет только нулевой вектор.

$$ row(A) cap null(A) = { mathbf 0 } $$

Ортогональность подпространств матрицы

Более того, ядро ортогонально пространству строк $row(A) perp null(A)$, так как их скалярное произведение равно нулю. Это следует из определения ядра $A mathbf x = mathbf 0$ (произведение $mathbf x$ на каждую вектор-строку $mathbf a_m$ равно нулю).

$$ begin{bmatrix} dots & mathbf a_1 & dots \ dots & mathbf a_2 & dots \ dots & dots & dots \ dots & mathbf a_m & dots end{bmatrix} begin{bmatrix} vdots \ mathbf x \ vdots end{bmatrix} = begin{bmatrix} 0 \ 0 \ 0 \ 0 end{bmatrix} $$

Более того, так как $null(A)$ содержит все векторы, ортогональные $row(A)$, то ядро можно считать ортогональным дополнением пространства строк в $R^n$: $null(A) = row(A)^{perp} $.

То же самое справедливо для пространства столбцов и коядра.

$$ col(A) perp leftnull(A) perp null(A^T) text{ в } R^m $$

$$ leftnull(A), null(A^T) = col(A)^{perp} $$

Количество решений системы уравнений

Систематизируем наши знания о подпространствах матрицы с точки зрения возможного количества решений системы уравнений.

Система не имеет решений

В случае если система не имеет решений, существует некоторый вектор $mathbf b $, при котором $A mathbf x = mathbf b $ не будет иметь решения.

$$ exists mathbf b implies A mathbf x not= mathbf b $$

С точки зрения матрицы $underset{m times n}{A}$, можно говорить о том, что некоторые строки линейно зависимы и после преобразования методом Гаусса обратятся в нули. Как следствие, ранг матрицы меньше количества строк, $r < m$.

Система имеет единственное решение

Если мы знаем, что система имеет единственное решение, то это означает, что нуль-пространство матрицы $A$ содержит только нулевой вектор, $null(A) = { mathbf 0 }$ и все столбцы линейно независимы, $ r = n $.

Система имеет множество решений

В этом случае решение состоит из частного решения и решения системы $A mathbf x not= mathbf 0 $. Другими словами, это означает, что нуль-пространство содержит не только нулевой вектор, а значит столбцы матрицы линейно зависимы и $ r < n $.

Теперь приведем пример, иллюстрирующий применение матрицы для моделирования физического процесса, а также посмотрим как подпространства такой матрицы одновременно характеризуют свойства этого процесса.

Источник