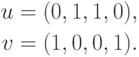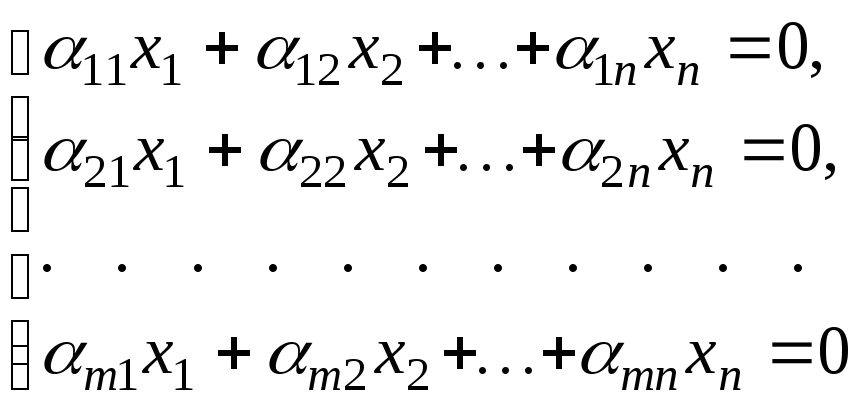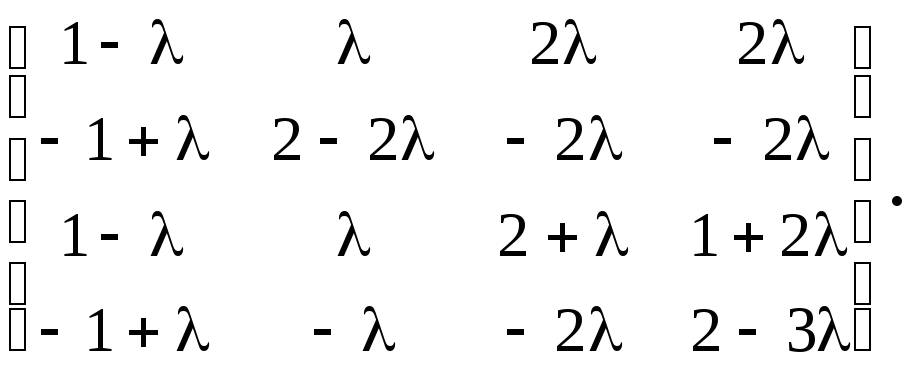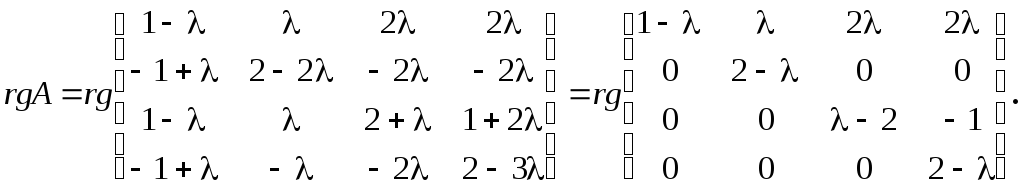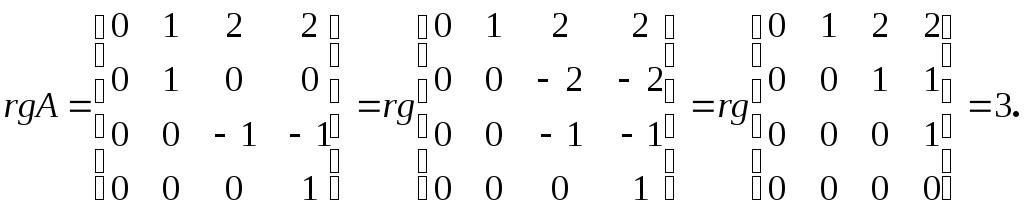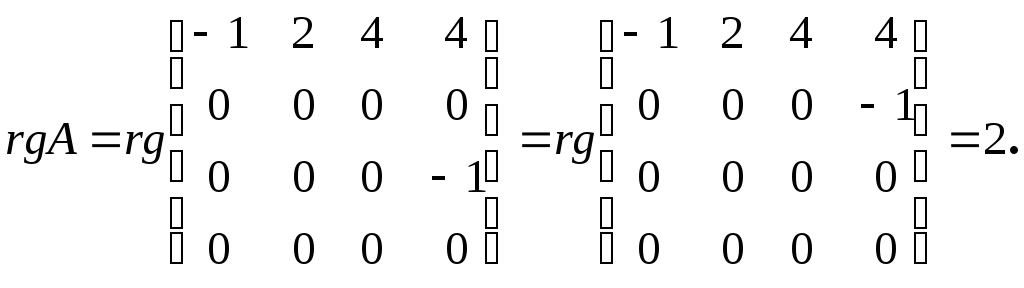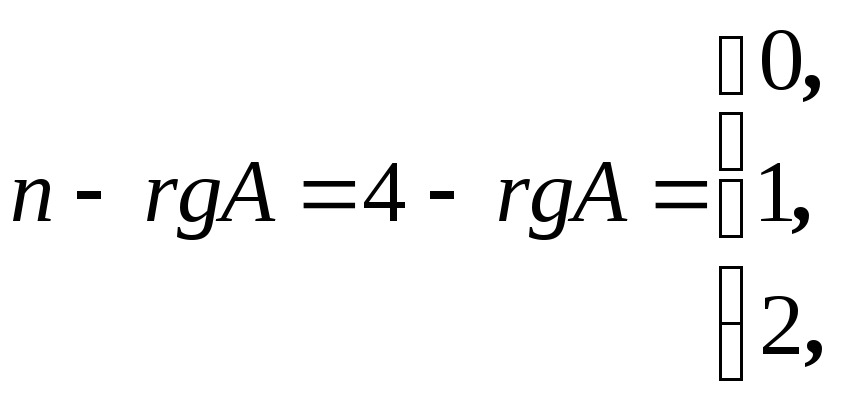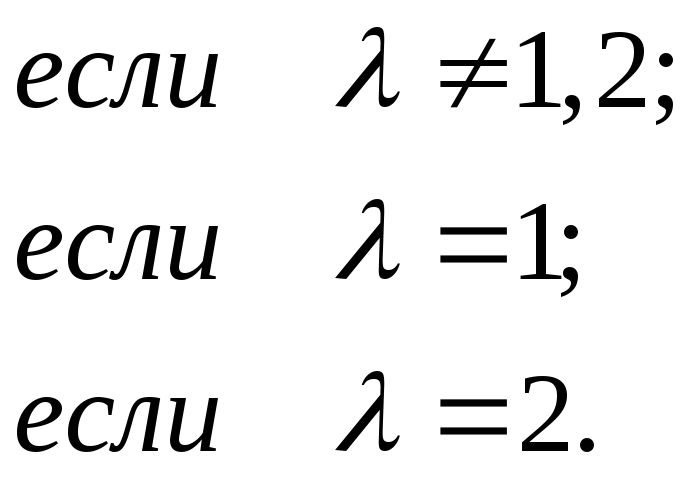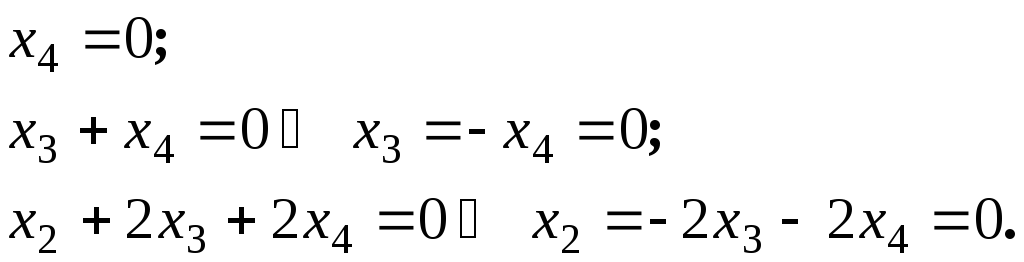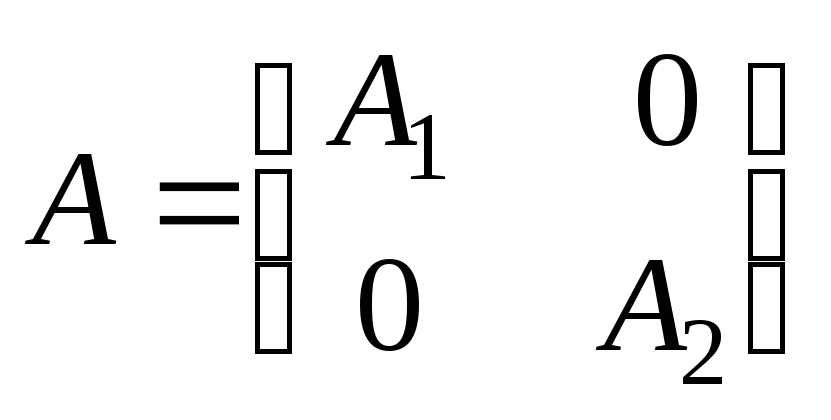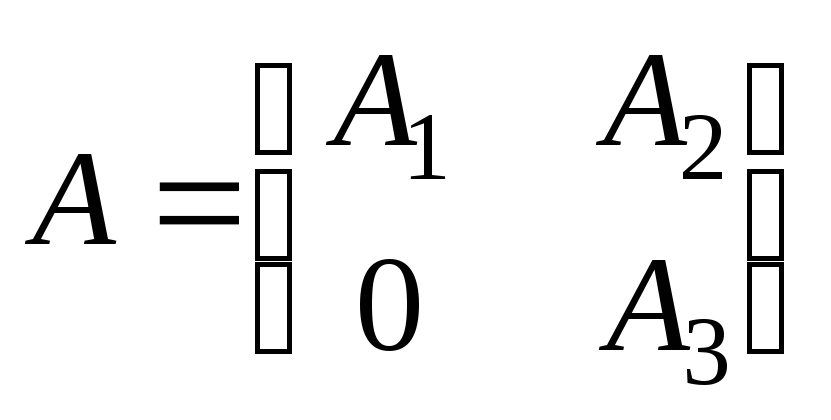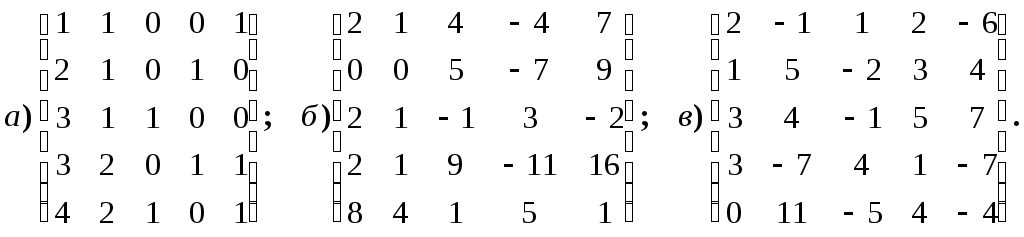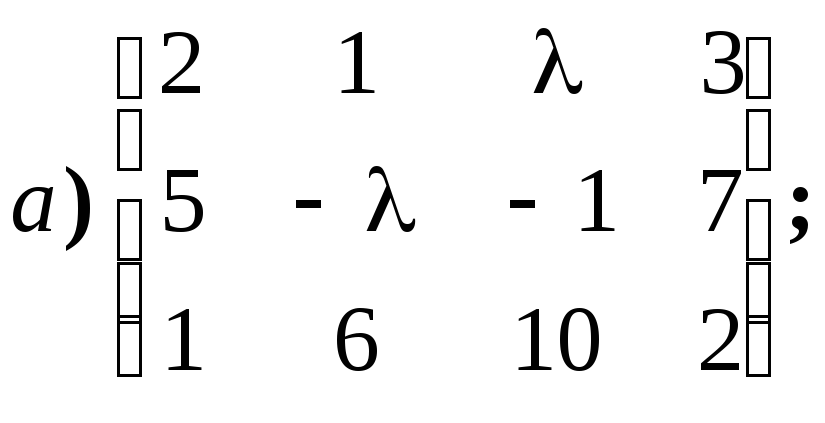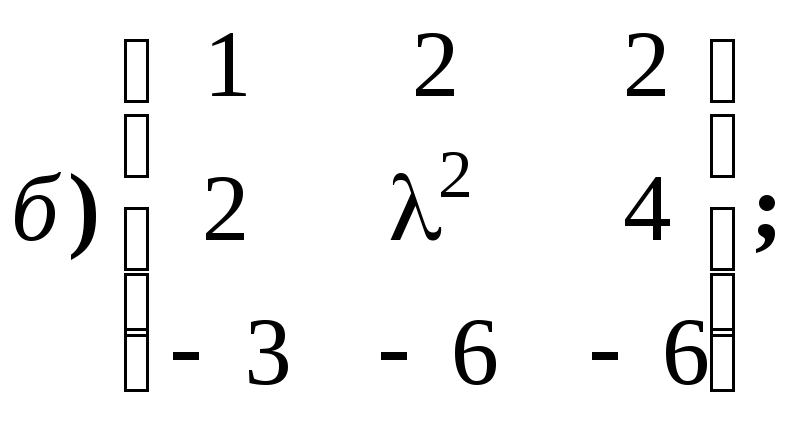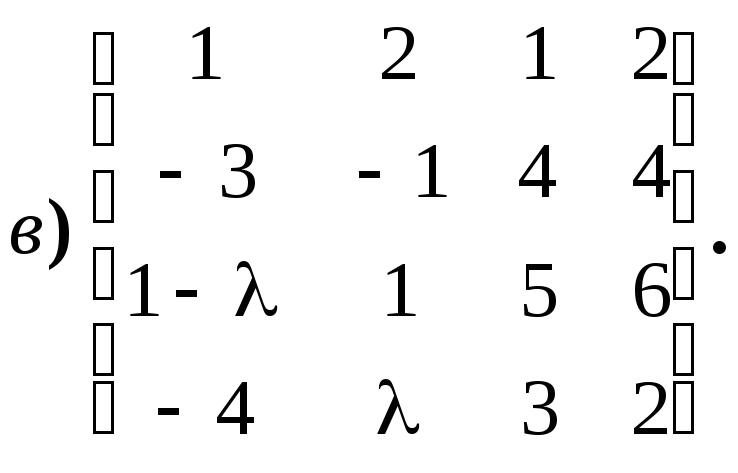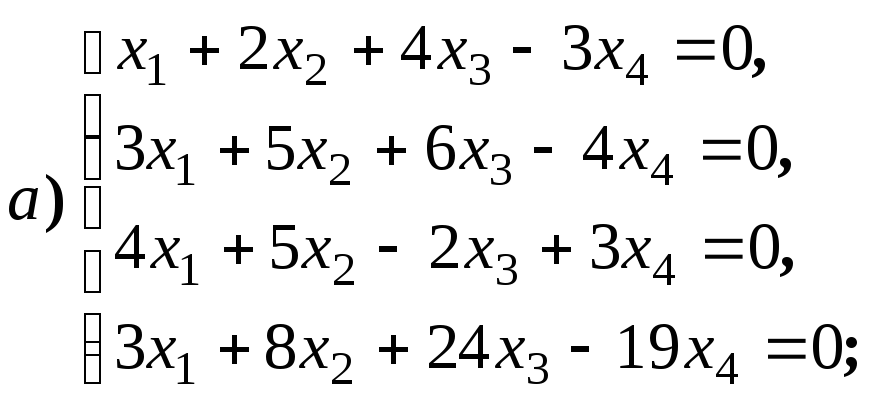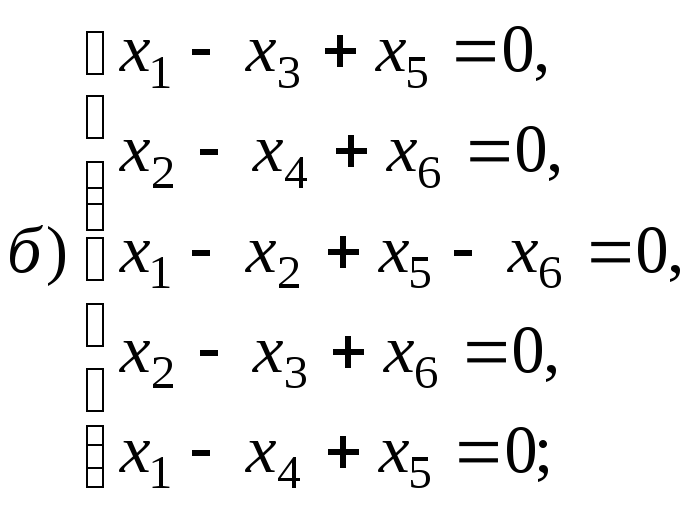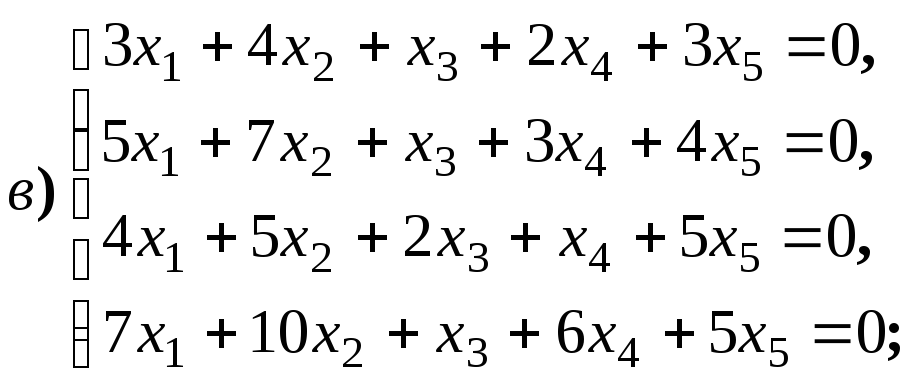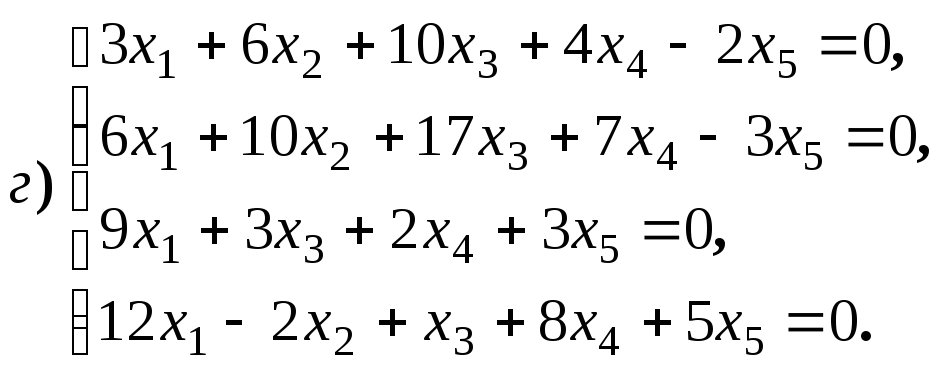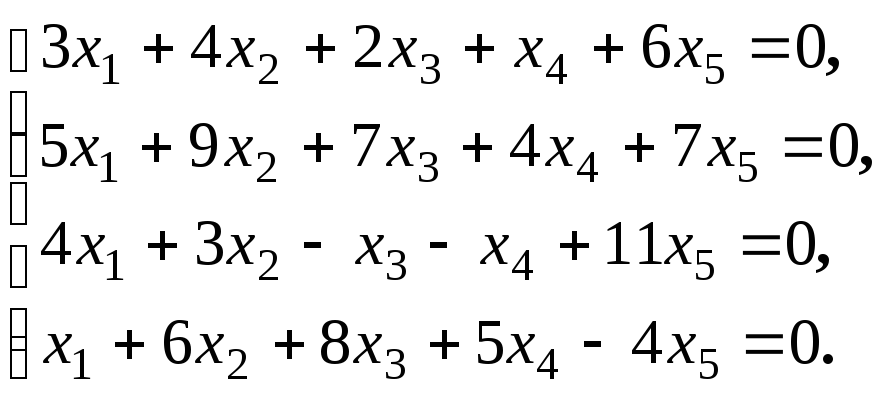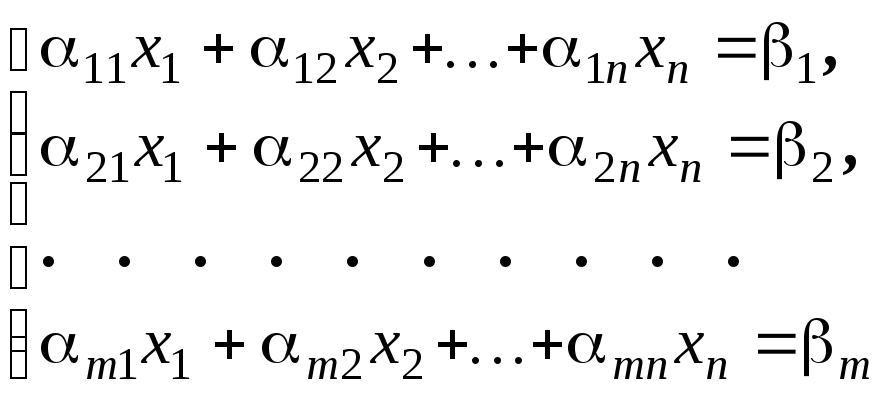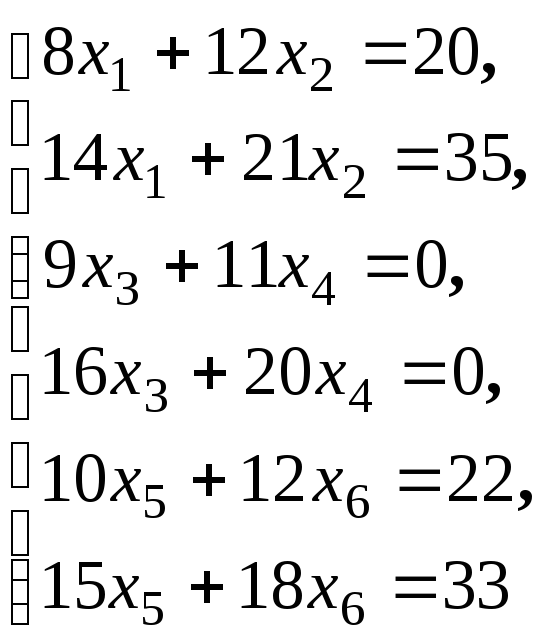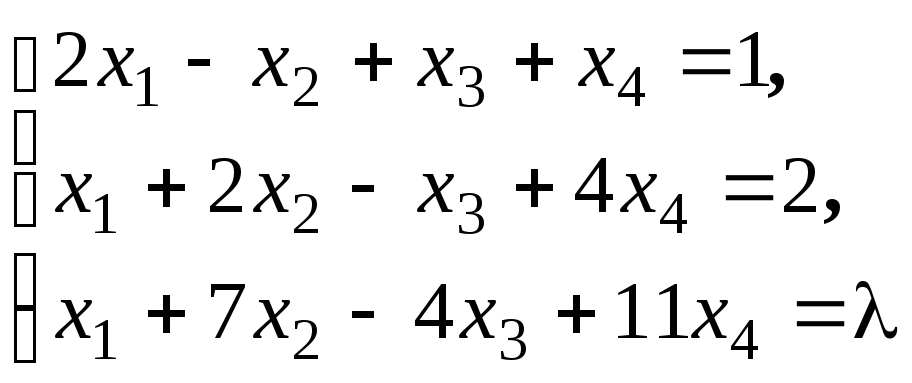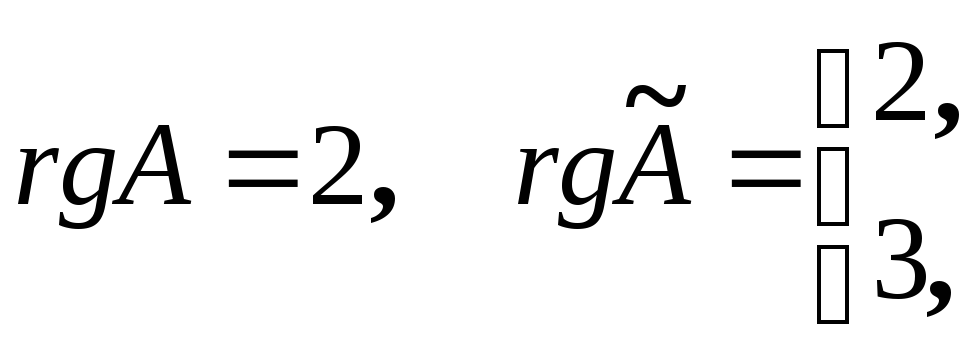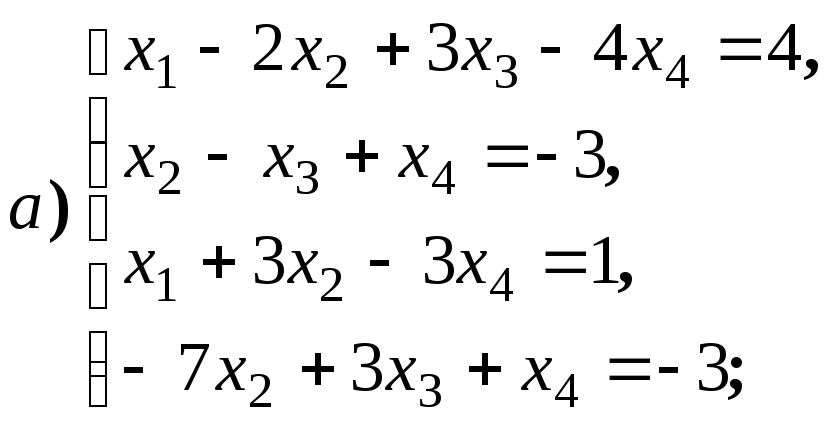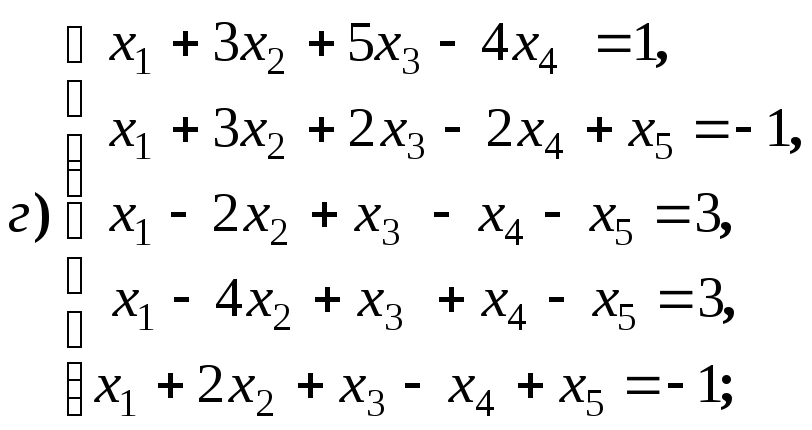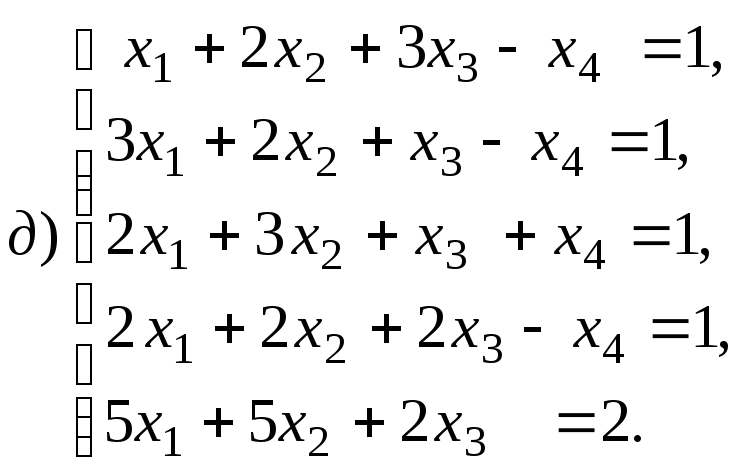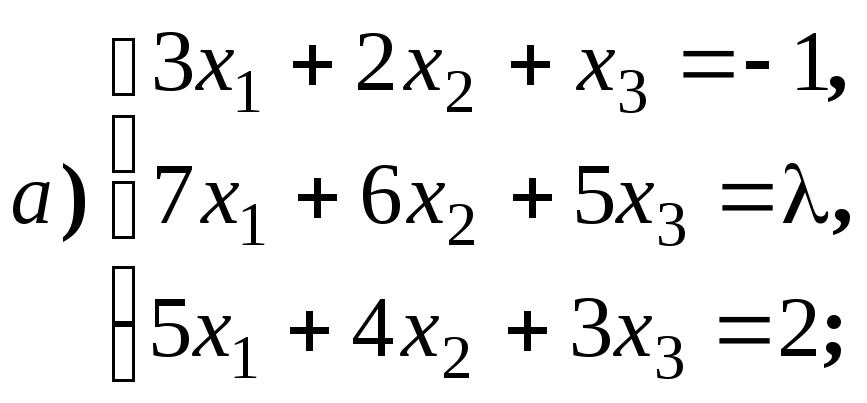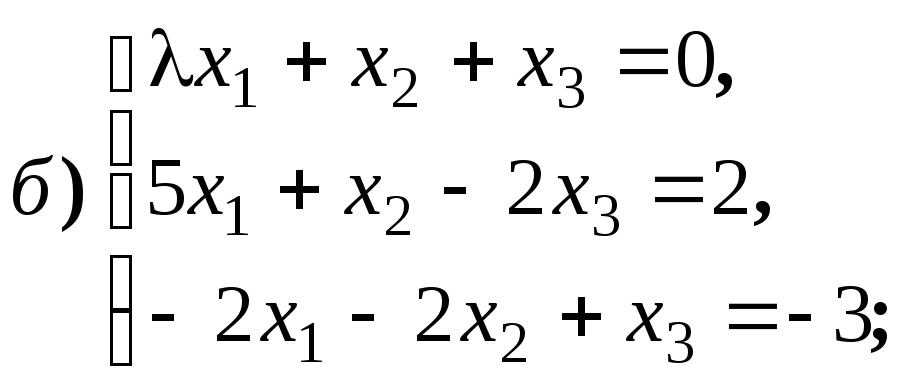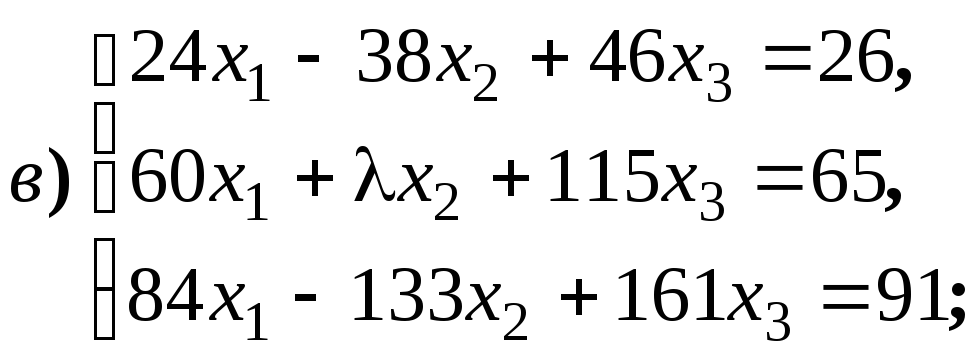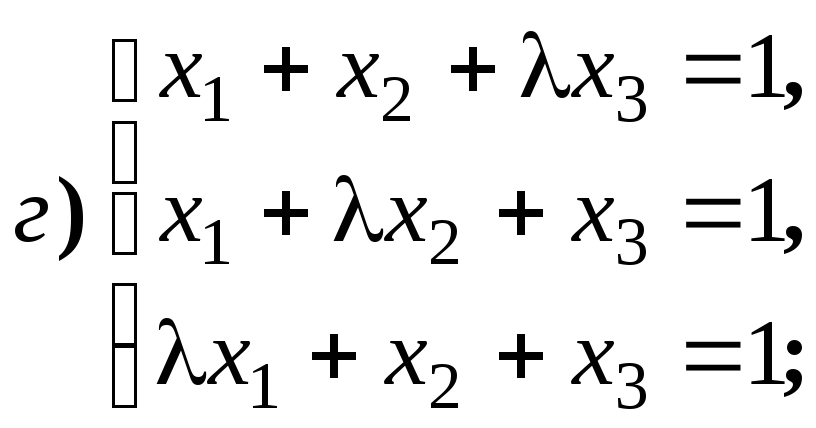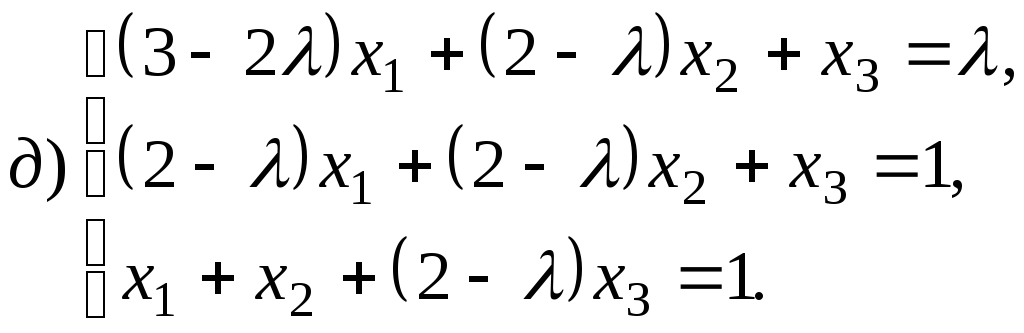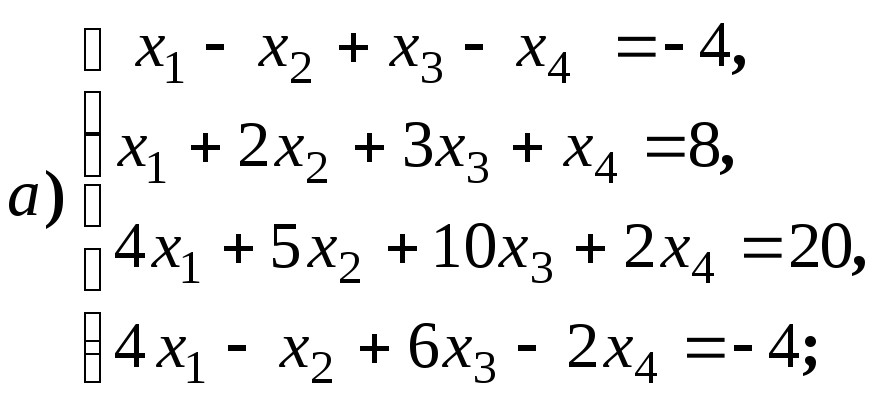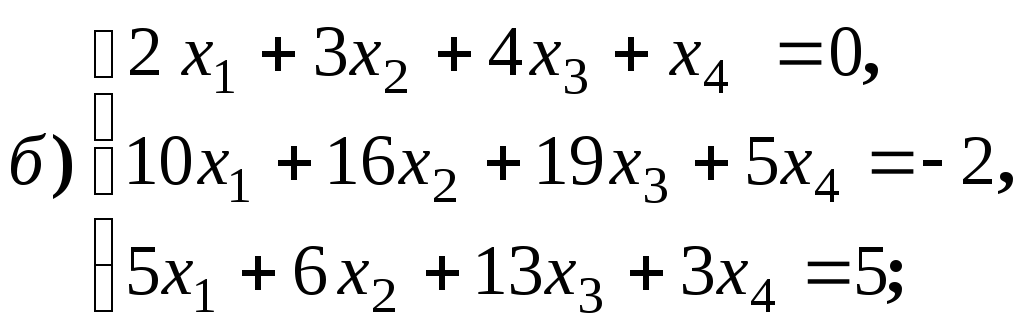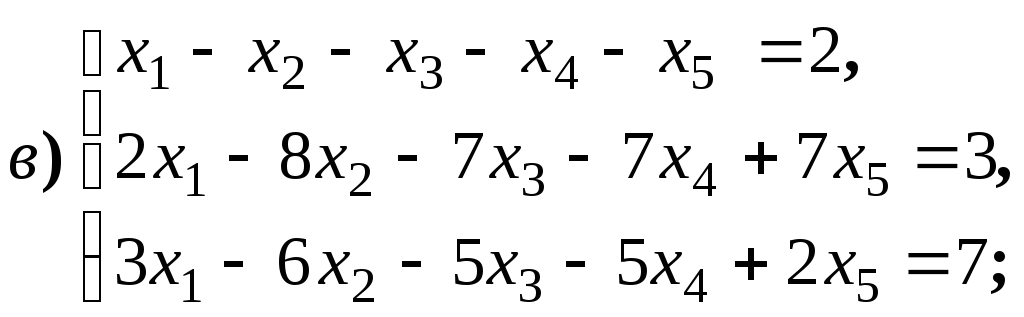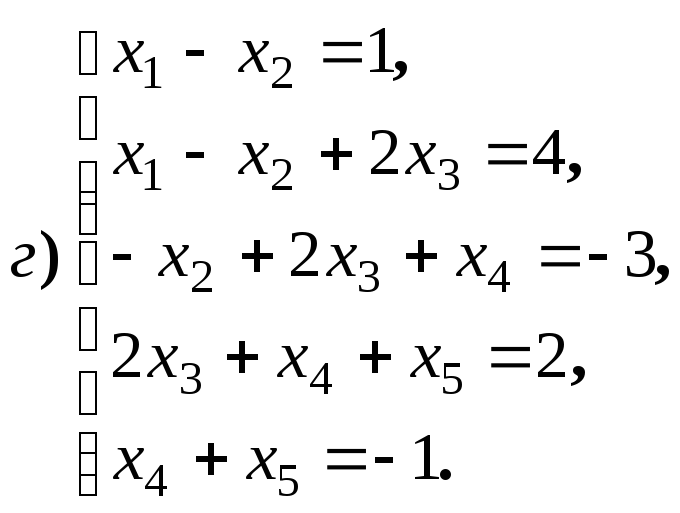Размерность пространства решений однородной системы линейных уравнений
Как мы отметили ранее, совокупность решений Xодн однородной системы линейных уравнений с матрицей 
Теорема 9.17.1. Если r=r(A)<n, то 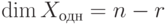
Доказательство. Для удобства записи переупорядочим неизвестные, если это необходимо, так, чтобы
Пусть 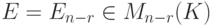

Эта система n-r строк-решений линейно независима (поскольку строки единичной матрицы, конечно, линейно независимы). Если
произвольное решение, то
Однако, конечно,
при этом 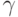
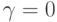
Итак, мы построили базис 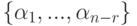
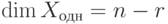
Замечание 9.17.2. Если вместо строк единичной матрицы En-r для свободных неизвестных брать строки всевозможных матриц 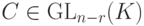
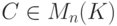
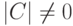
Замечание 9.17.2. Любой базис линейного пространства решений Xодн однородной системы линейных уравнений называется в ряде алгебраических текстов » фундаментальной системой решений однородной системы линейных уравнений «.
Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений
Пусть K — поле, 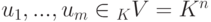
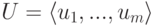
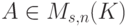
совпадает с U.
Если U — нулевое подпространство, то в качестве A мы можем взять любую матрицу 
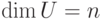




Рассмотрим матрицу 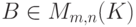

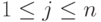
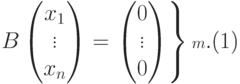 |
( 9.2) |
Ясно, что 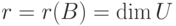
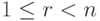
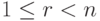
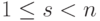
Пусть строки 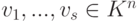
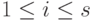
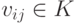
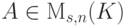
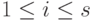
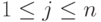
Действительно, по построению матрицы A любая строка из U (как линейная комбинация строк u1,…,um ) является решением однородной системы уравнений
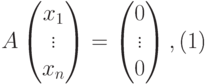 |
( 9.3) |
т. е. 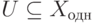
Следовательно, U=Xодн.
В заключение отметим, что матрица A определена неоднозначно. Например, другая матрица A’ может быть получена с помощью другой фундаментальной системы решений системы (9.2).
Полученное задание линейных подпространств оказывается полезным при решении ряда практических задач. Например, пусть 
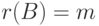
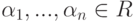
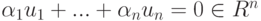
имеем 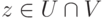
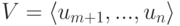
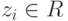

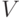
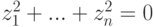
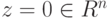
Но u1,…,um — линейно независимые строки, поэтому 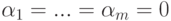
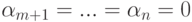
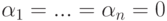
Таким образом, мы рассмотрели два способа задания линейных подпространств в K V=Kn :
- как множество решений Xодн однородной системы линейных уравнений;
- как линейную оболочку
строк
.
При этом мы научились переходить от первого задания ко второму (фундаментальная система решений) и от второго задания к первому. Первый способ задания удобен для задания пересечения 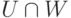
В следующем примере мы увидим комбинацию этих приемов.
Пример 9.18.1. Пусть 
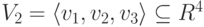

Решение Запишем строки u1, u2, u3, v1, v2, v3 по столбцам и приведем полученную матрицу к ступенчатому виду с помощью элементарных преобразований строк:
Поскольку 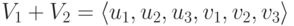

Поэтому v’_2=u’_1+u’_2+u’_3-v’_1 и, следовательно, v2=u1+u2+u3-v1. Для v’3 мы видим, что v’3+v’1=(2,0,2,0)*=2u’1+2u’3, поэтому v3=2u1+2u3-v1. Проведенные вычисления равносильны завершению приведения матрицы к главному ступенчатому виду:
Рассмотрим теперь 
Для V1:
система уже имеет ступенчатый вид, x1, x2, x3 — главные неизвестные, x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,1,-1,1). Итак, подпространство V1 совпадает с пространством решений однородной системы линейных уравнений
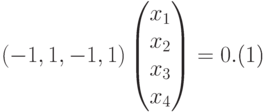 |
( 9.4) |
Для V2 :
и мы приходим к ступенчатому виду, при этом x1, x2, x3 — главные неизвестные, а x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,-1,1,1). Значит, однородная система линейных уравнений
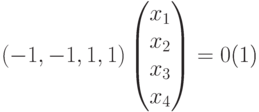 |
( 9.5) |
задает подпространство V2.
Ясно, что система
задает подпространство 
Решим эту систему:
x1, x2 — главные неизвестные, x3, x4 — свободные неизвестные. Фундаментальная система решений состоит из двух строк
Следовательно, {u,v} — базис линейного подпространства 
Системы линейных однородных уравнений
Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Свойства систем линейных однородных уравнений
Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.
Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.
Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3
Системы линейных однородных уравнений
Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы
1. Записываем матрицу системы:
и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:
.
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.
3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.
Примечание. К элементарным преобразованиям матрицы относят:
1. умножение (деление) строки на множитель, отличный от нуля;
2. прибавление к какой-либо строке другой строки, умноженной на любое число;
3. перестановка строк местами;
4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).
Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.
Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:
Полагаем , тогда
.
Размерность линейного пространства решений равна 3.
:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон
21. Пространство решений системы линейных однородных уравнений
Пусть дана система (30) линейных однородных уравнений с коэффициентами из поля Р.
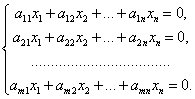
Так как столбец свободных членов в матрице А1 этой системы состоит только из нулей, то rang A = rang A1, т. е. система линейных однородных уравнений всегда совместна. В частности она всегда имеет нулевое решение. Рассмотрим множество всех возможных решений системы (30).
Пусть A =(A1, A2, … , An) и B =(B1, B2, … , Bn) – Любые два из них. Их можно рассматривать, как векторы в арифметическом n-мерном пространстве над полем Р. Пусть L – любой элемент поля Р. Тогда A +B = (A1 + B1, A2 + B2, … , An + Bn ), L×A = (LA1, LA2, … , LAn). Подставим компоненты этих векторов в произвольное S-е уравнение системы (30). Получим 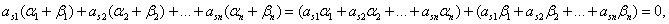
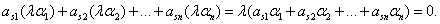
Теорема 27. Множество решений системы линейных однородных уравнений с N Переменными есть линейное подпространство арифметического пространства Аn .
Теорема 28. Размерность пространства решений системы линейных однородных уравнений равна N – r, Где N – Число неизвестных, r – ранг матрицы системы.
Доказательство. Пусть L – пространство решений системы (30). Тогда L Ì Аn . Пусть A = (A1, A2, … Ar, Ar+1, … , An) – произвольное решение системы. Пусть (Ar+1, … , An) – набор свободных неизвестных, соответствующий этому решению. Множество всех возможных наборов свободных неизвестных есть арифметическое (N – r)-мерное пространство Аn–r . Зададим отображение J: L ® Аn–r по правилу
Покажем, что J – изоморфизм (определение 24). Для этого нужно проверить три условия.
1. Покажем, что J – взаимнооднозначное отображение. Решению A = (A1, A2, … Ar, Ar+1, … , An) соответствует только один набор (Ar+1, … , An), следовательно, J – Однозначное отображение. Обратно, если задать элемент (Ar+1, … , An) из Аn–r , то по теореме Крамера найдётся только один набор (A1, A2, … Ar ) искомых неизвестных, т. е. каждый элемент J(A) из Аn–r соответствует единственному элементу из L .
Итак, пространство решений системы линейных однородных уравнений изоморфно арифметическому (N – r)-мерному пространству. Следовательно, размерность L равна (N – r).
Определение 29. Базис пространства решений системы линейных однородных уравнений называется её Фундаментальной системой решений.
Так как при изоморфизме базис пространства Аn–r соответствует базису пространства L , То для того. чтобы найти фундаментальную систему решений для системы (30), достаточно выбрать (N – r) линейно независимых наборов свободных неизвестных и для каждого из них найти решение данной системы.
Следствие. Если А1, а2, …, аN–r фундаментальная система решений системы линейных однородных уравнений (30) и С1, С2, … , СN–r – произвольные элементы поля Р, то С1А1 + С2А2 + … + СN–r АN–r – общее решение этой системы.
http://www.reshebnik.ru/solutions/10/3
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/21-prostranstvo-reshenii-sistemy-lineinykh-odnorodnykh-uravnenii
Глава
4
Системы
линейных уравнений
§
4.1. Ранг матрицы. Однородные системы.
Фундаментальная
система
решений
Рангом
матрицы
(обозначается
)
называется наивысший порядок
отличных
от нуля миноров этой матрицы.
Ранг
нулевой матрицы полагается равным нулю
по определению.
Для
любой прямоугольной матрицы ранги ее
систем векторов- строк и векторов-
столбцов совпадают и равны рангу матрицы.
Система
уравнений
называется
однородной.
Однородная система всегда совместна,
так как одним из ее частных решений
является нулевое решение.
Для
того, чтобы однородная система имела
ненулевое решение, необходимо и
достаточно, чтобы ранг матрицы системы
был меньше числа неизвестных.
Множество
решений однородной системы линейных
уравнений
образует линейное пространство
размерности
,
где
—
ранг матрицы системы. Любой базис
пространства решений однородной системы
называется фундаментальной
системой решений
этой системы.
Пример
1.
Найдите ранг матрицы в зависимости от
значения параметра
Решение.
При помощи элементарных преобразований,
не изменяющих ранг, приведем матрицу к
ступенчатому виду. Прибавив ко второй
строке первую, к третьей- первую,
умноженную на
,
к четвертой- первую, получим:
Если
,
то
Рассмотрим
теперь случай, когда
:
Очевидно,
что если
,
то
.
Пример
2.
Найдите размерность пространства
решений однородной системы линейных
уравнений с матрицей системы из примера
1.
Решение.
Размерность пространства решений равна
Пример
3.
Найдите общее решение и фундаментальную
систему решений однородной системы
линейных уравнений из примера 1.
Решение.
Если
система имеет только нулевое решение.
Пусть
.
Тогда, как было показано в примере 1,
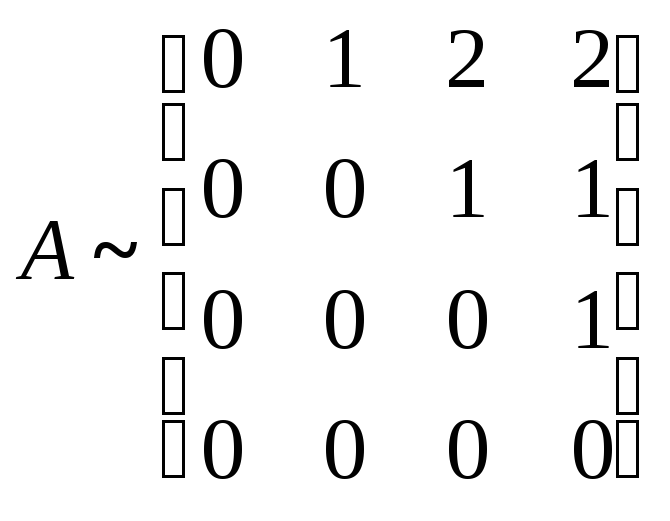
Пространство
решений одномерное и фундаментальная
система решений состоит из одного
вектора. Из
находим:
—
свободная переменная.
Общее
решение имеет вид:.
Фундаментальная система решений:.
Пусть
теперь
.
В этом случае
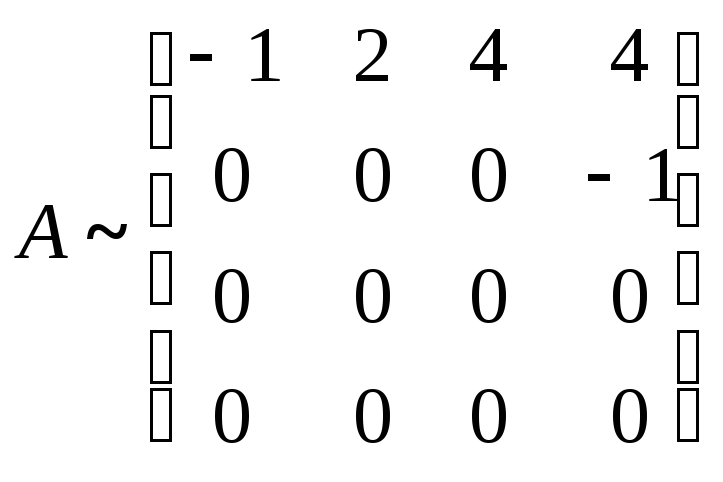
пространство
решений двумерное и фундаментальная
система решений состоит из двух векторов.
Из
получаем:
—
свободные переменные;
.
Общее
решение имеет вид:
.
Выбирая
значения свободных переменных в
соответствии с таблицей,
|
i |
|
|
|
1 |
1 |
0 |
|
2 |
0 |
1 |
записываем
фундаментальную систему решений:
и
.
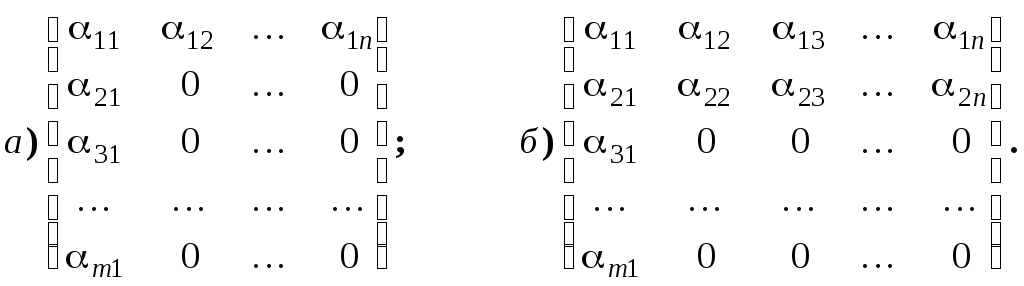
4.1.1.
Укажите всевозможные значения ранга
матриц вида:
4.1.2.Как
может измениться ранг матрицы, если
изменить значение одного ее элемента?
4.1.3.
Как может изменится ранг матрицы, при
изменении элементов лишь одной строки?
строк?
4.1.4.
Докажите, что ранг квазидиагональной
матрицы
равен сумме рангов матриц
и
.
4.1.5.
Верно ли следующее утверждение:
ранг квазитреугольной
матрицы
всегда равен сумме рангов матриц
и
?
-
Докажите,
что ранг суммы двух матриц не больше
суммы их рангов.
4.1.7.
Вычислите ранг матриц:
4.1.8.
Найдите ранг матриц в зависимости от
значений параметров:
4.1.9.
Найдите общее решение и фундаментальную
систему решений для систем уравнений:
4.1.10.
Образуют ли строки каждой из матриц
фундаментальную
систему решений для системы уравнений
§
4.2. Неоднородные системы. Теорема
Кронекера- Капелли
Согласно
теореме
Кронекера- Капелли неоднородная система
линейных уравнений
совместна
тогда и только тогда, когда ранг матрицы
этой системы
равен
рангу ее расширенной матрицы
т.е.
когда
.
Общее
решение
неоднородной системы представимо в
виде суммы общего решения
соответствующей однородной системы и
какого- либо частного решения
неоднородной системы.
Пример
1.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений
в
виде суммы частного решения этой системы
и линейной комбинации базисных решений
соответствующей однородной системы.
Решение.
Запишем систему уравнений в матричном
виде. Используя элементарные преобразования
над строками полученной матрицы, приведем
ее к ступенчатому виду и проверим
выполнимость условия
:
т.е.
по теореме Кронекера- Капелли система
уравнений совместна. Запишем ее общее
решение. Поскольку
будем иметь две свободные переменные.
—
свободная переменная,
—
свободная переменная,
Таким
образом,
.
Заметим,
что
,
а векторы
и
образуют фундаментальную систему
решений соответствующей однородной
системы уравнений.
Пример
2.
Подберите
так, чтобы система уравнений
имела
решение.
Решение.
Нужно найти такое значение параметра
,
при котором выполняется условие
.
По
теореме Кронекера- Капелли система
уравнений совместна при
4.2.1.
Исследуйте совместность и найдите общее
решение систем уравнений

4.2.2.
Исследуйте систему и найдите общее
решение в зависимости от значения
параметра
:
4.2.3.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений в виде суммы одного решения
этой системы и линейной комбинации
базисных решений соответствующей
однородной системы:
8
Соседние файлы в папке Задачник-1
- #
- #
- #
- #
- #
- #
- #
- #
- #

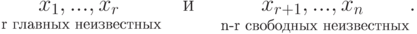
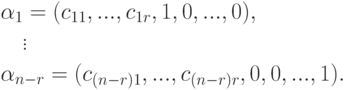
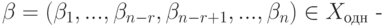
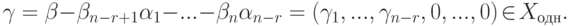
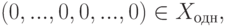
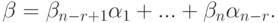
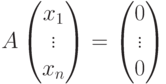
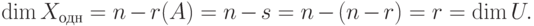
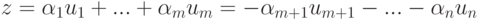
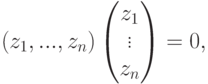

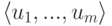 строк
строк 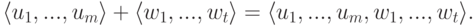
![begin{mult}
begin{gathered}
u_1 u_2 u_3,, ! v_1 v_2 v_3 kern53mm
\
left(
begin{array}{cccccc}
1 & 0 & 0 & 1 & 0 & 1\
1 & 1 & 0 & 0 & 2 & 2\
0 & 1 & 1 & 1 & 1 & 1\
0 & 0 & 1 & 0 & 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & 0 & 1\
0 & 1 & 0 & -1 & 2 & 1\
0 & 1 & 1 & phm 1 & 1 & 1\
0 & 0 & 1 & phm 0 & 1 & 2
end{array}right)to{}
end{gathered}
\[3mm]
begin{gathered}
kern55mm u'_1, u'_2, u'_3 v'_1; v'_2; v'_3
\
{}to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & phm 0 & 1\
0 & 1 & 0 & -1 & phm 2 & 1\
0 & 0 & 1 & phm 2 & -1 & 0\
0 & 0 & 1 & phm 0 & phm 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
multicolumn{1}{|c}{1} & 0 & 0 & phm 1 & phm 0 & phm 1\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & -1 & phm 2 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & phm 2 & -1 & phm 0\
cline{3-3}
0 & 0 & 0 & multicolumn{1}{|c}{phm 1} & -1 & -1\
cline{4-6}
end{array}right).
end{gathered}
end{mult}](https://intuit.ru/sites/default/files/tex_cache/dd0dbbb69869493ca81113a368c90d5a.png)
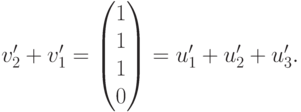

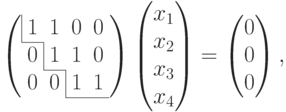
![begin{align*} & begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
1 & 2 & 1 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 2 & 0 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 1 & 0 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to!
%{}
%\[3mm]
%& quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 1 & 0 & 1\
0 & 2 & 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & 0 & 1 & phm 0\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & -1\
cline{3-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/9b3e5cd07c99c5ba9b0cfe865a6061bc.png)
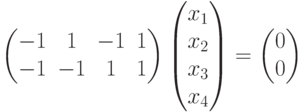
![begin{align*} & begin{pmatrix}
-1 & phm 1 & -1 & 1\
-1 & -1 & phm 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
phm 1 & -1 & 1 & -1\
-1 & -1 & 1 & phm 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & -1 & 1 & -1\
cline{1-1}
0 & multicolumn{1}{|c}{-2} & 2 & phm 0\
cline{2-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/514a0838571b1cf6b55788bbade81424.png)