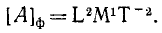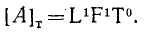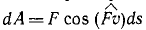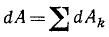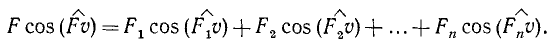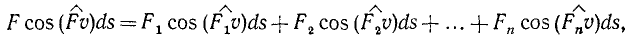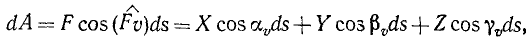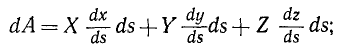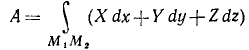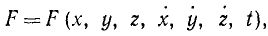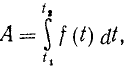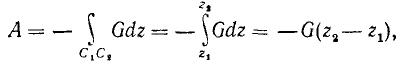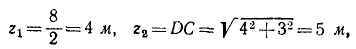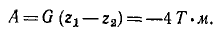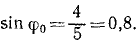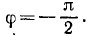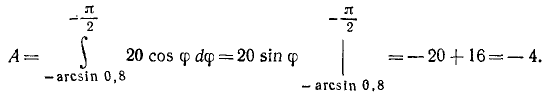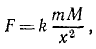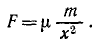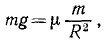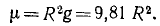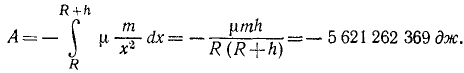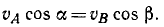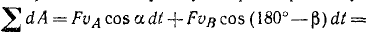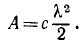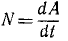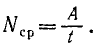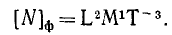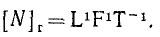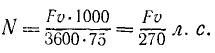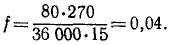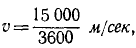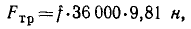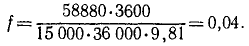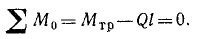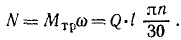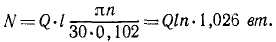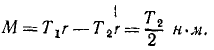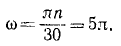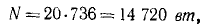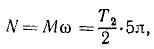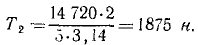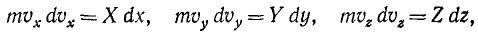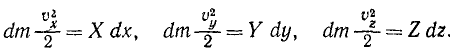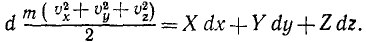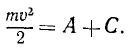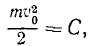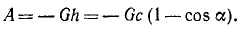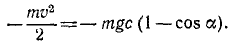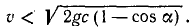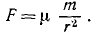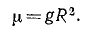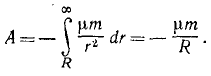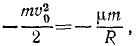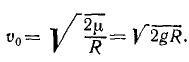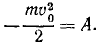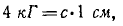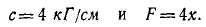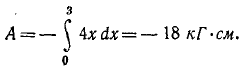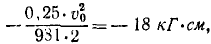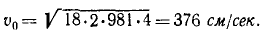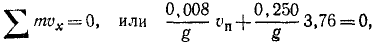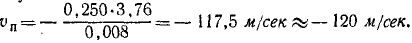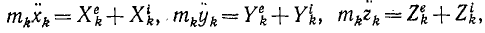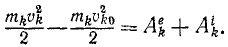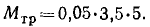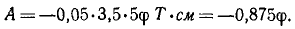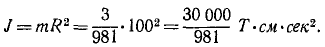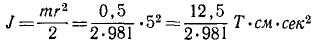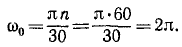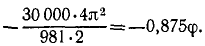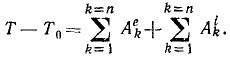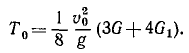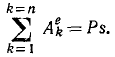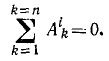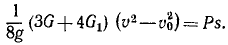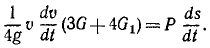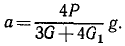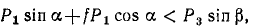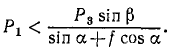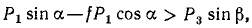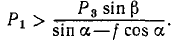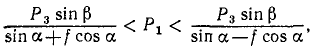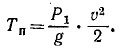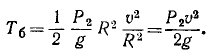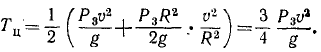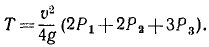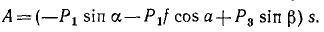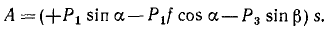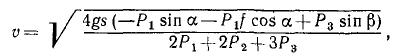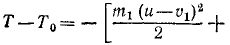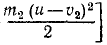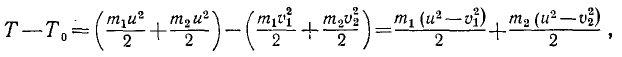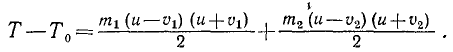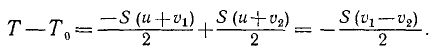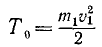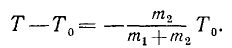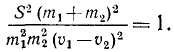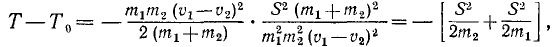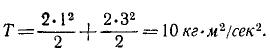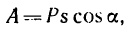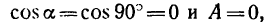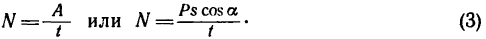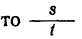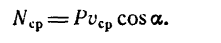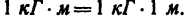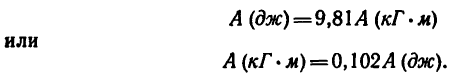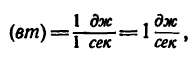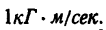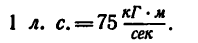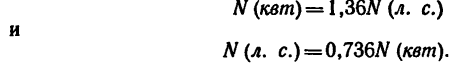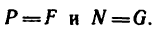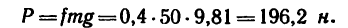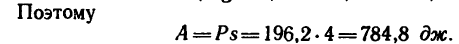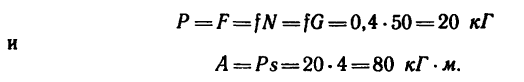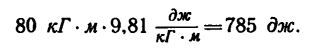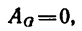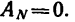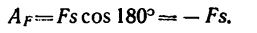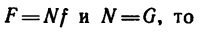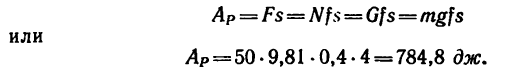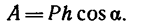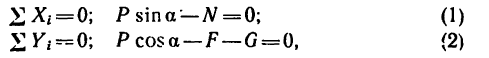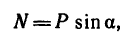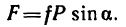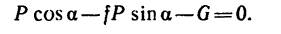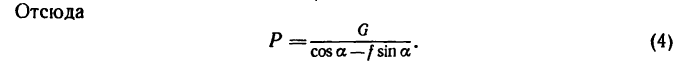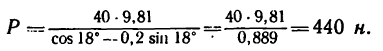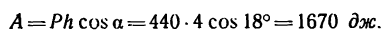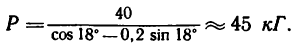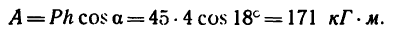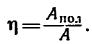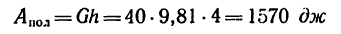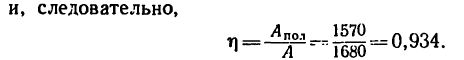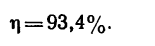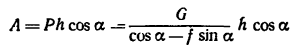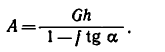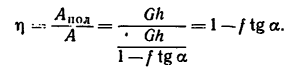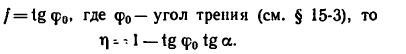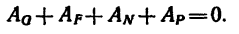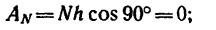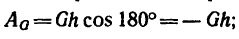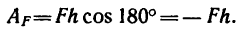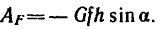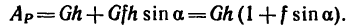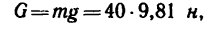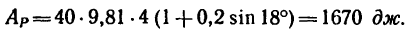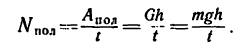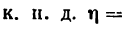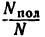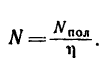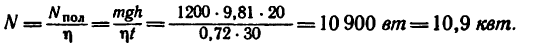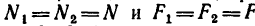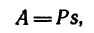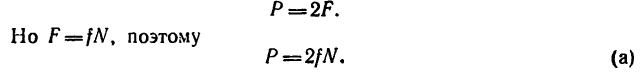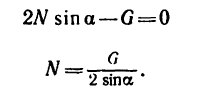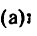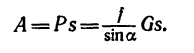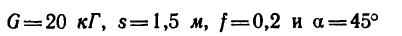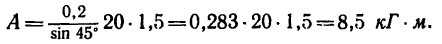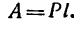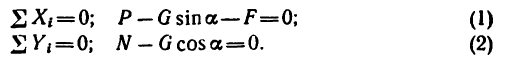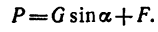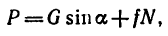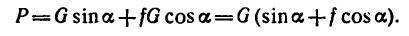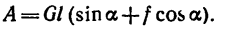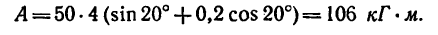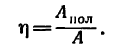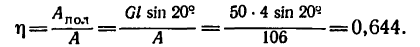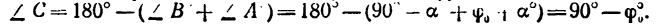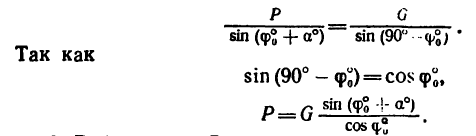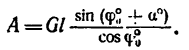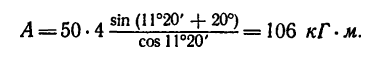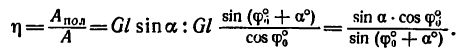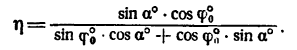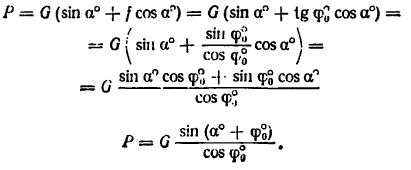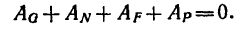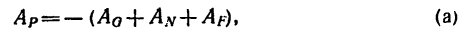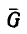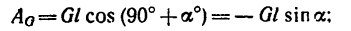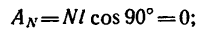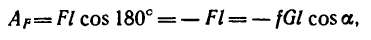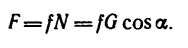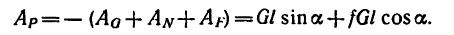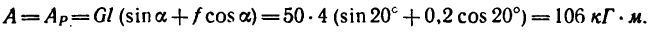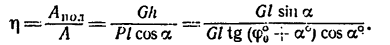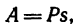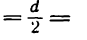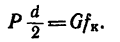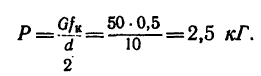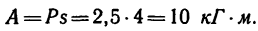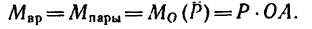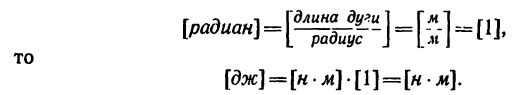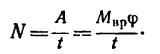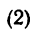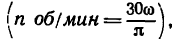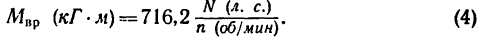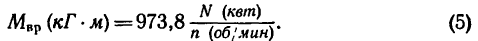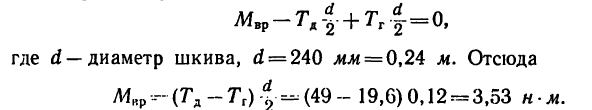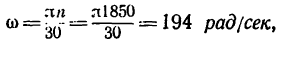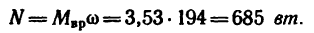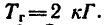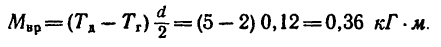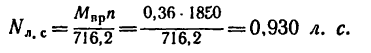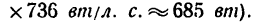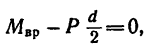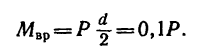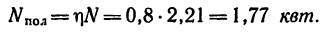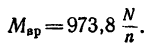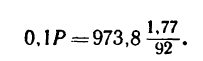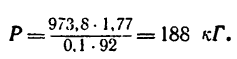Содержание:
Работа силы м мощность силы:
«Работа — это изменение формы движения, рассматриваемое с его количественной стороны» (Энгельс)
Понятие работы
Энергия может переходить из одного вида в другие. Например, потенциальная энергия воды, поднятой плотиной на гидроэлектростанции, переходит в кинетическую энергию вращающихся турбин, которая в свою очередь превращается в электрическую энергию, по проводам передается на большие расстояния, чтобы опять перейти в кинетическую энергию станков, в тепловую энергию электропечей, в световую, в звуковую и в прочие виды энергии. При всех этих явлениях исчезает (или возникает) такое же количество каждого вида энергии, сколько возникает (или исчезает) энергии всех прочих видов. Это изменение энергии, изменение формы движения, рассматриваемое с количественной стороны, Энгельс называет работой.
Из множества различных видов движения в теоретической механике интересуются только механическим движением. Переход механического движения в немеханическое или же, наоборот, немеханического в механическое происходит на протяжении некоторого пути и зависит от действующих сил. Поэтому понятие работы в механике связано с понятиями перемещения и силы.
Работу постоянной силы при прямолинейном движении выражают произведением модуля силы на величину перемещения материальной частицы и на косинус угла между направлением силы и перемещением А = Fs cos α
Работа постоянной силы при прямолинейном движении
Знакомство с понятием работы силы в механике начнем с частного случая — работы постоянной силы при прямолинейном движении точки ее приложения.
Пусть к некоторой материальной частице приложена сила F, постоянная по величине и по направлению. Пусть точка приложения силы переместилась на прямолинейный отрезок s . В таком случае произведение
A= Fs cos α (218)
выражает работу постоянной силы F при прямолинейном движении и характеризует механическое воздействие на материальную частицу со стороны других материальных объектов на данном пути.
Работа является скалярной величиной, она не имеет направления и вполне характеризуется величиной и знаком. В формуле (218) модуль силы F и длина пути s всегда положительны. Знак « + » или «—» определяются знаком косинуса угла α между направлением силы и перемещения или, так как при прямолинейном движении точки перемещение совпадает с направлением скорости υ, косинусом угла между направлением силы и скорости. Работа положительна, если угол (Fυ) острый, и отрицательна, если он тупой. Если направление F совпадает с направлением перемещения, то угол (
А =Fs.
Если же сила направлена противоположно перемещению, то (
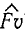
А = -Fs.
Сила, перпендикулярная к перемещению, работы не совершает, так как cos 90° = 0.
Определим размерность работы. В физической системе единиц
Единицей работы в СИ является джоуль2 — работа силы в 1 ньютон, действующей по направлению перемещения на пути в 1 метр (1 дж= 1 н ∙ 3t = l кг ∙ м2 ∙ ceκ-2).
Размерность работы в технической системе единиц
Если сила выражена в кГ, а длина — в м, то единицей работы является 1 килограммометр.
Размерности работы и кинетической энергии одинаковы.
Элементарной работой силы называют работу силы на столь малом перемещении точки ее приложения, при котором изменением силы можно пренебречь:
Элементарная работа силы
В общем случае, если сила переменна или движение точки приложения силы криволинейное, определять работу силы по (218) нельзя. Но, разбив мысленно весь путь на такие маленькие участки, которые можно считать прямолинейными и на которых можно пренебречь изменением величины и направления силы, мы определим на каждом из этих участков работу, называемую элементарной работой силы:
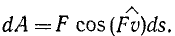
В этом равенстве ds выражает длину элементарного перемещения и является величиной всегда положительной.
Зная работу силы (219) на отдельных элементах пути, можно определить работу на конечном участке. Докажем некоторые теоремы о работе силы.
Элементарная работа равнодействующей равна сумме элементарных работ составляющих:
Теорема об элементарной работе равнодействующей. Пусть к точке О приложен пучок сил F1, F2,…, Fn. Обозначим равнодействующую этого пучка F. Спроецируем все силы пучка и равнодействующую на направление скорости точки О и приравняем проекцию равнодействующей сумме проекций составляющих:
Умножив теперь каждый член этого равенства на длину ds элементарного перемещения точки приложения сил, найдем, что элементарная работа равнодействующей равна сумме элементарных работ составляющих:
или
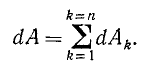
Под суммой следует понимать, конечно, алгебраическую сумму, потому что работа не имеет направления, но имеет знак.
Элементарная работа силы связана с проекциями силы на оси координат соотношением: dA = Xdx+ Ydy + Zdz
Выражение элементарной работы через проекции силы на оси координат
Разложим силу F на составляющие по осям координат и определим элементарную работу силы по сумме работ ее составляющих. Пусть составляющие силы направлены в положительном направлении осей координат. Тогда углы между составляющими силы и скоростью являются углами между скоростью и положительными направлениями осей координат, а их косинусы определяются формулами (62) направляющих косинусов скорости. В таком случае имеем
или, подставляя значения направляющих косинусов,
сокращая на ds, получаем окончательно
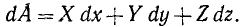
Формула (221) имеет очень большое значение в динамике. При. выводе этой формулы мы считали X, Y и Z направленными положительно по осям координат. Если какие-либо из составляющих силы направлены в противоположные стороны, то иным станет знак соответствующего косинуса. Поэтому в (221) X, Y и Z являются не модулями составляющих, а проекциями силы на оси координат, т.е. определяются не только величиной, но и знаком. Кроме того, в отличие от (219), где всегда ds>0, в (221) величины dx, dy и dz являются дифференциалами координат точки приложения силы и могут быть как положительными, так и отрицательными.
Заметим, что в общем случае дифференциальный трехчлен X dx + Y dy + Z dz не является полным дифференциалом и обозначение элементарной работы dA не следует понимать как полный дифференциал от А.
Работу силы на данном пути выражают пределом суммы всех элементарных работ силы на элементарных перемещениях, из абсолютных величин которых составляется данный путь:
Работа силы на данном пути. Возьмем какие-либо два положения M1 и M2 точки на ее криволинейной траектории. Работа А силы F на конечном перемещении M1M2 выразится суммой элементарных работ силы F на всех элементарных перемещениях, на которые разбит конечный участок пути M1M2.
Эта сумма состоит из бесчисленного множества бесконечно малых слагаемых. Такую сумму называют криволинейным интегралом, взятым по дуге M1M2, и обозначают так:
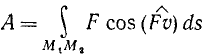
или, если воспользоваться выражением элементарной работы через проекции силы на оси координат,
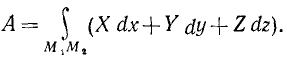
Если на точку действуют несколько сил, то, очевидно, работа равнодействующей на конечном участке пути равна сумме работ составляющих на том же участке пути.
Так как сила, вообще говоря, зависит от координат точки ее приложения, от проекций скоростей точки и от времени:
то мы можем вычислить интеграл (222′) только в случае, если известно движение точки. Подставив тогда вместо 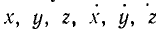
где t1 и t2 — мгновения, соответствующие положению точки в M1 и M2.
Работа графически выражается площадью, ограниченной кривой, изображающей зависимость проекции силы на скорость от пути, осью абсцисс и крайними ординатами
Графическое определение работы
Ввиду сложности математического вычисления работы па практике часто пользуются для этой цели графическим методом. Будем откладывать по оси абсцисс длину пути, пройденного точкой, а по оси ординат — соответствующую проекцию силы на направление скорости, учитывая и знак проекции. Получим некоторую кривую, изображающую зависимость между проекцией силы на направление скорости и путем точки. Площадь, ограниченная этой кривой, осью абсцисс и двумя крайними ординатами, изображает работу силы на данном пути. Если кривая или часть ее расположена по отрицательную сторону, вниз от оси абсцисс, то соответствующая площадь изображает отрицательную работу.
Для построения графика зависимости силы от пути имеются различные приборы. В частности, специальный прибор — индикатор— служит для записи давления в цилиндре в зависимости отхода поршня. Работу, вычисленную при помощи индикаторной диаграммы, т.е. диаграммы, начерченной этим прибором, называют индикаторной работой.
Работа силы тяжести не зависит от вида траектории центра тяжести тела и равна произведению веса тела на изменение высоты центра тяжести тела: AG=Gh
Работа силы тяжести
Складывая веса всех частиц тела, заменим их одной силой G, равной весу тела и приложенной в центре тяжести С. Пусть при движении тела центр тяжести тела переместился из C1(x1, yl, z1) в C2 (x2, y2, Z2) (рис. 210). Определим проекции веса на оси координат, считая, что Oz направлена вертикально вверх:
X=O; Y = 0; Z = -G,
и, подставив их в (222′), получим под знаком интеграла полный дифференциал, а потому
или
A = G (z1—z2) = Gh. (223)э
Рис. 210
Следовательно, работа силы тяжести не зависит от вида траектории точек тела и равна произведению веса тела на разность начальной и конечной высот центра тяжести. Если тело опускается, то сила тяжести тела совершает положительную работу, а если поднимается, то отрицательную. Так, например, если человек поднял гирю весом 10 кГ на высоту одного метра (безразлично—по вертикали или по иной траектории), то работа силы тяжести равна —10 кГ∙ м, а работа человека на преодоление силы тяжести равна +10 кГ∙ м.
Элементарная работа силы, приложенной к телу, закрепленному на неподвижной оси, равна произведению момента силы относительно оси вращения на бесконечно малый угол поворота: dА = Mdφ
Работа силы, приложенной к вращающемуся телу
Пусть тело вращается (или может вращаться) вокруг неподвижной оси и к какой-либо точке К этого тела приложена сила F. Примем ось вращения тела за ось Oz прямоугольной системы координат. Элементарная работа силы выразится равенством
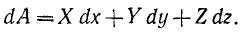
Припомним формулы Эйлера, связывающие проекции вращательной скорости точки К (х, у, z) с угловой скоростью и координатами этой точки:
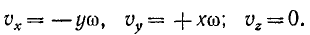
Умножая эти равенства на dt, найдем приращения координат точки приложения силы:
Подставим эти выражения dx, dy и dz в формулу (221)
Разность, стоящая в скобках, выражает момент данной силы относительно оси вращения Oz:
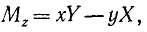
а следовательно, элементарная работа силы, приложенной к вращающемуся телу, равна произведению момента силы относительно оси вращения на дифференциал угла поворота:
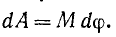
Если на тело действует несколько сил, то, составив такие равенства для определения работы каждой из них и просуммировав, найдем, что элементарная работа всех сил равна произведению главного момента сил относительно оси вращения на dφ.
Чтобы определить работу силы, действующей на тело при его повороте от φ1 до φ2, надо проинтегрировать уравнение (224) в этих пределах, выразив момент силы в функции угла поворота:
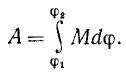
В частном случае постоянного момента силы
A = Mφ (226)
работа равна произведению момента силы на угол поворота тела.
Задача №1
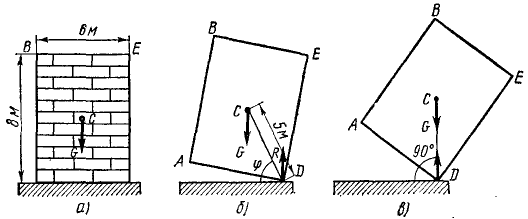
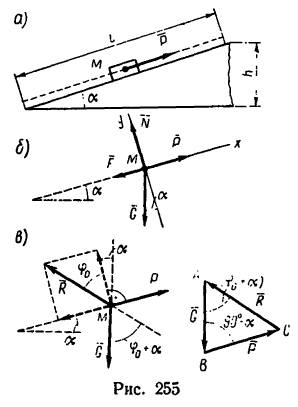
Однородный массив ABED, размеры которого указаны на чертеже (рис. 211, а), весит 4 Т. Определить работу, которую необходимо произвести, чтобы опрокинуть его вращением вокруг ребра D.
Рис. 211
Решение. 1-й способ. Рассматриваем опрокидывание массива. Какие силы действуют на массив? Их две: вес массива G=4 Т, приложенный в его центре тяжести С, и реакция фундамента. Во время опрокидывания реакция приложена в ребре D, вокруг которого происходит опрокидывание (рис. 211,6), как известно из статики). Но во время опрокидывания ребро D неподвижно, поэтому работа реакции равна нулю. Работу веса (силы тяжести) определим по (223). Для опрокидывания массива достаточно повернуть его до положения неустойчивого равновесия, изображенного на рис. 211, в, при котором центр тяжести находится в вертикальной плоскости, проходящей через ребро D; далее массив опрокинется сам. Имеем
Такова работа силы тяжести при опрокидывании массива. Чтобы опрокинуть массив, надо произвести работу, такую же по величине и обратную по знаку.
2-й способ. Несколько сложнее получится решение задачи, если мы воспользуемся формулой (225) о работе сил, приложенных к вращающемуся телу.
На поворачиваемый вокруг ребра D массив действуют вес и реакция в ребре D. Момент реакции относительно оси вращения равен нулю, следовательно, равна нулю и работа реакции. Момент веса — величина переменная — равен произведению силы 4 T на плечо CD cos φ, где φ (см. рис. 211, б) —угол, составляемый CD с горизонтальной плоскостью:
M = 20 cos φ.
Определим пределы интегрирования. При начале работы массив стоял вертикально, высота центра тяжести была 4 м и
Угол считаем отрицательным, так как отсчет производим по ходу часов:
φ0 = arcsin 0,8.
В конечном положении (см. рис. 211, в)
Подставляя в (225), получаем
Мы определили работу восстанавливающего момента, вызванного силой тяжести и стремящегося восстановить устойчивое равновесие массива. Работа на опрокидывание массива вращением вокруг ребра D равна ей по величине и противоположна по знаку.
Ответ. А = + 4 Тм.
Задача №2
Определить работу на преодоление силы земного притяжения при запуске на высоту 30 000 м ракеты массой m = 2000 кг, считая силу притяжения изменяющейся по закону всемирного тяготения. Радиус земного шара принять R = 6 370 000 м.
Решение. На ракету действует сила, направленная к центру Земли и равная
где k — постоянный коэффициент пропорциональности, M — масса Земли, 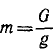
Обозначая kM через μ, имеем
При x=R ракета находится на поверхности Земли и F = mg,
откуда
Зная μ и k, можно определить массу Земли, потому что k = μ : M.
Работу переменной силы F на перемещение ракеты с поверхности Земли на высоту h= 30 000 м определим по (222):
Отрицательный знак показывает, что при подъеме ракеты сила тяготения ракеты к Земле направлена против движения. Чтобы преодолеть эту силу на заданном расстоянии, надо совершить работу, такую же по величине, но положительную по знаку.
Ответ. A = + 5 621 262 369 дж.
Задача №3
Доказать, что сумма работ внутренних сил абсолютно твердого тела при всяком перемещении тела равна нулю.
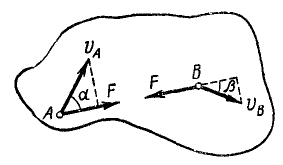
Решение. Рассмотрим две точки А и В твердого тела (рис. 212). Силы взаимодействия этих точек всегда равны между собой и направлены по прямой AB в противоположные стороны.
Проекции скоростей точек А и В на прямую AB всегда равны между собой:
Рис. 212
Поэтому при любом перемещении работы сил взаимодействия точек A и В равны по величине, но обратны по знаку, и сумма работ равна нулю
Доказательство проведено для двух точек абсолютно твердого тела, за которые мы можем принять любые точки тела, а потому оно относится ко всем точкам твердого тела. В случае упругого тела или изменяемой системы точек сумма работ внутренних сил не равна нулю. Так, например, при падении камня на Землю силы взаимодействия между камнем и Землей (внутренние силы системы Земля —камень) равны и противоположны, но сумма работ этих сил не равна нулю.
Ответ. Сумма работ всех внутренних сил в абсолютно твердом теле при всяком перемещении тела равна нулю.
Работа упругой силы равна половине произведения коэффициента жесткости на квадрат деформации:
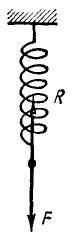
Работа упругой силы. Определим работу упругой силы F пружины при растяжении ее на λ см, если для растяжения этой пружины на 1 см необходима сила с кГ (рис. 213). Сначала определим работу, которую необходимо совершить для растяжения этой пружины на λ см.
Рис. 213
Согласно одному из основных законов теории упругости и сопротивления материалов, называемому законом Гука, растяжение нагруженного тела прямо пропорционально нагрузке:
F = сх,
де F — нагрузка, х—растяжение и с — коэффициент жесткости.
Подставляя это значение F в (221) и интегрируя в пределах от О до λ, найдем работу, необходимую для искомой деформации пружины:
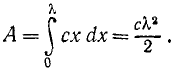
Если к пружине приложить силу, например растягивать пружину рукой, то со стороны пружины возникнет реакция, называемая упругой реакцией, или упругой силой, пружины. По принципу равенства действия и противодействия упругая сила равна и противоположна растягивающей силе F, а поэтому работа упругой силы определяется найденным значением. Знак работы упругой силы отрицателен, если сила упругости направлена против деформации, т. е. если деформация увеличивается, и положителен, если деформация уменьшается.
Задача №4
Применить графический метод для вывода формулы (227).
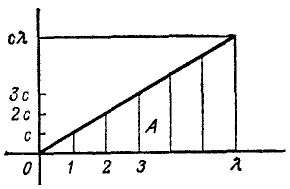
Решение. Будем откладывать (рис. 214) по оси абсцисс растяжение пружины, а по оси ординат—силу F, потребную для этого растяжения, затем построим по точкам кривую зависимости между силой и перемещением точки приложения силы. В нашем случае это кривая первого порядка, т. е. прямая линия.
Рис. 214
Первую точку поставим в начале координат, так как при отсутствии растягивающей силы растяжение пружины равно нулю. Чтобы растянуть пружину на 1 см, нужна сила с кГ, поэтому вторая точка кривой имеет координаты х=1, у =с Если сила с кГ будет продолжать действовать на пружину, то пружина будет оставаться растянутой на один сантиметр, но чтобы растянуть пружину еще на один сантиметр, надо увеличить силу еще на с кГ. Следовательно, координаты третьей точки x=2, y=2c и т. д. Для растяжения пружины на λ си нужна сила в cλ кГ. Точка x = λ, y = cλ лежит на прямой, соединяющей все нанесенные точки. Проведя ординату крайней точки, получим треугольник с основанием λ и высотой cλ.
Ответ. Работа выражается площадью этого треугольника, т. е.
Заметим, что работа упругой силы выражается полученным равенством не только в рассмотренном нами частном случае. Эта формула относится в равной мере ко всем случаям упругой деформации, в которых упругая реакция подчиняется закону Гука F = сх, где х—перемещение точки приложения реакции, отсчитанное от положения этой точки при недеформированном состоянии тела, ас — постоянный коэффициент. Сюда относятся растяжение и сжатие прямолинейного бруса, изгиб балки и т. п.
Величину, характеризующую быстроту приращения работы Силы и выражающуюся отношением элементарной работы к дифференциалу времени, называют мощностью силы:
Мощность силы
Одну и ту же работу можно произвести за различное время. Величину, характеризующую быстроту приращения работы, называют мощностью силы и обозначают буквой N. Разделив работу, произведенную силой, на время, в течение которого эта работа произведена, получим значение средней мощности силы:
B этом смысле говорят, хотя и несколько нечетко, что средняя мощность — это работа за единицу времени. При таком определении получается, что мощность является работой, или элементарной работой, чего не может быть, так как мощность имеет свою размерность. В физической системе единиц
Единицей мощности в СИ является мощность силы, производящей работу в один джоуль за одну секунду. Эту единицу называют ватт1 и обозначают вт. На практике часто употребляют единицу мощности киловатт (квт):
1 κвт= 1000вт =l02 кГ •м/сек.
В технической системе единиц
В технической системе в качестве единицы мощности силы обычно применяют кГм/сек. Употребляют также другую единицу мощности, называемую лошадиной силой:
1 л. с. = 75 кГ • м/сек = 736 вт.
Чем меньше промежуток времени, за который определена средняя мощность силы, тем ближе она соответствует мощности в данное мгновение, которую мы определим в пределе, если будем уменьшать промежуток времени, сохраняя начало этого промежутка:
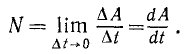
Таким образом, мощность силы выражают отношением элементарной работы к дифференциалу времени.
При некоторых частных выражениях работы мощность можно определить по другим формулам. Так, например, если сила направлена по скорости, то dA=Fds, и, подставляя в (228), найдем
N = F ∙υ, (229)
т. е. мощность можно выразить произведением силы на скорость. При езде на автомобиле по ровной хорошей дороге, где нужно получить большую скорость, но не надо преодолевать большие сопротивления, включают высшие передачи, а при подъеме или на плохой дороге, где нужно развить при полной мощности возможно большую силу тяги, хотя бы и за счет потери скорости, включают низшие передачи.
Если сила выражена в килограммах, скорость —в км/ч, а мощность надо выразить в л. с., то формула (229) принимает следующий вид:
При вращательном движении тела подставим вместо dA его выражение (224):
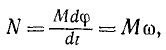
т. е. мощность выражается произведением вращающего момента и угловой скорости.
Задача №5
Тягач, развивая мощность 80 л. с., тянет по горизонтальной ледяной дороге со скоростью 15 км/ч сани с грузом 36 т. Определить коэффициент трения саней о дорогу.
Решение. За основные единицы примем: L — в км, F —в кГ, T — в ч.
На сани действуют следующие силы: 1) вес 36 000 кГ, направленный вертикально вниз, 2) реакция дороги, направленная вертикально вверх; 3) сила тяги тягача, направленная горизонтально вперед по ходу саней, и 4) сила трения полозьев о дорогу, направленная горизонтально назад.
Работа вертикальных сил при горизонтальном движении саней равна нулю, и эти силы нас не интересуют.
Сани движутся равномерно, откуда следует, что горизонтальные силы уравновешивают друг друга. Следовательно, сила тяги F уравновешена силой трения, равной, как известно, произведению коэффициента трения на нормальное давление (36 000 кГ). Подставляя эти данные, найдем
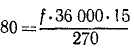
откуда
Решим теперь эту же задачу в СИ, т. е. примем L в м, M—в кг, T — в сек. Мощность силы, развиваемую тягачом, выразим в ваттах:
N = 80∙736 = 58 880 вт,
скорость —в метрах в секунду:
силу трения выразим в ньютонах:
и, пользуясь формулой (229), получим ответ.
Ответ.
Задача №6
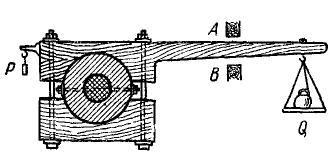
Определение мощности машины можно произвести следующим образом. На вал машины надевают чугунный шкив, который центрируют и закрепляют наглухо зинтами (рис. 215). На шкив надевают две связанные болтами деревянные подушки, одна из которых имеет плечо l с чашкой для грузов Q. Противовес P подбирают так, чтобы свободно надетый на шкив нажим находился в равновесии без гирь Q в горизонтальном положении, т. е. так, чтобы плечо проходило между двумя неподвижными балками А и В. Испытание начинают с того, что затягивают болты подушек до тех пор, пока машина не даст наперед заданное число оборотов n. Коромысло прижимается при этом к неподвижной балке А. Затем начинают накладывать на чашку гири до тех пор, пока плечо не отстанет от А и не займет горизонтальное положение между А и В.
Рис. 215
Определить мощность, если вес гирь известен и равен Q, длина плеча равна l а число оборотов в минуту n. Подобрать длину плеча так, чтобы мощность выражалась формулой N = Qn вт.
Решение. Центр тяжести подушек с противовесом P по условию задачи лежит на одной вертикали с осью шкива На шкив действуют вращающий момент и момент сил трения, сумма которых равна нулю, так как шкив вращается равномерно.
Чтобы определить момент сил трения, рассмотрим равновесие подушки и составим сумму моментов действующих на нее сил относительно оси вала:
Тогда, по (230),
Пусть вес выражен в кГ, а длина —в м, тогда для выражения мощности в вт надо эту величину разделить на 0,102 или умножить на 9,81:
Если l = 0,98 м, то N = Qn вт.
Ответ. N = 1,026 Qln вт. Если l = 0,98 м, то N = Qn вт.
Задача №7
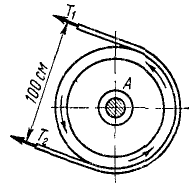
Посредством ремня (рис. 216) передается мощность 20 л. с. Радиус ременного шкива 50 см, число оборотов в минуту 150.
Предполагая, что натяжение T1 ведущей ветви вдвое больше натяжения T2 ведомой ветви, определить натяжение T1 и T2.
Рис. 216
Решение. Условие задачи дано в технической системе единиц, будем решать в СИ и выражать L — в .и, F — в н, Т —в сек.
Момент натяжения ремня, взятый относительно оси вращения шкива
Угловая скорость
Мощность 20 л. с. выразим в ваттах.
и по (230)
откуда
Натяжение ведущей ветви в два раза больше.
Ответ. T1 = 3750 н; T2= 1875 н. В задачнике И. В. Мещерского ответ дан в кГ, умножая число ньютонов на 0,102, выразим натяжение ремней в килограммах: T2 = 382 κΓ, T1= 191 кГ.
Теоремы об изменении кинетической энергии точки и системы
Изменение кинетической энергии материальной точки равно работе, приложенной к точке силы:
T-T0=A
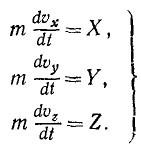
Умножим первое из этих уравнений на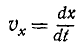
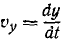
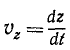
или
Сложим все три уравнения и заменим в левой части сумму дифференциалов дифференциалом суммы:
В числителе левой части имеем квадрат полной скорости (64), а правая часть выражает элементарную работу силы (221). Следовательно,
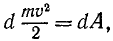
т. е. дифференциал кинетической энергии равен элементарной работе. Интегрируя равенство (231), получим
Постоянную интеграции определим из начальных данных. В начальное мгновение скорость точки υ = υ0, а работа равнялась нулю. Подставляя эти данные, получим
и окончательно
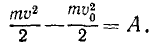
Равенство (232) словами можно прочитать так: изменение кинетической энергии материальной точки при перемещении этой точки на каком-либо участке пути равно работе силы, приложенной к точке, на том же участке пути. Уравнение (232) называют уравнением кинетической энергии.
Если на материальную точку действует несколько сил, то А означает работу равнодействующей приложенных к точке сил.
Уравнение (232) можно записать более коротко:
Т—Т0 = А. (232′)
Задача №8
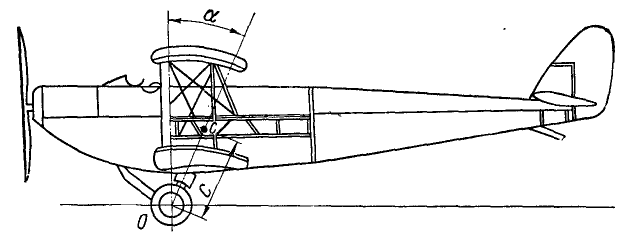
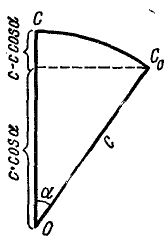
Самолет делает посадку с выключенным мотором на болотистую местность. Какую максимальную горизонтальную скорость v может иметь самолет, не рискуя капотировать (опрокинуться), если расстояние ОС центра тяжести от оси шасси равно с и угол наклона прямой СО с вертикалью в мгновение посадки равняется а (рис. 217).
Рис. 217
Решение. Опрокидывание самолета происходит от того, что при соприкосновении с Землей скорость шасси уменьшается, а корпус продолжает двигаться с постоянной скоростью. Для капота достаточно (и необходимо), чтобы центр тяжести, поднявшись, оказался на вертикали, проходящей через ось шасси.
Так как работа силы тяжести не зависит от траектории центра тяжести, а зависит лишь от его вертикального перемещения, то работа силы тяжести при опрокидывании (рис. 218)
Рис. 218
Вертикальная скорость самолета теряется при ударе о Землю, но горизонтальная сохраняется. Если при спуске самолета шасси остановится, то оставшаяся кинетическая энергия 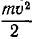
Решая это уравнение, находим ответ.
Ответ.
Задача №9
Пренебрегая сопротивлением атмосферы, определить, с какой наименьшей скоростью надо бросить материальную точку вертикально вверх, чтобы она не вернулась на Землю.
Решение. Сила, действующая на брошенную с Земли точку, пропорциональна массе точки и обратно пропорциональна квадрату расстояния точки от центра Земли:
Коэффициент пропорциональности был определен при решении задачи № 155:
Материальная точка, получив начальную скорость υ0, будет удаляться от Земли, при этом под действием силы F скорость ее будет уменьшаться, уменьшаться будет и сила F. Материальная точка не вернется на Землю, если в мгновение, когда скорость ее станет равной нулю, перестанет действовать и сила. Сила притяжения обратится в нуль при r = ∞.
Работу силы А при изменении r от R до ∞ выразим интегралом
Знак минус перед интегралом взят потому, что сила направлена в сторону, противоположную движению. Подставляем в (232):
откуда
Подставляя числовые данные, получим ответ.
Ответ. 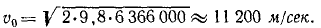
Задача №10
В автоматическом оружии отдача используется для выбрасывания пустой гильзы и вкладывания нового патрона. Это осуществляется посредством специального кожуха, сдерживаемого пружиной, который «принимает на себя» отдачу, отскакивает назад и под действием пружины возвращается обратно, производя упомянутые операции. Какова должна быть скорость пули, достаточная для того, чтобы работал автоматический пистолет, если вес пули 8 Г, вес кожуха 250 Г, расстояние, на которое отскакивает кожух, 3 см и сила, необходимая для сжатия пружины на 1 см, равна 4 кГ?
Решение. Путь кожуха 3 см. На этом пути начальная скорость кожуха υ0 уменьшается, достигая нуля. Механическое движение кожуха переходит в упругую энергию пружины. Следовательно, применима теорема об изменении кинетической энергии, пользуясь которой, определим начальную скорость кожуха, так как конечная скорость равна нулю:
Упругая сила пружины изменяется по закону Гука F = cx; подставляя вместо F и х их заданные значения, находим
Подставляя в (221) и интегрируя в пределах от 0 до 3, находим
Работа отрицательна, так как упругая сила пружины направлена против ее деформации и выражена в кГ. см. Выразив в тех же единицах кинетическую энергию кожуха, найдем его начальную скорость:
или
Итак, после выстрела кожух начал двигаться со скоростью 3,76 м/сек и, пройдя 3 см, остановился, затратив свое механическое движение на сжатие пружины.
После выстрела механическое движение получил не только кожух, но и пуля. Мы не будем больше рассматривать переход механического движения в упругую энергию пружины, а рассмотрим лишь механическое движение кожуха и пули.
Рассмотрим систему, состоящую из пистолета (с кожухом) и пули. Построим оси координат, проведя Ox вдоль дула пистолета. Проекция внешних сил на ось Ox равна нулю. Сила взрыва— внутренняя сила системы и, следовательно, центр масс системы не смещается по оси Ох, и сумма проекций количеств движения после выстрела, как и до выстрела, равна нулю:
откуда скорость пули
Знак минус показывает, что скорость пули направлена в сторону, противоположную скорости кожуха. Если скорость пули будет меньше, будет меньше и количество движения пули, а потому уменьшится и количество движения кожуха. Если же уменьшится количество движения кожуха, то уменьшится и его кинетическая энергия и ее будет недостаточно для совершения работы — сжатия пружины на 3 см, т. е. при меньшей начальной скорости пули пистолет не будет автоматически перезаряжаться. При большей скорости пули избыток кинетической энергии кожуха будет передаваться ударом на руку.
Ответ. υ=120 м/сек.
Изменение кинетической энергии материальной системы равно сумме работ внешних и внутренних сил системы: T-T0 = А
Теорема об изменении кинетической энергии материальной системы
Пусть механическая система состоит из п материальных точек. Разбив на две категории все силы, действующие на точки системы, напишем дифференциальные уравнения в форме (130):
где k = 1, 2, 3, …, n.
Рассмотрим отдельно какую-либо из точек системы и напишем для нее уравнение кинетической энергии. На эту точку действуют как внешние, так и внутренние силы, и в правой части уравнения кинетической энергии мы напишем сумму работ внешних и внутренних сил:
Составим такие же уравнения для всех точек и возьмем сумму:
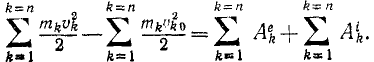
Припомним, что внутренние силы системы не вошли в уравнения проекций количеств движения системы (169) и в уравнения моментов системы (192). Однако они имеются в уравнении (233) кинетической энергии системы. Происходит это потому, что сумма проекций на любую ось и сумма моментов всех внутренних сил относительно любой оси всегда равны нулю, так как внутренние силы системы попарно равны и действуют по одной прямой в противоположные стороны. Но сумма работ внутренних сил системы в общем случае не равна нулю, как это было показано в задаче № 156.
Пусть, например, две точки системы отталкивают друг друга внутренними равными и противоположно направленными силами и под действием этих сил расстояние между точками увеличивается. Перемещения обеих точек направлены по силам, работы обеих сил положительны, и сумма работ этих сил не равна нулю. Внутренние силы системы можно рассматривать как силы взаимодействия точек, взятых по две. Поэтому сказанное о двух точках распространяется на все точки системы.
Силы взаимодействия между каждыми двумя частицами направлены в противоположные стороны по прямой, соединяющей эти частицы. Если расстояние между частицами не изменяется, то относительное перемещение этих частиц может быть только в направлении, перпендикулярном к этой прямой. Но силы, перпендикулярные к перемещениям, работы не совершают, а потому работа внутренних сил неизменяемой системы (абсолютно твердого тела) равна нулю.
Если система состоит из нескольких твердых тел, то работа внутренних сил каждого твердого тела равна нулю, но работы внутренних сил, действующих между каждыми двумя твердыми телами, принадлежащими к этой системе, в общем случае не равны нулю.
Задача №11
Цилиндрический вал диаметром 10 см и весом 0,5 T, на который насажено маховое колесо диаметром 2 м и весом 3 Т, вращается в данное мгновение с угловой скоростью 60 об/мин, а затем он предоставлен самому себе. Сколько оборотов еще сделает вал до остановки, если коэффициент трения в подшипниках равен 0,05? При решении задачи массу маховика считать равномерно распределенной по его ободу.
Решение. Примем следующие единицы измерения: L-в см, F — в Т, T — в сек.
Требуется определить количество оборотов вала до остановки. Механическое движение (вращение) вала с маховиком исчезает, переходит в другие виды движения. Для решения задачи применим теорему об изменении кинетической энергии (233′).
На вал с насаженным на него маховым колесом действуют силы: 1) вес всей системы, состоящий из веса махового колеса и веса вала, G = 3,5; 2) реакции в опорах; 3) сила трения в подшипниках, равная произведению веса на коэффициент трения; Fτp≈ 0,05-3,5.
Точка приложения первой из этих сил неподвижна, а потому работа первой из этих сил равна нулю.
Реакции перпендикулярны перемещениям, а потому работа реакции равна нулю.
Работу сил трения определим по (226) как работу силы, приложенной к вращающемуся телу. Момент силы трения относительно оси вращения равен произведению силы трения на плечо (на радиус вала):
Работа отрицательна, так как сила направлена против скорости, т. е. если вращение вала происходит против хода часовой стрелки (φ > 0), то Mтp < 0, а потому A = Mтp φ< 0; если же (φ < 0), то Mтp > 0, а потому А < 0:
Кинетическую энергию системы определим по (216) как кинетическую энергию вращающегося тела.
Момент инерции системы равен сумме момента инерции маховика и момента инерции вала. Хотя вес вала только в 6 раз меньше веса махового колеса, но момент инерции вала исчезающе мал по сравнению с моментом инерции махового колеса, так как момент инерции зависит не столько от массы тела, сколько от ее распределения. Действительно, если масса маховика равномерно распределена по ободу, то
Момент инерции цилиндрического вала определим как момент инерции цилиндра относительно его оси (см. задачу № 134):
Следовательно, момент инерции вала в 4800 раз меньше момента инерции маховика и при решении задачи моментом инерции вала можно пренебречь.
Определим начальную угловую скорость:
Конечная угловая скорость равна нулю.
Все полученные данные подставляем в (233′):
Из этого уравнения можно определить число оборотов вала до остановки. Так как φ выражен в радианах, а в каждом обороте 2π радиан, то, обозначая искомое число оборотов х, получим
φ = 2πx.
Подставляем φ в предыдущее уравнение и, решая, получаем ответ.
Ответ. Вал сделает до остановки 109,7 оборота.
Задача №12
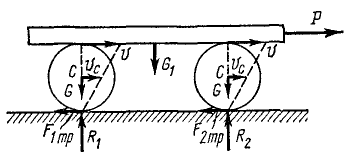
Доска весом G1 лежит на двух одинаковых цилиндрических катках весом G каждый, находящихся на горизонтальной плоскости. К доске приложена постоянная горизонтальная сила Р. При движении системы скольжение между катками и доской отсутствует. Определить ускорение доски, пренебрегая сопротивлением качению.
Решение. К механической системе, состоящей из доски и двух катков, применим теорему об изменении кинетической энергии в форме (233′):
Определим кинетическую энергию системы. При качении катка без скольжения его мгновенный центр скоростей находится в точке соприкосновения с неподвижной плоскостью. Кинетическую энергию каждого из цилиндрических катков определим по формуле (216′):
Кинетическую энергию доски, движущейся поступательно со скоростью о, равной скорости верхней точки обода каждого катка, определим по (214):
Величины скоростей точек фигуры пропорциональны расстояниям этих точек от мгновенного центра скоростей, следовательно,
υ = 2υc
Кинетическая энергия всей механической системы, т. е. двух цилиндрических катков и доски, равна
Аналогично
Определим работу внешних сил. Ha систему действует внешние силы (рис. 219); движущая сила Р, веса G1, G и G, нормальные реакции R1 и R2 неподвижной плоскости и силы трения скольжения F1 тр и F2 тр.
Рис. 219
Работа сил тяжести на горизонтальном перемещении их точек приложения равна нулю. Работа идеальных реакций и сил трения, приложенных в мгновенных центрах скоростей катков, равна нулю. Сумма работ всех внешних сил содержит только работу силы P на пути s, т. е.
Но в уравнение кинетической энергии системы входит также работа внутренних сил системы. Определим ее. Работа внутренних сил каждого из твердых тел всегда равна нулю. Работа внутренних сил взаимодействия между твердыми телами системы (между доской и каждым катком) в данном случае тоже
равна нулю, так как эти силы равны по модулю, противоположны по направлению и приложены к точкам, элементарные перемещения которых одинаковы, так как нет скольжения доски по каткам. Таким образом, имеем
Подставляя знамения Т, T0 и 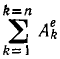
Продифференцировав это уравнение по времени, получим
Ответ.
Задача №13
Параллелепипед веса P1 (рис. 220) опирается на плоскость, наклоненную под углом а к плоскости горизонта; цилиндр веса P3 и радиуса R опирается образующей на плоскость, наклоненную под углом β. Оба тела соединены идеальной нитью, перекинутой через блок радиуса R и веса P2. Система выходит из состояния покоя. Определить скорость и параллелепипеда после того, как он переместится по плоскости на расстояние 3, если коэффициент трения его о плоскость равен f, а трением при качении цилиндра и вращении блока можно пренебречь. Массу блока считать равномерно распределенной по его поверхности.
Рис. 220
Решение. Рассмотрим движение системы, состоящей из параллелепипеда, цилиндра и блока. Для движения параллелепипеда вверх необходимо, чтобы
откуда
Для движения параллелепипеда вниз необходимо; чтобы
откуда
Если вес P1 параллелепипеда заключается в пределах
то система остается в равновесии. При прочих значениях P1 возникает движение системы. Для определения скорости определим кинетическую энергию системы.
В начальное мгновение кинетическая энергия системы равнялась нулю. Когда параллелепипед приобрел скорость у, то вследствие нерастяжимости нити такую же скорость получила и ось цилиндра. Кроме того, цилиндр получил угловую скорость 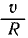
Кинетическая энергия T системы равна сумме кинетических энергий материальных тел, составляющих эту систему. Кинетическая энергия параллелепипеда
Кинетическая энергия блока
Кинетическая энергия цилиндра
Следовательно,
Работа сил при перемещении s параллелепипеда вверх по плоскости
Если же параллелепипед опустился на такое же расстояние, то
Приравнивая работу изменению кинетической энергии, получим ответ.
Ответ. Скорость параллелепипеда выражается равенствами: I) при подъеме:
2) при опускании:
Задача №14
Решить задачу применив теорему об изменении кинетической энергии.
Решение. Выразив все заданные величины в кГ, м и сек, вычислим конечную кинетическую энергию системы:
Начальная кинетическая энергия системы 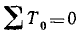
Вращающий момент приложен к первому валу. Когда второй вал сделает искомое число оборотов n2, первый вал повернется на 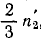
Подставляя эти данные в (233), имеем
Ответ. n2 = 2,344 оборота.
Потеря кинетической энергии при ударе
Потеря кинетической энергии системы, происходящая от ударов при встрече ее тел, равна кинетической энергии, соответствующей потерянным скоростям (Л. Карно):
Теорема Карно
Кинетическая энергия является мерой, характеризующей способность механического движения превращаться в эквивалентное количество других видов движения (теплота, электричество и т. и.). Удары тел всегда сопровождаются явлениями, требующими затраты энергии (нагревание тел, звук и пр.), поэтому удары, происходящие при встрече тел всякой механической системы, обязательно уменьшают кинетическую энергию системы.
Как было показано в § 45, мгновенный импульс при прямом центральном неупругом ударе двух тел может быть выражен любой из следующих формул:
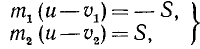
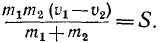
Кинетическую энергию системы двух тел до удара обозначим T0, а после удара Т. Изменение кинетической энергии
или
Если тела неупруги, то, принимая во внимание (174), получим
Подставив вместо S его значение (175), убедимся, что кинетическая энергия системы уменьшилась:
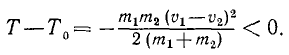
Если одно из тел, например второе, до удара было неподвижно (v2 = 0), то начальная кинетическая энергия системы равна кинетической энергии первого тела:
и
Следовательно, в этом случае потеря кинетической энергии зависит исключительно от отношения масс ударяющихся тел. При ковке металла переход кинетической энергии в тепловую целесообразен, а потому наковальня должна быть во много раз массивнее молота. Так, например, если молот в 99 раз легче наковальни, то T-T0=-0,99 T0, т. е. 99% энергии уходит главным образом на полезную работу (на ковку) и лишь 1% затрачивается на сотрясение наковальни. Напротив, при забивании свай надо сообщить свае возможно большую скорость, т. е. надо по возможности сохранить при ударе кинетическую энергию системы, а потому целесообразно ударять сваю массивной бабой. Так, например, если масса бабы в 99 раз больше массы сваи, то T-T0 = -0,01 T0 и 99 % энергии уходит на полезную работу (забивку сваи) и лишь 1 % теряется на звук, теплоту и пр.
Потерю кинетической энергии при ударе выразим более удобной формулой. Для этого возведем (175) в квадрат и потом разделим правую часть полученного равенства на левую:
Умножим теперь на полученное выражение (т. е. на единицу) равенство (234):
или в виду равенств (174)
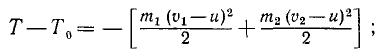
(υ1 — 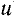
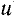
Аналогично можно показать, что в случае не вполне упругого удара потеря кинетической энергии равна 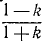
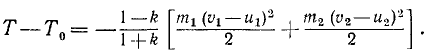
Если бы существовали абсолютно упругие тела (k = 1), то их соударение происходило бы без потери кинетической энергии, т. е. без нагревания, без звука и пр.
Задача №15
Определить потерю кинетической энергии при прямом центральном ударе двух тел, а также их скорости после удара, если ml = m2 = 2 кг, υ1 =4 м/сек, υ2 =0, k = 0,5.
Решение. Если бы удар был неупругим, то скорость тел после удара была бы по (176):
Учитывая коэффициент восстановления, скорости каждого из тел определим по (178):
Потерю кинетической энергии определим по (236′):
Напомним, что механическое движение имеет две меры: 1) количество движения, т. е. меру, характеризующую способность механического движения передаваться от одних материальных тел к другим в виде механического же движения, и 2) кинетическую энергию, характеризующую способность механического движения переходить в другие немеханические виды движения.
Поэтому кинетическая энергия системы теряется при ударе, переходит в теплоту, звук и пр. и 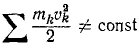
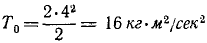
Потерянная системой двух тел кинетическая энергия 6 кгм2/сек2 перешла в другие немеханические виды движения.
Количество же движения системы лишь передалось от одного тела другому, но сохранилось в системе. В самом деле, K0 = 2∙4 = 8 κг∙м∕ceκ; K = 2∙1 + 2∙3 = 8 κг∙м∕ceκ, т. е. K-K0 = 0.
Ответ. T — T0 = 6 дж; 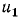
Коэффициент полезного действия
В этой главе рассмотрены задачи на определение работы, совершаемой постоянной силой, и развиваемой мощности при поступательном и вращательном движении тел.
Работа и мощность при поступательном движении
Работа постоянной силы Р на прямолинейном участке пути s, пройденном точкой приложения силы, определяется по формуле
где a — угол между направлением действия силы и направлением перемещения.
При a = 90°
т. e. работа силы, действующей перпендикулярно к направлению перемещения, равна нулю.
Если направление действия силы совпадает с направлением перемещения, то а = 0, поэтому cosa = cos O = 1 и формула (1) упрощается;
На точку или на тело обычно действует не одна сила, а несколько, поэтому при решении задач целесообразно использовать теорему о работе равнодействующей системы сил (Е. М. Н и к ит и и, § 89):
т. е. работа равнодействующей какой-либо системы сил на некотором пути равна алгебраической сумме работ всех сил этой системы на том же пути.
В частном случае, когда система сил уравновешена (тело движется равномерно и прямолинейно), равнодействующая системы сил равна нулю и, следовательно, 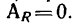
т. е. алгебраическая сумма работ уравновешенной системы сил на некотором пути равна нулю.
При этом силы, работа которых положительна, называются движущими, а силы, работа которых отрицательна, называются силами сопротивления. Например, при движении тела вниз—сила тяжести — движущая сила и ее работа положительны, а при движении тела вверх его сила тяжести является силой сопротивления и работа силы тяжести при этом отрицательна (§93, Е. М. Н и к и т и н).
При решении задач в случаях, когда неизвестна сила Р, работу которой нужно определить, можно рекомендовать два приема (метода).
1. При помощи сил, заданных в условии задачи, определить силу Р, а затем по формуле (1) или (1) вычислить ее работу.
2. Не определяя непосредственно силы Р, определить 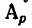
Мощность, развиваемая при работе постоянной силы, определяется по формуле
Если при определении работы силы Р скорость движения точки 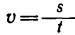
Если же скорость движения точки изменяется, 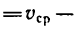
Коэффициент полезного действия (к. п. д.) при совершении работы можно определить как отношение работ
где 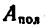
Единицей работы в СИ служит 1 джоуль (дж) =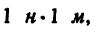
Так как единицей длины в обеих системах служит 1 м, а 1 кГ=9,81 н (или 1 н = 0,102 кГ), то
Единицей мощности в СИ служит 1 ватт
а в системе МКГСС—
При использовании системы МКГСС мощность обычно измеряют в лошадиных силах (л. с.), причем
При использовании СИ мощность измеряют в киловаттах (квт): 1 квт — 1,36 л. с.
Для перехода от одних единиц к другим следует пользоваться формулами
Задача №16
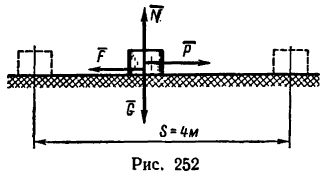
Какую работу производит человек, передвигая по горизонтальному полу на расстояние 4 м горизонтально направленным усилием ящик массой 50 кГ? Коэффициент трения f = 0,4.
Решение 1—методом определения движущей силы Р.
1. На ящик, поставленный на горизонтальный пол, действуют две силы: G и реакция пола N (рис. 252). Двигая ящик, че-
ловек прикладывает к нему силу Р, и тогда возникает сила трения F.
При равномерном передвижении ящика четыре силы образуют уравновешенную систему и поэтому, спроектировав их на горизонтальную и вертикальную оси, найдем, что
3. Работа, которую производит человек в данном случае, как видно, состоит в преодолении силы трения (P=F). Но так как
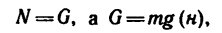
4. Если решить задачу в системе МКГСС, то
Легко убедиться, что оба ответа выражают одну и ту же работу:
Решение 2 —с применением теоремы о работе равнодействующей.
1. Как показано в первом решении, на ящик при его перемещении действуют четыре силы: сила тяжести G, реакция пола 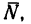
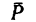
2. В этом уравнении работа силы тяжести Аа=0, так как сила G действует перпендикулярно к направлению перемещения; по этой же причине работа реакции N
Таким образом, искомая работа при перемещении ящика
3. Работу силы трения 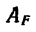
Подставим значение 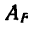
Так как F — Nf и N — G, то
AP=Fs — Nfs = Gfs=mgfs
Задача №17
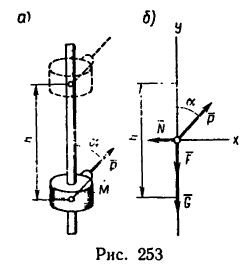
На тело М массой т—40 кг, могущее перемещаться вдоль вертикального направляющего бруска, действует некоторая сила Р, постоянно направленная под углом а =18° к вертикали. Под действием этой силы тело поднимается равномерно на высоту h = 4 м (рис. 253, а); коэффициент трения при скольжении тела вдоль направляющего бруса f=0,2. Определить произведенную работу и коэффициент полезного действия. Решение 1.
1. При равномерном перемещении вдоль бруска вверх на тело М действуют четыре силы: сила тяжести G, сила трения F, нормальная реакция N, равная давлению тела на брусок, и движущая сила Р (рис. 253. б).
2. Сила Р производит работу
Но чтобы определить ее, нужно сначала найти силу Р.
3. Расположив оси координат, как показано на рис. 253, б, выведем уравнения равновесия:
а также уравнение, выражающее основной закон трения:
Из уравнения (1)
поэтому уравнение (3) примет вид
Подставим полученное значение силы трения в уравнение (2):
4. Подставим в последнее выражение числовое значение силы тяжести G в единицах СИ (G=mg):
Тогда работа, произведенная силой,
5. Если подставить в уравнение (4) силу тяжести G, выраженную в технических единицах (G = 40 кГ), то
Работа этой силы в единицах МКГСС получит такое значение:
6. Определим коэффициент полезного действия:
Вся произведенная работа А = 1680 дж, а полезная работа состоит в том, что тело весом G — mg поднято на высоту h, т. е.
Умножив найденное значение 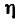
Примечание. Можно не определять отдельно числовое значение силы Р виде выражение работы для
(см. п. 4 и 5), а получить предварительно в общем данного случая:
и после деления числителя и знаменателя на cos а:
Но иногда в технических расчетах числовые значения девствующих сил необходимы для решения каких-либо других вопросов.
Если воспользоваться приведенным выше выражением работы, то выражение к. п. д. для данной задачи получит такой вид:
Таким образом, коэффициент полезного действия при передвижении тела М по вертикальному направляющему бруску зависит от коэффициента трения f и угла а, определяющего направление действия силы относительно вертикального бруска.
Если заменить
Решение 2.
1. В первом решении выяснено, что на тело М действует система четырех сил: G, F, N, Р (см. рис. 253, б).
2. Так как тело движется по бруску равномерно, система этих сил уравновешена и, следовательно, алгебраическая сумма их работ равна нулю:
3. Тело М движется вертикально вверх и поднимается на высоту h, поэтому работа силы N, направленной перпендикулярно к направлению перемещения:
работа силы тяжести G, направленной вертикально вниз,
работа силы трения F, также направленной вниз,
Известно, что F=Nf. Спроектировав на ось х (см. рис. 253,6) силы, приложенные к телу М, найдем, что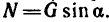
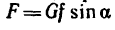
4. Подставим выражения работ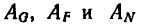
5. Вычислим работу в единицах СИ. Тогда
поэтому
Таким образом, вся работа, произведенная при подъеме тела М на высоту 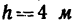
Задача №18
Какой мощности электродвигатель необходимо поставить на лебедку, чтобы она могла поднимать клеть со строительными материалами общей массой m=1200 кг на высоту 20 м за 30 сек. Коэффициент полезного действия лебедки
Решение (в единицах СИ).
1. Полезная мощность, развиваемая лебедкой при подъеме,
2. Мощность двигателя N найдем из выражения
3 Таким образом, мощность двигателя, необходимая для лебедки,
Двигатель должен иметь мощность не менее 10,9 квот.
Рекомендуется решить самостоятельно эту задачу в единицах МКГСС и найти мощность двигателя, выраженную в л. с.
Задача №19
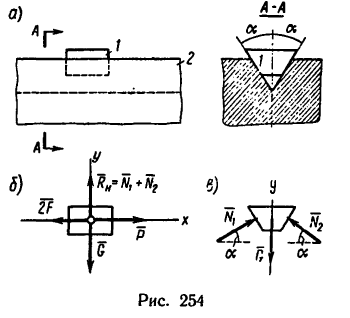
Какую работу необходимо произвести, чтобы равномерно передвинуть в горизонтальном направлении на расстояние ь клинчатый ползун 1 вдоль направляющих 2? Вес ползуна G, угол заострения ползуна и направляющих а (рис. 254, а), коэффициент трения между ползуном и направляющими f.
Решение.
1. На клинчатый ползун, когда он находится в горизонтально расположенных направляющих, действуют три силы: вес ползуна 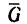
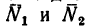
Для приведения ползуна в движение к нему нужно приложить параллельно направляющим силу 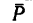
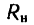
Таким образом, на ползун при его движении действуют всего шесть сил:
В данном случае нормальные реакции 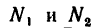
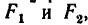
2. Работа при перемещении ползуна на расстояние s
но предварительно найдем числовое значение движущей силы Р.
3. Спроектировав приложенные к ползуну силы на ось х
(см. рис. 254, б), получим
Нормальную реакцию N найдем из уравнения проекций на ось у (см. рис. 254, в):
Подставляем найденное значение N в
4. Следовательно, работа при передвижении клинчатого ползуна на расстояние s
Например, при
Примечание. Входящая в формулу (б) величина 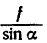
заострении ползуна и направляющих) коэффициент трения клинчатого ползуна резко увеличивается.
Решение задачи вторым способом с применением теоремы о работе равнодействующей силы рекомендуется выполнить самостоятельно.
Задача №20
Тело М весом G = 50 кГ равномерно перемещается вверх по наклонной плоскости, длина которой 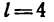
1. При движении тела М (примем его за материальную точку) вверх по наклонной плоскости на него действуют четыре силы: вес 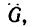
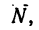
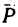
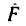
2. Работа силы Р при перемещении тела по длине наклонной плоскости
3. Найдем необходимую для перемещения тела М силу Р. Расположив оси координат, как показано на рис. 255, 6, составим два уравнения равновесия:
Дополним эти уравнения третьим уравнением, выражающим основной закон трения:
Из уравнения (1)
Вместо силы трения F подставим ее значение из уравнения (3):
а вместо нормальной реакции N подставим ее значение из уравнения (2):
4. Следовательно, работа силы P
После подстановки в это уравнение числовых значений
5. Находим к. п. д. наклонной плоскости:
Полезная работа состоит в подъеме тела весом G на высоту 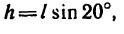
Решение 2.
1. Можно считать, что на тело М действуют не четыре, а три силы: G—вес тела, движущая сила 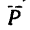
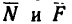
Реакция реальной связи R, как известно (§ 15-3), при движении отклоняется от нормали к поверхности связи на величину угла трения 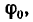
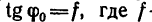
2. Так как на тело М действуют только три силы и они образуют уравновешенную систему (тело М, принятое за материальную точку, движется равномерно и прямолинейно), силовой треугольник АВС, построенный из этих сил, является замкнутым.
3. По рис. 255, в можно определить, что в силовом треугольнике AВС угол 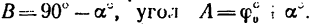
4. Применим к АВС теорему синусов’
5. Работа силы Р
Из равенства 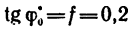
6. Находим к. п. д. наклонной плоскости:
Развернем знаменатель получившейся дроби:
Числитель и знаменатель разделим на произведение 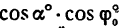
Подставив сюда значение угла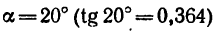
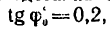
Примечания: I. Как видно, результаты обоих решений совпадают, хотя получившиеся формулы для силы Р внешне отличаются друг от друга.
Формулу для Р из первого решения легко преобразовать и привести к результату второго решения:
2. Выражение (I), полученное во втором решении, показывает, что к. п. д. наклонной плоскости зависит лишь от коэффициента трения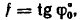
Решение 3.
1. Известно, что при действии на точку нескольких сил алгебраическая сумма работ всех сил на некотором пути равна работе равнодействующих этих сил.
2. В данном случае на тело М, которое примем за материальную точку, действуют четыре силы: вес 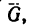
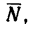
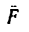
3. Точка М движется равномерно и прямолинейно. Равнодействующая сил, действующих на точку, равна нулю, и, следовательно, алгебраическая сумма работ, производимых силами 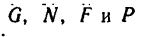
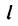
4. Находим отсюда работу силы Р:
где работа силы
работа силы 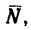
работа силы F
так как сила трения
Подставим в выражение (а) полученные значения работ:
Таким образом,
5. К п. д. наклонной плоскости найдем так же, как в п 5 первого решения.
Задача №21
Тело М весом G = 50 кГ равномерно перемещается вверх по наклонной плоскости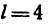
а=20 . Определить работу, произведенную силой, направленной параллельно основанию наклонной плоскости (рис. 256, а), также коэффициент полезного действия наклонной плоскости. Коэффициент трения f = 0,4.
Первое и третье решения задачи, аналогичные соответствующим решениям задачи 225-44, рекомендуется выполнить самостоятельно.
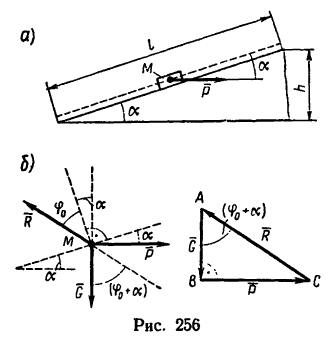
Решение. 2.
1. Приняв тело М за материальную точку, изобразим на рис. 256, б (слева) три действующие на нее силы: вес G, движущую силу Р и полную реакцию R наклонной плоскости, которая отклонена на угол 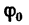
2. При равномерном движении тела по наклонной плоскости эти три силы образуют уравновешенную систему, и поэтому треугольник АВС, построенный из этих сил, является замкнутым (см. рис. 256, б — справа).
3. Силовой треугольник АВС получается в данном случае прямоугольным, так как вектор G перпендикулярен к вектору Р; угол 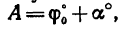
* Работа силы P в результате вычислений получается отрицательной, так как плоскость несамотормозящаяся (угол подъема 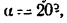
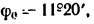
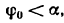
5. Подставим сюда числовые значения: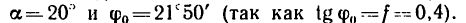
Как видно, по сравнению с задачей 225-44 работа получается несколько больше (на 24 кГм), потому что сила Р, действующая параллельно основанию наклонной плоскости, прижимает тело к наклонной плоскости, при этом увеличивается нормальное давление тела N, а вместе с ним и сила трения.
G. Определим коэффициент полезного действия. На основании изложенного, к. п. д. в данном случае уменьшится:
окончательно получаем формулу к. п. д. горизонтальном действии силы Р:
Подставим сюда значения углов:
По сравнению с к. п. д., полученным в задаче 225-44, к. п. д. наклонной плоскости в этой задаче уменьшается.
Следующую задачу рекомендуется решить самостоятельно.
Задача №22
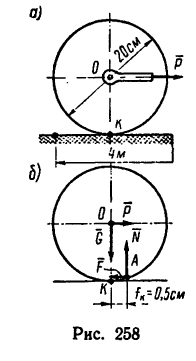
Определить работу, которую необходимо произвести, чтобы перекатить каток массой 50 кГ на расстояние 4 м по горизонтальной негладкой поверхности. Считать, что сила, двигающая каток, приложена к оси катка и горизонтальна (рис. 258, а).
Диаметр катка 20 см; коэффициент трения 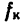
Решение.
1. Как известно из кинематики, движение катящегося катка называется плоскопараллельным и составляется из двух движений — поступательного и вращательного.
Ось катка передвигается поступательно, поэтому работу силы Р, приложенной к оси, можно определить по формуле
но предварительно нужно найти числовое значение силы Р.
2. На каток в неподвижном состоянии действуют две силы: вес катка G и реакция N горизонтальной поверхности, приложенная к катку в точке К (геометрическая точка касания катка с поверхностью). При качении на Каток действуют уже четыре силы (рис. 258, б): G — вес катка, Р -движущая сила и две составляющие N и F полной реакции поверхности, место приложения которой перемещается из точки К в точку А — вперед по ходу катка.
3. Если спроектировать все силы на вертикальную и горизонтальную оси, то N — G и Р = Р, т. е. на катящийся каток действуют две пары сил: катящая пара (Р; F) с плечом ОК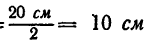
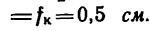
Отсюда находим силу Р, выразив силу тяжести в кГ (G — = 50 кГ)
4. Таким образом, работа, произведенная при перемещении катка,
Рекомендуется сопоставить этот результат с результатом, полученным в задаче 221-44. Следующую задачу решить самостоятельно.
Работа и мощность при вращательном движении
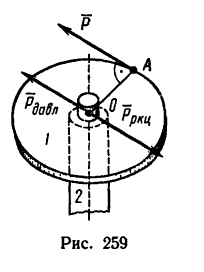
При вращательном движении тела движущим фактором является пара сил. Рассмотрим диск 1, могущий свободно вращаться вокруг оси 2 (рис. 259). Если к точке А на ободе диска приложить силу Р (направим ее вдоль касательной к боковой поверхности диска; направленная таким образом сила называется окружным усилием), то диск станет вращаться. Вращение диска обусловлено появлением пары сил. Сила Р, действуя на диск, прижимает его в точке О к оси (сила 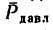
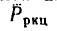
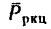
Как известно, вращающее действие пары сил измеряется ее моментом, но момент пары сил равен произведению модуля любой из сил на плечо пары, поэтому вращающий момент
Единицей момента пары сил, а также момента силы относительно точки или относительно оси является 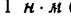
Работу при вращательном движении производят пары сил. Величина работы пары сил измеряется произведением момента пары (вращающего момента) на угол поворота, выраженный в радианах:
Таким образом, чтобы получить единицу работы, например, 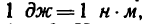
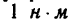
Мощность при вращательном движении
Если тело вращается с постоянной угловой скоростью, то, заменив в формуле (2) 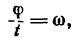
Мощность того или иного двигателя величина постоянная, поэтому
т. е. вращающий момент двигателя обратно пропорционален угловой скорости его вала.
Это означает, что использование мощности двигателя при различных угловых скоростях позволяет изменять создаваемый им вращающий момент. Используя мощность двигателя при малой угловой скорости, можно получить большой вращающий момент.
Так как угловая скорость вращающейся части двигателя (ротора электродвигателя, коленчатого вала двигателя внутреннего сгорания и т. п.) при его работе практически нс изменяется, то между двигателем и рабочей машиной устанавливается какой-либо механизм (редуктор, коробка скоростей и т. н.), могущий передавать мощность двигателя при различных угловых скоростях.
Поэтому формула (3), выражающая зависимость вращающего момента от передаваемой мощности и угловой скорости (Е. М. Н и-китнн, § 93), имеет очень важное значение.
Используя при решении задач эту зависимость, необходимо иметь в виду следующее. Формула (3) принимается для решения задач, если мощность N задана в ваттах, а угловая скорость—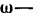
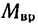
Соответственно, если мощность N подставлена в кет (киловаттах), то вращающий момент получится в к-нм (килоньютон-метрах).
Если передаваемая мощность выражена в л. с. (1 л. с. =
= 75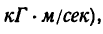
а вращающий момент нужно получить в кГм, то необходимо воспользоваться формулой
Если передаваемая мощность выражена в кет, угловая скорость — в об/мин, а вращающий момент нужно получить в кГ м, то необходимо воспользоваться формулой
Задача №23
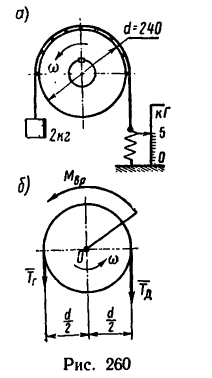
Для определения мощности электродвигателя через его шкив перекинута тормозная лента (рис. 260, а). Один конец ленты удерживается динамометром, а к другому концу прикрепленадвухкилограммовая гиря.
После запуска двигателя при установившейся угловой скорости n = 1850 об/мин динамометр показывает усилие 5 кГ. Определить мощность двигателя.
Решение 1—в единицах СИ.
1. Рассмотрим, какие силы действуют на шкив при установившемся равномерном вращении.
Шкив приводится во вращательное движение вращающим моментом 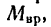
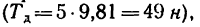
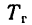
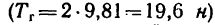
2. Определим вращающий момент двигателя.
Так как шкив вращается равномерно, то алгебраическая сумма моментов всех сил относительно оси вращения шкива равна нулю:
3. Переведя угловую скорость n =1850 об/мин в рид/сек:
из формулы (3) можно найти мощность двигателя!
Таким образом, мощность двигателя составляет 685 вт. Решение 2 —при помощи формулы (4).
1. На шкив действуют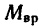
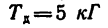
2. Определяем вращающий момент двигателя:
3. Теперь из формулы (4) определяем мощность двигателя:
Переведя получившуюся мощность из л. с. в вт, легко убедиться, что она такая же, как и в первом решении (0,930 л. с
Задачу можно решить еще при помощи формулы (5). Рекомендуется это решение выполнить самостоятельно.
Задача №24
Токарный станок приводится в движение электродвигателем, мощность которого N = 2,21 кет. Считая, что к резцу станка подводится лишь 0,8 мощности двигателя, определить вертикальную составляющую усилия резания, если диаметр обрабатываемой детали d = 200 мм, а шпиндель вращается со скоростью n=92 об/мин.
Решение — при помощи формулы (5).
1. Шпиндель станка с закрепленной в нем деталью вращается под действием вращающего момента, который уравновешивается моментом искомого вертикального усилия резания Р, т. е.
где d—200 лш = 0,2 м — диаметр обрабатываемой детали. Следовательно,
2. Мощность, подведенная к резцу, составляет 0,8 от всей мощности двигателя. Таким образом, к. п. д. передачи 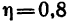
3. Подставим найденные значения 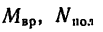
Тогда
Откуда
Решение задачи в единицах СИ рекомендуется выполнить самостоятельно.
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
- Основные законы динамики
- Колебания материальной точки
- Количество движения
- Момент количества движения
Механическая работа. Единицы работы.
В обыденной жизни под понятием «работа» мы понимаем всё.
В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа.
Рассмотрим примеры механической работы.
Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули при этом увеличивается.
Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.
Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.
Итак, механическая работа совершается, только когда на тело действует сила, и оно движется.
Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.
Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути.
Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:
работа = сила × путь
или
A = Fs,
где А — работа, F — сила и s — пройденный путь.
За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.
Единица работы — джоуль (Дж) названа в честь английского ученого Джоуля. Таким образом,
1 Дж = 1Н · м.
Используется также килоджоули (кДж) .
1 кДж = 1000 Дж.
Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.
Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.
Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.
A = -Fs.
Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:
A = 0.
В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.
Пример. Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м3 на высоту 20 м. Плотность гранита 2500 кг/м3.
Запишем условие задачи, и решим ее.
Дано:
V = 0,5 м3
ρ = 2500 кг/м3
h = 20 м
Решение:
A = Fs,
где F -сила, которую нужно приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, то есть F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, то есть путь равен высоте подъема.
Итак, m = 2500 кг/м3 · 0,5 м3 = 1250 кг.
F = 9,8 Н/кг · 1250 кг ≈ 12 250 Н.
A = 12 250 Н · 20 м = 245 000 Дж = 245 кДж.
А — ?
Ответ: А =245 кДж.
Рычаги. Мощность. Энергия
На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10-12 ч, трактор же с многолемешным плугом (лемех — часть плуга, подрезающая пласт земли снизу и передающая его на отвал; многолемешный — много лемехов), эту работу выполнит на 40-50 мин.
Ясно, что подъемный кран ту же работу совершает быстрее, чем рабочий, а трактор — быстрее чем лошадь. Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.
Мощность равна отношению работы ко времени, за которое она была совершена.
Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа.
мощность = работа/время.
или
N = A/t,
где N — мощность, A — работа, t — время выполненной работы.
Мощность — величина постоянная, когда за каждую секунду совершается одинаковая работа, в других случаях отношение A/t определяет среднюю мощность:
Nср = A/t .
За единицу мощности приняли такую мощность, при которой в 1 с совершается работа в Дж.
Эта единица называется ваттом (Вт) в честь еще одного английского ученого Уатта.
Итак,
1 ватт = 1 джоуль/ 1 секунда, или 1 Вт = 1 Дж/с .
Ватт (джоуль в секунду) — Вт (1 Дж/с).
В технике широко используется более крупные единицы мощности — киловатт (кВт), мегаватт (МВт) .
1 МВт = 1 000 000 Вт
1 кВт = 1000 Вт
1 мВт = 0,001 Вт
1 Вт = 0,000001 МВт
1 Вт = 0,001 кВт
1 Вт = 1000 мВт
Пример. Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 м3 в минуту.
Запишем условие задачи и решим ее.
Дано:
h = 25 м
V = 120 м3
ρ = 1000 кг/м3
t = 60 c
g = 9,8 м/с2
Решение:
Масса падающей воды: m = ρV,
m = 1000 кг/м3 · 120 м3 = 120 000 кг (12 · 104 кг).
Сила тяжести, действующая на воду:
F = gm,
F = 9.8 м/с2 · 120 000 кг ≈ 1 200 000 Н (12 · 105 Н)
Работа, совершаемая потоком в минуту:
A = Fh,
А — 1 200 000 Н · 25 м = 30 000 000 Дж (3 · 107 Дж).
Мощность потока: N = A/t,
N = 30 000 000 Дж / 60 с = 500 000 Вт = 0,5 МВт.
N — ?
Ответ: N = 0.5 МВт.
Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до сотен тысяч киловатт (водяные и паровые турбины).
Таблица 5.
Мощность некоторых двигателей, кВт.
| Вид транспортного средства | Мощность двигателя | Вид транспортного средства | Мощность двигателя |
|---|---|---|---|
| Автомобиль «Волга — 3102» | 70 | Ракета-носитель космического корабля | |
| Самолет Ан-2 | 740 | ||
| Дизель тепловоза ТЭ10Л | 2200 | «Восток» | 15 000 000 |
| Вертолет Ми — 8 | 2×1100 | «Энергия» | 125 000 000 |
На каждом двигателе имеется табличка (паспорт двигателя), на которой указаны некоторые данные о двигателе, в том числе и его мощность.
Мощность человека при нормальный условиях работы в среднем равна 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и еще бóльшую.
Зная мощность двигателя, можно рассчитать работу, совершаемую этим двигателем в течение какого-нибудь промежутка времени.
Из формулы N = A/t следует, что
A = Nt.
Чтобы вычислить работу, необходимо мощность умножить на время, в течение которого совершалась эта работа.
Пример. Двигатель комнатного вентилятора имеет мощность 35 Вт. Какую работу он совершает за 10 мин?
Запишем условие задачи и решим ее.
Дано:
N = 35 Вт
t = 10 мин
A = ?
Си 600 с.
Решение:
A = Nt,
A = 35 Вт * 600с = 21 000 Вт* с = 21 000 Дж = 21 кДж.
Ответ A = 21 кДж.
Простые механизмы.
С незапамятных времен человек использует для совершения механической работы различные приспособления.
Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно сдвинуть руками, можно сдвинуть с помощью достаточно длинной палки — рычага.
На данный момент считается, что с помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.
Во многих случаях, вместо того, чтобы поднимать тяжелый груз на некоторую высоту, его можно вкатывать или втаскивать на ту же высоту по наклонной плоскости или поднимать с помощью блоков.
Приспособления, служащие для преобразования силы, называются механизмами.
К простым механизмам относятся: рычаги и его разновидности — блок, ворот; наклонная плоскость и ее разновидности — клин, винт. В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить силу, действующую на тело, в несколько раз.
Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручивают и штампуют большие листы стали или вытягивают тончайшие нити, из которых делаются потом ткани. Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.
Рычаг. Равновесие сил на рычаге.
Рассмотрим самый простой и распространенный механизм — рычаг.
Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.
На рисунках показано, как рабочий для поднятия груза в качестве рычага, использует лом. В первом случае рабочий с силой F нажимает на конец лома B, во втором — приподнимает конец B.
Рабочему нужно преодолеть вес груза P — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О. Сила F, с которой рабочий действует на рычаг, меньше силы P, таким образом, рабочий получает выигрыш в силе. При помощи рычага можно поднять такой тяжелый груз, который своими силами поднять нельзя.
На рисунке изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В. На другом рисунке показана схема этого рычага. Обе силы F1 и F2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
- Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы. На рисунке показано, что ОА — плечо силы F1; ОВ — плечо силы F2 . Силы, действующие на рычаг могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F1 вращает рычаг по ходу часовой стрелки, а сила F2 вращает его против часовой стрелки.
Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы, зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу, или как направлена.
К рычагу (см рис.) по обе стороны от точки опоры подвешиваются различные грузы так, что каждый раз рычаг оставался в равновесии. Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н. При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.
На основании таких опытов было установлено условие (правило) равновесия рычага.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Это правило можно записать в виде формулы:
F1/F2 = l2/l1,
где F1 и F2— силы, действующие на рычаг, l1 и l2, — плечи этих сил (см. рис.).
Правило равновесия рычага было установлено Архимедом около 287—212 гг. до н. э. (но ведь в прошлом параграфе говорилось, что рычаги использовались египтянами? Или тут важную роль играет слово «установлено»?)
Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага бóльшую силу. Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.
Пример. С помощью рычага рабочий поднимает плиту массой 240 кг (см рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?
Запишем условие задачи, и решим ее.
Дано:
m = 240 кг
g =9,8 Н/кг
l1 = 2,4 м
l2 =0,6 м
Решение:
По правилу равновесия рычага F1/F2 = l2/l1, откуда F1 = F2 l2/l1, где F2 = Р — вес камня. Вес камня asd = gm, F = 9,8 Н · 240 кг ≈ 2400 Н
Тогда, F1 = 2400 Н · 0,6/2,4 = 600 Н.
F — ?
Ответ : F1 = 600 Н.
В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес камня (l1 : l2 = 2,4 м : 0,6 м = 4).
Применяя правило рычага, можно меньшей силой уравновесить бóльшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Момент силы.
Вам уже известно правило равновесия рычага:
F1 / F2 = l2 / l1,
Пользуясь свойством пропорции (произведение ее крайних членов, равно произведению ее средних членов), запишем его в таком виде:
F1l1 = F2l2 .
В левой части равенства стоит произведение силы F1 на ее плечо l1, а в правой — произведение силы F2 на ее плечо l2 .
Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы; он обозначается буквой М. Значит,
M = Fl.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов, можно записать в виде формулы:
М1 = М2
Действительно, в рассмотренном нами опыте, (§ 56) действующие силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 давления рычага, то есть моменты этих сил одинаковы при равновесии рычага.
Момент силы, как и всякая физическая величина, может быть измерена. За единицу момента силы принимается момент силы в 1 Н, плечо которой ровно 1 м.
Эта единица называется ньютон-метр (Н · м).
Момент силы характеризует действие силы, и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила. Гайку, лучше отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка вóрота, и т. д.
Рычаги в технике, быту и природе.
Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.
Выигрыш в силе мы имеем при работе с ножницами. Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.
Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.
Примеры применения рычагов — это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.
На принципе рычага основано действие и рычажных весов (рис.). Учебные весы, изображенные на рисунке 48 (с. 42), действуют как равноплечий рычаг. В десятичных весах плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.
Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.
Рычаги встречаются также в разных частях тела животных и человека. Это, например, руки, ноги, челюсти. Много рычагов можно найти в теле насекомых (прочитав книгу про насекомых и строение их тела), птиц, в строении растений.
Применение закона равновесия рычага к блоку.
Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускается веревка, трос или цепь.
Неподвижным блоком называется такой блок, ось которого закреплена, и при подъеме грузов не поднимается и не опускается (рис).
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис): ОА = ОВ = r. Такой блок не дает выигрыша в силе. (F1 = F2), но позволяет менять направление действие силы.
Подвижный блок — это блок. ось которого поднимается и опускается вместе с грузом (рис.). На рисунке показан соответствующий ему рычаг: О — точка опоры рычага, ОА — плечо силы Р и ОВ — плечо силы F. Так как плечо ОВ в 2 раза больше плеча ОА, то сила F в 2 раза меньше силы Р:
F = P/2 .
Таким образом, подвижный блок дает выигрыш в силе в 2 раза.
Это можно доказать и пользуясь понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р, а, значит, сама сила F в 2 раза меньше силы Р.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.). Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы. Например, позволяет поднимать груз, стоя на земле. Это пригождается многим людям или рабочим. Тем не менее, он даёт выигрыш в силе в 2 раза больше обычного!
Равенство работ при использовании простых механизмов. «Золотое правило» механики.
Рассмотренные нами простые механизмы применяются при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Естественно, возникает вопрос: давая выигрыш в силе или пути, не дают ли простые механизмы выигрыша в работе? Ответ на поставленный вопрос можно получить из опыта.
Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис.), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь s2 , а точка приложения большей силы F1 — меньший путь s1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
s1 / s2 = F2 / F1.
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.
Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:
F1 s1 = F2 s2, то есть А1 = А2.
Итак, при использовании рычага выигрыша в работе не получится.
Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Действуя же силой на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проигрываем в силе.
Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я переверну Землю!».
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали бы точку опоры (которая должна была бы быть вне Земли) и рычаг нужной длины.
Для подъема земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например, со скоростью 1 м/с, потребовались бы миллионы лет!
Не дает выигрыша в работе и неподвижный блок, в чем легко убедиться на опыте (см. рис.). Пути, проходимые точками приложения сил F и F, одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис.), переместить на высоту 2h.
Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок, на дает выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не дает выигрыш в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.
Уже древним ученым было известно правило, применимое ко всем механизмом: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.
Коэффициент полезного действия механизма.
Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. в этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной), равна полезной работе по подъему грузов или преодоления какого — либо сопротивления.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.
Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по определению силы трения в оси блока.
Какой мы механизм мы не взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Значит, обозначив полезную работу буквой Ап, полную(затраченную) работу буквой Аз, можно записать:
Ап < Аз или Ап / Аз < 1.
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД = Ап / Аз.
КПД обычно выражается в процентах и обозначается греческой буквой η, читается он как «эта»:
η = Ап / Аз · 100 %.
Пример: На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложена сила 250 Н. Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м. Найти КПД рычага.
Запишем условие задачи и решим ее.
Дано:
m = 240
g = 9,8 Н/кг
F = 250 Н
h1 = 0.08 м
h2 =0,04 м
Решение:
η = Ап / Аз · 100 %.
Полная (затраченная) работа Аз = Fh2.
Полезная работа Ап = Рh1
Р = gm.
Р = 9,8 · 100 кг ≈ 1000 Н.
Ап = 1000 Н · 0,08 = 80 Дж.
Аз = 250 Н · 0,4 м = 100 Дж.
η = 80 Дж/100 Дж · 100 % = 80 %.
η — ?
Ответ : η = 80 %.
Но «золотое правило» выполняется и в этом случае. Часть полезной работы — 20 % ее-расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.
КПД любого механизма всегда меньше 100 %. Конструируя механизмы, люди стремятся увеличить их КПД. Для этого уменьшаются трение в осях механизмов и их вес.
Энергия.
На заводах и фабриках, станки и машины приводятся в движения с помощью электродвигателей, которые расходуют при этом электрическую энергию (отсюда и название).
Автомобили и самолеты тепловозы и теплоходы, работают, расходуя энергию сгорающего топлива, гидротурбины — энергию падающей с высоты воды. Да и сами мы, чтобы жить, учиться и работать, возобновляем свой запас энергии при помощи пищи, которую мы едим.
Слово «энергия» употребляется нередко и в быту. Так, например, людей, которые могут быстро выполнять большую работу, мы называем энергичными, обладающими большой энергией. Что же такое энергия? Чтобы ответить на этот вопрос, рассмотрим примеры.
Сжатая пружина (рис), распрямляясь, совершить работу, поднять на высоту груз, или заставить двигаться тележку.
Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю).
Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа.
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, говорится, что они обладают энергией.
Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергия выражается в системе СИ в тех же единицах, что и работу, то есть в джоулях.
Чем большую работу может совершить тело, тем большей энергией оно обладает.
При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии.
Потенциальная и кинетическая энергия.
Потенциальной (от лат. потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.
Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия зависит от взаимного положения его и Земли. и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Еп, поскольку Е = А , а работа, как мы знаем, равна произведению силы на путь, то
А = Fh,
где F — сила тяжести.
Значит, и потенциальная энергия Еп равна:
Е = Fh, или Е = gmh,
где g — ускорение свободного падения, m — масса тела, h — высота, на которую поднято тело.
Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.
Потенциальную энергию молота копра (рис.) используют в строительстве для совершению работы по забиванию свай.
Открывая дверь с пружиной, совершается работа по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь.
Энергию сжатых и раскрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр.
Потенциальной энергией обладает всякое упругое деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д.
Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией.
Кинетическая энергия тела обозначается буквой Ек .
Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер.
От чего зависит кинетическая энергия? Обратимся к опыту (см. рис.). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он продвигает брусок, то есть совершает большую работу. Значит, кинетическая энергия тела зависит от его скорости.
За счет скорости большой кинетической энергией обладает летящая пуля.
Кинетическая энергия тела зависит и от его массы. Еще раз проделаем наш опыт, но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, то есть будет совершена бóльшая работа. Значит, и кинетическая энергия второго шарика, больше, чем первого.
Чем больше масса тела и скорость, с которой он движется, тем больше его кинетическая энергия.
Для того чтобы определить кинетическую энергию тела, применяется формула:
Ек = mv² /2,
где m — масса тела, v — скорость движения тела.
Кинетическую энергию тел используют в технике. Удерживаемая плотиной вода обладает, как было уже сказано, большой потенциальной энергией. При падении с плотины вода движется и имеет такую же большую кинетическую энергию. Она приводит в движение турбину, соединенную с генератором электрического тока. За счет кинетической энергии воды вырабатывается электрическая энергия.
Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций.
Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива.
Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией.
Мы познакомились с двумя видами механической энергии. Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики.
Превращение одного вида механической энергии в другой.
В природе, технике и быту можно часто наблюдать превращение одного вида механической энергии в другой: потенциальную в кинетическую и кинетическую в потенциальную. Например, при падении воды с плотины ее потенциальная энергия превращается в кинетическую. В качающемся маятнике периодически эти виды энергии переходят друг в друга.
Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображенном на рисунке. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.) Поднявшись вверх, диск снова падает, а затем снова поднимается. В этом опыте при движении диска вниз его потенциальная энергия превращается в кинетическую, а при движении вверх кинетическая превращается в потенциальную.
Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту.
Если поднять над стальной плитой стальной шарик (рис) и выпустить его из рук, он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик, примут свою первоначальную форму. Шарик отскочит от плиты, а их потенциальная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а значит, и его кинетическая энергия уменьшаются, потенциальная энергия увеличивается. отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся его кинетическая энергия вновь превратится в потенциальную.
Явления природы обычно сопровождается превращением одного вида энергии в другой.
Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы.
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Загрузить PDF
Загрузить PDF
В физике понятие «работа» имеет другое определение, чем то, которое используется в повседневной жизни. В частности, термин «работа» используется, когда физическая сила заставляет объект перемещаться. В общем, если мощная сила заставляет объект перемещаться очень далеко, то выполняется много работы. И если сила — небольшая или объект не перемещается очень далеко, — то только небольшая работа. Сила может быть рассчитана по формуле: Работа = F × D × косинус(θ), где F = сила (в Ньютонах), D = смещение (в метрах), и θ = угол между вектором силы и направлением движения.
-
1
Найдите направление вектора силы и направление движения. Чтобы начать, важно сначала определить в каком направлении движется объект, а также откуда применяется сила. Имейте в виду, что объекты не всегда движутся в соответствии с силой, приложенной к ним, — например, если вы потяните небольшую тележку за ручку, то вы применяете диагональную силу (если вы выше, чем тележка), чтобы переместить ее вперед. В этом разделе, однако, мы будем иметь дело с ситуациями, в которых сила (усилие) и перемещение объекта имеют одинаковое направление. Для получения информации о том, как найти работу, когда эти предметы не имеют одинакового направления, читайте ниже.
- Чтобы сделать этот процесс легким для понимания, давайте следовать примеру задачи. Скажем, игрушечный вагон тянется прямо вперед поездом перед ним. В этом случае вектор силы и направление движения поезда указывают на одинаковый путь — вперед. В следующих шагах мы будем использовать эту информацию, чтобы помочь найти работу, выполненную объектом.
-
2
Найдите смещение объекта. Первую переменную D или смещение, которая нам нужна для формулы работы, как правило, легко найти. Смещение — это просто расстояние, на которое сила заставила объект переместиться от его исходного положения. В учебных задачах эта информация, как правило, либо дана (известна), либо ее можно вывести (найти) из другой информации в задаче. В реальной жизни все, что вам нужно сделать, чтобы найти смещение, это измерить расстояние движения объектов.
- Обратите внимание, что единицы измерения расстояния должны быть в метрах в формуле для вычисления работы.
- В нашем примере игрушечного поезда, предположим, что находим работу, выполненную поездом, когда он проходит по трассе. Если он стартует в определенной точке и останавливается в месте около 2 метров по трассе, то мы можем использовать 2 метра для нашего значения «D» в формуле.
-
3
Найдите силу, применяющуюся к объекту. Далее найдите величину силы, которая используется для перемещения объекта. Это является мерой «прочности» силы — чем больше ее величина, тем сильнее она толкает объект и тем быстрее он ускоряет свой ход.[1]
Если величина силы не предусмотрена, ее можно вывести из массы и ускорения перемещения (при условии, что нет других конфликтующих сил, действующих на него) с помощью формулы F = M × A.[2]
- Обратите внимание, что единицы измерения силы должны быть в Ньютонах для вычисления формулы работы.
- В нашем примере, предположим, что не знаем величину силы. Тем не менее, давайте допустим, что знаем, что игрушечный поезд имеет массу 0,5 кг и что сила заставляет его ускоряться со скоростью 0,7 метров/секунду2. В этом случае можем найти величину путем умножения M × A = 0.5 × 0.7 = 0.35 Ньютон.
-
4
Умножьте Сила× Расстояние. После того, как узнаете величину силы, действующую на ваш объект, и расстояние, на которое он был перемещен, остальное будет сделать легко. Просто умножьте эти два значения друг на друга, чтобы получить значение работы.
- Пора решить наш пример задачи. При значении силы 0,35 Ньютон и значении смещения — 2 метра, наш ответ является вопросом простого умножения: 0.35 × 2 = 0.7 Джоулей.
- Вы, возможно, заметили, что в формуле, приведенной в введении, есть дополнительная часть к формуле: косинус (θ). Как обсуждалось выше, в этом примере сила и направление движения применяются в одном направлении. Это означает, что угол между ними равен 0o. Поскольку косинус (0) = 1, то мы не должны включать его — мы просто умножаем на 1.
-
5
Обозначьте ответ в Джоулях. В физике значения работы (и нескольких других величин) почти всегда даются в единице измерения, которая называется Джоуль. Один джоуль определяется как 1 Ньютон силы применяющейся на 1 метр, или другими словами, 1 Ньютон × метр.[3]
Это имеет смысл, — так как вы умножаете расстояние на силу, это логично, что ответ, который вы получите, будет иметь единицу измерения, равную умножению единицы величины вашей силы и расстояния.- Обратите внимание, что Джоуль также имеет альтернативное определение — 1 Ватт мощности, излучаемой за одну секунду.[4]
Читайте ниже о более детальном обсуждении мощности и ее соотношении к работе.
Реклама
- Обратите внимание, что Джоуль также имеет альтернативное определение — 1 Ватт мощности, излучаемой за одну секунду.[4]
-
1
Найдите силу и смещение, как обычно. Выше мы имели дело с задачей, в которой объект движется в том же направлении, что и сила, которая прилаживается к нему. На самом деле не всегда так бывает. В тех случаях, когда сила и движение объекта находятся в двух разных направлениях, разница между этими двумя направлениями также должна быть учтена в уравнении для получения точного результата. Для начала найдите величину силы и смещения объекта, как вы это обычно делаете.
- Давайте посмотрим на другой пример задачи. В этом случае, предположим, что мы тянем игрушечный поезд вперед, как в примере задачи выше, но, на этот раз мы на самом деле тянем вверх под диагональным углом. В следующем шаге будем принимать это во внимание, но сейчас будем придерживаться основ: перемещения поезда и величины силы, действующей на него. Для наших целей, скажем, сила имеет величину 10 Ньютон и что он проехал те же 2 метра вперед, как раньше.
-
2
Найдите угол между вектором силы и перемещением. В отличие от приведенных выше примеров с силой, которая находится в другом направлении, чем движение объекта, необходимо найти разницу между этими двумя направлениями в виде угла между ними. Если эта информация не предоставляется вам, то возможно, потребуется измерить угол самостоятельно или вывести его из другой информации в задаче.
- В нашем примере задачи, предположим, что сила, которая применяется, равна приблизительно 60o выше горизонтальной плоскости. Если поезд все еще движется прямо вперед (то есть, по горизонтали), то угол между вектором силы и движения поезда будет равен 60o.
-
3
Умножьте Force × Distance × Cosine(θ). После того, как узнаете смещение объекта, величину силы, действующей на него, и угол между вектором силы и его движением, решение почти такое же легкое, как и без того, чтобы принимать угол во внимание. Просто возьмите косинус угла (для этого может потребоваться научный калькулятор) и умножьте его на силу и перемещение, чтобы найти ответ на свою задачу в Джоулях.
- Решим пример нашей задачи. С помощью калькулятора находим, что косинус 60o равен 1/2. Включив это в формулу, можем решить задачу следующим образом: 10 Ньютонов × 2 метра × 1/2 = 10 Джоулей.
Реклама
-
1
Измените формулу, чтобы найти расстояние, силу или угол. Формула работы, указанная выше, является не просто полезной для нахождения работы — она также ценна для нахождения любых переменных в уравнении, когда вы уже знаете значение работы. В этих случаях просто выделите переменную, которую ищете, и решите уравнение в соответствии с основными правилами алгебры.
- Например, предположим, что мы знаем, что наш поезд тянут с силой в 20 Ньютон под диагональным углом более 5 метров пути для выполнения 86,6 Джоулей работы. Тем не менее, мы не знаем, угла вектора силы. Чтобы найти угол, мы просто выделим эту переменную и решим уравнение следующим образом:
-
- 86.6 = 20 × 5 × Косинус(θ)
- 86.6/100 = Косинус(θ)
- Arccos(0.866) = θ = 30o
-
- Например, предположим, что мы знаем, что наш поезд тянут с силой в 20 Ньютон под диагональным углом более 5 метров пути для выполнения 86,6 Джоулей работы. Тем не менее, мы не знаем, угла вектора силы. Чтобы найти угол, мы просто выделим эту переменную и решим уравнение следующим образом:
-
2
Разделите на время, проведенное в движении, чтобы найти мощность. В физике работа тесно связана с другим типом измерения под названием «мощность». Мощность — это просто способ определения количества скорости, с которой работа проводится в определенной системе в течение долгого периода времени. Таким образом, чтобы найти мощность, все, что вам нужно сделать, это разделить работу, используемую для перемещения объекта на время, которое требуется для завершения перемещения. Измерения мощности обозначаются в единицах — Вт (которые равны Джоуль/секунду).[5]
- Например, для примера задачи в указанном выше шаге, предположим, что перемещение поезда на 5 метров заняло 12 секунд. В этом случае, все, что нужно сделать, это разделить работу, выполненную для перемещения его на 5 метров (86,6 Дж), на 12 секунд, чтобы найти ответ для вычисления мощности: 86.6/12 = ‘7.22 Вт.
-
3
Используйте формулу TMEi + Wnc = TMEf, чтобы найти механическую энергию в системе. Работа также может быть использована, чтобы найти количество энергии, содержащееся в системе. В приведенной выше формуле TMEi = начальная полная механическая энергия в системе TMEf = окончательная полная механическая энергия в системе и Wnc = работа, выполненная в системах связи за счет не-консервативных сил.[6]
. В этой формуле, если сила применяется в направлении движения, то она — положительная, а если давит на (против) него, то она — отрицательная. Заметим, что обе переменные энергии можно найти по формуле (½)mv2, где m = масса и V = объем.- Например, для примера задачи в двух шагах выше, предположим, что поезд изначально имел общую механическую энергию 100 Дж. Поскольку сила в задаче тянет поезд в направлении, которое он уже проходил, она — положительная. В этом случае конечная энергия поезда — TMEi + Wnc = 100 + 86.6 = 186.6 Дж.
- Обратите внимание, что не-консервативные силы — это силы, чья мощность для воздействия на ускорение объекта зависит от пути, пройденного объектом. Трение является хорошим примером — объект, который толкнули по короткому, прямому пути, будет ощущать последствия трения в течение короткого времени, в то время как объект, который толкнули по длинному, извилистому пути к такому же конечному местонахождению, в целом будет ощущать больше трения.
Реклама
Советы
- Если вам удастся решить задачу, то улыбнитесь и порадуйтесь за себя!
- Тренируйтесь в решении как можно большего числа задач, это гарантирует полное понимание.
- Продолжайте практиковаться, и пробуйте снова, если вам не удастся в первый раз.
- Изучите следующие моменты, касающиеся работы:
- Работа, проделанная силой, может быть либо положительной, либо отрицательной. (В этом смысле термины «положительные или отрицательные» несут свой математический смысл, а обычное значение).
- Выполненная работа является отрицательной, когда сила действует в противоположном к перемещению направлении.
- Выполненная работа является положительной, когда сила действует в направлении перемещения.
Реклама
Об этой статье
Эту страницу просматривали 11 133 раза.
Была ли эта статья полезной?
Порядок выполнения работы.
В начале занятия студенты должны охарактеризовать общие правила конструирования систем единиц. Далее следует ознакомиться с основными и производными единицами системы СИ, с правилами написания обозначений единиц:
- — обозначения единиц ставят после их числовых значений и помещают в строку с ними;
- — в обозначениях единиц точку и знак сокращения не ставят;
— в буквенных обозначениях отношений единиц в качестве знака деления должна применятся только одна черта: косая или прямая. При применении косой черты обозначения единиц в числителе и знаменателе помещают в строку, произведение обозначений единиц в знаменателе заключают в скобки, например, Вт/(м2·К). Допускается вместо знака черты применять обозначения единиц в виде произведений единиц, возведённых в степени (); (Вт·м -2 К -1 ).
Затем студенты должны ознакомится с принципом образования наименьших кратных и дольных единиц.
В конце занятия следует выполнить ряд заданий, представленных преподавателем по применению теории размерностей, ответить на вопросы, касающиеся данной темы. Оформить отчёт.
Для проверки качества усвоения материала по теории размерностей рекомендуется выполнить следующие задания.
По определяющим уравнениям выразить размерности физических величин:
V = l/t dimV=diml/dimt=L/T=LT -1 м/с
a = V/t dim a=dimV/dimt=L/T 2 =LT -2 м/с 2
F = m·a dim F=dim m*dim a=ML*T 2 =MLT -2 H(кг*м/с 2 )
с = m·V dim p=dim m*dim V=ML*L 2 =ML -3 кг*м 3
P = F/S t dimP=dimF/dimS=MLT -2 /L 2 =ML -1 T -2 Па(Н/м 2 =кг*м -1 *с -2 )
A = F·l dim A=dim F*dim l=MLT -2 *L=ML 2 T -2 Дж(Н*м=кг*м 2 /с 2 )
P = A/t dimP=dimA/dimt=ML 2 T -2 /T=ML 2 T -3 Вт(Дж/с=кг*м 2 /с 3 )
По размерности физических величин определить основные формулы и обозначить единицы измерений:
L 2 T -1 =L 2 /T ?=?жидк/р м 2 /с
L 3 M -1 =L 3 /M d=P/V H/м 3
L -1 MT -1 =L -1 M/T n=рPT*? 4 /8lV Па*с
L 2 MT -2 I -2 =L 2 M/T -2 I -2 Gm=M0S/? Гн
удельное электрическое сопротивление
L 3 MT -2 I -2 = L 3 M/T -2 I -2 р=R*S/l Ом*м
Применение размерности для проверки правильности решения физических задач
Разделы: Физика
Цели:
- шире использовать полученные теоретические знания по физике;
- вооружить учащихся большим набором способов решения задач.
1. Понятие размерности
Для начала упорядочим некоторые понятия, с которыми мы имели дело раньше и с теми, которые встретятся нам в будущем. К таким физическим понятиям относятся: наименование, название физической величины, в выбранной системе единиц, размерность, обозначение и определяющее уравнение.
Разберём это на некоторых примерах взятых из раздела «Механика» и знакомых нам. Для краткости сведём всё это в таблицу.
Наименование
S
S = a 3
кв. метр
L 2
V
V = а 3
куб. метр
L 3
V
V = S/t
м/с; м с –1
метр в сек.
L T –1
а
а =
м/с 2 ; м с –2
метр в секунду
за секунду
L T –2
кг/м 3 ; кг м –3
кг на куб. метр
M L –3
| Название физ. величины | Обозначение | Определяющее уравнение | Размерность |
| Площадь | |||
| Объём | |||
| Скорость | |||
| Ускорение | |||
| Плотность |
Это простые и часто встречающиеся понятия, причём название физической величины вытекает из определяющего её уравнения. Но ряд физических величин имеют «клички». Название величины не следует прямо, как прежде, из определяющего уравнения.
Наименование величины – сила. Название единицы измерения – Ньютон. Вспомним материал 7-го класса. Что такое Ньютон? Это такая сила, которая за 1 секунду изменяет скорость тела массой 1 кг на 1 метр в секунду. Примером одной из сил является вес тела. Мы знаем, что вес тела равен Р = mg, где m – масса тела , а g – ускорение свободного падения.
Из физики 8-го класса мы знаем, что ускорение измеряется в м/с 2 . Значит, если речь идёт о весе тела Р, то он равен произведению массы тела на ускорение. Отсюда можно сделать вывод, что и любая другая сила F равна произведению массы тела на полученное в результате действия силы ускорение, т.е. F = ma.
Обратим внимание на то, что, если масса тела равна 1 кг и полученное ускорение равно 1 м/с 2 , то и сила будет равна единице силы, то есть 1-му Ньютону. Тогда размерность Ньютона будет
[ F ] = кг = кг м /с 2 = M L T –2 . Заметим, что определяющим уравнением будет уравнение F = ma. Обратите внимание, что название единицы силы не кг м/с 2 , а Ньютон – «кличка». Просто громоздкое наименование единицы заменили на «Ньютон» в честь знаменитого английского учёного Ньютона. Таких имён «кличек» которые носят единицы измерения физических величин много. В механике это Джоуль, Герц, Ватт.
Каждой такой единице присуща ей размерность, которая показывает, из каких основных единиц системы СИ «приготовлена», «сделана» такая единица, в какой степени входят в состав этой величины основные единицы и где они находятся в числителе или в знаменателе.
Что такое определяющее уравнение? Это уравнение, которое следует из определения физической величины.
1. Скорость – это физическая величина равная отношению пути, пройденного телом, ко времени за которое этот путь пройден. Отсюда следует определяющее уравнение V = S/t.
2. Работа – это физическая величина равная произведению силы, приложенной к телу на путь, который прошло тело под действием этой силы. Отсюда следует определяющее уравнение: A = F S.
До введения интернациональной системы единиц (СИ), существовал несколько систем единиц.
Так в одной из них основными единицами были: единица массы – грамм; единица длины – сантиметр; единица времени – секунда. Эта система единиц называлась СГС.
Были и другие системы единиц. Но масса есть масса в любой системе. Будь она в кг, или в г, или в мг. Поэтому, независимо от выбранной системы единиц, принято размерность выражать в символах. Масса – М. Длина – L. Время – Т.
В таблице выше соответствующая колонка называется просто размерность.
Задачи для самостоятельного решения.
1. Определить размерность Джоуля. Определяющее уравнение A = F S
2. Определить размерность Ватта. Определяющее уравнение N = A / t
3. Определить размерность Герца. Определяющее уравнение = 1 / Т
4. Определить размерность Паскаля. Определяющее уравнение р = F/S
5. Определить размерность момента силы. Определяющее уравнение М = F L.
2. Проверка правильности решения задач по размерности
«Видкиль воно взялось и на щоб воно сдалось» Украинская пословица.
Откуда взялась размерность мы рассмотрели. Рассмотрим где, и как она может быть применена и её особенности.
Рассмотрим решение нескольких задач:
1. Определить расстояние между Землёй и Солнцем, если луч света, двигаясь со скоростью 3 х 108 м/с, проходит это расстояние примерно за 8,5 минут?
2. Какое расстояние по прямой может пройти ракета за 1 минуту, двигаясь от места старта с ускорением 20 м/с 2 ?
3. Автомобиль, двигаясь со скоростью 54 км/ч, пошел на обгон и в течение 10 секунд двигался с ускорением 2 м/с 2 . Какой путь прошел автомобиль за это время?
4. Автомобиль, двигаясь со скоростью 54 км/ч, перед поворотом в течение 10 секунд двигался равнозамедленно с ускорением – 2 м/с 2 . Какой путь прошел автомобиль за это время?
Проанализируем решение этих задач.
1. Что общего было в этих задачах? (Определялся путь S)
2. В чём различие в этих задачах? (В каждой задаче описывается различное движение, а значит, применяются различные уравнения для определения пути)
То есть различие в том, что одна и та же величина (путь) определяется через различные величины. В № 1 через V и t. В № 2 через а и t. В № 3 и № 4 через Vо, a, t.
Эти величины имеют различные размерности, а в результате произведенных действий получается во всех случаях одна и та же размерность – метр.
Произведём, не используя модулей этих величин, предлагаемые действия только с размерностями.
1. S = V t = 2. S = . 3.4. S = V0t ± = ± =L±L= L
Отсюда следует закономерность: В правильно составленном уравнении, размерность правой его части равна размерности его левой части.
Эту закономерность можно применить для проверки правильности решения задач.
Допустим, задачу №3 решили с ошибкой (она очень часто встречается), записав
уравнение так S = Vо + at 2 /2 , тогда S = 15 + 2 х 10 2 /2 = 65 (м). Так как правильный ответ неизвестен, то неясно, как проверить правильность решения, и найти причину ошибки.
То ли ошибка в вычислениях, то ли в преобразованиях, то ли в неправильном написании правильно выбранного уравнения?
Проверяя правильность решения по наименованию можно найти причину ошибки.
Как это сделать? Вместо модулей величин подставить размерности величин и сравнить размерности левой и правой части уравнения. (использовать, указанную выше, закономерность )
Отсюда следует, L =/= 1 + Т. Задача решена неверно. Где ошибка? В правой части уравнение представляет двучлен. Одна его часть имеет размерность L, а другая L/T. Как из этого выражения L/T получить L? Нужно умножить его на Т. Тогда получим размерность первого члена L. Первый член и второй член правой части уравнения будут иметь размерность L, то есть L + L = L. Левая и правая части будут иметь одинаковую размерность. Значит, первый член правой части уравнения должен иметь вид не Vо, а Vо t.
Теперь, предположим, решающий допустил другую ошибку. В уравнении S = Vоt +at 2 /2 вместо знака «+» поставил знак «–». Поможет ли здесь метод размерности указать на ошибку? Решение задачи № 4 говорит о том, что задача решена правильно. L = L – L = L, но модуль величины другой.
Отсюда следует второй вывод: метод размерностей может подсказать ошибочность физического направления решения, но не может подсказать ошибочность математического действия.
Решим несколько задач по кинематике и сделаем проверку их правильности решения, применив метод размерности.
Задача № 1.
За время равное 2 с, тело, двигаясь прямолинейно и равноускоренно, прошло путь 20 м. Его скорость при этом увеличилась в 3 раза. Определить ускорение тела.
Сделаем проверку решения методом размерности.
Размерности левой и правой части уравнения совпадают, значит, задача решена правильно.
Задача №2.
Тело, двигаясь от остановки равноускоренно, за первые 5 секунд движения прошло путь 10 м. Какой путь пройдёт это тело за 10 секунд от начала движения?
Задача № 3. Тело, двигаясь равноускоренно, за 5 секунд движения прошло путь 100 м , а за 10 сек. – 300 м. Определить начальную скорость движения тела.
Мы проделали громоздкие преобразования. Не допустили ли мы ошибку? Воспользуемся знанием закономерности размерности и проверим свою работу.
L T–1 = Следовательно, задача решена верно.
Подставим числовое значение входящих величин и получим числовой ответ задачи.
V0 = (м/с)
Задача №4. Во сколько раз скорость пули при вылете её из ствола винтовки больше скорости этой пули при прохождении ею 1/3 ствола?
Работа определяется по уравнению A=F∙l где сила F = m ∙ a, m – масса, a – ускорение; l – длина перемещения. Рассчитайте размерность работы А: Готовое решение: Заказ №8095
Готовое решение: Заказ №8095
Тип работы: Задача
Статус: Выполнен (Зачтена преподавателем ВУЗа)
Предмет: Физика
Дата выполнения: 12.08.2020
Цена: 118 руб.
Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Работа определяется по уравнению
где сила F = m ∙ a, m – масса, a – ускорение; l – длина перемещения. Рассчитайте размерность работы А:
Решение:
Ускорение , где v- скорость, t — время
Я и моя команда оказывает помощь в учёбе по любым предметам и заданиям любой сложности.
Решение задач является неотъемлемой частью обучения в любом учебном заведении, и я смогу помочь в решение задач по любым предметам.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://urok.1sept.ru/articles/561983
http://natalibrilenova.ru/rabota-opredelyaetsya-po-uravneniyu-afl-gde-sila-f—m—a-m—massa-a—uskorenie-l—dlina-peremescheniya-rasschitajte-razmernost-rabotyi-a-gotovoe-reshenie-zakaz-8095/