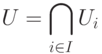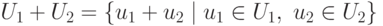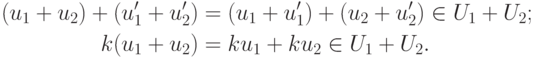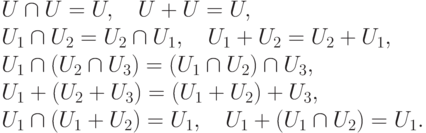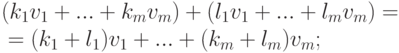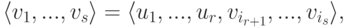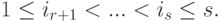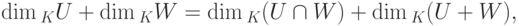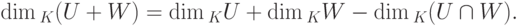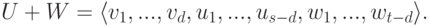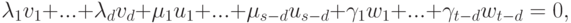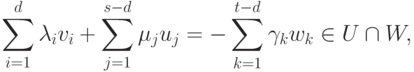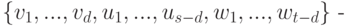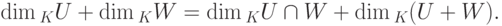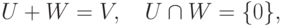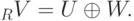Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Линейные оболочки и подпространства
Определение. Подпространством 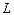
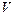
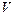

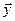
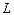
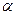
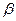
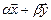
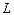
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 

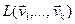
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 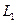



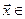
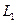
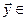

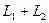
Утверждение. Сумма и пересечение подпространств 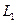

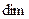
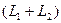
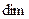
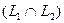

Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами 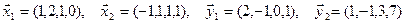
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 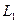
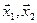
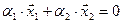
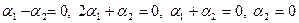
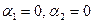
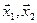
независимы и размерность подпространства 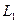
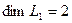

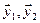
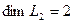
Вычислим теперь размерность пересечения подпространств 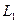


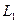
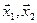
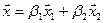

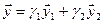
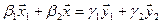
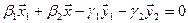

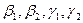
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим 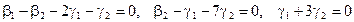
откуда 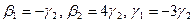
Полагая свободное неизвестное 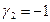
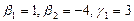
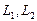
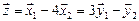
Размерность пересечения 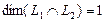
размерность суммы подпространств 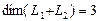
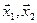
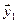
Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами 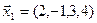
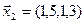

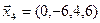
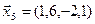
3.40. Найти размерность и какой-либо базис линейной оболочки векторов 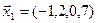
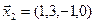
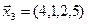
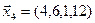
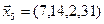
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 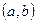
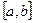
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве 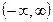
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а) 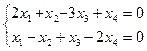
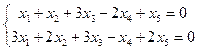
в) 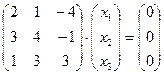
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению 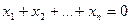
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами 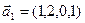
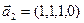
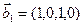
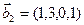
3.46. Найти размерность суммы и пересечения линейных оболочек векторов 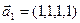
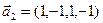
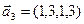

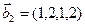
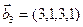
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
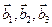
а) 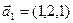
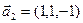
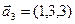
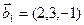
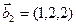
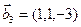
б) 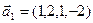
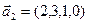
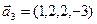
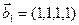
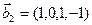
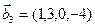
3.48. Найти базис суммы и пересечения линейных оболочек 
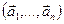

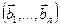
а) 
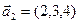
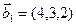
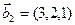
б) 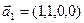
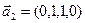
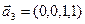
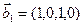
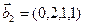
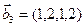
Является ли прямой сумма этих подпространств?
http://lektsii.org/10-6017.html
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Размерность суммы и пересечения линейных оболочек
|
|
07/04/15 |
Найти размерность суммы и пересечения линейных оболочек Если вектор Преобразуя методом Гаусса матрицу И получаем матрицу рангом 2, значит и размерность пересечения 2. Вроде все сошлось Правильно я вообще делаю?
|
|
|
|
|
Munin |
Re: Размерность суммы и пересечения линейных оболочек
|
||
30/01/06 |
Навскидку видно, что вы векторы с ошибками в матрицу переписали.
|
||
|
|
|||
|
ewert |
Re: Размерность суммы и пересечения линейных оболочек
|
||
11/05/08 |
Вообще искать размерность пересечения — занятие несколько противное. Зато легко и приятно ищется размерность суммы. И поскольку Вам всё равно она нужна — найдите сначала её, а потом размерности каждой оболочки по отдельности, отсюда и размерность пересечения получится.
|
||
|
|
|||
|
2old |
Re: Размерность суммы и пересечения линейных оболочек
|
|
07/04/15 |
Munin Вроде поправил. Наверное можно было вообще сразу без минусов переписать, оболочка осталось бы такой же, но я как-то не сообразил. ewert Я так себя проверял. Но там в следующем задании еще и базис просят все равно…
|
|
|
|
|
iifat |
Re: Размерность суммы и пересечения линейных оболочек
|
||
16/02/13 |
|||
|
|
|||
|
svv |
Re: Размерность суммы и пересечения линейных оболочек
|
||
23/07/08 |
2old По поводу первого сообщения. Нормальный метод, только матрицу (Я считал, что у Вас
|
||
|
|
|||
|
ex-math |
Re: Размерность суммы и пересечения линейных оболочек
|
||
24/02/12 |
Если Вы умеете записывать Ваши линейные оболочки в виде систем линейных уравнений (что само по себе полезно), то пересечение тоже найдется легко и приятно.
|
||
|
|
|||
|
2old |
Re: Размерность суммы и пересечения линейных оболочек
|
|
07/04/15 |
iifat Спасибо! svv Ура) Если без фальшивых, то слишком много придется гауссить ex-math Надо научиться. Ссылка iffat вроде тоже как раз об этом.
|
|
|
|
|
Brukvalub |
Re: Размерность суммы и пересечения линейных оболочек
|
||
01/03/06 |
Все эти «фокусы-покусы» давно разобраны по косточкам в учебной литературе:
|
||
|
|
|||
|
svv |
Re: Размерность суммы и пересечения линейных оболочек
|
||
23/07/08 |
то слишком много придется гауссить К сведению: и Кряквин (стр. 112 книги «Линейная алгебра. Пособие к решению задач…»), и Шевцов (стр. 150 книги «Линейная алгебра») ссылаются на одну и ту же задачу 1319 из книги Проскурякова «Сборник задач по линейной алгебре», в которой для нахождения базиса пересечения подпространств применяется метод, близкий к Вашему. Об этом алгоритме Кряквин пишет, что Цитата: По вычислительной сложности он приблизительно такой же, как и используемый здесь. («Используемый здесь» — это через объединение однородных систем уравнений.)
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Нахождение дополнения, суммы и пересечения подпространств
Нахождение алгебраического дополнения подпространства
Для заданного подпространства требуется найти алгебраическое дополнение подпространства
, т.е. такое подпространство
, что
.
В зависимости от способа описания подпространства , используем одно из следующих двух утверждений.
1. Если подпространство задано как линейная оболочка
столбцов матрицы
, то множество решений однородной системы
является его алгебраическим дополнением
, т.е.
(8.16)
2. Если подпространство задано как множество решений однородной системы
уравнений с
неизвестными, то линейная оболочка столбцов
транспонированной матрицы
является его алгебраическим дополнением
, т.е.
(8.17)
где — i-й столбец матрицы
.
Разумеется, в (8.16) и (8.17) указано одно из возможных алгебраических дополнений подпространства (см. свойство 3 алгебраических дополнений подпространств).
Докажем сначала справедливость (8.16) в одномерном случае , а потом в общем. Пусть
— одномерное подпространство
,
— ненулевой столбец. Найдем алгебраическое дополнение подпространства
. Рассмотрим уравнение
в координатной форме:
. Множество
решений однородной системы, состоящей из одного уравнения, образует подпространство
размерности
. Найдем пересечение
. Подставляя элемент
линейной оболочки
в уравнение
, получаем
, что возможно только при
, так как
. Следовательно, элемент
из
принадлежит подпространству
только тогда, когда
— нулевой столбец, т.е.
. Учитывая, что
, заключаем, что
— алгебраическое дополнение подпространства
в
.Таким образом,
(8.18)
Учитывая (8.18), докажем (8.16) в общем случае . Представим
в виде суммы
, где
. Из (8.15) следует, что
. Согласно (8.18), множество
решений однородной системы, состоящей из одного уравнения, дополняет
до всего пространства
. Пересечение множеств решений отдельных уравнений дает, разумеется, множество
решений системы этих уравнений. Поэтому
, что и требовалось доказать. Утверждение (8.17) доказывается аналогично, используя (8.18).
Пример 8.10. Найти алгебраическое дополнение подпространства в пространстве
многочленов не более, чем 3-й степени.
Решение. Сначала нужно переформулировать задачу для арифметического пространства (см. следствие теоремы 8.3 об изоморфизме конечномерных пространств). Для этого возьмем в стандартный базис
. Пространство
изоморфно
. Найдем координаты многочленов
и
в стандартном базисе. Раскладывая
по базису, получаем:
т.е. многочлену соответствует координатный столбец
— элемент пространства
. Аналогично получаем координатный столбец
для многочлена
.
Таким образом, исходная задача сводится к следующей: требуется найти алгебраическое дополнение подпространства в пространстве
. Используя правило (8.16), получаем, что
— это множество решений системы
, где
, т.е. системы
Решаем ее методом Гаусса. Приводим матрицу системы к упрощенному виду, прибавляя ко второй строке первую, умноженную на (-1), поделив вторую строку на 5, а затем прибавив ее, умноженную на 2, к первой:
Базисные переменные , свободные —
. Выражаем базисные переменные через свободные:
. Находим фундаментальную систему решений. Подставляя стандартные наборы свободных переменных (
и
), получаем решения:
, которые образуют фундаментальную систему решений и являются базисом алгебраического дополнения
Полученный результат переносим в пространство многочленов. По координатному столбцу
находим многочлен
Аналогично получаем . Искомое алгебраическое дополнение имеет вид
Проверим равенство . Для этого приравняем между собой линейные комбинации многочленов
и
Преобразовывая, получаем
Чтобы это равенство выполнялось тождественно, все его коэффициенты должны быть равны нулю:
Ранг матрицы этой системы равен 4 (находится, например, методом Гаусса). Поэтому однородная система имеет только нулевое решение
. Таким образом, равенство
выполняется.
Нахождение алгебраической суммы подпространств
Для заданных подпространств и
пространства
требуется найти размерность и базис их алгебраической суммы
. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы линейными оболочками своих образующих (внутреннее описание): и
. Тогда, приписывая к образующим
одного подпространства образующие
другого подпространства, получаем образующие суммы подпространств
и
(8.19)
поскольку любой вектор имеет вид
. Базис суммы
можно найти как максимальную подсистему линейно независимых столбцов.
Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): и
. Тогда, переходя к внутреннему описанию, сводим задачу к предыдущему случаю, а именно нужно выполнить следующие действия:
1) для каждой однородной системы и
найти фундаментальные системы решений
и
соответственно. При этом получим
и
, где
;
2) по правилу (8.19) найти сумму .
Пример 8.11. Найти размерность и базис алгебраической суммы подпространств
, если подпространство
задано системой уравнений
подпространство — линейной оболочкой своих образующих:
Решение. Образующие подпространства были найдены в примере 8.9:
, где
. По правилу (8.19) получаем
. Найдем базис этого подпространства как максимальную линейно независимую подсистему столбцов. Составляем из этих столбцов матрицу и приводим ее методом Гаусса к ступенчатому виду:
Первый, второй и четвертый столбцы полученной матрицы линейно независимы. Значит, соответствующие столбцы исходной матрицы так же линейно независимы (так как выполнялись элементарные преобразования только над строками). Поэтому они являются базисом
и
.
Нахождение пересечения подпространств
Для заданных подпространств и
пространства
требуется найти размерность и базис их пересечения
. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): и
. Тогда, приписывая к системе
, задающей одно подпространство, систему
, задающую другое подпространство, получаем систему
определяющую пересечение подпространств:
(8.20)
Базисом пересечения служит ее фундаментальная система решений.
Пусть подпространства и
пространства
заданы линейными оболочками своих образующих (внутреннее описание):
и
. Переходя от внутреннего описания подпространств к внешнему, можно свести задачу к предыдущему случаю. Однако удобнее сделать иначе. Пересечению
принадлежат только такие
, которые можно представить как равные между собой линейные комбинации столбцов
и столбцов
соответственно:
(8.21)
Представим второе равенство в (8.21) в матричном виде , где
— матрицы, составленные из данных столбцов,
— столбцы коэффициентов линейных комбинаций. Равенство
можно рассматривать как одно родную систему
уравнений с
неизвестными
и
. Каждому решению этой системы соответствует вектор
, при надлежащий пересечению
. Однако, на практике удобнее вместо системы
рассматривать однородную систему
, решения которой обладают теми же свойствами (тогда вектор
при надлежит пересечению
.
Поэтому для нахождения пересечения подпространств и
и базиса пересечения нужно выполнить следующие действия.
1. Составить блочную матрицу коэффициентов однородной системы уравнений
, где матрицы
образованы из заданных столбцов.
2. Для однородной системы с матрицей найти фундаментальную матрицу
. Матрица
имеет размеры
, где
.
3. Из первых строк матрицы
составить матрицу
. Столбцы матрицы
содержат искомые коэффициенты
линейных комбинаций (8.21).
4. Записать пересечение как линейную оболочку столбцов матрицы
.
5. Найти базис пересечения как максимальную линейно независимую подсистему образующих .
Пример 8.12. Найти размерности и базисы суммы и пересечения
подпространств
, если они заданы линейными оболочками своих образующих:
, где
Решение. Найдем базис и размерность суммы . Составим из данных столбцов блочную матрицу
Элементарными преобразованиями над строками приведем ее к ступенчатому виду:
По ступенчатому виду определяем, что первый, второй и четвертый столбцы линейно независимы. Следовательно, из 6 образующих
подпространства
максимальную линейно независимую подсистему составляют столбцы
(в этих столбцах расположен базисный минор матрицы). Следовательно, эти столбцы служат базисом суммы:
и
. По ступенчатому виду матрицы
можно также определить размерности подпространств. В блоке
две ненулевых строки, следовательно,
. Ненулевые строки блока В’ линейно независимы, следовательно,
.
Найдем базис и размерность пересечения .
1. Первый пункт алгоритма выполнен выше: матрица однородной системы
приведена к ступенчатому виду
.
2. Находим фундаментальную систему решений (используя алгоритм, описанный в разд. 5.5). Приводим матрицу системы к упрощенному виду:
Базисные переменные: ; остальные переменные — свободные. Выражаем базисные переменные через свободные:
. Придавая свободным переменным наборы значений
получаем линейно независимые решения
т.е. фундаментальная матрица имеет вид
3. Из первых трех строк матрицы
составляем матрицу
.
4. Вычисляем произведение
Столбцы этой матрицы являются образующими пересечения , где
— нулевой столбец,
.
5. Найдем базис пересечения . Для этого матрицу
приводим к ступенчатому виду
По ступенчатому виду определяем, что последние два столбца матрицы линейно независимы. Следовательно, два столбца
являются базисом пересечения
и
.
Проверим размерность пересечения подпространств, которую вычислим, используя формулу (8.13):
что совпадает с найденной ранее размерностью.
Пример 8.13. Найти размерности и базисы пересечения и суммы
подпространств
, если они заданы однородными системами уравнений:
Решение. Обозначим матрицы данных систем через и
соответственно. По правилу (8.20) пересечение
описывается однородной системой
Найдем базис пересечения — фундаментальную систему решений этой однородной системы уравнений. Составляем матрицу системы
и приводим ее к ступенчатому виду, а затем к упрощенному виду:
Базисные переменные: , свободная переменная —
. Выражаем базисные переменные через свободную:
. Фундаментальная система содержит одно решение
, которое получаем, задавая
. Следовательно,
и
.
Найдем теперь сумму . Фундаментальная система решений однородной системы
была найдена в примере 8.9. Следовательно,
, где
.
Найдем фундаментальную систему решений однородной системы . Для этого приводим матрицу системы к ступенчатому виду, а затем к упрощенному:
Базисные переменные: , свободные переменные:
. Выражаем базисные переменные через свободные:
. Фундаментальная система состоит из двух решений
, которые находим, придавая свободным переменным стандартные наборы значений (
и
). Следователь но,
и
.
По правилу (8.19) находим сумму . Чтобы определить базис, составим из столбцов
матрицу и приведем ее к ступенчатому виду:
Первые три столбца линейно независимы. Следовательно, и
.
Проверим размерность суммы подпространств. По формуле (8.13) получаем
что совпадает с найденной ранее размерностью.
Нахождение относительных алгебраических дополнений подпространств
Пусть дана цепочка подпространств . Требуется найти относительное дополнение
подпространства
до подпространства
.
Рассмотрим случай внешнего описания подпространств — как множеств решений однородных систем уравнений: и
. Согласно (8.17) базис пространства
образуют линейно независимые столбцы транспонированной матрицы
. Тогда относительное дополнение
составляют такие векторы
, которые удовлетворяют системе
. Если обозначить через
фундаментальную матрицу системы
, то линейно независимые столбцы матрицы
являются максимальной системой векторов подпространства
, линейно независимой над
, т.е. базисом относительного дополнения.
На практике нахождение базиса удобнее производить, используя ступенчатые виды матриц
и
, согласно следующей методике.
1. Привести матрицы и
при помощи элементарных преобразований строк к ступенчатому виду и удалить нулевые строки. В результате по лучим матрицы
и
модифицированного ступенчатого вида (строки каждой из этих матриц линейно независимые).
2. Найти фундаментальную матрицу однородной системы уравнений
.
3. Вычислить матрицу . Ее столбцы образуют искомый базис
.
Рассмотрим случай внутреннего описания подпространства как линейной оболочки своих образующих:
. Согласно (8.16) множество решений системы уравнений
(матрица
составлена из образующих) является алгебраическим дополнением
. Тогда множество решений системы
является относительным дополнением
, а ее фундаментальная система решений — базисом относительного дополнения.
Замечание 8.10. Способы описания подпространств комплексного линейного пространства, а также методы решения типовых задач аналогичны рассмотренным. В отличие от вещественного арифметического пространства вместо операции транспонирования матрицы в комплексном арифметическом пространстве
нужно использовать операцию сопряжения матрицы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Проверить,
являются ли заданные множества линейными
подпространствами; указать какой-нибудь
базис и размерность линейных
подпространств:-
Множество
всех геометрических векторов из V3,
компланарных фиксированной плоскости. -
Множество
геометрических векторов из V3,
удовлетворяющих условию (͞х ,͞а)=0, где͞
а-фиксированный вектор. -
Множество
всех геометрических векторов из V3,
удовлетворяющих условию |
̅х̅ |
=1. -
Множество
всех векторов из Rn
вида: ̅х=(0, х2,
0, х4,
х5,…хn) -
Множество
всех симметрических матриц порядка
n. -
Множество
решений линейной однородной системы
уравнений
-
x1+2x2
–
x3+x4
—
3x5=0
x2
–4
x3+x5=0
-
Множество
всех векторов из Rn,
координаты которых удовлетворяют
условию: х1=хn. -
Найти
размерность линейной оболочки L(x̅1,
x̅2)
арифметических векторов x̅1(1,
0, 2, -1), x̅2(0,
-1, 2, 0). Показать, что вектор x̅(1,
-1, 4, -1) принадлежит оболочке. -
Найти
размерность и какой-нибудь базис
линейной оболочки заданной системы
векторов x̅1(1,
0, 0, -1), x̅2(2,
1, 1, 0), x̅3(1,
1, 1, 1), x̅4(1,
2, 3, 4), x̅5(0,
1, 2, 3). -
Найти
размерность и какой-нибудь базис
линейной оболочки заданной системы
векторов x̅1(1,
1, 1, 1, 0), x̅2(1,
1, -1, -1, -1), x̅3(2,
2, 0, 0, -1), x̅4(1,
1, 5, 5, 2), x̅5(1,
-1, -1, 0, 0). -
Найти
размерность суммы и пересечения линейных
оболочек L(x̅1,
x̅2)
и L(y̅1,
y̅2):
x̅1(1,
2, 1, 0), x̅2(-1,
1, 1, 1);
y̅1(2,
-1, 0, 1), y̅2(1,
-1, 3, 7)
-
Найти
размерность суммы и пересечения линейных
оболочек L(x̅1,
x̅2,
x̅3)
и L(y̅1,
y̅2):
x̅1
(1,
2, -1, -2), x̅2
(3,
1, 1, 1), x̅3
(-1,
0, 1, -1);
y̅1
(2,
5, -6, -5), y̅2
(-1,
2, -7, -3)
-
Написать
уравнение геометрического образа
линейной оболочки
L(а̄)
и многообразия L(а̄)
+b̅,
если а̄= -2i̅
+ j̅
— k̅,
b̅=
2i̅
— j̅.
-
Написать
уравнение геометрического образа
линейной оболочки
L(а̄1,
a̅2)
и многообразия L(а̄1,
a̅2)
+ b̅,
если а̄1=
-i̅
+ j̅
+ k̅,
а̄2=2
j̅
— k̅
b̅=
i̅
+ k̅.
-
Задана
система уравнений
x1+
x2
–
3x3
—
x4
+ x5=1
3x1—
x2
+
x3
+
4x4
+ 3x5=4
x1—
5x2
—
9x3
—
8x4
+ x5=0.
Доказать,
что множество решений этой системы есть
линейное многообразие в пространстве
R5.Сдвигом
какого подпространства получается это
линейное многообразие? Найти ранг и
какой-нибудь базис этого подпространства.
Найти какой-нибудь вектор сдвига.
Ответы
к разделу 2
-
1.2.
является, dimL=1,
1.3.не является, 1.4. является, dimL=n-2,
1.5. является, dimL=n2
—
Cn2,
1.6. является, dimL=3,
1.7.является, dimL=n-1 -
dimL=2.
-
dimL=2
-
dimL=3.
-
Размерность
пересечения равна 1, базисный вектор
имеет координаты z̅
(5, -2, -3, -4); размерность суммы равна 3,
базис составлен, например, из векторов
z̅,
x̅1,
y̅1. -
Сумма
совпадает с первым пространством,
пересечение – со вторым. -
Линейная
оболочка – прямая, проходящая через
точку (0, 0, 0) параллельно вектору с
координатами (-2, 1, -1), линейное многообразие
— прямая, проходящая через точку (2,-1, 0)
параллельно вектору с координатами
(-2, 1, -1) -
Линейная
оболочка – плоскость -3x
– y
— 2z
=0, линейное многообразие – плоскость
-3x
– y
— 2z
+ 5=0. -
Множество
решений неоднородной системы есть
линейное многообразие, полученное из
подпространства размерности 3 решений
соответствующей однородной системы
сдвигом на произвольное частное решение
неоднородной системы. -
Доказать,
что пространство Rn
есть прямая сумма двух линейных
подпространств: L1,
заданного уравнением х1+х2+…+хn=0
и L2,
заданного системой уравнений х1=х2=…=хn. -
Пусть
линейное пространство L
является прямой суммой линейных
подпространств L1
и L2.
Доказать, что размерность L
равна сумме размерностей подпространств
L1
и L2,
причем любые базисы L1
и L2
дают вместе базис L. -
Доказать,
что сумма L
линейных подпространств L1
и L2
тогда и только тогда будет прямой
суммой, когда хотя бы один вектор x̅,
принадлежащий L,
представляется в виде x̅=
x̅1+
x̅2,
где x̅1
принадлежит L1,
x̅2
принадлежит L2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: В данной лекции рассматриваются линейные подпространства линейных пространств, приведены определения их суммы и их пересечения, рассмотрено понятие линейной оболочки элементов линейного пространства. Приведены доказательства основных теорем и задачи для самостоятельного рассмотрения
Линейные подпространства линейных пространств
Пусть K — поле, K V — линейное пространство над полем K. Непустое подмножество 
-
для всех
;
-
для всех
,
.
Ясно, что K U — линейное пространство относительно тех же операций сложения элементов и умножения на элементы из поля K, что и в линейном пространстве K V.
Если U — линейное подпространство в конечномерном линейном пространстве KV, 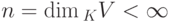

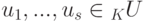


Если K U — линейное подпространство линейного пространства K V, 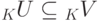


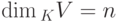
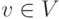
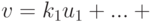
Пересечение линейных подпространств
Лемма 9.11.1. Пересечение
любого семейства линейных подпространств 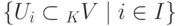
Доказательство. Если 
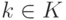


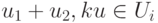


Следствие 9.11.2. Если U1 и U2 — линейные подпространства линейного пространства K V, то 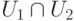
Сумма линейных подпространств
Если U1 и U2 — линейные подпространства линейного пространства K V, то сумма линейных подпространств
также является линейным подпространством. Действительно, если 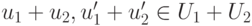
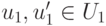
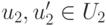
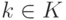
Замечание 9.12.1. U1+U2 — наименьшее линейное подпространство среди линейных подпространств, содержащих одновременно U1 и U2. Более того,
Замечание 9.12.2. Если U, U1, U2, U3 — линейные подпространства в K V, то
Линейная оболочка элементов линейного пространства
Пусть K V — линейное пространство, 
совокупность всех линейных комбинаций k1v1+…+kmvm элементов v1,…,vm с коэффициентами 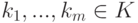
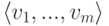
k(k1v1+…+kmvm)=(kk1)v1+…+(kkm)vm; если U — линейное подпространство в K V, 
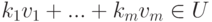

Замечание 9.13.1. Если 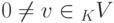
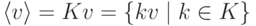
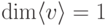
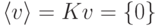
Замечание 9.13.2. 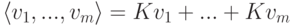
Замечание 9.13.3. 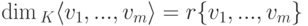
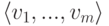
Основная лемма о линейной зависимости может быть сформулирована в следующей эквивалентной форме.
Теорема 9.13.4 (о замене). Пусть 

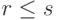
где
Доказательство. Так как 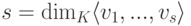
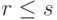

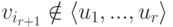
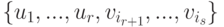
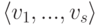
Следствие 9.13.5. Пусть U, W — линейные подпространства в K V и 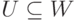
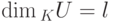

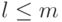
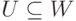
Теорема 9.13.6 (формула размерности). Пусть U, W — линейные подпространства в K V, 
или, что эквивалентно,
Доказательство. Пусть 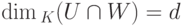
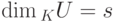

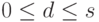

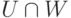
Если
то
поэтому 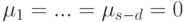
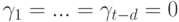

базис линейного подпространства U+W, откуда s+t = d+(s-d)+d+(t-d)=d+(d+(s-d)+(t-d)),
поэтому
Теорема 9.13.7 (о существовании прямого дополнения подпространства). Пусть 
(называемое прямым дополнением подпространства U в K V ; в этом случае также говорят, что линейное пространство K V является прямой суммой линейных подпространств U и W, обозначение: 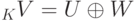
Доказательство. Если 
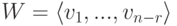
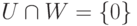
Замечание 9.13.8. Конечно, прямое дополнение определено неоднозначно, однако все прямые дополнения линейного пространства изоморфны (а именно, все они имеют размерность 
Замечание 9.13.9. Если 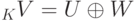
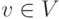
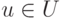
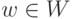
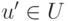
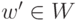

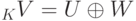


Пример 9.13.10 (прямого разложения). Пусть
Тогда
Действительно, 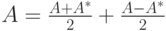


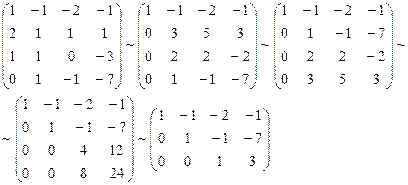
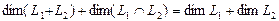



 лежит в пересечении подпространств, то его можно представить ввиде:
лежит в пересечении подпространств, то его можно представить ввиде:  и тогда
и тогда 

 и
и  .
. ) вырожденная, то биекции не будет, значит нужно умножать её на матрицу из базисных векторов ядра усеченных до
) вырожденная, то биекции не будет, значит нужно умножать её на матрицу из базисных векторов ядра усеченных до  и смотреть.
и смотреть.
 надо составлять из базисных векторов
надо составлять из базисных векторов  . (Тем более, что в таких заданиях обычно требуется сначала найти эти базисы.) Тогда «фальшивых» решений, вроде
. (Тем более, что в таких заданиях обычно требуется сначала найти эти базисы.) Тогда «фальшивых» решений, вроде  , все
, все  , не будет.
, не будет. — коэффициенты, а
— коэффициенты, а  — векторы, если всё наоборот, то, соответственно).
— векторы, если всё наоборот, то, соответственно). Я лучше поперемножаю, у меня строчки путаются из-за зрения очень медленный процесс выходит))
Я лучше поперемножаю, у меня строчки путаются из-за зрения очень медленный процесс выходит))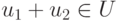 для всех
для всех 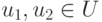 ;
; для всех
для всех