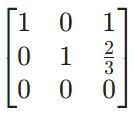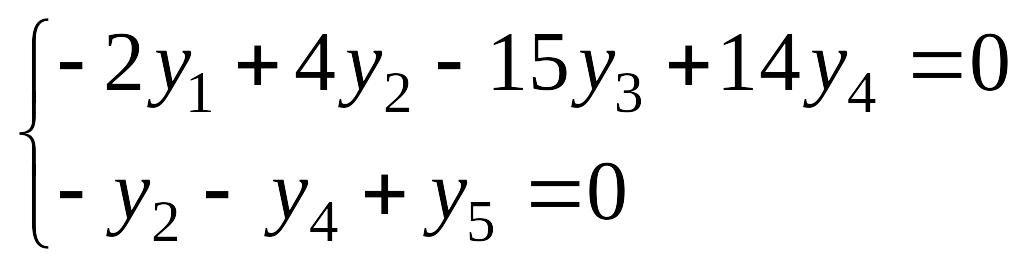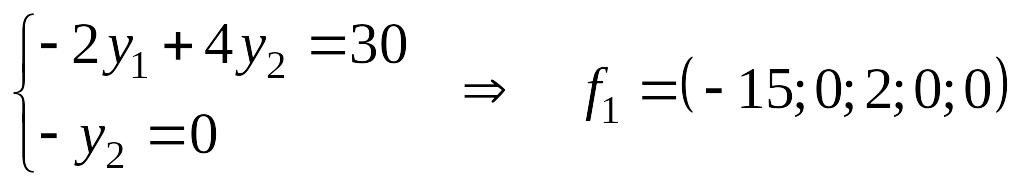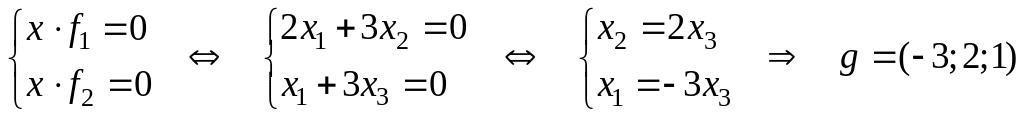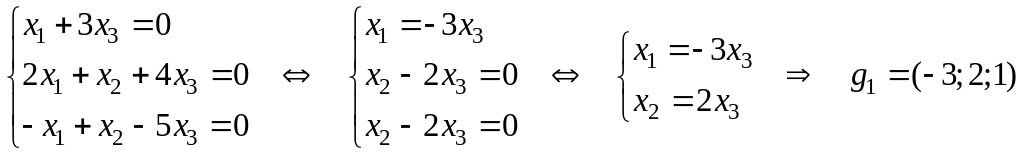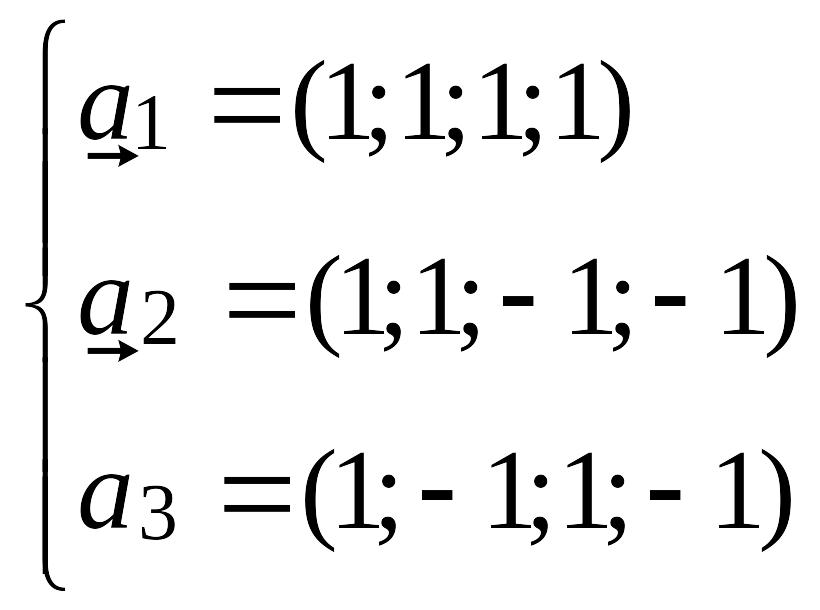Как найти размерность ядра по матрице - Исправление недочетов и поиск решений вместе с Examum.ru

Все курсы > Линейная алгебра > Занятие 6 (часть 1)

Сегодня мы еще раз рассмотрим полученные ранее знания о векторных пространствах, линейных преобразованиях, системе линейных уравнений и определителе матрицы в контексте новых понятий ранга и четырех фундаментальных подпространств матрицы, а именно пространства столбцов, пространства строк, ядра и коядра матрицы.

Продолжим работать в том же ноутбуке⧉

Ранг матрицы

При нулевом определителе в трехмерном пространстве матрица может «схлопнуть» пространство до плоскости, линии или точки (во всех трех случаях определитель равен нулю).

Ранее мы сказали, что для того чтобы в системе уравнений, например, трехмерная матрица $A$ при нулевом определителе все же имела решение, вектор $mathbf b$, на который матрица $A$ переводит вектор $mathbf x$, должен лежать на плоскости или линии, в которые «схлопывается» трехмерное пространство.

Размерность пространства после трансформации принято описывать рангом матрицы (rank).

Если преобразование трехмерной матрицы «сворачивает» размерность до линии, то ранг такого преобразования равен единице, до плоскости — двум и т.д. В случае матрицы $2 times 2$ самый высокий ранг матрицы — два. Это значит, что при преобразовании размерность сохранилась (и соответственно определитель не равен нулю).

Пространство столбцов

Пространством столбцов (column space, а также образом, image) называют множество всех возможных линейных комбинаций вектор-столбцов.

С точки зрения линейных преобразований, пространством столбцов называют векторы, которые определяют пространство после трансформации.

В случае линейно зависимых векторов таких векторов будет меньше, чем в исходной матрице. Приведем пример линейно зависимых векторов и рассчитаем ранг матрицы.

M = np.array([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

np.linalg.matrix_rank(M)

Приведем матрицу к упрощенному ступенчатому виду (reduced row-echelon form) с помощью Питона. Для этого воспользуемся методом .rref() библиотеки sympy.

from sympy import *

M = Matrix([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

M_rref = M.rref()

M_rref[0]

Как мы видим, с одной стороны, пространство сократилось до двух измерений (поэтому ранг матрицы равен двум), с другой, двумерное пространство можно описать первыми двумя столбцами (их еще называют разрещающими, ведущими или базисными, pivot columns), где все элементы кроме одного равны нулю.

Разрешающие столбцы и образуют пространство столбцов. Найдем пространство столбцов с помощью Питона.

# вторым элементом метод .rref() выводит

# индексы разрешающих столбцов (pivot columns),

# используем их для нахождения пространства столбцов

M.col(M.rref()[1])

# то же самое можно найти с помощью

# метода .columnspace()

M_columnspace = M.columnspace()

M_columnspace[0]

Откуда такое название? Столбцы матрицы говорят куда «приземлятся» координаты базисных векторов. В этом смысле, оболочка вектор-столбцов то же самое, что и пространство столбцов.

В матрице $2 times 2$ первый столбец показывает, где окажется вектор $mathbf i$, второй — вектор $mathbf j$. И оболочка этих столбцов определит пространство столбцов. Если, например, в матрице $2 times 2$ столбцы линейно независимы и преобразование не приводит к снижению размерности, то пространство столбцов задается этими двумя векторами.

Замечу, что столбцы, не являющиеся разрешающими, называются свободными (free).

Ядро матрицы

Если преобразование уменьшает размерность (например, преобразовывает плоскость в линию), то несколько векторов оказываются в начале координат (становятся нулевыми векторами). Видео ниже прекрасно иллюстрирует эту трансформацию.

Множество таких «исчезающих» векторов называется ядром матрицы или ее нуль-пространством (null space, kernel).

Видео про обратные матрицы, ранг и ядро⧉.

Система уравнений

$Ax = b$

Рассмотрим пространство столбцов и ядро с точки зрения системы линейных уравнений. В первую очередь представим пространство столбцов, как решение системы $ A mathbf x = mathbf b $, т.е. линейную комбинацию вектор-столбцов $A$, умноженных на компоненты $mathbf x$.

$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf b \ vdots end{bmatrix} $$

Всегда ли $A mathbf x = mathbf b$ будет иметь решение? Нет. Возьмем некоторую матрицу $A$ и соответствующие ей векторы $mathbf x$ и $mathbf b$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} b_1 \ b_2 \ b_3 \ b_4 end{bmatrix} $$

В такой системе будет много векторов $mathbf b$, которые не будут являться линейной комбинацией трех столбцов матрицы A.

В каком случае такое решение все-таки будет существовать? Если $mathbf b$ будет являться линейной комбинацией векторов $A$, т.е. будет находиться в пространстве столбцов $A$, $mathbf b in col(A) $.

Например, если $mathbf b$ будет равен одному из столбцов $A$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

Тогда решением может быть

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} $$

Что интересно, все возможные решения $mathbf x$ именно такой системы $A mathbf x = mathbf b$, где $mathbf b in col(A) $ сами по себе не образуют векторное пространство (хотя бы потому что нулевой вектор не включен в эти решения).

Дополнительно замечу, что так как в матрице $A$ только два линейно независимых вектора (третий вектор является суммой первых двух), то в данном случае мы имеем двумерное подпространство $R^4$.

$Ax = 0$

В системе линейных уравнений $A mathbf x = mathbf b$, если $mathbf b$ — нулевой вектор, т.е. $A mathbf x = mathbf 0$, то ядро дает все возможные решения этой системы (все возможные $mathbf x$). Можно также сказать, что ядро $mathbf x $ представляет собой комбинацию вектор-столбцов $A$, обращающихся в ноль.

В примере выше обратите внимание, что $col(A) in R^4$, в то время как $null(A) in R^3$. Решением же этой системы при нулевом векторе $mathbf b$, $A mathbf x = mathbf 0$ будет

$$ null(A) = k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

где $k in mathbb{R} $. Другими словами, $null(A)$ представляет собой линию в $R^3$.

Убедимся, что для матрицы $M$ выше мы правильно нашли ядро (а также решение $M mathbf x = 0$).

M = np.array([[1, 0, 1],

[2, 3, 4],

[—1, —3, —3]])

Null = np.array([—1, —2/3, 1])

M @ Null

Общее и частное решение

Приведем общее решение (complete solution) следующей системы, состоящее из частного решения (particular solution) системы $A mathbf x = mathbf b$ и ядра, то есть решения $A mathbf x = mathbf 0$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} + k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

Независимость векторов, базис и размерность

В свете новых знаний еще раз рассмотрим линейную независимость векторов и базис векторного пространства. Возьмем некоторую матрицу $A$.

Независимые вектор-столбцы

Можно сказать, что вектор-столбцы, образующие матрицу $A$ независимы, если ядро матрицы состоит только из нулевого вектора, $null(A) = { mathbf 0 }$ (решением $A mathbf x = mathbf 0$ будет только нулевой вектор $mathbf x$). Одновременно все столбцы такой матрицы являются разрешающими, и матрица имеет полный ранг, равный количеству столбцов $n$, $rank(A) = n$.

Если матрица $А$ квадратная и ее столбцы линейно независимы, то можно сказать, что

Вектор-столбцы матрицы образуют базис $R^n$
Такая матрица будет обратима (!)

Приведем примеры обратимых матриц, столбцы которых формируют базис.

$$ begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix}, begin{bmatrix} 1 & 2 & 3 \ 1 & 2 & 1 \ 2 & 5 & 8 end{bmatrix} $$

A = np.array([[1, 2, 3],

[1, 2, 1],

[2, 5, 8]])

np.linalg.matrix_rank(A)

array([[ 5.5, -0.5, -2. ],

[-3. , 1. , 1. ],

[ 0.5, -0.5, 0. ]])

Зависимые вектор-столбцы

Если же столбцы зависимы, то ядро матрицы содержит также ненулевые векторы и решением $A mathbf x = mathbf 0$ будет или будут некоторые ненулевые векторы $mathbf x$. Столбцы матрицы будут как разрешающими, так и свободными. Ранг матрицы будет равен количеству разрещающих столбцов.

Базис пространства будет определяться именно линейно независимыми векторами, входящими в пространство столбцов. Размерностью (dimension) векторного пространства будет как раз количество векторов базиса.

Например, возьмем следующую матрицу $A$.

$$ A = begin{bmatrix} 1 & 2 & 3 & 1 \ 1 & 1 & 2 & 1 \ 1 & 2 & 3 & 1 end{bmatrix} $$

В данном случае у матрицы два линейно независимых столбца. В частности, это

$$ col(A) = left{ begin{bmatrix} 1 \ 1 \ 1 end{bmatrix}, begin{bmatrix} 2 \ 1 \ 2 end{bmatrix} right} $$

Как следствие,

$$ dim(col(A)) = rank(A) = dim(basis) = text{# of pivots} = 2 $$

Одновременно, нулевое пространство задано векторами

$$ null(A) = left{ begin{bmatrix} -1 \ -1 \ 1 \ 0 end{bmatrix}, begin{bmatrix} -1 \ 0 \ 0 \ 1 end{bmatrix} right} $$

Как следствие,

$$ dim(null(A)) = text{# of free columns} = 2 $$

Код на Питоне для нахождения пространства столбцов и ядра приведен в ноутбуке к занятию⧉.

В качестве дополнения, замечу, что размерность векторного пространства характеризуется следом (trace) единичной матрицы этого пространства или суммой элементов главной диагонали. Например, размерность $R^3$ можно охарактеризовать через

$$ dim(col(A)) = tr left( begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix} right) = 3 $$

Пространство строк и коядро

Пространством строк (row space) называют множество всех возможных линейных комбинаций вектор-строк.

Если матрицу транспонировать, то можно сказать, что

$$ row(A) = col(A^T) $$

Коядром или левым нуль-пространством (left null-space, cokernel) матрицы $A$ будет ядро матрицы $A^T$.

$$ leftnull(A) = null(A^T) $$

Продемонстрируем, почему это пространством называется именно левым нуль-пространством. По определению ядра, как решения $A mathbf x = mathbf 0$, можно сказать, что коядро будет решением $A^T mathbf y = mathbf 0$.

$$ A^T mathbf y = mathbf 0 $$

$$ mathbf y^T(A^T)^T = mathbf 0^T $$

$$ mathbf y^T A = mathbf 0^T $$

Схематично это можно представить следующим образом.

Можно также сказать, что коядро $ mathbf y $ в системе $ A^T mathbf y = mathbf 0 $ дает все возможные комбинации столбцов $A^T$, обращающиеся в нулевой вектор (что то же самое, что линейные комбинации строк $mathbf x^T A = 0$). Приведем пример. Найдем коядро матрицы $A$.

A = Matrix([[1, 2, 3, 1],

[1, 1, 2, 1],

[1, 2, 3, 1]])

A.T.nullspace()[0]

Другими словами, нам нужно взять $-1R_1 + 0R_2 + 1R_3$, чтобы получить нулевой вектор. Проверим полученный результат.

A = np.array([[1, 2, 3, 1],

[1, 1, 2, 1],

[1, 2, 3, 1]])

Leftnull = np.array([—1, 0, 1])

Leftnull.T @ A

Фундаментальные подпространства матрицы

Обобщим изложенную выше информацию. Возьмем матрицу $A$ размерностью $m times n$. Тогда

$ null(A) in R^n$ (так как должно быть решением $A mathbf x = mathbf 0$)
$ col(A) in R^m $ (количество строк $A$)
$ row(A) = col(A^T) in R^n $ (количество столбцов $A$)
$ leftnull(A) = null(A^T) in R^m $ (так как должно быть решением $A^T mathbf y = mathbf 0$)

Тогда схематично эти подпространства можно представить следующим образом.

Несколько пояснений и дополнений:

$r$ означает ранг (rank) матрицы
$r+(n-r) = n$, т.е. столбцы матрицы $A$
$r+(m-r) = m$, т.е. строки матрицы $A$ или столбцы $A^T$

Про пересечение подпространств. Может ли вектор $mathbf v = begin{bmatrix} 1 \ 2 end{bmatrix}$ быть одновременно в нуль-пространстве и являться частью пространства строк A (или в целом строкой в A)? Нет.

$$ begin{bmatrix} 1 & 2 \ dots & dots end{bmatrix} begin{bmatrix} 1 \ 2 end{bmatrix} not= begin{bmatrix} 0 \ 0 end{bmatrix} $$

Пересечением пространства строк и нуль-пространства будет только нулевой вектор.

$$ row(A) cap null(A) = { mathbf 0 } $$

Ортогональность подпространств матрицы

Более того, ядро ортогонально пространству строк $row(A) perp null(A)$, так как их скалярное произведение равно нулю. Это следует из определения ядра $A mathbf x = mathbf 0$ (произведение $mathbf x$ на каждую вектор-строку $mathbf a_m$ равно нулю).

$$ begin{bmatrix} dots & mathbf a_1 & dots \ dots & mathbf a_2 & dots \ dots & dots & dots \ dots & mathbf a_m & dots end{bmatrix} begin{bmatrix} vdots \ mathbf x \ vdots end{bmatrix} = begin{bmatrix} 0 \ 0 \ 0 \ 0 end{bmatrix} $$

Более того, так как $null(A)$ содержит все векторы, ортогональные $row(A)$, то ядро можно считать ортогональным дополнением пространства строк в $R^n$: $null(A) = row(A)^{perp} $.

То же самое справедливо для пространства столбцов и коядра.

$$ col(A) perp leftnull(A) perp null(A^T) text{ в } R^m $$

$$ leftnull(A), null(A^T) = col(A)^{perp} $$

Количество решений системы уравнений

Систематизируем наши знания о подпространствах матрицы с точки зрения возможного количества решений системы уравнений.

Система не имеет решений

В случае если система не имеет решений, существует некоторый вектор $mathbf b $, при котором $A mathbf x = mathbf b $ не будет иметь решения.

$$ exists mathbf b implies A mathbf x not= mathbf b $$

С точки зрения матрицы $underset{m times n}{A}$, можно говорить о том, что некоторые строки линейно зависимы и после преобразования методом Гаусса обратятся в нули. Как следствие, ранг матрицы меньше количества строк, $r < m$.

Система имеет единственное решение

Если мы знаем, что система имеет единственное решение, то это означает, что нуль-пространство матрицы $A$ содержит только нулевой вектор, $null(A) = { mathbf 0 }$ и все столбцы линейно независимы, $ r = n $.

Система имеет множество решений

В этом случае решение состоит из частного решения и решения системы $A mathbf x not= mathbf 0 $. Другими словами, это означает, что нуль-пространство содержит не только нулевой вектор, а значит столбцы матрицы линейно зависимы и $ r < n $.

Теперь приведем пример, иллюстрирующий применение матрицы для моделирования физического процесса, а также посмотрим как подпространства такой матрицы одновременно характеризуют свойства этого процесса.

Источник

Решение. Очевидно,
что данное линейное преобразование
действует

,
т.к. умножение матриц

определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность

(т.к. в матрице A
5 строк).

Совокупность N
векторов x
таких, что Ax=0,
называется ядром
преобразования A.

Совокупность M
векторов вида Ax,
когда x
пробегает все R
(в нашем случае

)
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).

1) Находим ядро.
Пусть

— вектор столбец. Решаем систему уравнений

Решаем систему
методом Гаусса

Переменные

— базисные, а

— небазисная.

Находим все
фундаментальные решения. В нашем случае
оно одно: положив

,
получаем

— который и будет образовывать базис
ядра (т.к. все вектора вида

отображаются в 0). Размерность базиса
равна 1.

2) Находим образ.
Пусть

— вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

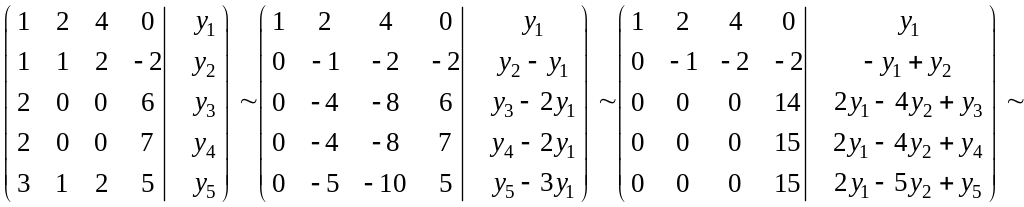
Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

Находим фундаментальные
решения (базис образа). Т.к. определитель
из коэффициентов при

:

,
то

— базисные, а

— небазисные.

1-е фундаментальное
решение. Положим

,
находим решение системы

— первое базисное
решение.

2-е фундаментальное
решение. Положим

,
находим решение системы

— второе базисное
решение.

3-е фундаментальное
решение. Положим

,
находим решение системы

— второе базисное
решение.

Итак, размерность
образа равна 3, базис – вектора

.

(Видно, что
размерность образа + размерность ядра
= размерности пространства R⁴).

7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .

Решение.

— ядро,

— образ. Преобразование

.

1) Находим ядро.
Решаем систему уравнений

Следовательно,
одно базисное решение

— базис ядра. Размерность

.

2) Находим образ.

Пусть

— вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

Отсюда,

—
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

— базис образа. Размерность

.

3) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

— фундаментальное
решение системы или базис

.

4) Найдем базис
линейной оболочки векторов

,

.
Т.к.

,
то заключаем, что

— базис в

,
и следовательно, размерность

.

5) Находим пространство
решений системы уравнений

— фундаментальное
решение системы или базис M.

6) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

Отсюда,

—
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

— базис

.
Размерность

.

7) Найдем базис
линейной оболочки векторов

Очевидно, что

,
а

— базис в

,
и следовательно, размерность

.

8. Пусть U
— подпространство
линейного пространства R⁴,
являющееся линейной оболочкой. векторов

,
V
— подпространство
линейного пространства R⁴являющееся
линейной оболочкой векторов

.
Найдите: базис U
+ V
и
базис

.

Решение.

1) Находим базис в
U.

rang=3
, сл-но,

— базис U.

1) Находим базис в
V.

rang=3
, сл-но,

— базис V.

3) Находим базис в
U
+ V.

Находим линейно
независимые вектора в объединении

.

,
а вектора

— базис U
+ V
, а размерность
dim(U
+ V)=4.

4) Найдем общие
вектора в U
и
V
.

Нам известно, что
в конечномерном пространстве
подпространства могут быть заданы
системами линейных уравнений. Тогда их
пересечение задаётся системой уравнений,
полученной объединением систем, задающих
подпространства.

Система уравнений
задающая U:

Для того, чтобы
вектор

принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Система уравнений
задающая V:

Для того, чтобы
вектор

Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Решаем общую
систему:

Отсюда фундаментальные
решения (которые получаются при

и при

),
а следовательно базис

есть:

.

9. Подпространство
L₁
в R⁴
порождено векторами (1;-4;6;7) и (0;1;-3;1), а
подпространство L₂
— векторами
(0;1;-4;5) и (1;-4;7;-11). Постройте базисы следующих
подпространств: пересечения

и ортогонального дополнения к сумме

.

Решение.

1) Находим базис в
L₁.
Т.к. матрица, составленная из координат
векторов

,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка

),
то заключаем, что вектора

=(1;-4;6;7)
и

=(0;1;-3;1)
линейно независимые и образуют базис
в L₁.

2) Аналогично,
заключаем, что вектора

=(0;1;-4;5)
и

=(1;-4;7;-11)
линейно независимые и образуют базис
в L₂.

3) Находим базис
L₁+
L₂.

Рассматриваем
объединенную систему векторов

=(1;-4;6;7),

=(0;1;-3;1),

=(0;1;-4;5),

=(1;-4;7;-11)

и находим среди
них линейно независимые. Находим ранг
матрицы, столбцами которой являются
координаты

:

Ранг = 4, следовательно,
все вектора

— линейно независимые и образуют базис
в L₁+
L₂.

4)
Находим базис ортогонального дополнения

Каждый вектор из

ортогонален любому вектору из L₁+
L₂.
Следовательно, скалярные произведения

на вектора базиса из L₁+
L₂
равны 0. Получаем однородную систему

Т.к. определитель
системы не равен 0 (показано выше, что
ранг=4), то система имеет единственное
тривиальное решение

.

Следовательно,

состоит
только из одного вектора

.

(Это и так было
видно, т.к. линейная оболочка

,
ибо 4 линейно независимых вектора

образуют базис в

,
а

).

5) Находим систему
уравнений описывающую L₁.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Находим систему
уравнений описывающую L₂.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

— искомая система
линейных уравнений.

Решаем общую
систему:

Т.к. определитель
матрицы коэффициентов

,
то система имеет единственное решение

.
Следовательно,

состоит из
одного вектора (0;0;0;0).

(Это и так было
видно, т.к. вектора

— линейно независимые,
линейные оболочки

не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов

не может дать вектора

,
а следовательно и их линейные комбинации).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задача №1. В арифметическом пространстве [math]mathbb{R}^4[/math] линейный оператор [math]displaystyle varphi[/math] задан матрицей

[math]A= left(!!begin{array}{rrrr} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{array}!!right)[/math]

Найти базисы ядра и образа, ранг и дефект линейного оператора. Найти операторы, индуцированныe в ядре и образе.

Решение.
1) По определению ядро линейного оператора [math]displaystyle varphi[/math] ([math]displaystyle ker varphi[/math]) есть множество всех векторов [math]displaystyle x[/math], которые [math]displaystyle varphi[/math] переводит в нулевой вектор. Это означает, что [math]displaystyle ker varphi[/math] состоит из векторов, координаты которыx [math]displaystyle x_1, x_2, x_3, x_4[/math] (в некотором базисе [math]displaystyle { e_1, e_2, e_3, e_4 }[/math]) удовлетворяет условию:

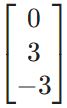
[math]begin{pmatrix} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{pmatrix}!!! begin{pmatrix} x_1\ x_2 \ x_3 \ x_4 end{pmatrix}!=! begin{pmatrix} 0\ 0 \ 0 \ 0 end{pmatrix}[/math]. То есть, [math]kervarphi[/math] cooтветствует пространству [math]L[/math] решений системы [math]begin{cases}x_1-2x_2+x_3+3x_4=0,\ -2x_1+5x_2+6x_3-12x_4=0,\ 5x_1+9x_2+13x_3+9x_4=0,\ -x_1+3x_2+7x_3-9x_4=0.end{cases}[/math]

Общим решением системы является семейство векторов [math]left(-frac{15}{4}C , 0, frac{3}{4}C, C right)[/math]. Полагая [math]C=4[/math], находим базис [math]ker varphi[/math]: [math](-15,,0,,3,,4)[/math].

2) Дефектом линейного оператора называется размерность его ядра ([math]dim ker varphi[/math]). Здесь [math]dim ker varphi=1[/math], т.к. в ядре существует лишь один линейно независимый вектор.

Верны ли мои рассуждения?

3) Не знаю, как найти образ линейного отображения [math]varphi[/math] ([math]im varphi[/math]). Подскажите идею.

4) Рангом линейного отображения [math]varphi[/math] называется размерность его образа ([math]dim im varphi[/math]). Здесь всё ясно.

5) Что такое операторы, индуцированные в ядре и образе?

Задача №2. Найти матрицу, область значений и ядро оператора [math]A[/math] проектирования на плоскость [math]x-z=0[/math]. Если [math]x={x_1, x_2, x_3 }[/math], то [math]Ax={x_1-x_2-x_3, -2x_1+3x_2, x_2- x_3 }[/math].

1) Cовершенно не знаю, как найти матрицу. И что означает проектирование на плоскость?

2) Если найду матрицу, то можно найти ядро.

3) Область значений — это синоним образа или что-то другое?

И ещё один вопрос общего характера. Существует ли какое-то обозначение для базиса линейного пространства (как, например, для ядра или размерности)?

Источник

Consider a linear map $f∈L(Π2(Bbb R),Bbb R^2) $ whose matrix $f_{G,B}$ in the basis $mathcal B$ of $prod_2(Bbb R)$ and

$G={(1,1) , (1,-1)}$ of $Bbb R^2$ is

$$f_{G,B} = begin{pmatrix}
-4 & -8 \ 7 & 4\ 5 & 0
end{pmatrix} ^T$$
(This is suppose to be a $Bbb R^{2×3}$ matrix)

From the information i need to find: dim ker $f$

Im a bit confused am i suppose to use the matrix of $f_{G.B}$?
*From a previous part of the question i found the rank$f =2$ if that helps at all.

To find the kernel i multiplies the $fG,B$ matrix by $(x, y)^T$ and equated it to $(0,0)^T$ and solved this using the row reduced matrix . So I got $x1 + 1/2×3 = 0$ and $x2 + x3 = 0$ and let $x3= λ$. Therfore $x1 = -1/2λ$ , $x2 = -λ$ and $x3 = λ$

Im not sure if what i did so far is correct. I think i need to use span, but i dont know how exactly.

Would really appreciate your help, thank you so much guys!

Источник

Помогаю со студенческими работами здесь

Найдите базисы ядра и образа линейного оператора
Здравствуйте. Решите, пожалуйста, задачу: В действительном линейном пространстве V линейный…

Базисы и размерности ядра и образа линейного оператора
В пространстве А4 линейный оператор φ вектор x=(x1,x2,x3,x4) переводит в вектор…

Задан линейный оператор A(f). Какова размерность ядра оператора А?
Дано линейное пространство комплексных периодических функций f(x) на интервале и задан линейный…

Базисы ядра и образа. Неясно условие
Я не понимаю, из какой части мне нужны векторы, из левой или правой.

f:R3 -> R3, v->f(v),
при…

Доказать утверждение о размерностях ядра и образа при отображении
Подскажите, пожалуйста, как доказать следующее утверждение :

dim(V) = dim( Ker(f) ) + dim(…

Сборка ядра с нуля и запись Linux на флешку в виде iso-образа
Добрый день, друзья!

Не подскажите по такому вопросику:

Необходимо скомпилировать любое ядро…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник