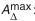Построение и расчет размерных цепей
Основные термины и определения
Рассмотрим фрагмент конструкции (рис. 4.1).
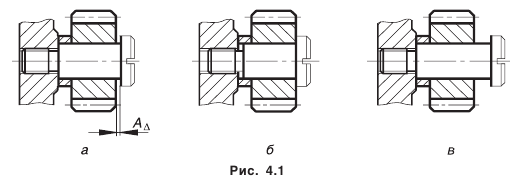
Для свободного вращения зубчатого колеса на оси необходим зазор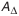 
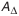
. Величина получается автоматически при сопряжении деталей, контуры которых выделены. Если размеры их выполнены неверно (рис. 4.1 6, в), то либо зазора не будет вовсе, либо он будет слишком большой, что сделает невозможным нормальное функционирование узла.
Установим те размеры деталей, которые при сборке автоматически создадут необходимый зазор (рис. 4.2). Обозначив размеры деталей, которые влияют на зазор , мы тем самым построим размерную цепь.
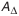
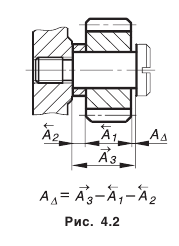
Размерной цепью называется совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур (ГОСТ 16319-80).
По виду задач, в решении которых участвуют цепи, они делятся на конструкторские, технологические и измерительные.
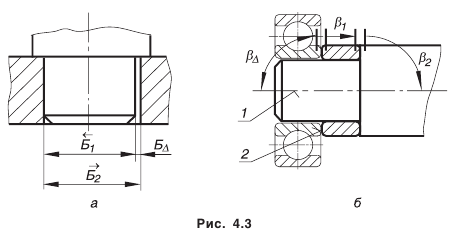
Конструкторские размерные цепи решают задачу по обеспечению точности при конструировании. Они устанавливают связь размеров детали в изделии. На рис. 4.3 приведены примеры сборочных размерных цепей.
На рис. 4.3, а приведена элементарная сборочная размерная цепь, решающая задачу обеспечения точности сопряжения двух деталей. На рис 4.3, 6 тоже показана сборочная цепь, которая решает задачу обеспечения перпендикулярности поверхности 2 к оси 1, необходимой для базирования подшипника качения.
Технологические размерные цепи решают задачу по обеспечению точности при изготовлении машин. Они устанавливают связь размеров деталей на разных этапах технологического процесса. На рис. 4.4, а изображена деталь с размерами, которые следует выдержать при изготовлении. Последовательность получения размеров приведена на рис. 4.4, 6, в, г. На основании предложенного маршрута обработки построена технологическая размерная цепь (см. рис 4.4, д). При обработке детали выдерживаются размеры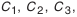 
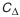
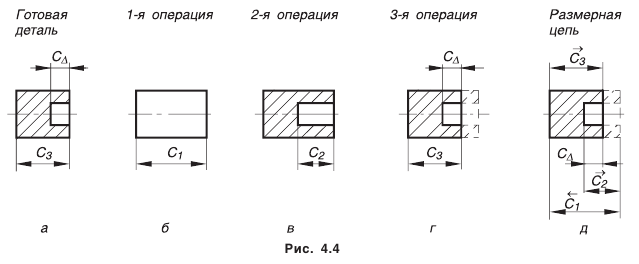
а размер 
получается автоматически.
Измерительные размерные цепи решают задачу обеспечения точности при измерении. Они устанавливают связь между звеньями, которые влияют на точность измерения.
Размеры, образующие размерную цепь, называются звеньями. В зависимости от расположения звеньев, цепи делятся на плоские (звенья расположены в одной или параллельных плоскостях) и пространственные. В зависимости от вида звеньев различают линейные размерные цепи (звеньями являются линейные размеры, рис. 4.2, 4.3, а) и угловые (рис. 4.3, б). Звенья линейной размерной цепи обозначают какой-либо одной прописной буквой русского алфавита с соответствующим числовым индексом, звенья угловых цепей — строчной буквой греческого алфавита.
Любая размерная цепь состоит из составляющих звеньев и одного замыкающего. Замыкающее звено (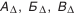
и т. д.) — то звено, которое непосредственно не выдерживается, а получается в результате выполнения размеров составляющих звеньев.
Составляющие звенья делятся на увеличивающие и уменьшающие. Увеличивающие звенья
— те, с увеличением которых замыкающее звено увеличивается, а уменьшающие
— те, с увеличением которых замыкающее звено уменьшается. При правильном определении увеличивающих и уменьшающих звеньев стрелки над буквами должны указывать движение в одном направлении по замкнутому контуру размерной цепи.
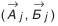
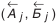
Принципы построения конструкторских размерных цепей
Перед тем как построить размерную цепь, следует выявить замыкающее звено, которое, допустим, определяет нормальное функционирование механизма. Размер или предельное отклонение замыкающего звена назначают или рассчитывают исходя из условий работы и (или) требуемой точности.
Например, размер и предельные отклонения 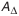(см. рис. 4.2) принимаются такими, которые обеспечивали бы свободное вращение зубчатого колеса при минимальном возможном смещении его вдоль оси. Несовпадение вершины делительного конуса конической шестерни с осью вращения конического колеса (рис. 4.7, а, б) определяется степенью точности зубчатых колес, а его предельные значения находятся по соответствующему стандарту.
В курсовом проекте замыкающее звено и допуск на него уже заданы. Надо только установить, между какими деталями стоит размер замыкающего звена, а затем связать эти детали цепью размеров.
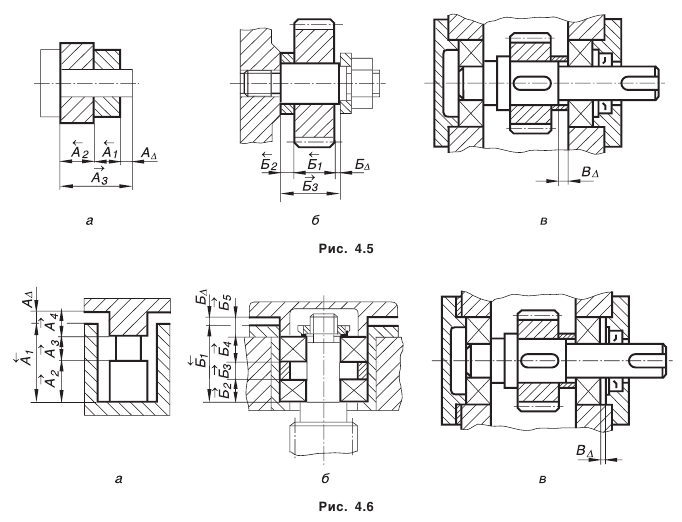
Например, на рис. 4.5, б размер замыкающего звена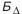 
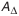
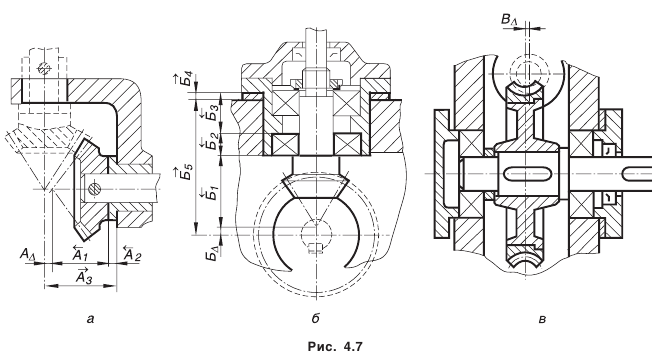
стоит между осью и торцом зубчатого колеса; на рис. 4.7, а стоит между осью отверстия в корпусе и вершиной делительного конуса конического колеса и т. д.
Рассмотрим наиболее типичные варианты сборочных размерных цепей’. Первый вид размерных цепей приведен на рис. 4.5, второй — на рис. 4.6, третий — на рис. 4.7.
При построении размерных цепей следует руководствоваться их основными свойствами:
• цепь должна быть замкнута;
• размер любого звена сборочной цепи должен относиться к элементам одной и той же детали; исключением является замыкающее звено, которое всегда соединяет элементы разных деталей;
• цепь должна быть проведена наикратчайшим способом, т. е. деталь своими элементами должна входить в размерную цепь только один раз.
Основные соотношения размерных цепей
Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей с номинальными звеньями она имеет следующий вид:
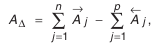
где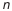 
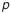
и 
— число увеличивающих и уменьшающих звеньев в размерной цепи соответственно.
Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем вначале наибольшее значение замыкающего звена:
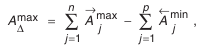
затем наименьшее значение:
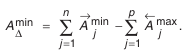
Вычтем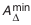 
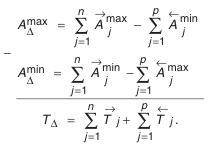
из 
Окончательно получим:
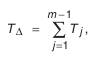
где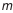 
— количество звеньев размерной цепи, включая замыкающее звено.
Из формулы (4.2) следует, что разброс размеров замыкающего звена равен сумме разбросов размеров составляющих звеньев. Поэтому, чтобы обеспечить наибольшую точность замыкающего звена, размерная цепь должна состоять из возможно меньшего числа звеньев, т. е. необходимо при конструировании машин и проектировании технологических процессов соблюдать принцип наикратчайшей размерной цепи. Аналогичным образом находится верхнее отклонение замыкающего звена:
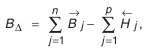
нижнее отклонение:
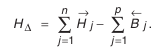
Координата середины поля допуска замыкающего звена рассчитывается следующим образом:
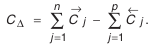
Если известны размеры и поля допусков, составляющих звеньев размерной цепи, то по формулам (4.1 )-(4.5) можно определить все параметры замыкающего звена.
Расчет размерных цепей
Обычно при конструировании возникает необходимость определить параметры составляющих звеньев размерной цепи при известном замыкающем звене. Решением данной задачи может быть большое количество вариантов сочетаний допусков и предельных отклонений составляющих звеньев. лишь бы они удовлетворяли основным соотношениям.
Обычно в прикидочных расчетах пользуются способом равных допусков, т. е.:
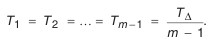
При большой разнице в номинальных размерах составляющих звеньев такой способ является некорректным, так как к большим звеньям будут предъявляться более жесткие требования по точности.
Смысл корректного расчета размерной цепи заключается в том, чтобы допуски на составляющие звеньев размерной цепи были бы одного или двух ближайших квалитетов.
Известно, что допуск есть произведение единицы допуска на коэффициент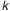 
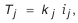
. Это справедливо и для любого звена размерной цепи:
где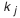 
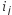
— число единиц допуска (величина постоянная для одного квалитета);
— единица допуска, характеризующая ту часть допуска, которая меняется с изменением размера.
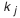
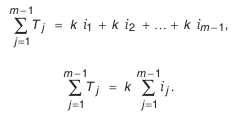
Итак, чтобы добиться одинаковых требований к точности изготовления составляющих звеньев, необходимо, чтобы коэффициенты были бы одинаковыми у всех звеньев. Просуммируем допуски составляющих звеньев размерной цепи:
Подставим полученную зависимость в формулу (4.2):
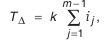
откуда
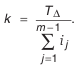
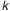
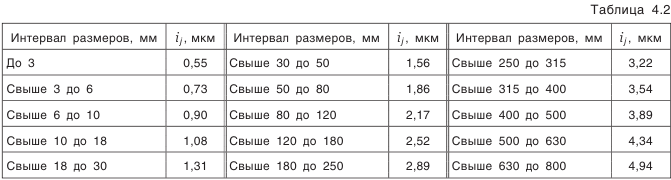
Значение характеризует точность, с которой следует получать все составляющие звенья размерной цепи. Рассчитанное по формуле значение к в общем случае не будет соответствовать строго определенному квалитету, поэтому для назначения допусков на соответствующие звенья выбирают ближайшие квалитеты по табл. 4.1.
Значения единицы допуска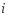 
для размеров до 800 мм приведены в табл. 4.2.
Обеспечить заданную точность замыкающего звена можно несколькими методами (ГОСТ 16320-80).
Метод полной взаимозаменяемости
Метод, при котором требуемая точность замыкающего звена размерной цепи получается при любом сочетании размеров составляющих звеньев. При этом предполагают, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний (все увеличивающие звенья с верхними предельными размерами, а уменьшающие с нижними, или наоборот). Такой метод расчета, который учитывает эти неблагоприятные сочетания, называется методом расчета на максимум — минимум.
Пример
На рис. П.8.2 изображен фрагмент конструкции, у которой необходимо обеспечить при сборке осевой зазор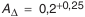 
между торцом крышки и наружным кольцом подшипника. Осевой зазор необходим для компенсации тепловых деформаций деталей, возникающих во время работы узла.
Требуется назначить допуски и отклонения на составляющие звенья для обеспечения 100% годности собираемых механизмов при любом сочетании размеров составляющих звеньев.
Допуски и отклонения на ширину подшипниковых колец и монтажную высоту подшипников качения, входящих в размерную цепь, назначать условно, как и на другие детали.
Решение
- Определение номинальных размеров составляющих звеньев.
Номинальные размеры стандартных деталей, например подшипников качения, находят по соответствующим стандартам. Остальные размеры составляющих звеньев, кроме звена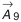 
, определяют непосредственно по чертежу узла.
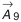
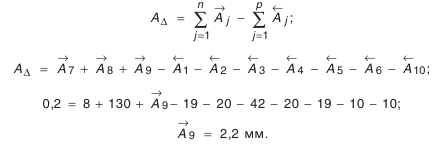
Для нахождения номинального размера воспользуемся зависимостью (4.1):
- Определение средней точности размерной цепи.
По формуле (4.7.) найдем значение :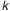
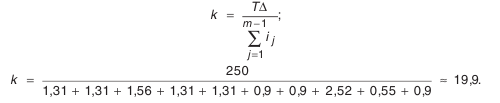
Найденное число единиц допуска лежит в пределах стандартных значений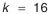 
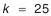
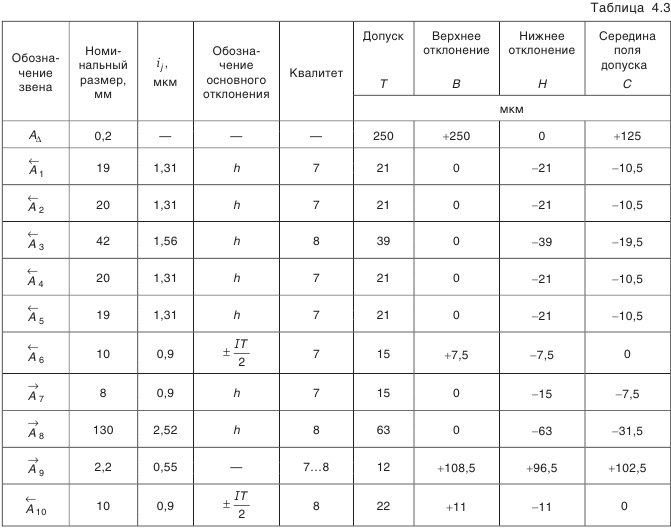
(7-й ква-литет) и 
(8-й квалитет). Отсюда следует, что часть звеньев должна изготавливаться по
7-му квалитету, а часть — по 8-му. При этом следует назначать допуски таким образом, чтобы допуск звена 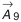лежал в пределах между 7-м и 8-м квалитетами либо соответствовал одному из этих квалитетов.
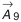
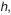
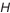
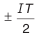
Предельные отклонения на составляющие звенья, кроме , рекомендуется назначать на размеры, относящиеся к валам — по 
относящиеся к отверстиям — по 
; на остальные — 
, т. е. симметричные предельные отклонения. 2
Результаты поэтапных расчетов внесены в табл. 4.3.
- Определение допуска звена
. Воспользуемся формулой (4.2):
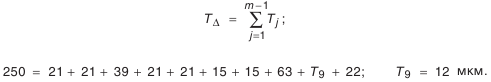
- Определение предельных отклонений звена . Из формулы (4.3):
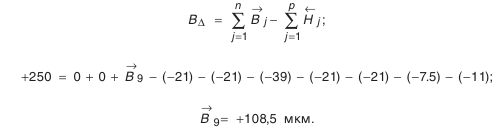
Из формулы (4.4):
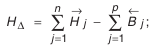
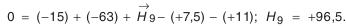
- Проверка.
Чтобы убедиться в правильности проведенных расчетов, воспользуемся зависимостью (4.5) для координат середины полей допусков:
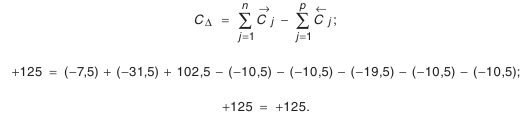
Это говорит о правильности проведенных вычислений.
Метод неполной взаимозаменяемости
Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.
Сборка осуществляется без пригонки, регулировки и подбора звеньев.
Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер и вероятность того, что все звенья с самыми неблагоприятными сочетаниями окажутся в одном изделии, весьма мала.
Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных сочетаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допуска. При этом расширяются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовления деталей.
Задачей расчета является назначение допусков на составляющие звенья, соответствующих одинаковой степени точности.
Учитывая случайный характер сочетаний действительных размеров деталей в изделии, воспользуемся уравнением для определения дисперсии суммы независимых случайных величин:
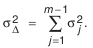
Допустим, что погрешность всех звеньев изменяется по закону нормального распределения, а границы рассеяния размеров для составляющих звеньев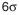 
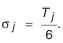
совпадают с границами полей допусков, тогда:
Для замыкающего звена допустим, что:
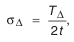
где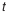 
— коэффициент риска.
Тогда:
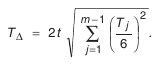
Обозначим через
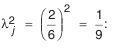
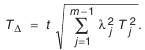
Формула (4.8) устанавливает связь между допуском на замыкающий размер и допусками на составляющие звенья.
Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, воспользуемся известной формулой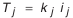 
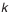
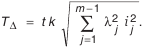
и подставим ее в выражение (4.8). Потребуем, чтобы 
у всех звеньев были одинаковыми, тогда:
Окончательно получим:
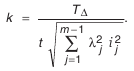
Значение 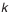характеризует точность, с которой следует изготовить все составляющие звенья размерной цепи при заданных условиях.
При обработке деталей разброс размеров у них может распределяться и не по закону Гаусса. В этом случае можно также воспользоваться формулой (4.9), только при этом следует поставить другие значения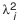 
.
Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то
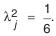
При неизвестном характере рассеяния размеров рекомендуется принимать закон равной вероятности с
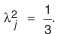
На основании предельных теорем теории вероятностей независимо от характера рассеяния размеров составляющих звеньев разброс размеров замыкающего звена размерной цепи будет близок к закону нормального распределения.
В зависимости от принятого процента риска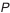 
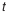
значения выбирают из ряда, приведенного в табл. 4.4.
Пример
Вероятностный метод расчета рассмотрим на том же узле (см. рис. П.8.2). По техническим требованиям необходимо обеспечить осевой зазор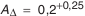 
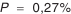
. Требуется назначить допуски и отклонения на составляющие звенья при 
и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).
Допуски и отклонения на ширину подшипниковых колец и монтажную высоту подшипников качения, входящих в размерную цепь, назначать условно, как и на другие детали.
Решение
- Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум — минимум.
- Определение средней точности размерной цепи. Воспользуемся зависимостью (4.9):
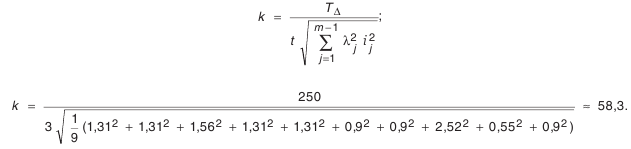
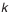
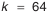
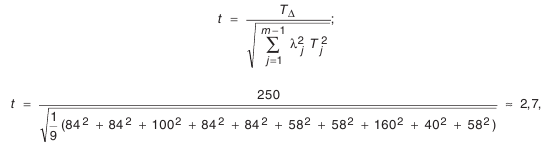
Найденное число единиц допуска лежит ближе к стандартному значению 
, что соответствует 10-му квалитету. Допуски на все звенья назначаются по 10-му квалитету. 3. Определение истинного процента брака. Из формулы (4.8):
что соответствует 0.693% брака (значения процента брака определяется по табл. П.7.1 приложения).
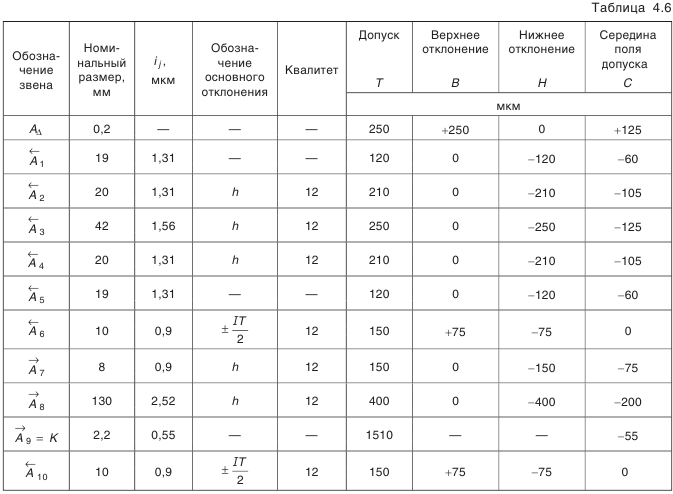
Полагаем, что такой процент брака нас устраивает. Если же количество брака мы сочли бы чрезмерным, тогда необходимо было бы допуски на ряд звеньев назначить по 9-му квалитету. Результаты поэтапных расчетов внесены в табл. 4.5.
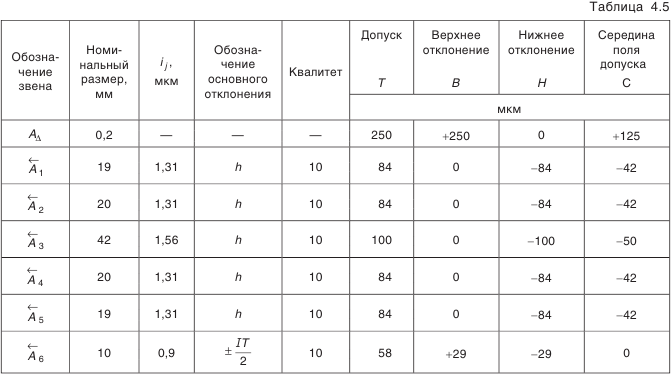
- Определение предельных отклонений звена .
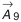
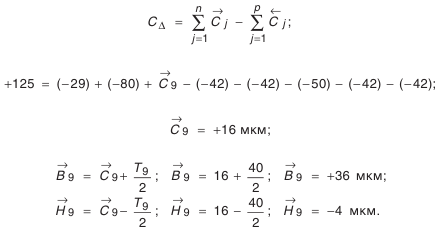
Вначале определим координату середины поля допуска звена по формуле (4.5):
Метод пригонки
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена путем снятия с компенсатора слоя металла. Его суть состоит в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, например по 12-14-му квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора.
Смысл расчета заключается в определении припуска на пригонку, достаточного для компенсации величины превышения предельных значений замыкающего звена и вместе с тем наименьшего для сокращения объема пригоночных работ.
Роль компенсатора обычно выполняет деталь, наиболее доступная при разборке механизма, несложная по конструкции и неточная, например прокладки, шайбы, проставочные кольца и т. п.
Пример
Определить размеры заготовки компенсатора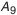 
для размерной цепи (см. рис. П.8.2, приложение 8). Замыкающее звено должно быть 
.
Решение
- Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум — минимум.
- Выбор и назначение допусков на составляющие звенья.
Считаем, что для размеров звеньев экономически приемлемым является 12-й квалитет. Назначаем по этому квалитету допуски на все размеры, кроме допусков на монтажную высоту шариковых радиальных подшипников, которые условно принимаются по табл. П.7.2 приложения 7, и на звено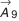 
, которое выбрали в качестве компенсатора.
- Определение наибольшей величины компенсации. По формуле (4.2):
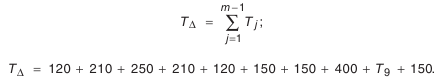
Нетрудно заметить, что сумма допусков составляющих звеньев значительно превосходит допуск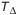 
, т. е. колебание размера замыкающего звена от изделия к изделию значительно увеличится.
Наибольшая расчетная компенсация избыточного колебания размера замыкающего звена:
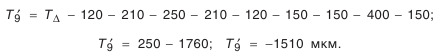
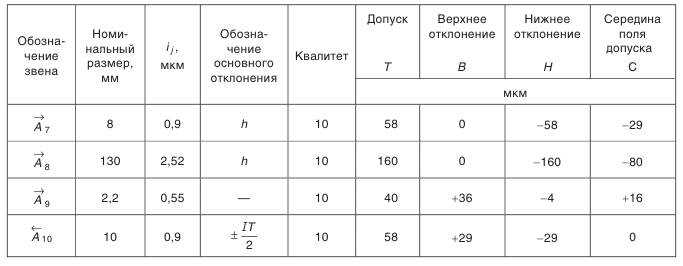
Следовательно, при самом неблагоприятном сочетании размеров надо с компенсатора снять слой материала толщиной 1,51 мм, чтобы замыкающее звено попало в предписанные пределы. Результаты расчетов представлены в табл. 4.6.
- Определение предельных размеров компенсатора звена .
Вначале определим координату середины поля допуска звена :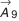
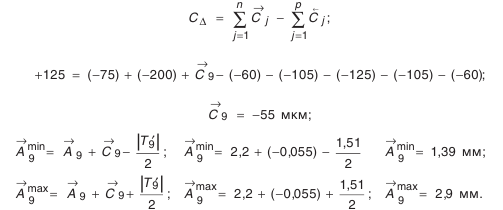
- Определение размера заготовки компенсатора.
Исполнительный размер заготовки компенсатора определяется его наибольшей величиной, так как в прочих случаях он будет подгоняться.
Для изготовления компенсатора на него надо назначить приемлемый допуск, например, по тому же 12-му квалитету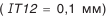 
, но так, чтобы его наименьший размер был не менее 2,9 мм:
Метод регулирования с применением неподвижного компенсатора
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением компенсирующего звена без снятия слоя металла.
Его суть состоит в том, что избыток поля рассеивания замыкающего звена устраняют путем подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различными размерами.
Смысл расчета заключается в определении наименьшего количества компенсаторов в комплекте.
Пример
Определить размеры компенсационных прокладок в комплекте для размерной цепи (см. рис. П.8.2, приложение 8). Замыкающее звено должно быть
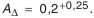
Решение
Прежним порядком (см. метод пригонки) устанавливаем номинальные размеры и назначаем допуски на составляющие звенья размерной цепи. Рассчитываем величину компенсации
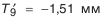
и наименьший размер компенсатора в комплекте
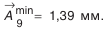
- Определение числа компенсаторов в комплекте.
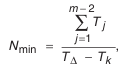
где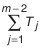 
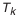
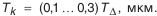
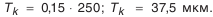
— сумма допусков всех составляющих звеньев без допусков на компенсатор; 
— допуск на отдельный компенсатор в комплекте. Допуск на отдельный компенсатор выбирается в пределах:
Принимаем
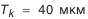
(10-й квалитет);
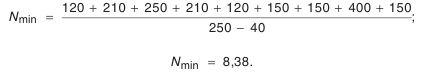
Найденное число компенсаторов в комплекте следует всегда округлять в бблыиую сторону, так как по формуле (4.10) определяется наименьшее число компенсаторов.
Принимаем:
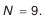
- Величина ступени компенсации.
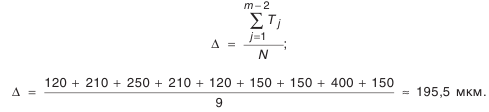
- Размеры компенсаторов в комплекте.
Эта лекция взята со страницы лекций по допускам и посадкам:
Допуски и посадки: ГОСТы и особенности применения
Возможно вам будут полезны эти страницы:
Расчет размерных цепей онлайн. Прямая задача.
Задание:
Рассчитать заданную размерную цепь (см. рис. 1) по методу полной взаимозаменяемости (max/min).
Допуски на составляющие звенья определять способом равных квалитетов (одного квалитета).
Сделать проверку выполненных расчетов.
Исходные данные:
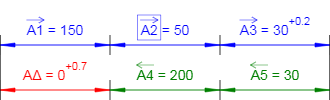
Рисунок 1 — Схема размерной цепи. Исходные данные.
Звенья размерной цепи:
A1 = 150 (мм)
A2 = 50 (мм)
A3 = 30+0,2 (мм) — звено с известным допуском;
A4 = 200 (мм)
A5 = 30 (мм)
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5;
Компенсирующее звено: A2
Замыкающее звено: AΔ
Верхнее отклонение замыкающего звена Es(AΔ) = 0,7 мм
Нижнее отклонение замыкающего звена: Ei(AΔ) = 0 мм
Решение:
1. Определение характеристик замыкающего звена.
1.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
 |
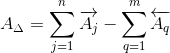(1) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
Тогда для заданной размерной цепи формула (1) принимает вид:
AΔ = A1 + A2 + A3 — (A4 + A5)
AΔ = 150 + 50 + 30 — (200 + 30) = 0(мм)
1.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
| T(A Δ ) = Es(A Δ ) — Ei(A Δ ) | (2) |
где
Es(A Δ ) – верхнее отклонение замыкающего звена;
Ei(A Δ ) – нижнее отклонение замыкающего звена;
тогда
T(AΔ) = 0,7 — 0 = 0,7(мм)
2. Определение характеристик составляющих звеньев размерной цепи.
2.1. Определение допусков составляющих звеньев
2.1.1 Определение значений единиц допуска составляющих звеньев.
По таблице 1 принимаем количество единиц допуска для каждого звена.
Таблица 1 — Значение единиц допуска i для различных интервалов размеров.
| Интервалы размеров, мм | 1-3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i, мкм | 0,55 | 0,73 | 0,90 | 1,08 | 1,31 | 1,56 | 1,86 | 2,17 | 2,52 | 2,90 | 3,23 | 3,54 |
A1 = 150, i1 = 2,52;
A2 = 50, i2 = 1,56;
A4 = 200, i4 = 2,89;
A5 = 30, i5 = 1,31;
2.1.2 Определение числа единиц допуска.
Число единиц допуска «а» находим по формуле:
 |
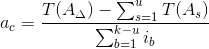(3) |
где
T(A Δ) — допуск замыкающего звена;
T(A s ) — допуск звена с известным допуском;
k – число звеньев размерной цепи;
u — число звеньев с известным допуском;
s — индекс звена с известным допуском;
b — индекс звена с неизвестным допуском;
ib — значение единицы допуска, мкм
Тогда для заданной размерной цепи формула (3) принимает вид:
| аc = | T(AΔ) — T(A3) | |
| i1 + i2 + i4 + i5 |
тогда
| аc = | 700 — 200 | = 60,4 |
| 2,52 + 1,56 + 2,89 + 1,31 |
2.1.3 Определение квалитетов составляющих звеньев.
По числу единиц допуска аc=60,4 принимаем квалитет 9 (см. табл.2).
Таблица 2 — Число единиц допуска, содержащихся в допуске по квалитетам, коэффициент точности «а».
| Квалитет IT | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэф. точн. а | 7 | 10 | 16 | 25 | 40 | 64 | 100 | 160 | 250 | 400 | 640 | 1000 |
На составляющие звенья назначаем допуски по 9 квалитету (см. табл.3).
На увеличивающие размеры допуски назначаем по H
На уменьшающие размеры допуски назначаем по h
A1 = 150H9(+0,1) (мм);
A4 = 200h9(-0,115) (мм);
A5 = 30h9(-0,052) (мм);
Таблица 3 — Величины допусков (мкм) для различных интервалов размеров (мм) и квалитетов
| Квалитеты | Интервалы (свыше) – до, мм | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| До 3 | 3-6 | 6-10 | 10-18 | 18-30 | 30-50 | 50-80 | 80-120 | 120-180 | 180-250 | 250-315 | 315-400 | 400-500 | |
| 5 | 4 | 5 | 6 | 8 | 9 | 11 | 13 | 15 | 18 | 20 | 23 | 25 | 27 |
| 6 | 6 | 8 | 9 | 11 | 13 | 16 | 19 | 22 | 25 | 29 | 32 | 36 | 40 |
| 7 | 10 | 12 | 15 | 18 | 21 | 25 | 30 | 35 | 40 | 46 | 52 | 57 | 63 |
| 8 | 14 | 18 | 22 | 27 | 33 | 39 | 46 | 54 | 63 | 72 | 81 | 89 | 97 |
| 9 | 25 | 30 | 36 | 43 | 52 | 62 | 74 | 87 | 100 | 115 | 130 | 140 | 155 |
| 10 | 40 | 48 | 58 | 70 | 84 | 100 | 120 | 140 | 160 | 185 | 210 | 230 | 250 |
| 11 | 60 | 75 | 90 | 110 | 130 | 160 | 190 | 220 | 250 | 290 | 320 | 360 | 400 |
| 12 | 100 | 120 | 150 | 180 | 210 | 250 | 300 | 350 | 400 | 460 | 520 | 570 | 630 |
| 13 | 140 | 180 | 220 | 270 | 330 | 390 | 460 | 540 | 630 | 720 | 810 | 890 | 970 |
| 14 | 250 | 300 | 360 | 430 | 520 | 620 | 740 | 870 | 1000 | 1150 | 1300 | 1400 | 1550 |
| 15 | 400 | 480 | 580 | 700 | 840 | 1000 | 1200 | 1400 | 1600 | 1850 | 2100 | 2300 | 2500 |
| 16 | 600 | 750 | 900 | 1100 | 1300 | 1600 | 1900 | 2200 | 2500 | 2900 | 3200 | 3600 | 4000 |
2.3. Определение середины поля допуска i-го звена
Середину поля допуска i-го звена определим по формуле:
 |
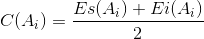(4) |
где
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
тогда
| С(A1) = | (0,1 + 0) | = 0,05 |
| 2 |
| С(A3) = | (0,2 + 0) | = 0,1 |
| 2 |
| С(A4) = | (0 + (-0,115)) | = -0,0575 |
| 2 |
| С(A5) = | (0 + (-0,052)) | = -0,026 |
| 2 |
3. Определение характеристик компенсирующего звена.
Компенсирующее звено: A2 — увеличивающее звено
3.1. Определение допуска компенсирующего звена.
Допуск компенсирующего звена определим по формуле:
 |
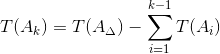(5) |
где
Т(А i ) – допуск любого составляющего звена;
T(A k) — допуск компенсирующего звена;
Тогда для заданной размерной цепи формула (5) принимает вид:
T(A2к) = T(AΔ) — (T(A1) + T(A3) + T(A4) + T(A5))
тогда
TA2к = 0,7 — (0,1 + 0,2 + 0,115 + 0,052) = 0,233 (мм)
3.2. Определение середины поля допуска компенсирующего звена
Середину поля допуска компенсирующего звена определим по формуле:
 |
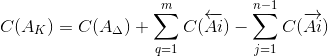(6) |
где
C(A j ) — координата середины поля допуска любого увеличивающего звена;
C(A q ) — координата середины поля допуска любого уменьшающего звена;
C(A Δ) — координата середины поля допуска замыкающего звена
Тогда для заданной размерной цепи формула (6) принимает вид:
C(A2к) = C(AΔ) + (C(A4) + C(A5)) — (C(A1) + C(A3))
тогда
С(A2к) = 0,35 + ((-0,0575) + (-0,026)) — (0,05 + 0,1) = 0,1165
3.3. Определение верхнего отклонения компенсирующего звена
Верхнее отклонение компенсирующего звена определим по формуле:
| Es(Ak ) = C(Ak ) + 0,5⋅T(k ) | (7) |
где
C(A k) — координата середины поля допуска компенсирующего звена;
тогда
Es(Aк) = 0,1165 + (0,5⋅0,233) = 0,233
3.4. Определение нижнего отклонения компенсирующего звена
Нижнее отклонение компенсирующего звена определим по формуле:
| Ei(Ak ) = C(Ak ) — 0,5⋅T(k ) | (8) |
тогда
Ei(Aк) = 0,1165 — (0,5⋅0,233) = 0
Результаты расчета.
Звенья размерной цепи с определенными допусками:
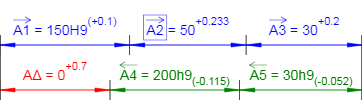
A1 = 150H9(+0,1) (мм);
A2 = 50+0,233 (мм);
A3 = 30+0,2 (мм);
A4 = 200h9(-0,115) (мм);
A5 = 30h9(-0,052) (мм);
Рисунок 2 — Схема размерной цепи. Результаты расчета.
Проверка расчета.
Проверка правильности решения задачи производится по формулам:
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
 |
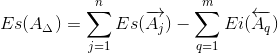(9) |
где
Es(A j ) – верхнее отклонение любого увеличивающего звена;
Ei(A q ) – нижнее отклонение любого уменьшающего звена;
Тогда для заданной размерной цепи формула (9) принимает вид:
Es(AΔ) = Es(A1) + Es(A2) + Es(A3) — (Ei(A4) + Ei(A5))
тогда
Es(AΔ) = 0,1 + 0,233 + 0,2 — ((-0,115) + (-0,052)) = 0,7
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
 |
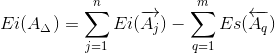(10) |
где
Ei(A i ) – нижнее отклонение любого увеличивающего звена;
Es(A q ) – верхнее отклонение любого уменьшающего звена;
Тогда для заданной размерной цепи формула (10) принимает вид:
Ei(AΔ) = Ei(A1) + Ei(A2) + Ei(A3) — (Es(A4) + Es(A5))
тогда
Ei(AΔ) = 0 + 0 + 0 — (0 + 0) = 0
Расчет размерных цепей онлайн. Прямая задача.
Шестая лекция
5. Размерные цепи
План
Общие сведения о
размерных цепях.
Виды размерных
цепей
Задачи
расчета размерных
цепей
Численный пример
проектного расчета размерной цепи
Взаимозаменяемость
определяется не только точностью
попарных соединений, но часто – суммарной
точностью комплекса элементов конструкции
(машины, прибора).
Размерная цепь
(РЦ) – совокупность размеров, относящихся
к изделию, непосредственно участвующих
в решении поставленной задачи
(конструкторской, технологической,
измерительной) и образующих замкнутый
контур (цепь). Каждый размер – звено
такой цепи.
В любой РЦ всегда
есть одно звено, называемое замыкающим,
которое физически получается последним
(при изготовлении, сборке или при
измерении). При постановке задачи расчета
РЦ это звено – исходное.
Рис.
5.1. Схема измерительной размерной цепи
Так, для случая
измерения размера АΔ
показанной на рис. 5.1 детали этот размер
и является замыкающим звеном, поскольку
его можно определить только после
измерения других размеров образуемой
здесь цепи – замкнутого контура размеров
А1
— АΔ
— А3
— А2
— А1.
Схема конструкции,
иллюстрирующей сборочную РЦ, приведена
на рис. 5.2.
Основу этой конструкции представляет
корпус 1. В нем установлены два центрирующих
узла (2 и 2′), которые обеспечивают
центрированное положение относительно
них чувствительного элемента 3
инерциального прибора (система поддержания
его положения соосно с узлами 2 и 2′ не
рассматривается). Замыкающим звеном в
соответствующей размерной цепи (рис.
5.3) является суммарный зазор (АΔ‘
+ АΔ»).
Рис. 5.2.
Схема конструкции макета системы осевого
магнитного центрирования поплавкового
чувствительного элемента: 1 – корпус;
2, 2/
— центрирующие узлы; 3 – центрируемый
элемент.
Рис.
5.3. Схема размерной цепи конструкции
макета системы осевого центрирования
Остальные размеры
РЦ – составляющие.
Все они по отношению к замыкающему
(исходному) звену делятся на увеличивающие
и уменьшающие
размеры (звенья), в зависимости от того,
увеличивается или уменьшается замыкающий
размер при увеличении рассматриваемого
составляющего звена.
Самый элементарный
частный случай РЦ – соединение вала и
отверстия (рассмотрим для положительного
зазора):
Рис. 1.5.4. Представление
посадки как частного случая РЦ: А1
– размер отверстия, А2
– размер вала, А0
– зазор (замыкающее звено); а) схемы
конструкций; б) схема РЦ
Размерную цепь
(РЦ) называют линейной,
если ее звеньями являются линейные
размеры. Размерные цепи, звеньями которых
являются, угловые размеры, называются
угловыми
размерными цепями.
Размерная цепь называется плоской, если
все звенья ее лежат в одной или нескольких
параллельных плоскостях. Пространственной
называют размерную цепь, все или часть
звеньев которой расположены в
непараллельных плоскостях.
Наиболее простыми
являются одномерные (коллинеарные)
линейные РЦ (рис. 5.1, 5.3, 5.4,б). Если звенья
РЦ не расположены параллельно, то Aj
берется как проекция соответствующего
вектора на линию замыкающего размера.
Задачи расчета
размерных цепей
Эксплуатационные
свойства машин, приборов и многих других
изделий зависят в основном от замыкающего
звена РЦ. Именно для замыкающего звена
при разработке конструкции должен быть
установлен интервал (АΔэ,нм,
АΔэ, нб)
эксплуатационных допустимых значений.
Точность составляющих звеньев РЦ играет
подчиненную роль: интервалы допустимых
значений этих размеров должны
устанавливаться исходя из заданного
интервала (АΔэ,нм,
АΔэ, нб)
. Совершенно обоснованно замыкающее
звено именуется также исходным.
Основная задача,
решаемая на этапе проектирования (задача
проектного расчета РЦ):
определить интервалы допустимых значений
размеров составляющих звеньев по
заданному интервалу (АΔэ,нм,
АΔэ, нб)
эксплуатационно допустимых значений
замыкающего звена. Данная задача (еще
называемая задачей синтеза) может быть
сформулирована и в отношении предельных
отклонений.
Если предельные
отклонения составляющих размеров
известны (в результате решения проектной
задачи), то для проверки их соответствия
интервалу (АΔэ,нм,
АΔэ, нб)
решают обратную задачу.
Расчетные
соотношения, необходимые для решения
задач РЦ
Отправное
соотношение, связывающее параллельно
расположенные звенья:
, (5.1)
где m – число
увеличивающих размеров; p — общее число
звеньев (вместе с исходным).
Из (5.1) следуют
выражения для наибольшего и наименьшего
значений АΔ
:
; (5.2)
. (5.3)
Отсюда, на основании
определения допуска Т размера А как
T = Aнб
– Aнм
(5.4)
легко получить
формулу, связывающую допуски всех
звеньев:
. (5.5)
То есть допуск
замыкающего звена равен сумме допусков
составляющих звеньев, что имеет совершенно
очевидный смысл: нельзя
получить высокую суммарную точность
изготовления, сборки, измерения без
соответственно высокой точности
элементов, из которых складывается
результат указанных процессов.
Для решения задач
РЦ необходимо располагать еще и
соотношениями, связывающими предельные
отклонения звеньев. Они также могут
выведены из отправных выражений (5.2),
(5.3) с учетом того, что
Ajнб
= Aj
+ Es(Aj);
Ajнм
= Aj
+ Ei(Aj), (5.6)
где ES,
Ei
– верхнее и нижнее предельные отклонения.
Тогда
; (5.7)
. (5.8)
Теперь можно решать
задачи расчета РЦ. Следует особо
подчеркнуть, что полученные выше формулы
применяют для решения задач при
условии полной взаимозаменяемости
(метод
максимума-минимума).
Способы решения
задачи проектного расчета РЦ
Здесь необходимо,
во-первых, распределить допуск замыкающего
звена по составляющим звеньям, а,
во-вторых, назначить предельные
отклонения. Первая часть задачи может
быть выполнена двумя способами:
— равных допусков;
— равноточных
допусков.
Более простой, но,
вместе с тем, грубый – способ
равных допусков:
Tj
= Tср
= TΔ
/ (p-1),
(5.9)
Полученное значение
следует округлить до стандартного(ых),
после чего проверить выполнение условия
. 
. (5.10)
Этот способ дает
хорошие результаты только для РЦ с
близкими по величине составляющими
звеньями. Если же составляющие размеры
цепи существенно отличаются по величине,
то будут сильно различаться и квалитеты
их точности. Например, допуск IT = 25 мкм
соответствует 9-му квалитету для размера
3 мм и 5-му квалитету для размера 400 мм.
Такое различие квалитетов точности
неэкономично (ведь, как уже отмечалось,
каждый более точный квалитет дается
при нелинейно возрастающей стоимости).
При решении задачи
способом равноточных
допусков
стремятся получить допуски составляющих
размеров по одинаковым квалитетам.
Следовательно, в допуске каждого звена
должно содержаться одно и то же число
n единиц допуска.
Здесь исходят,
таким образом, из формулы
ITj
= nср
* ij(A)
, (5.11)
где ij(A)
– единица допуска размера А.
Отсюда искомое
число единиц допуска находится как
. (5.12)
Полученное значение
nср
дает возможность выбрать №№ квалитетов
так, чтобы выполнялось условие (5.10).
После того, как
допуски назначены, остается найти
предельные отклонения. Сделать это
удобнее всего, следуя известному правилу
[1, 2, 3]: полем допуска каждого из размеров
охватывающих внутренних элементов
считать поле допуска основного отверстия
(рис.5.5,а), полем допуска каждого из
размеров охватываемых наружных элементов
считать поле допуска основного вала
(рис. 5.5,б), а поля допусков звеньев, не
относящихся ни к валам ни к отверстиям
считать симметричными относительно
линии номинального размера (рис. 5.5,в).
Это правило надо применить ко всем
составляющим размерам, за исключением
одного – увязочного или резервного.
Два предельных отклонения этого
резервного звена остаются неизвестными,
определяемыми из двух уравнений.
Рис.
5.5.
К выбору предельных отклонений
составляющих звеньев размерной цепи
(проектный расчет)
Далее предлагается численный пример
проектного расчета РЦ.
Дано. Размерная цепь (рис. 5.3), относящаяся
к конструкции, приведенной на рис. 1.5.2.
Величина магнитного зазора АΔ
задана в следующем эксплуатационном
интервале: 40 ≤ АΔ ≤ 150 мкм.
Номинальные размеры:
А1 =А3 = 10 мм; А2 = 80 мм; А4
= 60 мм.
Требуется определить предельные
отклонения Ei(Aj) — ?, Es(Aj)
— ?
Решение. Число единиц допуска ncр
рассчитывается по формуле (5.12) при
следующих значениях единиц допуска ij:
i1
= i3 =
0,9 мкм; i2
= i4
=1,9 мкм.
ncр = 110 / 5,6 = 19,6 .
Полученное число, дает основания взять
допуски по квалитетам 7 и 8. Пусть
IT1 =
IT3 =
22 мкм (8-й
кв.); IT2
= IT4
= 30 мкм (7-й
кв.)
Σ ITj = 104 мкм, что меньше ширины
заданного эксплуатационного интервала
примерно на 6%.
Теперь надо определить границы полей
допусков Ei(Aj) — ?, Es(Aj)
— ?
Увязочным (резервным) звеном назначим
А2 (расстояние между торцевыми
поверхностями корпуса). Для размера А4
примем поле допуска основного вала
(рис. 5.5), а для размеров А1, А3
– симметричные относительно линии
номинального размера поля допусков.
Уравнения (5.7), (5.8) в рассматриваемом
случае имеют вид:
ESΔ
= ES2
– Ei1
— Ei3
— Ei4
;
EiΔ
= Ei2
– ES1
– ES3
– ES4
.
Из этих уравнений и определяются
неизвестные ES2 и Ei2 :
Es2 = 150 – 22 – 30 = 98 мкм; Ei2 = 40 +
22 + 0 = 62 мкм.
Допуск Т = 36 мкм округлим до стандартного
IT = 30 мкм.
Литература
-
Белкин В.М. Допуски
и посадки (Основные нормы взаимозаменяемости).
– М.: Машиностроение, 1992.- 528 с. -
Дунин-Барковский
И.В. Взаимозаменяемость, стандартизация
и технические измерения. – М.: Издательство
стандартов, 1987. — 352 с. -
Якушев А.И.
Взаимозаменяемость, стандартизация и
технические измерения. – М.:
Машиностроение,1986.
Соседние файлы в папке КЛ
- #
- #
- #
- #
- #
- #
- #
- #
Допуски размеров, входящих в размерные цепи
Основные понятия, термины и определения
Машины, механизмы и создаваемые человеком сооружения образованы множеством соединений деталей, которые образуют узлы, агрегаты и прочие элементы конструкций. Каждая деталь имеет свои линейные, угловые и диаметральные размеры, которые, как нам уже известно, не могут соответствовать идеалу, называемому номинальным размером – всегда присутствуют погрешности размеров, обусловленные несовершенством технологий производства, средств измерений и другими факторами.
По этой причине каждая сопрягаемая деталь механизма имеет по замыслу конструкторов определенные отклонения от номинала и допуски на те или иные размеры, формы и т. п.
А когда все эти детали в механизме или машине образуют взаимосвязанную цепочку, допуски размеров каждого составляющего звена этой цепи оказывают влияние на размеры и допуски размеров всех остальных звеньев.
Поэтому обеспечение правильной работы всей машины или какого-либо элемента ее конструкции может быть достигнуто рациональным подбором предельных отклонений каждой детали.
Для определения оптимального соотношения предельных взаимосвязанных размеров одной или нескольких деталей, входящих в этот сборочный узел, проводят размерный анализ, предварительно построив размерные цепи.
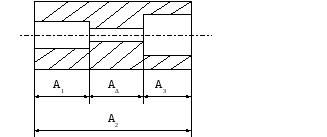
Размерной цепью (рис. 1) называют совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи (РД 50-635-87 «Цепи размерные. Основные понятия. Методы расчета линейных и угловых цепей»).
Если в такую совокупность входят размеры одной детали, то такую цепь называют подетальной размерной цепью (рис. 2), а если участвуют размеры нескольких деталей, то сборочной размерной цепью (рис. 3).
Для анализа размерной цепи необходимым условием является замкнутость размерного контура, т. е. цепь должна замкнуться.
***
Виды размерных цепей
По взаимному расположению размеров и их характеру размерные цепи делятся на линейные, угловые, плоские и пространственные.
Линейными называют размерные цепи, звеньями которых являются линейные размеры. Соответственно, угловыми называют размерные цепи, звеньями которых являются угловые размеры.
Если все звенья цепи лежат в одной или в нескольких параллельных плоскостях, такую цепь называют плоской, а если звенья цепи не параллельны одно другому и лежат в непараллельных плоскостях, то такую цепь называют пространственной.
По назначению размерные цепи подразделяют на следующие виды:
- конструкторские – обеспечивают точность изделия на этапе его проектирования;
- технологические – выражают связь размеров обрабатываемой детали с технологическим процессом;
- измерительные – решают задачу измерения определенных звеньев, характеризующих точность изделия.
***
Звенья размерных цепей
Размеры, составляющие размерную цепь, называются звеньями.
Звено, которое является исходным при постановке задачи или получается последним в процессе обработки детали, ее измерения или сборки изделия, называют замыкающим (на рис. 3 замыкающим звеном является зазор «S»).
Таким звеном может быть звено, точность которого определяет точность изготовления детали в целом (для подетальной цепи) или всего собранного узла (для сборочной цепи).
Номинальный размер и точность замыкающего звена зависят от точности всех остальных звеньев цепи, которые называются составляющими звеньями. Изменение их размеров приводит к изменению размеров замыкающего звена (но недолжно вызвать изменения размеров исходного звена).
Исходным называют звено, к которому предъявляются основные требования – точность в соответствии с техническими условиями, от которого зависит работоспособность узла. При сборке исходное звено, как правило, получается последним, поэтому оно также называется замыкающим.
Составляющие звенья обозначаются на схемах или чертежах прописными буквами русского алфавита (А, Б, В и т. д.) или строчными буквами греческого алфавита (кроме букв α, β, ω, ξ, λ) с соответствующим порядковым номером 1, 2, 3, ….., m. При этом замыкающее звено обозначается соответствующей буквой с индексом Δ (например, АΔ).
Размерную цепь удобно представлять в виде замкнутого векторного контура, в котором векторы направлены либо по часовой стрелке, либо против нее (рис. 5).
Звенья цепи, по отношению к замыкающему звену, могут быть увеличивающими и уменьшающими. Увеличение размеров увеличивающих звеньшев приводит к увеличению и замыкающего звена при неизменном исходном звене.
И наоборот — увеличение размеров уменьшающих звеньев приводит к уменьшению размеров замыкающего звена.
На схемах уменьшающие звенья имеют направления, одинаковые с направлением замыкающего звена (←), а увеличивающие – противоположное (→).
***
Анализ размерных цепей
Анализ размерных цепей и их расчет проводят с целью:
- определения числовой взаимосвязи размеров, обеспечивающих эксплуатационные требования и экономически целесообразную точность выполнения этих размеров;
- экономически выгодного вида взаимозаменяемости (полной или неполной);
- допусков размеров и рационального порядка их простановки на чертежах.
Задачи размерного анализа делятся на два вида:
- прямая задача решается при конструировании деталей и узлов для определения допусков и предельных отклонений составляющих звеньев по заданным номинальным размерам всех размеров цепи и заданным предельным размерам исходного звена;
- обратная задача, решение которой позволяет определить номинальный размер, предельные отклонения и допуск замыкающего или исходного звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев. Задача решается, как правило, при проверке правильности решения прямой задачи.
***
Методы расчета размерных цепей
Существует несколько методов решения прямой и обратной задачи в условиях полной и неполной взаимозаменяемости. Наиболее распространены следующие методы:
- расчет на максимум – минимум (обеспечивает полную взаимозаменяемость);
- теоретико-вероятностный (обеспечивает полную или частичную взаимозаменяемость);
- групповой взаимозаменяемости;
- равных допусков;
- регулирования;
- пригонки и др.
Рассмотрим некоторые из них на примере расчета размерной цепи подшипникового узла (рис. 4).
***
Метод расчета на максимум – минимум (обратная задача)
Известны: Аi; ESAi; EIi; TАi.
Определить: AΔ; ESAΔ; EIAΔ; TAΔ.
Расчет осуществляется в следующем порядке.
1. Составляется схема размерной цепи, определяется m – общее число звеньев цепи (рис. 5).
2. Определяется характер звеньев: AΔ – замыкающее звено; А1 – увеличивающее звено; А2; А3; А4 – уменьшающие звенья. При этом n – число увеличивающих звеньев; p – число уменьшающих звеньев; m — общее число звеньев, включая замыкающее.
Тогда n + p = m — 1.
3. Составляется уравнение номинальных размеров для частного случая:
АΔ = А1 – (А2 + А3 + А4),
в общем случае это уравнение будет иметь вид: АΔ = ∑ Аi ув — ∑ Ai ум.
4. Определяется допуск замыкающего звена, для чего составляется уравнение допусков:
ТАΔ = АΔmax — АΔmin,
а предельные размеры замыкающего звена равны:
АΔmax = ∑ Аi ув max — ∑ Ai ум min;
АΔmin = ∑ Аi ув min — ∑ Ai ум max.
Поскольку разность между предельными размерами звеньев есть их допуск, можно записать:
ТАΔ = ∑ ТАi ув — ∑ ТAi ум, (1)
а так как сумма увеличивающих и уменьшающих звеньев равна n + p = m — 1, то
ТАΔ = ∑ТАi,
т. е. допуск замыкающего или исходного звена равен сумме допусков составляющих звеньев.
5. Находятся предельные размеры замыкающего звена, т. е. определяются его верхнее и нижнее отклонение:
ESАΔ = ∑ ESАi ув — ∑ ESAi ум;
EIАΔ = ∑ EIАi ув — ∑ EIAi ум.
6. По предельным отклонениям определяются предельные размеры замыкающего или исходного звена:
АΔmax = АΔ + ESAΔ;
АΔmin = АΔ + EIAΔ.
Поскольку расчеты показали, что допуск замыкающего звена равен сумме допусков всех составляющих звеньев (формула 1), необходимо стремиться, чтобы число звеньев в цепи было минимальным, тогда минимальной будет и погрешность.
***
При решении прямой задачи размерного анализа можно воспользоваться методом равных допусков, основанный на предположении, что допуски всех составляющих звеньев равны, или методом одинаковой точности (метод допусков одного квалитета точности).
В условиях массового и крупносерийного производства расчет размерных цепей изложенными выше методами часто не дает экономически выгодного результата. Поэтому в этих видах производства целесообразно использовать теоретико-вероятностные методы расчета, которые основаны на суммировании средних размеров, определенных с учетом случайных погрешностей. При этом замыкающее звено размерной цепи принимается за случайную величину, являющуюся суммой независимых случайных переменных размеров составляющих звеньев.
Для подробного ознакомления с другими методами размерного анализа целесообразно изучить документ РД 50-635-87 «Методические указания. Цепи размерные. Основные понятия. Методы расчета размерных и угловых цепей».
***
Допуски и посадки резьбовых соединений