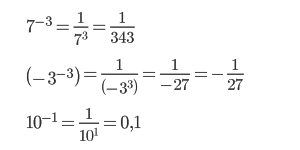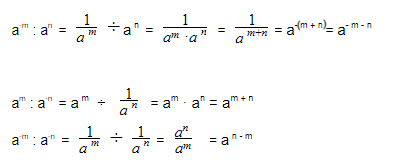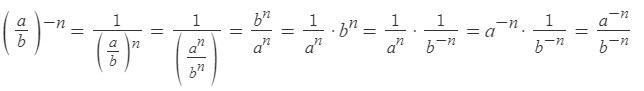Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.
23+ 34= 8 + 81= 89
63— 33= 216 — 27 = 189
- Если есть скобки — начинать вычисления нужно внутри них
- Только потом возводим этот результат из скобок в степень
- Затем выполняем остальные действия: сначала умножение и деление по порядку (слева направо), а в конце — сложение и вычитание по порядку (слева направо)
Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 23+ 24= 8 + 16= 24
Сложение степеней с разными основаниями
В целом это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые показатели. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 34+ 54=81 + 625 = 706
- 14+ 72= 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно так же, как и в предыдущем примере. Если показатели степени одинаковые, а основания разные — нельзя сложить основания и затем эту сумму возводить в степень.
- 63+ 33= 216 + 27 = 243
В уравнениях с этим все проще. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a2.
- 2a2 + 3a2 = 5a2
2,3, 5 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
- 63— 33= 216 — 27 = 189
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые показатели степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 54— 44= 625 — 256 = 369
- 74— 32= 2401 — 9 = 2392
Вычитание степеней с одинаковыми показателями
Все точно так же, как и со сложением. Если показатели степени одинаковые, а основания разные — нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
- 63— 33= 216 — 27 = 189
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a2) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a2.
- 5a2 — 3a2 = 2a2
5, 3, 2 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Умножение и деление степеней
Здесь всё не так однозначно, как со сложением и вычитанием — общие правила для всех случаев выделить не получится. Все зависит от оснований и показателей степеней, с которыми нужно выполнить манипуляции.
Например, действия со степенями с разными основаниями будут отличаться от действий с числами, у которых основания одинаковые. Работа с показателями — одинаковыми и разными — тоже отличается. Давайте разбираться.
Умножение степеней с одинаковыми показателями
Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:
- an · bn = (a · b)n , где
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
- a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
- 35 · 45 = (3·4)5 = 125 = 248 832
- 16a2 = 42·a2 = (4a)2
Умножение степеней с одинаковыми основаниями
Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:
am · an= am+n, где
a — основание степени
m, n — показатели степени, любые натуральные числа
- 35 · 32 = 35 + 2 = 37 = 2 187
- 28 · 81= 28 · 23 = 28 + 3 = 211 = 2048
Умножение степеней с разными основаниями и показателями
Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 28 · 81= 28 · 23 = 211 = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:
- 33 · 52 = 27·25 = 675
Деление степеней с одинаковыми основаниями и одинаковыми показателями
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Деление чисел с одинаковыми показателями степени
При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:
- an : bn = (a : b)n , где
a, b — основание степени, любые числа, b ≠ 0,
n — показатель степени, натуральное число
Пример:
Деление степеней с разными основаниями и показателями
Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:
- 33 ÷52 = 27÷25 = 1,08
Степень с отрицательным показателем и её свойства
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
- a3÷a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
am · an = am+n
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
Как представить число в виде степени
Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.
Например, представим в виде степени число 243:
243 = 3 × 3 × 3 × 3 × 3 = 35
|
Как вычитать числа с одинаковым основанием и разными степенями?Vyacheslav 8 лет назад
Rafail 8 лет назад Либо вычислить сами числа а затем произвести вычитание, либо сначала вынести за скобку число с меньшим показателем степени. Проще объяснить на примере. Например: 2^7-2^5=128-32=96, или 2^7-2^5=2^5*(2^2-1)=2^5*(4-1)=2^5*3=(3*2^5)=32*3=96, но можно и оставить в виде 3*2^5. автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
0
Как вычитать числа с одинаковым основанием и разными степенями?
1 ответ:
1
0
Либо вычислить сами числа а затем произвести вычитание, либо сначала вынести за скобку число с меньшим показателем степени. Проще объяснить на примере.
Например: 2^7-2^5=128-32=96, или 2^7-2^5=2^5*(2^2-1)=2^5*(4-1)=2^5*3=(3*2^5)=32*3=96, но можно и оставить в виде 3*2^5.
Читайте также
Для того чтобы возвести число в дробную степень нужно выполнить две операции: во-первых, возвести число в степень числителя дробной степени (числитель — это то что у дроби находится сверху), во-вторых, из того что получилось после возведения в степень нужно извлеч корень той степени чему равен знаменатель дробной степени (знаменатель — это то что стоит внизу дроби). Например, нам нужно возвести 3 в степень 3/7, сначало мы возводим 3 в степень числителя т.е. в куб, получаем 27, а затем извлекаме корень седьмой степени. Если дробная степень представленна с целой частью, то есть например нужно 2 возвести в степень 1 целая 1/3 то степень нужно представить в виде обычной дроби т.е. в данном случае это будет 4/3, а затем производить вычисления, 2 возводим в 4 степень получаем 16 и затем берем кубический корень из 16. Таким же образом в случае если нужно возвести число в степень 1,5, степень можно представить в виде обычной дроби 15/10 или 3/2 и произвести вычисления.
Очевидно, что если бы все вычисления в вопросе проводились в числах, записанных в десятичной системе счисления, то вопрос бы большого смысла не имел. Не имеет смысла спрашивать, чему равно 84, если всё проводится с обычными десятичными числами. То есть методом исключения мы определили, что в примере с умножением применена какая-то иная система, не десятичная. Нужно выяснить, какая именно. Мы видим, что результат, который должен был бы равен 64, записывается в той системе как 54. Нет сомнения, что 5 — это цифра десятков, а 4 — цифра единиц. Обозначим переменной x пока неизвестное нам искомое основание системы. Составим уравнение:
5x + 4 = 64,
откуда:
5x = 60;
x = 12.
Мы нашли, что умножение проводилось по двенадцатеричной системе. Теперь мы можем найти, чему равно двенадцатеричное число 84 по нашей общепринятой десятичной системе:
8 * 12 + 4 = 96 + 4 = 100.
Ответ: 84 (12) = 100 (10). В скобках — основания систем счисления.
Пусть рубашка стоит 100 единиц, тогда брюки будут стоить 130 единиц, а пиджак будет стоить 169 единиц. Он дороже брюк на 39 единиц. Единиц, но не процентов. А вот 39 единиц от 130 единиц будут составлять всего 30%.
Ответ: пиджак дороже брюк на 30%.
Насколько я понял, R – это значок функции, например f(x). Поэтому запишем ваш первый интеграл так I = int[f(sinx)cosxdx]. Сюда входят и синус и косинус. Самый простой способ решения это заменить косинус на синус, или наоборот. При этом надо знать следующее равенство: d(sinx) = cosxdx. Или cosxdx = d(sinx). Тогда ваш интеграл примет более удобный вид I = int[f(sinx)dsinx]. Сюда входит только одна функция sinx. Чтобы было еще понятней, сделаем такую замену переменных: sinx = z. Тогда I = int[f(z)dz]. Для того чтобы решить этот интеграл, надо знать конкретный вид функции f(z).
Возьмем ваш второй интеграл I = int[f(cosx)sinxdx]. Метод решения тот же самый. Но надо вспомнить дифференциал от косинуса. Он тоже есть в таблицах. d(cosx) = -sinxdx. То есть sinxdx = — d(cosx). Тогда ваш второй интеграл примет вид I = -int[f(cosx)d(cosx)]. Для удобства введем замену переменных cosx = z. Имеем I = -int[f(z)d(z)]. Интегралы в алгебраическом виде решать проще, чем в тригонометрическом виде. И здесь надо знать конкретный вид функции f(z).
Теперь ваш третий интеграл int[f(sinx,cosx)dx]. Сделаем такую же замену переменных, как и в предыдущем случае. Здесь уже сложнее. Надо в подинтегральном выражении оставить только синус или только косинус, сделать что проще. Например, выразим sinx через cosx. Из тригонометрии мы знаем, что sin^2(x) + cos^2(x) = 1. То есть сумма квадратов синуса и косинуса равна 1. Отсюда sin^2(x) = 1 — cos^2(x). Тогда sinx = корень[1 — cos^2(x)]. Где корень[ ] означает взять квадратный корень из выражения, стоящего в квадратных скобках. То есть мы заменили синус на косинус. Остается интеграл только от косинуса. I = int[f(cosx)]dx. Например, имеем интеграл I = int[cos^2x * sinxdx]. Заменим синус на косинус. I = int{cos^2x * корень[1 — cos^2(x)]dx}. Получилось сложное выражение. Но метод решения вашего интеграла – надо выразить синус через косинус или косинус через синус, и выбрать что проще. Для решения интеграла int[f(cosx)]dx тоже бывает проще перейти к алгебраическому выражению. Сделаем замену переменных cosx = z. Но dz = dcosx = -sinxdx = — корень[1 – cos^2x]dx = — корень[1 – z^2]dx. Отсюда dx = -dz/корень[1 – z^2]. Имеем I = int[f(cosx)]dx = -int[f(z)dz/корень(1 – z^2)].
Криволинейная трапеция – это плоская фигура, контуры которой ограниченны: а) внизу – осью абсцисс, б) по бокам – вертикальными прямыми, в) верхний контур – графиком неотрицательной неприрывной функции. Как и любая плоская фигура, криволинейная трапеция имеет площадь (без названия).
А вот ФОРМУЛА, с помощью которой определяется эта площадь, название имеет. Вычисление площади проводят с применением интеграла.
В 19 веке идеи интегральных исчислений были приведены в математическую систему английским физиком Иссаком Ньютоном и немецким философом, математиком и физиком Вильгемом Лейбницом. К окончательному верному выводу ученые шли разными путям. И дабы не обидеть никого из них, по решению других ученых, было принято такое решение.
Формула, с помощью которой определяется площадь криволинейной трапеции носит название этих двух ученых – формула Ньютона-Лейбница.
6 Простые шаги для добавления и вычитания в научной записи
Главный / 8 -й класс / 6 Простые шаги для добавления и вычитания в научной нотации
Вот как добавить и вычесть в научной записи
. Когда Сложение и вычитание в научном представлении степени чисел, которые вы складываете или вычитаете, должны быть равны. Если они уже равны, то можно просто сложить коэффициенты. Если показатели степени не равны, то вы должны сделать их равными, переместив один из десятичных знаков. Самый простой способ сделать десятичные дроби равными — сделать меньшую степень равной большей, переместив десятичную дробь влево. Вы добавляете единицу к показателю степени для каждого пробела, на который вы перемещаете десятичную точку влево. Когда показатели равны, вы можете добавить или вычесть коэффициенты. Последний шаг для Сложение и вычитание в экспоненциальном представлении для обеспечения того, чтобы коэффициент был между 1 и 10. Если это не так, вы должны переместить десятичную точку так, чтобы она была.
Общий базовый стандарт: 8.EE.A.3
Связанные темы: Квадратные корни, кубические корни, иррациональные числа, степени 10, введение в экспоненциальную запись, преобразование чисел в экспоненциальную запись, преобразование чисел из экспоненциальной записи , Умножение в экспоненциальном представлении, Деление в экспоненциальном представлении
Пример задачи на сложение и вычитание в экспоненциальном представлении
При сложении и вычитании в экспоненциальном представлении степени слагаемых или вычитаемых чисел должны быть эквивалентны. В том случае, если они эквивалентны, можно просто объединить коэффициенты вместе. Если степени не эквивалентны, вы должны сделать их эквивалентными, переместив один из десятичных знаков так, чтобы степени стали эквивалентными. Последним шагом для сложения и вычитания в экспоненциальном представлении является проверка того, что коэффициент находится где-то в диапазоне от 1 до 10.
6 быстрых шагов для сложения или вычитания в экспоненциальном представлении
- Проверьте, равны ли степени в степени десятков.
- Если степени равны, то вы можете добавить или вычесть коэффициенты.
- Если степени не равны, вы должны сделать их равными, переместив десятичную точку.
- Перемещение десятичной точки влево будет прибавлять к показателю степени для каждой цифры, которую она перемещает влево.
- Когда степени равны, вы можете складывать или вычитать коэффициенты.
- Убедитесь, что ваш коэффициент находится между единицей и десятью, так как он должен быть записан в научной нотации.
Посмотрите объяснение сложения и вычитания в экспоненциальном представлении видео
Посмотрите наше бесплатное видео о том, как решить сложение и вычитание в экспоненциальном представлении . В этом видео показано, как решить проблемы, которые есть на нашем бесплатном 9Рабочий лист 0003 Adding and Subtracting in Scientific Notation , который вы можете получить, отправив свой адрес электронной почты выше.
Посмотрите бесплатное видео «Сложение и вычитание в экспоненциальном представлении» на YouTube здесь: «Сложение и вычитание в экспоненциальном представлении»
Расшифровка видео:
Это видео посвящено сложению и вычитанию в экспоненциальном представлении. Вы можете получить рабочий лист, который мы используем в этом видео, бесплатно, нажав на ссылку в описании ниже.
Первая задача, которую мы собираемся использовать, чтобы показать вам сложение и вычитание экспоненциальной записи, дает нам 9 умножить на 10 до 9 минус 2 умножить на 10 до 9. При сложении или вычитании в экспоненциальном представлении вы будете брать коэффициенты каждого числа, которое добавляется или вычитается, и вы собираетесь либо складывать, либо вычитать эти два вместе. В этом случае у нас есть 9 и 2, которые мы в конечном итоге будем складывать или вычитать вместе. Вторая часть добавления или вычитания научной записи, о которой вам нужно знать, заключается в том, что наши степени 10 должны быть равны.
Другими словами, показатель степени 10 должен быть одинаковым. Например, если бы это было, скажем, 10 в седьмой степени, мы не могли бы вычесть их, потому что этот показатель равен 9.и этот показатель равен 7. Нам нужно было бы изменить 7 на 9, и когда это было 9, мы могли бы складывать или вычитать, но в случае нашего первого примера у нас есть совпадающие показатели степени.
Итак, мы собираемся решить эту проблему. При решении этой задачи мы возьмем наши коэффициенты, равные 9 и 2, и вычтем их друг из друга, а затем перепишем нашу степень числа 10 прямо рядом с ним. Мы будем делать 10 раз в 9-й степени, при сложении или вычитании степень 10 должна быть равна. Как только показатель степени равен, вы сохраните показатель степени в своем ответе. Следующим шагом будет фактически пойти дальше и вычесть коэффициент. 9минус 2 равно 7, а затем мы перепишем времена, а затем нашу степень 10, которая равна 10 в 9-й степени. Таким образом, наш ответ в научных обозначениях будет 7 умножить на 10 в 9-й степени, потому что мы не меняем степень 10 в нашем ответе.
Число 2 очень похоже на число 1. Нам дано 3 шесть раз по десять до семи плюс две целых один раз по десять до седьмого. Мы знаем, что добавляем, теперь мы собираемся сложить наши коэффициенты вместе, что составляет три целых шесть десятых плюс две целых один десятых. Мы продолжим и напишем, что три целых шесть десятых плюс две целых десятых. Теперь, если вы посмотрите на нашу степень 10, наш показатель степени одинаков для каждой степени 10. 10 в седьмой здесь и десять в седьмой здесь. Нам не нужно менять показатель в степени 10, потому что он уже равен, мы просто перепишем 10 в седьмой степени под нашей задачей. Затем мы продолжим и добавим наши коэффициенты: три целых шесть десятых плюс две целых десятых — это пять целых семь десятых, а затем умножим на 10, а затем уменьшим семерку. Таким образом, наше решение будет пять целых семь десятых в седьмой степени.
Число три немного сложнее, потому что оно имеет один дополнительный шаг: семь целых семь целых трижды десять до пятой минус пять целых три десятых до четвертой.
Теперь в этом случае мы не можем вычесть их друг из друга, потому что наши показатели степени не совпадают. Вы заметите, что у этого есть четыре, и у этого есть показатель степени пять. Они не равны, что означает, что мы не можем их вычесть, мы должны изменить одно из них на другое, а затем, когда они равны, вы можете их вычесть.
Самый простой способ изменить показатель степени 10 — всегда превращать меньший показатель в больший. Что мы собираемся сделать, так это изменить это 4 на 5. Как мы это делаем, мы перемещаем десятичную дробь влево и ставим ее здесь, а затем добавляем единицу к нашему показателю степени. Каждый раз, когда вы перемещаете десятичную дробь влево, вы добавляете единицу к показателю степени. Например, предположим, что мы перемещаем десятичную дробь вместо того, чтобы перемещать ее сразу, мы перемещаем ее один раз два раза, а затем добавляем два к этому показателю степени. Это было бы четыре плюс два, но если бы мы сделали 4 плюс 2, это было бы 6, и мы не пытаемся получить 6, мы пытаемся получить пять, поэтому добавление двух не имеет смысла.
Что мы собираемся сделать, так это сдвинуть его влево один раз, а затем добавить один, потому что четыре плюс один равно пяти, и мы пытаемся получить пять. Мы пытаемся сделать показатели равными, поэтому давайте перепишем нашу задачу.
Теперь мы знаем, что у нас есть семь целых семь десятых три на этой стороне, умноженное на 10 в пятой степени минус, и теперь на этой стороне у нас есть пять целых 3, потому что мы сдвигаем десятичную дробь влево на один раз. 10 в пятой степени, потому что это 4 плюс 1, что будет равно 5. Теперь наши показатели степени равны, здесь у нас 5, а здесь 5, так что мы можем продолжить и вычесть наши коэффициенты. Мы сделаем семь целых семь десятых три минус 0,53, а затем перепишем, умноженный на 10. А затем нашу степень 10, которая равна 10 в пятой степени, потому что это то, что мы создали, чтобы сделать их равными. Затем мы продолжим и вычтем наши коэффициенты, семь целых семь десятых три минус 0,53 будет семь целых две десятых умножить на 10 в пятой степени.
И семь целых два десятых в пятой степени будет нашим решением.
Видео с вопросами: вычитание чисел в стандартной форме
Стенограмма видео
Найдите значение 8,7, умноженное на
10 в отрицательной пятой степени минус 7,7, умноженное на 10 в отрицательной четвертой степени
власть, давая свой ответ в стандартной форме.
Эти номера нам дали
в стандартной форме, также известной как научная нотация, что означает, что они
сформируйте 𝑎, умноженное на 10 в 𝑛-й степени, где абсолютное значение 𝑎 равно
больше или равно единице и меньше 10, а 𝑛 — целое число. Нам не нужно брать эти цифры
из стандартной формы, чтобы вычесть их. Но есть одна вещь, которую мы должны
сделать сначала. Нам нужно убедиться, что оба числа
имеют одинаковую степень 10. Итак, мы начнем с требования одного из
они должны быть переписаны, чтобы сделать степени 10 одинаковыми.
Для отрицательных способностей проще
перепишите вариант с более высокой степенью так, чтобы он имел ту же мощность 10, что и
с меньшей мощностью. Так что в данном случае это будет
7,7 умножить на 10 в минус четыре степени. Мы хотим переписать это как число
умножить на 10 в минус пятой степени. Мы можем начать с записи 10 в
отрицательную четвертую степень как 10 к единице добавить отрицательную пятую степень, видя как единицу и
минус пять дает нам минус четыре.
В этот момент запомните
правило экспоненциального произведения: 𝑥 в степени 𝑚 умножается на 𝑥 в степени 𝑛 равно 𝑥
к 𝑚 добавить силу 𝑛. Мы можем использовать это, чтобы записать 10 в
один прибавляет отрицательную степень пять как 10 к первой степени, умноженной на 10 к
отрицательная пятая степень. На самом деле мы можем просто записать 10 в
первая степень равна 10.
Помните, что наша цель здесь состоит в том, чтобы мы
хотите получить что-то, умноженное на 10 в отрицательной пяти степени. Итак, теперь мы умножаем 7,7 на 10, чтобы
получить 77 умножить на 10 в отрицательной степени пять.
Теперь, когда оба номера одинаковы
степень 10, мы вычитаем. Итак, мы вычисляем 8,7, умноженное на
на 10 в отрицательной пятой степени минус 77 умножить на 10 в отрицательной пятой степени
сила. Это точно так же, как 8.7
минус 77 умножить на 10 в минус пятой степени. Это дает нам отрицательное значение 68,3.
умножить на 10 в минус пятой степени.
Этого номера на самом деле нет в
стандартная форма, потому что стандартная форма требует абсолютного значения 𝑎, которое равно
68,3, чтобы быть между 1 и 10. Итак, нам нужно преобразовать
этот результат в стандартную форму. Мы можем сделать это аналогично
ранее, используя правило произведения экспоненты.
Зачем уметь умножать и делить степени?
Умение умножать степени важно в математике, т.к. оно помогает быстро вычислять произведения и деления многих чисел со степенями, что может быть полезно в решении различных задач, таких как вычисление площади, объема или поверхности фигур, вычисление значений функций и т.д.
Умножение и деление степеней может использоваться в различных областях математики и науки, таких как:
- Алгебра: для умножения и деления многочленов, вычисления различных формул и выражений.
- Геометрия: для вычисления площади, объема или поверхности фигур, расчета расстояний и углов.
- Физика: для вычисления силы, энергии, давления и т.д.
- Информатика: для вычисления сложности алгоритмов, мощности вычислительных систем и т.д.
- Другие науки: в экономике, биологии, медицине и других областях умножение и деление степеней используется для вычисления различных показателей и метрик.
Кроме того, если вы любите поддерживать в тонусе свой мозг, вам тоже очень пригодится умение работать со степенями, потому что оно позволит решать намного больше интересных примеров и задач. Естественно, это навык крайне важен в школе и институте, ведь от него в большой степени зависит успеваемость учащегося.
Умение умножать и делить степени пригодится школьнику и студенту, а также любому человеку, чья деятельность связана с вычислениями. А прежде, чем учиться умножать и делить степени, важно усвоить несколько базовых основ.
Что такое степенные выражения?
Первое определение степени гласит, что степень n для числа a – это произведение множителей, равных величине a, взятой n раз.
Возьмем, например, an. Здесь a является основанием степени, а n определяет показатель этой степени.
Исходя из этого, можно получить формулу:
an = a × a × a … × a
А сама запись так и читается: a в степени n.
Можно сказать проще: степень (конкретно ее показатель) указывает на то, сколько раз нужно умножить основание степени само на себя.
Есть также и второе определение степени, согласно которому, степенное выражение – это выражение, в составе которого имеется степень.
В принципе, все просто, но перед освоением действий со степенными выражениями важно запомнить свойства степеней.
Свойства степеней
Если вы хотите грамотно и правильно работать со степенями, нужно раз и навсегда запомнить пять их свойств:
- Произведение степеней. В случае, когда у степеней, которые нужно умножить, имеются одинаковые основания, основание остается неизменным, а показатели степеней суммируются. К примеру, an × am = an + m. Основанием степени тут является a, а n и m являются показателями степени в виде натуральных чисел.
- Частное степеней. Если делятся степени, имеющие одинаковые основания, основание остается неизменным, а показатель степени делимого уменьшается на показатель степени делителя. К примеру, am/an = am — n. Основанием степени тут является a, а m и n являются показателями степени в виде натуральных чисел, и при этом m > n.
- Возведение степени в степень. Если степень возводится в степень, основание остается неизменным, а показатели перемножаются. К примеру, (an)m = anm. Основанием степени тут является a, а n и m являются показателями степени в виде натуральных чисел.
- Степень произведения. Если требуется возвести в степень произведение, все множители возводятся в эту степень. Полученные результаты перемножаются. К примеру, (a × b)n = an х bn. Основаниями степени тут являются a и b, а n является показателем степени в виде натурального числа.
- Степень частного. Если требуется возвести в степень частное, в эту степень нужно по отдельности возвести делимое и делитель. Первый полученный результат делится на второй. К примеру, (a/b)n = an/bn. Основаниями степени тут являются a и b, а n является показателем степени в виде натурального числа.
Запомнив эти правила, можно переходить к действиям со степенями.
Умножение степеней
Первое правило умножения степеней гласит, что при умножении степеней с разными основаниями, но одинаковыми показателями нужно умножить между собой их основания, а показатель остается неизменным.
Формула:
an × bn = (a × b)n
Пример:
a3 × b3 = (a × a × a)(b × b × b) = (a × b)3 = (ab)(ab)(ab) = (ab)3
35 × 44 = (3 × 4)5 = 125 = 248832
16a2 = 42 × a2 = (4a)2
Второе правило умножения степеней гласит, что при поиске произведения степеней, обладающих одинаковыми основаниями, складываются показатели степеней.
Формула:
an × am = an + m
Пример:
35 × 33 = 35 + 3 = 38 = 6561
28 × 81 = 28 × 23 = 211 = 2048
Если числа отличаются и по основаниям, и по степеням, и какое-либо одно основание не получается преобразовать в число со степенью, как у второго числа, нужно по отдельности возвести в степень каждое число, а затем сложить два результата. Например: 34 х 43 = 81 + 64 = 145.
Деление степеней
Первое правило деления степеней гласит, что при делении степеней с одинаковыми основаниями, но разными показателями нужно найти разность их показателей, а основание остается неизменным.
Формула:
am/an = an– m (не забывайте, что n > m)
Пример:
(113 х 44)/(11 х 43) = 113 – 1 х 44 – 2 = 112 х 42 = (11 х 4)2 = 1936
2a4/2a3 = 2a4 – 3 = 2a
Второе правило деления степеней гласит, что при делении степеней с разными основаниями, но одинаковыми показателями нужно возвести результат частного имеющихся чисел в эту степень.
Формула:
an/bn = (a/b)n
Пример:
512/312 = (5/3)12
Если числа отличаются и по основаниям, и по степеням, нужно возвести в степень каждое число, а после этого разделить результаты. Например: 33/52 = 27/25 = 1,08.
Чтобы было проще усвоить умножение и деление степеней, вы также можете запомнить несколько важных теорем, касающихся все рассмотренных нами операций.
Основные теоремы
Всего есть пять теорем, которые требуют внимания:
- Теорема 1. Для любого числа a и натуральных чисел n и m будет справедливым равенство an × am = an + m. Умножая степени с одинаковыми основаниями, вы складываете показатели, а основание оставляете без изменений.
- Теорема 2. Для любого числа a и любых натуральных чисел n и m (при этом n > m) будет справедливым равенство an/am = an – m. Деля степени с одинаковыми основаниями, вы отнимаете показатели, а основание оставляете без изменений.
- Теорема 3. Для любого числа a и натуральных чисел n и m будет справедливым равенство (an)m = anm.
Имейте в виду, что эти три теоремы относятся к степеням с одинаковыми основаниями, а далее мы рассмотрим теоремы для степеней с одинаковыми показателями.
- Теорема 4. Для любых чисел a и b и любого натурального числа n будет справедливым равенство an × bn = (ab)n. Перемножая степени с одинаковыми показателями, просто перемножьте их основания, а показатель оставьте без изменений.
- Теорема 5. Для любых чисел a и b (при условии, что b ≠ 0) и любого натурального числа n будет справедливым равенство an/bn = (a/b)n. Деля друг на друга степени с одинаковыми показателями, просто разделите одно основание на другое, а показатель оставьте без изменений.
Несложно увидеть, что расчеты со степенями не вызывают особых трудностей. Чтобы научиться умножать и делить степени, нужно лишь немного попрактиковаться и наработать навык. После этого подобные примеры и задания вы сможете щелкать, как орешки.
Вопросы и ответы
А также предлагаем вашему внимание ответы на часто задаваемые вопросы по умножению и делению степеней.
Что происходит при умножении степеней с одинаковыми основаниями?
При умножении степеней с одинаковыми основаниями степени суммируются.
Что происходит при делении степеней с одинаковыми основаниями?
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Можно ли упростить выражение an × am до одной степени?
Да, выражение an × am можно упростить до одной степени так: am + n.
Чем отличается умножение степеней с одинаковыми основаниями от умножения степеней с разными основаниями?
Умножение степеней с одинаковыми основаниями приводит к сложению показателей, в то время как умножение степеней с разными основаниями не дает степень.
Можно ли умножать разные степени с разными основаниями?
Да, можно умножать разные степени с разными основаниями. В этом случае основания нужно по отдельности возвести в степень, а затем сложить результаты.