Содержание:
- Сложение комплексных чисел
- Вычитание комплексных чисел
Сложение комплексных чисел
Определение
Суммой двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называется
комплексное число
$z$, которое равно
$z=left(a_{1}+a_{2}right)+left(b_{1}+b_{2}right) i$
То есть суммой двух комплексных чисел есть комплексное число,
действительная и мнимая части
которого есть суммой действительных и мнимых частей чисел-слагаемых соответственно.
Пример
Задание. Найти сумму
$z_{1}+z_{2}$, если
$z_{1}=5-6 i$,
$z_{2}=-3+2 i$ .
Решение. Искомая сумма равна
$z_{1}+z_{2}=5-6 i+(-3+2 i)=(5+(-3))+(-6+2) i=2-4 i$
Ответ. $z_{1}+z_{2}=2-4 i$
Вычитание комплексных чисел
Определение
Разностью двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называется комплексное число
$z=z_{1}-z_{2}$, действительная и мнимая части
которого есть разностью действительных и мнимых частей чисел
$z_{1}$ и
$z_{2}$ соответственно:
$z=left(a_{1}-a_{2}right)+left(b_{1}-b_{2}right) i$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти разность
$z_{1}-z_{2}$, если
$z_{1}=5-6 i$,
$z_{2}=-3+2 i$ .
Решение. Действительная часть искомого комплексного числа равна разности действительных частей чисел
$z_{1}$ и
$z_{2}$ , а мнимая — мнимых частей этих чисел, то есть
$z_{1}-z_{2}=5-6 i-(-3+2 i)=(5-(-3))+(-6-2) i=8-8 i$
Ответ. $z_{1}-z_{2}=8-8 i$
Читать дальше: умножение комплексных чисел.
В данной публикации мы рассмотрим формулы, с помощью которых можно найти сумму или разность двух комплексных чисел, представленных в алгебраической форме. Также приведены примеры для лучшего понимания теоретического материала.
- Сложение комплексных чисел
- Вычитание комплексных чисел
Сложение комплексных чисел
Если сложить два комплексных числа x = a1 + b1i и y = a2 + b2i, то получится тоже комплексное число z:
z = x + y = (a1 + a2) + (b1 + b2) ⋅ i
Таким образом, мы отдельно складываем действительные и мнимые части суммируемых чисел.
Пример 1
Найдем сумму комплексных чисел: x = 8 + 3i и y = 5 – i.
Решение:
x + y = (8 + 5) + (3i – i) = 13 + 2i.
Вычитание комплексных чисел
Разность двух комплексных чисел x = a1 + b1i и y = a2 + b2i вычисляется по формуле:
z = x – y = (a1 – a2) + (b1 – b2) ⋅ i
То есть получится комплексное число, действительная и мнимая части которого равны разности соответствующих частей x и y.
Пример 2
Вычтем из x = 12 – 7i число y = -8 + 4i.
Решение:
x – y = (12 – (-8)) + (-7i – 4i) = 20 – 11i.
Заказать задачи по любым предметам можно здесь от 10 минут
Найти сумму, разность, произведение и частное комплексных чисел
Пусть даны два комплексных числа в алгебраической форме $z_1 = a + bi, z_2 = c + di$, тригонометрической форме $z_1 = r_1 (cos varphi_1 + isin varphi_1), z_2 = r_2(cos varphi_2 + isin varphi_2)$ и показательной форме $z_1 = r_1 e^{varphi_1 i} , z_2 = r_2 e^{varphi_2 i}$.
| Формула суммы и разности |
|
В алгебраической форме $$z_1 + z_2 = (a+bi) + (c+di) = (a + c) + (b + d)i, $$ $$z_1 — z_2 = (a+bi) — (c+di) = (a-c) + (b — d)i, $$в тригонометрической и показательной форме тоже можно выполнять сложение и вычитание, но удобнее это делать в алгебраической. |
| Формула произведения |
|
В алгебраической форме $$z_1 cdot z_2 = (a+bi) cdot (c+di) = (ac — bd) + i(ad + bc),$$ в тригонометрической форме $$z_1 cdot z_2 = r_1 r_2 (cos (varphi_1 + varphi_2) + isin (varphi_1 + varphi_2)),$$в показательной форме $$z_1 cdot z_2 = r_1 r_2 e^{(varphi_1+varphi_2)i}.$$ |
| Формула деления |
| В алгебраической форме $$frac{z_1}{z_2} =frac{z_1 overline{z_2}}{z_2 overline{z_2}} = frac{ac+bd}{c^2+d^2} + frac{bc-ad}{c^2+d^2}i, $$в тригонометрической форме $$frac{z_1}{z_2} = frac{r_1}{r_2} (cos(varphi_1 — varphi_2)+isin(varphi_1-varphi_2)),$$в показательной форме $$frac{z_1}{z_2} = frac{r_1}{r_2}e^{(varphi_1 — varphi_2)i}.$$ |
Введите первое комплексное число
Введите второе комплексное число
| Пример 1 |
| Найти сумму, разность, произведение, частное комплексных чисел $$z_1 = 1+2i, z_2 = -2+i.$$ |
| Решение |
|
Сначала находим сумму. Для этого раскрываем скобки и проводим вычисления с подобными $$z_1 + z_2 = (1+2i) + (-2+i) = 1+2i — 2 + i = (1-2) + (2i+i) = -1 + 3i.$$ Тоже самое делаем для того, чтобы найти разность. Раскрываем скобки и вычисляем $$z_1 — z_2 = (1+2i) — (-2+i) = 1+2i + 2 — i = 3 + i.$$ Теперь найдем произведение чисел. Раскрываем скобки попарно перемножая слагаемые в скобках. Но не забываем, что $i = sqrt{-1}$, а это значит, что $i^2 = -1$, получаем $$z_1 cdot z_2 = (1+2i)cdot (-2+i) = -2 + i — 4i + 2i^2 = $$ $$ = -2 — 3i — 2 = -4-3i.$$ Выполним деление комплексных чисел. Здесь необходимо числитель и знаменатель домножить на комплексно-сопряженное число к знаменателю, чтобы избавиться от дроби $$frac{z_1}{z_2} = frac{1+2i}{-2+i} = frac{(1+2i)(-2-i)}{(-2+i)(-2-i)} = $$ В числителе и знаменателе раскрываем скобки, то есть выполняем умножение комплексных чисел по соответствующей формуле. И не забываем про то, что $i^2 = -1$ $$ = frac{-2-i-4i-2i^2}{4+2i-2i-i^2} = frac{-2-5i+2}{4+1} = frac{-5i}{5} = -i.$$ |
| Ответ |
| $$z_1 + z_2 = -1+3i, z_1 — z_2 = 3+i, z_1 cdot z_2 = -4-3i, frac{z_1}{z_2} = -i$$ |
| Пример 2 |
| Найти произведение и частное комплексных чисел $z_1 = 2(cos frac{pi}{3} + isin frac{pi}{3})$ и $z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6})$ |
| Решение |
|
Начнем с умножения двух чисел. Вычисляем произведение модулей и складываем аргументы синуса и косинуса $$z_1 cdot z_2 = 2(cos frac{pi}{3} + isin frac{pi}{3}) cdot 4(cos frac{pi}{6} + isin frac{pi}{6}) = $$ $$ = 8 (cos (frac{pi}{3} + frac{pi}{6}) + isin (frac{pi}{3}+frac{pi}{6})) = 8(cosfrac{pi}{2} + isin frac{pi}{2}).$$ Деление выполняется наоборот. Ищем частное модулей и разность аргументов $$frac{z_1}{z_2} = frac{2}{4} (cos (frac{pi}{3} — frac{pi}{6}) +isin (frac{pi}{3}-frac{pi}{6}) = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6}).$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$z_1 cdot z_2 = 8(cosfrac{pi}{2} + isin frac{pi}{2}), frac{z_1}{z_2} = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6})$$ |
| Пример 3 |
| Найти произведение и частное комплексных чисел $ z_1 = 6e^{frac{pi}{2}i} $ и $ z_2 = 2e^{frac{pi}{4}i} $ |
| Решение |
|
Для умножения двух комплексных чисел необходимо перемножить их аргументы и сложить показатели степеней $$z_1 cdot z_2 = 6e^{frac{pi}{2}i} cdot 2e^{frac{pi}{4}i} = 12e^{(frac{pi}{2}+frac{pi}{4})i} = 12e^{frac{3pi}{4}i}.$$ Для деления нужно найти частное аргументов двух комплексных чисел и вычислить разницу показателей степеней $$frac{z_1}{z_2} = frac{6e^{frac{pi}{2}i}} {2e^{frac{pi}{4}i}} = frac{6}{2} e^{(frac{pi}{2}-frac{pi}{4})i} = 3e^{frac{pi}{4}i}.$$ |
| Ответ |
| $$z_1 cdot z_2 = 12e^{frac{3pi}{4}i}, frac{z_1}{z_2} = 3e^{frac{pi}{4}i}$$ |
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Определение 1
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством
[z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )cdot i.]
Другими словами, суммой двух заданных комплексных чисел является комплексное число, действительная и мнимая части которого определяется как сумма соответственно действительных и мнимых частей исходных слагаемых.
Примечание 1
Сумму любого количества заданных комплексных чисел можно найти путем суммирования действительных частей и суммирования мнимых частей слагаемых.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Примечание 2
Для операции суммы комплексных чисел справедливо следующее правило:
(от перестановки слагаемых сумма не меняется).
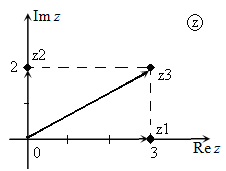
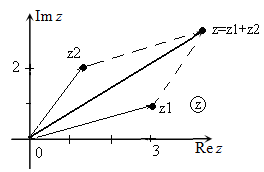
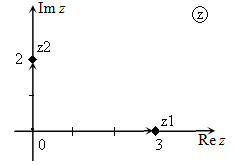
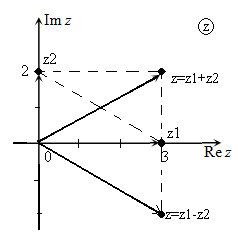
Иллюстрация примера сложения комплексных чисел с использованием комплексной плоскости приведена на рис.1-2.
Рис. 1
Рис. 2
Пример 1
Найти сумму $z_{1} +z_{2} $ для комплексных чисел:
1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.
Решение:
Для сложения комплексных чисел воспользуемся определением и получим:
1) $z_{1} +z_{2} =(3+2i)+(1-2i)=(3+1)+(2-2)i=4+0cdot i=4$
2) $z_{1} +z_{2} =(3+0cdot i)+(1+5i)=(3+1)+(0+5)i=4+5i$
3) $z_{1} +z_{2} =(3+9i)+(0-7i)=(3+0)+(9-7)i=3+2i$
«Сложение и вычитание комплексных чисел» 👇
Пример 2
Найти модуль суммы $|z_{1} +z_{2} |$ двух заданных комплексных чисел:
1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$; 3) $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$.
Решение:
Для сложения комплексных чисел воспользуемся определением. Для вычисления модуля комплексного числа воспользуемся формулой:
[|z|=sqrt{a^{2} +b^{2} } .]
1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:
[z_{1} +z_{2} =(1+2i)+(1-5i)=(1+1)+(2-5)i=2+(-3)cdot i]
[|z_{1} +z_{2} |=sqrt{2^{2} +(-3)^{2} } =sqrt{4+9} =sqrt{13} .]
2) Для чисел $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$ получим:
[z_{1} +z_{2} =(sqrt{3} +0cdot i)+(0+sqrt{5} cdot i)=(sqrt{3} +0)+(0+sqrt{5} )i=sqrt{3} +sqrt{5} cdot i]
[|z_{1} +z_{2} |=sqrt{(sqrt{3} )^{2} +(sqrt{5} )^{2} } =sqrt{3+5} =sqrt{8} =2sqrt{2} .]
3) Для чисел $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$ получим:
[z_{1} +z_{2} =(sqrt{3} +9i)+(0-7i)=(sqrt{3} +0)+(9-7)i=sqrt{3} +2cdot i]
[|z_{1} +z_{2} |=sqrt{(sqrt{3} )^{2} +2^{2} } =sqrt{3+4} =sqrt{7} .]
Определение 2
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством
[z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )cdot i.]
Примечание 4
Модуль разности двух заданных комплексных чисел равен расстоянию между точками, которые изображают эти числа на комплексной плоскости:
[|z_{1} -z_{2} |=sqrt{(a_{1} -a_{2} )^{2} +(b_{1} -b_{2} )^{2} } .]
Пример 3
Найти разность $z_{1} -z_{2} $ для комплексных чисел:
1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.
Решение:
Для нахождения разности комплексных чисел воспользуемся определением и получим:
1) $z_{1} -z_{2} =(3+2i)-(1-2i)=(3-1)+(2-(-2))i=2+4i$
2) $z_{1} -z_{2} =(3+0cdot i)-(1+5i)=(3-1)+(0-5)i=2-5i$
3) $z_{1} -z_{2} =(3+9i)-(0-7i)=(3-0)+(9-(-7))i=3+16i$
Пример 4
Найти модуль разности двух заданных комплексных чисел:
1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$; 3) $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$.
Решение:
Воспользуемся формулой из примечания 4.
1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:
[|z_{1} -z_{2} |=sqrt{(1-1)^{2} +(2+5)^{2} } =sqrt{0^{2} +7^{2} } =sqrt{49} =7.]
2) Для чисел $z_{1} =sqrt{3} $ и $z_{2} =sqrt{5} i$ получим:
[|z_{1} -z_{2} |=sqrt{(sqrt{3} -0)^{2} +(0-sqrt{5} )^{2} } =sqrt{(sqrt{3} )^{2} +(-sqrt{5} )^{2} } =sqrt{3+5} =sqrt{8} =2sqrt{2} .]
3) Для чисел $z_{1} =sqrt{3} +9i$ и $z_{2} =-7i$ получим:
[|z_{1} -z_{2} |=sqrt{(sqrt{3} -0)^{2} +(9+7)^{2} } =sqrt{(sqrt{3} )^{2} +16^{2} } =sqrt{3+256} =sqrt{259} .]
Примечание 5
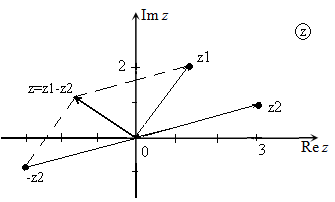
На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рис. 3), используя следующий алгоритм:
- построить на плоскости комплексное число $-z_{2} $;
- найти сумму $-z_{2} $ и $z_{1} $ по правилу параллелограмма.
Рис. 3
Примечание 6
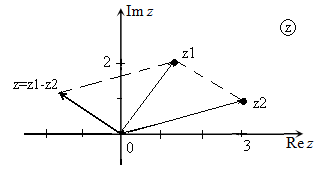
На комплексной плоскости операцию вычитания можно реализовать, используя другой алгоритм:
- соединить точки, изображающие исходные комплексные числа;
- достроить параллелограмм;
- радиус-вектор, параллельный прямой, соединяющей точки, изображающие исходные комплексные числа, изображает разность исходных комплексных чисел — $z=z_{1} -z_{2} $.
Рис. 4
Пример 6
Построить на комплексной плоскости сумму и разность изображенных на плоскости комплексных чисел (рис.5): $z_{1} +z_{2} ,z_{1} -z_{2} $.
Рис. 5
Решение:
Для построения воспользуемся примечаниями 4 и 6.
Рис. 6
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Найти сумму или разность двух комплексных чисел — такие задачи часто возникают при изучении высшей математики. В этой статье подробно рассматриваются операции сложения и вычитания комплексных чисел в алгебраической форме.
Если вам необходимо вспомнить, что же такое комплексные числа, то обратитесь к этой статье.
Сложение комплексных чисел
Чтобы сложить два комплексных числа, мы складываем каждую часть (действительную и мнимую) отдельно и получаем формулу сложения комплексных чисел:
( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i
Пример сложения комплексных чисел:
( 4 + 6 i ) + (8 — 3 i) = ( 4 + 8 ) + ( 6 — 3 ) i = 12 + 3 i
Вычитание комплексных чисел
Чтобы вычесть одно комплексное число из другого, для этого нужно также вычесть каждую часть отдельно:
( a + b i ) — ( c + d i ) = ( a — c ) + ( b — d ) i
Пример вычитания комплексных чисел:
( 2 + 11 i ) — ( 9 + 6 i ) = ( 2 — 9 ) + ( 11 — 6 ) i = -7 + 5 i
Еще примеры:
5 — ( 3 + 2 i) = ( 5 + 0 i ) — ( 3 + 2 i ) = ( 5 — 3 ) + ( 0 — 2 ) i = 2 — 2 i
( 7 — 8 i ) + 4 i = ( 7 — 8 i ) + ( 0 + 4 i ) = ( 7 + 0 ) + ( — 8 + 4 ) i = 7 — 4 i
Следующим этапом вы можете освоить операцию умножения комплексных чисел, перейдя по этой ссылке.